Electroosmosis-Optimized Thermal Model for Peristaltic Transportation of Thermally Radiative Magnetized Liquid with Nonlinear Convection
Abstract
:1. Introduction
2. Problem Formulation
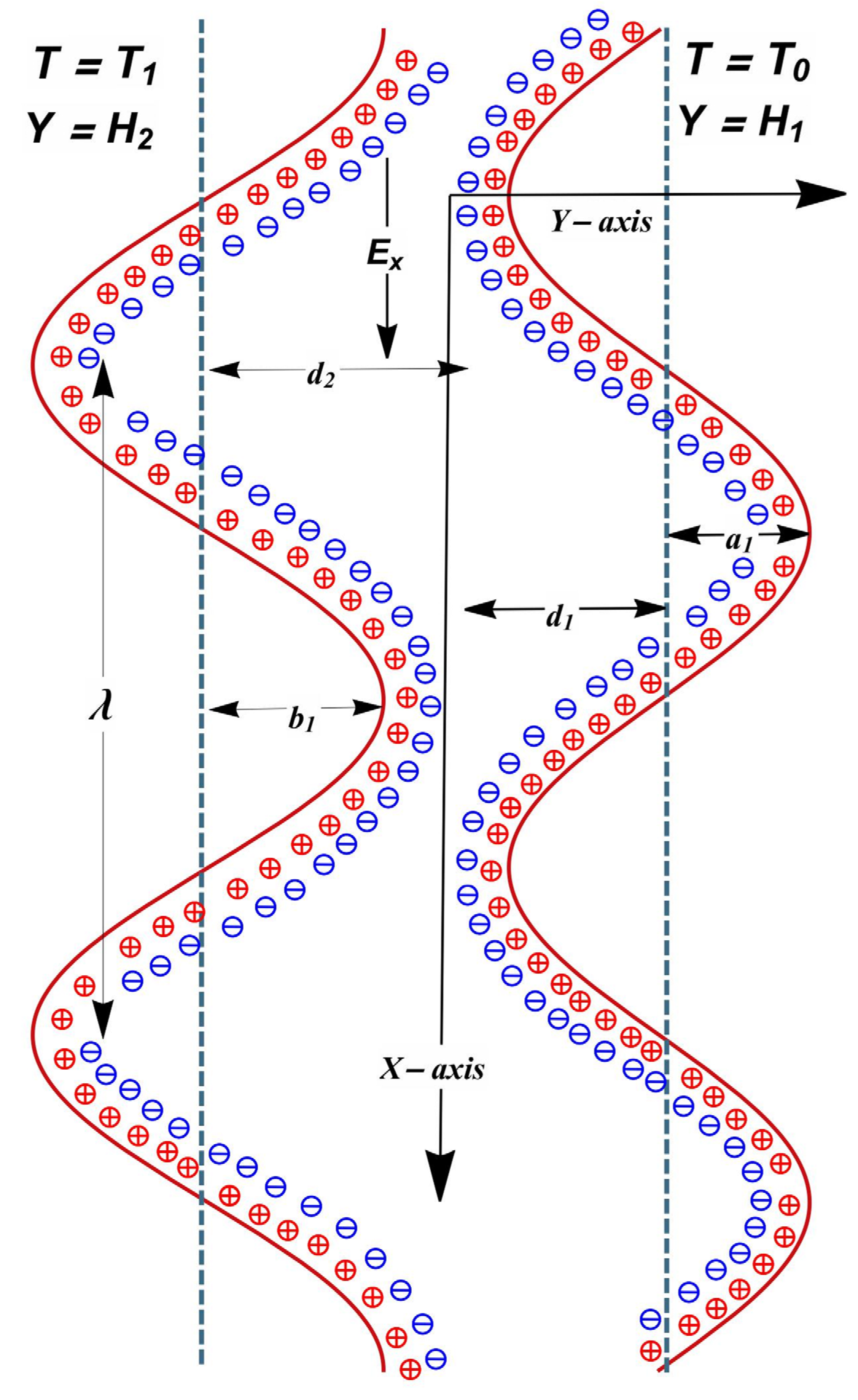
2.1. Flow Regime
2.2. Electro and Magnetohydrodynamics
2.3. Governing Equations
2.4. Dimensionless Quantities
2.5. Boundary Conditions
3. Entropy Generation Analysis
4. Results and Discussion
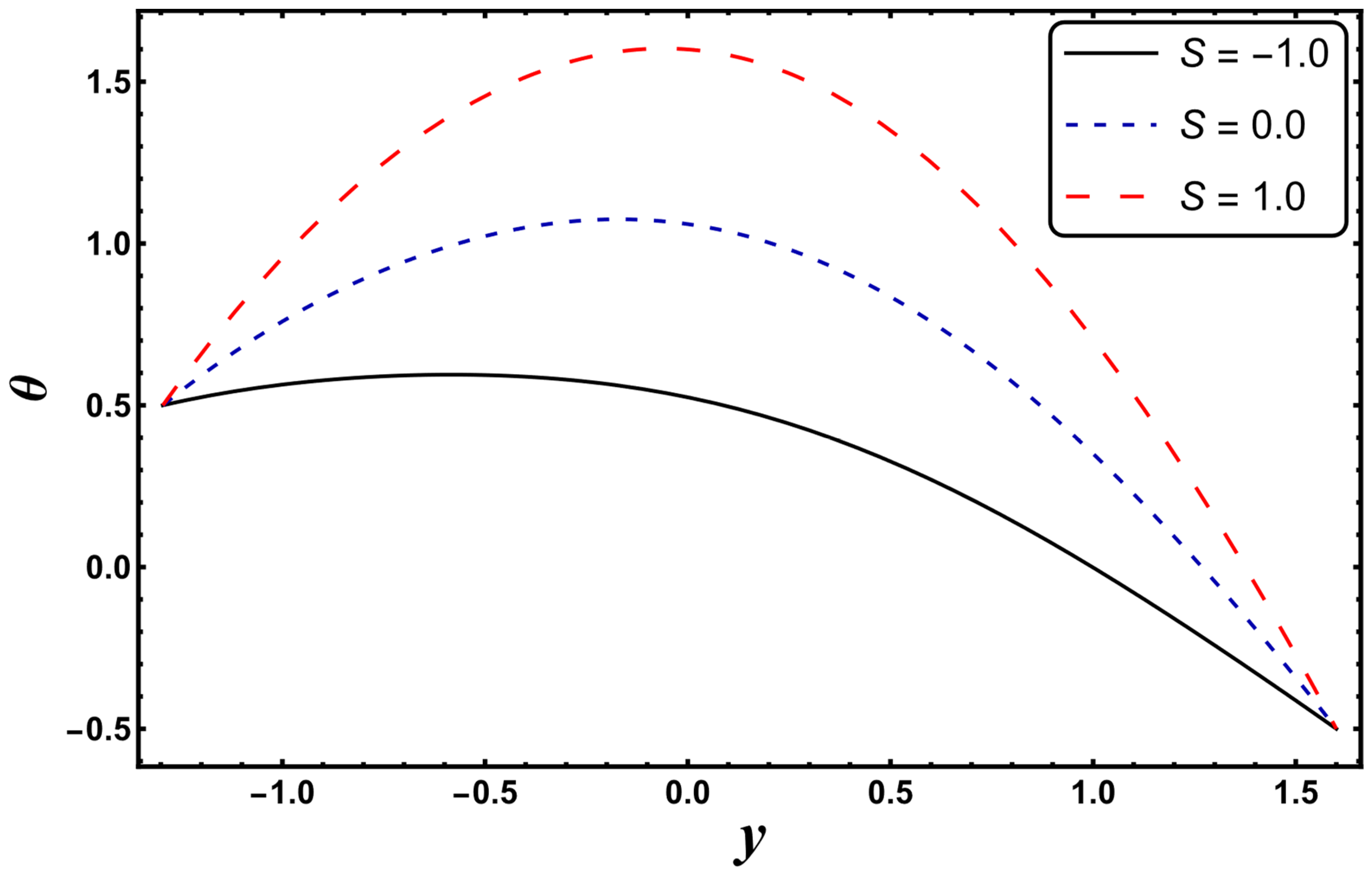
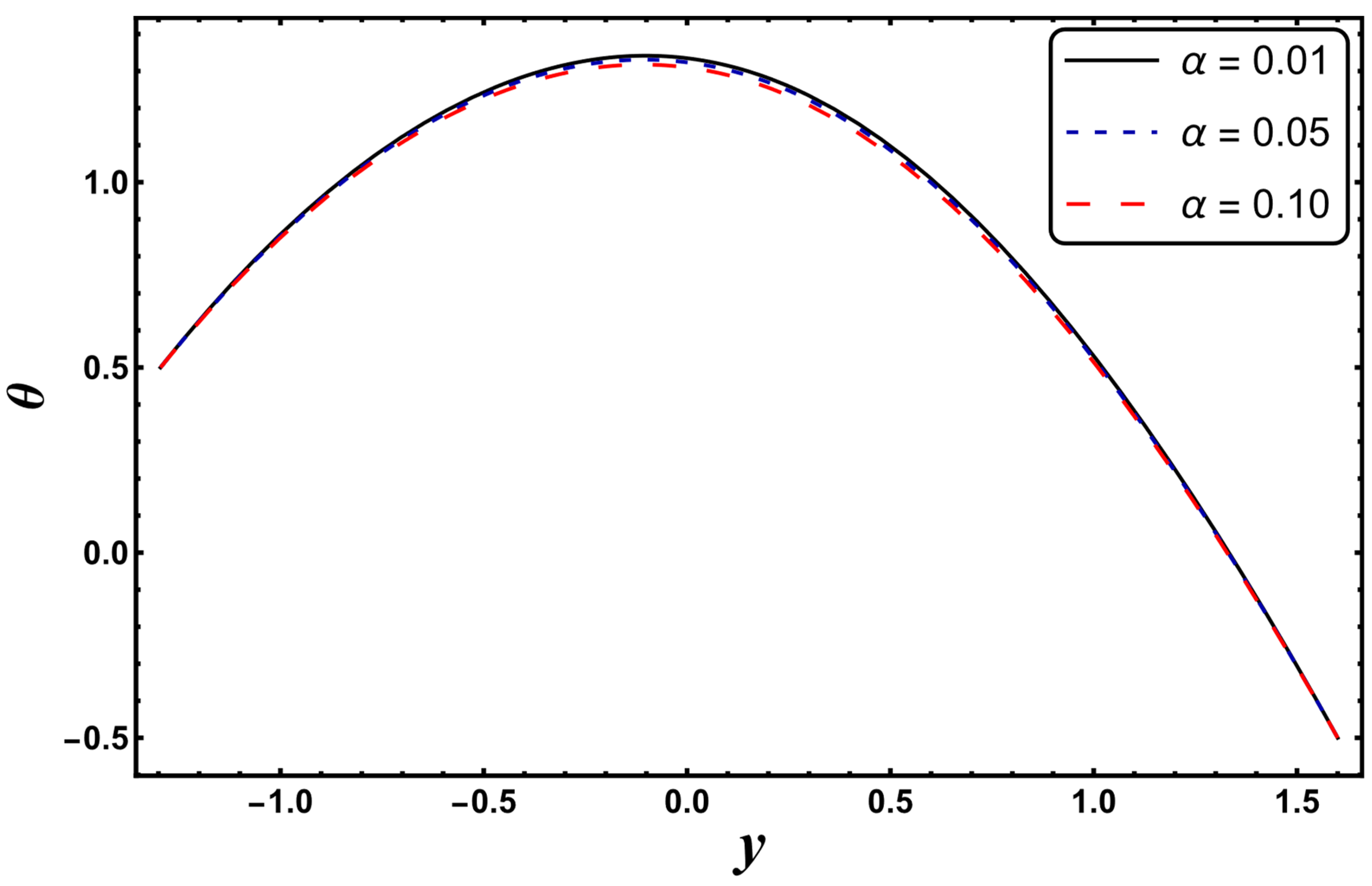
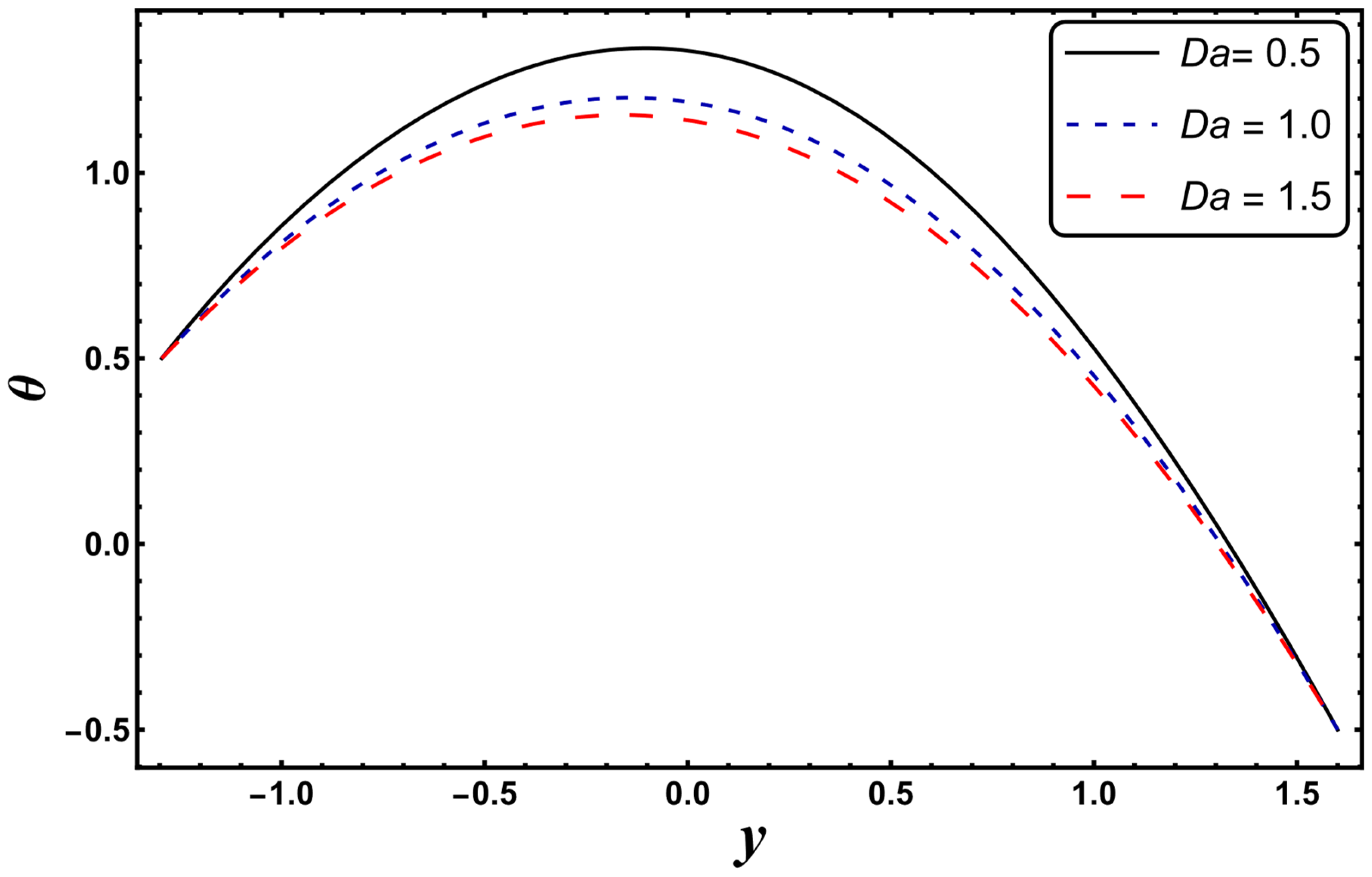
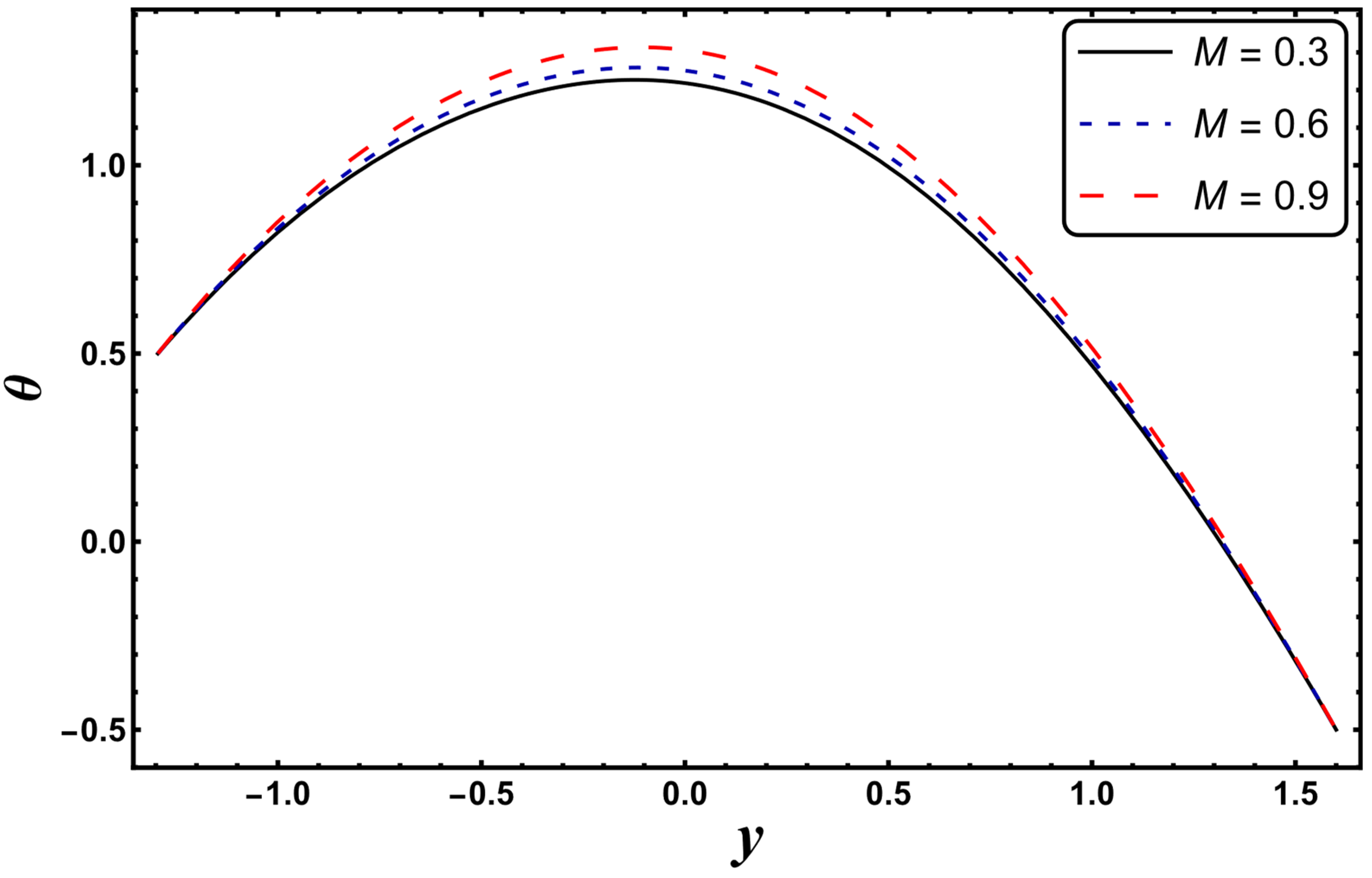
4.1. Temperature Profile
4.2. Heat Transfer Rate at the Wall
4.3. Temperature at Channel Center
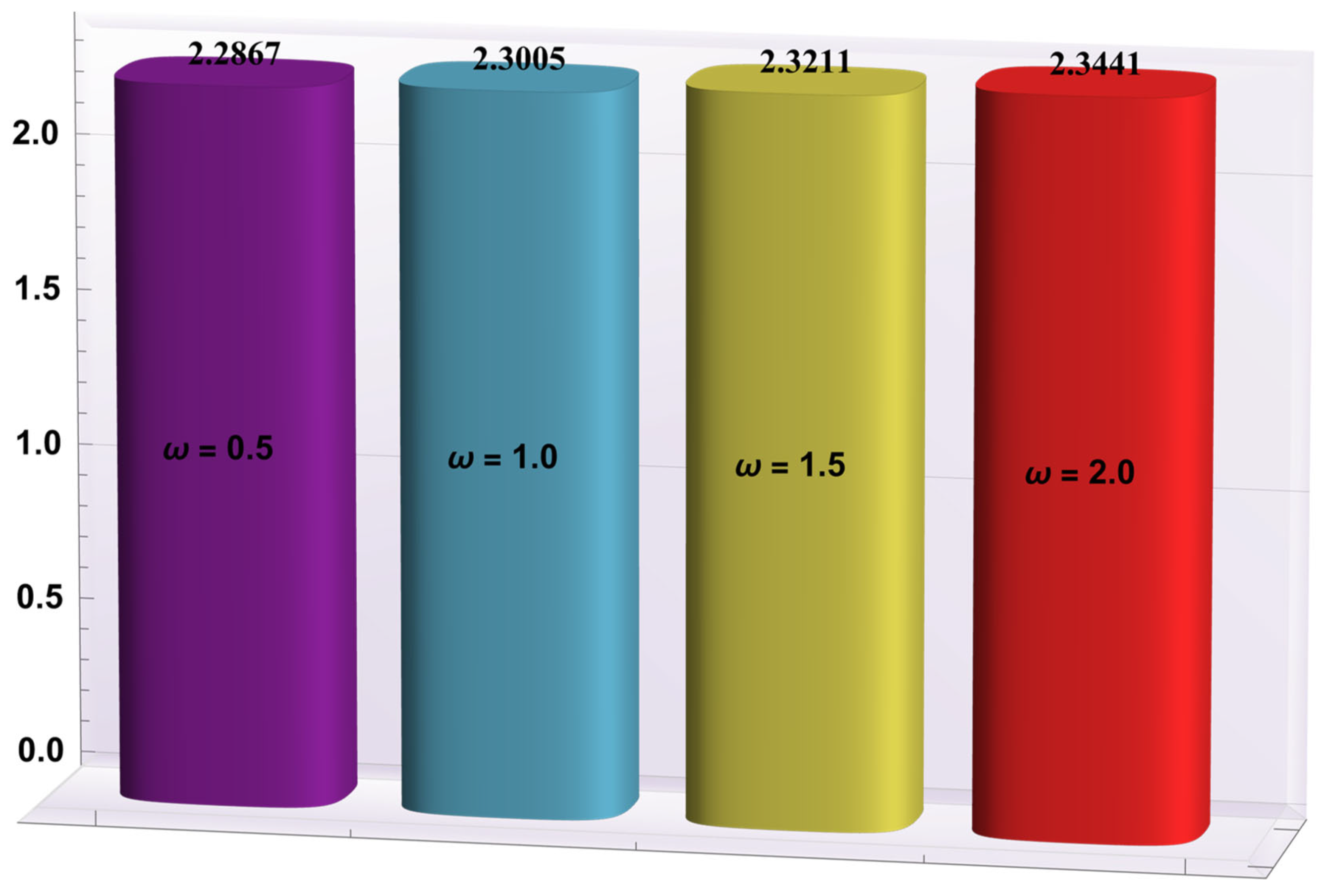
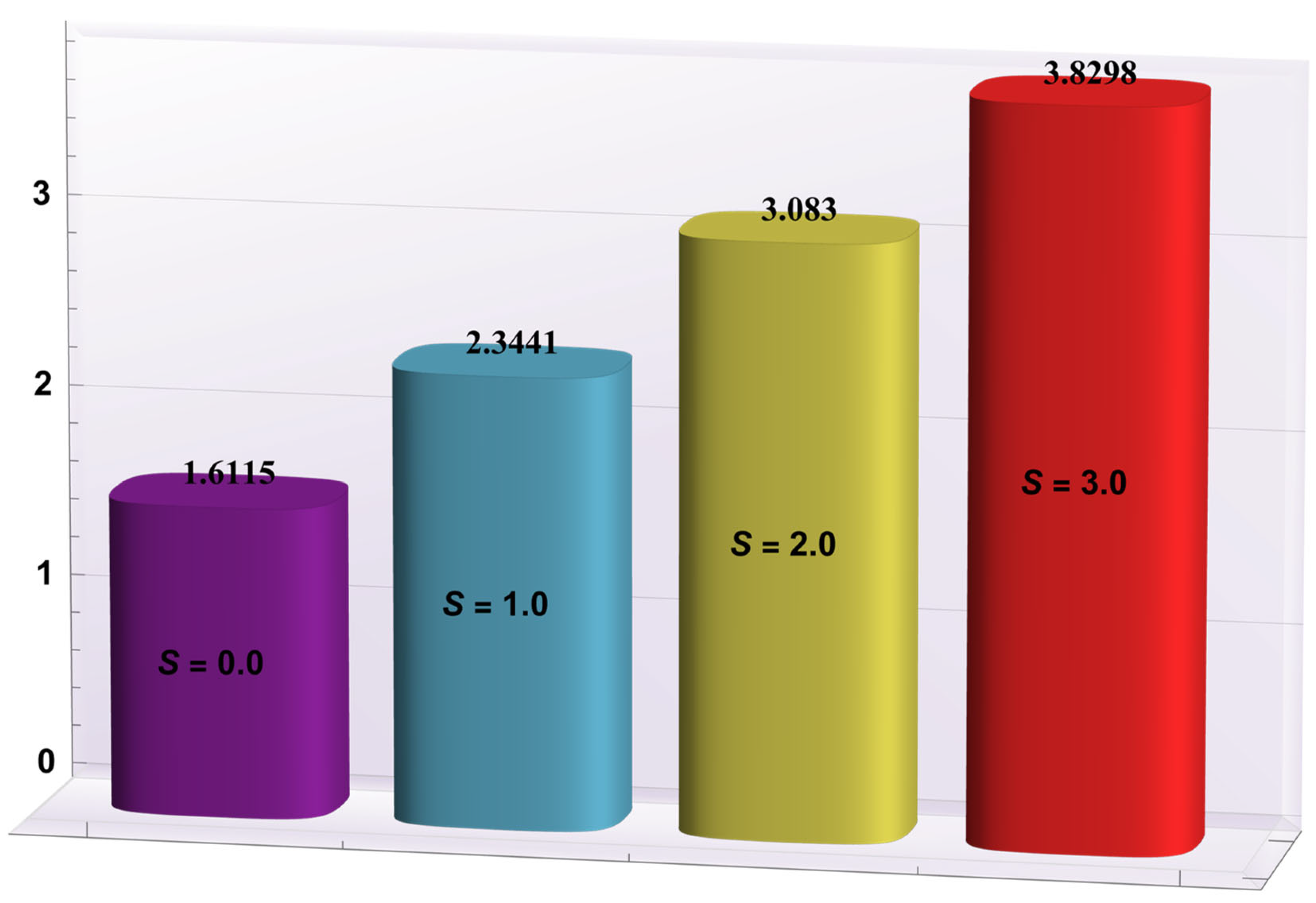
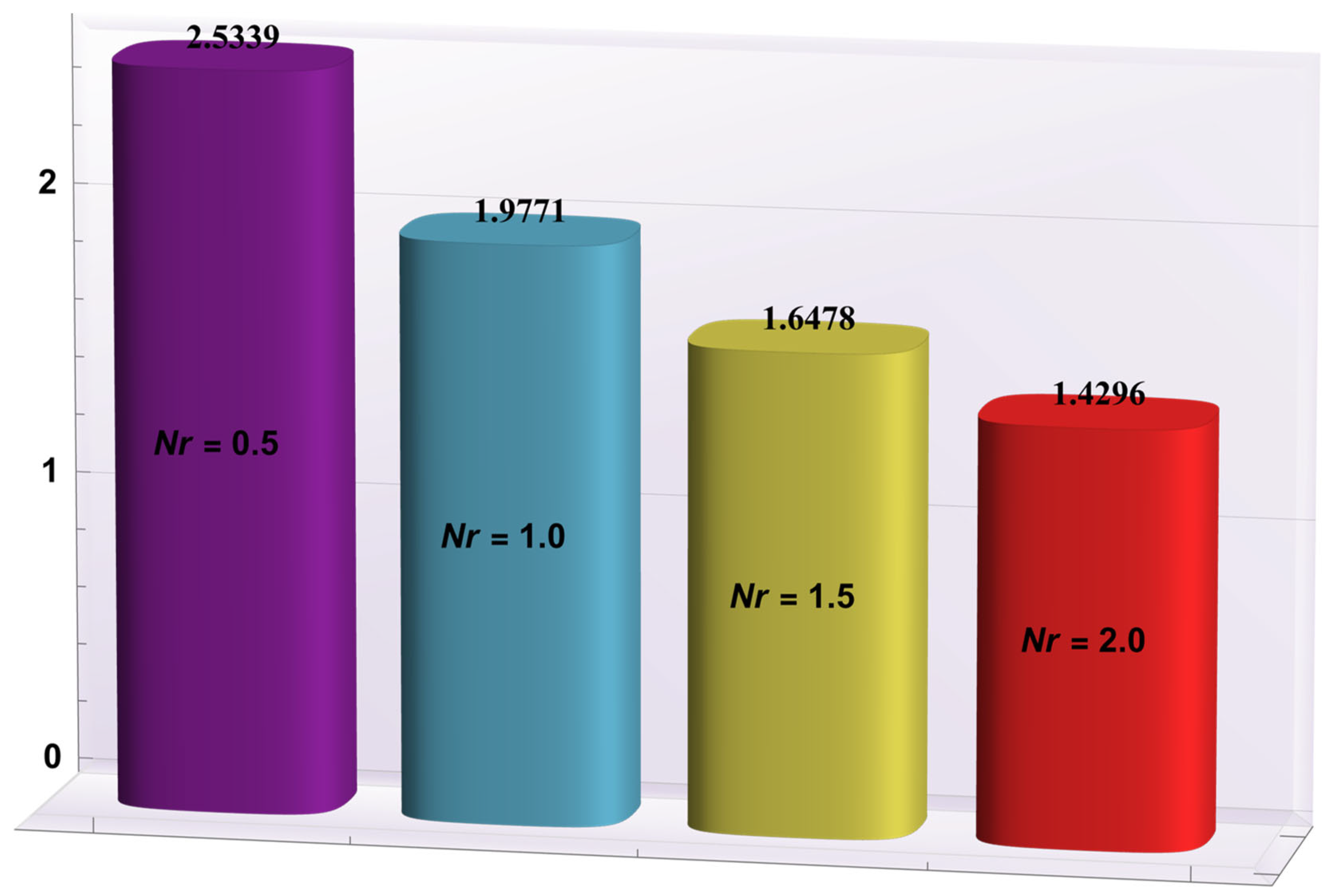
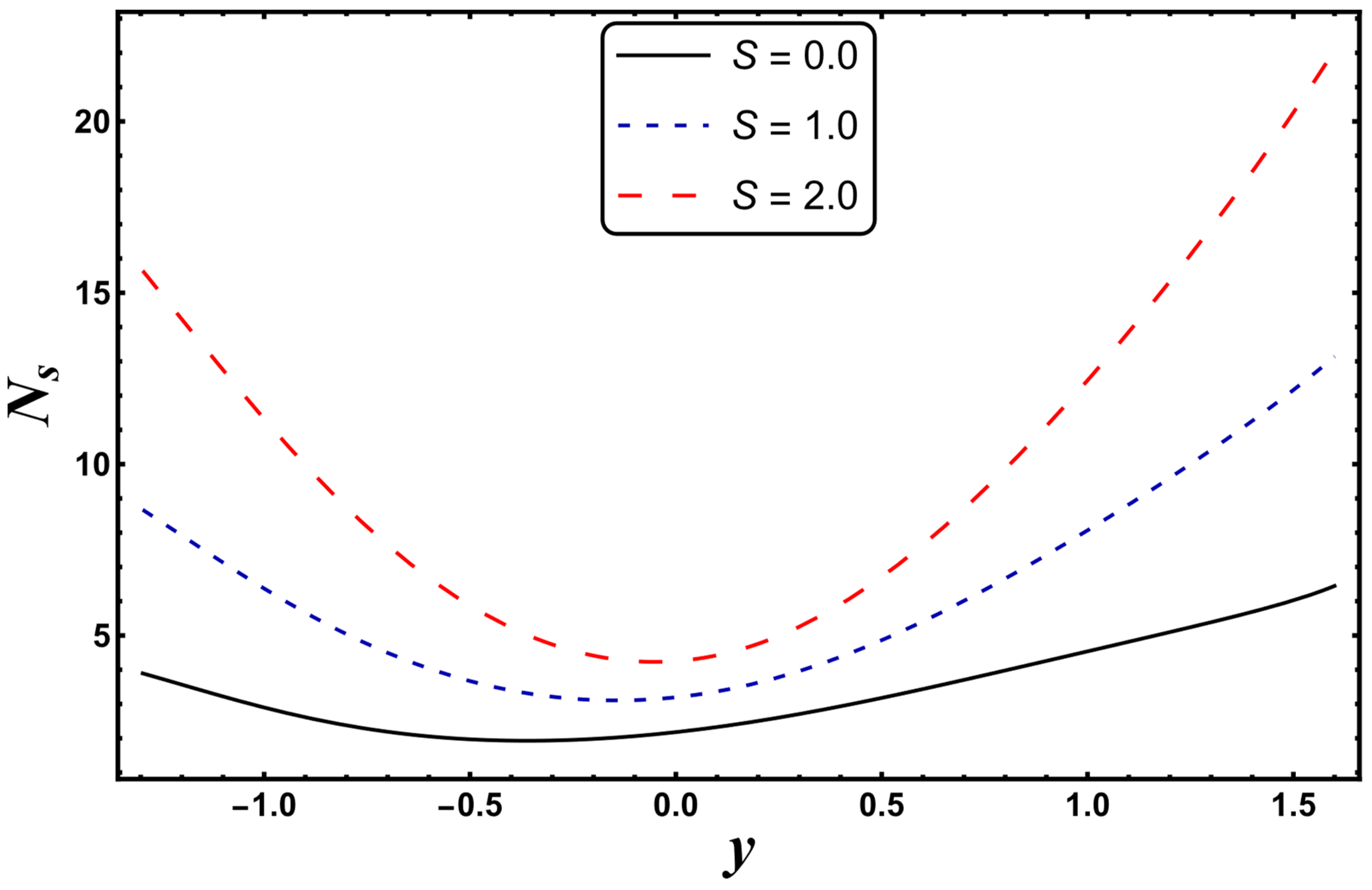
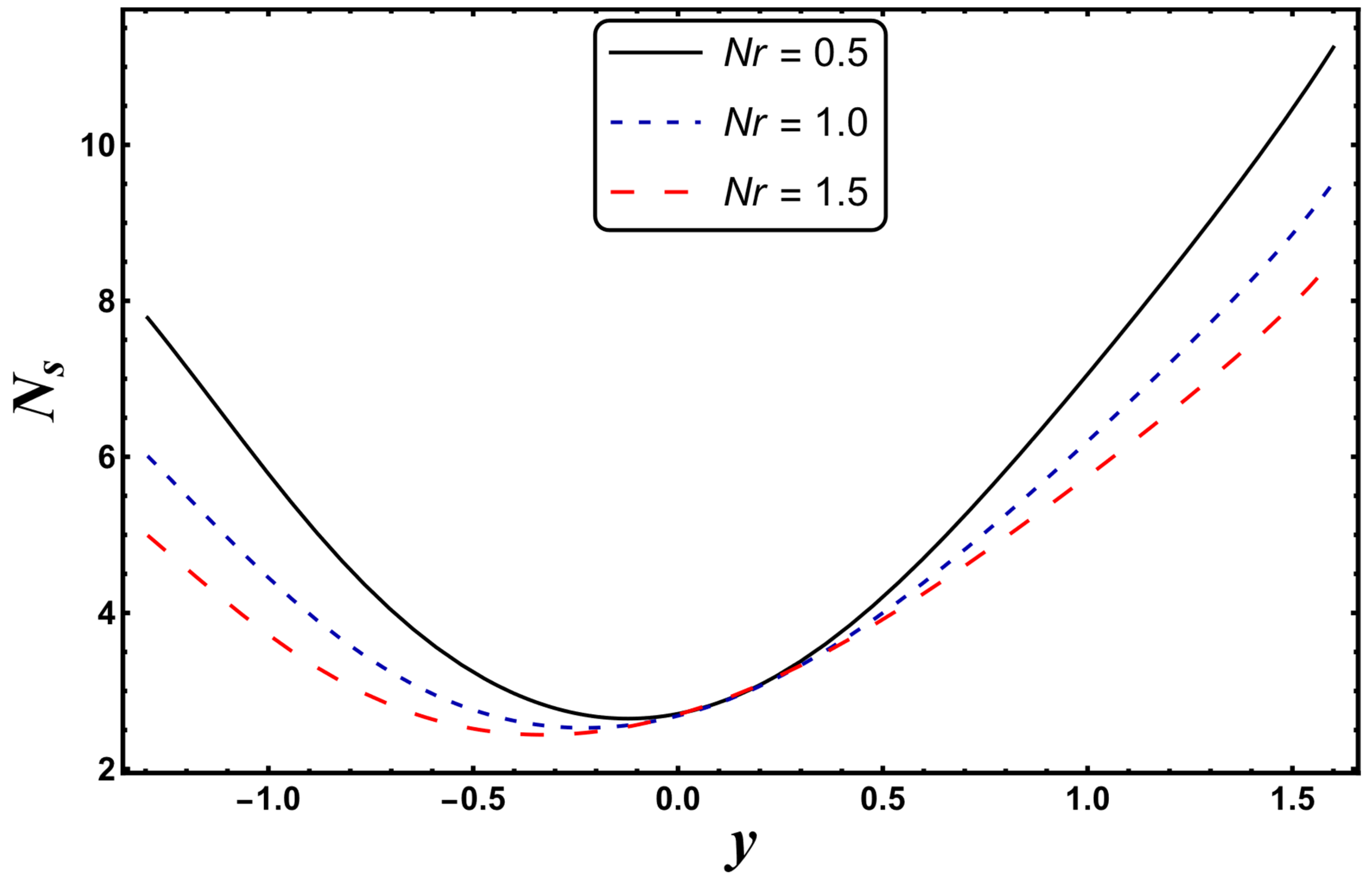
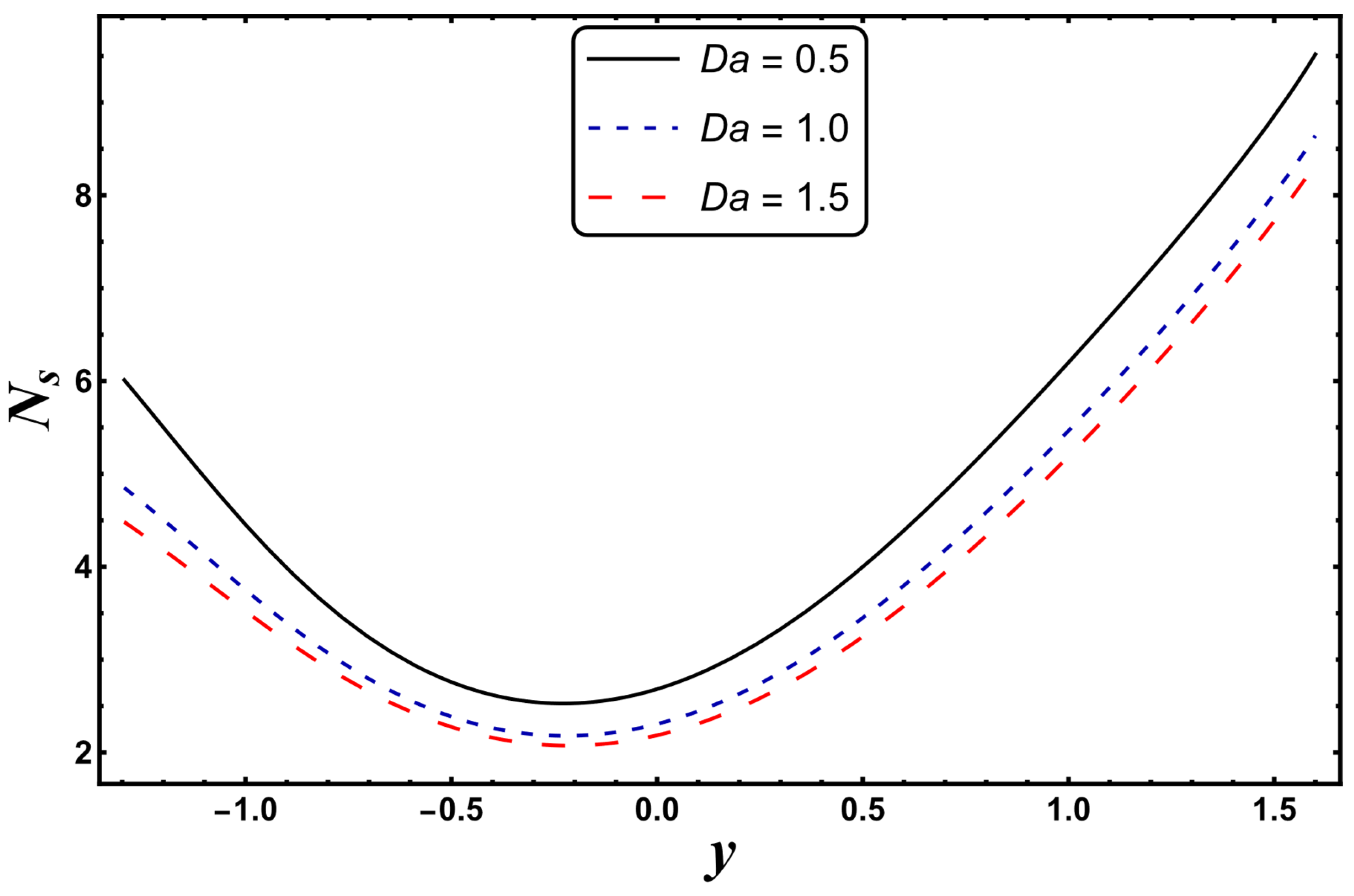
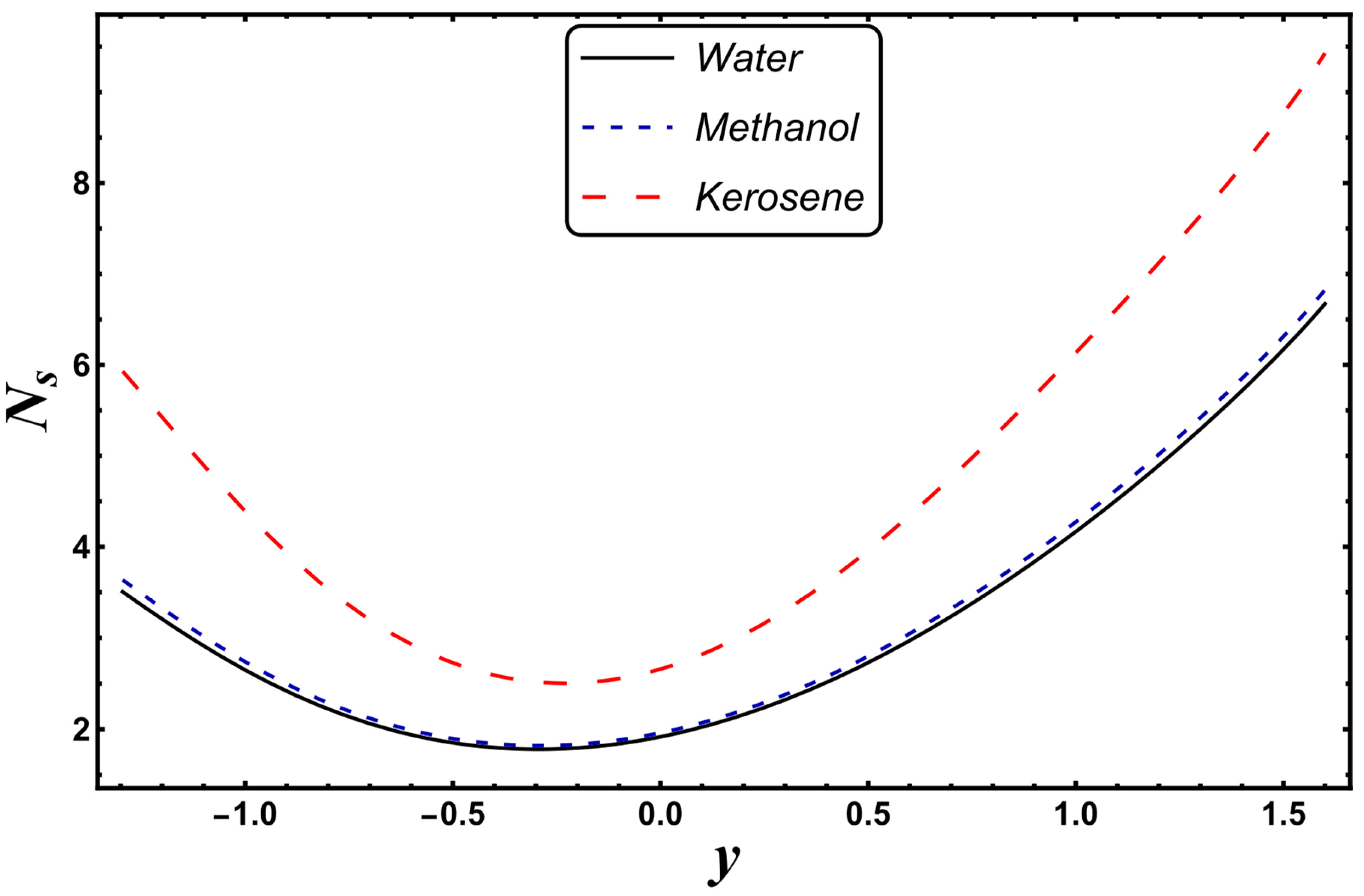
4.4. Entropy Generation
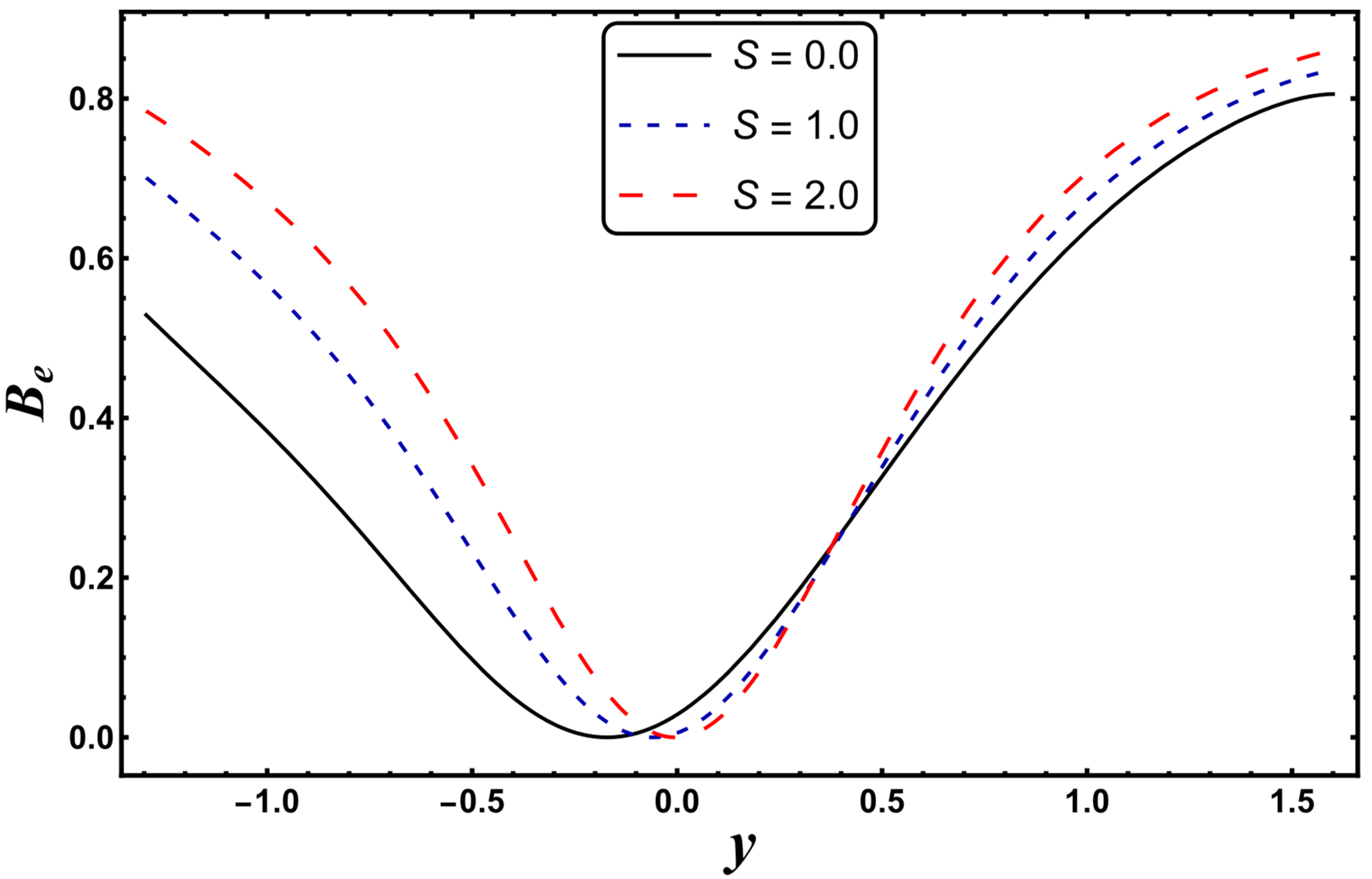
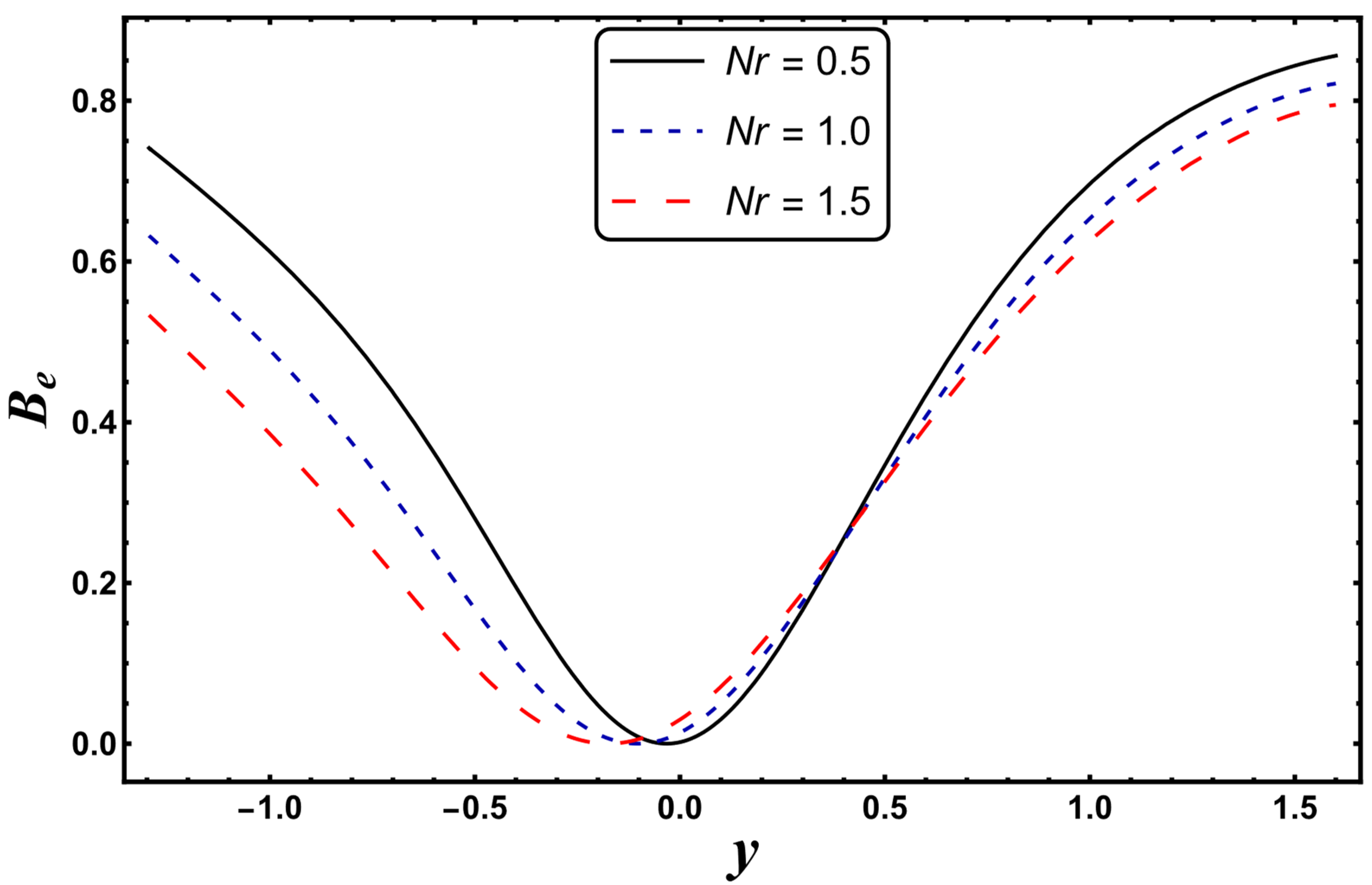
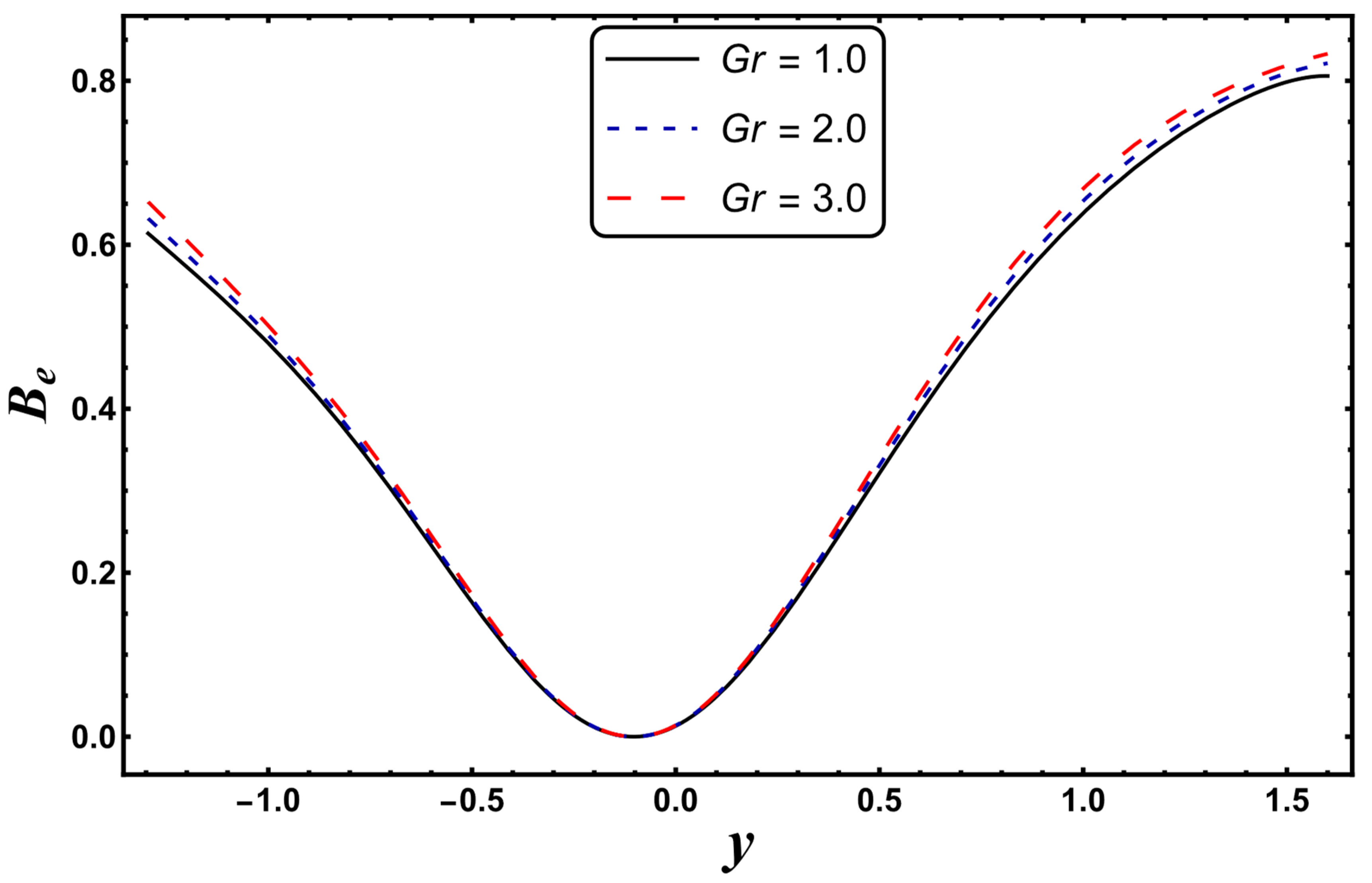
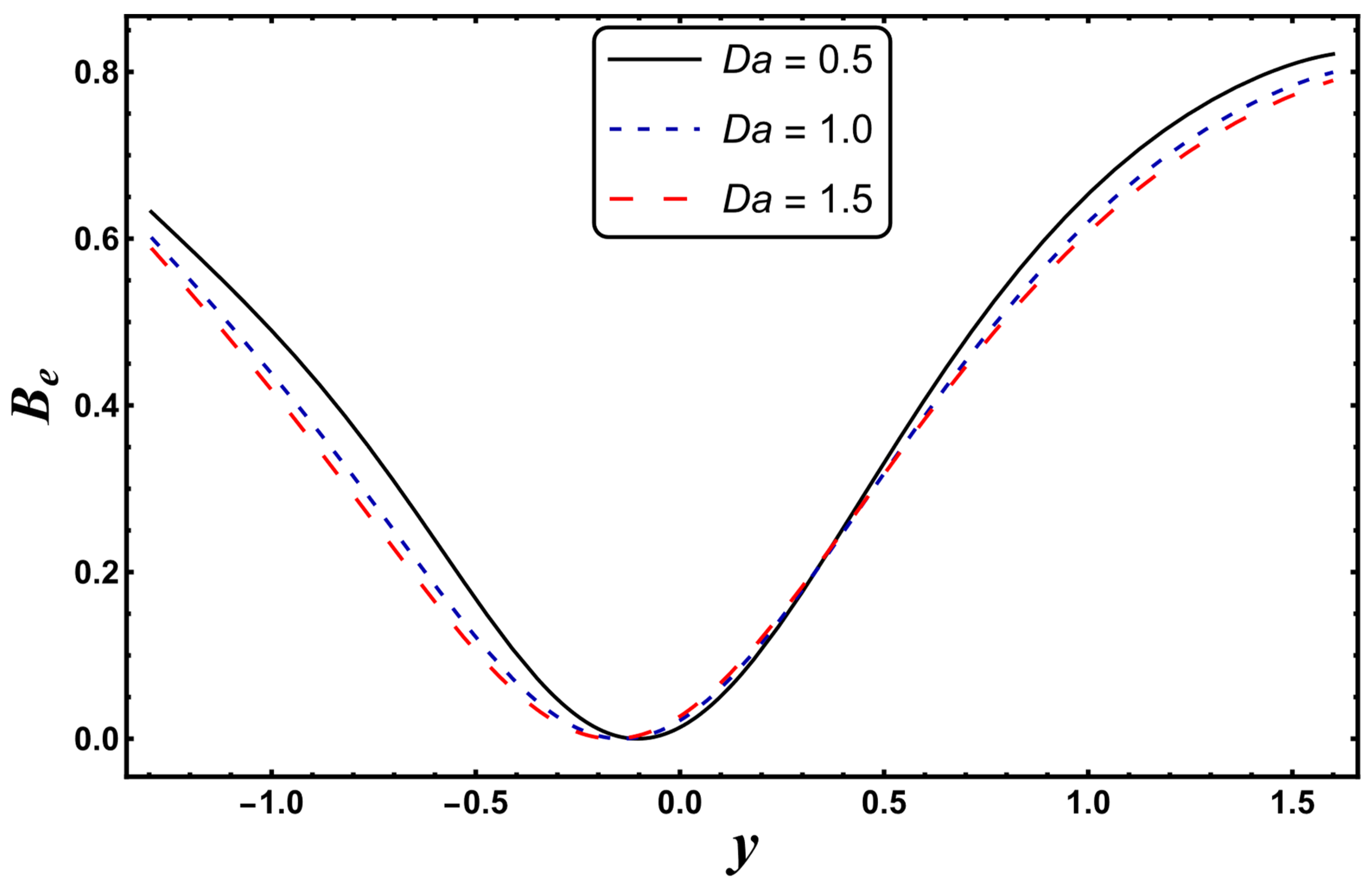
4.5. Bejan Number
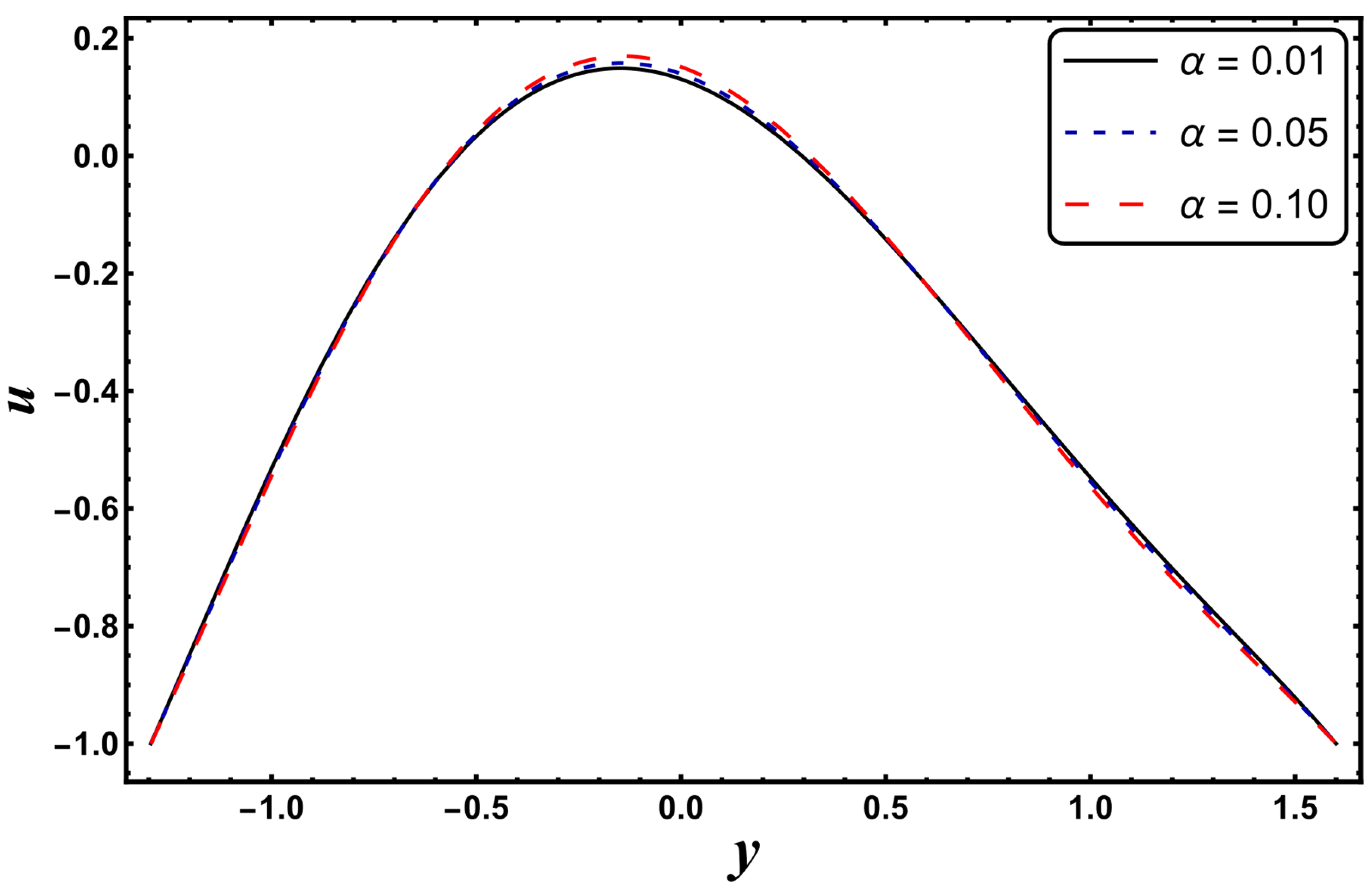
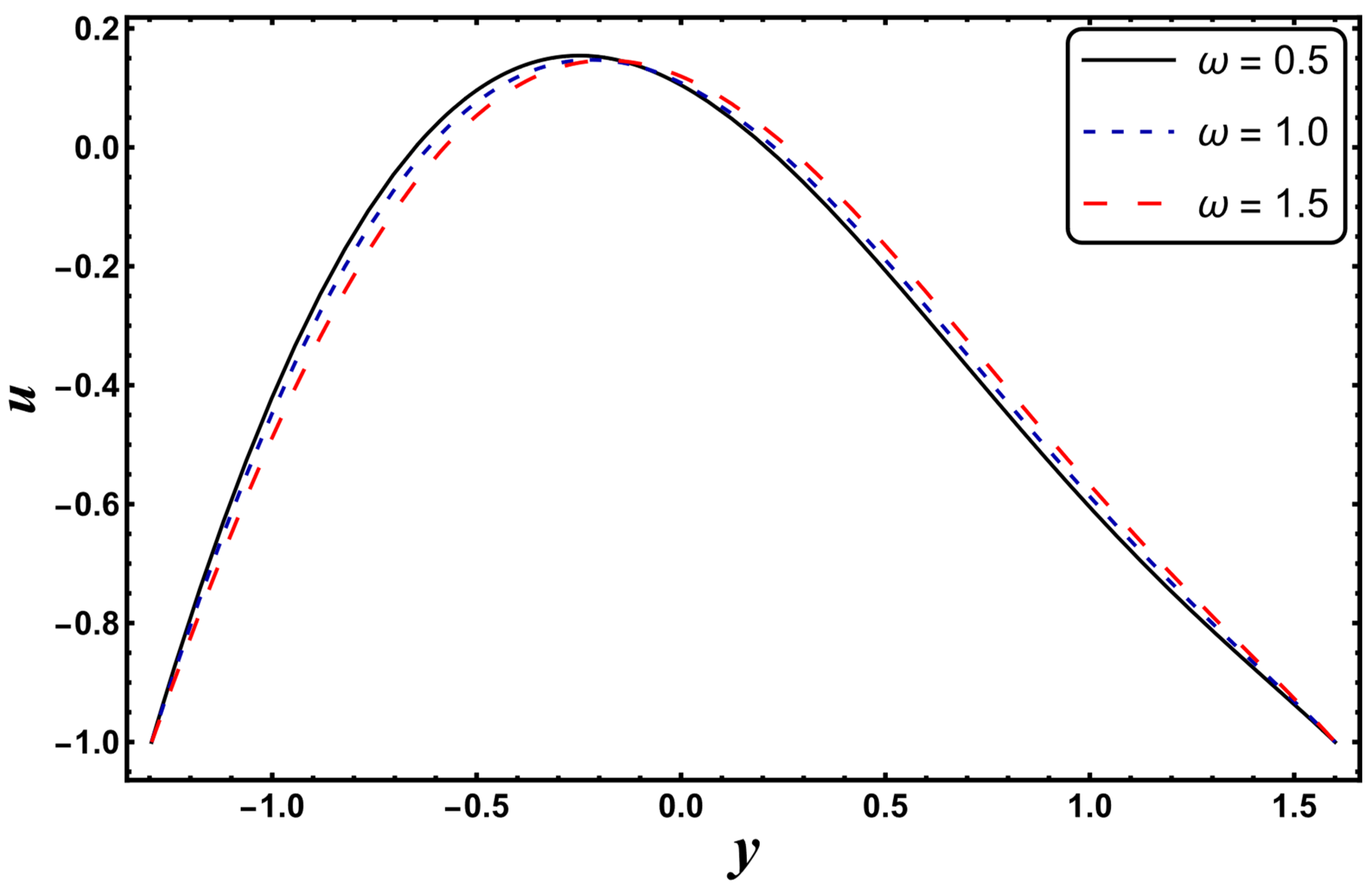
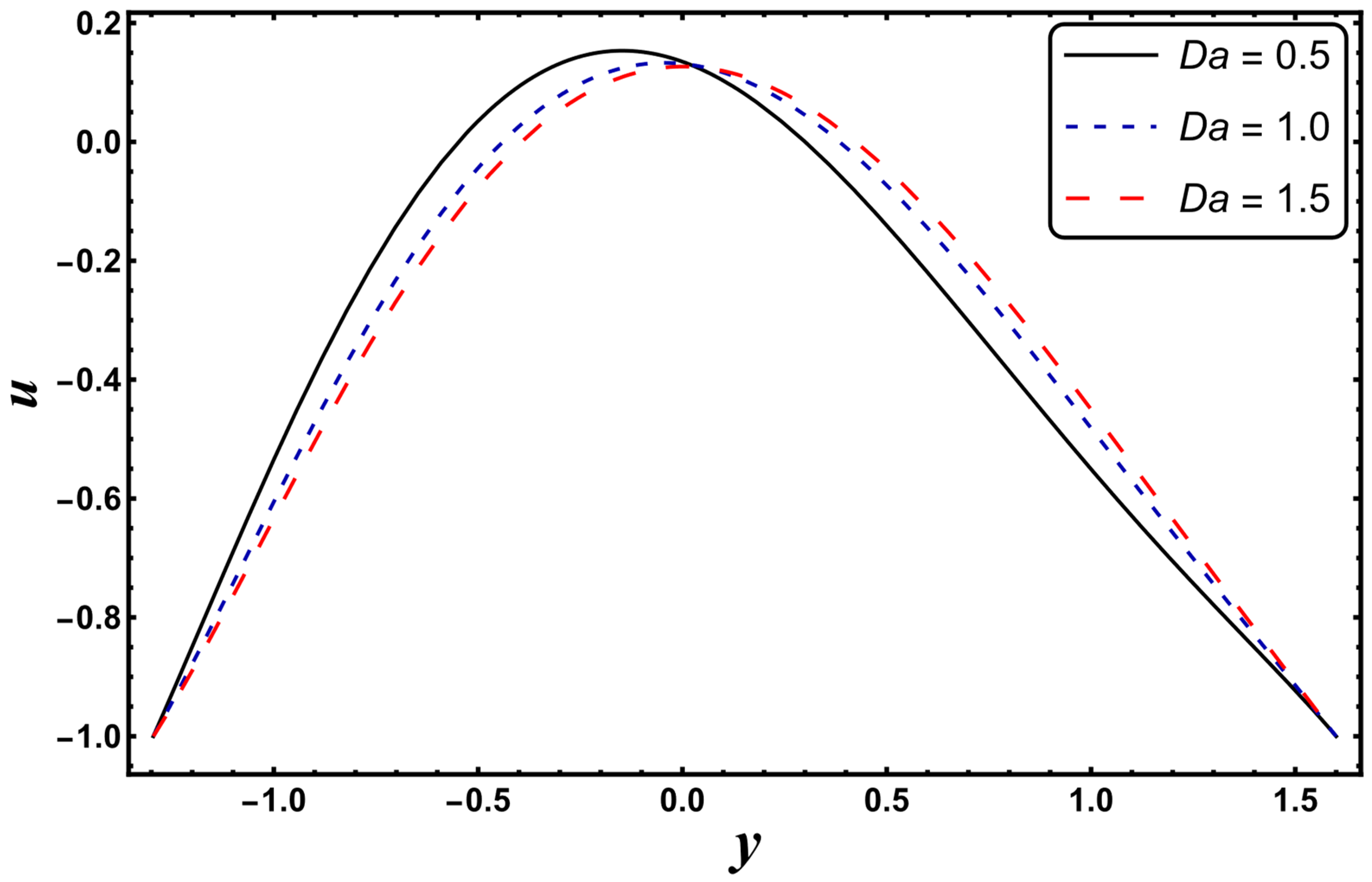
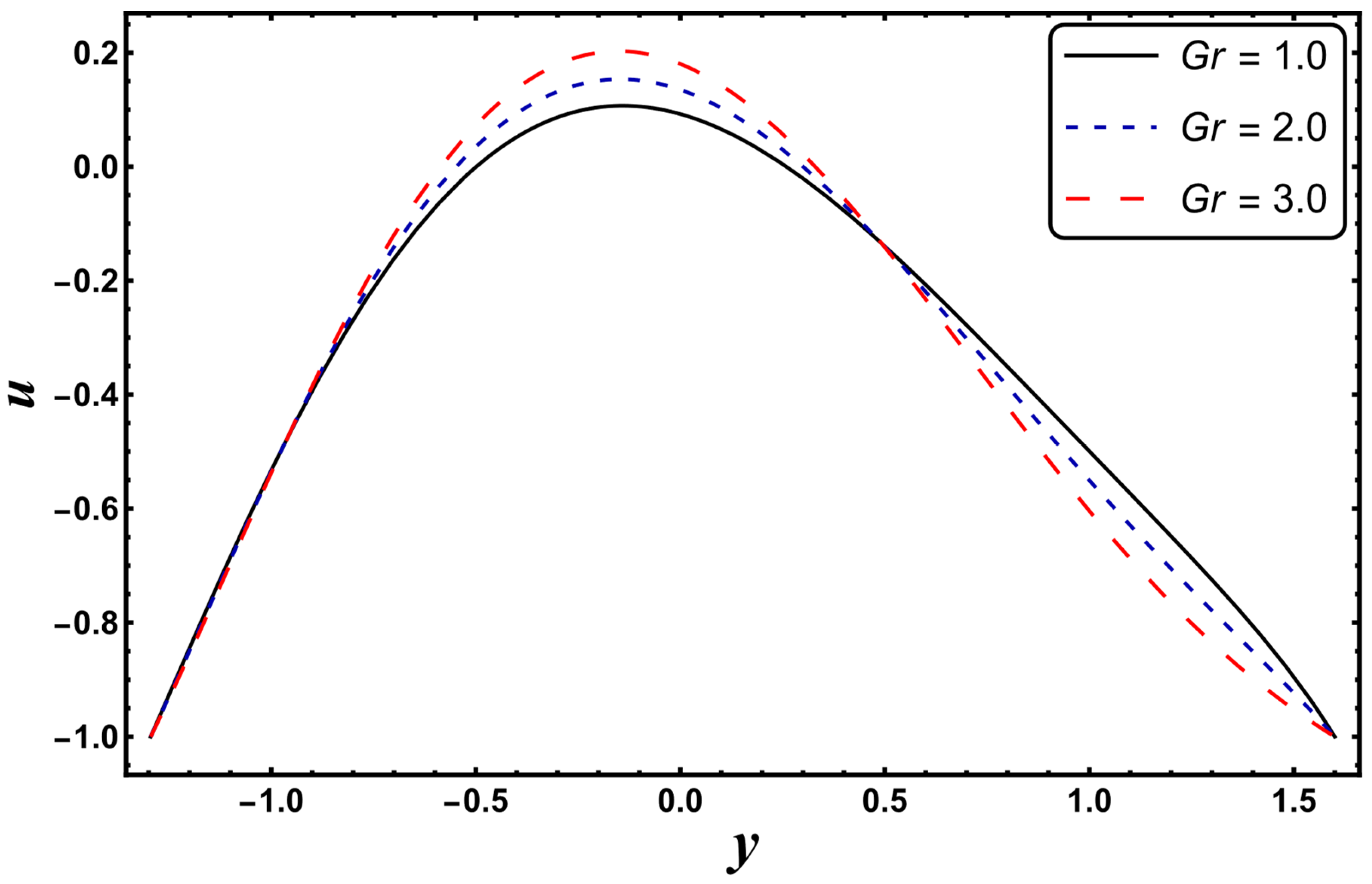
4.6. Velocity Profile
4.7. Velocity at Channel Center
5. Concluding Remarks
- Temperature increased in the presence of electroosmotic and Joule heating parameters.
- A decrement in the heat transfer rate at the wall was encountered for the case of a higher Grashoff number.
- The radiation parameter was found to be very important for minimizing the generation of entropy. However, more irreversibility was created by mounting the values of the Joule heating parameter.
- The Bejan number decreased for the case of a higher Darcy’s number.
- Fluid velocity can be regulated by adjusting the magnetic field intensity and Helmholtz–Smoluchowski velocity.
- The nonlinear convection and viscosity parameter was an increasing function of velocity at the channel center. However, the reverse trend was noted for a higher Helmholtz–Smoluchowski velocity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| (, ) | coordinates in wave frame (m) |
| (, ) | velocity components in lab frame (m s−1) |
| (, ) | velocity components in wave frame |
| c | speed of peristaltic wave (m/s) |
| current density | |
| applied magnetic field (N A−1 m−2) | |
| applied electric field (N/C) | |
| Cf | specific heat of fluid |
| μf | viscosity of fluid (Ns m−2) |
| T | dimensional temperature (K) |
| δ | wave number |
| electric conductivity of fluid (S/m) | |
| g | acceleration due to gravity (m s−2) |
| Φ | dimensional heat generation/absorption parameter (Wm−2K−1) |
| ε | dimensionless heat generation/absorption parameter |
| (, ) | coordinates in lab frame |
| P | dimensional pressure |
| Tw | temperature at channel wall |
| p | dimensionless pressure (N/m2) |
| T0 | temperature of wall |
| F | dimensionless flow rate in wave frame |
| θ | dimensionless temperature |
| ψ | stream function |
| η | dimensionless flow rate in laboratory frame |
| Pr | Prandtl number |
| Kf | thermal conductivity of fluid |
| Re | Reynolds number |
| Br | Brinkman number |
| Ec | Eckert number |
| ρf | density of fluid (kg m−3) |
| Gr | Grashoff number |
| M | Hartman number |
References
- Aicher, T.; Martin, H. New correlations for mixed turbulent natural and forced convection heat transfer in vertical tubes. Int. J. Heat Mass Transf. 1997, 40, 3617–3626. [Google Scholar] [CrossRef]
- Bae, Y.Y.; Kim, H.Y.; Kang, D.J. Forced and mixed convection heat transfer to supercritical CO2 vertically flowing in a uniformly heated circular tube. Exp. Therm. Fluid Sci. 2010, 34, 1295–1308. [Google Scholar] [CrossRef]
- Kumar, N.; Doshi, J.B.; Vijayan, P.K. Investigations on the role of mixed convection and wall friction factor in single-phase natural circulation loop dynamics. Ann. Nucl. Energy 2011, 38, 2247–2270. [Google Scholar] [CrossRef]
- Pretorius, J.P.; Kröger, D.G. Critical evaluation of solar chimney power plant performance. Sol. Energy 2006, 80, 535–544. [Google Scholar] [CrossRef]
- Liu, D.; Gu, H. Mixed convection heat transfer in a 5 × 5 rod bundles. Int. J. Heat Mass Transf. 2017, 113, 914–921. [Google Scholar] [CrossRef]
- Jackson, J.D. Fluid flow and convective heat transfer to fluids at supercritical pressure. Nucl. Eng. Des. 2013, 264, 24–40. [Google Scholar] [CrossRef]
- Bae, J.H.; Yoo, J.Y.; Choi, H.; McEligot, D.M. Effects of large density variation on strongly heated internal air flows. Phys. Fluids 2006, 18, 075102. [Google Scholar] [CrossRef]
- Venugopal, G.; Balaji, C.; Venkateshan, S.P. Experimental study of mixed convection heat transfer in a vertical duct filled with metallic porous structures. Int. J. Therm. Sci. 2010, 49, 340–348. [Google Scholar] [CrossRef]
- Izadi, M.; Behzadmehr, A.; Shahmardan, M.M. Effects of inclination angle on mixed convection heat transfer of a nanofluid in a square cavity. Int. J. Comput. Methods Eng. Sci. Mech. 2015, 16, 11–21. [Google Scholar] [CrossRef]
- Majdi, H.S.; Abed, A.M.; Habeeb, L.J. Mixed Convection Heat Transfer of CuO-H2O Nanofluid in a Triangular Lid-Driven Cavity with Circular Inner Body. J. Mech. Eng. Res. Dev. 2021, 44, 164–175. [Google Scholar]
- Latham, T.W. Fluid Motions in a Peristaltic Pump. Ph.D. Thesis, Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA, 1966. [Google Scholar]
- Abdelsalam, S.I.; Bhatti, M.M. The study of non-Newtonian nanofluid with hall and ion slip effects on peristaltically induced motion in a non-uniform channel. RSC Adv. 2018, 8, 7904–7915. [Google Scholar] [CrossRef] [Green Version]
- Abdelsalam, S.I.; Bhatti, M.M. The impact of impinging TiO2 nanoparticles in Prandtl nanofluid along with endoscopic and variable magnetic field effects on peristaltic blood flow. Multidiscip. Modeling Mater. Struct. 2018, 14, 530–548. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Vafai, K. Combined effects of magnetic field and rheological properties on the peristaltic flow of a compressible fluid in a microfluidic channel. Eur. J. Mech. -B/Fluids 2017, 65, 398–411. [Google Scholar] [CrossRef]
- Eldesoky, I.M. Influence of slip condition on peristaltic transport of a compressible Maxwell fluid through porous medium in a tube. Int. J. Appl. Math. Mech. 2012, 8, 99–117. [Google Scholar]
- Mekheimer, K.S.; Komy, S.R.; Abdelsalam, S.I. Simultaneous effects of magnetic field and space porosity on compressible Maxwell fluid transport induced by a surface acoustic wave in a microchannel. Chin. Phys. B 2013, 22, 124702. [Google Scholar] [CrossRef]
- Kothandapani, M.; Prakash, J. Effect of radiation and magnetic field on peristaltic transport of nanofluids through a porous space in a tapered asymmetric channel. J. Magn. Magn. Mater. 2015, 378, 152–163. [Google Scholar] [CrossRef]
- Abumandour, R.M.; Eldesoky, I.M.; Abdelwahab, E.T. On the performance of peristaltic pumping for the MHD slip flow under the variation of elastic walls features. ERJ. Eng. Res. J. 2020, 43, 231–244. [Google Scholar] [CrossRef]
- Rice, C.L.; Whitehead, R. Electrokinetic flow in a narrow cylindrical capillary. J. Phys. Chem. 1965, 69, 4017–4024. [Google Scholar] [CrossRef]
- Tang, G.H.; Li, X.F.; He, Y.L.; Tao, W.Q. Electroosmotic flow of non-Newtonian fluid in microchannels. J. Non-Newton. Fluid Mech. 2009, 15, 133–137. [Google Scholar] [CrossRef]
- Ramesh, K.; Prakash, J. Thermal analysis for heat transfer enhancement in electroosmosis-modulated peristaltic transport of Sutterby nanofluids in a microfluidic vessel. J. Therm. Anal. Calorim. 2019, 138, 1311–1326. [Google Scholar] [CrossRef]
- Akram, J.; Akbar, N.S.; Maraj, E.N. A comparative study on the role of nanoparticle dispersion in electroosmosis regulated peristaltic flow of water. Alex. Eng. J. 2020, 59, 943–956. [Google Scholar] [CrossRef]
- Akbar, Y.; Iqbal, J.; Hussain, M.; Khan, H.; Alotaibi, H. Peristaltic transportation of Carreau–Yasuda magneto nanofluid embedded in a porous medium with heat and mass transfer. Waves Random Complex Media 2022, 1–21. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Sahin, A.Z.; Wongwises, S. Entropy generation during Al2O3/water nanofluid flow in a solar collector: Effects of tube roughness, nanoparticle size, and different thermophysical models. Int. J. Heat Mass Transf. 2014, 78, 64–75. [Google Scholar] [CrossRef]
- Mahian, O.; Mahmud, S.; Zeinali Heris, S. Effect of uncertainties in physical properties on entropy generation between two rotating cylinders with nanofluids. J. Heat Transf. 2012, 134, 101704. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu–H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ashorynejad, H.R.; Rana, P. Lattice Boltzmann simulation of nanofluid heat transfer enhancement and entropy generation. J. Mol. Liq. 2016, 214, 86–95. [Google Scholar] [CrossRef]
- Khan, A.; Khan, I.; Alkanhal, T.A.; Ali, F.; Khan, D.; Nisar, K.S. Entropy generation in MHD conjugate flow with wall shear stress over an infinite plate: Exact analysis. Entropy 2019, 21, 359. [Google Scholar] [CrossRef] [Green Version]
- Akbar, Y.; Abbasi, F.M. Impact of variable viscosity on peristaltic motion with entropy generation. Int. Commun. Heat Mass Transf. 2020, 118, 104826. [Google Scholar] [CrossRef]
- Zahid, U.M.; Akbar, Y.; Abbasi, F.M. Entropy generation analysis for peristaltically driven flow of hybrid nanofluid. Chin. J. Phys. 2020, 67, 330–348. [Google Scholar] [CrossRef]
- Tlau, L.; Ontela, S. Effect of shape of nanoparticles on mixed convection nanofluid flow in a porous medium with variable permeability: Analysis of the second law of thermodynamics. Pramana 2021, 95, 1–12. [Google Scholar] [CrossRef]
- Ali, Z.; Qasim, M.; Ashraf, M.U. Thermodynamic analysis of nonlinear convection in peristaltic flow. Int. Commun. Heat Mass Transf. 2021, 129, 105686. [Google Scholar] [CrossRef]









| α | Nr | Da | Gr | S | Water | Methanol | Kerosene |
|---|---|---|---|---|---|---|---|
| 0.02 | 1.0 | 0.5 | 2.0 | 0.5 | 0.9806 | 1.0013 | 1.3317 |
| 0.04 | 0.9793 | 0.9999 | 1.3262 | ||||
| 0.06 | 0.9781 | 0.9984 | 1.3206 | ||||
| 0.03 | 0.5 | 1.2938 | 1.3222 | 1.7818 | |||
| 1.0 | 0.9800 | 1.0006 | 1.3289 | ||||
| 1.5 | 0.7930 | 0.8092 | 1.0655 | ||||
| 0.5 | 0.9800 | 1.0006 | 1.3289 | ||||
| 1.0 | 0.9387 | 0.9536 | 1.1912 | ||||
| 1.5 | 0.9239 | 0.9368 | 1.1418 | ||||
| 0.0 | 0.9720 | 0.9912 | 1.2874 | ||||
| 1.0 | 0.9756 | 0.9955 | 1.3061 | ||||
| 2.0 | 0.9800 | 1.0006 | 1.3289 | ||||
| 0.0 | 0.7184 | 0.7386 | 1.0597 | ||||
| 1.0 | 1.2419 | 1.2629 | 1.5994 | ||||
| 2.0 | 1.7668 | 1.7889 | 2.1448 |
| α | Uhs | Gr | λ1 | Water | Methanol | Kerosene |
|---|---|---|---|---|---|---|
| 0.02 | 1.0 | 2.0 | 0.5 | 0.1076 | 0.1090 | 0.1328 |
| 0.04 | 0.1108 | 0.1123 | 0.1373 | |||
| 0.06 | 0.1141 | 0.1156 | 0.1420 | |||
| 0.03 | –0.5 | 0.0949 | 0.0964 | 0.1200 | ||
| 0.0 | 0.0808 | 0.0821 | 0.1052 | |||
| 0.5 | 0.0666 | 0.0680 | 0.0905 | |||
| 0.0 | 0.0508 | 0.0509 | 0.0520 | |||
| 1.0 | 0.0798 | 0.0805 | 0.0924 | |||
| 2.0 | 0.1092 | 0.1106 | 0.1350 | |||
| 0.0 | 0.1092 | 0.1106 | 0.1350 | |||
| 0.1 | 0.1156 | 0.1174 | 0.1483 | |||
| 0.2 | 0.1220 | 0.1241 | 0.1591 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbar, Y.; Alotaibi, H. Electroosmosis-Optimized Thermal Model for Peristaltic Transportation of Thermally Radiative Magnetized Liquid with Nonlinear Convection. Entropy 2022, 24, 530. https://doi.org/10.3390/e24040530
Akbar Y, Alotaibi H. Electroosmosis-Optimized Thermal Model for Peristaltic Transportation of Thermally Radiative Magnetized Liquid with Nonlinear Convection. Entropy. 2022; 24(4):530. https://doi.org/10.3390/e24040530
Chicago/Turabian StyleAkbar, Yasir, and Hammad Alotaibi. 2022. "Electroosmosis-Optimized Thermal Model for Peristaltic Transportation of Thermally Radiative Magnetized Liquid with Nonlinear Convection" Entropy 24, no. 4: 530. https://doi.org/10.3390/e24040530
APA StyleAkbar, Y., & Alotaibi, H. (2022). Electroosmosis-Optimized Thermal Model for Peristaltic Transportation of Thermally Radiative Magnetized Liquid with Nonlinear Convection. Entropy, 24(4), 530. https://doi.org/10.3390/e24040530







