Testability of Instrumental Variables in Linear Non-Gaussian Acyclic Causal Models
Abstract
:1. Introduction
- 1.
- We propose a necessary condition for detecting variables that cannot serve as (conditional) IVs by the so-called generalized independent noise (GIN) condition [24], which is called instrumental variable generalized independent noise (IV-GIN) condition. We characterize the graphical implications of IV-GIN condition in linear non-Gaussian acyclic causal models.
- 2.
- We then further show whether and how the graphical criteria of an instrumental variable can be checked by exploiting the IV-GIN conditions.
- 3.
- We develop a method to select the set of candidate IVs for the target causal influence from the observational data by IV-GIN conditions.
- 4.
- We demonstrate the efficacy of our algorithm on both synthetic and real-word data.
2. Related Work
2.1. Instrument Variable Models
2.2. Causal Graphical Models
3. Preliminaries
3.1. Notation and Graph Terminology
3.2. Instrumental Variable Model
- 1.
- contains only nondescendants of Y in G;
- 2.
- d-separates Z from Y in the graph obtained by removing the edge from G;
- 3.
- does not d-separates Z from X in G.
3.3. Problem Setup
4. Necessary Condition for Instrumental Variable
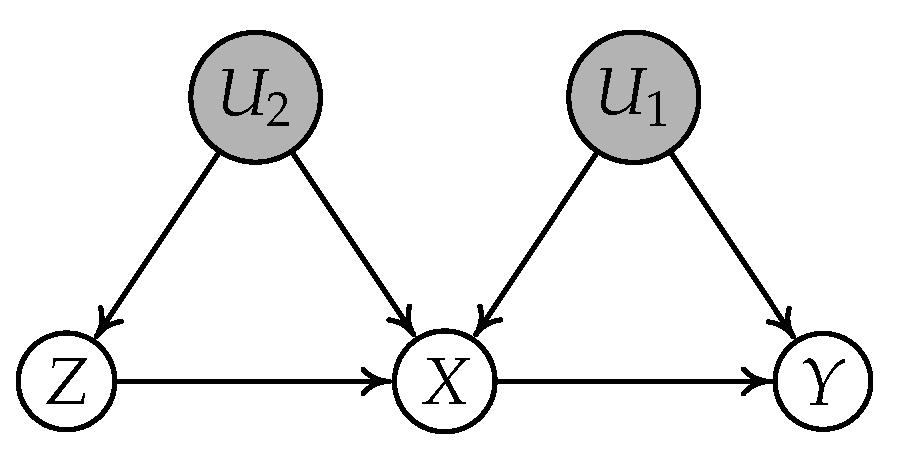
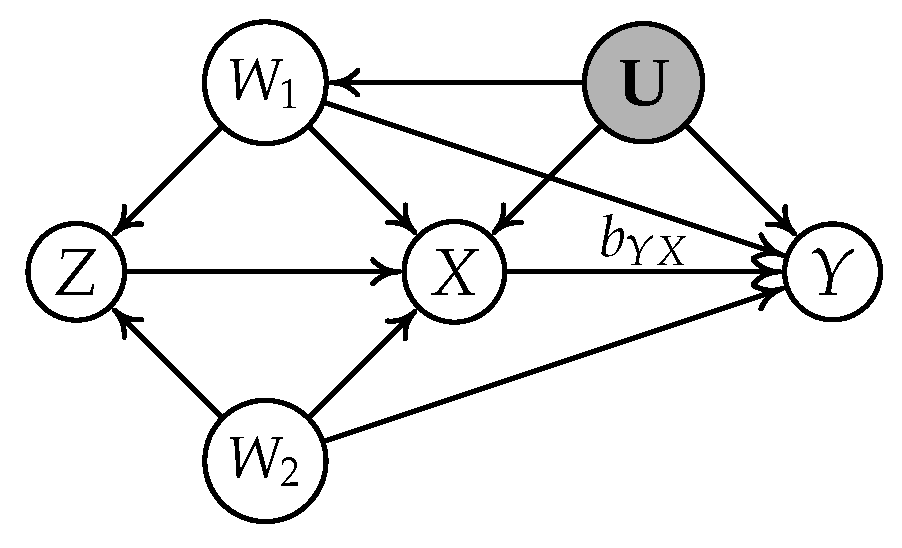
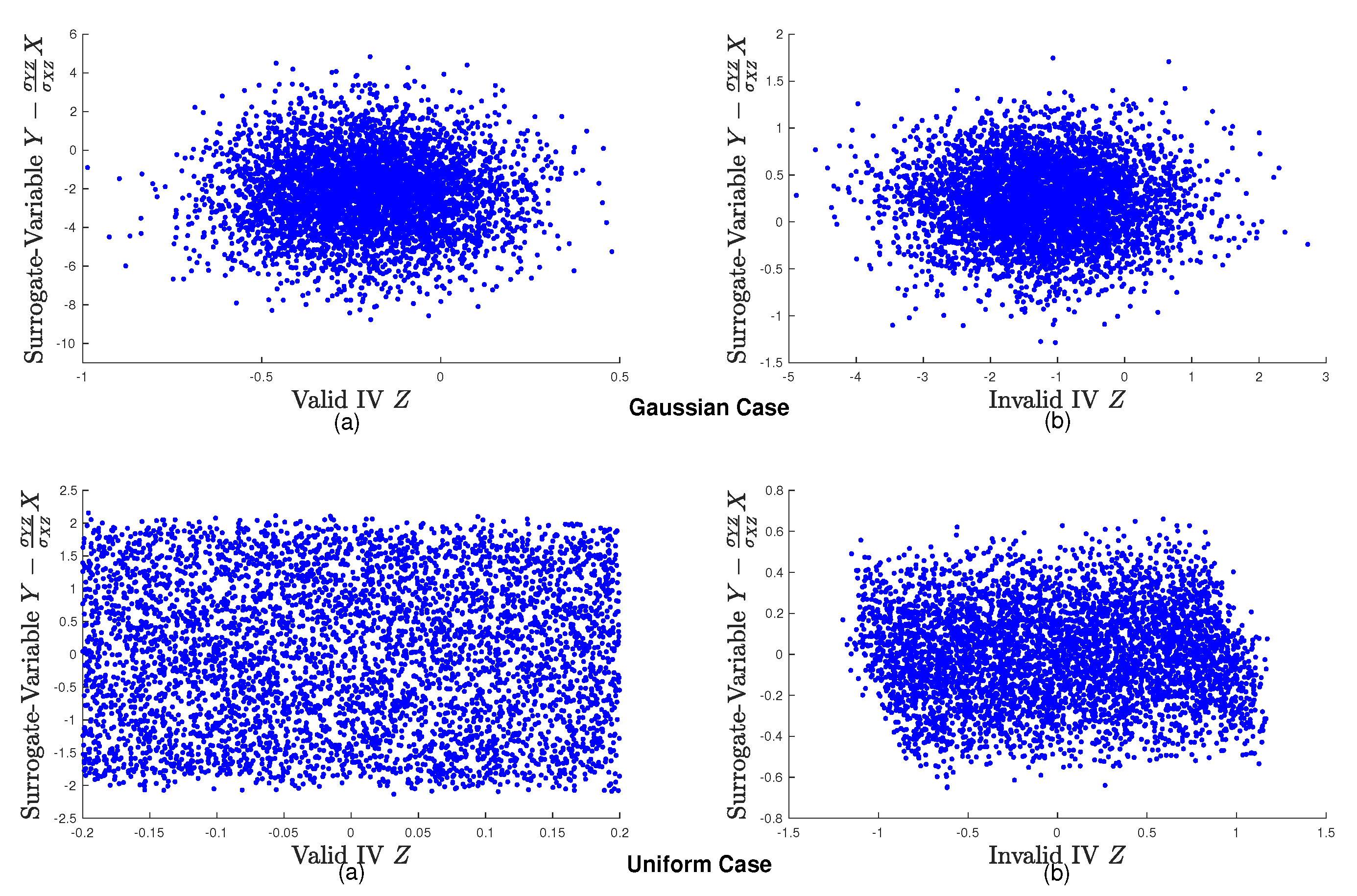
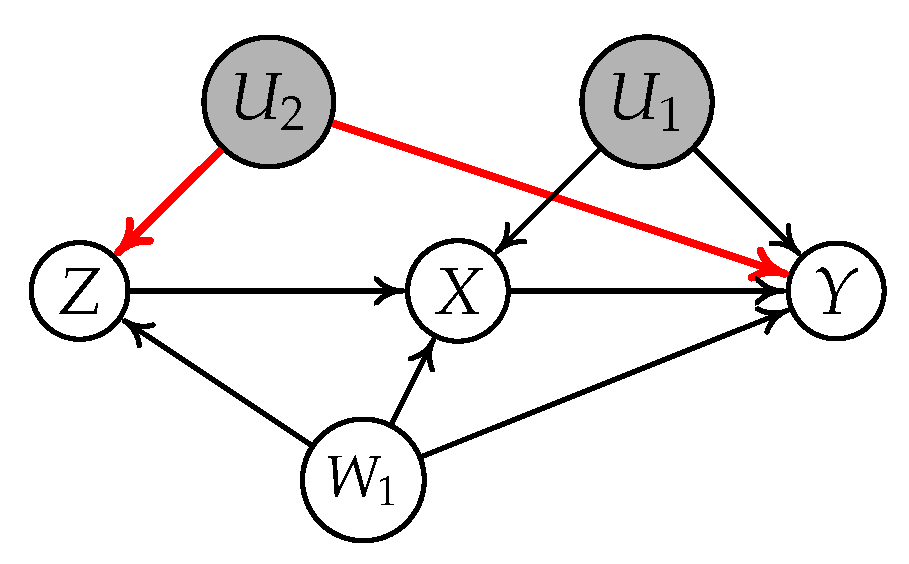
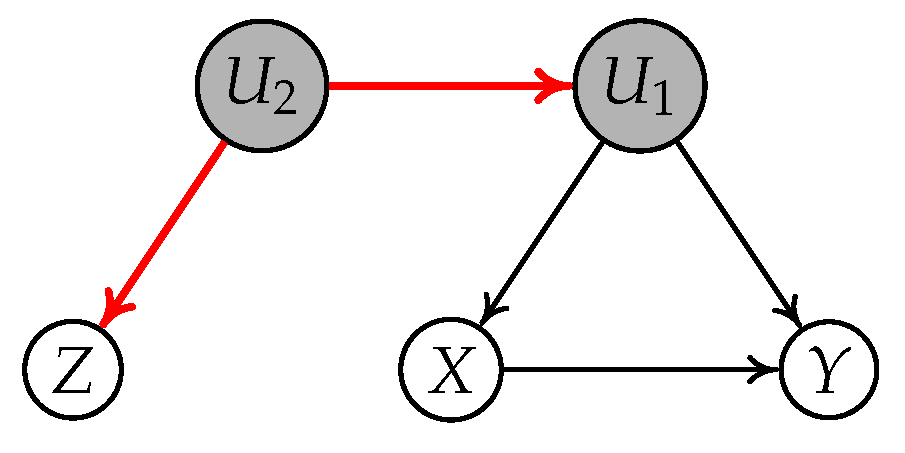
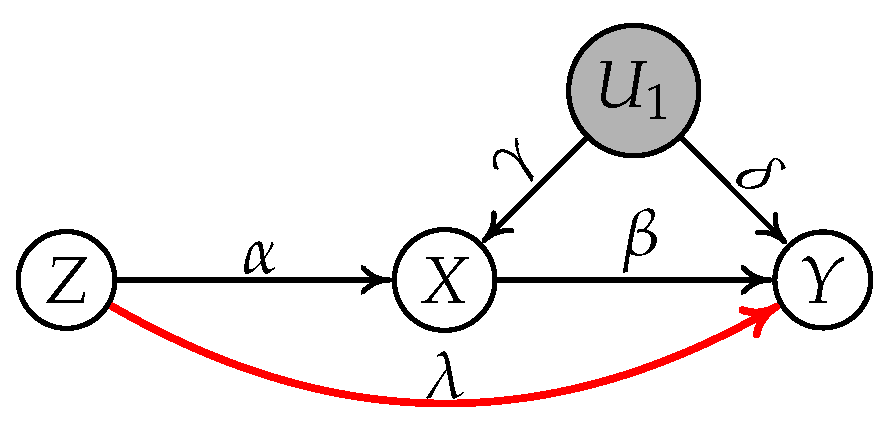
4.1. A Motivating Example
- Subgraph (a): , , , and ;
- Subgraph (b): , , , and .
- Gaussian Case: All noise terms in subgraphs (a) and (b) are generated from the standard Gaussian distributions.
- Uniform Case: All noise terms in subgraphs (a) and (b) are generated from the uniform distributions over the interval .
4.2. IV-GIN Condition for Instrumental Variable
4.3. Graphical Implications of IV-GIN Condition in Linear non-Gaussian causal Models
- 1.
- There exists a node , , such that for every trek π between a node and a node , (a) π goes through at least one node in , denoted by , and (b) has its arrow pointing to in π. (In other words, is causally earlier (according to the causal order) than on π.)
- 2.
- There is at least one directed path between any one node in and any one node in .
- 3.
- There is no proper subset of to satisfy conditions 1 and 2.
5. Testability of Instrument Criteria Validity in Terms of IV-GIN Conditions
5.1. Condition 1 of Instrument Criteria
5.2. Condition 2 of Instrument Criteria
- 2a.
- There is no active nondirected path between Z and Y that does not include X;
- 2b.
- There is no active directed path from Z to Y that does not include X.
5.2.1. Subcondition 2a
5.2.2. Subcondition 2b
6. Algorithm for Selecting the Candidate IVs
| Algorithm 1: IV-GIN |
| Input: Treatment X, outcome Y, and set of observed variables . Output: Set of candidate and its corresponding conditional set . 1: Initialize the set of candidate IVs: , the conditional set: , the length of conditional set: , and ; 2: while do 3: for each variable do 4: repeat 5: Select a subset from such that ; 6: if follows the IV-GIN condition then 7: Add into , and delete from ; 8: Set ; 9: Break the repeat loop of line 4; 10: end if 11: until all subsets with length in are selected; 12: end for 13: ; 14: end while 15: Return: and |
7. Experiments on Synthetic Data
- Correct-selecting rate: The number of correctly selected valid IVs divided by the total number of valid IVs in the ground-truth graph.
- Selection commission: The number of falsely detected IVs divided by the total number of selected IVs in the output of the current algorithm.
- T1.
- Sensitivity on the effect of sample size. We considered different sample sizes , where k = 1000.
- T2.
- Sensitivity on the effect of unmeasured confounders between X and Y. The coefficients between and are set such that , at two levels, , as that in [21]. The sample size N is 5000.
8. Application to Vitamin D Data
9. Discussion
10. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proofs
Appendix A.1. Proof of Theorem 3
Appendix A.2. Proof of Theorem 2
Appendix A.3. Proof of Proposition 1
Appendix A.4. Proof of Proposition 2
Appendix A.5. Proof of Theorem 4
References
- Wright, P.G. Tariff on Animal and Vegetable Oils; Macmillan Company: New York, NY, USA, 1928. [Google Scholar]
- Goldberger, A.S. Structural equation methods in the social sciences. Econom. J. Econom. Soc. 1972, 40, 979–1001. [Google Scholar] [CrossRef]
- Bowden, R.J.; Turkington, D.A. Instrum. Var.; Number 8; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Pearl, J. Causality: Models, Reasoning, and Inference, 2nd ed.; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Imbens, G.W. Instrumental Variables: An Econometrician’s Perspective. Stat. Sci. 2014, 29, 323–358. [Google Scholar] [CrossRef]
- Imbens, G.W.; Rubin, D.B. Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Hernán, M.A.; Robins, J.M. Instruments for causal inference: An epidemiologist’s dream? Epidemiology 2006, 17, 360–372. [Google Scholar] [CrossRef] [PubMed]
- Baiocchi, M.; Cheng, J.; Small, D.S. Instrumental variable methods for causal inference. Stat. Med. 2014, 33, 2297–2340. [Google Scholar] [CrossRef] [PubMed]
- Bound, J.; Jaeger, D.A.; Baker, R.M. Problems with instrumental variables estimation when the correlation between the instruments and the endogenous explanatory variable is weak. J. Am. Stat. Assoc. 1995, 90, 443–450. [Google Scholar] [CrossRef]
- Pearl, J. On the testability of causal models with latent and instrumental variables. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; pp. 435–443. [Google Scholar]
- Manski, C.F. Partial Identification of Probability Distributions; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Palmer, T.M.; Ramsahai, R.R.; Didelez, V.; Sheehan, N.A. Nonparametric bounds for the causal effect in a binary instrumental-variable model. Stata J. 2011, 11, 345–367. [Google Scholar] [CrossRef]
- Kitagawa, T. A test for instrument validity. Econometrica 2015, 83, 2043–2063. [Google Scholar] [CrossRef]
- Wang, L.; Robins, J.M.; Richardson, T.S. On falsification of the binary instrumental variable model. Biometrika 2017, 104, 229–236. [Google Scholar] [CrossRef] [PubMed]
- Kédagni, D.; Mourifié, I. Generalized instrumental inequalities: Testing the instrumental variable independence assumption. Biometrika 2020, 107, 661–675. [Google Scholar] [CrossRef]
- Gunsilius, F.F. Nontestability of instrument validity under continuous treatments. Biometrika 2021, 108, 989–995. [Google Scholar] [CrossRef]
- Kuroki, M.; Cai, Z. Instrumental variable tests for Directed Acyclic Graph Models. In Proceedings of the International Workshop on Artificial Intelligence and Statistics, Bridgetown, Barbados, 6–8 January 2005; pp. 190–197. [Google Scholar]
- Spearman, C. Pearson’s contribution to the theory of two factors. Br. J. Psychol. 1928, 19, 95–101. [Google Scholar] [CrossRef]
- Kang, H.; Zhang, A.; Cai, T.T.; Small, D.S. Instrumental variables estimation with some invalid instruments and its application to Mendelian randomization. J. Am. Stat. Assoc. 2016, 111, 132–144. [Google Scholar] [CrossRef]
- Silva, R.; Shimizu, S. Learning instrumental variables with structural and non-gaussianity assumptions. J. Mach. Learn. Res. 2017, 18, 1–49. [Google Scholar]
- Sullivant, S.; Talaska, K.; Draisma, J. Trek separation for Gaussian graphical models. Ann. Stat. 2010, 38, 1665–1685. [Google Scholar] [CrossRef]
- Spirtes, P. Calculation of Entailed Rank Constraints in Partially Non-linear and Cyclic Models. In Proceedings of the Twenty-Ninth Conference on Uncertainty in Artificial Intelligence; AUAI Press: Arlington, VA, USA, 2013; pp. 606–615. [Google Scholar]
- Xie, F.; Cai, R.; Huang, B.; Glymour, C.; Hao, Z.; Zhang, K. Generalized Independent Noise Conditionfor Estimating Latent Variable Causal Graphs. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; pp. 14891–14902. [Google Scholar]
- Choi, M.J.; Tan, V.Y.; Anandkumar, A.; Willsky, A.S. Learning latent tree graphical models. J. Mach. Learn. Res. 2011, 12, 1771–1812. [Google Scholar]
- Chandrasekaran, V.; Parrilo, P.A.; Willsky, A.S. Latent variable graphical model selection via convex optimization. In Proceedings of the 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 29 September–1 October 2010; pp. 1935–1967. [Google Scholar]
- Meng, Z.; Eriksson, B.; Hero, A. Learning latent variable Gaussian graphical models. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1269–1277. [Google Scholar]
- Zorzi, M.; Sepulchre, R. AR identification of latent-variable graphical models. IEEE Trans. Autom. Control. 2015, 61, 2327–2340. [Google Scholar] [CrossRef]
- Wu, C.; Zhao, H.; Fang, H.; Deng, M. Graphical model selection with latent variables. Electron. J. Stat. 2017, 11, 3485–3521. [Google Scholar] [CrossRef]
- Kumar, S.; Ying, J.; de Miranda Cardoso, J.V.; Palomar, D.P. A Unified Framework for Structured Graph Learning via Spectral Constraints. J. Mach. Learn. Res. 2020, 21, 1–60. [Google Scholar]
- Ciccone, V.; Ferrante, A.; Zorzi, M. Learning latent variable dynamic graphical models by confidence sets selection. IEEE Trans. Autom. Control. 2020, 65, 5130–5143. [Google Scholar] [CrossRef]
- Alpago, D.; Zorzi, M.; Ferrante, A. A scalable strategy for the identification of latent-variable graphical models. IEEE Trans. Autom. Control. 2021. [Google Scholar] [CrossRef]
- Bertsimas, D.; Cory-Wright, R.; Johnson, N.A. Sparse Plus Low Rank Matrix Decomposition: A Discrete Optimization Approach. arXiv 2021, arXiv:2109.12701. [Google Scholar]
- Spirtes, P.; Meek, C.; Richardson, T. Causal inference in the presence of latent variables and selection bias. In Proceedings of the Eleventh Conference on Uncertainty in Artificial Intelligence; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1995; pp. 499–506. [Google Scholar]
- Colombo, D.; Maathuis, M.H.; Kalisch, M.; Richardson, T.S. Learning high-dimensional directed acyclic graphs with latent and selection variables. Ann. Stat. 2012, 40, 294–321. [Google Scholar] [CrossRef]
- Kitson, N.K.; Constantinou, A.C.; Guo, Z.; Liu, Y.; Chobtham, K. A survey of Bayesian Network structure learning. arXiv 2021, arXiv:2109.11415. [Google Scholar]
- Hoyer, P.O.; Shimizu, S.; Kerminen, A.J.; Palviainen, M. Estimation of causal effects using linear non-Gaussian causal models with hidden variables. Int. J. Approx. Reason. 2008, 49, 362–378. [Google Scholar] [CrossRef]
- Entner, D.; Hoyer, P.O. Discovering unconfounded causal relationships using linear non-gaussian models. In JSAI International Symposium on Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; pp. 181–195. [Google Scholar]
- Tashiro, T.; Shimizu, S.; Hyvärinen, A.; Washio, T. ParceLiNGAM: A causal ordering method robust against latent confounders. Neural Comput. 2014, 26, 57–83. [Google Scholar] [CrossRef] [PubMed]
- Salehkaleybar, S.; Ghassami, A.; Kiyavash, N.; Zhang, K. Learning Linear Non-Gaussian Causal Models in the Presence of Latent Variables. J. Mach. Learn. Res. 2020, 21, 1–24. [Google Scholar]
- Ciccone, V.; Ferrante, A.; Zorzi, M. Robust identification of “sparse plus low-rank” graphical models: An optimization approach. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; pp. 2241–2246. [Google Scholar]
- Alpago, D.; Zorzi, M.; Ferrante, A. Identification of sparse reciprocal graphical models. IEEE Control. Syst. Lett. 2018, 2, 659–664. [Google Scholar] [CrossRef]
- Frot, B.; Nandy, P.; Maathuis, M.H. Robust causal structure learning with some hidden variables. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2019, 81, 459–487. [Google Scholar] [CrossRef]
- Agrawal, R.; Squires, C.; Prasad, N.; Uhler, C. The DeCAMFounder: Non-Linear Causal Discovery in the Presence of Hidden Variables. arXiv 2021, arXiv:2102.07921. [Google Scholar]
- Brito, C.; Pearl, J. Generalized instrumental variables. In Proceedings of the Eighteenth Conference on Uncertainty in Artificial Intelligence; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2002; pp. 85–93. [Google Scholar]
- Bollen, K.A. Structural Equations with Latent Variable; John Wiley & Sons: Hoboken, NJ, USA, 1989. [Google Scholar]
- Shimizu, S.; Hoyer, P.O.; Hyvärinen, A.; Kerminen, A. A linear non-Gaussian acyclic model for causal discovery. J. Mach. Learn. Res. 2006, 7, 2003–2030. [Google Scholar]
- Kagan, A.M.; Rao, C.R.; Linnik, Y.V. Characterization Problems in Mathematical Statistics; John Wiley: New York, NY, USA, 1973. [Google Scholar]
- Fisher, R.A. Statistical Methods for Research Workers; Springer: Berlin/Heidelberg, Germany, 1950. [Google Scholar]
- Zhang, Q.; Filippi, S.; Gretton, A.; Sejdinovic, D. Large-scale kernel methods for independence testing. Stat. Comput. 2018, 28, 113–130. [Google Scholar] [CrossRef]
- Skaaby, T.; Husemoen, L.L.N.; Martinussen, T.; Thyssen, J.P.; Melgaard, M.; Thuesen, B.H.; Pisinger, C.; Jørgensen, T.; Johansen, J.D.; Menné, T.; et al. Vitamin D status, filaggrin genotype, and cardiovascular risk factors: A Mendelian randomization approach. PLoS ONE 2013, 8, e57647. [Google Scholar]
- Martinussen, T.; Nørbo Sørensen, D.; Vansteelandt, S. Instrumental variables estimation under a structural Cox model. Biostatistics 2019, 20, 65–79. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.; Shimizu, S. Learning Instrumental Variables with Non-Gaussianity Assumptions: Theoretical Limitations and Practical Algorithms. arXiv 2015, arXiv:1511.02722. [Google Scholar]
- Hyvärinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 46. [Google Scholar]
- Hoyer, P.O.; Janzing, D.; Mooij, J.M.; Peters, J.; Schölkopf, B. Nonlinear causal discovery with additive noise models. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2009; pp. 689–696. [Google Scholar]
- Zhang, K.; Hyvärinen, A. On the identifiability of the post-nonlinear causal model. In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence; AUAI Press: Arlington, VA, USA, 2009; pp. 647–655. [Google Scholar]
- Peters, J.; Mooij, J.M.; Janzing, D.; Schölkopf, B. Causal Discovery with Continuous Additive Noise Models. J. Mach. Learn. Res. 2014, 15, 2009–2053. [Google Scholar]



| Correct-Selecting Rate ↑ | Selection Commission ↓ | ||||||
|---|---|---|---|---|---|---|---|
| Algorithm | IV-GIN (Ours) | sisVIVE | IV-TETRAD | IV-GIN (Ours) | sisVIVE | IV-TETRAD | |
| Scenario | 1k | 0.92 | 0.76 | 0.84 | 0.12 | 0.0 | 0.16 |
| 3k | 0.95 | 0.81 | 0.96 | 0.03 | 0.0 | 0.04 | |
| 5k | 0.97 | 0.85 | 0.96 | 0.0 | 0.0 | 0.04 | |
| Scenario | 1k | 0.9 | 0.92 | 0.03 | 0.03 | 0.08 | 0.0 |
| 3k | 0.95 | 0.93 | 0.02 | 0.0 | 0.02 | 0.0 | |
| 5k | 1.0 | 0.94 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Scenario | 1k | 0.75 | 0.29 | 0.05 | 0.1 | 0.59 | 0.1 |
| 3k | 0.86 | 0.2 | 0.02 | 0.05 | 0.7 | 0.05 | |
| 5k | 0.93 | 0.24 | 0.02 | 0.02 | 0.63 | 0.0 | |
| Correct-Selecting Rate ↑ | Selection Commission ↓ | ||||||
|---|---|---|---|---|---|---|---|
| Algorithm | IV-GIN (Ours) | sisVIVE | IV-TETRAD | IV-GIN (Ours) | sisVIVE | IV-TETRAD | |
| Scenario | 0.96 | 0.83 | 0.92 | 0.06 | 0.01 | 0.08 | |
| 0.85 | 0.72 | 0.86 | 0.01 | 0.0 | 0.01 | ||
| Scenario | 0.98 | 0.93 | 0.02 | 0.04 | 0.06 | 0.0 | |
| 0.92 | 0.91 | 0.0 | 0.08 | 0.1 | 0.0 | ||
| Scenario | 0.89 | 0.22 | 0.05 | 0.03 | 0.58 | 0.02 | |
| 0.85 | 0.2 | 0.03 | 0.07 | 0.61 | 0.0 | ||
| Metrics | Scenario | Scenario | Scenario |
|---|---|---|---|
| Correct-selecting rate ↑ | 0.1 | 0.1 | 0.09 |
| Selection commission ↓ | 0.0 | 0.12 | 0.3 |
| Metrics | Scenario | Scenario | Scenario |
|---|---|---|---|
| Correct-selecting rate ↑ | 0.96 | 1.0 | 0.92 |
| Selection commission ↓ | 0.01 | 0.0 | 0.04 |
| Testability of Instrument Criteria | |||
|---|---|---|---|
| Method | Scenario | Scenario | Scenario |
| IV-GIN (ours) | Fully | Partially | None |
| IV-TETRAD | None | Fully | None |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, F.; He, Y.; Geng, Z.; Chen, Z.; Hou, R.; Zhang, K. Testability of Instrumental Variables in Linear Non-Gaussian Acyclic Causal Models. Entropy 2022, 24, 512. https://doi.org/10.3390/e24040512
Xie F, He Y, Geng Z, Chen Z, Hou R, Zhang K. Testability of Instrumental Variables in Linear Non-Gaussian Acyclic Causal Models. Entropy. 2022; 24(4):512. https://doi.org/10.3390/e24040512
Chicago/Turabian StyleXie, Feng, Yangbo He, Zhi Geng, Zhengming Chen, Ru Hou, and Kun Zhang. 2022. "Testability of Instrumental Variables in Linear Non-Gaussian Acyclic Causal Models" Entropy 24, no. 4: 512. https://doi.org/10.3390/e24040512
APA StyleXie, F., He, Y., Geng, Z., Chen, Z., Hou, R., & Zhang, K. (2022). Testability of Instrumental Variables in Linear Non-Gaussian Acyclic Causal Models. Entropy, 24(4), 512. https://doi.org/10.3390/e24040512






