Cancer Segmentation by Entropic Analysis of Ordered Gene Expression Profiles
Abstract
1. Introduction
2. Materials and Methods
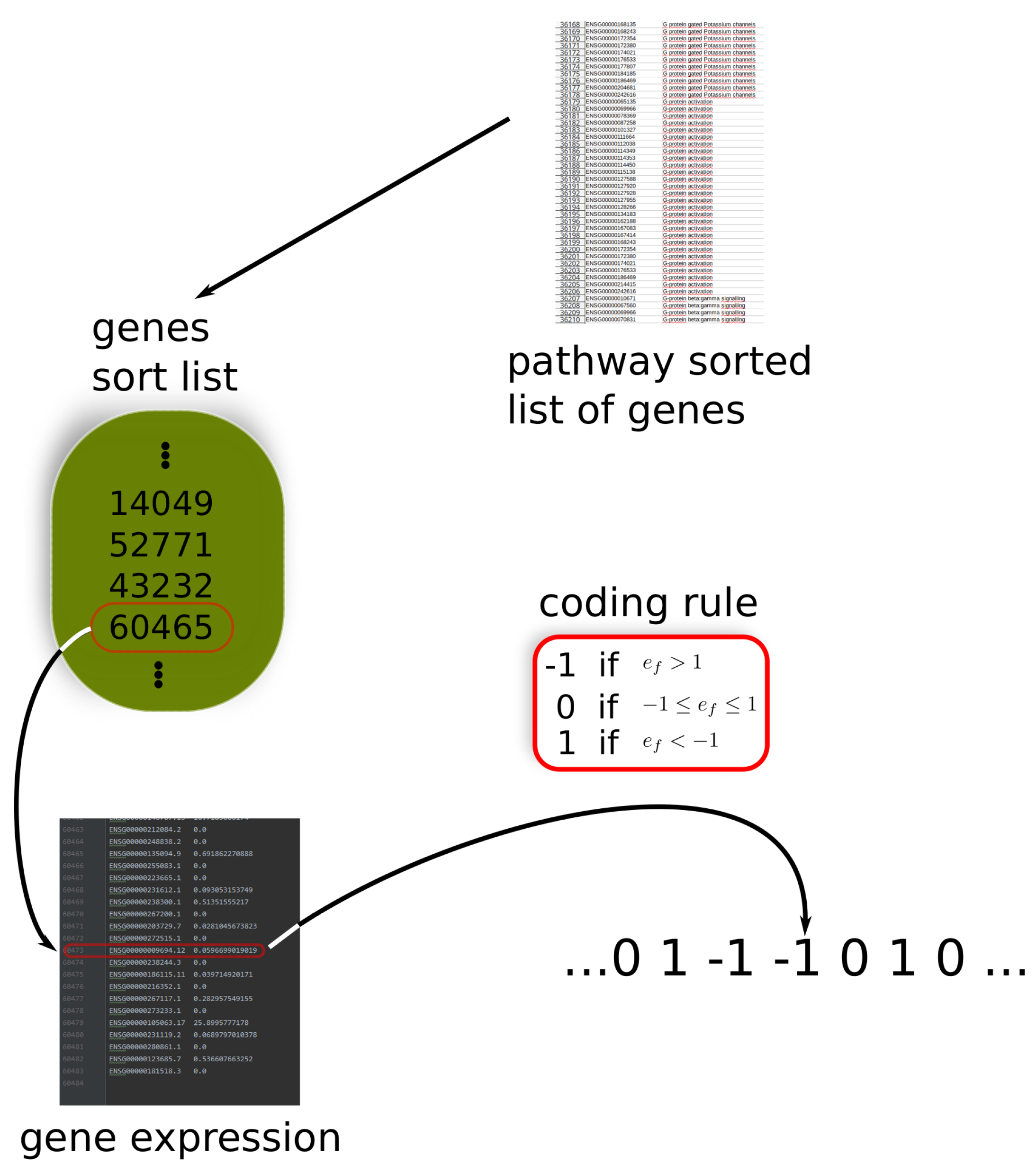
2.1. Gene Expression Level and Gene Expression Coding
2.2. Reactome Pathways and Ordered Sequences
2.3. Entropic Measures
2.4. Lempel–Ziv Estimates
3. Results
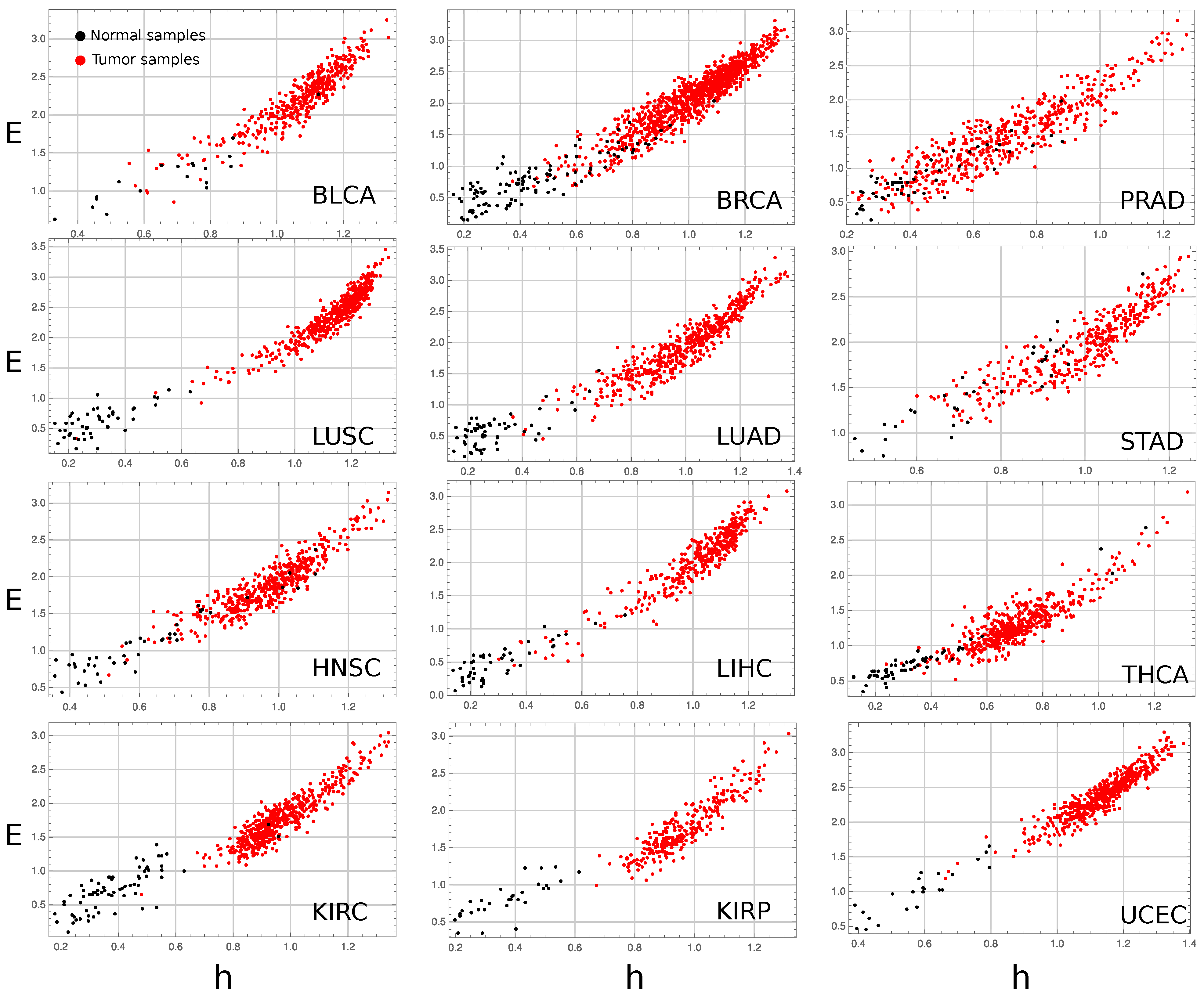
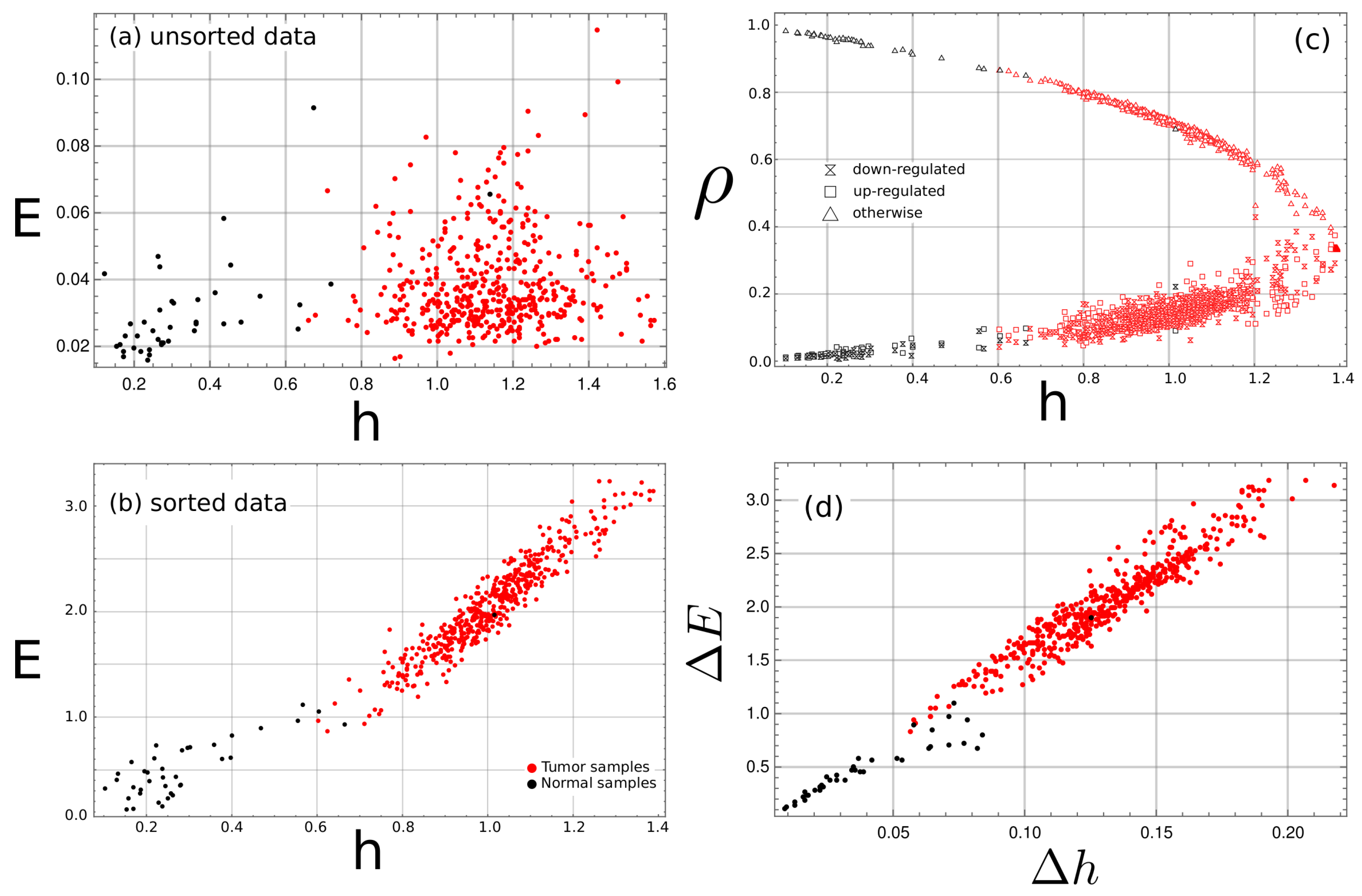
3.1. Complexity–Entropy Maps
3.2. Discrimination by Information Distance Measure
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TCGA | The Cancer Genome Atlas |
| RNA | Ribonucleic Acid |
| FPKM | Fragments Per Kilobase of transcript per Million mapped reads |
| H | Shannon Block Entropy |
| h | Entropy Density |
| E | Effective Measure Complexity |
| NN | Nearest Neighbors |
| K | Kolmogorov Complexity |
Appendix A
Appendix A.1. Cancer Coding and Number of Samples
| Number of Samples | |||
|---|---|---|---|
| TCGA | Tumor | Normal | Tumor |
| BLCA | Bladder Urothelial Carcinoma | 19 | 421 |
| BRCA | Breast Invasive Carcinoma | 112 | 1096 |
| COAD | Colon Adenocarcinoma | 41 | 474 |
| HNSC | Head and Neck Squamous Cell Carcinoma | 44 | 502 |
| KIRC | Kidney Renal Clear Cell Carcinoma | 72 | 539 |
| KIRP | Kidney Renal Papillary Cell Carcinoma | 32 | 289 |
| LIHC | Liver Hepatocellular Carcinoma | 50 | 374 |
| LUAD | Lung Adenocarcinoma | 59 | 535 |
| LUSC | Lung Squamous Cell Carcinoma | 49 | 502 |
| PRAD | Prostate Adenocarcinoma | 52 | 499 |
| STAD | Stomach Adenocarcinoma | 32 | 375 |
| THCA | Thyroid Carcinoma | 58 | 510 |
| UCEC | Uterine Corpus Endometrial Carcinoma | 23 | 552 |
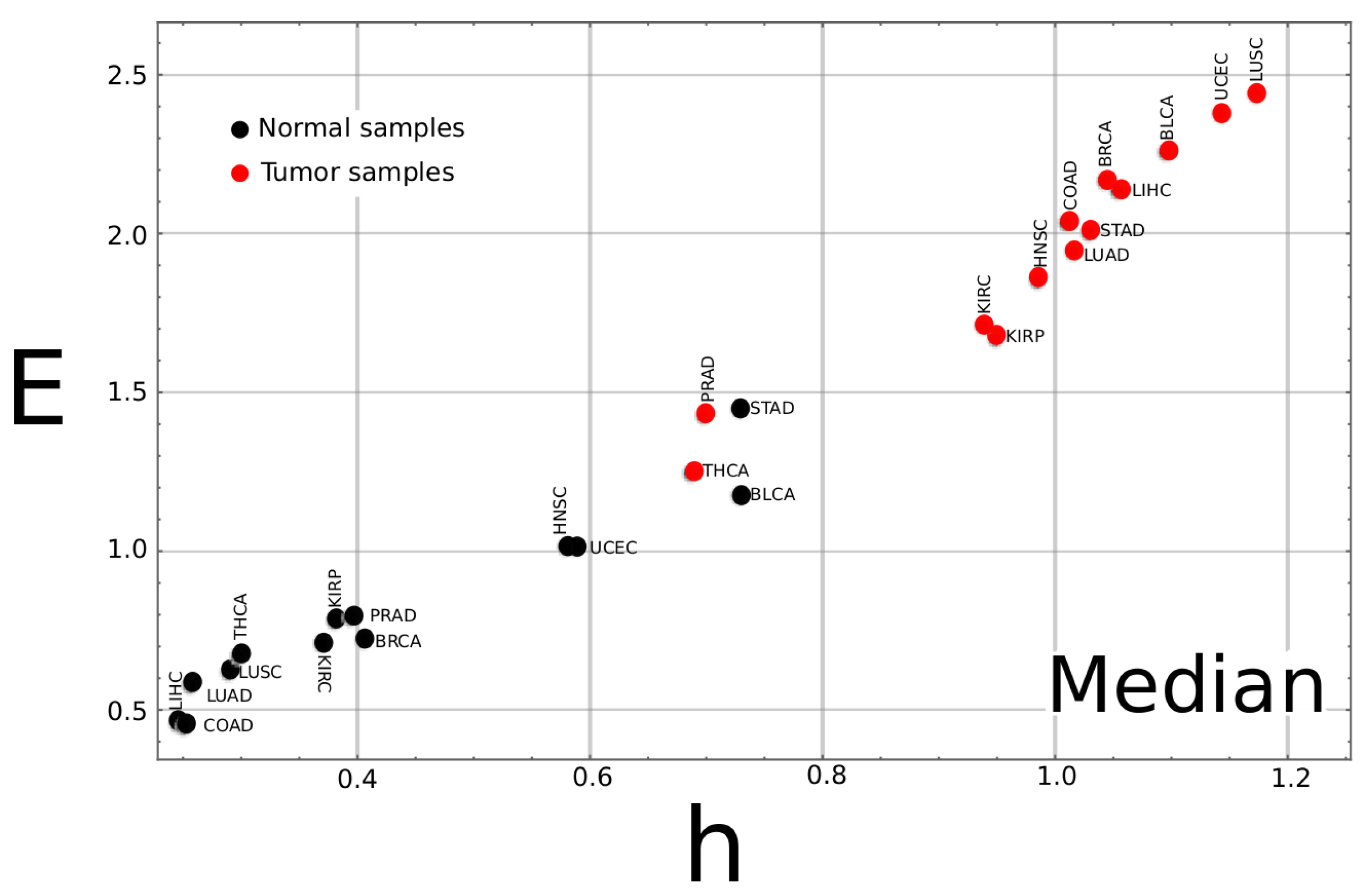
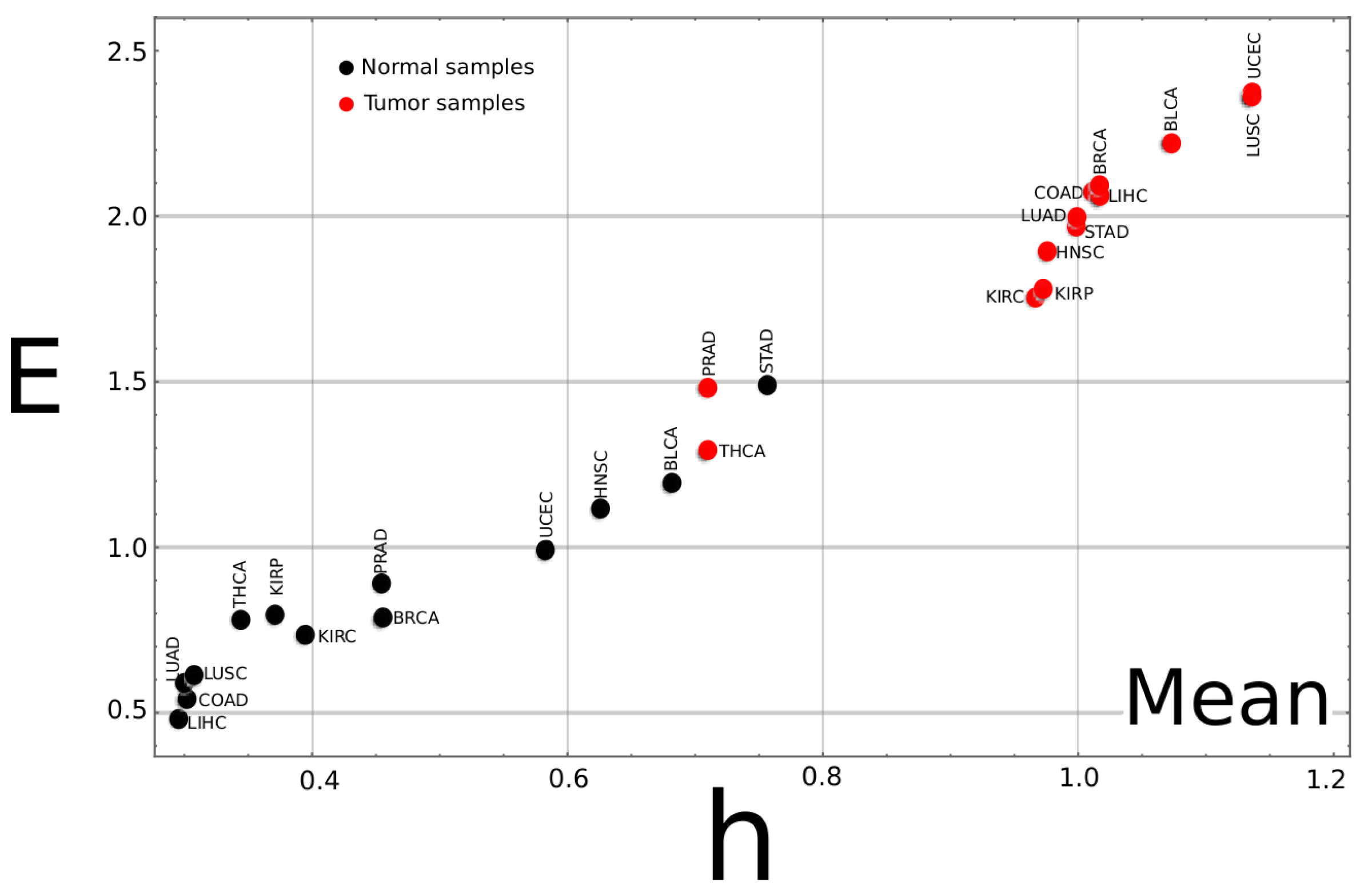
Appendix A.2. Complexity–Entropy Map for the Median Values of All Studied Cancer Types
Appendix A.3. Complexity–Entropy map for All Studied Cancer Types
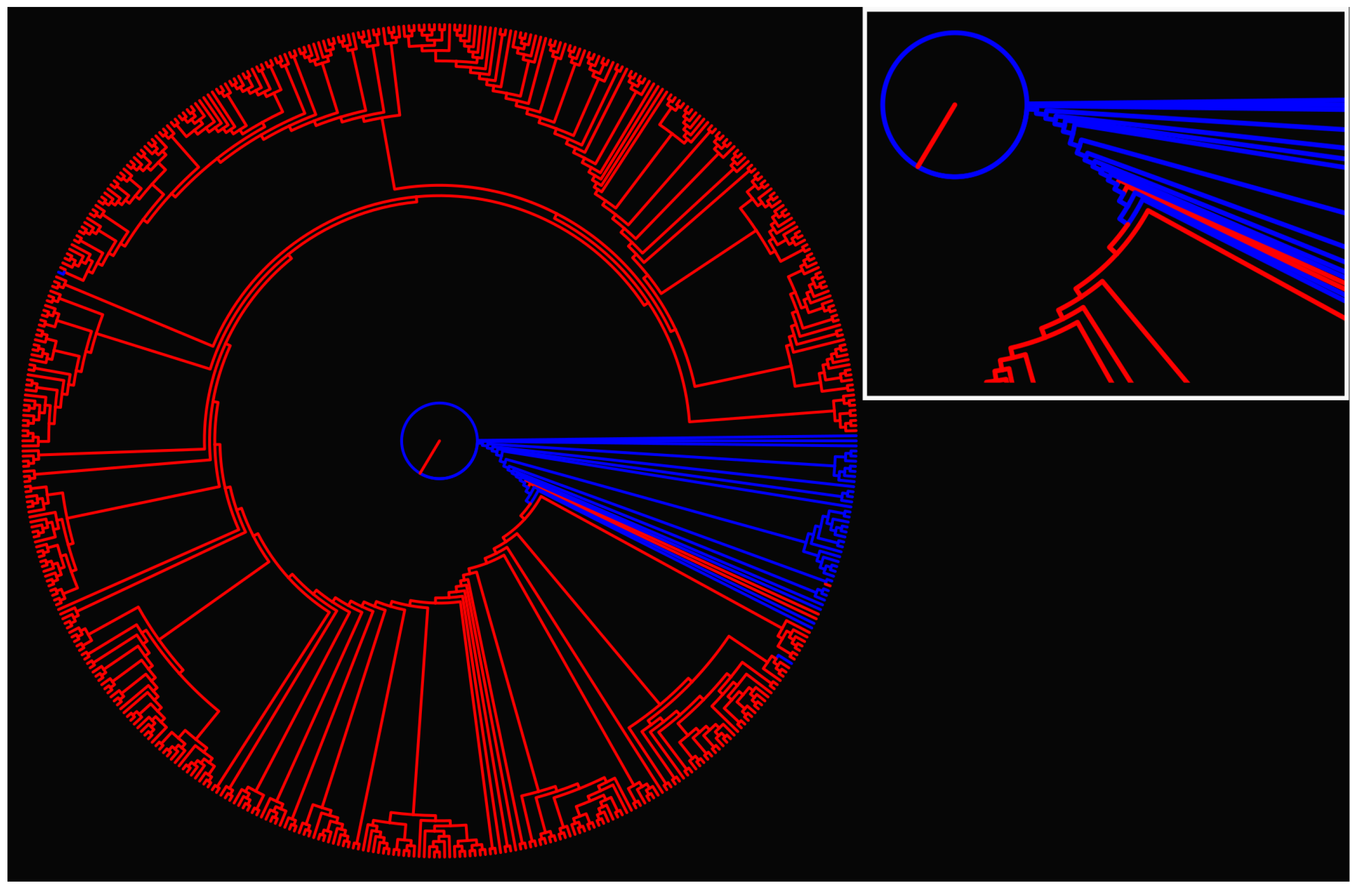
Appendix A.4. Dendrogram for All Studied Cancer Types
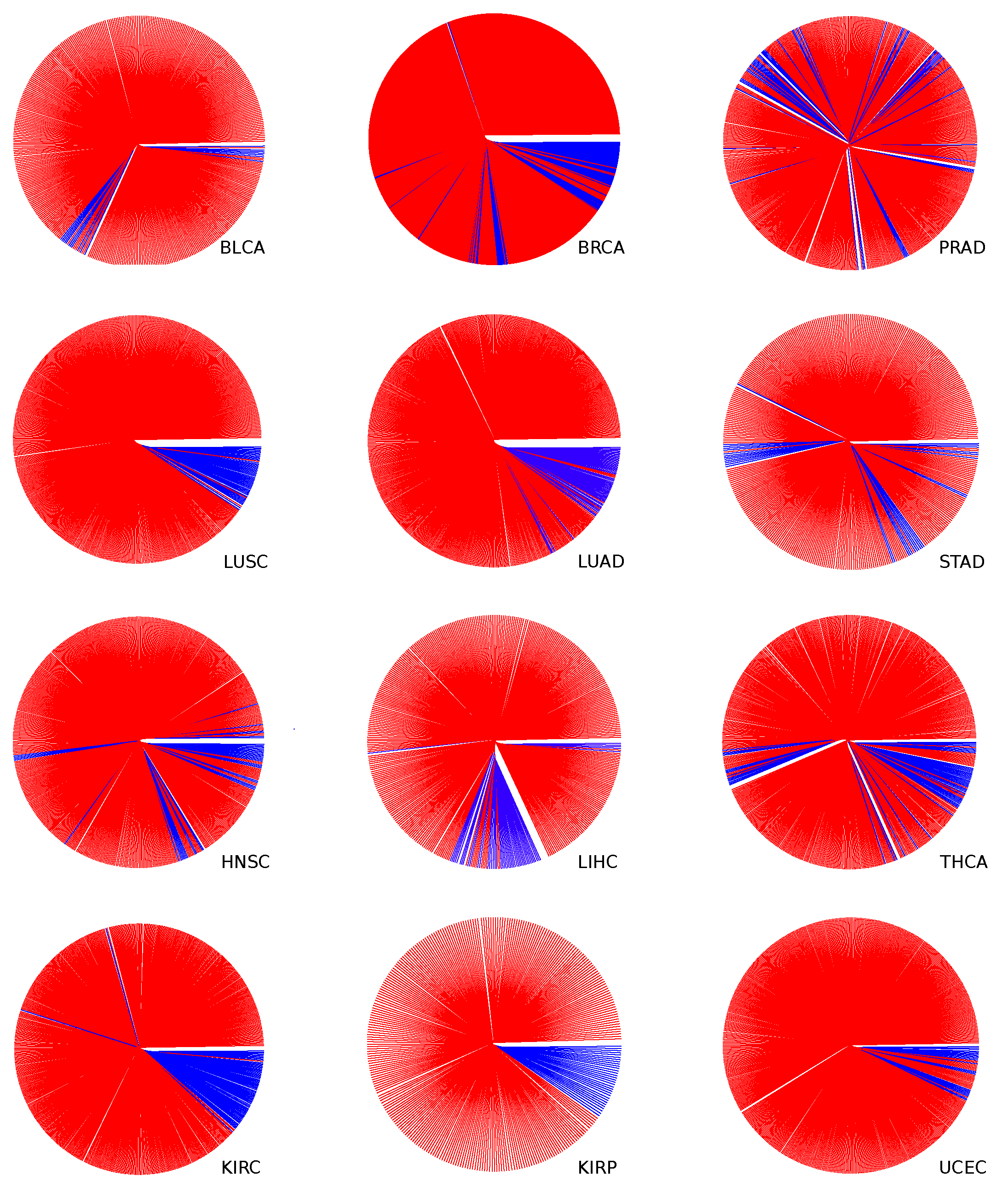
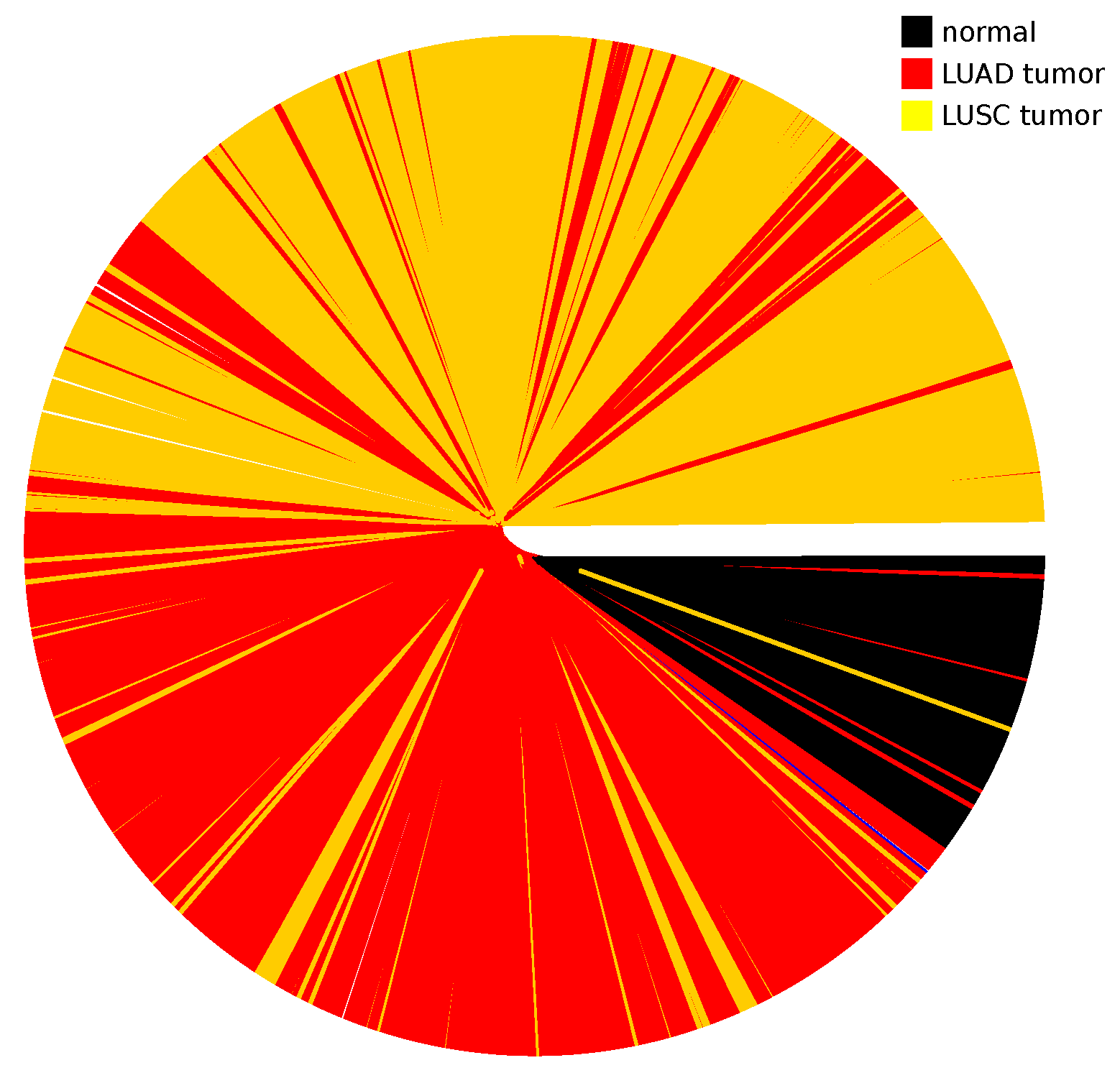
Appendix A.5. Dendrogram for LUAD and LUSC Cancer Types
References
- Crutchfield, J.P. Between order and chaos. Nat. Phys. 2012, 8, 17–24. [Google Scholar] [CrossRef]
- Montemuro, M.A.; Zanette, D. Towards the quantification of the semnatic information encoded in written language. Adv. Complex. Syst. 2010, 13, 135–153. [Google Scholar] [CrossRef]
- Amancio, D.R.; Atmann, E.G.; Rybski, D.; Oliveira, O.N.; da Costa, F.L. Probing the statistical properties of unknown texts: Application to the Voynich manuscripts. PLoS ONE 2013, 8, e67310. [Google Scholar] [CrossRef] [PubMed]
- Estevez-Rams, E.; Mesa-Rodriguez, A.; Estevez-Moya, D. Complexity–entropy analysis at different levels of organisation in written language. PLoS ONE 2019, 14, e0214863. [Google Scholar] [CrossRef]
- Sigaki, H.Y.D.; Perc, M.; Ribeiro, H.V. History of art painting through the lens of entropy and complexity. Proc. Natl. Acad. Sci. USA 2018, 115, e8585–e8594. [Google Scholar] [CrossRef]
- Daikoku, T. Neurophysiological markers of statistical learning in music and language: Hierarchy, entropy, and uncertainty. Brain Sci. 2018, 8, 114. [Google Scholar] [CrossRef]
- Farach, M.; Noordewier, M.; Savari, S.; Shepp, L.; Wyner, A. On the entropy of DNA: Algorithms and measurements based on memory and rapid convergence. In Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 14 July 1995; pp. 48–57. [Google Scholar]
- Schmitt, A.O.; Herzel, H. Estimating the Entropy of DNA Sequences. J. Theor. Biol. 1997, 188, 369–377. [Google Scholar] [CrossRef]
- Weiss, O.; Jiménez-Montaño, M.A.; Herzel, H. Information content of protein sequences. J. Theor. Biol. 2000, 206, 379–386. [Google Scholar] [CrossRef]
- Vinga, S.; Ameida, J.S. Rényi continuous entropy of DNA sequences. J. Theor. Biol. 2004, 231, 377–388. [Google Scholar] [CrossRef] [PubMed]
- Hariri, A.; Weber, B.; Olmstead, J. On the validity of Shannon-information calculations for molecular biological sequence. J. Theor. Biol. 1990, 147, 235–254. [Google Scholar] [CrossRef] [PubMed]
- Shekin, P.S.; Erman, B.; Mastrandea, L.D. Information-theoretical entropy as a measure of sequence variability. Proteins 1991, 11, 297. [Google Scholar] [CrossRef] [PubMed]
- Lipshutz, R.J.; Morris, D.; Chee, M.; Hubbell, E.; Kozal, M.J.; Shah, N.; Fodor, S.P. Using oligonucleotide probe arrays to access genetic diversity. Biotechniques 1995, 19, 442–447. [Google Scholar] [PubMed]
- Schena, M.; Shalon, D.; Davis, R.W.; Brown, P.O. Quantitative monitoring of gene expression patterns with a complementary DNA microarray. Science 1995, 270, 467–470. [Google Scholar] [CrossRef] [PubMed]
- Lockhart, D.J.; Winzeler, E.A. Genomics, gene expression and DNA arrays. Nature 2000, 405, 827–836. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, A.; Williams, B.A.; McCue, K.; Schaeffer, L.; Wold, B. Mapping and quantifying mammalian transcriptomes by RNA-Seq. Nat. Methods 2008, 5, 621–628. [Google Scholar] [CrossRef] [PubMed]
- Lowe, R.; Shirley, N.; Bleackley, M.; Dolan, S.; Shafee, T. Transcriptomics technologies. PLoS Comput. Biol. 2017, 13, e1005457. [Google Scholar] [CrossRef]
- Sherlock, G. Analysis of large-scale gene expression data. Curr. Opin. Immunol. 2000, 12, 201–205. [Google Scholar] [CrossRef]
- Jiang, D.; Tang, C.; Zhang, A. Cluster analysis for gene expression data: A survey. IEEE Trans. Knowl. Data Eng. 2004, 16, 1370–1386. [Google Scholar] [CrossRef]
- Madeira, S.C.; Oliveira, A.L. Biclustering algorithms for biological data analysis: A survey. IEEE/ACM Trans. Comput. Biol. Bioinform. 2004, 1, 24–45. [Google Scholar] [CrossRef]
- Almugren, N.; Alshamlan, H. A survey on hybrid feature selection methods in microarray gene expression data for cancer classification. IEEE Access 2019, 7, 78533–78548. [Google Scholar] [CrossRef]
- Dudoit, S.; Yang, Y.H.; Callow, M.J.; Speed, T.P. Statistical methods for identifying differentially expressed genes in replicated cDNA microarray experiments. Stat. Sin. 2002, 12, 111–139. [Google Scholar]
- Mar, J.C. The rise of the distributions: Why non-normality is important for understanding the transcriptome and beyond. Biophys. Rev. 2019, 11, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Daoud, M.; Mayo, M. A survey of neural network-based cancer prediction models from microarray data. Artif. Intell. Med. 2019, 97, 204–214. [Google Scholar] [CrossRef]
- Danaee, P.; Ghaeini, R.; Hendrix, D.A. A deep learning approach for cancer detection and relevant gene identification. In Proceedings of the Pacific Symposium on Biocomputing 2017, Kohala Coast, HI, USA, 4–8 January 2017; pp. 219–229. [Google Scholar]
- Alter, O.; Brown, P.O.; Botstein, D. Singular value decomposition for genome-wide expression data processing and modeling. Proc. Natl. Acad. Sci. USA 2000, 97, 10101–10106. [Google Scholar] [CrossRef]
- Tomfohr, J.; Lu, J.; Kepler, T.B. Pathway level analysis of gene expression using singular value decomposition. BMC Bioinform. 2005, 6, 1–11. [Google Scholar] [CrossRef]
- Aziz, R.; Verma, C.K.; Srivastava, N. A novel approach for dimension reduction of microarray. Comput. Biol. Chem. 2017, 71, 161–169. [Google Scholar] [CrossRef]
- Li, Z.; Xie, W.; Liu, T. Efficient feature selection and classification for microarray data. PLoS ONE 2018, 13, e0202167. [Google Scholar] [CrossRef]
- Cilia, N.D.; De Stefano, C.; Fontanella, F.; Raimondo, S.; Scotto di Freca, A. An experimental comparison of feature-selection and classification methods for microarray datasets. Information 2019, 10, 109. [Google Scholar] [CrossRef]
- Alon, U.; Barkai, N.; Notterman, D.A.; Gish, K.; Ybarra, S.; Mack, D.; Levine, A.J. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. Natl. Acad. Sci. USA 1999, 96, 6745–6750. [Google Scholar] [CrossRef]
- Alizadeh, A.A.; Eisen, M.B.; Davis, R.E.; Ma, C.; Lossos, I.S.; Rosenwald, A.; Staudt, L.M. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature 2000, 403, 503–511. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Richards, W.G.; Staunton, J.; Li, C.; Monti, S.; Vasa, P.; Meyerson, M. Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses. Proc. Natl. Acad. Sci. USA 2001, 98, 13790–13795. [Google Scholar] [CrossRef]
- Dudoit, S.; Fridlyand, J.; Speed, T.P. Comparison of discrimination methods for the classification of tumors using gene expression data. J. Am. Stat. Assoc. 2002, 97, 77–87. [Google Scholar] [CrossRef]
- Dettling, M.; Bühlmann, P. Boosting for tumor classification with gene expression data. Bioinformatics 2003, 19, 1061–1069. [Google Scholar] [CrossRef] [PubMed]
- Quackenbush, J. Microarray analysis and tumor classification. N. Engl. J. Med. 2006, 354, 2463–2472. [Google Scholar] [CrossRef] [PubMed]
- Reyna, M.A.; Haan, D.; Paczkowska, M.; Verbeke, L.P.; Vazquez, M.; Kahraman, A.; Raphael, B.J. Pathway and network analysis of more than 2500 whole cancer genomes. Nat. Commun. 2020, 11, 729. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Li, M.; Vitanyi, P. An Introduction to Kolmogorov Complexity and Its Applications; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Regularities unseen, randomness observed: Levels of entropy convergence. Chaos Interdiscip. J. Nonlinear Sci. 2003, 13, 25–54. [Google Scholar] [CrossRef]
- Schürmann, T.; Grassberger, P. Entropy estimation of symbol sequences. Chaos Interdiscip. J. Nonlinear Sci. 1996, 6, 414–427. [Google Scholar] [CrossRef]
- Feldman, D.P.; McTague, C.S.; Crutchfield, J.P. The organization of intrinsic computation: Complexity–entropy diagrams and the diversity of natural information processing. Chaos Interdiscip. J. Nonlinear Sci. 2008, 18, 043106. [Google Scholar] [CrossRef]
- Li, M.; Chen, X.; Li, X.; Ma, B.; Vitányi, P.M. The similarity metric. IEEE Trans. Inf. Theory 2004, 50, 3250–3264. [Google Scholar] [CrossRef]
- Lesne, A.; Blanc, J.L.; Pezard, L. Entropy estimation of very short symbolic sequences. Phys. Rev. E 2009, 79, 046208. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Ziv, J. Coding theorems for individual sequences. IEEE Trans. Inf. Theory 1978, 24, 405–412. [Google Scholar] [CrossRef]
- Amigó, J.M.; Kennel, M.B. Variance estimators for the Lempel–Ziv entropy rate estimator. Chaos Interdiscip. J. Nonlinear Sci. 2006, 16, 043102. [Google Scholar] [CrossRef]
- Estevez-Rams, E.; Lora-Serrano, R.; Nunes, C.A.J.; Aragón-Fernández, B. Lempel–Ziv complexity analysis of one-dimensional, cellular automata. Chaos Interdiscip. J. Nonlinear Sci. 2015, 25, 123106. [Google Scholar] [CrossRef]
- Estevez-Rams, E.; Estevez-Moya, D.; Garcia-Medina, K.; Lora-Serrano, R. Computational capabilities at the edge of chaos for one-dimensional, system undergoing continuous transitions. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 043105. [Google Scholar] [CrossRef]
- Melchert, O.; Hartmann, A.K. Analysis of the phase transition in the two-dimensional Ising ferromagnet using a Lempel–Ziv string-parsing scheme and black-box data-compression utilities. Phys. Rev. E 2015, 91, 023306. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Three approaches to the quantitative definition of information. Probl. Inf. Transm. 1965, 1, 1–7. [Google Scholar] [CrossRef]
- Felsenstein, J. Phylogenetic inference package (PHYLIP), version 3.2. Cladistics 1989, 5, 164–166. [Google Scholar]
- Mootha, V.K.; Lindgren, C.M.; Eriksson, K.F.; Subramanian, A.; Sihag, S.; Lehar, J.; Groop, L.C. PGC-1α-responsive genes involved in oxidative phosphorylation are coordinately downregulated in human diabetes. Nat. Genet. 2003, 34, 267–273. [Google Scholar] [CrossRef]
- Weinberg, R.A.; Hanahan, D. The hallmarks of cancer. Cell 2000, 100, 57–70. [Google Scholar]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]
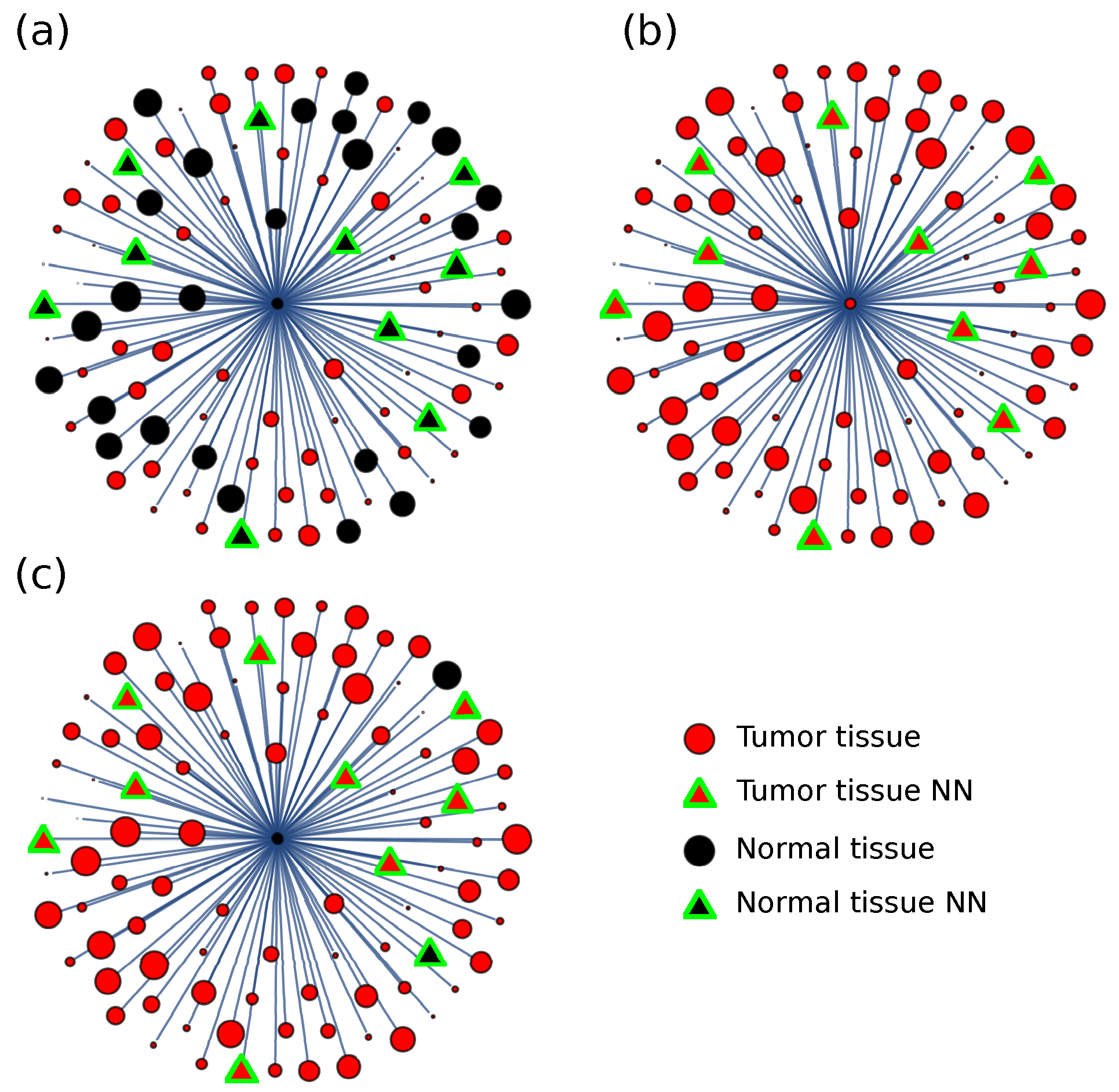
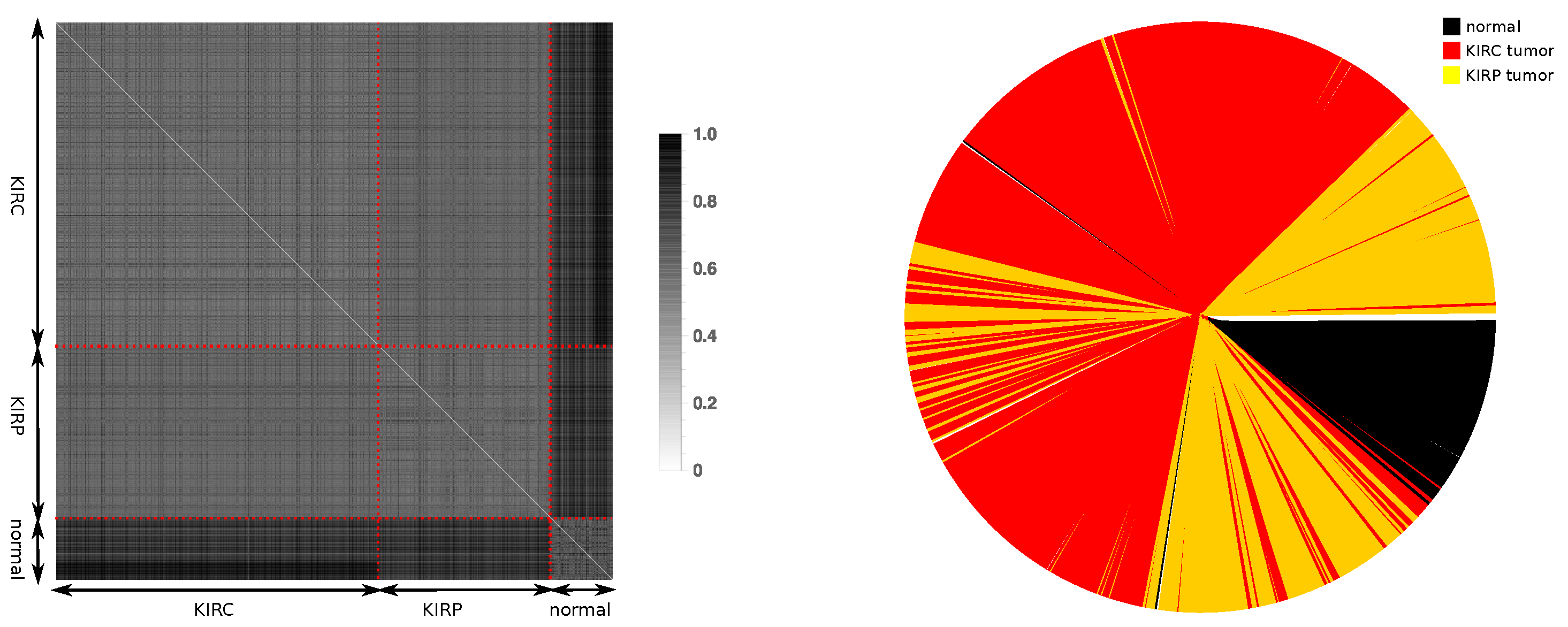
| Mean | Median | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tumor | Normal | Tumor | Normal | |||||||
| h | E | h | E | d | h | E | h | E | d | |
| BLCA | 1.073 | 2.222 | 0.683 | 1.192 | 1.101 | 1.098 | 2.260 | 0.730 | 1.178 | 1.143 |
| BRCA | 1.017 | 2.097 | 0.456 | 0.785 | 1.426 | 1.045 | 2.169 | 0.408 | 0.722 | 1.581 |
| COAD | 1.012 | 2.067 | 0.304 | 0.537 | 1.686 | 1.013 | 2.037 | 0.251 | 0.460 | 1.751 |
| HNSC | 0.975 | 1.891 | 0.626 | 1.119 | 0.847 | 0.985 | 1.864 | 0.583 | 1.016 | 0.939 |
| KIRC | 0.967 | 1.754 | 0.395 | 0.733 | 1.170 | 0.941 | 1.706 | 0.371 | 0.705 | 1.152 |
| KIRP | 0.973 | 1.772 | 0.372 | 0.797 | 1.145 | 0.950 | 1.682 | 0.384 | 0.790 | 1.057 |
| LIHC | 1.018 | 2.060 | 0.295 | 0.480 | 1.738 | 1.057 | 2.138 | 0.249 | 0.469 | 1.854 |
| LUAD | 0.999 | 1.964 | 0.301 | 0.581 | 1.549 | 1.017 | 1.946 | 0.259 | 0.584 | 1.559 |
| LUSC | 1.137 | 2.382 | 0.308 | 0.611 | 1.955 | 1.172 | 2.439 | 0.291 | 0.620 | 2.021 |
| PRAD | 0.712 | 1.481 | 0.454 | 0.896 | 0.639 | 0.700 | 1.435 | 0.394 | 0.796 | 0.708 |
| STAD | 1.000 | 1.989 | 0.757 | 1.486 | 0.558 | 1.031 | 2.010 | 0.730 | 1.449 | 0.636 |
| THCA | 0.710 | 1.296 | 0.346 | 0.780 | 0.632 | 0.691 | 1.246 | 0.301 | 0.678 | 0.689 |
| UCEC | 1.138 | 2.382 | 0.585 | 1.002 | 1.486 | 1.144 | 2.378 | 0.589 | 1.012 | 1.474 |
| Mean | Median | |||
|---|---|---|---|---|
| Cancer | Normal | Cancer | Normal | |
| BLCA | 0.917 | 0.947 | 0.903 | 0.947 |
| BRCA | 0.912 | 0.937 | 0.912 | 0.937 |
| COAD | 0.979 | 0.976 | 0.983 | 0.976 |
| HNSC | 0.880 | 0.750 | 0.934 | 0.750 |
| KIRC | 0.983 | 0.958 | 0.991 | 0.958 |
| KIRP | 0.979 | 1.000 | 0.990 | 1.000 |
| LIHC | 0.933 | 1.000 | 0.930 | 1.000 |
| LUAD | 0.933 | 0.983 | 0.938 | 0.983 |
| LUSC | 0.972 | 1.000 | 0.966 | 1.000 |
| PRAD | 0.681 | 0.731 | 0.735 | 0.731 |
| STAD | 0.723 | 0.656 | 0.723 | 0.656 |
| THCA | 0.872 | 0.914 | 0.916 | 0.879 |
| UCEC | 0.987 | 1.000 | 0.985 | 1.000 |
| Cancer | Normal | |
|---|---|---|
| BLCA | 0.997 | 0.210 |
| BRCA | 0.995 | 0.821 |
| COAD | 1.000 | 0.872 |
| HNSC | 0.996 | 0.454 |
| KIRC | 0.998 | 0.972 |
| KIRP | 1.000 | 0.969 |
| LIHC | 0.973 | 0.760 |
| LUAD | 0.994 | 0.847 |
| LUSC | 0.998 | 0.959 |
| PRAD | 0.994 | 0.404 |
| STAD | 0.987 | 0.719 |
| THCA | 0.986 | 0.845 |
| UCEC | 0.996 | 0.609 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesa-Rodríguez, A.; Gonzalez, A.; Estevez-Rams, E.; Valdes-Sosa, P.A. Cancer Segmentation by Entropic Analysis of Ordered Gene Expression Profiles. Entropy 2022, 24, 1744. https://doi.org/10.3390/e24121744
Mesa-Rodríguez A, Gonzalez A, Estevez-Rams E, Valdes-Sosa PA. Cancer Segmentation by Entropic Analysis of Ordered Gene Expression Profiles. Entropy. 2022; 24(12):1744. https://doi.org/10.3390/e24121744
Chicago/Turabian StyleMesa-Rodríguez, Ania, Augusto Gonzalez, Ernesto Estevez-Rams, and Pedro A. Valdes-Sosa. 2022. "Cancer Segmentation by Entropic Analysis of Ordered Gene Expression Profiles" Entropy 24, no. 12: 1744. https://doi.org/10.3390/e24121744
APA StyleMesa-Rodríguez, A., Gonzalez, A., Estevez-Rams, E., & Valdes-Sosa, P. A. (2022). Cancer Segmentation by Entropic Analysis of Ordered Gene Expression Profiles. Entropy, 24(12), 1744. https://doi.org/10.3390/e24121744






