Spike Spectra for Recurrences
Abstract
1. Introduction
2. Method
3. Results
- (1)
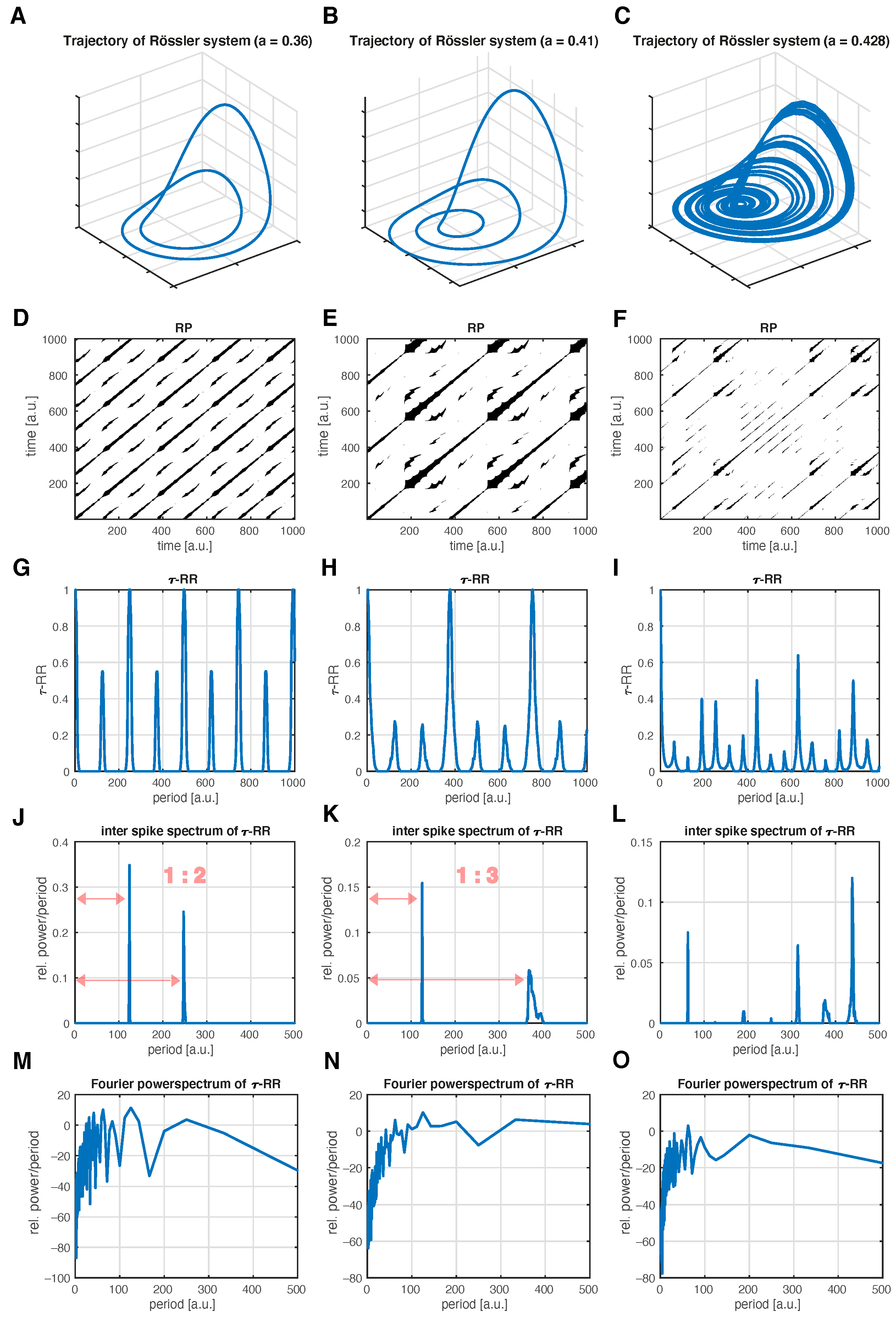
- Compute an RP of the trajectory of the system, Equation (1). If only univariate data are available, perform a state space reconstruction for obtaining the trajectory first.
- (2)
- Compute the -RR of the RP, as shown in Equation (2).
- (3)
- Transform the -RR into the proposed inter-spike spectrum, see Section 2.
3.1. Period Estimation for Different Dynamics in the Rössler System
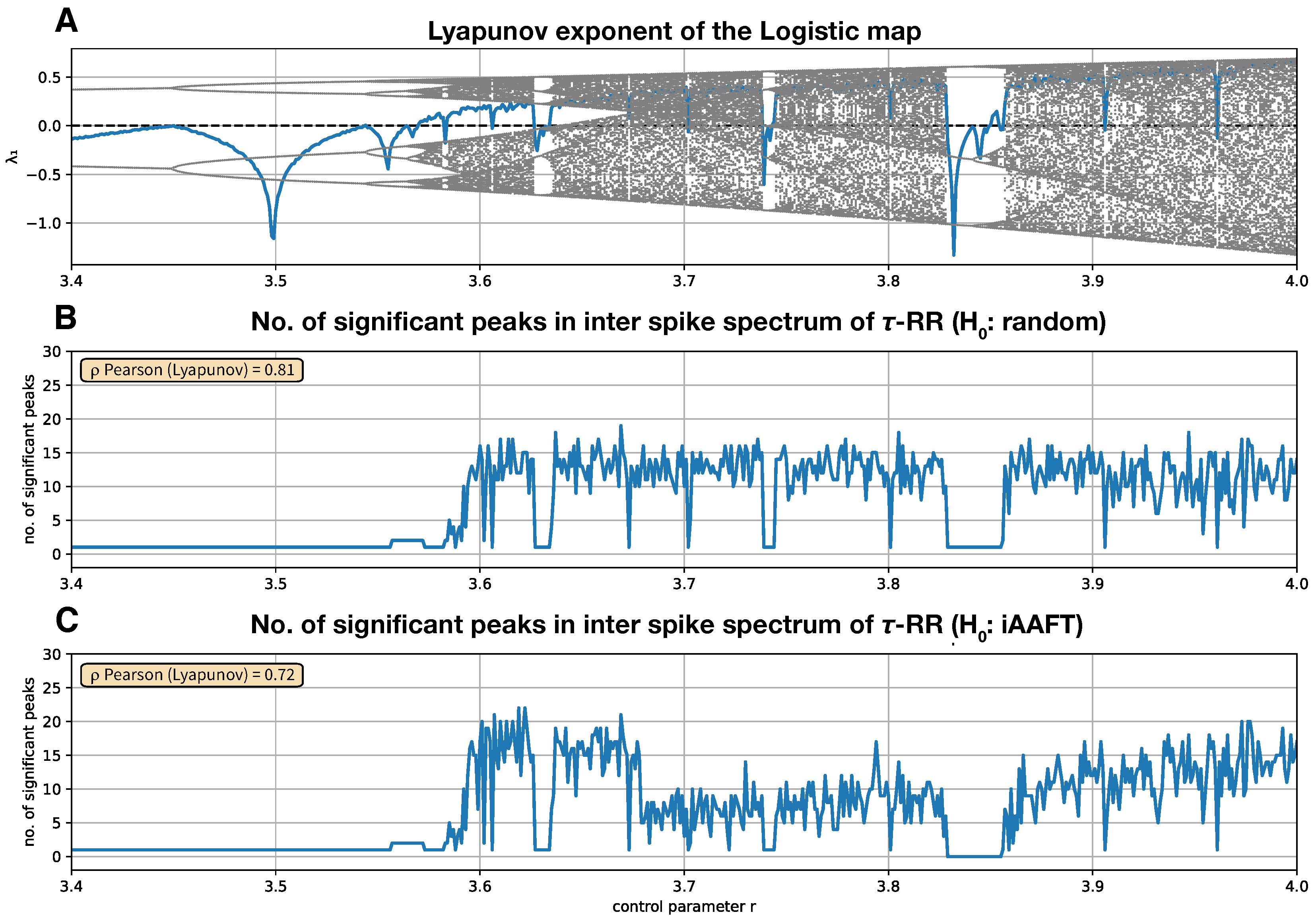
3.2. Bifurcations in the Logistic Map
- (1)
- A time series of length is computed with a random initial condition , neglecting the first 1000 samples as transients;
- (2)
- (3)
- The time series and its iAAFT surrogates are embedded in a 2-dimensional state space using a time delay of unity;
- (4)
- The two-dimensional trajectories RPs, as shown in Equation (1), are computed under a threshold ,
- (5)
- -RR, as shown in Equation (2), is computed from the RP of the signal and from the RPs of the surrogates;
- (6)
- Inter-spike spectra are obtained from -RR of the signal and from the -RRs of the surrogates, as can be seen in Section 2;
- (7)
- Finally, from the distribution of the surrogate inter-spike spectra, the 95th percentile is computed. The peaks of the inter-spike spectrum of the signal which exceed this percentile are counted.
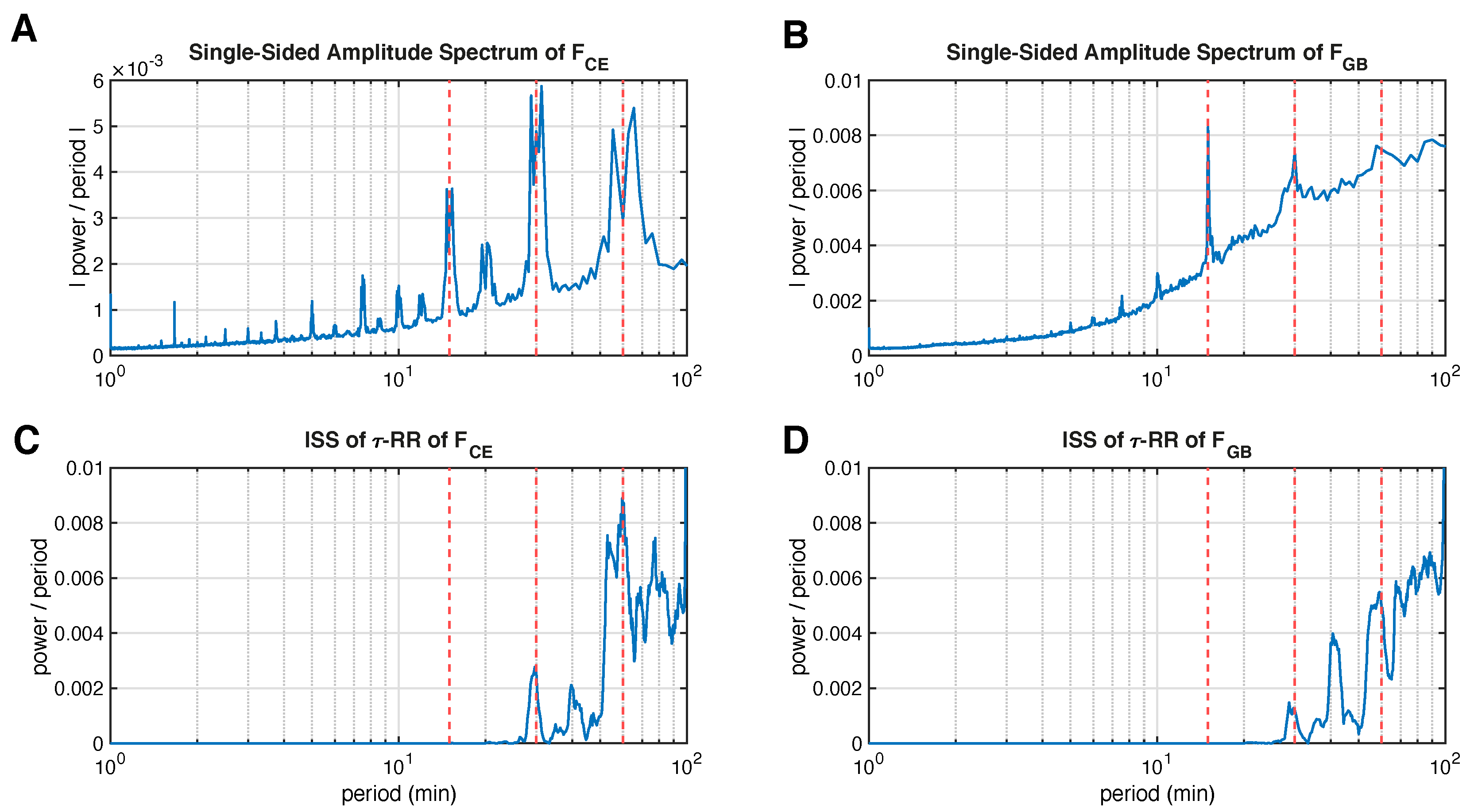
3.3. Inter-Spike Spectra of Power Grid Frequency Data
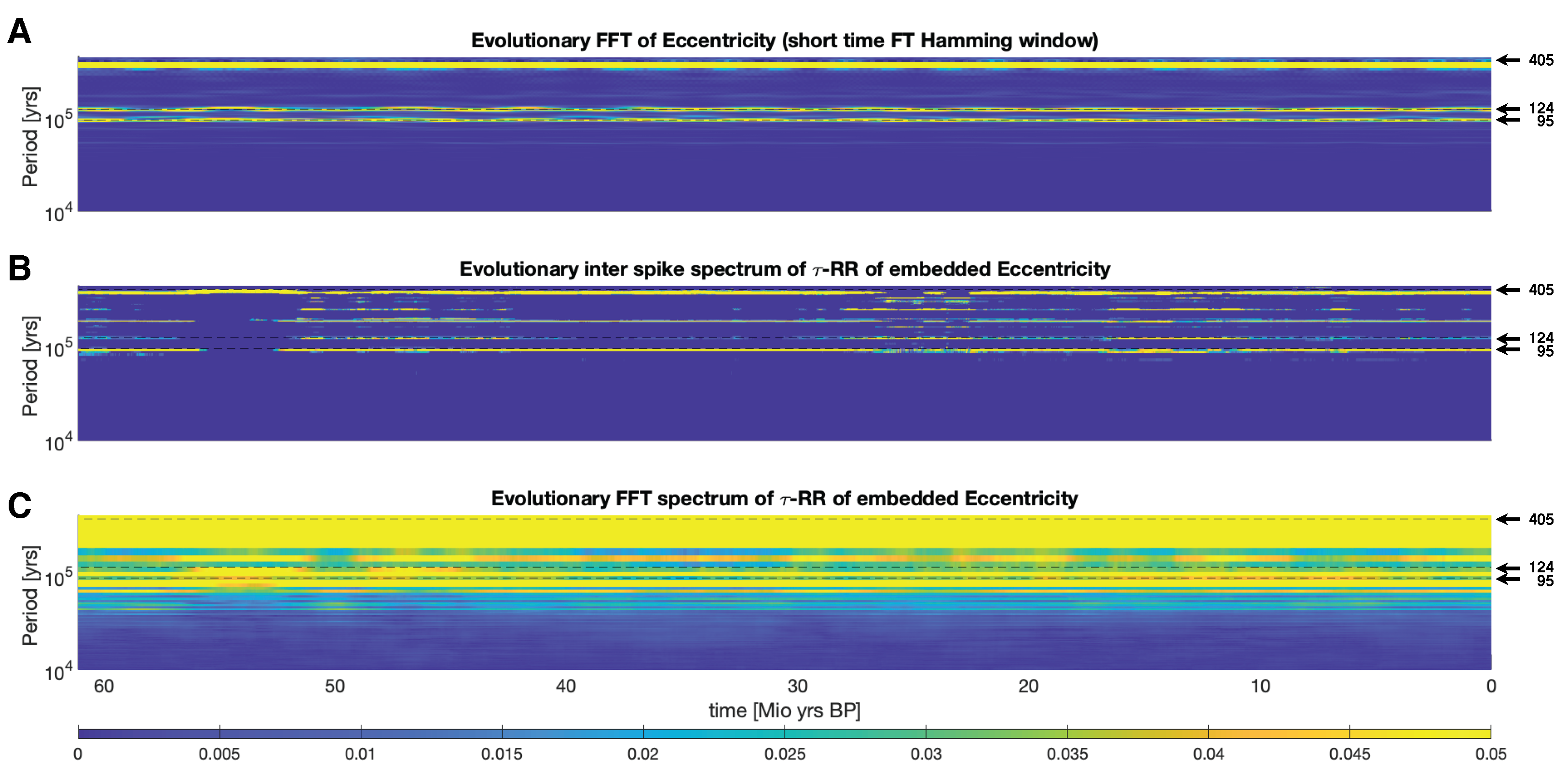
3.4. Evolutionary Inter-Spike Spectra of Earth’s Orbit Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Exemplary Models
Appendix A.1. Lorenz System
Appendix A.2. Rössler System
Appendix B. Power Grid Frequency Time Series


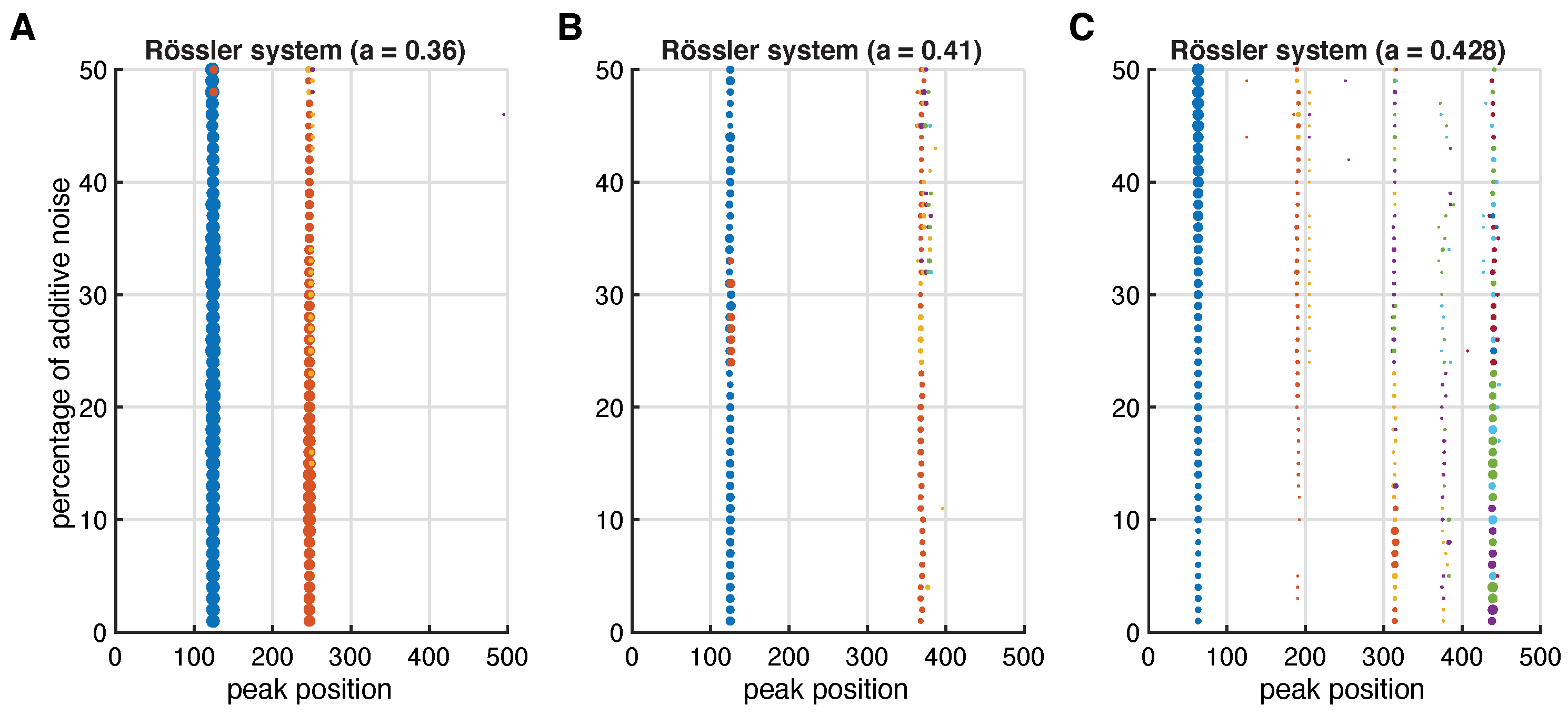
Appendix C. Inter-Spike Spectra for Noisy R össler System



Appendix D. Regularizationparameters for Different Sparse Regression Techniques

References
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence Plots for the Analysis of Complex Systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Marwan, N. A Historical Review of Recurrence Plots. Eur. Phys. J. Spec. Top. 2008, 164, 3–12. [Google Scholar] [CrossRef]
- Webber, C.L., Jr.; Marwan, N. Recurrence Quantification Analysis—Theory and Best Practices; Springer: Cham, Switzerland, 2015; p. 421. [Google Scholar] [CrossRef]
- Dummer, B.; Wieland, S.; Lindner, B. Self-consistent determination of the spike-train power spectrum in a neural network with sparse connectivity. Front. Comput. Neurosci. 2014, 8, 104. [Google Scholar] [CrossRef] [PubMed]
- Orcioni, S.; Paffi, A.; Apollonio, F.; Liberti, M. Revealing Spectrum Features of Stochastic Neuron Spike Trains. Mathematics 2020, 8, 1011. [Google Scholar] [CrossRef]
- Marwan, N.; Wessel, N.; Meyerfeldt, U.; Schirdewan, A.; Kurths, J. Recurrence Plot Based Measures of Complexity and its Application to Heart Rate Variability Data. Phys. Rev. E 2002, 66, 026702. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Goswami, B.; Hirata, Y.; Eroglu, D.; Merz, B.; Kurths, J.; Marwan, N. Recurrence analysis of extreme event-like data. Nonlinear Process. Geophys. 2021, 28, 213–229. [Google Scholar] [CrossRef]
- Kajikawa, Y.; Hackett, T.A. Entropy analysis of neuronal spike train synchrony. J. Neurosci. Methods 2005, 149, 90–93. [Google Scholar] [CrossRef]
- Canale, A.; Lijoi, A.; Nipoti, B.; Prünster, I. Inner spike and slab Bayesian nonparametric models. Econom. Stat. 2021. [Google Scholar] [CrossRef]
- Kraemer, K.H.; Donner, R.V.; Heitzig, J.; Marwan, N. Recurrence threshold selection for obtaining robust recurrence characteristics in different embedding dimensions. Chaos: Interdiscip. J. Nonlinear Sci. 2018, 28, 085720. [Google Scholar] [CrossRef]
- March, T.K.; Chapman, S.C.; Dendy, R.O. Recurrence plot statistics and the effect of embedding. Phys. D 2005, 200, 171–184. [Google Scholar] [CrossRef]
- Baptista, M.S.; Ngamga, E.J.; Pinto, P.R.F.; Brito, M.; Kurths, J. Kolmogorov-Sinai entropy from recurrence times. Phys. Lett. A 2010, 374, 1135–1140. [Google Scholar] [CrossRef]
- Kraemer, K.H.; Marwan, N. Border effect corrections for diagonal line based recurrence quantification analysis measures. Phys. Lett. A 2019, 383, 125977. [Google Scholar] [CrossRef]
- Marwan, N.; Kurths, J. Nonlinear analysis of bivariate data with cross recurrence plots. Phys. Lett. A 2002, 302, 299–307. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Marwan, N. The Wiener–Khinchin theorem and recurrence quantification. Phys. Lett. A 2008, 372, 6622–6626. [Google Scholar] [CrossRef]
- Kraemer, K.H.; Datseris, G.; Kurths, J.; Kiss, I.Z.; Ocampo-Espindola, J.L.; Marwan, N. A unified and automated approach to attractor reconstruction. New J. Phys. 2021, 23, 033017. [Google Scholar] [CrossRef]
- Schild, D. An Efficient Method for the Fourier Transform of a Neuronal Spike Train. Int. J. Neurosci. 1982, 17, 179–182. [Google Scholar] [CrossRef]
- Córdoba, A. Dirac combs. Lett. Math. Phys. 1989, 17, 191–196. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London. Ser. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Biagetti, G.; Crippa, P.; Orcioni, S.; Turchetti, C. Homomorphic Deconvolution for MUAP Estimation From Surface EMG Signals. IEEE J. Biomed. Health Inform. 2017, 21, 328–338. [Google Scholar] [CrossRef]
- Bracewell, R.N.; Bracewell, R.N. The Fourier Transform and its Applications; McGraw-Hill: New York, NY, USA, 1986; Volume 31999. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection Via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D: Nonlinear Phenom. 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Gorjão, L.R.; Anvari, M.; Kantz, H.; Beck, C.; Witthaut, D.; Timme, M.; Schäfer, B. Data-driven model of the power-grid frequency dynamics. IEEE Access 2020, 8, 43082–43097. [Google Scholar] [CrossRef]
- Anvari, M.; Gorjão, L.R.; Timme, M.; Witthaut, D.; Schäfer, B.; Kantz, H. Stochastic properties of the frequency dynamics in real and synthetic power grids. Phys. Rev. Res. 2020, 2, 013339. [Google Scholar] [CrossRef]
- Meyer, P.G.; Anvari, M.; Kantz, H. Identifying characteristic time scales in power grid frequency fluctuations with DFA. Chaos: Interdiscip. J. Nonlinear Sci. 2020, 30, 013130. [Google Scholar] [CrossRef]
- Weißbach, T.; Welfonder, E. High frequency deviations within the European power system: Origins and proposals for improvement. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–6. [Google Scholar]
- Laskar, J.; Fienga, A.; Gastineau, M.; Manche, H. La2010: A new orbital solution for the long-term motion of the Earth. Astron. Astrophys. 2011, 532, A89. [Google Scholar] [CrossRef]
- Laskar, J.; Robutel, P.; Joutel, F.; Gastineau, M.; Correia, A.C.M.; Levrard, B. A long-term numerical solution for the insolation quantities of the Earth. Astron. Astrophys. 2004, 428, 261–285. [Google Scholar] [CrossRef]
- Westerhold, T.; Marwan, N.; Drury, A.J.; Liebrand, D.; Agnini, C.; Anagnostou, E.; Barnet, J.S.K.; Bohaty, S.M.; De Vleeschouwer, D.; Florindo, F.; et al. An astronomically dated record of Earth’s climate and its predictability over the last 66 million years. Science 2020, 369, 1383–1387. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, K.H.; Gelbrecht, M.; Pavithran, I.; Sujith, R.I.; Marwan, N. Optimal state space reconstruction via Monte Carlo decision tree search. Nonlinear Dyn. 2022, 108, 1525–1545. [Google Scholar] [CrossRef]
- Hegger, R.; Kantz, H. Improved false nearest neighbor method to detect determinism in time series data. Phys. Rev. E 1999, 60, 4970–4973. [Google Scholar] [CrossRef]
- Pecora, L.M.; Moniz, L.; Nichols, J.; Carroll, T.L. A unified approach to attractor reconstruction. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 013110. [Google Scholar] [CrossRef]
- Datseris, G. DynamicalSystems.jl: A Julia software library for chaos and nonlinear dynamics. J. Open Source Softw. 2018, 3, 598. [Google Scholar] [CrossRef]
- Rackauckas, C.; Nie, Q. Differentialequations.jl–a performant and feature-rich ecosystem for solving differential equations in julia. J. Open Res. Softw. 2017, 5, 15. [Google Scholar] [CrossRef]
- Zhang, S.; Widmann, D.; Barreira, D.S. JuliaOptimalTransport/OptimalTransport.jl: v0.3.19, Zenodo. 2022. Available online: https://zenodo.org/record/5920148#.Y3SbbORByUk (accessed on 16 November 2022).
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Rössler, O. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- National Grid, Frequency Data (2014–2018). Available online: https://power-grid-frequency.org/database/ (accessed on 25 July 2022).
- Haehne, H.; Schottler, J.; Waechter, M.; Peinke, J.; Kamps, O. The footprint of atmospheric turbulence in power grid frequency measurements. EPL (Europhys. Lett.) 2018, 121, 30001. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kraemer, K.H.; Hellmann, F.; Anvari, M.; Kurths, J.; Marwan, N. Spike Spectra for Recurrences. Entropy 2022, 24, 1689. https://doi.org/10.3390/e24111689
Kraemer KH, Hellmann F, Anvari M, Kurths J, Marwan N. Spike Spectra for Recurrences. Entropy. 2022; 24(11):1689. https://doi.org/10.3390/e24111689
Chicago/Turabian StyleKraemer, K. Hauke, Frank Hellmann, Mehrnaz Anvari, Jürgen Kurths, and Norbert Marwan. 2022. "Spike Spectra for Recurrences" Entropy 24, no. 11: 1689. https://doi.org/10.3390/e24111689
APA StyleKraemer, K. H., Hellmann, F., Anvari, M., Kurths, J., & Marwan, N. (2022). Spike Spectra for Recurrences. Entropy, 24(11), 1689. https://doi.org/10.3390/e24111689






