A Novel Fault Diagnosis Method for Rolling Bearing Based on Hierarchical Refined Composite Multiscale Fluctuation-Based Dispersion Entropy and PSO-ELM
Abstract
1. Introduction
- A novel fault feature extraction method based on HRCMFDE is proposed. The method quantifies the high-frequency and low-frequency features of the measured time series by introducing the hierarchical theory algorithm, which effectively overcomes the problem of high-frequency information loss caused by the coarse-grained process. Meanwhile, HRCMFDE maps each element of the time series to different classes and generates different fluctuation dispersion patterns, which not only has strong anti-noise capability but also avoids the defect of losing amplitude information.
- The performance of the proposed rolling bearing fault diagnosis method is verified using two typical rotating machinery fault datasets. The experimental results show that the proposed fault diagnosis method can not only accurately identify the fault types with varying loads, but also have a high fault identification effect even under load migration.
2. Methodologies
2.1. Feature Extraction
2.1.1. Multiscale Fluctuation-Based Dispersion Entropy (MFDE)
2.1.2. Refined Composite Multiscale Fluctuation-Based Dispersion Entropy (RCMFDE)
2.1.3. Hierarchical Refined Composite Multiscale Fluctuation-Based Dispersion Entropy (HRCMFDE)
- Basic Principle
- Parameter Selection
- 1.
- Embedding dimension .
- 2.
- The number of classes .
- 3.
- Time delay .
- 4.
- Maximum scale factor .
- 5.
- Number of hierarchical layers .
- Simulation Signal Analysis
2.2. Fault Identification
2.2.1. Extreme Learning Machine (ELM)
2.2.2. Particle Swarm Optimization-Based Extreme Learning Machine (PSO-ELM)
3. Proposed Method
3.1. Data Preprocessing
3.2. Training Process
3.3. Testing Process
4. Experiments
4.1. Case 1: CWRU Dataset
4.1.1. Experiment Setup
4.1.2. Feature Extraction
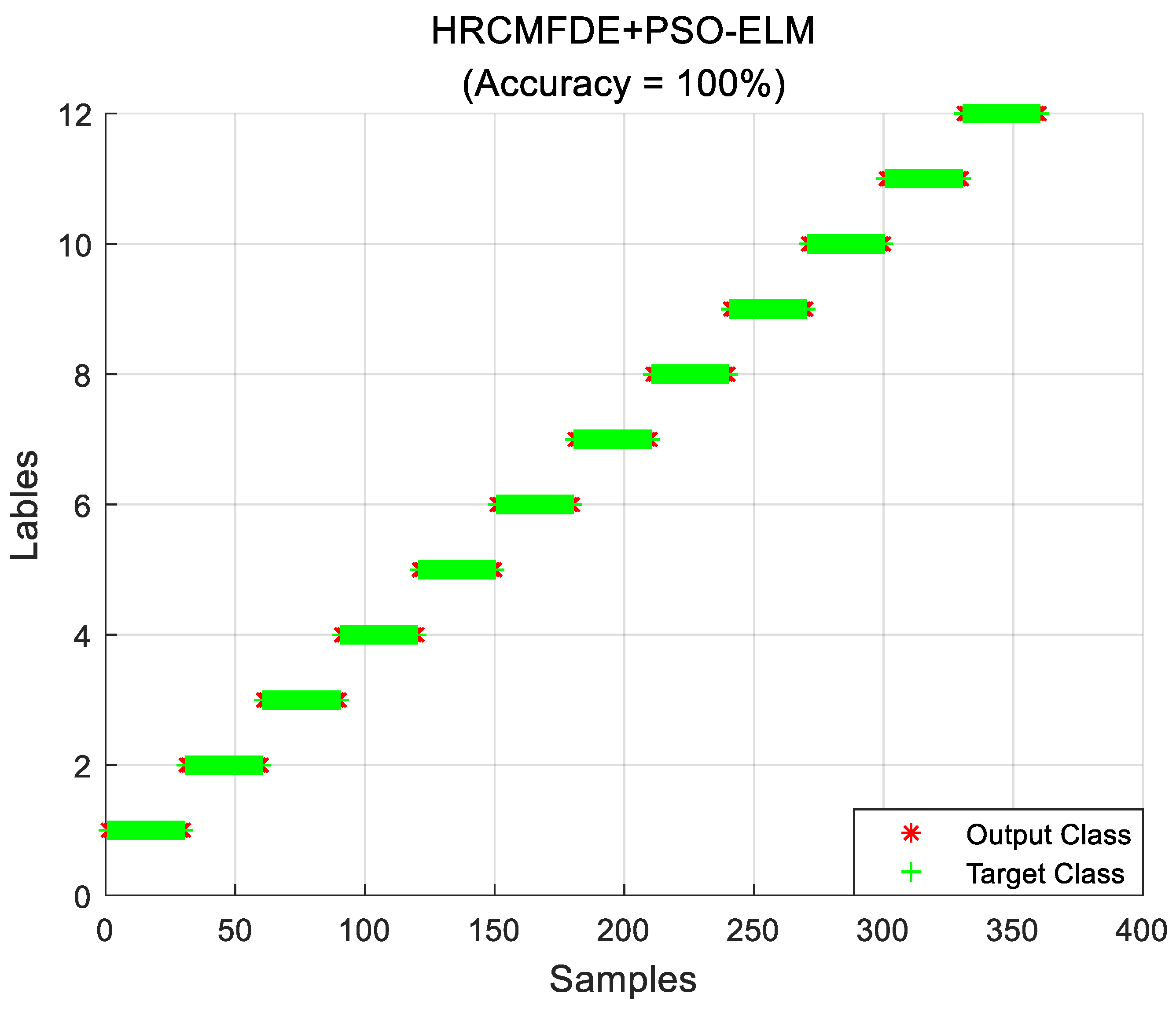
4.1.3. Fault Identification
4.1.4. Performance Comparison
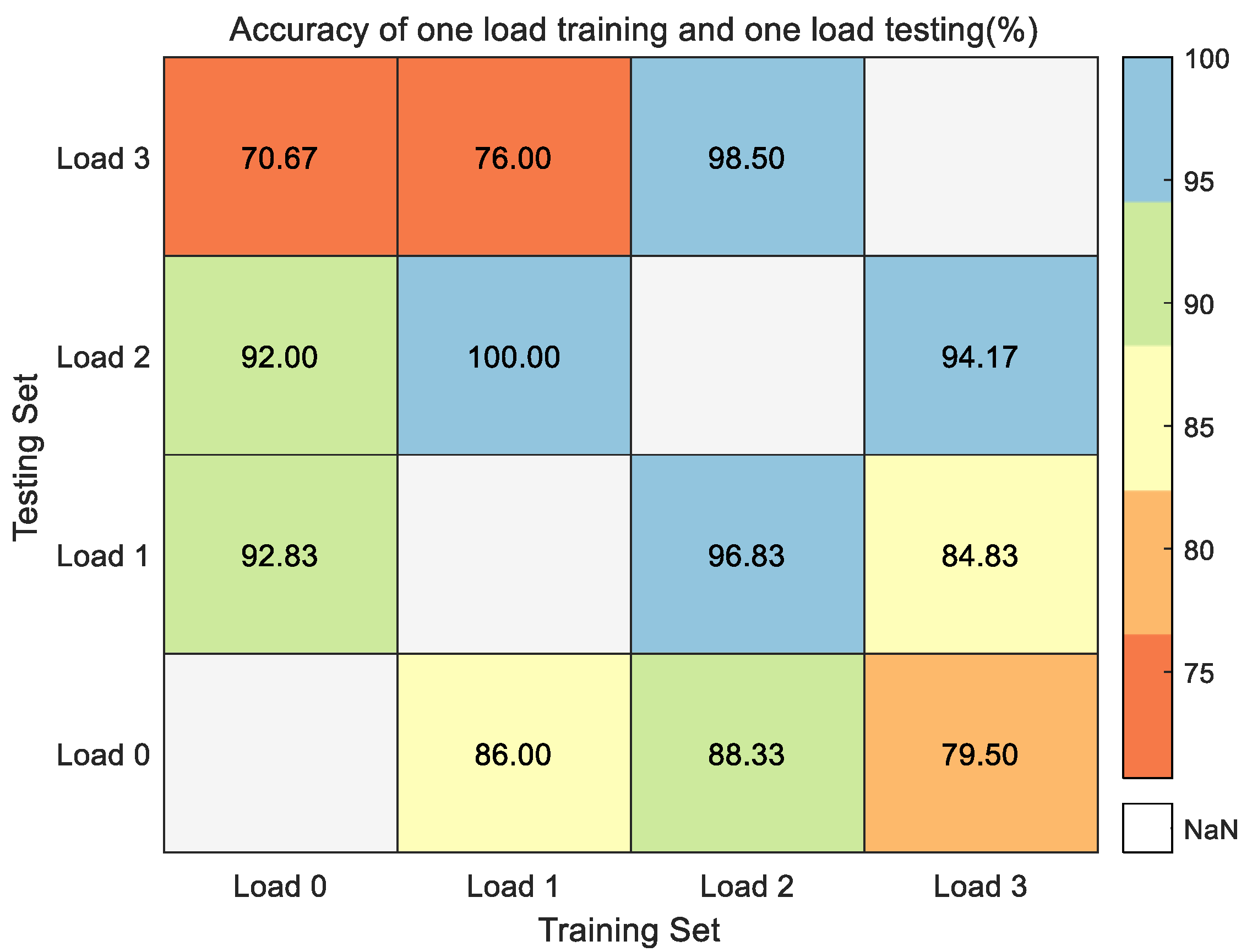
4.1.5. Load Migration
4.2. Case 2: MFPT Fault Dataset
4.2.1. Experiment Setup
4.2.2. Feature Extraction
4.2.3. Fault Identification
4.2.4. Performance Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AAPE | Amplitude aware permutation entropy |
| ANN | Artificial neural network |
| ApEn | Approximate entropy |
| CMFDE | Composite multiscale fluctuation-based dispersion entropy |
| CNN | Convolutional neural network |
| CVs | Coefficients of variation |
| CWRU | Case Western Reserve University |
| CWT | Continuous wavelet transform |
| DE | Dispersion entropy |
| DLZC | Dispersion Lempel-Ziv complexity |
| EEMD | Ensemble empirical mode decomposition |
| ELM | Extreme learning machine |
| EMD | Empirical mode decomposition |
| FDE | Fluctuation-based dispersion entropy |
| FDLZC | Fluctuation-based DLZC |
| GA-ELM | Genetic algorithm optimized extreme learning machine |
| GRCMFE | Generalized refined composite multiscale fuzzy entropy |
| GSA-SVM | Gravitational search algorithm optimized support vector machine |
| HCNN | Hierarchical convolutional neural network |
| HFDE | Hierarchical fluctuation-based dispersion entropy |
| HRCMFDE | Hierarchical refined composite multiscale fluctuation-based dispersion entropy |
| IFBE | Improved frequency band entropy |
| IMFs | Intrinsic mode functions |
| KELM | Kernel extreme learning machine |
| k-NN | K-nearest neighbor |
| LMD | Local mean decomposition |
| LSVM | Linear support vector machine |
| LZC | Lempel-Ziv complexity |
| MAAPE | Multiscale amplitude aware permutation entropy |
| MFDE | Multiscale fluctuation-based dispersion entropy |
| MFPT | Machinery Fault Prevention Technology |
| M-RVM | Multiclass relevance vector machine |
| MSE | Multiscale entropy |
| MSST | Multi-synchro-squeezing transform |
| NCDF | Normal cumulative distribution function |
| NPLSSMM | Non-parallel least squares support matrix machine |
| PCA | Principal component analysis |
| PE | Permutation entropy |
| PSO | Particle swarm optimization |
| PSO-ELM | Particle swarm optimization-based extreme learning machine |
| RCMFDE | Refined composite multiscale fluctuation-based dispersion entropy |
| RCMFDLZC | Refined composite multiscale FDLZC |
| RNN | Recurrent neural network |
| SD | Standard deviation |
| SE | Sample entropy |
| SFC-DL | Sparse feature coding based on dictionary learning |
| SLFN | Single-hidden layer feedforward neural network |
| sps | sample per second |
| STMSST | Second-order time-reassigned multi-synchro-squeezing transform |
| SVM | Support vector machines |
| VMD | Variational mode decomposition |
| WGN | White Gaussian noise |
| WPT | Wavelet packet transform |
| WT | Wavelet transform |
| WTFD | Wavelet time-frequency diagram |
References
- Yan, X.; Jia, M. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, T.; Zhao, W.; Luo, Z.; Lin, H. Rotating machinery fault diagnosis based on improved multiscale amplitude-aware permu-tation entropy and multiclass relevance vector machine. Sensors 2019, 19, 4542. [Google Scholar] [CrossRef] [PubMed]
- Rai, A.; Upadhyay, S. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Yang, L.; Chen, H. Fault diagnosis of gearbox based on RBF-PF and particle swarm optimization wavelet neural network. Neural Comput. Appl. 2018, 31, 4463–4478. [Google Scholar] [CrossRef]
- Li, C.; Zheng, J.; Pan, H.; Tong, J.; Zhang, Y. Refined Composite Multivariate Multiscale Dispersion Entropy and Its Application to Fault Diagnosis of Rolling Bearing. IEEE Access 2019, 7, 47663–47673. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, D. Total variation on horizontal visibility graph and its application to rolling bearing fault diagnosis. Mech. Mach. Theory 2020, 147, 103768. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the Complexity of Finite Sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Jiao, S.; Geng, B.; Li, Y.; Zhang, Q.; Wang, Q.; Li, Y.; Wang, W. Comparative study of feature extraction and classification based on dispersion Lempel-Ziv complexity. Int. J. Numer. Model. Electron. Netw. Devices Fields 2021, 35, e2949. [Google Scholar] [CrossRef]
- Mao, X.; Shang, P.; Xu, M.; Peng, C.-K. Measuring time series based on multiscale dispersion Lempel–Ziv complexity and dispersion entropy plane. Chaos Solit. Fract. 2020, 137, 109868. [Google Scholar] [CrossRef]
- Li, Y.; Jiao, S.; Geng, B. Refined composite multiscale fluctuation-based dispersion Lempel–Ziv complexity for signal analysis. ISA Trans. 2022, in press. [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, J.; Tang, H.; Liu, X.; Zhong, Y. Minimum entropy deconvolution based on simulation-determined band pass filter to detect faults in axial piston pump bearings. ISA Trans. 2018, 88, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Ali, J.B.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Application of EEMD and improved frequency band entropy in bearing fault feature extraction. ISA Trans. 2019, 88, 170–185. [Google Scholar] [CrossRef]
- Liu, H.; Han, M. A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings. Mech. Mach. Theory 2014, 75, 67–78. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, T.; Luo, Z.; Sun, K. A Novel Rolling Bearing Fault Diagnosis and Severity Analysis Method. Appl. Sci. 2019, 9, 2356. [Google Scholar] [CrossRef]
- Ding, J.; Xiao, D.; Li, X. Gear Fault Diagnosis Based on Genetic Mutation Particle Swarm Optimization VMD and Probabilistic Neural Network Algorithm. IEEE Access 2020, 8, 18456–18474. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Liu, Z.; Liang, X.; Si, S. The Entropy Algorithm and Its Variants in the Fault Diagnosis of Rotating Machinery: A Review. IEEE Access 2018, 6, 66723–66741. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Chen, G.; Ding, J. Modified multiscale weighted permutation entropy and optimized support vector machine method for rolling bearing fault diagnosis with complex signals. ISA Trans. 2021, 114, 470–484. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy (ApEn) as a complexity measure. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation Entropy: A Natural Complexity Measure for Time Series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Azami, H.; Escudero, J. Amplitude-aware permutation entropy: Illustration in spike detection and signal segmentation. Comput. Methods Programs Biomed. 2016, 128, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, T.; Zhao, W.; Luo, Z.; Sun, K. Fault Diagnosis of Rolling Bearing Using Multiscale Amplitude-Aware Permutation Entropy and Random Forest. Algorithms 2019, 12, 184. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Amplitude- and Fluctuation-Based Dispersion Entropy. Entropy 2018, 20, 210. [Google Scholar] [CrossRef]
- Azami, H.; Arnold, S.E.; Sanei, S.; Chang, Z.; Sapiro, G.; Escudero, J.; Gupta, A.S. Multiscale fluctuation-based dispersion entropy and its applications to neurological dis-eases. IEEE Access 2019, 7, 68718–68733. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lee, K.Y.; Lin, S.G. Modified multiscale entropy for short-term time series analysis. Phys. A Stat. Mech. Its Appl. 2013, 392, 5865–5873. [Google Scholar] [CrossRef]
- Gan, X.; Lu, H.; Yang, G. Fault Diagnosis Method for Rolling Bearings Based on Composite Multiscale Fluctuation Dispersion Entropy. Entropy 2019, 21, 290. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, X.; Shen, J.; Liu, W. Fault Diagnosis of Hydraulic Pumps Using PSO-VMD and Refined Composite Multiscale Fluctuation Dispersion Entropy. Shock Vib. 2020, 2020, 8840676. [Google Scholar] [CrossRef]
- Jiang, Y.; Peng, C.-K.; Xu, Y. Hierarchical entropy analysis for biological signals. J. Comput. Appl. Math. 2011, 236, 728–742. [Google Scholar] [CrossRef]
- Ke, Y.; Yao, C.; Song, E.; Dong, Q.; Yang, L. An early fault diagnosis method of common-rail injector based on improved CYCBD and hierarchical fluctuation dispersion entropy. Digit. Signal Process. 2021, 114, 103049. [Google Scholar] [CrossRef]
- Tian, J.; Morillo, C.; Azarian, M.H.; Pecht, M. Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled With K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2015, 63, 1793–1803. [Google Scholar] [CrossRef]
- Zheng, J.; Pan, H.; Tong, J.; Liu, Q. Generalized refined composite multiscale fuzzy entropy and multi-cluster feature selection based intelligent fault diagnosis of rolling bearing. ISA Trans. 2021, 123, 136–151. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.; Gao, L. A New Two-Level Hierarchical Diagnosis Network Based on Convolutional Neural Network. IEEE Trans. Instrum. Meas. 2019, 69, 330–338. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Tian, Y.; Ma, J.; Lu, C.; Wang, Z. Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mech. Mach. Theory 2015, 90, 175–186. [Google Scholar] [CrossRef]
- Mao, W.; He, L.; Yan, Y.; Wang, J. Online sequential prediction of bearings imbalanced fault diagnosis by extreme learning machine. Mech. Syst. Signal Process. 2017, 83, 450–473. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Net-works, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Langdon, W.B.; Poli, R. Evolving Problems to Learn About Particle Swarm Optimizers and Other Search Algorithms. IEEE Trans. Evol. Comput. 2007, 11, 561–578. [Google Scholar] [CrossRef]
- Han, F.; Yao, H.-F.; Ling, Q.-H. An improved evolutionary extreme learning machine based on particle swarm optimization. Neurocomputing 2013, 116, 87–93. [Google Scholar] [CrossRef]
- Chen, S.; Shang, Y.; Wu, M. Application of PSO-ELM in electronic system fault diagnosis. In Proceedings of the 2016 IEEE International Con-ference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016; pp. 1–5. [Google Scholar]
- He, C.; Wu, T.; Gu, R.; Jin, Z.; Ma, R.; Qu, H. Rolling bearing fault diagnosis based on composite multiscale permutation entropy and reverse cog-nitive fruit fly optimization algorithm–extreme learning machine. Measurement 2021, 173, 108636. [Google Scholar] [CrossRef]
- Yan, X.; Liu, Y.; Huang, D.; Jia, M. A new approach to health condition identification of rolling bearing using hierarchical dispersion entropy and improved Laplacian score. Struct. Health Monit. 2020, 20, 1169–1195. [Google Scholar] [CrossRef]
- Zhou, F.; Han, J.; Yang, X. Multivariate hierarchical multiscale fluctuation dispersion entropy: Applications to fault diagnosis of rotating machinery. Appl. Acoust. 2021, 182, 108271. [Google Scholar] [CrossRef]
- Rao, D.; Shi, X.; Zhou, J.; Yu, Z.; Gou, Y.; Dong, Z.; Zhang, J. An Expert Artificial Intelligence Model for Discriminating Microseismic Events and Mine Blasts. Appl. Sci. 2021, 11, 6474. [Google Scholar] [CrossRef]
- The Case Western Reserve University Bearing Data Center. Available online: https://csegroups.case.edu/bearingdatacenter/pages/download-data-file (accessed on 17 June 2021).
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2011, 42, 513–529. [Google Scholar] [CrossRef]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Zheng, J.; Dong, Z.; Pan, H.; Ni, Q.; Liu, T.; Zhang, J. Composite multi-scale weighted permutation entropy and extreme learning machine based intelligent fault diagnosis for rolling bearing. Measurement 2019, 143, 69–80. [Google Scholar] [CrossRef]
- Yang, Z.; Ce, L.; Lian, L. Electricity price forecasting by a hybrid model, combining wavelet transform, ARMA and kernel-based extreme learning machine methods. Appl. Energy 2017, 190, 291–305. [Google Scholar] [CrossRef]
- Meng, L.; Liu, M.; Wei, P.; Qin, H. Rolling Bearing Fault Diagnosis Based on Improved VMD And GA-ELM. In Proceedings of the 2021 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 4414–4419. [Google Scholar]
- Li, X.; Yang, Y.; Pan, H.; Cheng, J.; Cheng, J. Non-parallel least squares support matrix machine for rolling bearing fault diagnosis. Mech. Mach. Theory 2019, 145, 103676. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, X.; Zhu, Q. A novel classification method based on ICGOA-KELM for fault diagnosis of rolling bearing. Appl. Intell. 2020, 50, 2833–2847. [Google Scholar] [CrossRef]
- Yuan, L.; Lian, D.; Kang, X.; Chen, Y.; Zhai, K. Rolling Bearing Fault Diagnosis Based on Convolutional Neural Network and Support Vector Machine. IEEE Access 2020, 8, 137395–137406. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Yang, J. A novel fault diagnosis method for rolling bearing based on EEMD-PE and multiclass relevance vector machine. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Turin, Italy, 22–25 May 2017; pp. 1–6. [Google Scholar]
- Machinery Failure Prevention Technology (MFPT). Available online: https://mfpt.org/fault-data-sets (accessed on 26 October 2021).
- Zuo, L.; Zhang, L.; Zhang, Z.-H.; Luo, X.-L.; Liu, Y. A spiking neural network-based approach to bearing fault diagnosis. J. Manuf. Syst. 2020, 61, 714–724. [Google Scholar] [CrossRef]
- Wang, Z.; Shangguan, W.; Peng, C.; Cai, B. A fault diagnosis method based on data feature reconstruction and deep transfer learning. In Proceedings of the 2022 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2022; pp. 1–5. [Google Scholar]
- Sun, G.; Gao, Y.; Lin, K.; Hu, Y. Fine-Grained Fault Diagnosis Method of Rolling Bearing Combining Multisynchrosqueezing Transform and Sparse Feature Coding Based on Dictionary Learning. Shock Vib. 2019, 2019, 1531079. [Google Scholar] [CrossRef]
- Sun, G.; Gao, Y.; Xu, Y.; Feng, W. Data-Driven Fault Diagnosis Method Based on Second-Order Time-Reassigned Multisynchrosqueezing Transform and Evenly Mini-Batch Training. IEEE Access 2020, 8, 120859–120869. [Google Scholar] [CrossRef]
















| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| m = 2 | 0.0211 | 0.0042 | 0.0066 | 0.0051 | 0.0140 | 0.0134 | 0.0105 | 0.0036 |
| m = 3 | 0.0217 | 0.0045 | 0.0070 | 0.0057 | 0.0156 | 0.0132 | 0.0096 | 0.0038 |
| m = 4 | 0.0211 | 0.0037 | 0.0067 | 0.0065 | 0.0169 | 0.0137 | 0.0101 | 0.0042 |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| m = 2 | 0.0951 | 0.0061 | 0.0045 | 0.0048 | 0.0112 | 0.0162 | 0.0116 | 0.0112 |
| m = 3 | 0.0972 | 0.0063 | 0.0044 | 0.0051 | 0.0115 | 0.0175 | 0.0134 | 0.0121 |
| m = 4 | 0.0970 | 0.0052 | 0.0045 | 0.0055 | 0.0115 | 0.0180 | 0.0140 | 0.0129 |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| c = 3 | 0.0301 | 0.0061 | 0.0102 | 0.0074 | 0.0950 | 0.1109 | 0.4438 | 0.4776 |
| c = 6 | 0.0211 | 0.0042 | 0.0066 | 0.0051 | 0.0140 | 0.0134 | 0.0105 | 0.0036 |
| c = 9 | 0.0176 | 0.0038 | 0.0061 | 0.0047 | 0.0108 | 0.0115 | 0.0127 | 0.0123 |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| c = 3 | 0.1147 | 0.0085 | 0.0096 | 0.0062 | 0.0259 | 0.0533 | 0.1814 | 0.3336 |
| c = 6 | 0.0951 | 0.0061 | 0.0045 | 0.0048 | 0.0112 | 0.0162 | 0.0116 | 0.0112 |
| c = 9 | 0.0492 | 0.0046 | 0.0056 | 0.0037 | 0.0131 | 0.0208 | 0.0123 | 0.0119 |
| Entropy | Embedding Dimension | Number of Classes | Time Delay | Number of Hierarchical Layers | Maximum Scale Factor |
|---|---|---|---|---|---|
| HFDE | m = 2 | c = 6 | d = 1 | n = 3 | \ |
| MFDE | m = 2 | c = 6 | d = 1 | \ | τ max = 20 |
| RCMFDE | m = 2 | c = 6 | d = 1 | \ | τ max = 20 |
| HRCMFDE | m = 2 | c = 6 | d = 1 | n = 3 | τ max = 20 |
| Fault Types | Severity (Inch) | Load (hp) | |||
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | ||
| Normal | - | √ | √ | √ | √ |
| Ball fault | 0.007 | √ | √ | √ | √ |
| 0.014 | √ | √ | √ | √ | |
| 0.021 | √ | √ | √ | √ | |
| 0.028 | √ | √ | √ | √ | |
| Inner race fault | 0.007 | √ | √ | √ | √ |
| 0.014 | √ | √ | √ | √ | |
| 0.021 | √ | √ | √ | √ | |
| 0.028 | √ | √ | √ | √ | |
| Outer race fault | 0.007 | √ | √ | √ | √ |
| 0.014 | √ | √ | √ | √ | |
| 0.021 | √ | √ | √ | √ | |
| 0.028 | * | * | * | * | |
| Labels | Fault Types | Abbreviations | Severity (inch) | Number of Training/Testing Samples |
|---|---|---|---|---|
| 1 | Normal | N | - | 20/30 |
| 2 | Ball fault | B007 | 0.007 | 20/30 |
| 3 | B014 | 0.014 | 20/30 | |
| 4 | B021 | 0.021 | 20/30 | |
| 5 | B028 | 0.028 | 20/30 | |
| 6 | Inner race fault | I007 | 0.007 | 20/30 |
| 7 | I014 | 0.014 | 20/30 | |
| 8 | I021 | 0.021 | 20/30 | |
| 9 | I028 | 0.028 | 20/30 | |
| 10 | Outer race fault | O007 | 0.007 | 20/30 |
| 11 | O014 | 0.014 | 20/30 | |
| 12 | O021 | 0.021 | 20/30 |
| Load | Fault Types | Number of Training Samples | Number of Testing Samples | Average Accuracy |
|---|---|---|---|---|
| 0 hp | N B IR OR | 20 80 80 60 | 30 120 120 90 | 99.86% |
| 1 hp | N B IR OR | 20 80 80 60 | 30 120 120 90 | 99.78% |
| 2 hp | N B IR OR | 20 80 80 60 | 30 120 120 90 | 100% |
| 3 hp | N B IR OR | 20 80 80 60 | 30 120 120 90 | 100% |
| Feature Extraction | Fault Identification | Load 0 hp | Load 1 hp | Load 2 hp | Load 3 hp | Average Accuracy |
|---|---|---|---|---|---|---|
| HFDE [33] | PSO-ELM | 99.72% | 100% | 100% | 99.81% | 99.88% |
| MFDE [28] | PSO-ELM | 94.03% | 96.69% | 99.61% | 99.42% | 97.44% |
| RCMFDE [31] | PSO-ELM | 98.36% | 99.39% | 100% | 99.92% | 99.42% |
| HRCMFDE | PSO-ELM | 99.86% | 99.78% | 100% | 100% | 99.91% |
| Num. | Feature Extraction | Fault Identification | Accuracy (%) | Training Time (s) | Testing Time (s) |
|---|---|---|---|---|---|
| 1 | HRCMFDE | ELM [51] | 99.56 ± 0.53 | 0.0285 | 0.0085 |
| 2 | HRCMFDE | KELM [52] | 97.94 ± 2.87 | 0.0046 | 0.0013 |
| 3 | HRCMFDE | GA-ELM [53] | 99.86 ± 0.16 | 231.3569 | 28.6741 |
| 4 | HRCMFDE | PSO-ELM | 99.91 ± 0.11 | 11.3320 | 1.2427 |
| Literature | Feature Extraction | Fault Identification | Number of Classes | Average Accuracy (%) |
|---|---|---|---|---|
| [54] | WTFD | NPLSSMM | 10 | 99.64 |
| [55] | VMD+MPE | KPCA+CGOA-KELM | 4 | 99.67 |
| [56] | CWT | CNN-SVM | 12 | 98.75 |
| [25] | MAAPE | RF | 10 | 96.00 |
| [57] | EEMD+PE | M-RVM | 4 | 99.58 |
| [11] | RCMFDLZC | DAC | 12 | 96.08 |
| This paper | HRCMFDE | PSO-ELM | 12 | 99.91 |
| Fault Classes | Fault Types | Load (lb) | Sample Rate (sps) | Sample Time (s) | Data Points |
|---|---|---|---|---|---|
| Normal | Baseline | 270 | 97,656 | 6 | 585,936 |
| Outer Race Fault | Outer Race Fault | 270 | 97,656 | 6 | 585,936 |
| More Outer Race Fault | 25 | 48,828 | 3 | 146,484 | |
| 50 | 48,828 | 3 | 146,484 | ||
| 100 | 48,828 | 3 | 146,484 | ||
| 150 | 48,828 | 3 | 146,484 | ||
| 200 | 48,828 | 3 | 146,484 | ||
| 250 | 48,828 | 3 | 146,484 | ||
| 300 | 48,828 | 3 | 146,484 | ||
| Inner Race Fault | Inner Race Fault | 0 | 48,828 | 3 | 146,484 |
| 50 | 48,828 | 3 | 146,484 | ||
| 100 | 48,828 | 3 | 146,484 | ||
| 150 | 48,828 | 3 | 146,484 | ||
| 200 | 48,828 | 3 | 146,484 | ||
| 250 | 48,828 | 3 | 146,484 | ||
| 300 | 48,828 | 3 | 146,484 |
| Labels | Fault Classes | Number of Total Samples | Number of Training Samples | Number of Testing Samples |
|---|---|---|---|---|
| 1 | Normal | 360 | 144 | 216 |
| 2 | Outer Race Fault | 790 | 316 | 474 |
| 3 | Inner race fault | 425 | 170 | 255 |
| Num. | Feature Extraction | Fault Identification | Accuracy (%) | Training Time (s) | Testing Time (s) |
|---|---|---|---|---|---|
| 1 | HRCMFDE | ELM | 97.90 ± 0.49 | 0.0318 | 0.0198 |
| 2 | HRCMFDE | KELM | 97.71 ± 0.49 | 0.0371 | 0.0293 |
| 3 | HRCMFDE | GA-ELM | 99.49 ± 0.48 | 318.0357 | 150.4896 |
| 4 | HRCMFDE | PSO-ELM | 99.43 ± 0.38 | 17.6277 | 5.1201 |
| Literature | Feature Extraction | Fault Identification | Number of Classes | Average Accuracy (%) |
|---|---|---|---|---|
| [56] | CWT | CNN-SVM | 3 | 98.89 |
| [59] | LMD | SNN | 3 | 99.31 |
| [60] | WT | IGoogLeNet | 3 | 99.40 |
| [61] | MSST+SFC-DL | LSVM | 3 | 95.83 |
| [62] | STMSST | CNN | 3 | 98.67 |
| [11] | RCMFDLZC | DAC | 3 | 96.05 |
| This paper | HRCMFDE | PSO-ELM | 3 | 99.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yuan, Z.; Chen, J.; Sun, K. A Novel Fault Diagnosis Method for Rolling Bearing Based on Hierarchical Refined Composite Multiscale Fluctuation-Based Dispersion Entropy and PSO-ELM. Entropy 2022, 24, 1517. https://doi.org/10.3390/e24111517
Chen Y, Yuan Z, Chen J, Sun K. A Novel Fault Diagnosis Method for Rolling Bearing Based on Hierarchical Refined Composite Multiscale Fluctuation-Based Dispersion Entropy and PSO-ELM. Entropy. 2022; 24(11):1517. https://doi.org/10.3390/e24111517
Chicago/Turabian StyleChen, Yinsheng, Zichen Yuan, Jiahui Chen, and Kun Sun. 2022. "A Novel Fault Diagnosis Method for Rolling Bearing Based on Hierarchical Refined Composite Multiscale Fluctuation-Based Dispersion Entropy and PSO-ELM" Entropy 24, no. 11: 1517. https://doi.org/10.3390/e24111517
APA StyleChen, Y., Yuan, Z., Chen, J., & Sun, K. (2022). A Novel Fault Diagnosis Method for Rolling Bearing Based on Hierarchical Refined Composite Multiscale Fluctuation-Based Dispersion Entropy and PSO-ELM. Entropy, 24(11), 1517. https://doi.org/10.3390/e24111517







