Coupled Electromagnetic-Dynamic Modeling and Bearing Fault Characteristics of Induction Motors considering Unbalanced Magnetic Pull
Abstract
1. Introduction
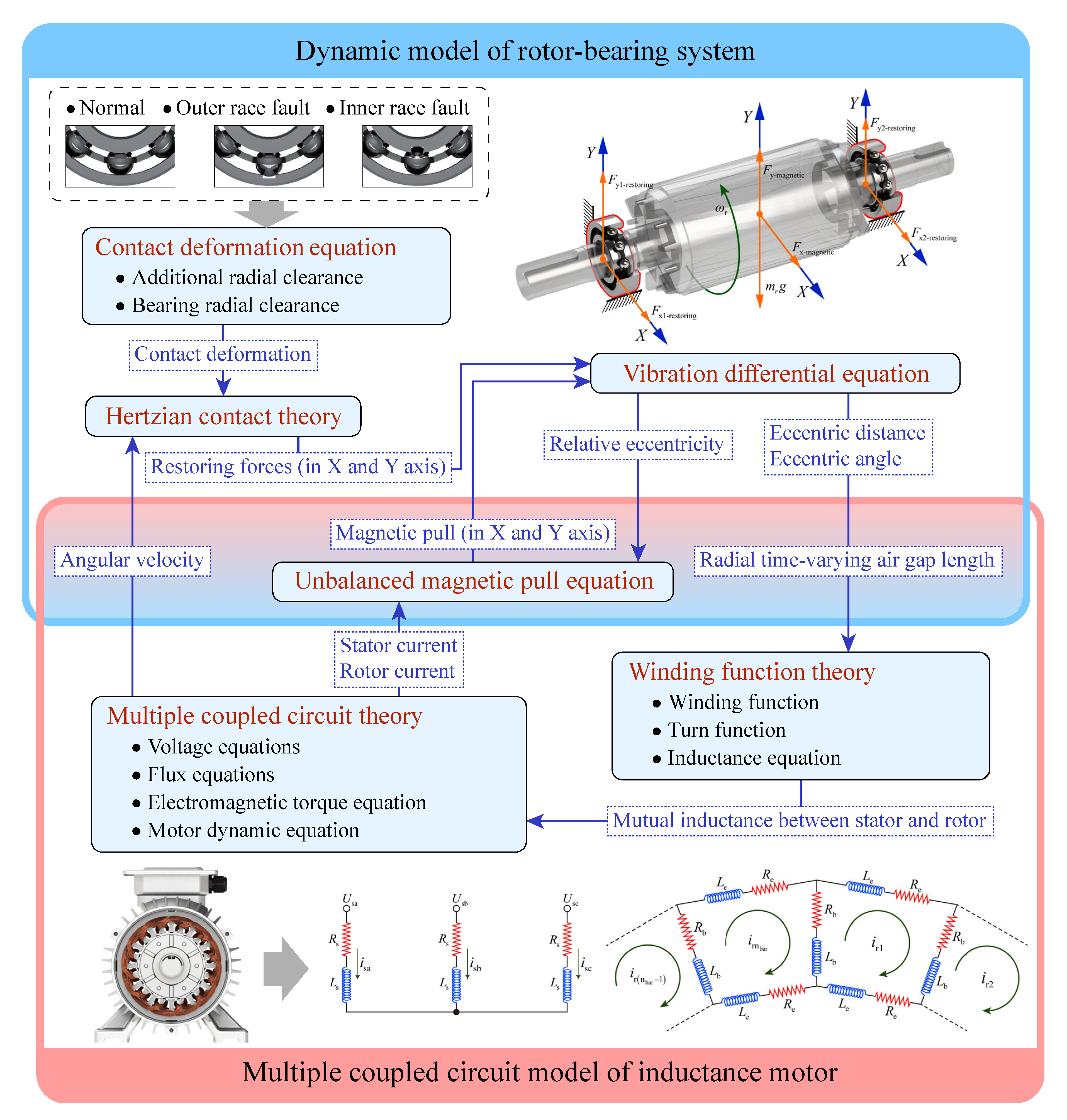
2. Electromagnetic-Dynamic Coupled Modeling Process Considering Unbalanced Magnetic Pull
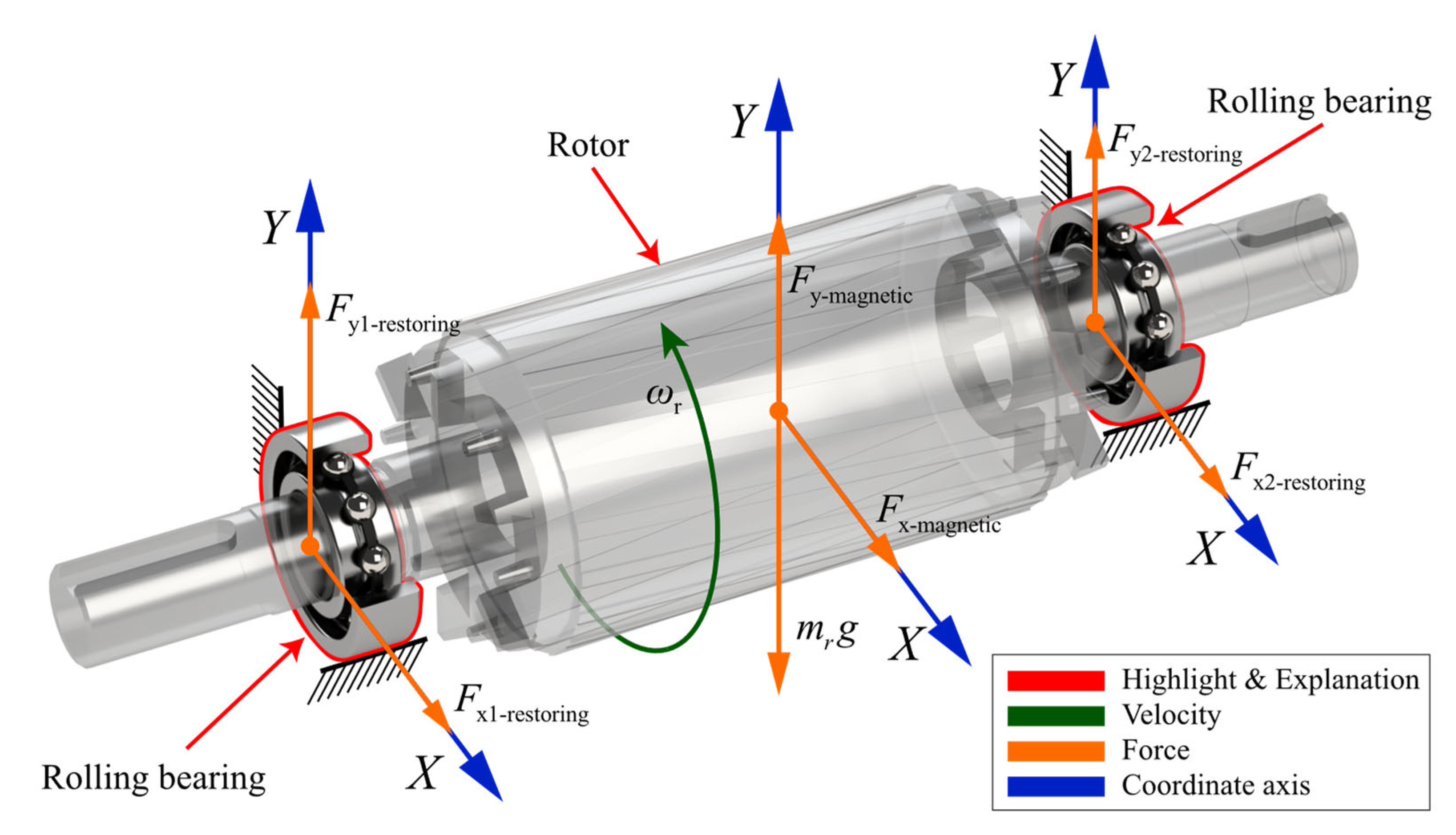
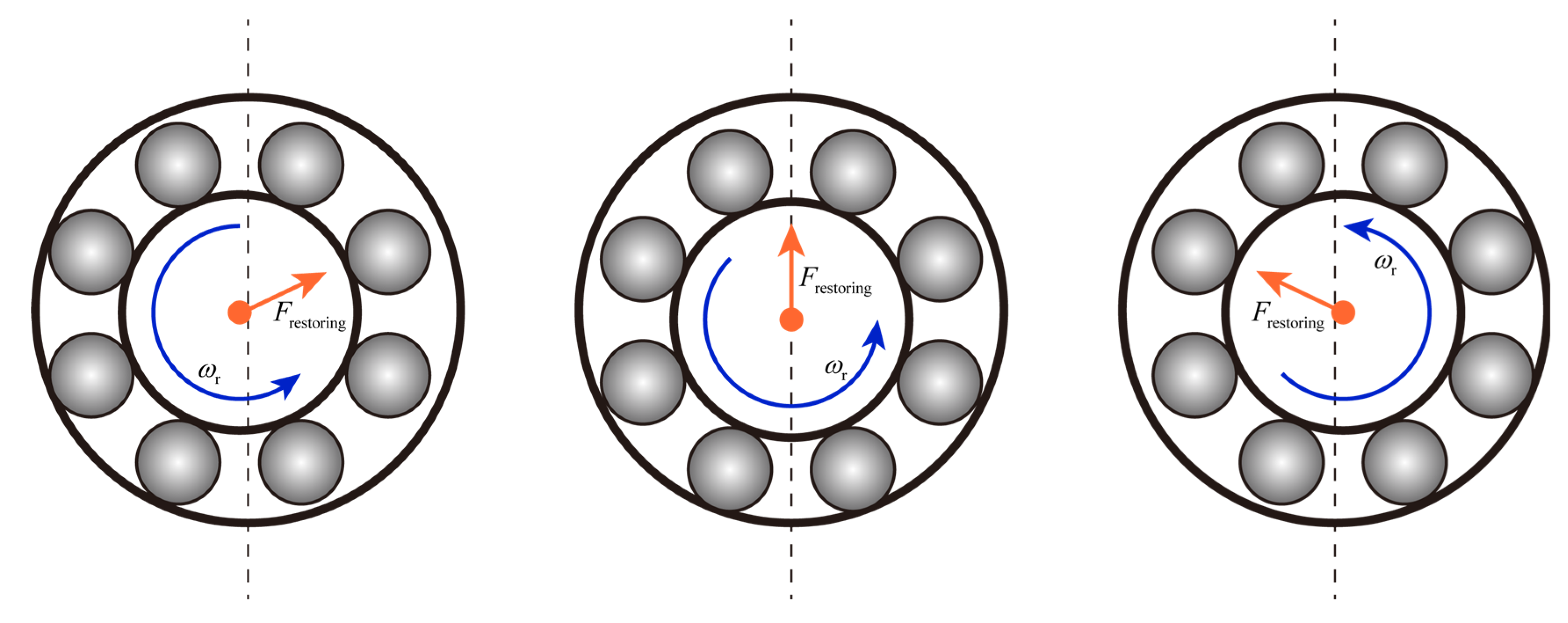
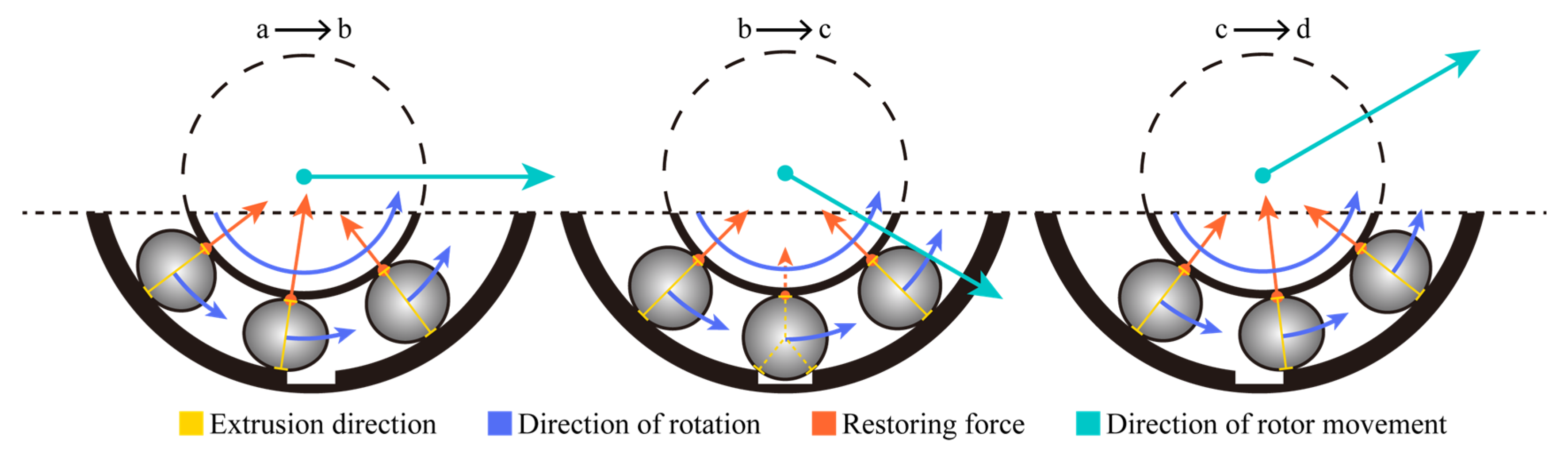
2.1. Rotor-Bearing Dynamic Model
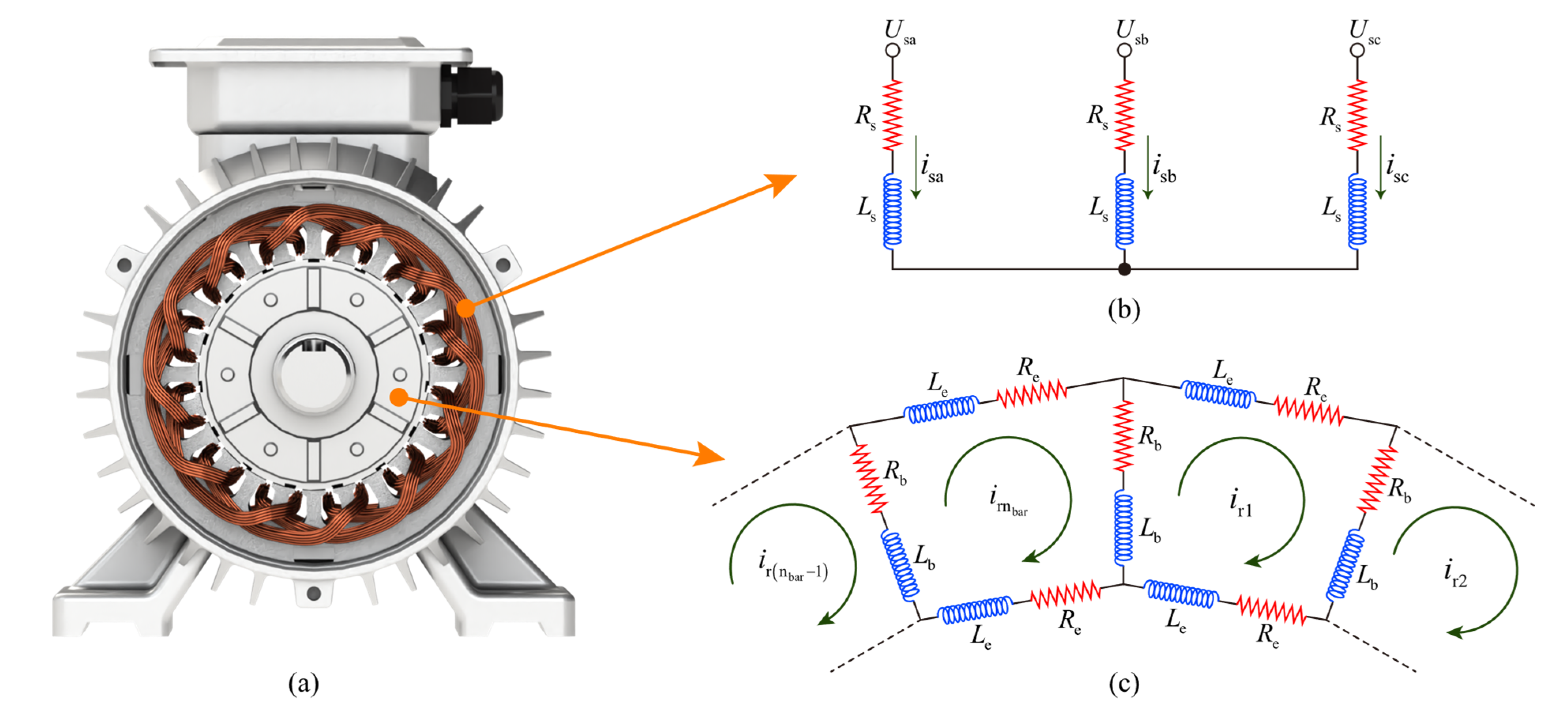
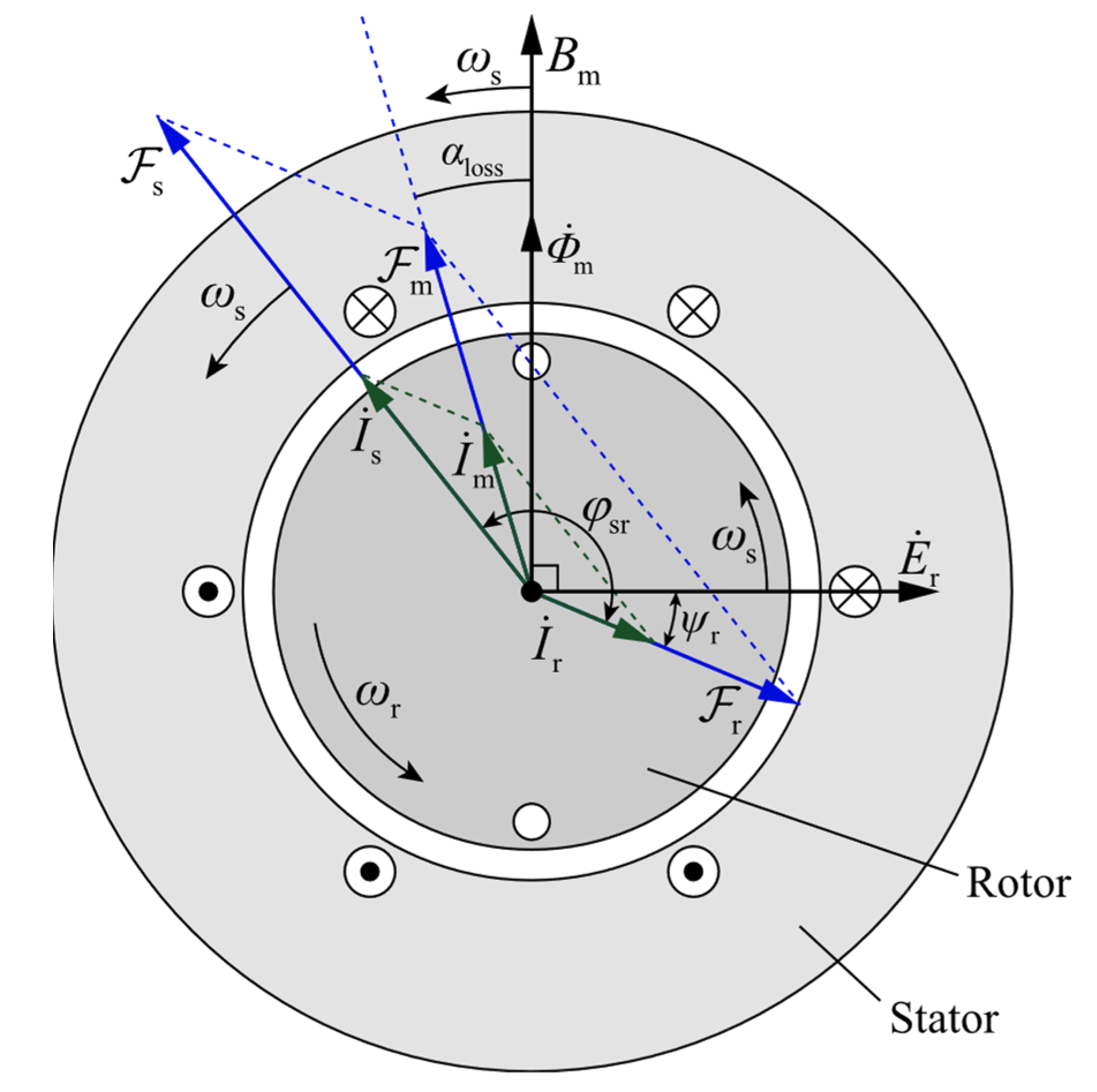
2.2. Electromagnetic Model Based on Multiple Coupled Circuit Theory
- The motor is powered by a balanced three-phase voltage source;
- Hysteresis loss, eddy current loss, and friction loss are ignored;
- Rotor bars are insulated from each other.
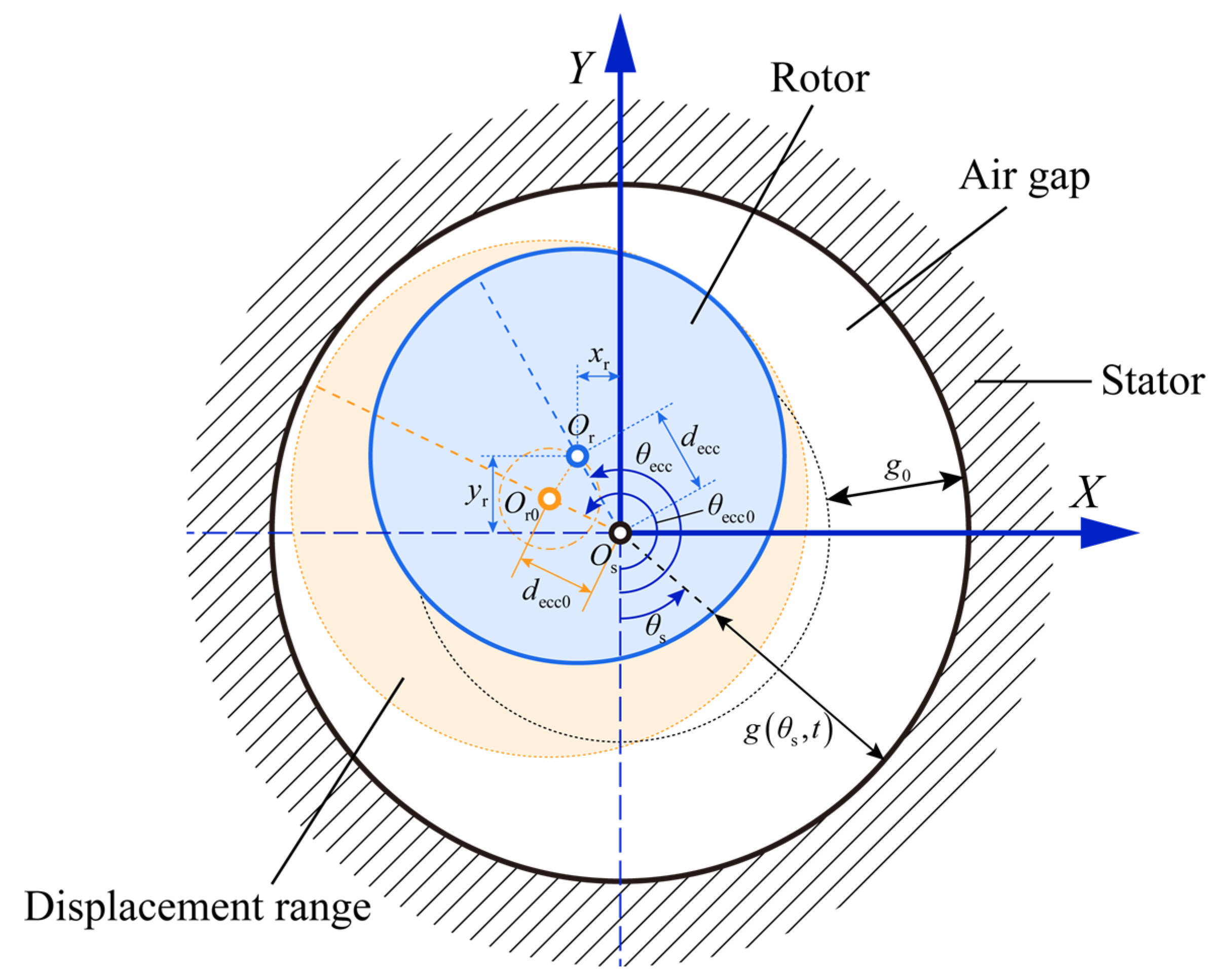
2.3. Calculation of Inductance and Unbalanced Magnetic Pull
- The flux linkage passes through the air gap radially, that is, the axial flux linkage is ignored;
- The magnetic permeability of magnetic materials is infinite;
- There is a negligible slot effect.
2.4. Electromagnetic-Dynamic Coupled Model Framework
3. Simulation, Experimentation, and Analysis of Results
3.1. Model Parameters and Experimental Conditions
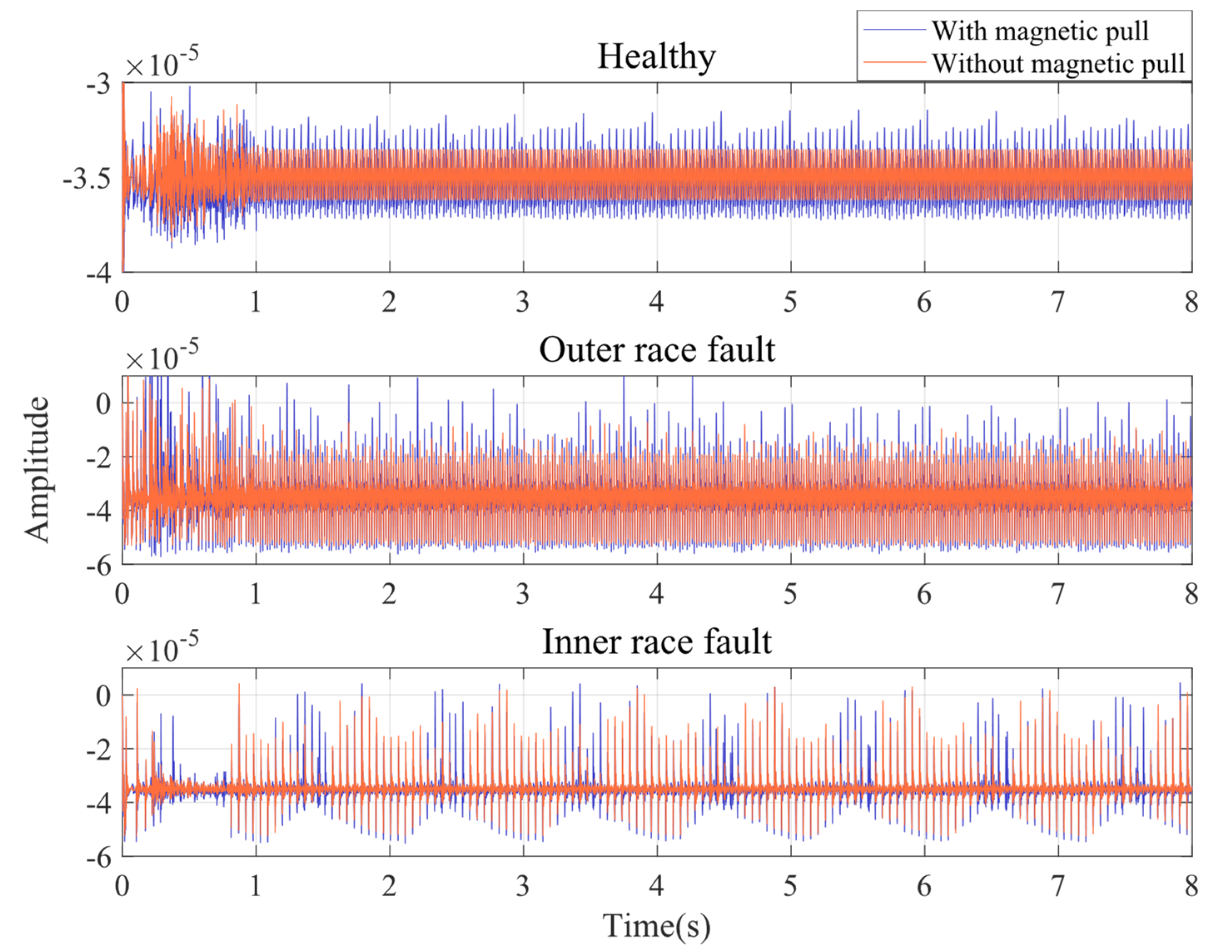
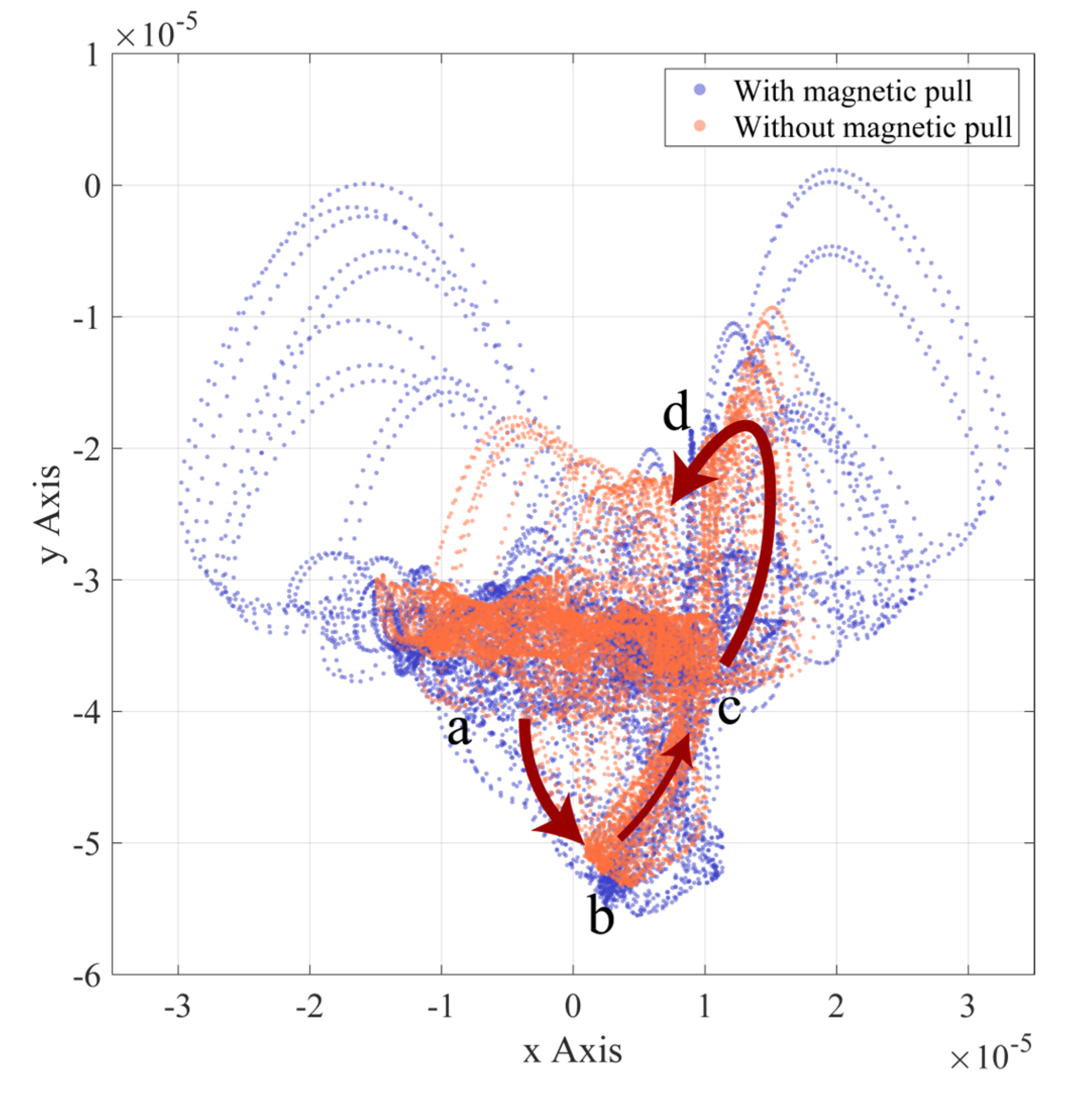
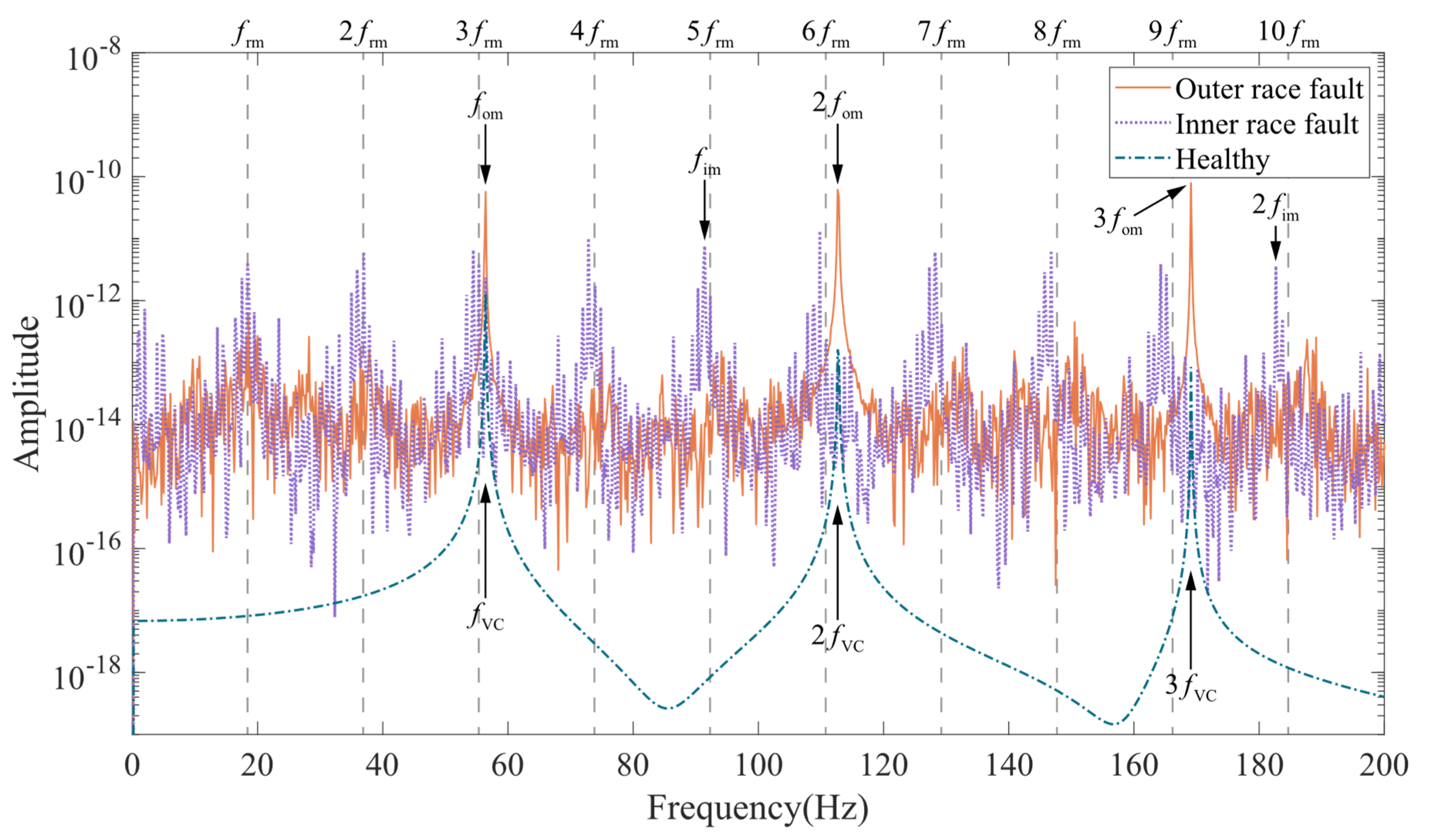
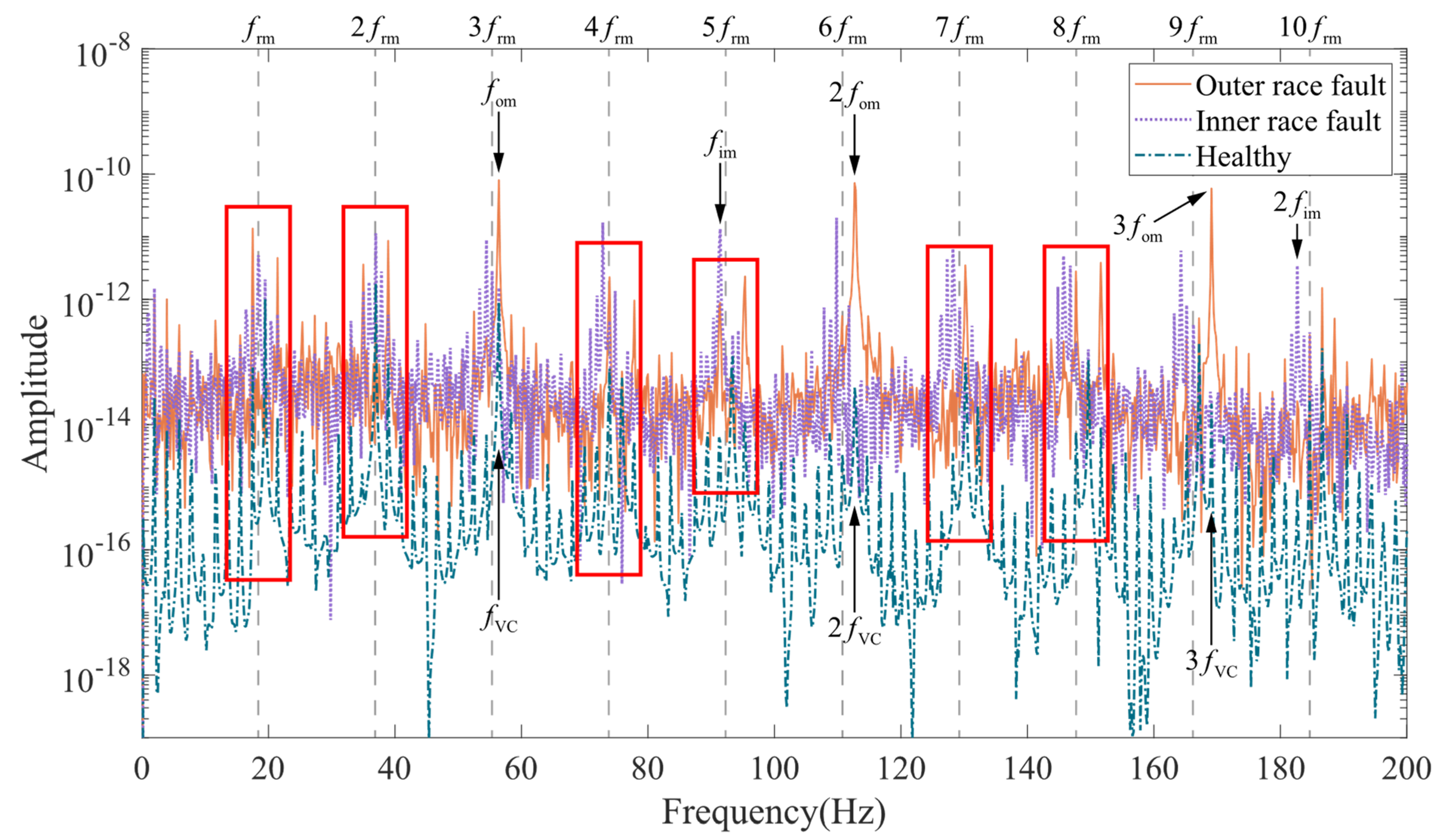
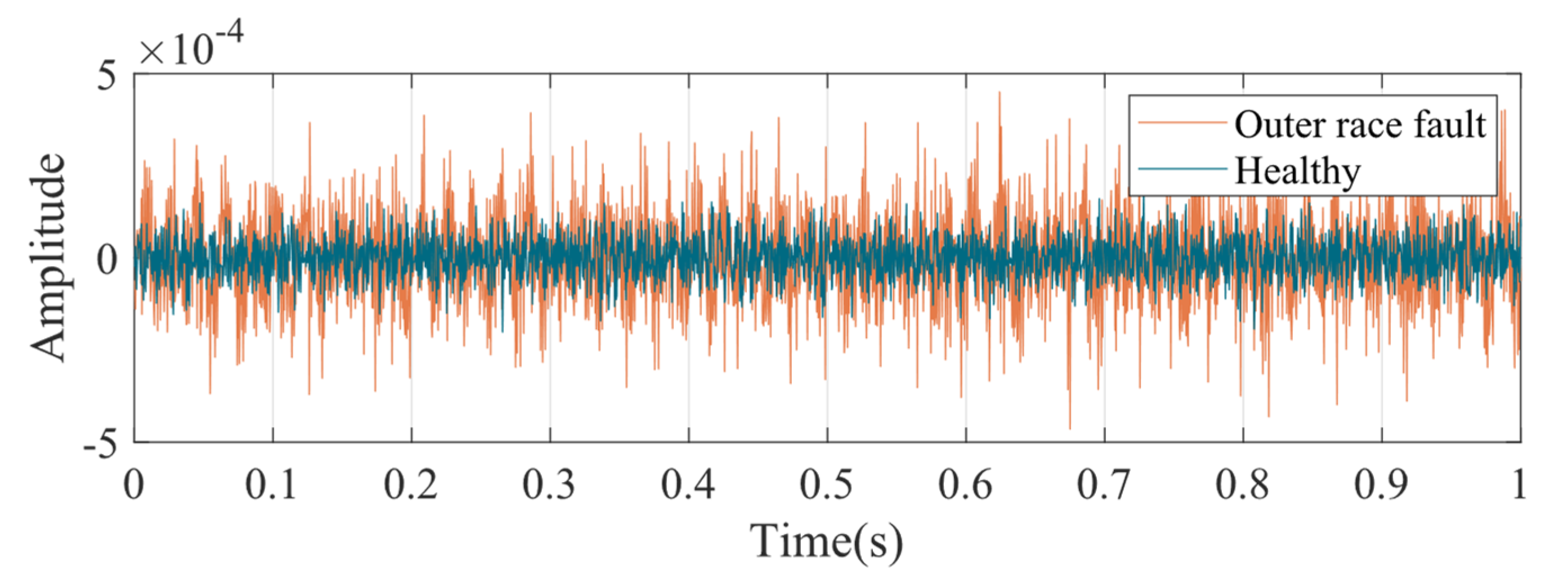
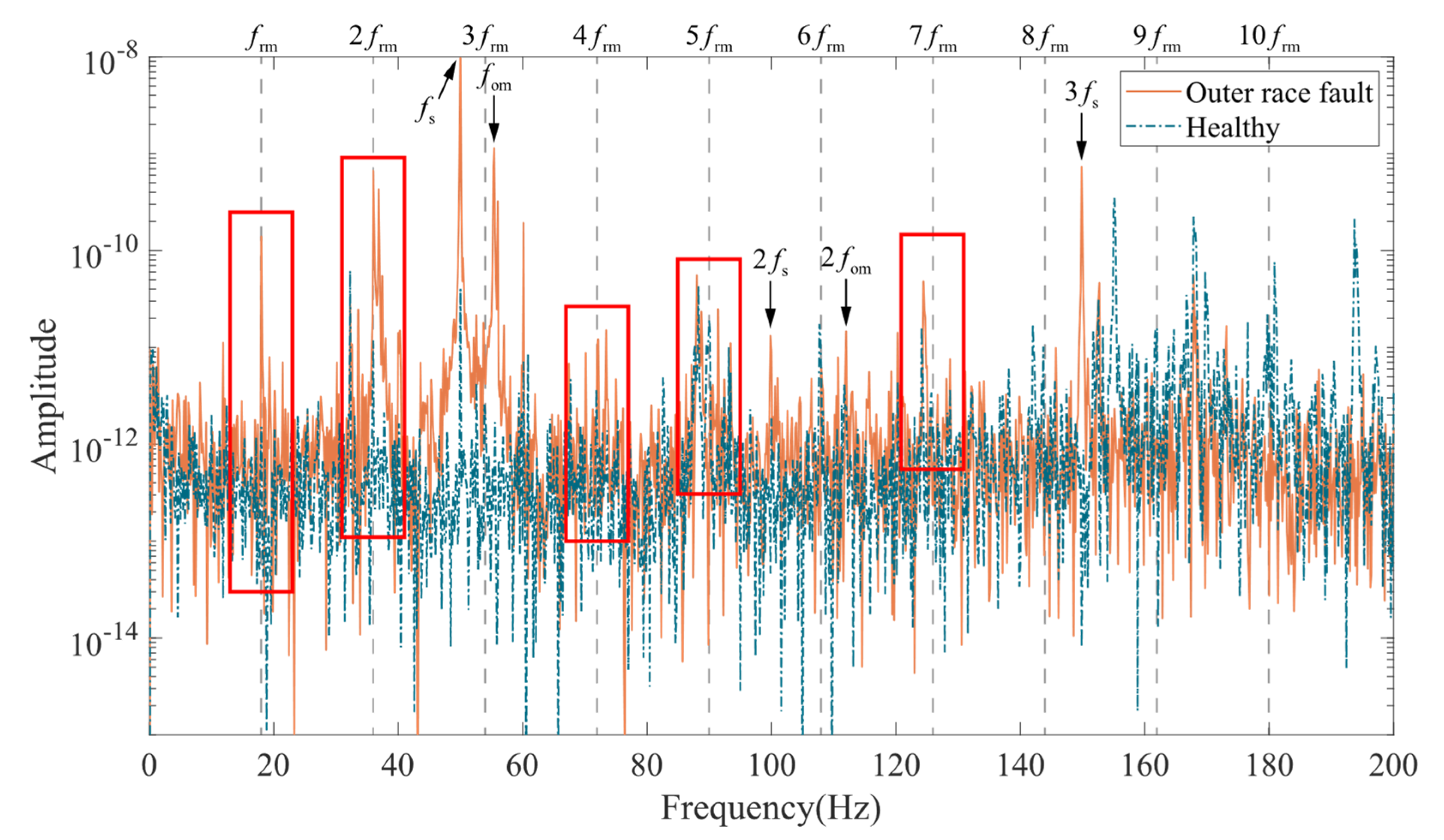
3.2. Vibration Characteristics Analysis
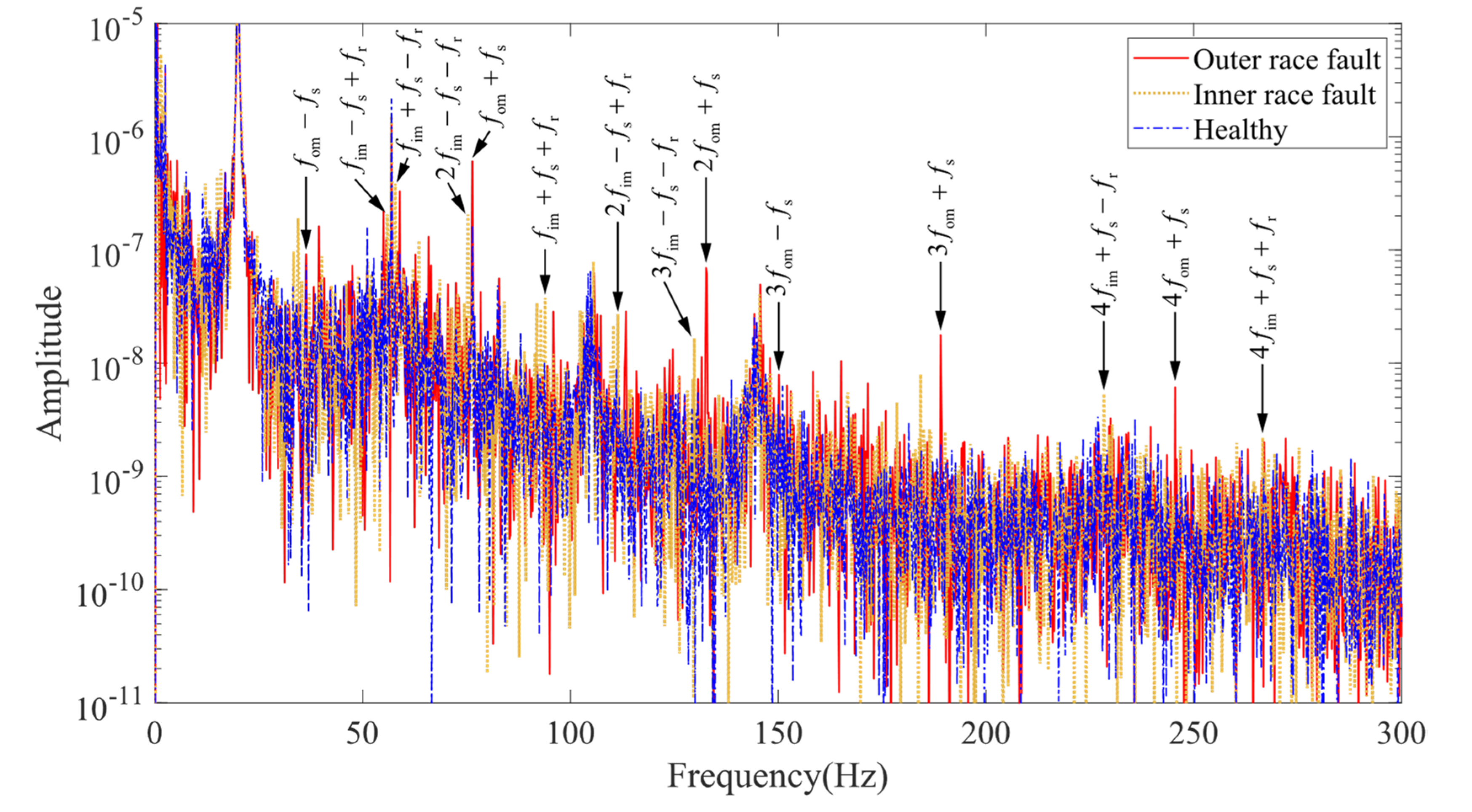
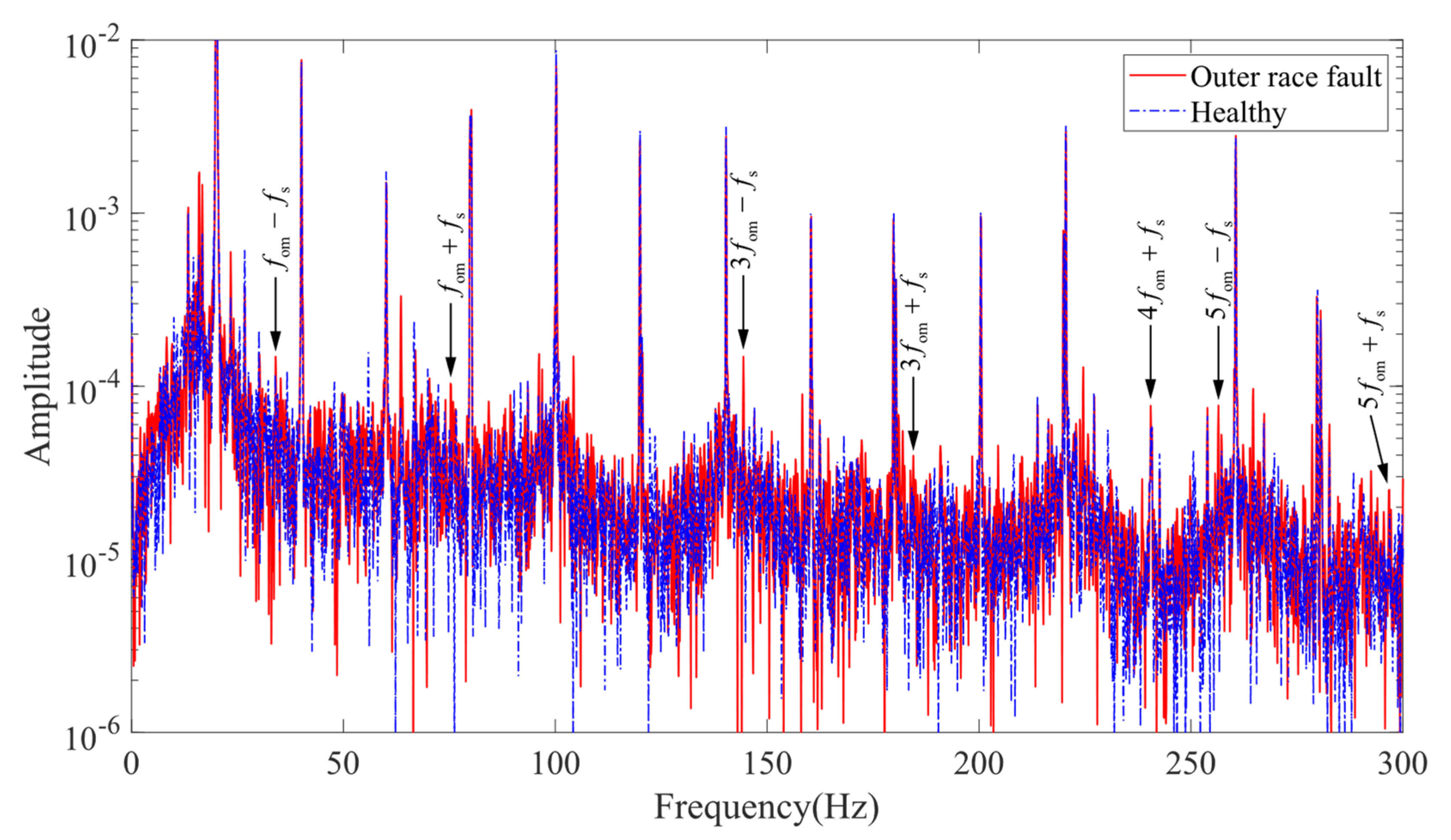
3.3. Current Characteristics Analysis
- Outer race fault:
- Inner race fault:
- Ball fault:
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| Contact deformation of the j-th ball | |
| Rotor displacement in X direction | |
| Rotor displacement in Y direction | |
| Bearing radial clearance | |
| Additional radial clearance when the j-th ball passes through the spalling position | |
| Equivalent spalling depth considering the ball does not touch the bottom of the spalling | |
| Spalling starting angle position | |
| Spalling angle | |
| Spalling width | |
| Bearing outer race diameter | |
| Bearing inner race diameter | |
| Bearing ball diameter | |
| Contact stiffness | |
| Angle position of the j-th ball | |
| Rotor mass | |
| Rotor damping | |
| Restoring force of the j-th bearing in the X direction | |
| Restoring force of the j-th bearing in the Y direction | |
| Unbalanced magnetic pull of the rotor in the X direction | |
| Unbalanced magnetic pull of the rotor in the Y direction | |
| Gravitational acceleration | |
| Bearing pitch diameter | |
| Number of bearing balls | |
| Bearing contact angle | |
| Contact coefficient of the j-th ball | |
| Stator voltage vector | |
| Stator and rotor current vectors | |
| Stator and rotor resistance matrix | |
| Stator and rotor flux linkage vectors | |
| Stator three-phase voltage | |
| Stator three-phase winding currents | |
| Single-phase stator winding resistance under the assumption of symmetrical stator | |
| Flux linkages on three-phase stator windings | |
| Number of rotor bars | |
| Single rotor bar resistance | |
| End ring resistance | |
| Current through the i-th rotor circuit | |
| Flux linkage through i-th rotor circuit | |
| Current through the end ring | |
| Flux linkage through the end ring | |
| Stator self-inductance matrix | |
| Rotor self-inductance matrix | |
| Stator–rotor mutual inductance matrix | |
| Rotor–stator mutual inductance matrix | |
| Mutual inductance between stator phase i and stator phase j | |
| Mutual inductance between stator phase i and rotor circuit j | |
| Mutual inductance between the i-th and j-th rotor circuits | |
| Rotor bar leakage inductance | |
| End ring leakage inductance | |
| Number of motor poles | |
| Electric angle | |
| Electromagnetic torque | |
| Rotor inertia | |
| Rotor mechanical angular velocity | |
| Load torque | |
| Rotor eccentricity | |
| Rotor eccentricity angle | |
| Relative eccentricity | |
| Uniformly distributed air gap length | |
| Air gap length function | |
| Permeability of air gap | |
| Air gap left radius | |
| Stack length | |
| Turn function of coil | |
| Winding function of coil | |
| Inverse function of air gap length | |
| Stator space angle position | |
| The average value of the air gap inverse function | |
| Time | |
| Rotor mechanical angular position | |
| Rotor electric angular velocity | |
| Stator and rotor magnetomotive force amplitude | |
| Fourier coefficient of air gap permeability | |
| Number of phases/imputed number of phases | |
| Total number of series turns per phase/imputed total number of series turns per phase | |
| Fundamental winding factor | |
| Fundamental wave pitch factor | |
| Fundamental distribution factor | |
| Bearing outer race fault frequency (in vibration) | |
| Bearing inner race fault frequency (in vibration) | |
| Bearing ball fault frequency (in vibration) | |
| Bearing outer race fault frequency (in stator current) | |
| Bearing inner race fault frequency (in stator current) | |
| Bearing ball fault frequency (in stator current) | |
| Bearing cage rotation frequency |
References
- Report of Large Motor Reliability Survey of Industrial and Commercial Installations, Part I. IEEE Trans. Ind. Appl. 1985, IA-21, 853–864. [CrossRef]
- Report of Large Motor Reliability Survey of Industrial and Commercial Installations, Part II. IEEE Trans. Ind. Appl. 1985, IA-21, 865–872. [CrossRef]
- Report of Large Motor Reliability Survey of Industrial and Commercial Installations: Part 3. IEEE Trans. Ind. Appl. 1987, IA-23, 153–158. [CrossRef]
- Albrecht, P.; Appiarius, J.; McCoy, R.; Owen, E.; Sharma, D. Assessment of the Reliability of Motors in Utility Applications—Updated. IEEE Trans. Energy Convers. 1986, EC-1, 39–46. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, H.; Xu, J.; Deng, W. Performance Prediction Using High-Order Differential Mathematical Morphology Gradient Spectrum Entropy and Extreme Learning Machine. IEEE Trans. Instrum. Meas. 2019, 69, 4165–4172. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, N.; Shen, C. A new data-driven transferable remaining useful life prediction approach for bearing under different working conditions. Mech. Syst. Signal Process. 2020, 139, 106602. [Google Scholar] [CrossRef]
- Cui, H.; Guan, Y.; Chen, H.; Deng, W. A Novel Advancing Signal Processing Method Based on Coupled Multi-Stable Stochastic Resonance for Fault Detection. Appl. Sci. 2021, 11, 5385. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Y.; Zheng, H.; Wang, R.; Xu, M. A new dynamic model and transfer learning based intelligent fault diagnosis framework for rolling element bearings race faults: Solving the small sample problem. ISA Trans. 2021, 121, 327–348. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, B.; Bin Zhang, B.; Yang, S. Establishment of Dynamic Model for Axle Box Bearing of High-Speed Trains Under Variable Speed Conditions. Chin. J. Mech. Eng. 2022, 35, 47. [Google Scholar] [CrossRef]
- Randall, R.B. The Use of Simulation Models to Generate Data Corresponding to Faults in Machines. In Proceedings of the 8th International Conference on Reliability, Maintainability and Safety(ICRMS 2009), Chengdu, China; pp. 256–261.
- Gray, A.; Pertsch, J.G. Critical review of the bibliography on unbalanced magnetic pull in dynamo-electric machines. Trans. Am. Inst. Electr. Eng. 1918, 37, 1417–1424. [Google Scholar] [CrossRef]
- Behrend, B. On the mechanical forces in dynamos caused by magnetic attraction. Trans. Am. Inst. Electr. Eng. 1900, 17, 613–633. [Google Scholar] [CrossRef]
- Dorrell, D.; Smith, A. Calculation and measurement of unbalanced magnetic pull in cage induction motors with eccentric rotors. Part 2: Experimental investigation. IEE Proc.-Electr. Power Appl. 1996, 143, 202–210. [Google Scholar] [CrossRef]
- Smith, A.; Dorrell, D. Calculation and measurement of unbalanced magnetic pull in cage induction motors with eccentric rotors. Part 1: Analytical model. IEE Proc.-Electr. Power Appl. 1996, 143, 193–201. [Google Scholar] [CrossRef]
- Dorrell, D.G. Sources and characteristics of unbalanced magnetic pull in 3-phase cage induction motors with axial-varying rotor eccentricity. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 240–247. [Google Scholar] [CrossRef]
- Guo, D.; Chu, F.; Chen, D. The unbalanced magnetic pull and its effects on vibration in a three-phase generator with eccentric rotor. J. Sound Vib. 2002, 254, 297–312. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, S.; Peng, Z. Nonlinear vibration for PMSM used in HEV considering mechanical and magnetic coupling effects. Nonlinear Dyn. 2015, 80, 541–552. [Google Scholar] [CrossRef]
- Han, X.; Palazzolo, A. Unstable force analysis for induction motor eccentricity. J. Sound Vib. 2016, 370, 230–258. [Google Scholar] [CrossRef]
- Zhang, A.; Bai, Y.; Yang, B.; Li, H. Analysis of Nonlinear Vibration in Permanent Magnet Synchronous Motors under Unbalanced Magnetic Pull. Appl. Sci. 2018, 8, 113. [Google Scholar] [CrossRef]
- Cheng, M.; Meng, G.; Jing, J. Non-Linear Dynamics of a Rotor-Bearing-Seal System. Arch. Appl. Mech. 2006, 76, 215–227. [Google Scholar] [CrossRef]
- Li, Y.; Cao, H.; Tang, K. A general dynamic model coupled with EFEM and DBM of rolling bearing-rotor system. Mech. Syst. Signal Process. 2019, 134, 106322. [Google Scholar] [CrossRef]
- Yan, D.; Wang, W.; Chen, Q. Fractional-order modeling and nonlinear dynamic analyses of the rotor-bearing-seal system. Chaos Solitons Fractals 2020, 133, 109640. [Google Scholar] [CrossRef]
- Cheng, H.; Zhang, Y.; Lu, W.; Yang, Z. Mechanical characteristics and nonlinear dynamic response analysis of rotor-bearing-coupling system. Appl. Math. Model. 2021, 93, 708–727. [Google Scholar] [CrossRef]
- Fourati, A.; Bourdon, A.; Feki, N.; Rémond, D.; Chaari, F.; Haddar, M. Angular-based modeling of induction motors for monitoring. J. Sound Vib. 2017, 395, 371–392. [Google Scholar] [CrossRef]
- Han, Q.; Ding, Z.; Xu, X.; Wang, T.; Chu, F. Stator current model for detecting rolling bearing faults in induction motors using magnetic equivalent circuits. Mech. Syst. Signal Process. 2019, 131, 554–575. [Google Scholar] [CrossRef]
- Zhou, S.; Guo, W.; Xiao, Q.; Zhu, J.; Zhou, X.; Tu, W. Vibration Characteristics Analysis of EMU Traction Motor Rotor Under Eccentric Faults. Eng. Mech. 2021, 38, 216–225. [Google Scholar]
- Schoen, R.; Habetler, T.; Kamran, F.; Bartfield, R. Motor bearing damage detection using stator current monitoring. IEEE Trans. Ind. Appl. 1995, 31, 1274–1279. [Google Scholar] [CrossRef]
- Blodt, M.; Granjon, P.; Raison, B.; Rostaing, G. Models for Bearing Damage Detection in Induction Motors Using Stator Current Monitoring. IEEE Trans. Ind. Electron. 2008, 55, 1813–1822. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| bearing designation | SKF 6203 |
| bearing outer race diameter | 40 mm |
| bearing inner race diameter | 17 mm |
| bearing ball diameter | 6.747 mm |
| number of bearing balls | 8 |
| bearing clearance | 3 × 10−2 mm |
| spalling width | 3 mm |
| rotor mass | 2.2299 kg |
| rotor damping | 600 N∙s/m |
| Parameter | Value |
|---|---|
| number of phases | 3 |
| number of poles | 2 |
| rated power | 1/3 Hp |
| number of stator slots | 24 |
| number of stator coil turns | 126 |
| stator resistance | 2.2 Ω |
| number of rotor bars | 34 |
| rotor length | 60 mm |
| rotor bar resistance | 8 × 10−5 Ω |
| end ring resistance | 2.375 × 10−5 Ω |
| center radius of air gap | 40.25 mm |
| initial length of air gap | 0.7 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Shen, G.; Hu, N.; Chen, L.; Yang, Y. Coupled Electromagnetic-Dynamic Modeling and Bearing Fault Characteristics of Induction Motors considering Unbalanced Magnetic Pull. Entropy 2022, 24, 1386. https://doi.org/10.3390/e24101386
Huang L, Shen G, Hu N, Chen L, Yang Y. Coupled Electromagnetic-Dynamic Modeling and Bearing Fault Characteristics of Induction Motors considering Unbalanced Magnetic Pull. Entropy. 2022; 24(10):1386. https://doi.org/10.3390/e24101386
Chicago/Turabian StyleHuang, Liangyuan, Guoji Shen, Niaoqing Hu, Ling Chen, and Yi Yang. 2022. "Coupled Electromagnetic-Dynamic Modeling and Bearing Fault Characteristics of Induction Motors considering Unbalanced Magnetic Pull" Entropy 24, no. 10: 1386. https://doi.org/10.3390/e24101386
APA StyleHuang, L., Shen, G., Hu, N., Chen, L., & Yang, Y. (2022). Coupled Electromagnetic-Dynamic Modeling and Bearing Fault Characteristics of Induction Motors considering Unbalanced Magnetic Pull. Entropy, 24(10), 1386. https://doi.org/10.3390/e24101386






