1. Introduction
Sadi Carnot had a crucial contribution to thermostatics that designated him as a co-founding researcher of equilibrium thermodynamics. He has shown that the efficiency of a thermo-mechanical engine is bounded by the Carnot efficiency
ηC [
1]. Assuming an isothermal source at
THS, and an isothermal sink at
TCS <
THS, and in between the cycle composed by two isothermals in perfect thermal contact with the source and sink, and two isentropics, he obtained:
Since that time, many papers have used the keyword “Carnot engine” (1290 papers from Web of Science on 17 September 2021). That same day on Web of Science, we noted 104 papers related to the keyword “Carnot efficiency”.
Among these papers, some are related to the connection between energy, efficiency, and power optimization. The most cited paper is probably that of Curzon and Ahlborn [
2,
3]. These authors proposed in 1975 an expression of the efficiency according to the first law of thermodynamics
at the maximum mechanical energy and at the maximum power
for the endo-reversible configuration of the Carnot cycle (no internal irreversibility for the converter in contact with two isothermal heat reservoirs):
This result is well-known as the
nice radical, and it has been recently reconsidered in the previous Special Issue
Carnot Cycle and Heat Engine Fundamentals and Applications I [
3] and particularly in [
4]. This last paper reports on the progress in Carnot and Chambadal modeling of thermomechanical engines by considering entropy production and heat transfer entropy in the adiabatic case (without heat losses).
The proposed paper gives back the basis of the modeling and a summary of the main results obtained recently for an endo-irreversible Carnot engine. Furthermore, the performance analysis of an extended Chambadal configuration is considered by including the converter irreversibilities. Emphasis is placed on the entropy production method, which is preferred over the ratio method.
2. Summary of Obtained Results for Carnot Endo-Irreversible Configuration
The consideration of
endo-irreversible Carnot engine modeling was recently developed [
5]. The approach considering as a reference the heat transfer entropy released at the sink Δ
SS (maximum entropy available at the source in the reversible case) [
5] confirmed that the work per cycle results (see
Appendix A):
where Δ
SI is the entropy production due to the internal irreversibilities of the cycle throughout the four thermodynamic transformations (two adiabatic and two isothermal ones).
For an engine without thermal losses, the following expression of the thermal efficiency was retrieved:
where
is a coefficient of the converter’s internal irreversibility during the cycle.
This parameter was introduced by Novikov [
6] and Ibrahim et al. [
7] in slightly different forms.
The reversible limit (dI = 0) in Equation (4) restores the Carnot cycle efficiency associated with equilibrium thermodynamics.
Since the reversibility is unattainable, it appears that the optimization (maximization) of the mechanical energy at the given parameters (Δ
SS,
THS, and
TCS) is related to the minimization of the entropy production (as was proposed by Gouy [
8]).
The assumption that each of the four transformations of the endo-irreversible cycle takes place with a duration
τi (
i = 1–4), leading to the inverse proportionality to
τi of the corresponding entropy production:
where
CIi represents the irreversibility coefficients, whose unit is Js/K [
5].
These coefficients are irreversible entropic actions by analogy to the energy (mechanical) action (Js).
By performing cycle energy optimization using the Lagrange multipliers method with the constraint of the cycle’s finite time duration
τ, one obtains the maximum work per cycle [
5]:
where Δ
TS =
THS −
TCS.
The efficiency at the maximum finite time work becomes
where
is the available entropic transfer action of the cycle.
The new result provided by Equation (7) gives back the Carnot efficiency limit for the reversible case (
CIi = 0). These calculations have been pursued for the case of power optimization, where Δ
SS,
THS, and
TCS remain parameters. It was shown that a value of the cycle duration
corresponding to
, the mean power output over the cycle, exists, and it is expressed as
and
Equation (9) proves that
is a decreasing function of the total entropic action of the cycle and that the associated efficiency with the maximum of the mean power corresponds to half the Carnot efficiency, as appeared repeatedly in some recent works [
9,
10,
11].
3. Summary of the Obtained Results for the Chambadal Configuration
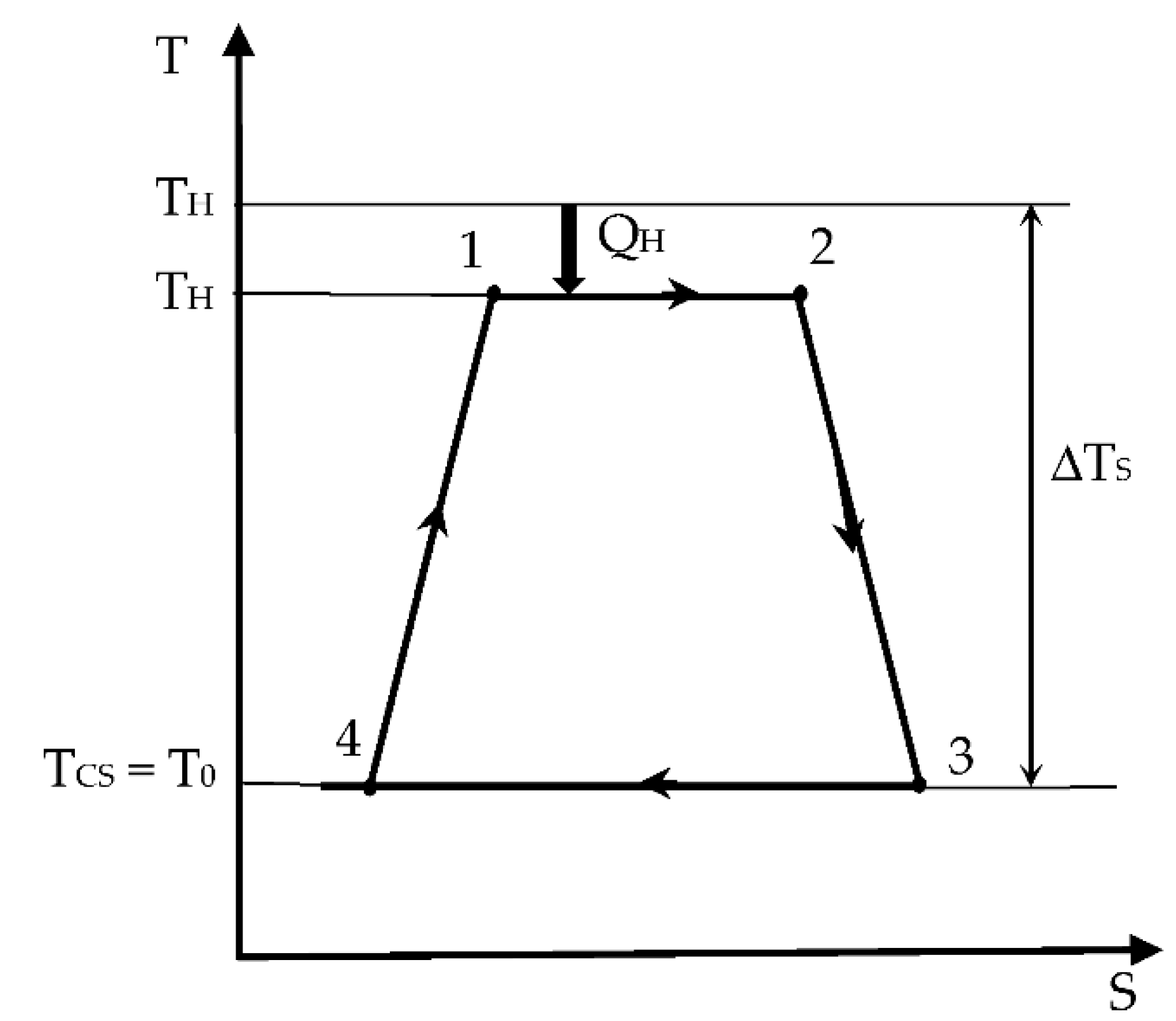
In the present paper, we intend to reconsider the approach of the Chambadal model of a Carnot engine [
12]. This configuration is common for thermomechanical engines, since the cold sink mainly refers to the environment (i.e., the atmosphere or water sink). This corresponds to the Chambadal approach (
Figure 1), with a temperature gradient at the hot source (
THS,
TH) but with perfect thermal contact at the sink (
TCS or
T0 at ambient temperature).
We propose here to extend the results (Equations (6)–(9)) to enhance the Chambadal configuration modeling. This extension starts from the endo-irreversible case, to which external irreversibilities due to heat transfer between the hot finite source and the converter are added. Thus, the new results obtained complete the endo-irreversible Carnot model [
5] and an earlier paper on Chambadal configuration [
12].
3.1. The Modified Chambadal Engine
To help understand the extension of the modeling in
Section 3, we report here the case with the following hypothesis:
Equation (10) corresponds to the heat expense of the engine.
Note that other heat transfer laws, namely the Stefan–Boltzmann radiation law, the Dulong–Petit law, and another phenomenological heat transfer law can be considered in the maximum power regime search [
13];
- 3.
Presence of irreversibility in the converter (internal irreversibility).
Two approaches are proposed in the literature, which introduce the internal irreversibility of the engine by (1) the
irreversibility ratio IH, [
6,
7], respectively (2) the
entropy production over the cycle Δ
SI, [
5].
We preconized this second approach for a long time. We also note that the original model of Chambadal is endo-reversible [
14]. Hence, we prefer to name the present model the “modified Chambadal model” due to some other differences that will be specified hereafter.
Note that only the second approach regarding the presence of irreversibilities in the converter will be considered in the following section.
3.2. Optimization of the Work per Cycle of the Modified Chambadal Engine with the Entropy Production Method
The first law of thermodynamics applied to the cycle implies conservation of energy, written as
where
and
are defined in
Appendix A.
One supposes here that Δ
SI is a parameter representing the total production of entropy over the cycle composed by four irreversible transformations. Thus, the entropy balance corresponds to
By combining Equations (11) and (12), we easily obtained
If
(Δ
Sconv) is a given parameter, we retrieve the Gouy-Stodola theorem stating that
Max W corresponds to min Δ
SI with the known consequences reported in
Section 4.1.
3.3. Optimization of the Work per Cycle of the Modified Chambadal Engine with the Heat Transfer Constraint
In this case, the energy balance between the source and isothermal transformation implies the combination of Equations (13) and (A1):
Knowing
QH from Equation (10), one obtains
where
.
The maximum of
W with respect to
TH is obtained for
where
, a specific ratio relative to the irreversible isothermal transformation
TH.
Finally, the expression of
yields
4. Complement to the Previous Results
Now, we will consider the time variable related to entropy production for each thermodynamic transformation, defined as . This form of the entropy production satisfying the second law induces that the entropy production method is well adapted to subsequent optimizations of energy and power as well.
4.1. Work Optimization Relative to the Time Variables
The expression of with GH as an extensive parameter (Equation (17)) shows that is always the optimum in the endo-reversible case. Nevertheless, if there are separate irreversibilities for each cycle transformation (as is the case with finite entropic actions), the irreversibility on the high temperature isotherm possesses a specific role (see Equation (17) and the ratio).
The constraint on the transformation duration or preferably frequencies
fi (finite cycle duration) allows one to seek for the optimal transformation duration allocation (see
Appendix B for the derivation).
We obtained
for the following optimal durations:
and
where
λ is given in
Appendix B and
i =
Ex,
C,
Co.Thus, the second optimization of
W (see
Appendix B) leads to
Furthermore, a third sequential optimization could be performed by considering the finite entropic action as a new constraint. This case is not developed here for brevity reasons.
4.2. Power Optimization in the Case of a Finite Heat Source (When GH Is the Parameter)
The mean power of the modified Chambadal cycle for the condition of maximum work
is defined by
where
is the mechanical work output of the endo-reversible engine.
The power is maximized with respect to the cycle period
τ. Thus, the expression of the optimum period is
This expression is analogous to the similar results obtained in [
5], leading to
The action of entropy production appearing in
N diminishes the mean power of the engine. At the given endo-reversible work, the maximum power corresponds to the minimum of the
N function, depending on the four entropy actions of the cycle, such that
The main difference between Equation (23) and the previous results [
5] comes from the imperfect heat transfer between the source and the converter in the Chambadal model.
5. Discussion
This paper proposed that the Special Issue
Carnot Cycle and Heat Engine Fundamentals and Applications II completes the previous paper [
12] published in Special Issue 1 and adds new results to a recently published paper [
5].
Whatever variable is chosen for the modified Chambadal model work optimization (TH or ΔS), the same optimum for the work per cycle is obtained with parameters GH, THS, and T0.
It appears that by introducing the duration of each transformation τi and the period of the cycle τ, the modified Chambadal model satisfies the Gouy-Stodola theorem. At the minimum of entropy production, the optimal durations are dependent on the transformation entropy actions. This result is new to our knowledge.
This new concept [
5] allows a new subsequent sequential optimization. The optimal allocation of the entropy action coefficients is slightly different from the equipartition (a new form of the equipartition theorem [
15,
16]).
Thus, the fundamental aspect related to irreversibilities through the new concept of entropy production action seems promising. Furthermore, this new concept could contribute to the improvement of the global system analysis by conducting optimal dimension allocation. In this respect, finite physical dimensions analysis could be a complementary way to correlate with exergy analysis.
Further extensions of this work are foreseen in the near future.
6. Conclusions
Similarities and differences present in the literature regarding the optimization of energy, first law efficiency, and power of the modified Chambadal engine have been resituated and summarized since the publication of [
12].
This approach allows for highlighting the evolution of the obtained results from the reversible Carnot engine case (thermostatics) to the endo-irreversible models related to the approaches of Novikov [
6] and Ibrahim et al. [
7] or to the entropy production method that we promote.
By generalizing a proposal from Esposito et al. [
9] and defining the new concept of entropic action through a coefficient
CI (Js/K) for the entropy production of transformations all along the cycle, we achieved a new form of power optimization different from the one of Curzon and Ahlborn, since the internal converter irreversibilities and the heat transfer irreversibility between the heat source and converter were accounted for.
The maximum work per cycle was obtained for the irreversible cycle case. It depended on the entropic action coefficient of the four transformations of the cycle CIi, after which the power of the engine was sequentially optimized.
An optimal period of the cycle
τ* appeared, corresponding to the maximum mean power of the cycle. It generalized the recent published results [
5] for a modified Chambadal engine.
This research continues to be developed by our team to obtain more general results.
Author Contributions
Conceptualization, M.F.; methodology, M.F.; software, M.C.; validation, M.F. and M.C.; formal analysis, M.F. and M.C.; writing—original draft preparation, M.F.; writing—review and editing, M.C.; visualization, M.F. and M.C.; supervision, M.F.; project administration, M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Work per Cycle of the Modified Chambadal Engine with the Entropy Production Method
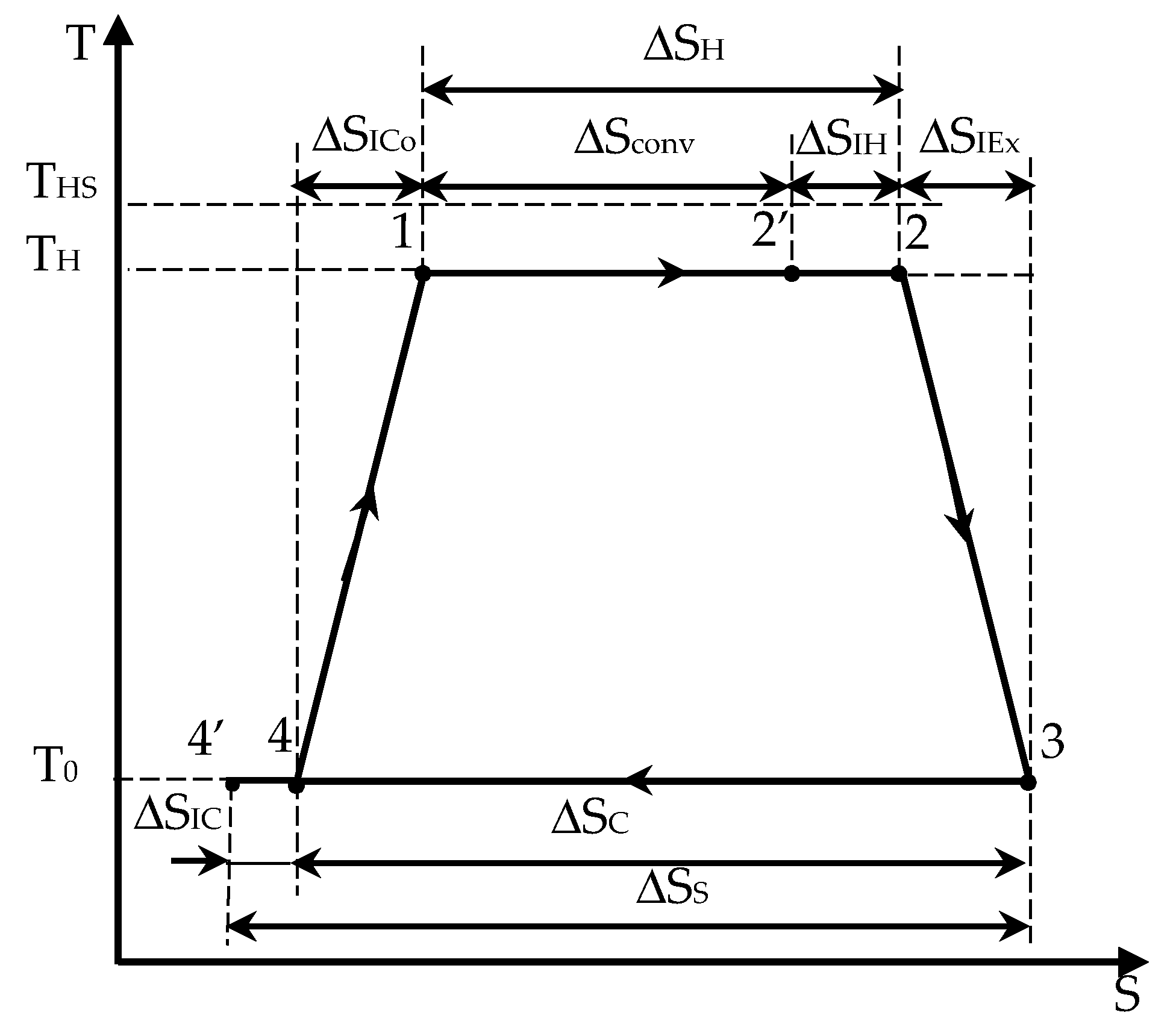
Figure A1.
Carnot engine cycle with internal irreversibilities along the four transformations of the cycle, illustrated in a T-S diagram.
Figure A1.
Carnot engine cycle with internal irreversibilities along the four transformations of the cycle, illustrated in a T-S diagram.
It results from
Figure A1 that the various heats exchanged over the irreversible cycle (1–2–3–4) are expressed as follows:
is the heat received by the cycled medium from the hot source (energy expense), corresponding to the heat transfer at the hot side;
, heat converted in mechanical energy during the isothermal process at
, with corresponding production of entropy
such that:
, where .
Note that is the entropy production during the irreversible isotherm at T0 and is the entropy rejected to the sink such that .
Thus, the entropy balance over the cycle is
The total entropy production over the cycle
is represented by
where
ΔSIH is the entropy production during the isothermal transformation at TH, ΔSIE is the entropy production during the adiabatic expansion from TH to T0, ΔSIC is the entropy production during the isothermal transformation at T0, and ΔSICo, is the entropy production during the adiabatic compression from T0 to TH.
The energy balance over the cycle for the system comprising the converter, the heat source, and the sink (with the source and sink as perfect thermostats) provides
Various forms of mechanical energy are obtainable from this point by combining the preceding relations. Thus, one may express W as follows:
With
as the reference entropy:
With
as the reference entropy:
With
or
as the reference entropy:
We prefer to choose between Equations (A6) and (A7). Note that Equation (A7) was the one used by Esposito et al. [
9].
We use Equation (A6) here because it gave back known results, particularly the Gouy-Stodola theorem, with
being a parameter. Thus, the maximum energy occurs when
such that
This corresponds to the endo-reversible model of Chambadal.
In
Section 3, we proposed a complete Chambadal model taking account entropy production all along the cycle.
Appendix B. Work Optimization Relative to Time (Frequency)
Using the Lagrange multipliers method with the frequencies
as variables, we get the following function:
The vector of optimal values is
Additionally, the following is a non-linear equation to solve numerically for
:
In the reasonable case of low irreversibility on the
TH isotherm
, a good approximation of
is
The finitude constraint on
allows for determining the
expression as
where
References
- Carnot, S. Réflexion sur la Puissance Motrice du feu et des Machines Propres à Développer Cette Puissance; Albert Blanchard: Paris, France, 1953. (In French) [Google Scholar]
- Curzon, F.L.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Feidt, M. Carnot Cycle and Heat Engine Fundamentals and Applications. Entropy 2020, 22, 348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feidt, M. The History and Perspectives of Efficiency at Maximum Power of the Carnot Engine. Entropy 2017, 19, 369. [Google Scholar] [CrossRef]
- Feidt, M.; Feidt, R. Endo-irreversible thermo-mechanical Carnot engine with new concept of entropy production action coefficient. Eur. Phys. J. Appl. Phys. 2021, 94, 30901. [Google Scholar] [CrossRef]
- Novikov, I. The efficiency of atomic power stations (a review). J. Nucl. Energy 1958, 7, 125–128. [Google Scholar] [CrossRef]
- Ibrahim, O.M.; Klein, S.A.; Mitchell, J.W. Optimum Heat Power Cycles for Specified Boundary Conditions. J. Eng. Gas Turbines Power 1991, 113, 514–521. [Google Scholar] [CrossRef]
- Gouy, G. Sur l’énergie utilizable. J. Phys. 1889, 8, 501–508. (In French) [Google Scholar]
- Esposito, M.; Kawai, R.; Lindenberg, K.; Van den Broeck, C. Efficiency at Maximum Power of Low-Dissipation Carnot Engines. Phys. Rev. Lett. 2010, 105, 150603. [Google Scholar] [CrossRef] [PubMed]
- Feidt, M.; Costea, M. From Finite Time to Finite Physical Dimensions Thermodynamics: The Carnot Engine and Onsager’s Relations Revisited. J. Non-Equilib. Thermodyn. 2018, 43, 151–161. [Google Scholar] [CrossRef]
- Dorfman, K.E.; Xu, D.; Cao, J. Efficiency at maximum power of a laser quantum heat engine enhanced by noise-induced coherence. Phys. Rev. E 2018, 97, 042120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feidt, M.; Costea, M. Progress in Carnot and Chambadal Modeling of Thermomechanical Engine by Considering Entropy Production and Heat Transfer Entropy. Entropy 2019, 21, 1232. [Google Scholar] [CrossRef] [Green Version]
- Barranco-Jimenez, M.A. Finite-time thermoeconomic optimization of a non endoreversible heat engine model. Rev. Mex. Fís. 2009, 55, 211–220. [Google Scholar]
- Chambadal, P. Les Centrales Nucléaires; Armand Colin: Paris, France, 1957. (In French) [Google Scholar]
- Tondeur, D. Optimisation Thermodynamique: Équipartition de Production d’entropie. Available online: https://hal.archives-ouvertes.fr/hal-00560251/ (accessed on 25 October 2021). (In French).
- Tondeur, D. Optimisation Thermodynamique. Equipartition: Exemples et Applications. Available online: https://hal.archives-ouvertes.fr/hal-00560257/ (accessed on 25 October 2021). (In French).
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).