1. Introduction
Symmetric positive-definite matrices have wide usage in many fields of information science, such as stability analysis of signal processing, linear stationary systems, optimal control strategies and imaging analysis [
1,
2,
3]. Its importance is beyond words [
4,
5]. Instead of considering a single matrix, contemporary scientists tend to comprehend the global structure of the set consisting of all
symmetric positive-definite matrices. This set is known as
.
can be endowed with various structures. The most traditional Euclidean metric is induced as submanifold metric from the Euclidean inner product on the space of matrices. X. Pennec, P. Fillard et al. [
6] defined the affine-invariant Riemannian metric. V. Arsigny, P. Fillard et al. [
7] showed the Lie group [
8] structure on
, which admits a bi-invariant metric called the Log-Euclidean metric.
Recently, by constructing a principle bundle, Y. Li, M. Wong et al. [
9] and S. Zhang et al. [
10] defined a new Riemannian metric on
whose geodesic distance is equivalent to the Wasserstein-2 [
11,
12] distance, the so-called Wasserstein metric. This distance rather than the metric has been widely used in artificial intelligence [
13]. In geometry, encouragingly, T. Asuka [
14] and E. Massart, P.-A. Absil [
15] gave a series of expressions for geometric quantities theoretically. However, these expressions are too general or complicated to be applied. In this paper, we derive more computationally feasible expressions in a concrete case. Moreover, we give the Jacobi field and scalar curvature.
Along the blooming of data science, point cloud processing, especially denoising, plays an increasingly important role in data relevant researches and engineering. There are immense literature in point cloud denoising and widely used algorithms packed as inline functions of softwares such as PCL [
16]. These methods share a common drawback when high density noise is added to point clouds. Utilizing the geometric structure of
, we design a novel algorithm to overcome this drawback. Compared to traditional methods, our algorithm is more accurate and less dependent on artificial parameters.
In addition to that, we involve our theory for image edge detection, which is a classical problem in image processing and design a new detecting algorithm. Different from traditional gradient-based filters, such as Sobel, Prewitt and Laplacian, we present the connection between Wasserstein sectional curvature and edges. Experiments show the feasibility of our algorithm.
The paper is organized as follows. In
Section 2, we introduce some basic knowledge of the Riemannian manifold
, and consider the symmetry of the
as well. In
Section 3, we describe the Wasserstein geometry of
, including the geodesic, exponential map, connection and curvature. In particular, we prove the geodesic convexity and the nonexistence of cut locus and conjugate pair. In
Section 4, we design an adaptive algorithm to denoise point clouds. In
Section 5, we develop a curvature-based method to detect image edge. Proofs and detailed numerical results are presented in the
Appendix B.
2. Preliminary
2.1. Notation
In this paper, we adopt conventional notations in algebra and geometry. Riemannian manifolds are denoted as pairs of . For example, our mainly interesting object is , meaning endowed with Wasserstein metric. is the n-dimensional Euclidean space. represents the set of matrices, means the set of symmetric matrices, and means the set of orthogonal matrices. is conventionally the tangent space of M at a point A.
always represents a diagonal matrix. For an matrix A, or means an eigenvalue or the i-th eigenvalue of A, respectively. The components of matrix A with the entries will always be noted as . The identity matrix is denoted as I. In this paper, we conventionally express points on manifolds as and vector fields as .
Sylvester equation is one of the most classical matrix equations. The following special case of Sylvester equation plays a key role in understand the geometry of
We denote the solution about
K of (
1) as
. Then, the matrix
satisfies
From geometric aspects, we can ensure the existence and uniqueness of the solution in the case involved in this paper. Some properties of
can be found in
Appendix A. More details about the Sylvester equation are presented in [
17].
We recall an algorithm to solve this kind of Sylvester equations, which offers an explicit expression of the solution. This expression only depends on the eigenvalue decomposition. More details can be found in [
10].
Algorithm 1 will be used frequently in the following passage, and it helps us to comprehend the geometry of
. Note that this algorithm can also be used for general
. In particular, when
X is symmetric (skew-symmetric),
is also symmetric (skew-symmetric). Moreover, this algorithm will be simplified if
A is diagonal.
| Algorithm 1 Solution of Sylvester Equation. |
Input: Output: - 1:
Eigenvalue decomposition, , where are eigenvalues of A; - 2:
; - 3:
; - 4:
.
|
2.2. Wasserstein Metric
In this part, we introduce the Wasserstein metric on .
Definition 1. For any , , define In the second equation, we use the facts that
are all symetric and that
. One can check that
is a symmetric and non-degenerated bilinear tensor fields on
[
18]. We call
the Wasserstein metric.
Denote as Euclidean metric on . Then, we have the following conclusions.
Proposition 1. The projectionis a Riemannian submersion [19], which means that is surjective and Remark 1. The general linear group with Euclidean metric and projection σ is a trivial principal bundles on with orthogonal group as the structure group. This bundle structure establishes two facts [10]: , and remains invariant under the group action of . Before giving more conclusions, we review some concepts. For any , we say that the tangent vector is vertical if , and is horizontal if for all vertical vecters . In addition to that, if , we call as a lift of X, where . Using the notation , we can find the horizontal lift of .
Proposition 2. For any , and any , there is a unique to be the horizontal lift of X at —that is, Using Proposition 2, we can obtain the representations of horizontal and vertical vectors.
Proposition 3. For any , has the following orthogonal decompositionwhere consists of all horizontal vectors, consists of all vertical vectors, and Proofs of Proposition 2 and 3 can be found in [
10].
2.3. Symmetry
Now we study the symmetry of
. Consider orthogonal group action
defined by
One can check that
is a group action of
and that
are isometric for all
, which means that
is isomorphic to a subgroup of the isometry group
on
. Precisely, we have
According to (
10), when we study local geometric characteristics, we only need to consider the sorted diagonal matrices as the representational elements under the orthogonal action rather than all general points on
. Therefore, some pointwise quantities, such as the scalar curvature and the bounds of sectional curvatures, depend only on the eigenvalues.
At the end of this part, we give the symmetry degree of , which is defined by the dimension of .
Proposition 4. has its symmetry degree controlled by Proof. The famous interval theorem [
20] about isometric group shows the nonexistence of isometric groups with dimension between
and
, for any
m-dimensional Riemannian manifold, except
.
On one hand, For an n-dimensional Riemannian manifold, the dimension of isometry group achieves maximum if and only if it has constant sectional curvature. However, we will show later that has no constant sectional curvature, which means its symmetry degree is less than the highest.
On the other hand, Equation (
10) shows that the dimension of Wasserstein isometric group is higher than the dimension of
. Therefore, by
and
, we obtain the desired result. □
3. Wasserstein Geometry of
3.1. Geodesic
In this part, we give the expression of geodesic on , including the geodesic jointing of two points and the geodesic with initial values. Then, we will show that the whole Riemannian manifold is geodesic convex, which means that we can always find the minimal geodesic jointing any two points. To some extent, geodesic convexity may make up for the incompleteness of .
To prove the geodesic convexity of , we need the following theorem.
Theorem 1. For any , let be the fixed lift of , there exists a lift of such that the line segment is horizontal and non-degenerated. Proof of Theorem 1 can be found in
Appendix B. This theorem brings some geometrical and physical facts.
Corollary 1. (geodesic convexity) is a geodesic convex Riemannian manifold. Between any two points , there exists a minimal Wasserstein geodesicwhere lies on strictly. Thus, is geodesic convex. The similar expression of geodesic can also be found in several papers [
14,
15].
Theorem 2. For any two points in , there exists a unique geodesic jointing them. From geometric aspect, there is no cut locus on any geodesic.
Proof. We have proved the existence of minimal geodesic jointing any two points in Corollary 1. Assume that the there exists two minimal geodesics jointing
. Fix
as the horizontal lift of
A and lift horizontally these two geodesic, we will find two horizontal lifts of
B. Denote these two lifts as
. Then,
and
are both solutions of the following optimization problem
Since the compactness of
, this problem has a unique solution. Thus, we prove the uniqueness of minimal geodesic. □
Remark 2. Due to the nonexistence of cut locus, there exists no conjugate pair on .
3.2. Exponential Map
Following Lemma A1, we can directly write down the Wasserstein logarithm on
, for any
,
By solving the inverse problem of above equation, we gain the expression of the Wasserstein exponential.
Theorem 3. In a small open ball in , the Wasserstein exponential at A, is explicitly expressed by Proof. By choosing the normal coordinates [
21] at
A, there always exist neighborhoods where
is well-defined. From (
15), given
as well-defined, this satisfies
This equation can convert to the Sylvester equation, and we can express its solution as
Therefore, we have
which finishes this proof. □
Remark 3. We call the first two terms of right hand as the Euclidean exponential, and the last term of right hand as the Wasserstein correction for this bend manifold.
Corollary 2. The geodesic equations with initial conditions on have the following explicit solution Using an exponential map, one can directly construct Jacobi fields with the geodesic variation.
Theorem 4. Along a geodesic with , there exists a unique normal Jacobi vector field with initial conditions , where . We have As in [
18],
is constructed by
substituting (
16) into (
22), and Theorem 4 comes from direct computation.
Subsequently, the next natural question is what is the maximal length of the extension of a geodesic. This question is equivalent to what is the largest domain of the exponential. We still focus on diagonal matrices.
Theorem 5. For any and , is well-defined if and only ifwhere is the minimal eigenvalue of . Proof. Evidently,
. By (
19), we have
where
is the eigenvalue of
. Thus,
. □
Corollary 3. The Wasserstein metric on is incomplete.
Corollary 3 can be directly obtained from Hopf–Rinow theorem [
22]. Theorem 5 and the next theorem help us to comprehend the size of
from sense of each point.
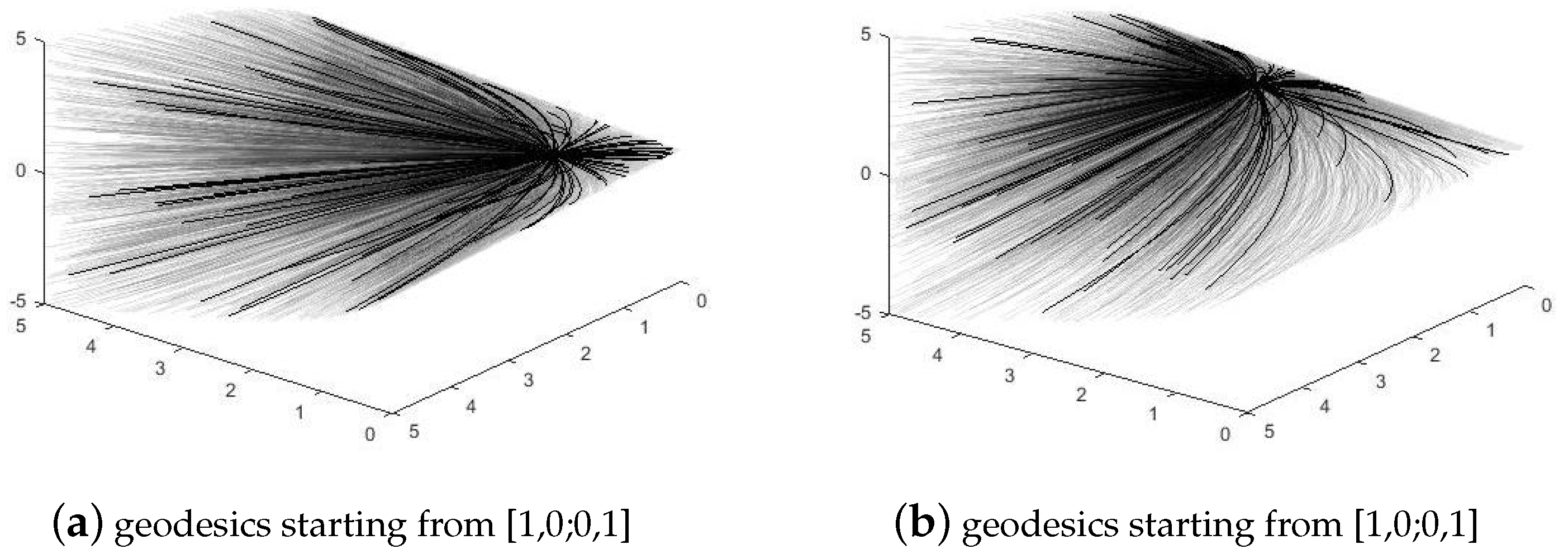
Figure 1 shows geodesics starting from different origins on
. From this group of pictures, we can observe the outline of the manifold and some behaviors of geodesics.
Using , we can obtain the injectivity radius . Geometrically speaking, is the maximal radius of the ball in which is well-defined.
Theorem 6. The Wasserstein radius can be given byand the function is continuous. Proof of Theorem 6 can be found in
Appendix C. Due to the geodesic convexity, the radius actually defines the Wasserstein distance of a point on
to the ’boundary’ of the manifold. It also measures the degenerated degree of a positive-definite symmetric matrix by
.
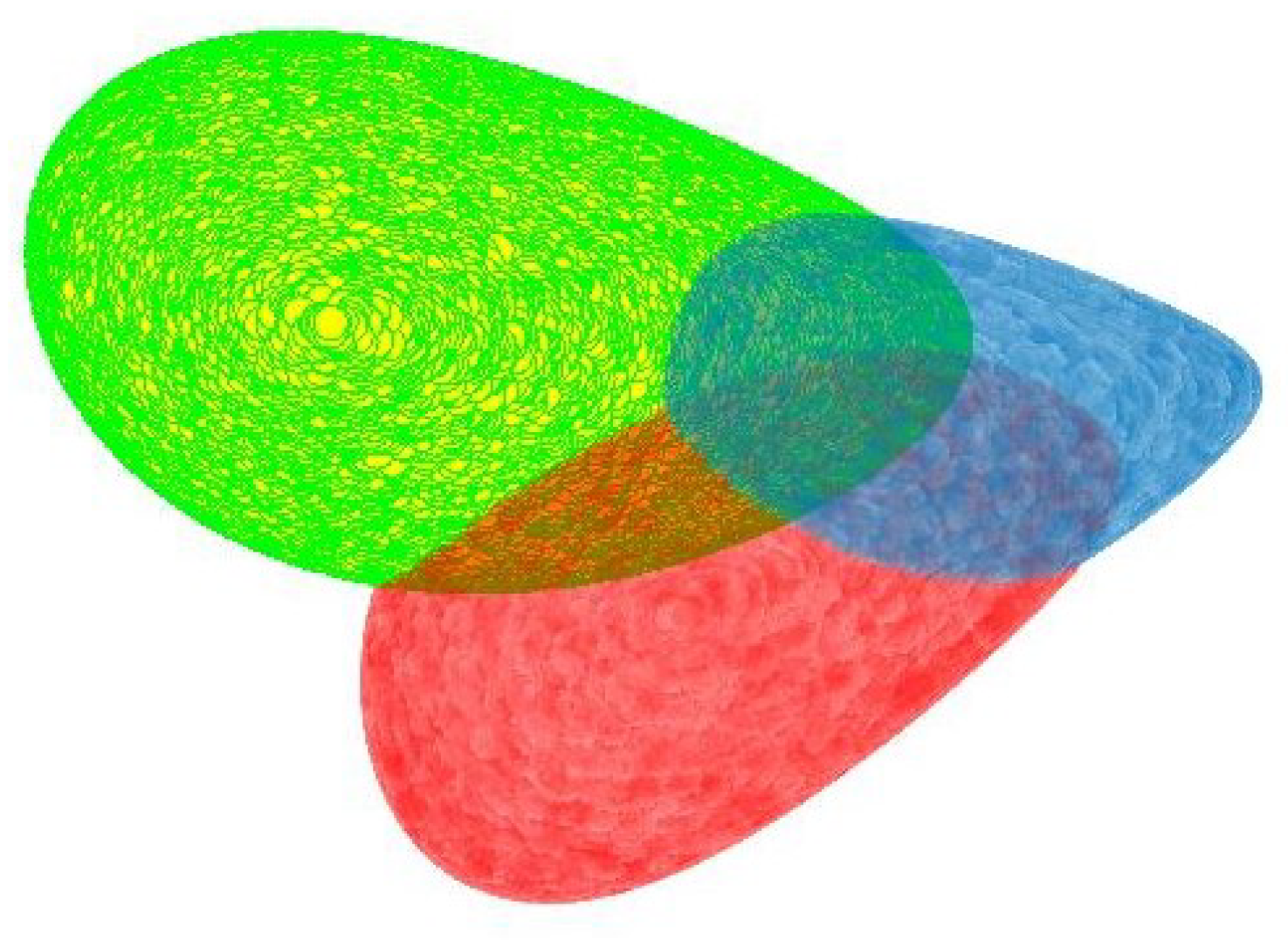
Figure 2 shows three maximal geodisical balls with different centers on
. From the viewpoint of
, the three balls have different sizes in the sense of Euclidean distance, but on
, all of them have the same radius.
3.3. Connection
In this section, we will study the Riemannian connection of , called a Wasserstein connection. The flatness of and the structure of the Riemannian submersion will take a series of convenience to our work. During computation, we denote both tensor actions of on and on by . Then, we denote the Euclidean connection as D and the Wasserstein connection as ∇.
The main idea to express the Wasserstein connection is to compute the horizontal term of the Euclidean covariant derivative of lifted vector fields. We shall prove:
Lemma 1. The Euclidean connection is a lift of the Wasserstein connection. For any smooth vector fields X and Y on , and and are their horizontal lifts, respectively, the following equation holds Proof of Lemma 1 can be found in
Appendix D. This lemma holds for general Riemannian submersion. The reason we reprove it for the case is that we will need use some middle results of the proof later. Using Lemma 1, we can find a direct corollary, which is one of the essential results in this paper.
Corollary 4. The Wasserstein connection has an explicit expression:where is a Euclidean directional derivative. Proof. From Lemma 1 and (
A14) (in
Appendix D), we have
The linearity, Leibnitz’s law and symmetry of Wasserstein connection are easily checked from the expression. □
The vertical component of lifted covariant derivative of
Y along
X is a vector field in
whose value at
is defined by
We say
is an
-tensor. The whole vector field is denoted as
. By definition and previous results, we can obtain the expression of
.
Proposition 5. is a antisymmetric bilinear map: , and it satisfies Proof. Using (
A12) (in
Appendix D), (
6) and (
27), we have
where (
31) shows that
depends only on
and the vectors on
. The multi-linearity and
are easily checked. □
In the following parts, we will show the tensor plays a significant role for computing curvature.
3.4. Curvature
In this part, we tend to understand the curvature of . Although there exists some relevant results giving abstract expressions for general cases, we obtain simpler expressions and derive the scalar curvature via a special basis.
3.4.1. Riemannian Curvature Tensor
First, we derive the Riemannian curvature of . We denote the Euclidean curvature on bundle (null entirely) as , and the Wasserstein (Riemannian) curvature on as R.
Theorem 7. For any , and are smooth vector fields on , the Wasserstein curvature tensor at A has an explicit expression Proof of Theorem 7 can be found in
Appendix E. The expression
has been derived before by other research group in similar way. However, here we use another way to calculate curvature tensor and find a more explicit expression, which is easier than expanding
directly. In addition to that, from
and (
A23) (in
Appendix E), we can obtain the following corollary.
Corollary 5. has non-negative curvatures, namely By solving the Sylvester equation with Algorithm 1, we can simplify the expression. We give the sectional curvature
K of the section
where we use the same donations as Algorithm 1. In particular, in diagonal cases, we obverse that the sectional curvature conforms to the inverse ratio law
These results conform with our visualized views of
, as presented in
Figure 1, where the manifold tends to be flat when
k increases.
3.4.2. Sectional Curvature
Now, we derive more explicit expressions for sectional curvature and scalar curvature. Conventionally, we only need to consider diagonal cases. Before that, we introduce a basis on
, which is the tangent space of
. Define
as
where the superscripts
marks the nonzero elements in
and
is the Kronecker delta. Apparently,
forms a basis of
. For simplicity, we sometimes sign
with
, respectively. In this way, we can express the curvature under this basis.
By direct calculation, we have
By Algorithm 1, we know that
(
in the decomposition of
). Note that the elements of
are all positive; therefore, we have
According to the anti-symmetry of curvature tensor, the non-vanishing curvature means that
. Moreover, by definition we know
. Without loss of generality, we only need to consider the following particular case:
Theorem 8. For any diagonal matrix , where , Wasserstein sectional curvature satisfieswhere . Proof of Theorem 8 can be found in
Appendix F. With the above expansion for sectional curvatures, we can easily find that sectional curvature can be controlled by the secondly minimal eigenvalue, which implies that the curvature will seldom explode even on a domain almost degenerated. Only when the matrices degenerate at over two dimensions will the curvatures be very large. This phenomenon ensures the curvature information makes sense in most applications. Some examples for this phenomenon can be observed later.
3.4.3. Scalar Curvature
In the last part of this section, we calculate the scalar curvature directly.
Theorem 9. For any , its scalar curvature iswhere the diagonal matrix is orthogonal similar to A, and . Proof of Theorem 9 can be found in
Appendix G.
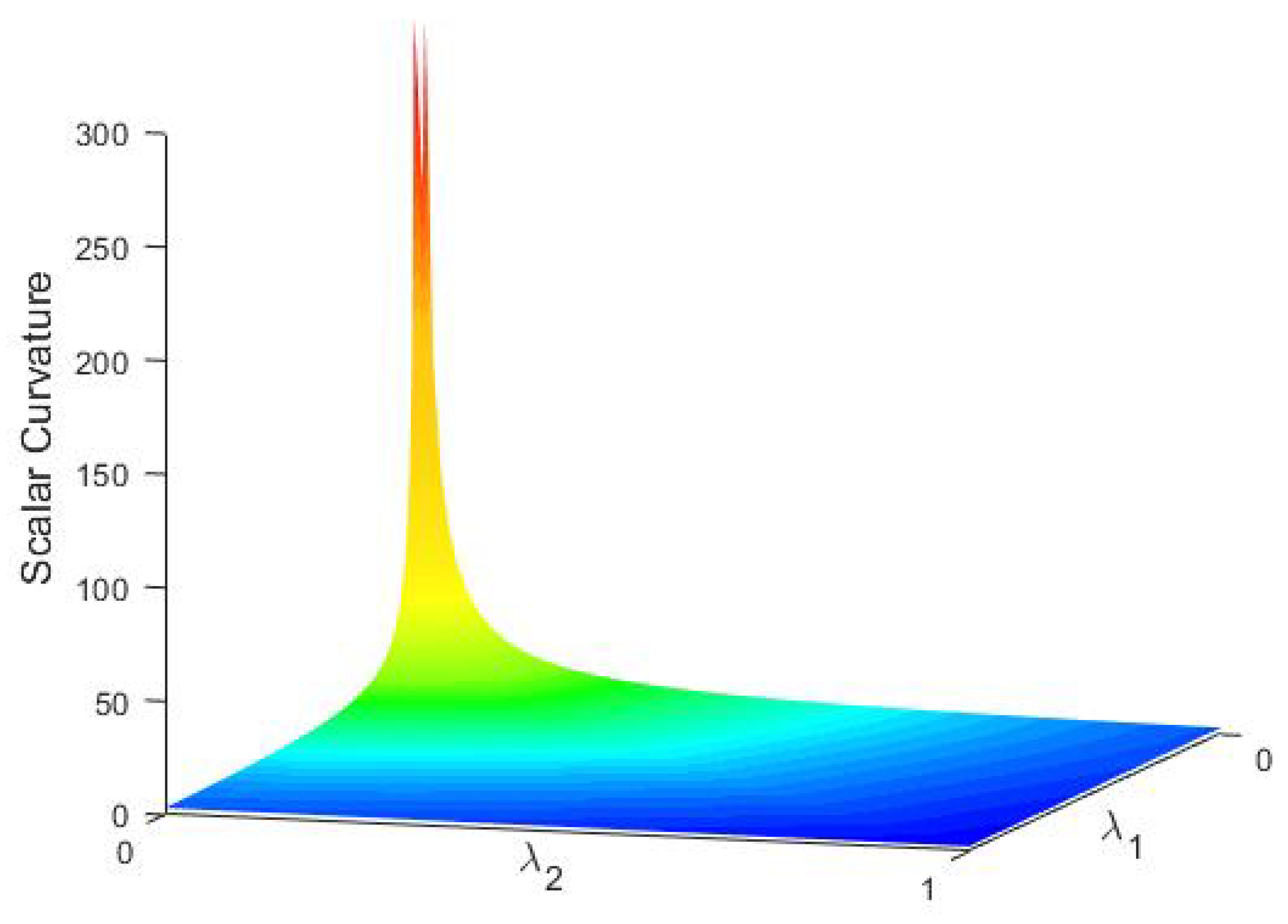
Figure 3 presents some examples for scalar curvatures on
, which shows our argument in the last part of
Section 3.4.2.
4. Point Cloud Denoising
Denoising or outlier removal is a fundamental step of point cloud preprocessing since real-world data are often polluted by noise. There are immense literature in point cloud denoising and widely used algorithms packed as inline functions of softwares. For example, PCL [
16] is a popular platform for point cloud processing, which collects four denoising schemes. However, these methods fail to give satisfactory performance when point clouds are polluted by high density noise. To solve this problem, we consider both the statistical and geometrical structure of data and design a new algorithm.
The idea is that by embedding the original point cloud from Euclidean space into , the Wasserstein scalar curvature gives essential information about noise and true data. Therefore, our new algorithm mainly contains two steps: First, we give the desired embedding by fitting a Gaussian distribution locally at each point. Then, we identify noise by looking at the histogram of the Wasserstein scalar curvature. Due to the flatness of the space of noise, it is reasonable to classify points with small curvature to be noise. The threshold is set to be the first local minimum of the histogram. We call this new scheme adaptive Wasserstein curvature denoising (AWCD).
In the following, we introduce two traditional denoising methods called radius outlier removal (ROR) and statistical outlier removal (SOR). Then, we explain details about AWCD. Additionally, we carry out experiments using different datasets, with a comparison to two classical methods. From the experimental results, AWCD presents better performance regardless of the data size and the density of noise. We also give a time complexity analysis for each denoising algorithm. The results show that AWCD is as efficient as other classical methods. Thus, it is applicable in many practical tasks.
4.1. Radius Outlier Removal
In Radius Outlier Removal, called ROR (seeing Algorithm 2), points are clustered into two categories according to their local density, i.e., points with low density tend to be recognized as noise, whereas points with high density are recognized as true data. ROR requires two parameters: a preset parameter
d as the radius for local neighborhoods and
as the least number of points in each neighborhood.
| Algorithm 2 Radius Outlier Removal. |
Input: initial point cloud , parameters d, Output: cleaned point cloud - 1:
search d-radius neighborhood for each point , where
- 2:
if number of neighbors then put into ; - 3:
return.
|
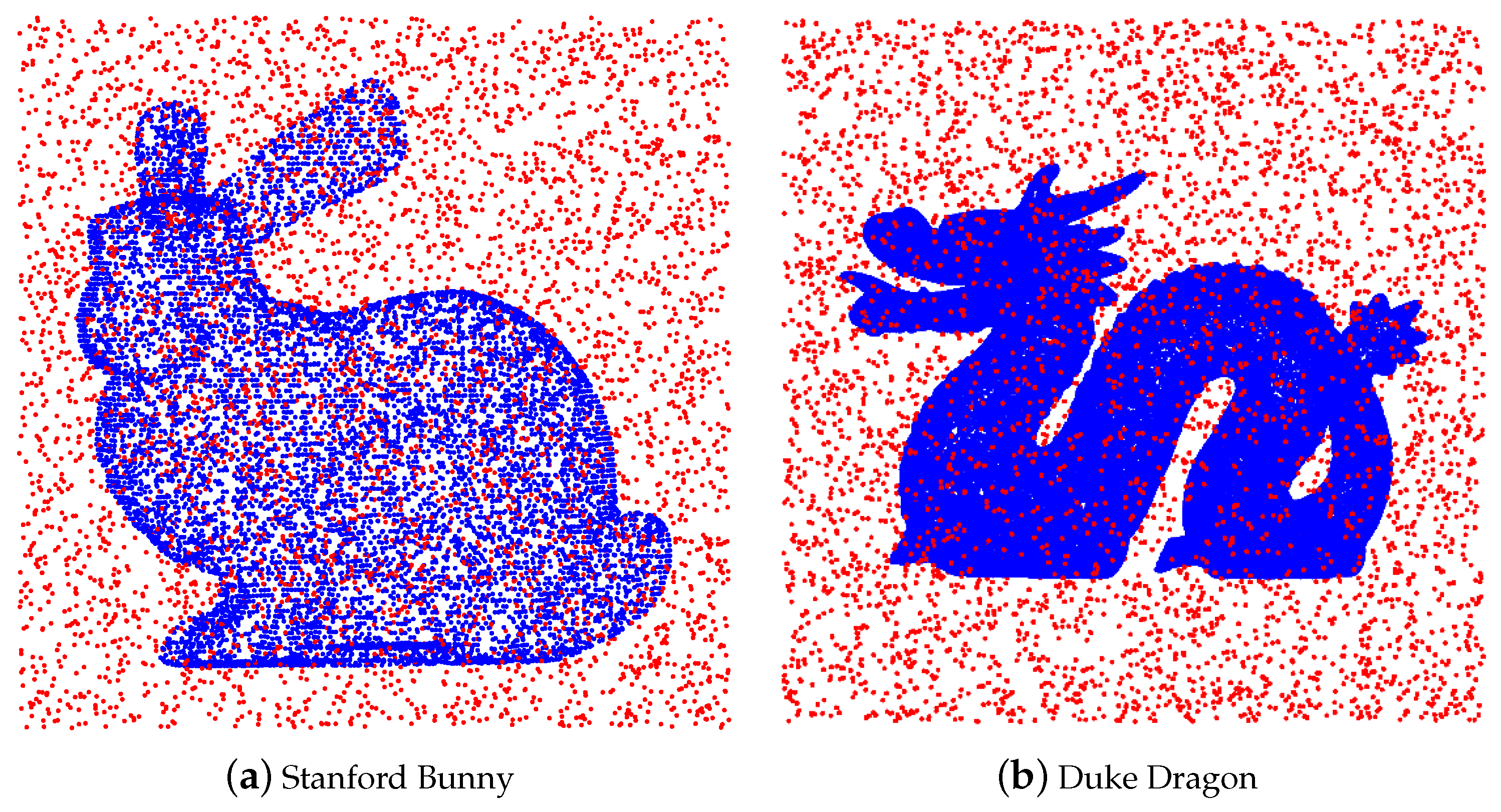
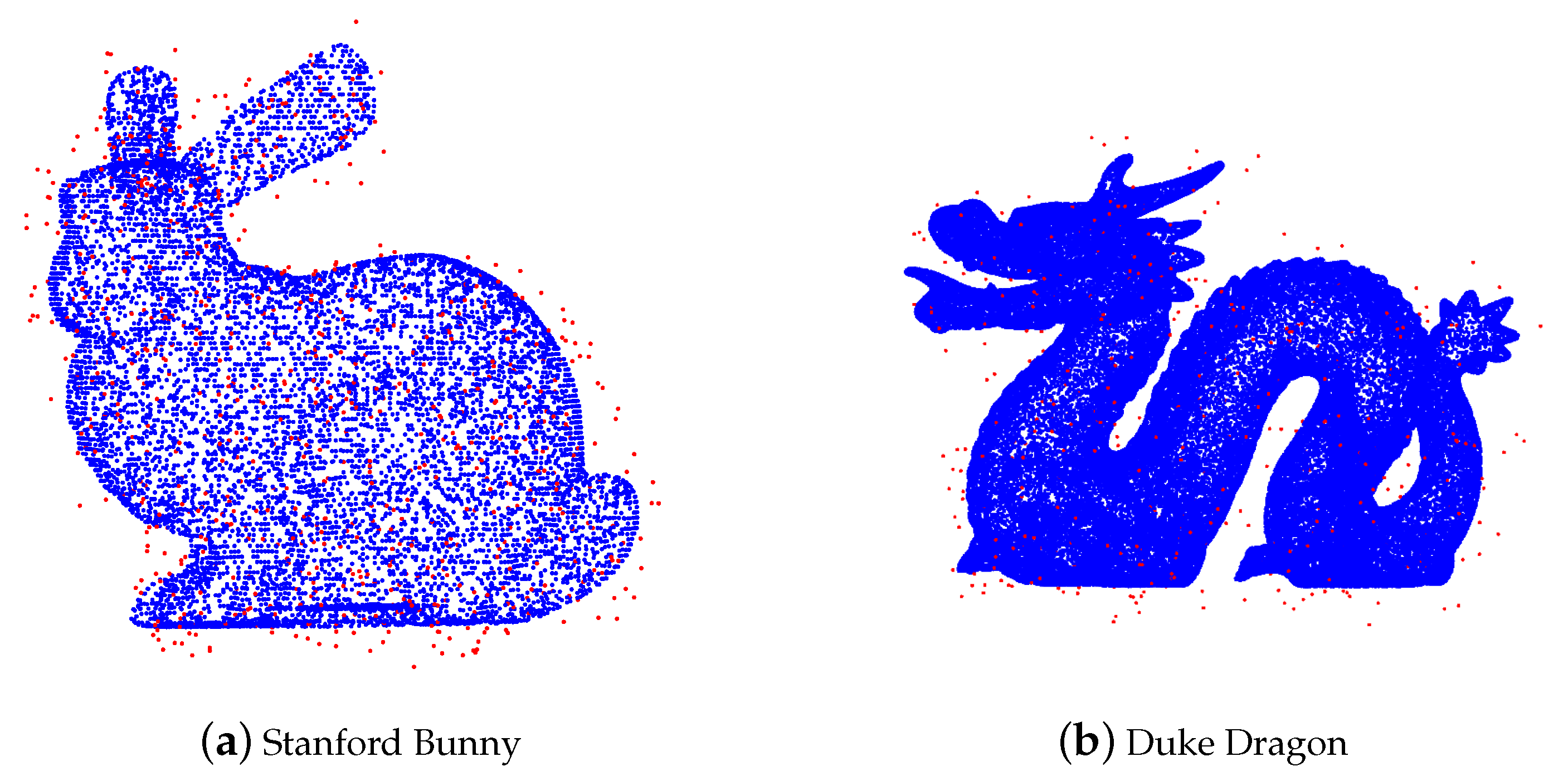
As an illustration, we add uniform noise to the Stanford Bunny with 10,000 points (see
Figure 4).
Then, we apply ROR to denoise the polluted point cloud. The result is shown in
Figure 5. From a visual observation, ROR preserves almost all true points but fails to recognize a small portion of noise at any area.
In fact, from a series of repetitive experiments we find that ROR is sensitive to the choice of manual parameters. A small radius will make ROR inefficient, while a large radius will wrongly recognize true points as noise. One of the disadvantages of ROR is that there exists no universal method to determine the best parameters. Further, since ROR uses the kernel method to find the undetermined closest neighbors, the time complexity can reach to where n is the number of points. Thus, in practice, it is often difficult to make a trade-off between efficiency and effect of ROR.
4.2. Statistical Outlier Removal
Compared to ROR, Statistical Outlier Removal (SOR) considers more detailed local structures than density does. SOR showed in Algorithm 3 is one of the most popular methods to preprocess point clouds due to its efficiency when dealing with low density noise. However, SOR gives worse performance than ROR when the noise is of high density. The main idea of SOR comes from one-sigma law from classical statistics [
23]. An outlier is believed to be far from the center of its k-nearest neighborhood. Conversely, a true point should lie in a confidence area of its neighborhoods. Let
be a
d-variate Gaussian distribution with expectation
and covariance
, and let
P be a fixed point in
. Then,
induces a Gaussian distribution on the line
where
. In fact, we write the eigendecomposition of
as
, where
is an orthogonal matrix. If we write
the projected Gaussian distribution in direction
has null expectation and variance
. According to one-sigma law, we say
P is in the confidence area of
if
which is equivalent to
This inequality is a generalization of one-sigma law in high dimensions.
| Algorithm 3 Statistical Outlier Removal. |
Input: initial point cloud , parameter k Output: cleaned point cloud - 1:
search kNN for each point ; - 2:
compute local mean and local covariance
- 3:
ifthen put into ; - 4:
return.
|
Thus, SOR consists of three steps: first we search the k-nearest neighbors (kNN) for every point. Then, we compute the empirical mean and covariance under the assumption of Gaussian distribution for each neighborhood. Finally, true points are identified using (
46). SOR requires a single parameter
k for kNN. Again, as an illustration, we use the data in
Figure 4. After SOR, the result is shown in
Figure 6.
We use KD-tree in kNN search. Thus, the time complexity is known as where k is the number of neighbors and n is the number of points. The remaining steps are finished in time. Therefore, the total time complexity is .
4.3. Adaptive Wasserstein Curvature Denoising
Note that the key step in SOR is to compute the local covariance, which is a positive-definite matrix. Motivated by the idea of SOR, we extract the covariance matrix at each point, which is equivalent to embed the original point cloud into . From an intuitive perspective, since the true data presents a particular pattern, the covariance matrices should have a large Wasserstein curvature. Conversely, for noise, the covariance matrices form a flat region. Hence, AWCD is based on a principal hypothesis that the Wasserstein curvature of true data is larger than noise.
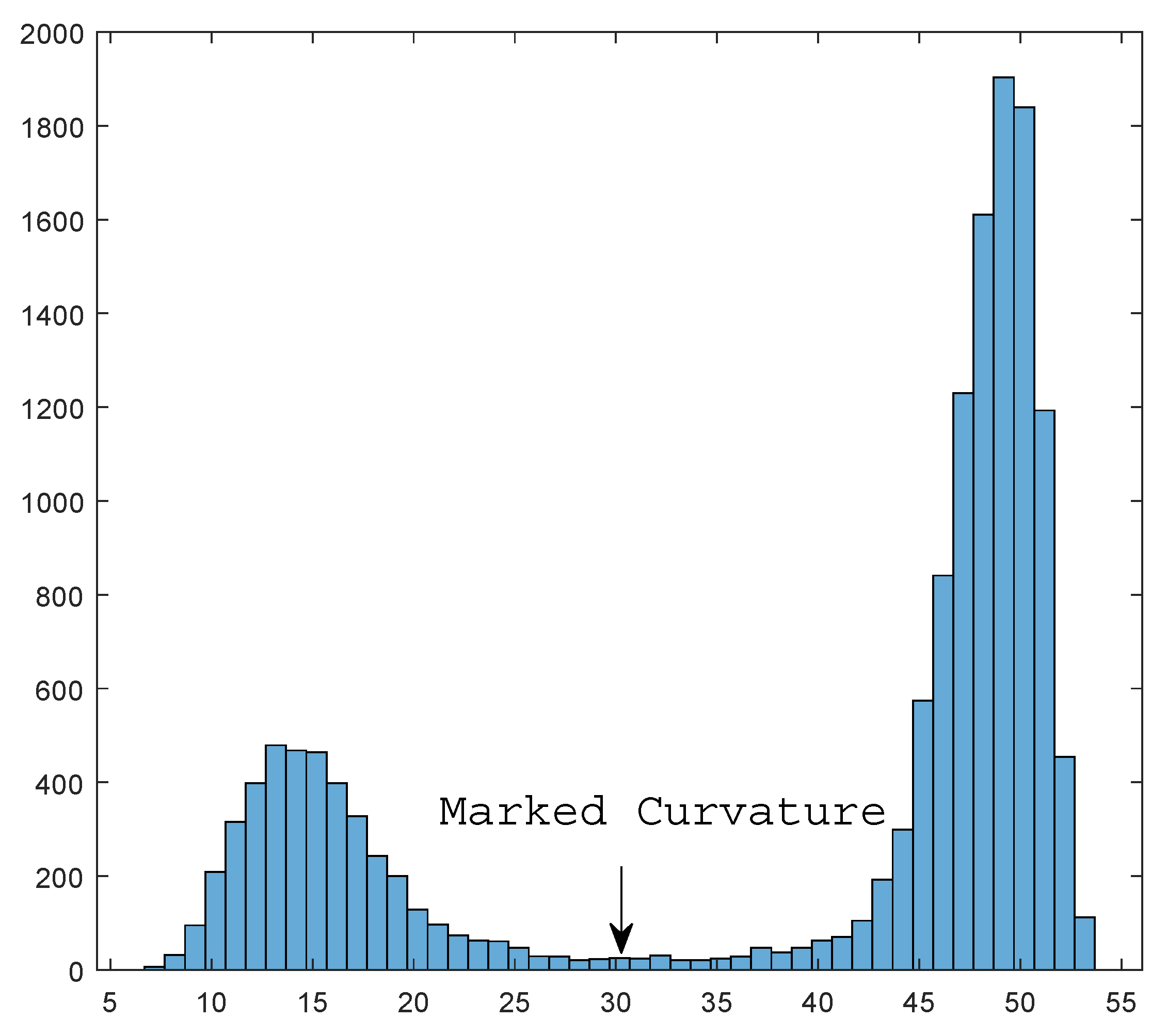
Under such a hypothesis, what we need to do is to set a threshold to pick out points with a small Wasserstein curvature. To do so, we gather all information in a histogram counting the number of points of different curvature. By the continuity of curvature function, true data and noise will form two different ’hills’.
Figure 7 shows an example for the histogram.
The phase change happens at the borderline of two hills, i.e., we seek to find the second minimal value of the histogram. In
Figure 7, the critical value is annotated as ’marked curvature’. In this way, we do not need to set the threshold manually and, instead, achieve an adaptive selection process. Algorithm 4 shows the processing of this adaptive denoising via wasserstein curvature.
| Algorithm 4 Adaptive Wasserstein Curvature Denoising. |
Input: initial point cloud , parameter k Output: cleaned point cloud - 1:
search kNN neighbors for each point ; - 2:
compute local mean and local covariance as before; - 3:
compute Wasserstein curvature as ( 43); - 4:
construct curvature histogram and determine the marked curvature ; - 5:
ifthen put into ; - 6:
return.
|
We use the same example as in
Figure 4. The performance of AWCD is shown in
Figure 8.
In this example, AWCD removes almost all noise far from Stanford Bunny, and remains almost all true data. The only problem is that a small portion of noise lying on the dragon cause the false positiveness and some true data located on the flat part are wrongly removed.
Since the main step in AWCD is also kNN, the time complexity is the same as SOR, which is . Therefore, AWCD is applicable in practice. It is remarkable that AWCD is effective for data with dense noise and robust to the unique parameter k.
4.4. Experiments
We use ROR, SOR and AWCD to denoise polluted data sets with noise of different levels of densities. The point clouds are from the Stanford 3D scanning repository, including Stanford Bunny, Duke Dragon, Armadillo, Lucy and Happy Buddha. For each data set, we add noise and record its signal-noise ratio (SNR). To show the influence of data size, we downsample the original data sets of different scales.
We adopt three criteria to measure the performance of the algorithms, including true positive rate (TPR), false positive rate (FPR) and signal-noise rate growing (SNRG). TPR describes the accuracy to preserve true points from unpolluted data sets. FPR describes the success rate to remove noisy points. SNRG explicates the promotion of SNR after processing. For any polluted point cloud
, where
D is the points set of true data and
N is the set of noise. We obtain the cleaned point cloud
after the denoising algorithms. Then, the computation of these measurements are
where
denotes the cardinality or size of a finite set. Intuitively, higher TPR, SNRG and lower FPR mean better performance of an algorithm. The experimental results are shown in
Table A1 in
Appendix I. In each experiment, we highlight the lowest FPR, the highest TPR and the SNRG over 99%.
Table A1 shows the superiority of AWCD to ROR and SOR. In general, AWCD can remove almost all noise and meanwhile preserves the true data, except for Armadillo.
5. Edge Detection
In this part, we attempt to apply the Wasserstein curvatures to detect the edges of images with noises. This application follows the idea that the edge parts contain more local information while the relatively flat parts tend to be regarded locally as white noise. Hence, the Wasserstein curvatures have natural advantages to depict the local information. This leads to the following Wasserstein sectional curvature edge detection (WSCED) of Algorithm 5.
| Algorithm 5 Wasserstein sectional curvature edge detection. |
Input: initial grayscale with pixels of , parameter k Output: edge figure - 1:
search kNN for each point ; - 2:
compute every local covariance to obtain the covariance image , which is a matrix constructed by matrixes ; - 3:
determine the section for every point on by computing tangent vectors ; - 4:
compute the Wasserstein sectional curvature for every with ( 36) to obtain the curvature image , which is a real matrix; - 5:
return.
|
Similar to what we have done in the last section, the first step of WSCED is computing the local mean and variance after kNN, which can be regarded as a two-dimensional embedding from a image into
. Every pixel coordinate
determines a local covariance matrix
. In the second step, we compute the sectional curvature for every
. The chosen section
is determined by two difference vectors along
x-axis and
y-axis,
According to (
36), we obtain the chosen curvature
on
. Then, we obtain a curvature image
. Finally, with some appropriate image transformation, we can detect edges on
.
In simulations, we compare WSCED to traditional edge detecting filters, including Sobel, Prewitt and Laplacian [
24]. We tend to detect edges for images with noises in high density. From
Figure 9, we find that WSCED approaches the same outcome as Sobel and Prewitt filters, which implies the potential connection between Wasserstein curvature and edges. This result also shows the robustness of WSCED to noises. We present more effects of digital experiments in
Figure A1 in
Appendix H.
6. Conclusions and Future Work
In this paper, we studied the geometric characteristics of , including geodesics, the connection, Jacobi fields and curvatures. Compared with the existing results, our results are simpler in form and more suitable for computation. Based on these results, we designed novel algorithms for point cloud denoising and image edge detection. Numerical experiments showed that these geometry-based methods were valid for applications. From both a theoretical and practical prospective, we gained a more comprehensive understanding regarding the Wasserstein geometry on , which shows that the Wasserstein metric has both deep application potential and mathematical elegance.
In our future work, on the one hand, we aim to study Wasserstein geometry on other matrix manifolds, such as the Stiefel manifold [
25], Grassman manifold [
26] and some complex matrix manifolds [
27]. On the other hand, we would like to generalize geometry-based methods to solve more problems in image, signal processing [
28] and data science.