Generalized Poisson Hurdle Model for Count Data and Its Application in Ear Disease
Abstract
1. Introduction
2. Basic Model
2.1. Generalized Poisson Regression
2.2. Hurdle Model
2.3. Generalized Poisson Hurdle Regression Model
3. Estimation
3.1. Parameter Estimation
3.2. Asymptotic Property and Efficiency
- (i)
- The covariateis a non-random variable;
- (ii)
- The weight matrixis positive definite matrix;
- (iii)
- .
- (i)
- andare continuous functions inwith probability one;
- (ii)
- andare continuously differentiable in a neighborhoodof.
4. Algorithm
- Choose point, , and .
- Calculate .
- Compute , where is a reflection coefficient. If , then , else go as follows:
- If , then calculate , where is an expansion coefficient. Next, If , then , else .
- If , then calculate , where is a contraction coefficient. Next, if , then , else go to Step 4.
- If , then calculate . Next, if , then , else go to Step 4.
- , where and .
5. Real Data Analysis
5.1. Data Description
5.2. Empirical Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Consul, P.C.; Jain, G.C. A generalization of the Poisson distribution. Technometrics 1973, 15, 791–799. [Google Scholar] [CrossRef]
- Consul, P.C.; Famoye, F. Generalized Poisson regression model. Commun. Stat.-Theory Methods 1992, 21, 89–109. [Google Scholar] [CrossRef]
- Famoye, F. Restricted generalized Poisson regression model. Commun. Stat.-Theory Methods 1993, 22, 1335–1354. [Google Scholar] [CrossRef]
- Noriszura, I.; Jemain, A.A. Handling overdispersion with negative binomial and generalized Poisson regression models. Casualty Actuar. Soc. Forum 2007, 2007, 103–158. [Google Scholar]
- Obubu, M.; Babalola, A.; Ikediuwa, U.C.; Peace, A. Modelling count data; a generalized linear model framework. Am. J. Math. Stat. 2018, 8, 179–183. [Google Scholar]
- Rivas, L. Zero inflated waring distribution zero inflated waring distribution. Commun. Stat.-Simul. Comput. 2021, 50, 1–16. [Google Scholar] [CrossRef]
- Cheung, Y. Zero-inflated models of regression analysis of count data: A study of growth and development. Stat. Med. 2002, 21, 1361–1469. [Google Scholar] [CrossRef] [PubMed]
- Lambert, D. Zero-Inflated Poisson Regression, with an Application to Defects in Manufacturing. Technometrics 1992, 34, 1–14. [Google Scholar] [CrossRef]
- Truong, B.-C.; Pho, K.-H.; Dinh, C.-C.; McALEER, M. Zero-inflated poisson regression models: Applications in the sciences and social sciences. Ann. Financ. Econ. 2021, 16, 1–19. [Google Scholar] [CrossRef]
- Bekalo, D.B.; Kebede, D.T. Zero-Inflated Models for Count Data: An Application to Number of Antenatal Care Service Visits. Ann. Data Sci. 2021. [Google Scholar] [CrossRef]
- Czado, C.; Erhardt, V.; Min, A.; Wagner, S. Zero-inflated generalized Poisson models with regression effects on the mean, dispersion and zero-inflation level applied to patent outsourcing rates. Stat. Model. Int. J. 2007, 7, 125–153. [Google Scholar] [CrossRef]
- Famoye, F.; Preisser, J.S. Marginalized zero-inflated generalized Poisson regression. J. Appl. Stat. 2017, 45, 1247–1259. [Google Scholar] [CrossRef]
- Famoye, F.; Singh, K. On inflated generalized Poisson regression models. Adv. Appl. Stat. 2003, 3, 145–158. [Google Scholar]
- Famoye, F.; Singh, K.P. Zero-Inflated Generalized Poisson Regression Model with an Application to Domestic Violence Data. J. Data Sci. 2006, 4, 117–130. [Google Scholar] [CrossRef]
- Kamalja, K.K.; Wagh, Y.S. Estimation in zero-inflated Generalized Poisson distribution. J. Data Sci. 2021, 16, 183–206. [Google Scholar] [CrossRef]
- Amin, M.; Akram, M.N.; Majid, A. On the estimation of Bell regression model using ridge estimator. Commun. Stat.-Simul. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Moreno-Arenas, G.; Castellares, F. Zero-inflated Bell regression models for count data. J. Appl. Stat. 2019, 47, 265–286. [Google Scholar] [CrossRef]
- Tawiah, K.; Iddi, S.; Lotsi, A. On Zero-Inflated Hierarchical Poisson Models with Application to Maternal Mortality Data. Int. J. Math. Math. Sci. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Mullahy, J. Specification and testing of some modified count data models. J. Econ. 1986, 33, 341–365. [Google Scholar] [CrossRef]
- Feng, C.X. A comparison of zero-inflated and hurdle models for modeling zero-inflated count data. J. Stat. Distrib. Appl. 2021, 8, 1–19. [Google Scholar] [CrossRef]
- Noh, M.; Lee, Y. Extended negative binomial hurdle models. Stat. Methods Med Res. 2018, 28, 1540–1551. [Google Scholar] [CrossRef]
- Bocci, C.; Grassini, L.; Rocco, E. A multiple inflated negative binomial hurdle regression model: Analysis of the Italians’ tourism behaviour during the great recession. Stat. Medthods Appl. 2020. [Google Scholar] [CrossRef]
- Park, M.H.; Kim, J.H.T. Hierarchical mixture-of-experts models for count variables with excessive zeros. Commun. Stat.-Theory Methods 2020, 1–25. [Google Scholar] [CrossRef]
- Hasanah, S.; Abdullah, S.; Lestari, D. Bayesian method for hurdle regression. ICSA-Int. Conf. Stat. Anal. 2019, 2019, 143–154. [Google Scholar]
- Chen, J.; Cheng, S. GMM Estimation of a Partially Linear Additive Spatial Error Model. Mathematics 2021, 9, 622. [Google Scholar] [CrossRef]
- Muris, C. Efficient GMM Estimation with Incomplete Data. Rev. Econ. Stat. 2020, 102, 518–530. [Google Scholar] [CrossRef]
- Sarvi, F.; Moghimbeigi, A.; Mahjub, H. GEE-based zero-inflated generalized Poisson model for clustered over or under-dispersed count data. J. Stat. Comput. Simul. 2019, 89, 2711–2732. [Google Scholar] [CrossRef]
- Mahpolah, M.; Suharto, S.; Wibowo, A.; Otok, B.W. The Estimation of Generalized Method Moment Poisson Regression Model on the Prevalence of Acute Respiratory Tract Infection (RTI) in South Kalimantan. CAUCHY 2018, 5, 161–168. [Google Scholar] [CrossRef]
- Allo, C.B.G.; Otok, B.W. Purhadi Estimation Parameter of Generalized Poisson Regression Model Using Generalized Method of Moments and Its Application. IOP Conf. Ser. Mater. Sci. Eng. 2019, 546, 052050. [Google Scholar] [CrossRef]
- Yogita, S.; Kirtee, K. Zero-inflated models and estimation in zero-inflated Poisson distribution. Commun. Stat.-Simul. Comput. 2018, 47, 2248–2265. [Google Scholar]
- Lee, D.; Youk, A.; Goldstein, N.A. A Meta-Analysis of Swimming and Water Precautions. Laryngoscope 1999, 109, 536–540. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, L.; Carney, A.; Esterman, A.; Sparrow, K.; Turner, D. Do esaccess to saltwater swimming pools reduce ear pathology and hearing loss in school children of remote arid zone aboriginal communities? A prospective three year cohort study. Clin. Otolaryngol. 2019, 44, 736–742. [Google Scholar] [CrossRef] [PubMed]
- Subtil, J.; Jardim, A.; Araujo, J.; Moreira, C.; Eça, T.; McMillan, M.; Dias, S.S.; Cruz, P.V.; Voegels, R.; Paço, J.; et al. Effect of Water Precautions on Otorrhea Incidence after Pediatric Tympanostomy Tube: Randomized Controlled Trial Evidence. Otolaryngol. Neck Surg. 2019, 161, 514–521. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, A.; Arom, G.; Perez, H.A.; Royal, L.; O-Lee, T. Are water precautions necessary after tympanostomy tube placement? A cadaver study. Int. J. Pediatr. Otorhinolaryngol. 2021, 143, 110632. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Famoye, F. Modeling household fertility decisions with generalized Poisson regression. J. Popul. Econ. 1997, 10, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Hansen, L.P. Large Sample Properties of Generalized Method of Moments Estimators. Econometrica 1982, 50, 1029. [Google Scholar] [CrossRef]
- Hansen, L.P.; Heaton, J.; Yaron, A. Finite-sample properties of some alternative Gmm estimators. J. Bus. Econ. Stat. 1996, 14, 262–280. [Google Scholar]
- Newey, W.; Mcfadden, D. Large sample estimation and hypothesis testing. In Handbook of Econometrics; Elsevier: Amsterdam, The Netherlands, 1994; Volume 4, pp. 2111–2245. [Google Scholar]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Galántai, A. A convergence analysis of the Nelder-Mead simplex method. Acta Polytech. Hung. 2021, 18, 93–105. [Google Scholar] [CrossRef]
- Han, L.; Neumann, M. Effect of dimensionality on the Nelder—Mead simplex method. Optim. Methods Softw. 2006, 21, 1–16. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- McKinnon, K.I.M. Convergence of the Nelder-Mead Simplex Method to a Nonstationary Point. SIAM J. Optim. 1998, 9, 148–158. [Google Scholar] [CrossRef]
- Bűrmen, Á.; Puhan, J.; Tuma, T. Grid restrained nelder-mead algorithm. Comput. Optim. Appl. 2006, 34, 359–375. [Google Scholar] [CrossRef][Green Version]
- Price, C.; Coope, I.; Byatt, D. A Convergent Variant of the Nelder—Mead Algorithm. J. Optim. Theory Appl. 2002, 113, 5–19. [Google Scholar] [CrossRef]
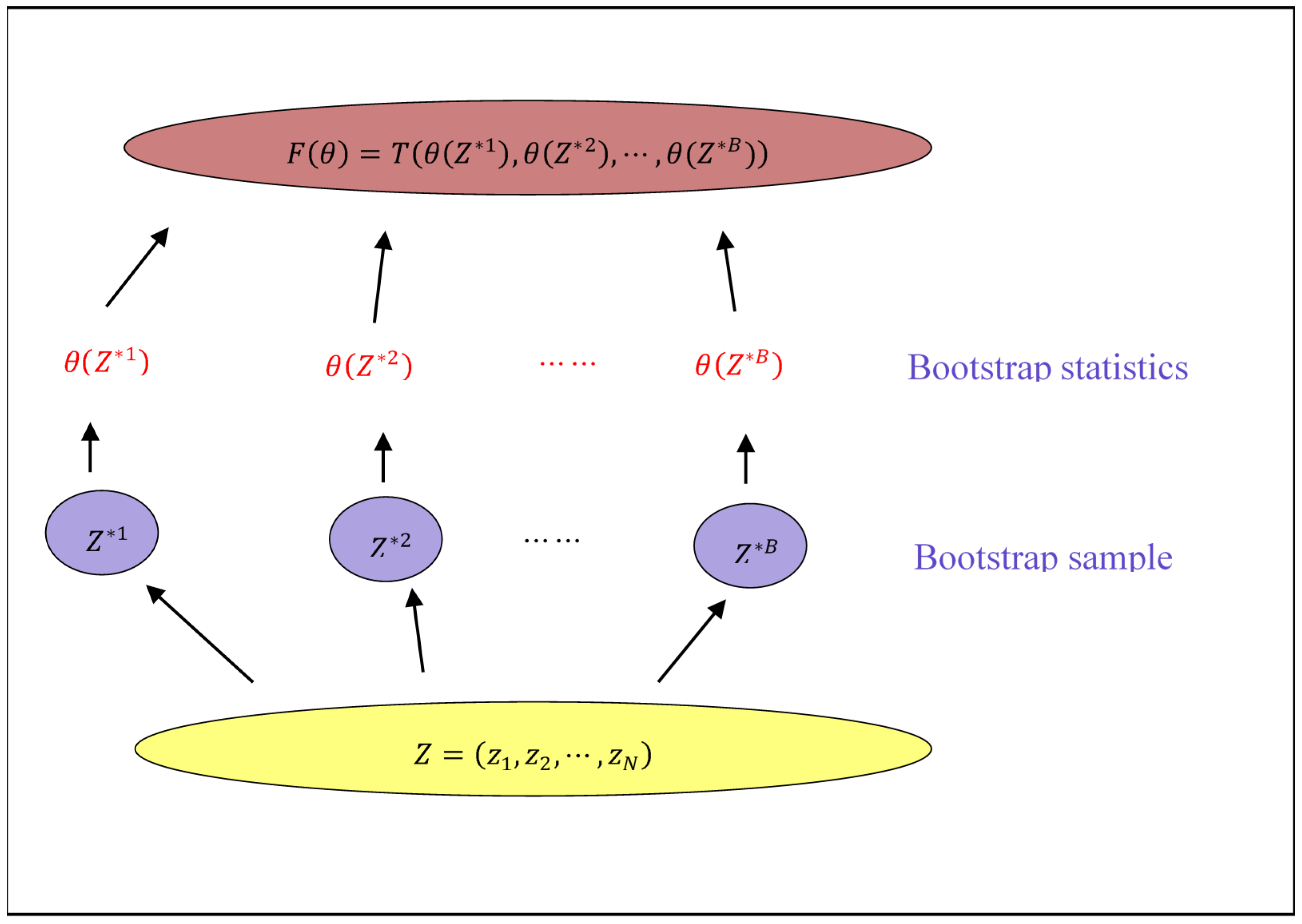
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Chapman and Hall: London, UK, 1993. [Google Scholar]
- Zhou, Y. Estimation Method of Generalized Estimation Equation; Science Press: Beijing, China, 2013; pp. 27–62. [Google Scholar]
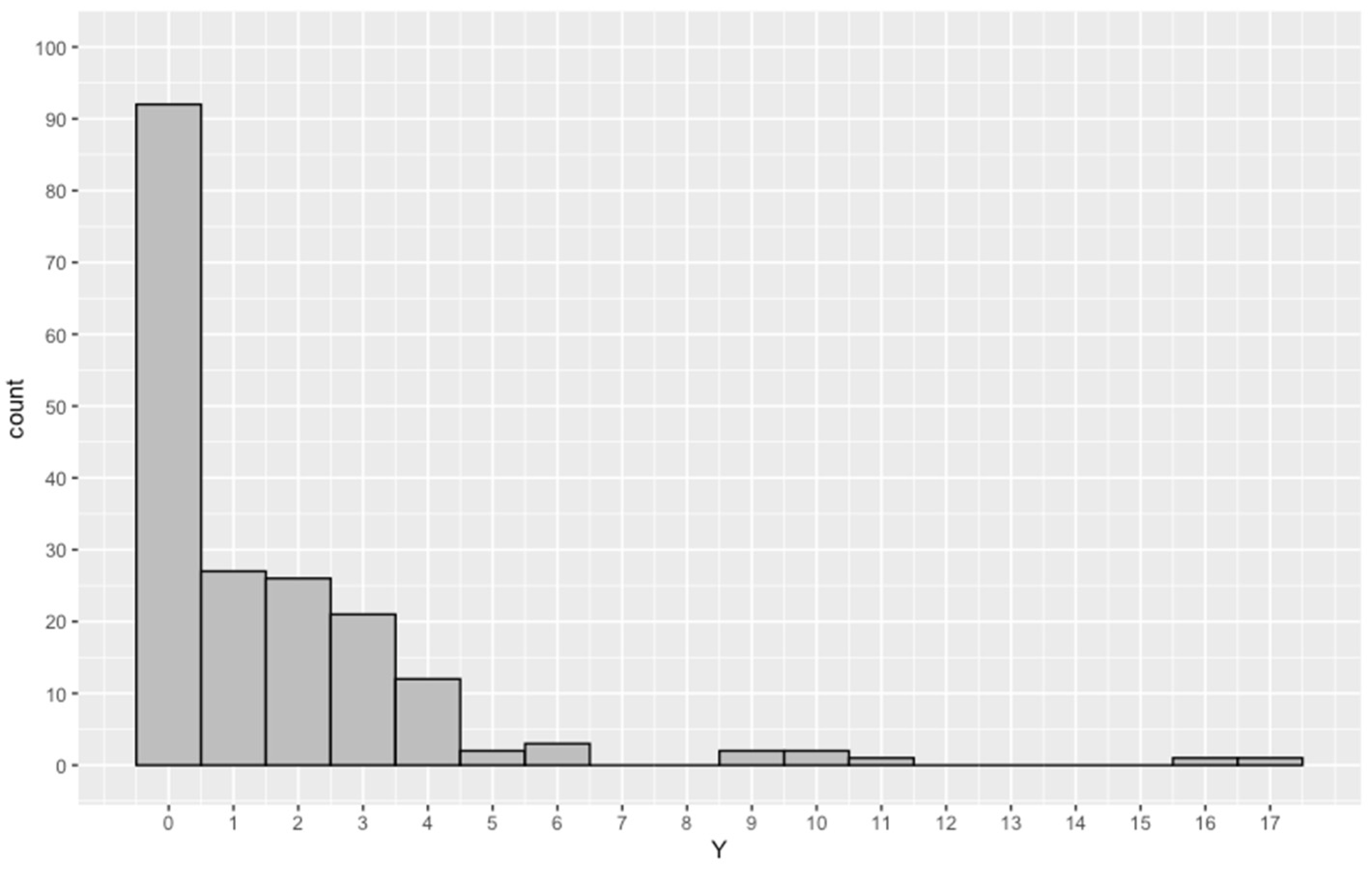
| Variable | Min. | 1st Qu. | Med. | Mean | 3rd Qu. | Max. | Var. |
|---|---|---|---|---|---|---|---|
| NED | 0.0 | 0.0 | 1.0 | 1.6 | 2.0 | 17.0 | 6.5 |
| Variables | GPHR | PH | GP | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MLE | GMM | MLE | GMM | MLE | GMM | |||||||
| Coefficient | SE | Coefficient | SE | Coefficient | SE | Coefficient | SE | Coefficient | SE | Coefficient | SE | |
| DIS | 0.28 (0.1, 0.4) | 0.09 (0.002) | 0.17 (0.07, 0.3) | 0.05 (<0.001) | − | − | − | − | 0.59 (0.4, 0.8) | 0.10 (<0.001) | 0.52 (0.4, 0.6) | 0.06 (<0.001) |
| INT1 | −0.48 (−1.8, 0.8) | 0.66 (0.474) | −0.42 (−0.6, −0.3) | 0.07 (<0.001) | −0.08 (−0.8, 0.7) | 0.38 (0.837) | 0.09 (−0.2, −0.01) | 0.04 (0.002) | −1.56 (−2.8, −0.3) | 0.64 (0.016) | −1.43 (−1.5, −1.3) | 0.06 (<0.001) |
| FRE1 | 0.63 (0.1, 1.1) | 0.26 (0.016) | 0.67 (0.5, 0.8) | 0.08 (<0.001) | 0.55 (0.2, 0.9) | 0.16 (<0.001) | 0.41 (0.3, 0.6) | 0.08 (<0.001) | 0.75 (0.2, 1.3) | 0.26 (0.004) | 0.71 (0.6, 0.8) | 0.06 (<0.001) |
| PLA1 | 0.07 (−0.1, 0.2) | 0.10 (0.513) | 0.11 (0, 0.2) | 0.06 (0.06) | 0.06 (−0.05, 0.2) | 0.06 (<0.001) | 0.03 (−0.1, 0) | 0.05 (0.543) | 0.23 (0.03, 0.4) | 0.10 (0.017) | 0.20 (0.1, 0.3) | 0.04 (<0.001) |
| INT2 | 2.29 (0.6, 4.0) | 0.85 (0.007) | 2.35 (2.2, 2.4) | 0.07 (<0.001) | −2.29 (−3.9, −0.6) | 0.85 (0.007) | 2.08 (−2.2, −2.0) | 0.05 (<0.001) | − | − | − | − |
| FRE2 | −0.71 (−1.3, −0.02) | 0.35 (0.040) | −0.72 (−1, −0.4) | 0.14 (<0.001) | 0.71 (0.02, 1.3) | 0.35 (0.004) | 0.83 (0.7, 0.9) | 0.05 (<0.001) | − | − | − | − |
| PLA2 | −0.37 (−0.6, −0.1) | 0.13 (0.004) | −0.29 (−0.4, −0.1) | 0.07 (<0.001) | 0.37 (0.1, 0.6) | 0.13 (0.004) | 0.57 (0.5, 0.6) | 0.03 (<0.001) | − | − | − | − |
| AIC | 639.90 | 745.64 | 643.31 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, G.; Fu, K.; Dai, X.; Zhang, L. Generalized Poisson Hurdle Model for Count Data and Its Application in Ear Disease. Entropy 2021, 23, 1206. https://doi.org/10.3390/e23091206
Zuo G, Fu K, Dai X, Zhang L. Generalized Poisson Hurdle Model for Count Data and Its Application in Ear Disease. Entropy. 2021; 23(9):1206. https://doi.org/10.3390/e23091206
Chicago/Turabian StyleZuo, Guoxin, Kang Fu, Xianhua Dai, and Liwei Zhang. 2021. "Generalized Poisson Hurdle Model for Count Data and Its Application in Ear Disease" Entropy 23, no. 9: 1206. https://doi.org/10.3390/e23091206
APA StyleZuo, G., Fu, K., Dai, X., & Zhang, L. (2021). Generalized Poisson Hurdle Model for Count Data and Its Application in Ear Disease. Entropy, 23(9), 1206. https://doi.org/10.3390/e23091206






