2. Convergence to a Max-Semistable Law for Dynamical Systems
We now consider a measure preserving dynamical system
, on the probability space
. Here,
,
a Borel
-algebra on
, and
is an
f-invariant probability measure supported on
. Given an observable
, i.e., a measurable function, we consider the stationary stochastic process
defined as
and its associated maximum process
defined as
As in the i.i.d. case, much attention has been to determine the existence of sequences
such that
for some non-degenerate distribution function
,
. Under general assumptions on the observable function, the measure density and the mixing properties of the dynamical system, it is found that the sequences
,
and limit
G are determined in much a similar way as to the i.i.d. case.
Here, the distribution function tail
takes the form
. The regularity of
depends on the regularity of the measure
, and on the regularity of the observable
. We focus on one-dimensional dynamical systems, and consider those with an absolutely continuous invariant measure
. For
-a.e.
the density
is well defined and takes values in
. There may be exceptional points where
, or is undefined. For the observable function
, we consider those which are maximised at a distinguished point
. Moreover, we consider observable functions of the form
, where
denotes the Euclidean distance on
and
is a monotone decreasing function. Functions of this form have been the main focus in the study of extremes for one-dimensional dynamical systems; see [
6]. For example, it can be shown that the max-stable GEV limit distributions are applicable for describing the statistics of extremes in the cases: (i)
; (ii)
, and (iii)
, (with
). The problem we consider is the case where
is not regularly varying, and hence not in the domain of attraction of a classical max-stable GEV distribution. For one-dimensional dynamical systems where the density of
is a smooth function (e.g., the density is
-a.e. Hölder continuous), the regularity of
(or lack thereof) depends on the regularity of the observable function
(through
). Hence, we seek conditions on the dynamical system process, and observable function
for which a max-semistable law limit exists. We cannot use the same methods of proof as in the i.i.d. case, since the dynamical system processes are dependent.
Going beyond one-dimensional dynamical systems, proving existence (or otherwise) of a max-stable GEV distribution limit is non-trivial. This is a relevant problem to consider, especially from a practical viewpoint of using dynamical systems for weather and climate models. For non-uniformly hyperbolic systems, e.g., those giving rise to chaotic attractors as in [
7,
8], the regularity considerations of the invariant measure will feature prominently in the determination of the limit law for the extremes (if such a limit law exists). Numerical results indicate slow or oscillatory convergence in the estimation of the tail parameter; see [
6,
9,
10,
11]. Within these references, it is shown that lack of regular variation for the function
is possible. This remains the case even if the observable function is sufficiently smooth, in the sense of
, and the function
regularly varying. The lack of regular variation of
is due to the fractal, and (approximate) self-similar structure of the chaotic attractor. In particular, the invariant measure
is longer absolutely continuous with respect to volume (Lebesgue) measure. Hence, it is natural to ask the validity of a max-semistable GEV distribution limit description for the extremes. We discuss this further in
Section 4.
2.1. Main Results
Suppose that is a piecewise expanding map, with finitely many pieces of continuity. For simplicity, we take . We assume that there is a partition such that f is differentiable on each , . Let be the corresponding partition for . We distinguish between finite and countable partitions. In the case of a finite partition , there is a such that every partition element of has a diameter of at least . In the case where the partition is countable, we assume that there is a such that for all n holds whenever .
We assume that
f is uniformly expanding, i.e., that there is a constant
such that
. Moreover, we assume that
f has bounded distortion, and that
is an ergodic measure
with exponential decay of correlations for functions of bounded variation against
. This means that there exists a constant
such that
and for functions
for some
. Here, the density of the measure
should be a function of bounded variation (BV) and
denotes the BV-norm [
12]. Recall that the
-norm is defined as
.
Examples of systems satisfying our assumption are piecewise expanding maps with finitely many pieces and an absolutely continuous invariant measure
, such as the
-transformation
, (
); the Gauss map
; or the first return map to
for a Manneville–Pomeau map [
13] with an absolutely continuous invariant measure
. For more details about the statistical properties of these maps see [
12,
14]. We consider specific case studies in
Section 3. We state the following result.
Theorem 1. Suppose that is a piecewise uniformly expanding interval map, with ergodic measure μ. Given , suppose that , with monotone decreasing. Suppose that there exists , regularly varying with index , a periodic function ν and sequences , such that where , and a continuity point of ν. Then for μ-a.e. , there exists a sequence with (where c is the period of ν), and We make several remarks on Theorem 1; it is proved in
Section 2.2. The first remark is that an example function
that fits the hypothesis of Theorem 1 is given by
It is straightforward to generalise to other functional forms. Another example includes:
which is connected to the St. Petersburg distribution; see [
5]. In a dynamical system setting, this type of limit distribution arises in the context of hitting time statistics to cylinder sets; see [
15]. Note that the observable
is defined implicitly through the function
. In general it is not possible to give an explicit formula for
(or
) even when the density of
is explicit. The problem is inverting
. If
is made explicit, such as specifying
for some periodic function
, then the problem is to determine the regularity
. This becomes relevant for dynamical systems, where it is natural to specify
first (rather than
). We state the following corollary.
Corollary 1. Suppose that is a piecewise uniformly expanding interval map, with ergodic measure μ. Given , suppose that , where and satisfies . The function is assumed periodic with period c, and differentiable with . Then for μ-a.e. , there exists a sequence with , and where also has period c, and is the density of μ at . The corollary is proved in
Section 2.3. To keep the exposition concise, we have focused on piecewise uniformly expanding (interval) maps. It is possible to generalise to dynamical systems which are not uniformly expanding, such as the dynamical systems considered in [
16,
17,
18]. The main purpose of our results is to demonstrate that max-semistable laws are the natural limits to consider for the maxima process, especially for observables that lack regular variation properties. The results we obtain are commensurate with the i.i.d. case. See also [
19] for results in the context of certain stationary processes, building upon [
20,
21].
For hyperbolic systems, such as those considered in [
7,
8], we make further remarks in
Section 4. In the context of semistable laws for suitably normalised Birkhoff sums (rather than extremes); see recent work of [
22,
23].
2.2. Proof of Theorem 1
The proof of Theorem 1 uses the blocking method adapted from [
16,
21]. See also ([
6] Chapter 6), in particular Proposition 6.3.3 within. We summarise the approach as follows. Given
n, consider integers
defined so that
as
. We take
and
, but other rates are possible. We now divide up our process in blocks of size
p, and take
q such blocks. Each consecutive block will be separated by a time scale
t. Block
consists of the time series
for
. Using the fact that the process is stationary, and an application of the inclusion-exclusion principle, the maxima of each block satisfies:
Since
t represents a correlation time-lag it is natural to replicate the i.i.d. argument leading to an estimate of the form:
where the error term
is composed of three significant terms, which we write as
An error term
which depends on the decay of correlations associated to separating the blocks by lag
t. This is bounded by
where
is power law in
n when
and
is the exponential decay of correlation decay rate. The functions
are indicator functions of the set
and have
-norm of 1, bounded variation norm of 2. Hence,
exponentially fast as
An error term
associated to the decomposition in (
9). This is bounded as follows
For observables of the form
, it is shown that for
-a.e.
that
for some
. See [
18].
A remainder error term of the form which arises from the requirement that are integers. By choice of and , we see that for some .
Hence, there exists
such that
and therefore
To complete the proof, we must relabel the sequence indexing. We choose
,
so that
and for
, we consider instead
. This means we take
. We obtain
for some
. By choice of
, and since
is a log-periodic function of log-period
, we can choose
proportional to
as required. This concludes the proof.
2.3. Proof of Corollary 1
To prove the corollary, it suffices to analyse the regularity of , such as its periodicity and regular variation properties. The following lemma is elementary and sets up an equivalence for log-periodicity of regular varying functions and their inverses.
Lemma 1. Suppose that , where is periodic with period c. Suppose that is differentiable and . Then admits the representation , where is also periodic with period c.
The requirement
ensures that
is a monotone decreasing function, and is therefore injective so that
is well defined. To show the periodicity property of
, we proceed as follows. First note that
, since
. We now compare
with
:
Hence, . Put , for some real-valued function . Then we see that as required. This completes the proof.
2.4. On the Role of the Extremal Index
For dependent processes, a further important parameter of statistical relevance is the extremal index . It is defined as follows:
Definition 1. Suppose , and let be a sequence such that Then we say that an extreme value law with extremal index holds for if If
is an i.i.d. process, then Equation (
12) holds for
. For dynamical systems, natural examples where the extremal index is non-trivial are for observables
maximised at periodic points. Following, e.g., [
15,
24], versions of Theorem 1 can be shown to hold. To see where the extremal index arises more explicitly, consider the following example. Take
, where
is an i.i.d. sequence with distribution function
. We assume
is differentiable, periodic with period
c and
. Defining
, we get identically
. Thus, along the sequence
, we have
. (We can take
.) If
denotes the maximum of a general random variable sequence
, then we see that
. Hence, taking
and
, we have
Now the convergence criteria to a max-semistable law are characterised by sequences
satisfying the asymptotic ratio condition
for some
. We can take
. The limit distribution is represented by
with
and
. Notice that this construction does not pick up the extremal index. This is due to the fact that the sequence
can be defined up to arbitrary multiplication constants. In the max-stable case, we work precisely along the given sequence
, and
,
are chosen by the requirement
. If instead we took
, then we would take
,
, and obtain
thus picking up an extremal index of 1/2.
From a practical viewpoint, the extremal index measures ‘clustering phenomena’ and this is a separate phenomenon associated to irregularity of the tails. We explore in the next section whether numerical methods still pick up the non-trivial extremal index, despite the extremal index itself not featuring directly in the limiting max-semistable GEV representation. We note that even in the classical max-stable GEV representation the extremal index is not formally incorporated. It is hidden within the scale and location parameters. Regarding Equation (
12), the sequence
appearing within is not required to satisfy any particular regularity condition, i.e., as associated to a linear scaling distributional limit for
(which indeed will not always exist).
4. Discussion
In this article, we have shown the existence of max-semistable limit laws for certain dynamical systems. For the systems we have considered, the existence on the type of limit law for the maxima process depends on the regularity of the observable function. For more general non-uniformly expanding (interval) maps, such as those that preserve an absolutely continuous invariant measure, then we expect similar conclusions to apply relative to Theorem 1 and Corollary 1. The corresponding results obtained would essentially depend on the regularity of the observable
and the measure density in the vicinity of the maxima
. As mentioned in
Section 2, for dynamical systems giving rise to chaotic attractors, regularity considerations of the invariant measure will be important in determining the existence (or otherwise) of a limit law for the extremes, whether that limit law be max-stable, or max-semistable. Unless the fractal structure of the chaotic attractor is strictly self-similar, then establishing existence of a max-semistable law would depend on finer (statistical) self-similar properties of the attractor, and local properties of the invariant measure in the vicinity of the point
. This is the case when taking an observable function of the form
. See [
6,
9,
10,
11]. When a max-semistable law description is valid, an ongoing work is to explore statistical methods to capture more formally the periodic behaviour, such as the computation of the periodicity constant for
. In the case of estimating the periodicity constant for i.i.d. processes; see [
4].
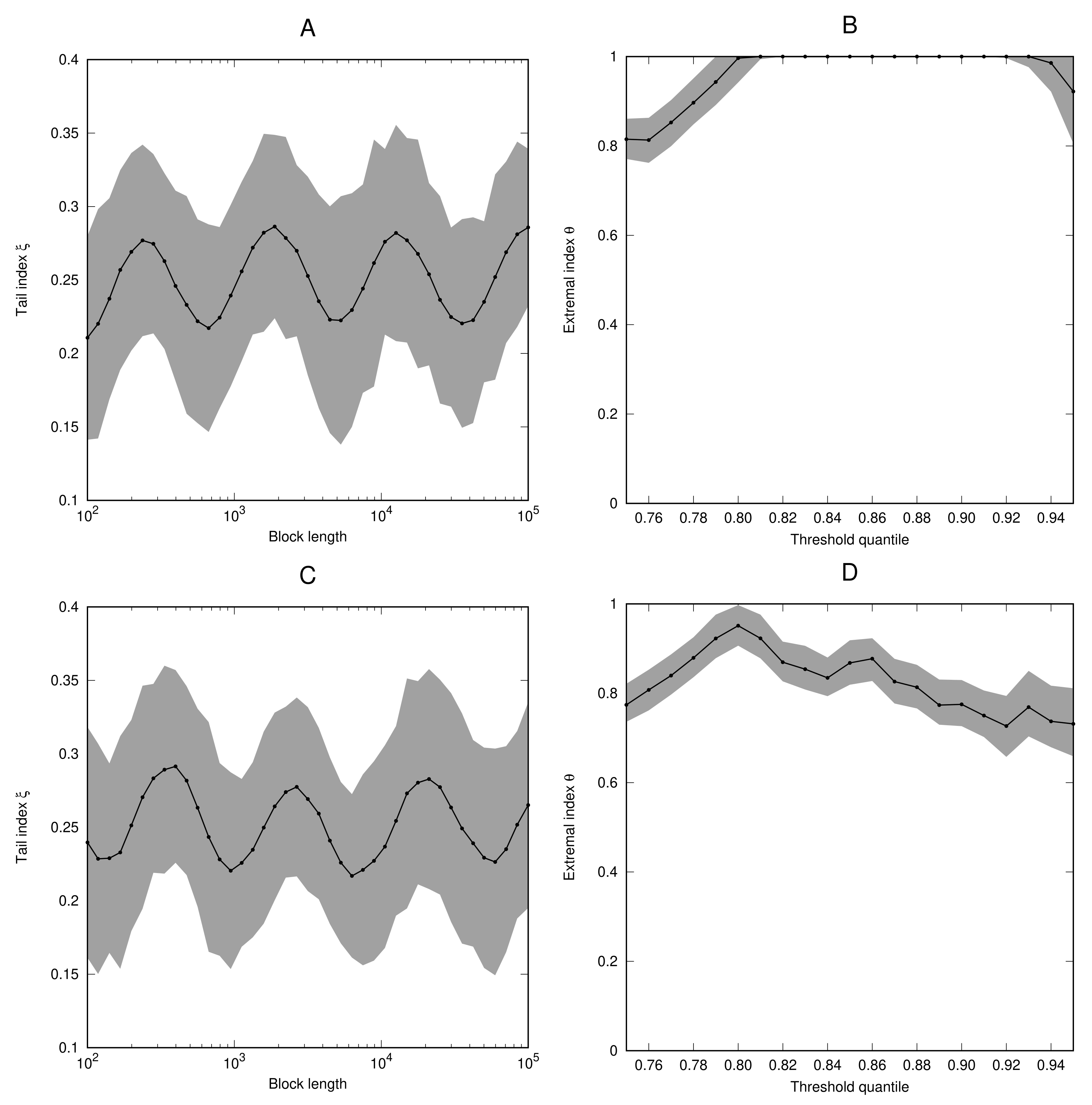
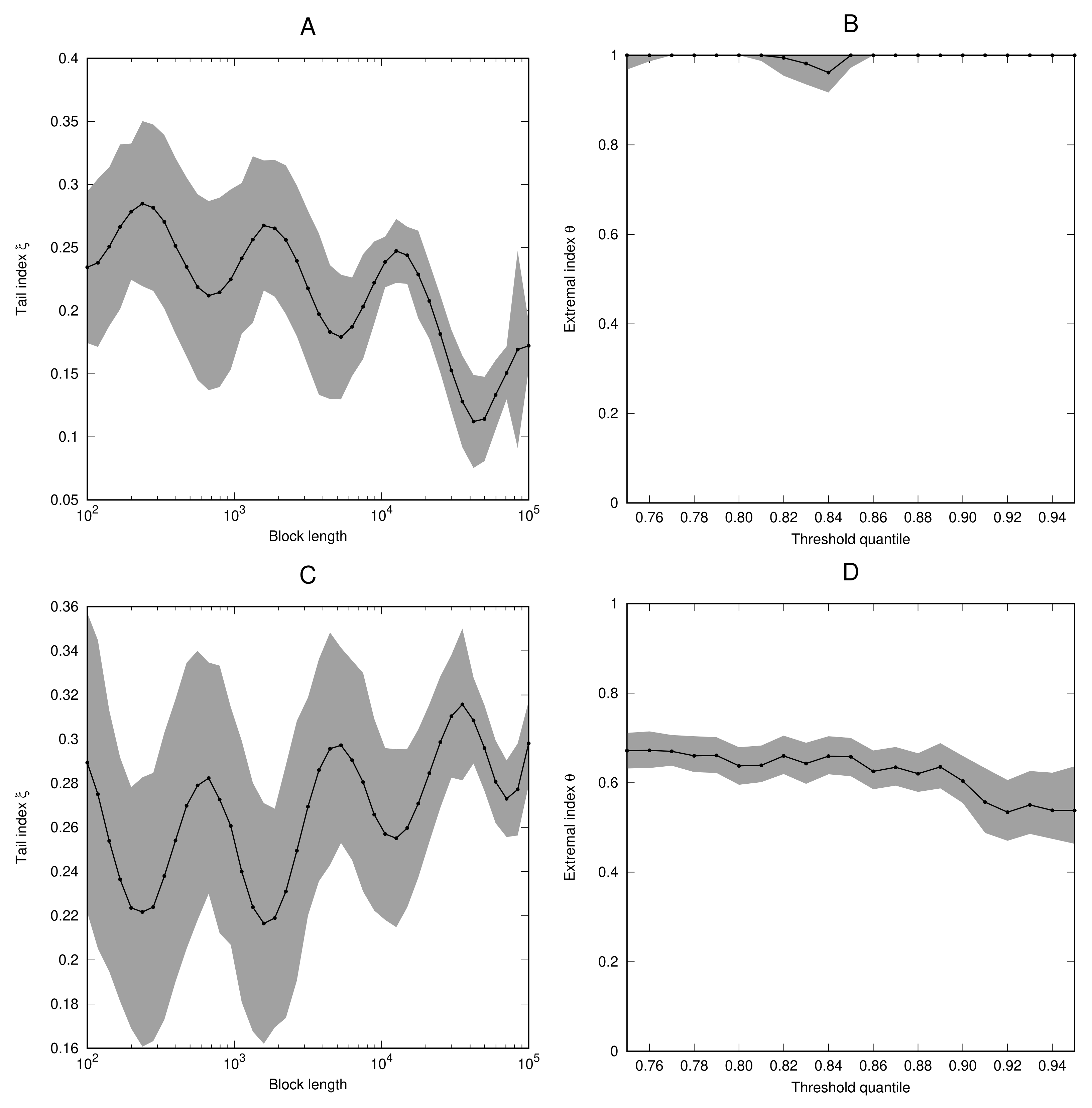
In our studies, the numerical computation of the extremal index has conformed accurately to the theoretical results. As we have pointed out in
Section 2.4, the extremal index does not appear (naturally) in the GEV representation, and therefore the oscillation behaviour of the periodic function
within is unlikely to affect the computation of the extremal index. Numerical accuracy in extremal index estimation has been due to dynamical considerations, such as presence of a neutral fixed point discussed in Example 8.