Plaintext-Related Dynamic Key Chaotic Image Encryption Algorithm
Abstract
:1. Introduction
2. Basic Theory
2.1. Lorenz System

2.2. Arnold Mapping
3. Encryption and Decryption Algorithm Design
3.1. Encryption Scheme
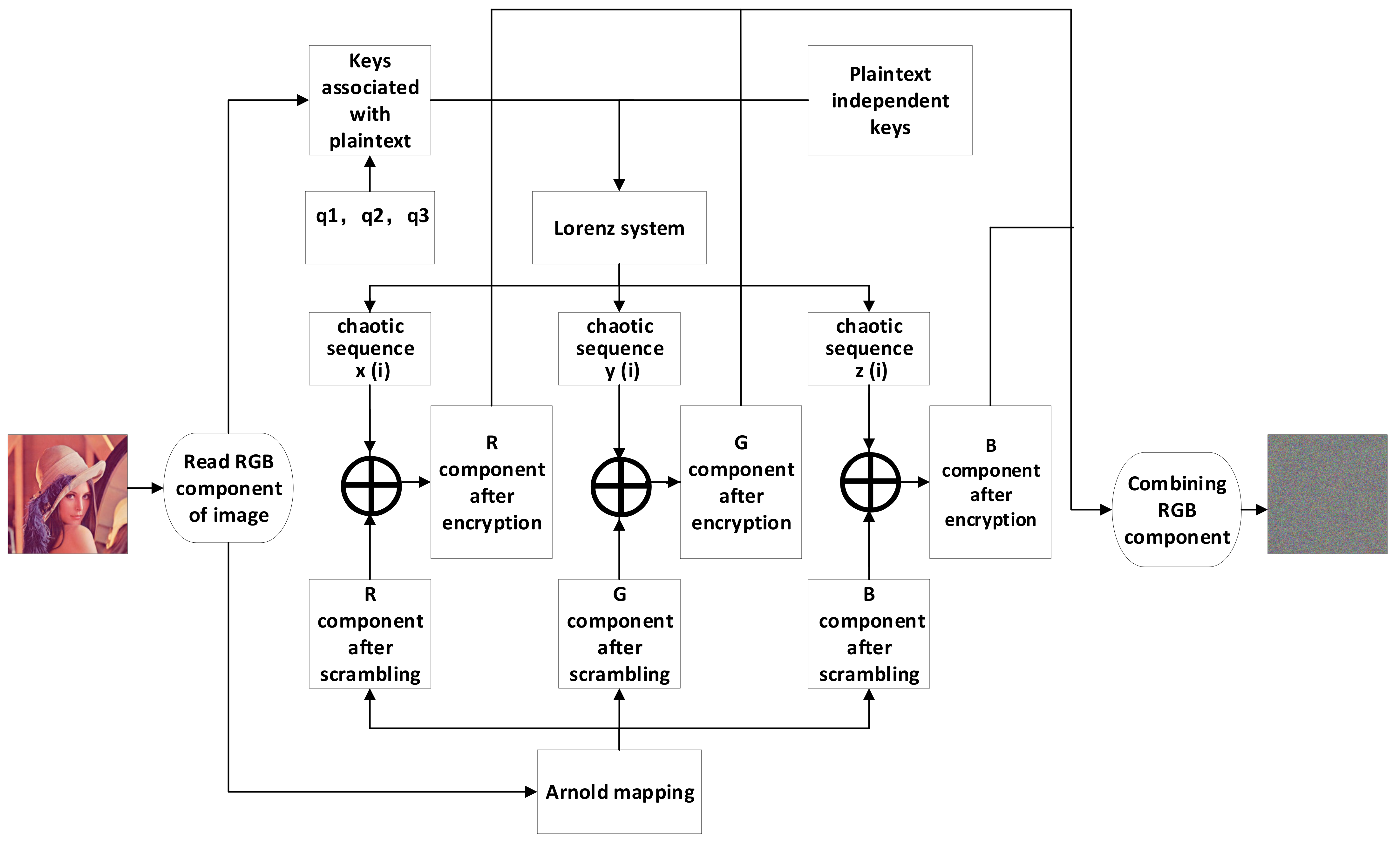
3.2. Decryption Scheme
4. Simulation Experiments and Performance Analysis
4.1. Encryption and Decryption
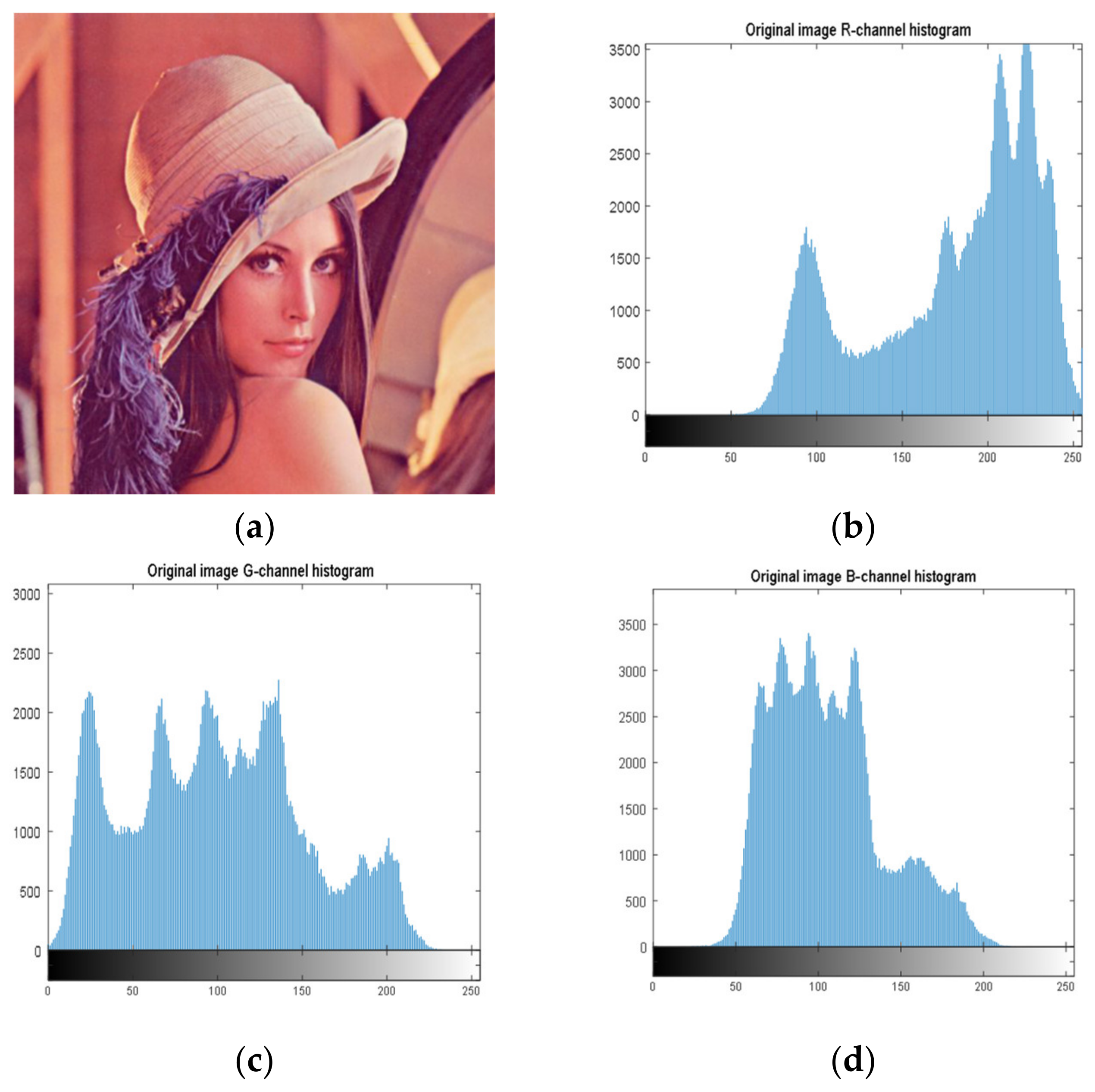
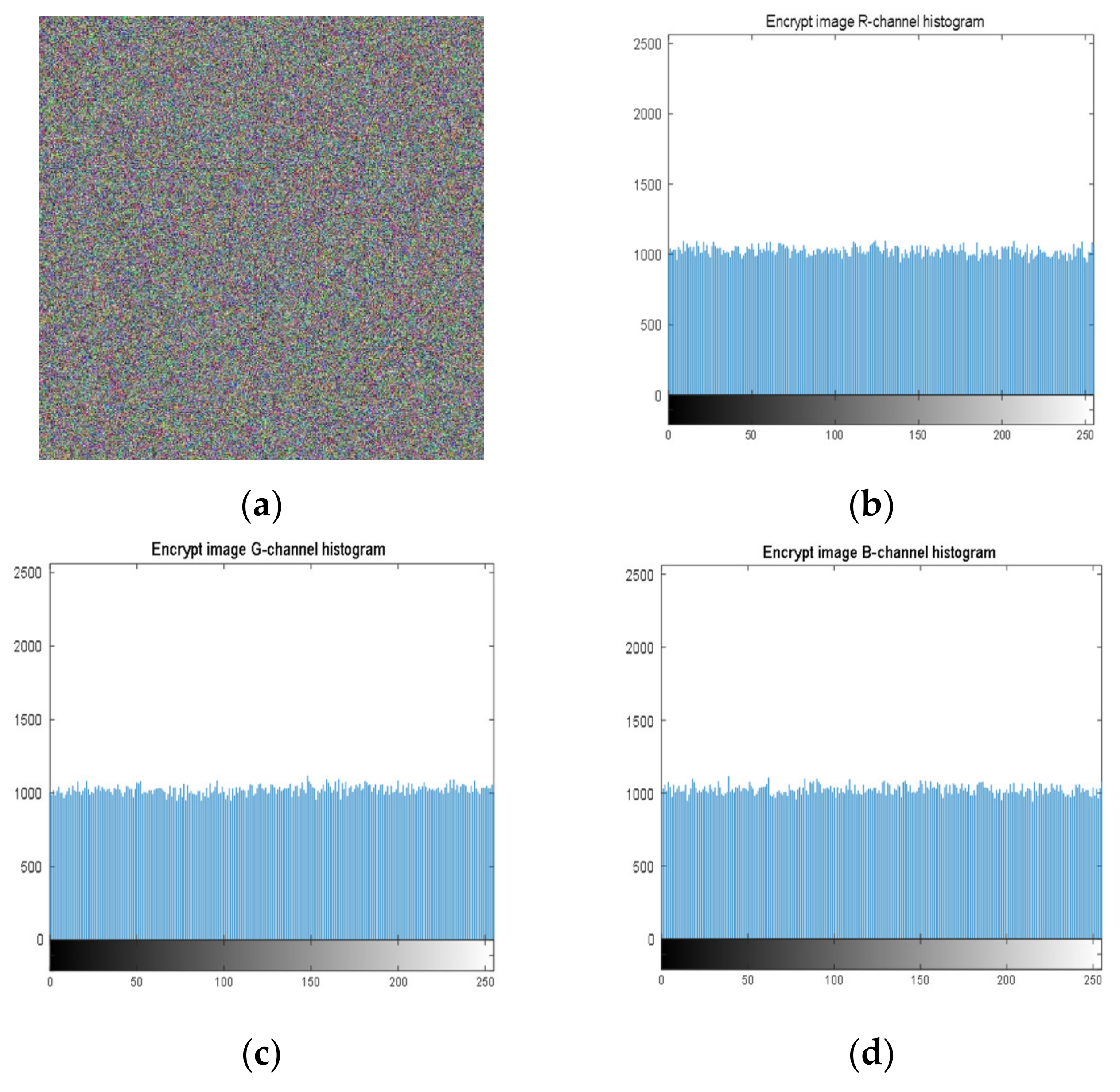
4.2. Histogram Analysis
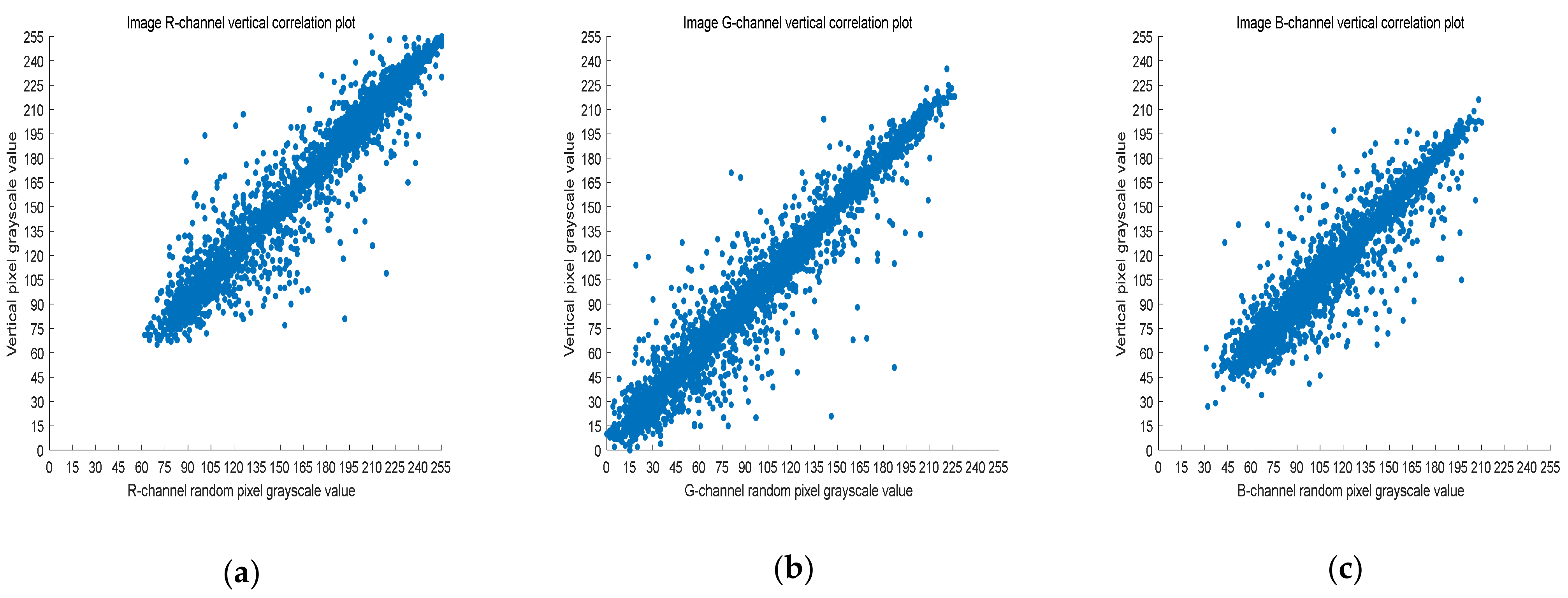
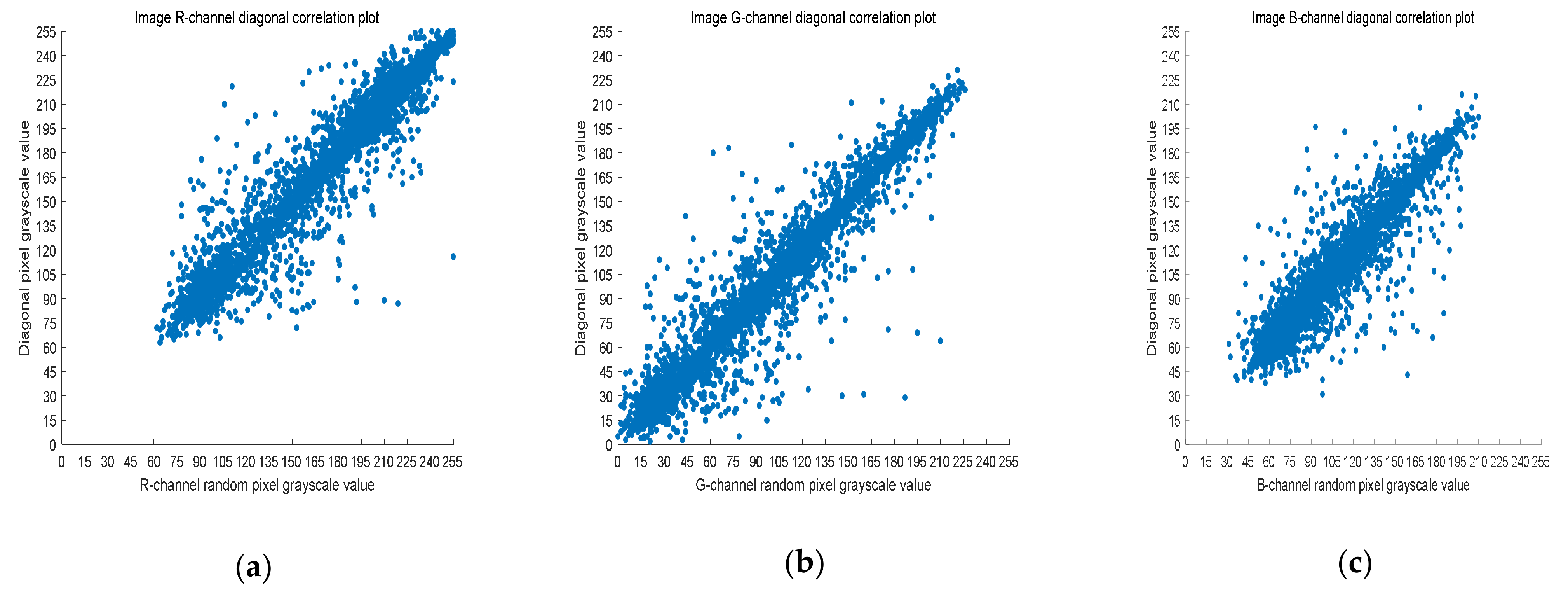
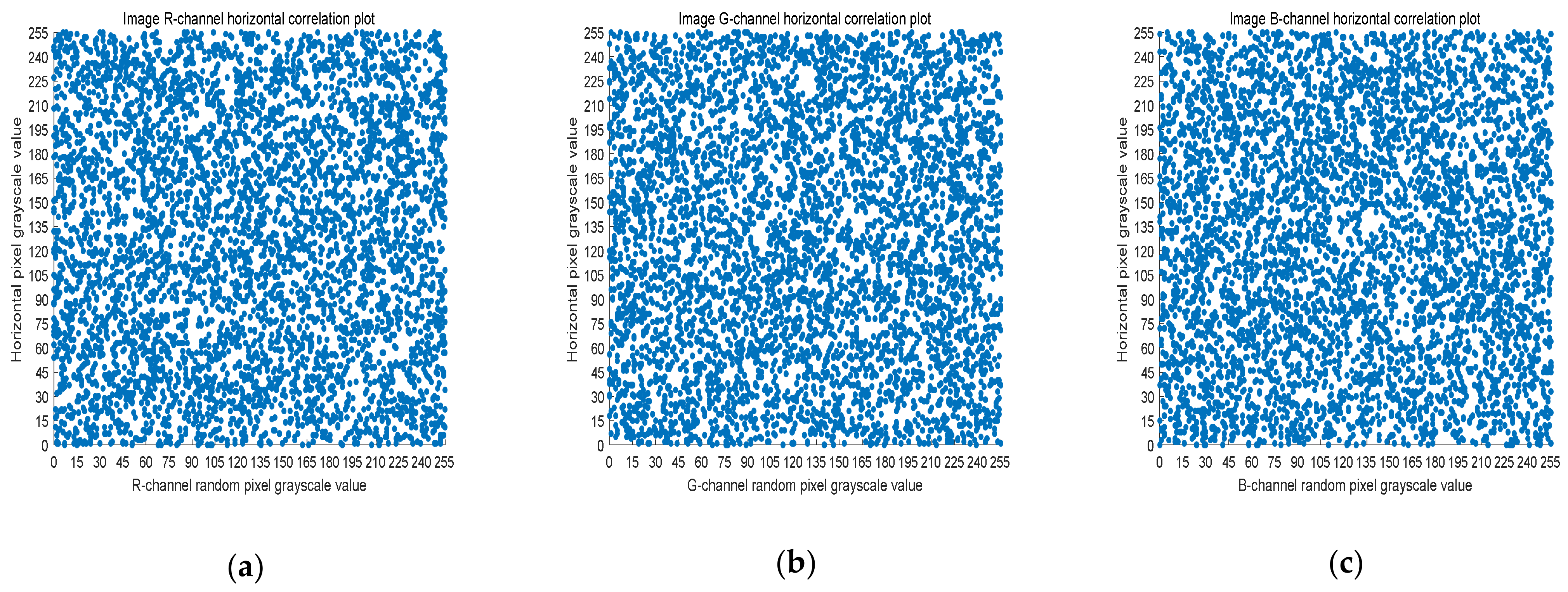
4.3. Correlation Analysis
4.4. Information Entropy
5. Security Analysis
5.1. Key Space Analysis
5.2. Key Sensitivity Analysis
5.3. Differential Attacks
5.4. Anti-Noise Capability Analysis


5.5. Analysis of Shear Resistance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matthews, R. On the derivation of a “Chaotic” encryption algorithm. Cryptologia 1989, 8, 29–41. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.W.; Liao, X.; Chen, G. A new chaos-based fast image encryption algorithm. Appl. Soft Comput. 2011, 11, 514–522. [Google Scholar] [CrossRef]
- Sun, J. A chaotic image encryption algorithm combining 2D chaotic system and random XOR diffusion. Phys. Scr. 2021, 96, 105208. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, N.; Li, Y. Image encryption algorithm based on chaotic mapping and dynamic S-box. J. Chin. Acad. Electron. Sci. 2019, 14, 1129–1135. [Google Scholar]
- Chen, S.; Tang, Y. Triple dislocation algorithm for RGB color images based on chaotic system. J. Chongqing Univ. Posts Telecommun. Nat. Sci. Ed. 2018, 30, 812–818. [Google Scholar]
- Hu, Y.; Yu, S.; Zhang, Z. On the Security Analysis of a Hopfield Chaotic Neural Network-Based Image Encryption Algorithm. Complexity 2020, 2020, 2051653. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S. Single Neuronal Dynamical System in Self-Feedbacked Hopfield Networks and Its Application in Image Encryption. Entropy 2021, 23, 456. [Google Scholar] [CrossRef]
- Chen, L.; Yin, H.; Huang, T.; Yuan, L.; Zheng, S.; Yin, L. Chaos in fractional-order discrete neural networks with application to image encryption. Neural Netw. 2020, 125, 174–184. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, X. Multiple-image encryption algorithm based on DNA encoding and chaotic system. Multimed. Tools Appl. 2018, 78, 7841–7869. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Y. Multiple-image encryption algorithm based on the 3D scrambling model and dynamic DNA coding. Opt. Laser Technol. 2021, 141, 107073. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J. A Multidimensional Chaotic Image Encryption Algorithm based on DNA Coding. Multimed. Tools Appl. 2020, 79, 21579–21601. [Google Scholar] [CrossRef]
- Zhu, J.; Ermann, N.; Chen, K.; Keyser, U.F. Image Encoding Using Multi-level DNA Barcodes with Nanopore Readout. Small 2021, 2100711. [Google Scholar] [CrossRef] [PubMed]
- Xie, D. Public Key Image Encryption Based on Compressed Sensing. IEEE Access 2019, 7, 131672–131680. [Google Scholar] [CrossRef]
- Yamac, M.; Ahishali, M.; Passalis, N.; Raitoharju, J.; Sankur, B.; Gabbouj, M. Multi-Level Reversible Data Anonymization via Compressive Sensing and Data Hiding. IEEE Trans. Inf. Forensics Secur. 2020, 16, 1014–1028. [Google Scholar] [CrossRef]
- Musanna, F.; Kumar, S. A novel image encryption algorithm using chaotic compressive sensing and nonlinear exponential function. J. Inf. Secur. Appl. 2020, 54, 102560. [Google Scholar] [CrossRef]
- Dou, Y.; Li, M. An Image Encryption Algorithm Based on Compressive Sensing and M Sequence. IEEE Access 2020, 8, 220646–220657. [Google Scholar] [CrossRef]
- Pourasad, Y.; Ranjbarzadeh, R.; Mardani, A. A New Algorithm for Digital Image Encryption Based on Chaos Theory. Entropy 2021, 23, 341. [Google Scholar] [CrossRef]
- Shi, H.; Wang, L.D. A multi-process image encryption scheme based on compressed sensing and multidimensional chaotic systems. J. Phys. 2019, 68, 39–52. [Google Scholar]
- Azam, N.A.; Hayat, U.; Ayub, M. A Substitution Box Generator, its Analysis, and Applications in Image Encryption. Signal Process. 2021, 187, 108144. [Google Scholar] [CrossRef]
- Wang, Y.; Li, A.; Wang, S.; Wang, J.Y.; Hu, J.J. Image encryption algorithm based on the combination of CNN and traditional S-box. Electro-Opt. Control 2021, 28, 34–38, 57. [Google Scholar]
- Yang, Y.G.; Guan, B.W.; Li, J.; Li, D.; Zhou, Y.H.; Shi, W.M. Image compression-encryption scheme based on fractional order hyper-chaotic systems combined with 2D compressed sensing and DNA encoding. Opt. Laser Technol. 2019, 119, 105661. [Google Scholar] [CrossRef]
- Sun, C.; Wang, E.; Zhao, B. Image Encryption Scheme with Compressed Sensing Based on a New Six-Dimensional Non-Degenerate Discrete Hyperchaotic System and Plaintext-Related Scrambling. Entropy 2021, 23, 291. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, X.; Wu, X.; Zhang, Y. Image encryption algorithm based on multiple mixed hash functions and cyclic shift. Opt. Lasers Eng. 2018, 107, 370379. [Google Scholar] [CrossRef]
- Wang, K.; Wu, X.; Wang, H.; Kan, H.; Kurths, J. New color image cryptosystem via SHA-512 and hybrid domain. Multimed. Tools Appl. 2021, 80, 18875–18899. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, G.-Y.; Zhu, M.; Chen, J.-X.; Lei, W.-M. A Fast Chaos-Based Colour Image Encryption Algorithm Using a Hash Function. Informatica 2018, 29, 651–673. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.G.; Xu, P.; Yang, R.; Zhou, Y.H.; Shi, W.M. Quantum Hash function and its application to privacy amplification in quantum key distribution, pseudo-random number generation and image encryption. Sci. Rep. 2016, 6, 19788. [Google Scholar] [CrossRef] [Green Version]
- Zhou, N.; Chen, W.; Yan, X.; Wang, Y. Bit-level quantum color image encryption scheme with quantum cross-exchange operation and hyper-chaotic system. Quantum Inf. Process. 2018, 17, 137. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, M.; Zhang, Y. Review of Quantum Image Processing. Arch. Comput. Methods Eng. 2021, 1–25. [Google Scholar] [CrossRef]
- Butt, K.K.; Li, G.; Masood, F.; Khan, S. A Digital Image Confidentiality Scheme Based on Pseudo-Quantum Chaos and Lucas Sequence. Entropy 2020, 22, 1276. [Google Scholar] [CrossRef]
- Plas-Garza, M.A.; Zambrano-Serrano, E.; Rodríguez-Cruz, J.R.; Posadas-Castillo, C. Implementation of an encrypted-compressed image wireless transmission scheme based on chaotic fractional-order systems. Chin. J. Phys. 2020, 71, 22–37. [Google Scholar] [CrossRef]
- Wang, K.; Wu, X.; Gao, T. Double color images compression–encryption via compressive sensing. Neural Comput. Appl. 2021, 1–22. [Google Scholar] [CrossRef]
- Masood, F.; Ahmad, J.; Shah, S.A.; Jamal, S.S.; Hussain, I. A Novel Hybrid Secure Image Encryption Based on Julia Set of Fractals and 3D Lorenz Chaotic Map. Entropy 2020, 22, 274. [Google Scholar] [CrossRef] [Green Version]
- Masood, F.; Boulila, W.; Ahmad, J.; Arshad, A.; Sankar, S.; Rubaiee, S.; Buchanan, W. A Novel Privacy Approach of Digital Aerial Images Based on Mersenne Twister Method with DNA Genetic Encoding and Chaos. Remote. Sens. 2020, 12, 1893. [Google Scholar] [CrossRef]
- Chen, L.-P.; Yin, H.; Yuan, L.-G.; Lopes, A.M.; Machado, J.A.T.; Wu, R.-C. A novel color image encryption algorithm based on a fractional-order discrete chaotic neural network and DNA sequence operations. Front. Inf. Technol. Electron. Eng. 2020, 21, 866–879. [Google Scholar] [CrossRef]
- Ahmad, J.; Masood, F.; Shah, A.; Jamal, S.S.; Hussain, I. A Novel Secure Occupancy Monitoring Scheme Based on Multi-Chaos Mapping. Symmetry 2020, 12, 350. [Google Scholar] [CrossRef] [Green Version]
- Gao, X. A color image encryption algorithm based on an improved Hénon map. Phys. Scr. 2021, 96, 065203. [Google Scholar] [CrossRef]
- Munir, N.; Khan, M.; Hazzazi, M.M.; Aijaedi, A.; Ismail, A.A.K.H.; Alharbi, A.R.; Hussain, I. Cryptanalysis of Internet of Health Things Encryption Scheme Based on Chaotic Maps. IEEE Access 2021, 9, 105678–105685. [Google Scholar] [CrossRef]
- Al-Hazaimeh, O.M.; Al-Jamal, M.F.; Alhindawi, N.; Omari, A. Image encryption algorithm based on Lorenz chaotic map with dynamic secret keys. Neural Comput. Appl. 2019, 31, 2395–2405. [Google Scholar] [CrossRef]
- Ye, G.; Zhao, H.; Chai, H. Chaotic image encryption algorithm using wave-line permutation and block diffusion. Nonlinear Dyn. 2015, 83, 2067–2077. [Google Scholar] [CrossRef]
- Yu, J.Z.; Vinc, T.L. Control study of chaotic Lorena systems. J. Phys. 1998, 47, 397–402. [Google Scholar]
- Wu, C. Discrete Arnold transform improvement and its application in image dislocation encryption. J. Phys. 2014, 63, 91–110. [Google Scholar]
- Li, C.; Luo, G.; Li, C. Image encryption scheme based on skew tent chaotic mapping and Arnold transform. Comput. Appl. Res. 2018, 35, 3424–3427. [Google Scholar]
- Zhou, S.; Wang, X.; Wang, M.; Zhang, Y. Simple colour image cryptosystem with very high level of security. Chaos Solitons Fractals 2020, 141, 110225. [Google Scholar] [CrossRef]
- Yildirim, M. A color image encryption scheme reducing the correlations between R, G, B components. Optik 2021, 237, 166728. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, C.; Chen, H. A Novel Color Image Encryption Algorithm Based on Hyperchaotic System and Permutation-Diffusion Architecture. Int. J. Bifurc. Chaos 2019, 29. [Google Scholar] [CrossRef]







| N | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 3 | 10 | 12 | 8 | 6 | |
| N | 9 | 10 | 11 | 12 | 25 | 50 | 60 |
| 12 | 30 | 5 | 12 | 50 | 150 | 60 | |
| N | 100 | 120 | 125 | 128 | 256 | 480 | 512 |
| 150 | 60 | 250 | 96 | 192 | 240 | 384 |
| Horizontal Correlation | Vertical Correlation | Diagonal Correlation | ||
|---|---|---|---|---|
| Original image | R | 0.97247 | 0.98656 | 0.96164 |
| G | 0.97322 | 0.98675 | 0.96296 | |
| B | 0.94617 | 0.97208 | 0.92864 | |
| The encryption method proposed in this paper | R | –0.0096211 | –0.011037 | –0.00084143 |
| G | 0.00096321 | –0.0014868 | –0.012429 | |
| B | 0.0022199 | 0.0015614 | 0.0045217 | |
| Literature [31] | R | 0.0046 | 0.0046 | 0.0005 |
| G | 0.0052 | 0.0058 | 0.0031 | |
| B | 0.0063 | 0.0084 | 0.0102 | |
| The large aerial images in the literature [33] | RGB average correlation | –0.0014 | 0.0039 | –0.0027 |
| Information Entropy | |||
|---|---|---|---|
| Image | R | G | B |
| original image | 7.2682 | 7.5901 | 6.9951 |
| Image encrypted in this article | 7.9992 | 7.9993 | 7.9994 |
| Literature [32] | 7.9974 | 7.9971 | 7.9975 |
| Literature [34] | 7.9973 | 7.9972 | 7.9966 |
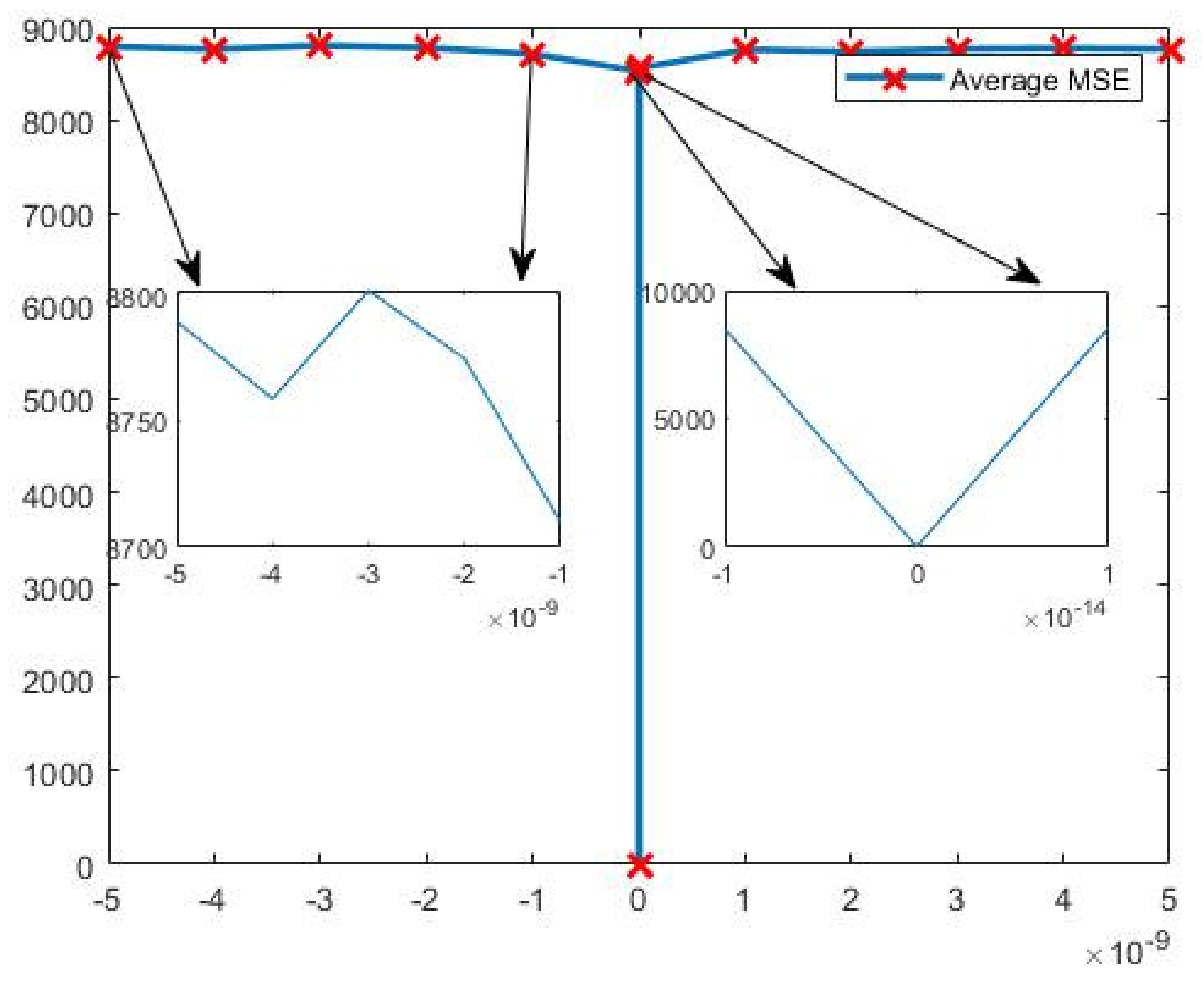
| Algorithms | MSE Values |
|---|---|
| Methodology of this article | 8932.0 |
| Literature [35] | 7775.0 |
| Literature [33] | 9875.5 |
| AES | 4600 |
| Lena (512 × 512) | NPCR | UACI | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| Methodology of this article | 0.99611 | 0.99627 | 0.99616 | 0.33400 | 0.33329 | 0.33483 |
| Tiffany image in the literature [32] | 0.9961 | 0.9961 | 0.9961 | 0.3626 | 0.3626 | 0.3626 |
| Literature [44] | 0.99602 | 0.99607 | 0.99601 | 0.334689 | 0.334965 | 0.334155 |
| Literature [45] | 0.99640 | 0.99633 | 0.99647 | 0.33488 | 0.33493 | 0.33509 |
| Image (PSNR) | R | G | B |
|---|---|---|---|
| Pepper noise density 0.0001 | 48.0455 | 47.0210 | 50.5779 |
| Pepper noise density 0.001 | 37.9455 | 38.6270 | 40.1578 |
| Pepper noise density 0.01 | 27.6638 | 28.3126 | 29.5434 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Pan, P.; Sun, C.; Zhao, B. Plaintext-Related Dynamic Key Chaotic Image Encryption Algorithm. Entropy 2021, 23, 1159. https://doi.org/10.3390/e23091159
Wu Z, Pan P, Sun C, Zhao B. Plaintext-Related Dynamic Key Chaotic Image Encryption Algorithm. Entropy. 2021; 23(9):1159. https://doi.org/10.3390/e23091159
Chicago/Turabian StyleWu, Zeming, Ping Pan, Chunyang Sun, and Bing Zhao. 2021. "Plaintext-Related Dynamic Key Chaotic Image Encryption Algorithm" Entropy 23, no. 9: 1159. https://doi.org/10.3390/e23091159
APA StyleWu, Z., Pan, P., Sun, C., & Zhao, B. (2021). Plaintext-Related Dynamic Key Chaotic Image Encryption Algorithm. Entropy, 23(9), 1159. https://doi.org/10.3390/e23091159






