Attention-Based Fault-Tolerant Approach for Multi-Agent Reinforcement Learning Systems
Abstract
:1. Introduction
2. Related Work
2.1. MARL Models Designed for Normal Environments
2.2. MARL Models Designed for Noisy Environments
3. Background
3.1. Partially Observable Markov Games
3.2. Policy Gradient and Actor–Critic
4. Our Approach
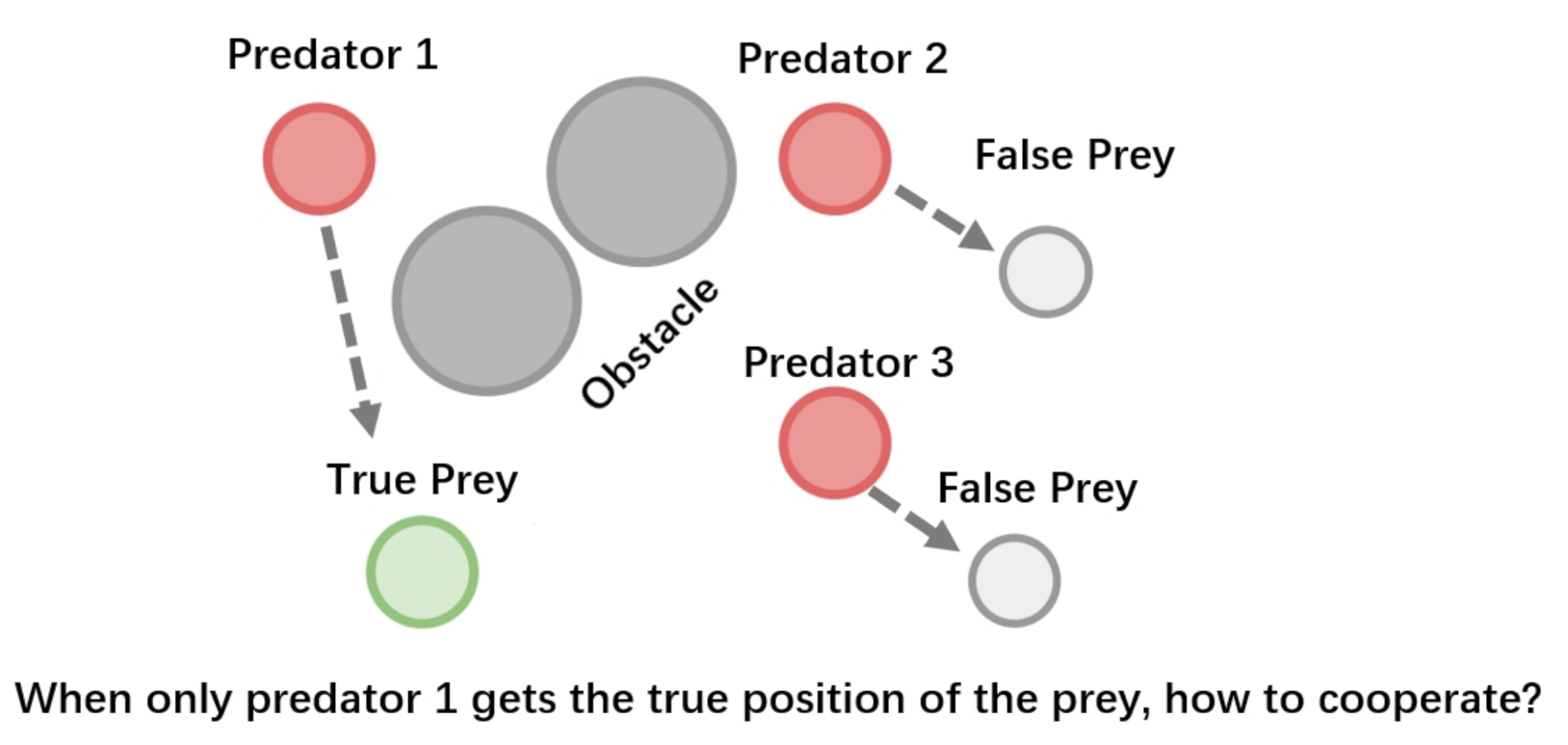
4.1. Problem Formulation
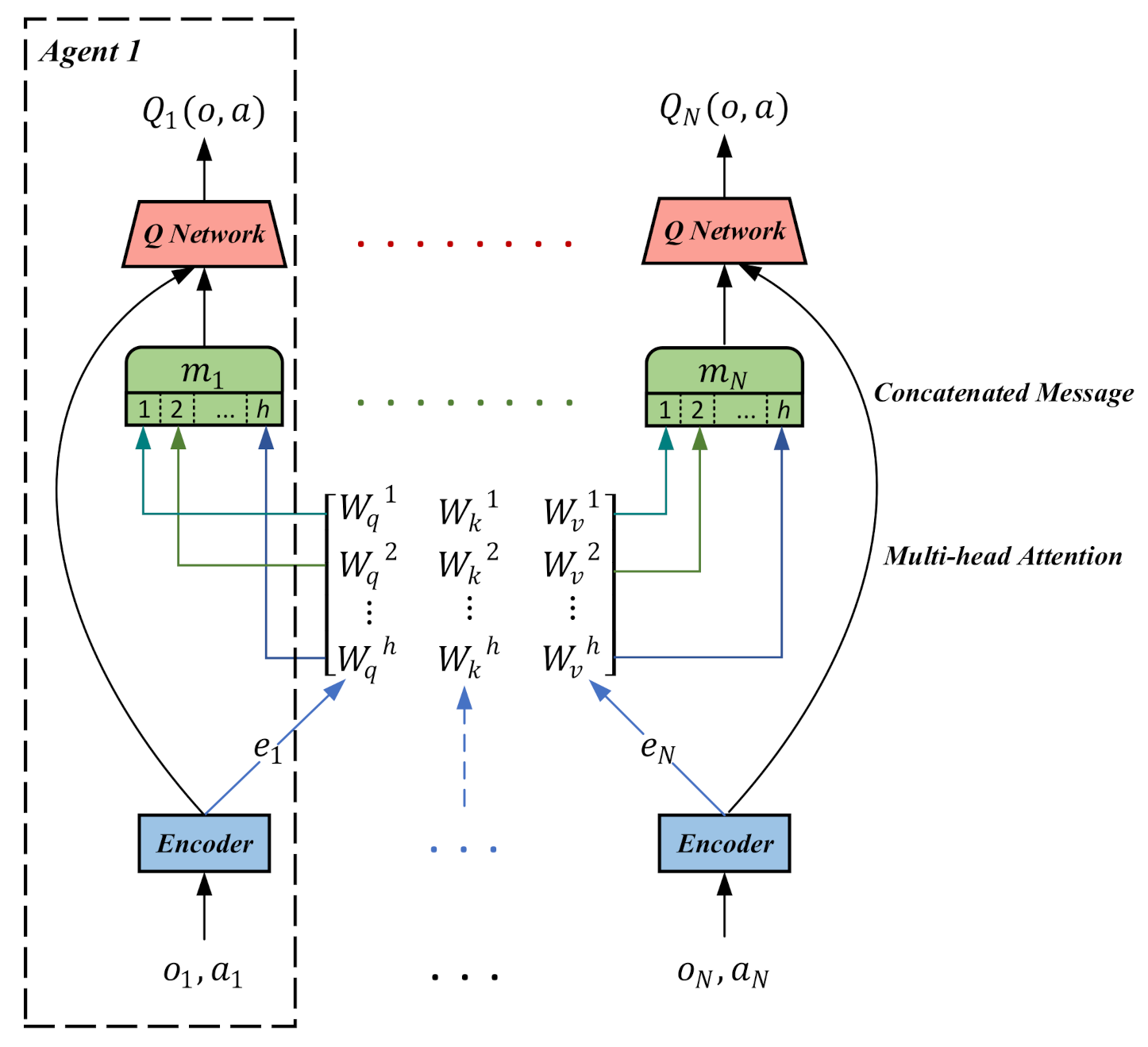
4.2. Attention-Based Fault-Tolerant Mechanism
4.3. Training Details of FT-Attn
| Algorithm 1 Training procedure for FT-Attn. |
| Input: Initialize the environments with N agents; initialize replay buffer, D. |
| 1: for num episodes do |
| 2: Observe initial state for each agent i, |
| 3: for steps per episode do |
| 4: Select actions for each agent i. |
| 5: Execute the action and get , for all agents. |
| 6: Store transitions in D. |
| 7: Sample minibatch , and unpack. |
| 8: Calculate for all i in parallel, , using target policies, |
| 9: Set , |
| 10: Update critic by minimizing the loss:
|
| 11: Update policy:
|
| 12: Update target critic and policy parameters:
|
| 13: end for |
| 14: end for |
5. Experiments
5.1. Experimental Setting and Baseline Methods
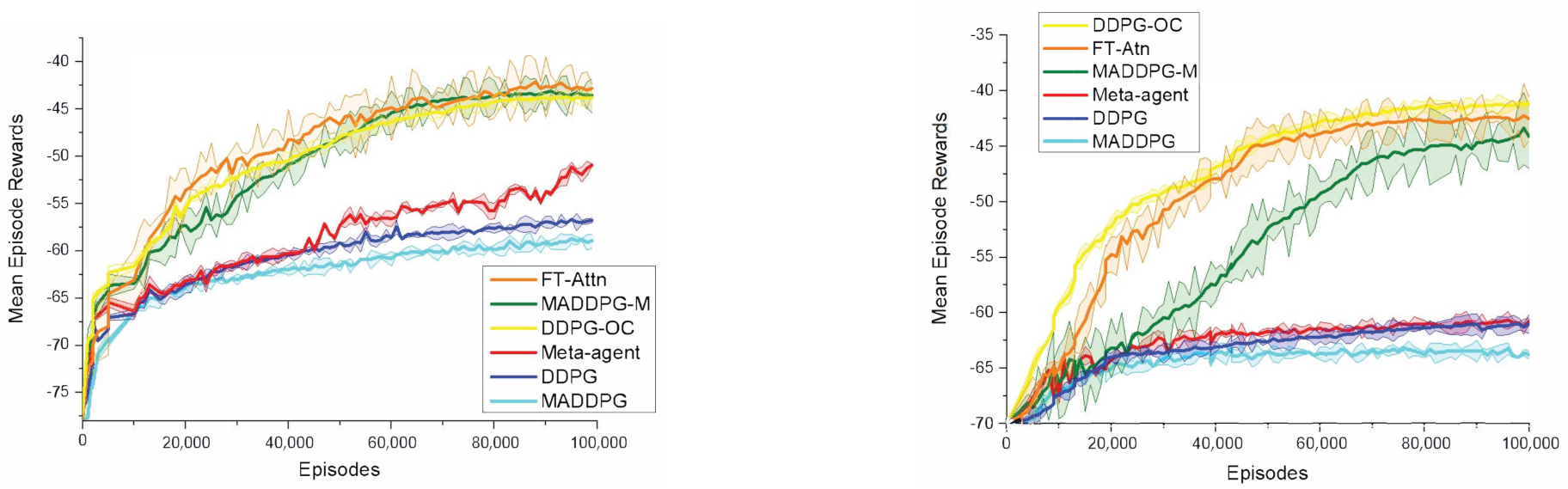
5.2. Performance Comparison in a Modified Cooperative Navigation Scenario
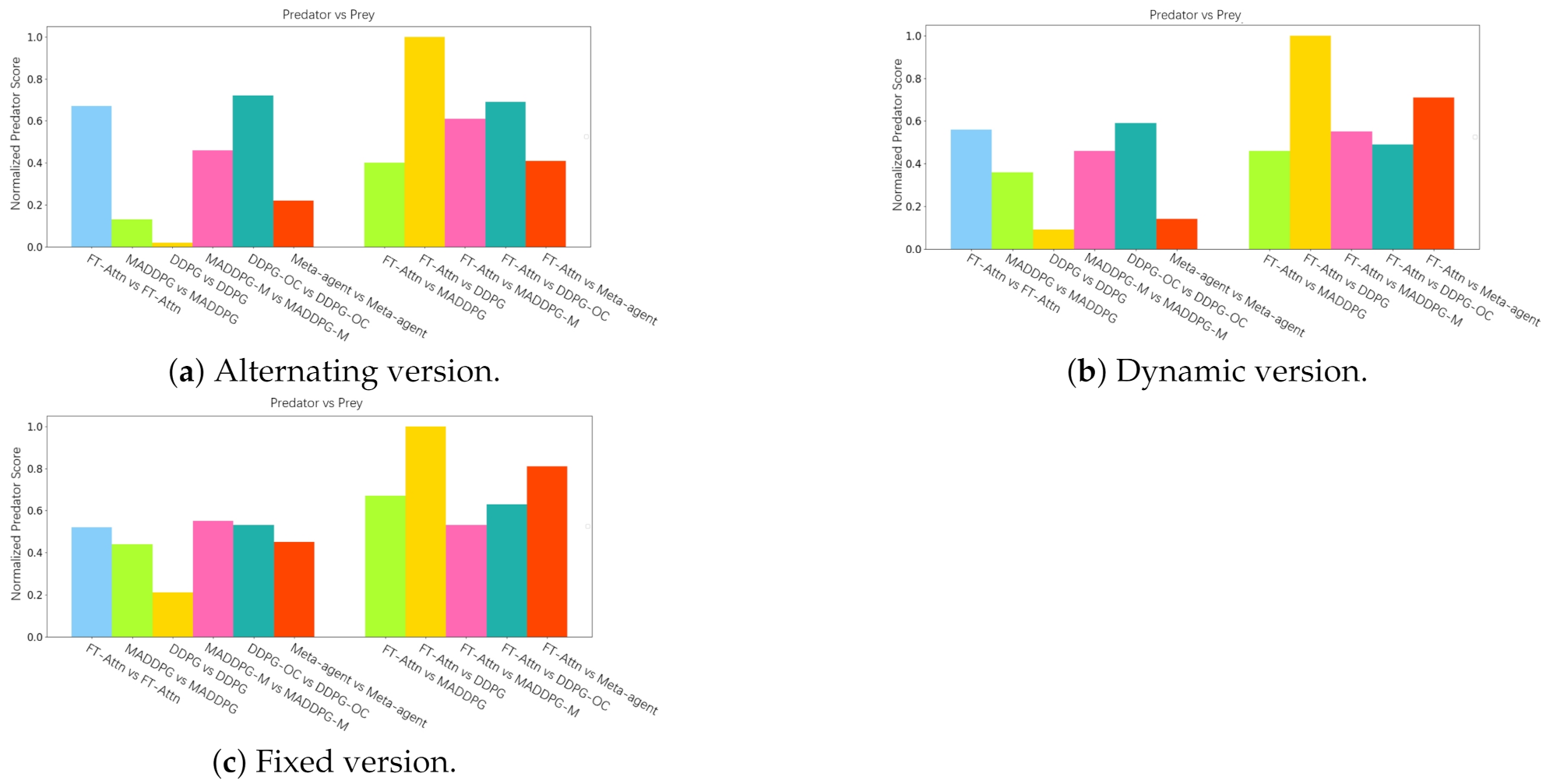
5.3. Performance Comparison in the Modified Predator and Prey Scenario
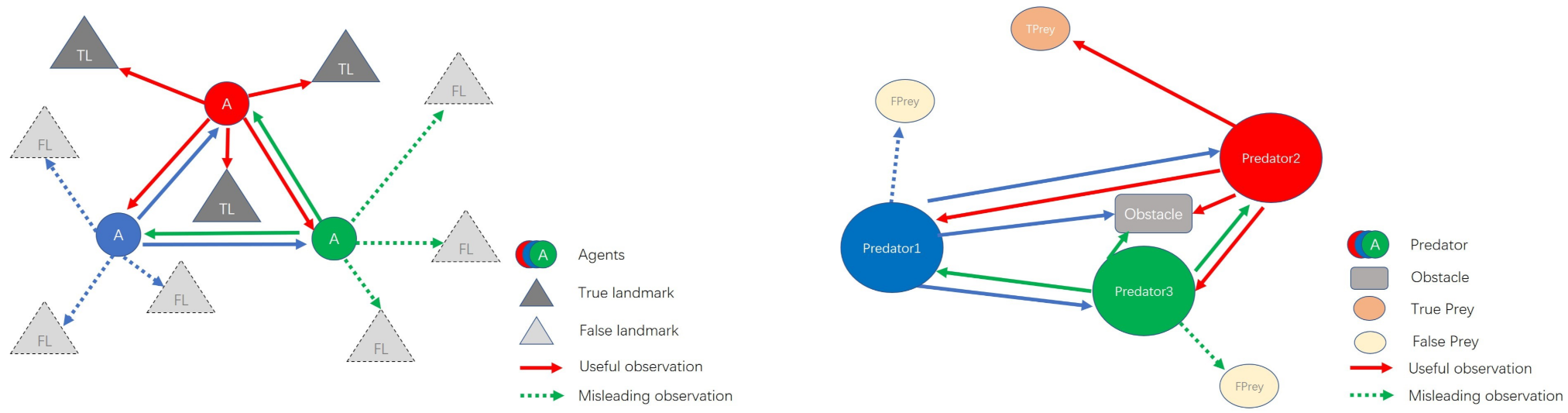
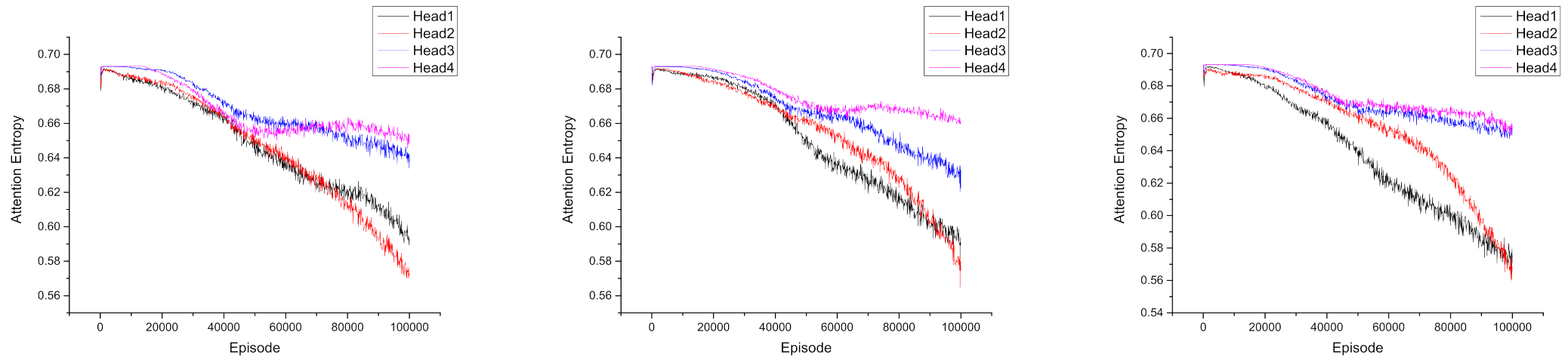
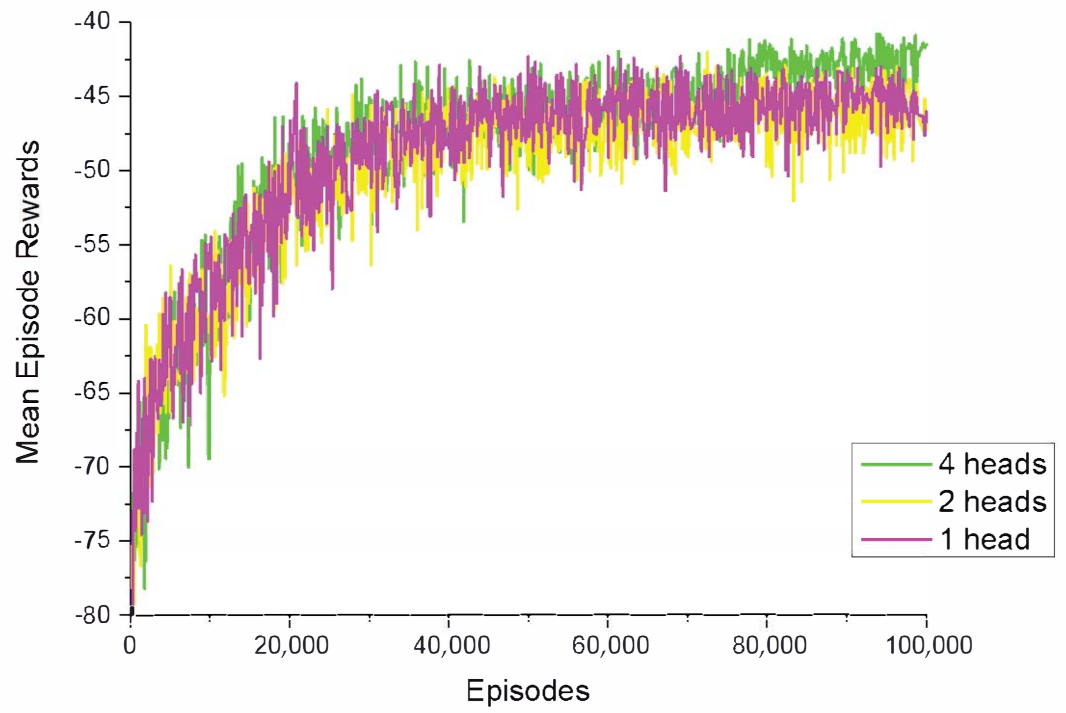
5.4. Attention Visualization
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Geng, M.; Zhou, X.; Ding, B.; Wang, H.; Zhang, L. Learning to cooperate in decentralized multirobot exploration of dynamic environments. In International Conference on Neural Information Processing; Springer: Cham, Switzerland, 2018; pp. 40–51. [Google Scholar]
- Higgins, F.; Tomlinson, A.; Martin, K.M. Survey on security challenges for swarm robotics. In Proceedings of the 2009 Fifth International Conference on Autonomic and Autonomous Systems, Valencia, Spain, 20–25 April 2009; pp. 307–312. [Google Scholar]
- Dresner, K.; Stone, P. A multiagent approach to autonomous intersection management. J. Artif. Intell. Res. 2008, 31, 591–656. [Google Scholar] [CrossRef] [Green Version]
- Pipattanasomporn, M.; Feroze, H.; Rahman, S. Multi-agent systems in a distributed smart grid: Design and implementation. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, Seattle, WA, USA, 15–18 March 2009; pp. 1–8. [Google Scholar]
- Geng, M.; Xu, K.; Zhou, X.; Ding, B.; Wang, H.; Zhang, L. Learning to cooperate via an attention-based communication neural network in decentralized multirobot exploration. Entropy 2019, 21, 294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, X.; Wang, H.; Ding, B.; Peng, W.; Wang, R. Multi-objective evolutionary computation for topology coverage assessment problem. Knowl.-Based Syst. 2019, 177, 1–10. [Google Scholar] [CrossRef]
- Ota, J. Multi-agent robot systems as distributed autonomous systems. Adv. Eng. Inform. 2006, 20, 59–70. [Google Scholar] [CrossRef]
- Amato, C. Decision-Making Under Uncertainty in Multi-Agent and Multi-Robot Systems: Planning and Learning. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligenge, Stockholm, Sweden, 13–19 July 2018; pp. 5662–5666. [Google Scholar]
- Guan, X.; Zhang, X.; Lv, R.; Chen, J.; Michal, W. A large-scale multi-objective flights conflict avoidance approach supporting 4D trajectory operation. Sci. China Inf. Sci. 2017, 60, 112202. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Wang, H.; Peng, W.; Ding, B.; Wang, R. Solving multi-scenario cardinality constrained optimization problems via multi-objective evolutionary algorithms. Sci. China Inf. Sci. 2019, 62, 192104. [Google Scholar] [CrossRef] [Green Version]
- Fang, H.; Shang, C.; Chen, J. An optimization-based shared control framework with applications in multirobot systems. Sci. China Inf. Sci. 2018, 61, 014201. [Google Scholar] [CrossRef] [Green Version]
- Millard, A.G.; Timmis, J.; Winfield, A.F. Towards exogenous fault detection in swarm robotic systems. In Proceedings of the Conference towards Autonomous Robotic Systems, Oxford, UK, 20–23 August 2013; pp. 429–430. [Google Scholar]
- Kilinc, O.; Montana, G. Multi-agent deep reinforcement learning with extremely noisy observations. arXiv 2018, arXiv:1812.00922. [Google Scholar]
- Buşoniu, L.; Babuška, R.; De Schutter, B. Multi-agent reinforcement learning: An overview. In Innovations in Multi-Agent Systems and Applications-1; Springer: Berlin/Heidelberg, Germany, 2010; pp. 183–221. [Google Scholar]
- Fischer, F.; Rovatsos, M.; Weiss, G. Hierarchical reinforcement learning in communication-mediated multiagent coordination. In Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems, New York, NY, USA, 19–23 July 2004; Volume 4, pp. 1334–1335. [Google Scholar]
- Littman, M.L. Markov games as a framework for multi-agent reinforcement learning. In Machine Learning Proceedings; Elsevier: Cambridge, MA, USA, 1994; pp. 157–163. [Google Scholar]
- Busoniu, L.; Babuska, R.; De Schutter, B. A comprehensive survey of multiagent reinforcement learning. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2008, 38, 156–172. [Google Scholar] [CrossRef] [Green Version]
- Tan, M. Multi-agent reinforcement learning: Independent vs. cooperative agents. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 June 1993; pp. 330–337. [Google Scholar]
- Tampuu, A.; Matiisen, T.; Kodelja, D.; Kuzovkin, I.; Korjus, K.; Aru, J.; Aru, J.; Vicente, R. Multiagent cooperation and competition with deep reinforcement learning. PLoS ONE 2017, 12, e0172395. [Google Scholar] [CrossRef] [PubMed]
- Gupta, J.K.; Egorov, M.; Kochenderfer, M. Cooperative multi-agent control using deep reinforcement learning. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Sao Paulo, Brazil, 8–12 May 2017; pp. 66–83. [Google Scholar]
- Sunehag, P.; Lever, G.; Gruslys, A.; Czarnecki, W.M.; Zambaldi, V.F.; Jaderberg, M.; Lanctot, M.; Sonnerat, N.; Leibo, J.Z.; Tuyls, K.; et al. Value-Decomposition Networks For Cooperative Multi-Agent Learning Based On Team Reward. In Proceedings of the 17th International Conference on Autonomous Agents and Multi-Agent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 2085–2087. [Google Scholar]
- Sukhbaatar, S.; Fergus, R.; Szlam, A. Learning multiagent communication with backpropagation. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2244–2252. [Google Scholar]
- Foerster, J.N.; Assael, Y.M.; de Freitas, N.; Whiteson, S. Learning to communicate to solve riddles with deep distributed recurrent q-networks. arXiv 2016, arXiv:1602.02672. [Google Scholar]
- Peng, P.; Yuan, Q.; Wen, Y.; Yang, Y.; Tang, Z.; Long, H.; Wang, J. Multiagent bidirectionally-coordinated nets for learning to play starcraft combat games. arXiv 2017, arXiv:1703.10069. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Abbeel, O.P.; Mordatch, I. Multi-agent actor–critic for mixed cooperative-competitive environments. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6379–6390. [Google Scholar]
- Jiang, J.; Lu, Z. Learning attentional communication for multi-agent cooperation. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 7254–7264. [Google Scholar]
- Iqbal, S.; Sha, F. Actor-attention-critic for multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 2961–2970. [Google Scholar]
- Kim, D.; Moon, S.; Hostallero, D.; Kang, W.J.; Lee, T.; Son, K.; Yi, Y. Learning to schedule communication in multi-agent reinforcement learning. arXiv 2019, arXiv:1902.01554. [Google Scholar]
- Luo, C.; Liu, X.; Chen, X.; Luo, J. Multi-agent Fault-tolerant Reinforcement Learning with Noisy Environments. In Proceedings of the 2020 IEEE 26th International Conference on Parallel and Distributed Systems (ICPADS), Hong Kong, China, 2–4 December 2020; pp. 164–171. [Google Scholar]
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. In Advances in Neural Information Processing Systems; MIT Press: Denver, CO, USA, 2000; pp. 1008–1014. [Google Scholar]
- Foerster, J.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual multi-agent policy gradients. arXiv 2017, arXiv:1705.08926. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]

| Method | Fixed | Alternating | Dynamic |
|---|---|---|---|
| Meta-agent | −39.95 ± 4.50 | −51.42 ± 7.70 | −60.98 ± 8.82 |
| MADDPG | −54.00 ± 7.43 | −58.67 ± 8.90 | −63.44 ± 9.88 |
| DDPG | −56.00 ± 8.96 | −56.50 ± 8.51 | −60.66 ± 8.68 |
| MADDPG-M | −39.73 ± 5.09 | −43.34 ± 7.29 | −43.91 ± 7.75 |
| FT-Attn | −40.89 ± 5.42 | −43.30 ± 7.83 | −42.48 ± 7.36 |
| DDPG-OC (upper-bound) | −39.26 ± 4.45 | −43.44± 5.92 | −41.25 ± 5.24 |
| Method | Fixed | Alternating | Dynamic |
|---|---|---|---|
| MADDPG-M | 99.98% ± 0.02 | 99.54% ± 0.56 | 88.82% ± 5.91 |
| FT-Attn | 99.23% ± 0.33 | 99.68% ± 0.42 | 91.76% ± 5.34 |
| Method | 1 Faulted | 2 Faulted | 3 Faulted | 4 Faulted |
|---|---|---|---|---|
| Meta-agent | −66.31 ± 5.48 | −66.98 ± 6.12 | −67.92 ± 7.27 | −69.73 ± 6.25 |
| MADDPG | −72.50 ± 8.35 | −72.83 ± 7.42 | −72.79 ± 9.56 | −72.68 ± 8.65 |
| DDPG | −72.20 ± 7.12 | −72.67 ± 5.79 | −73.03 ± 5.62 | −72.95 ± 5.43 |
| MADDPG-M | −66.73± 5.43 | −66.89 ± 8.43 | −67.13 ± 6.64 | −66.95 ± 6.65 |
| FT-Attn | −65.20 ± 4.38 | −66.25 ± 8.62 | −66.68 ± 6.57 | −67.00 ± 6.25 |
| DDPG-OC (upper-bound) | −64.92 ± 4.23 | −65.89 ± 7.73 | −66.14 ± 6.42 | −66.42 ± 7.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, S.; Geng, M.; Lan, L. Attention-Based Fault-Tolerant Approach for Multi-Agent Reinforcement Learning Systems. Entropy 2021, 23, 1133. https://doi.org/10.3390/e23091133
Gu S, Geng M, Lan L. Attention-Based Fault-Tolerant Approach for Multi-Agent Reinforcement Learning Systems. Entropy. 2021; 23(9):1133. https://doi.org/10.3390/e23091133
Chicago/Turabian StyleGu, Shanzhi, Mingyang Geng, and Long Lan. 2021. "Attention-Based Fault-Tolerant Approach for Multi-Agent Reinforcement Learning Systems" Entropy 23, no. 9: 1133. https://doi.org/10.3390/e23091133
APA StyleGu, S., Geng, M., & Lan, L. (2021). Attention-Based Fault-Tolerant Approach for Multi-Agent Reinforcement Learning Systems. Entropy, 23(9), 1133. https://doi.org/10.3390/e23091133






