Clifford Wavelet Entropy for Fetal ECG Extraction
Abstract
1. Introduction and Motivation
2. FECG Extraction Brief Review
3. Two Wavelet/Multiwavelet Processors
3.1. The Haar–Faber–Schauder System
3.2. Clifford Wavelets and Multiwavelets
3.3. Brief Comparison between the Two Classes of Wavelets/Multiwavelets
4. Methodology
4.1. Wavelet/Multiwavelet Processing
4.2. Wavelet/Multiwavelet Entropy
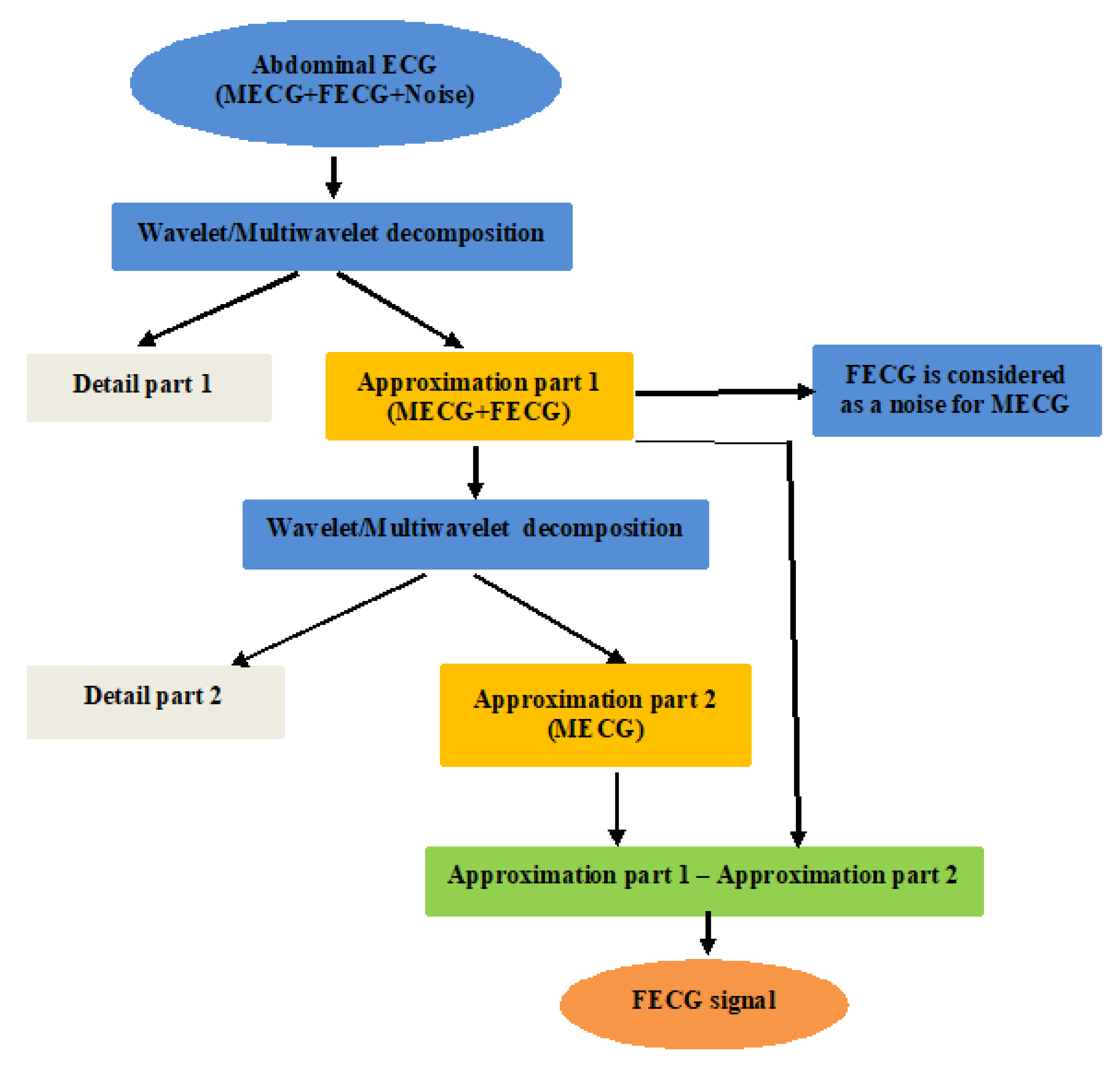
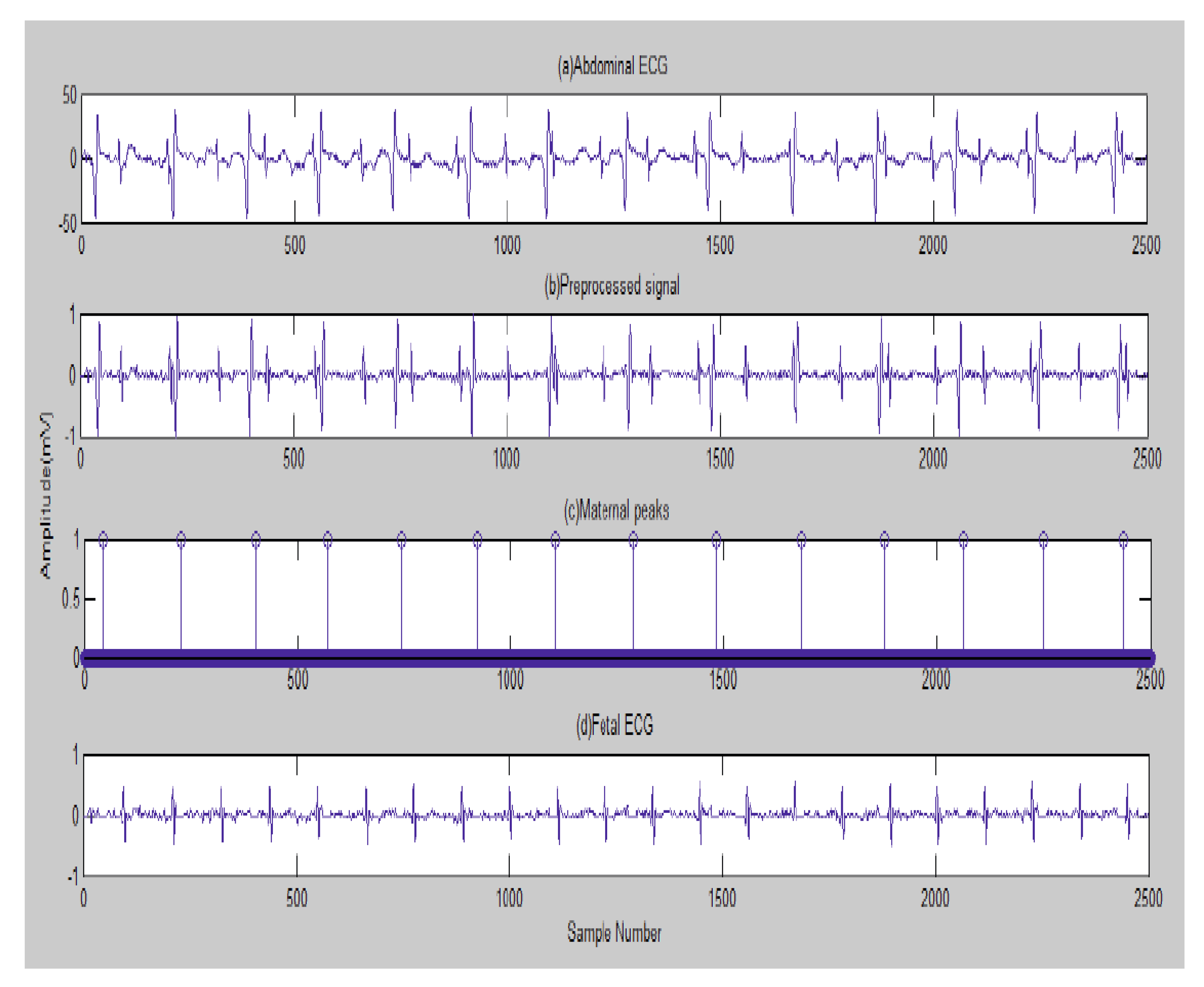
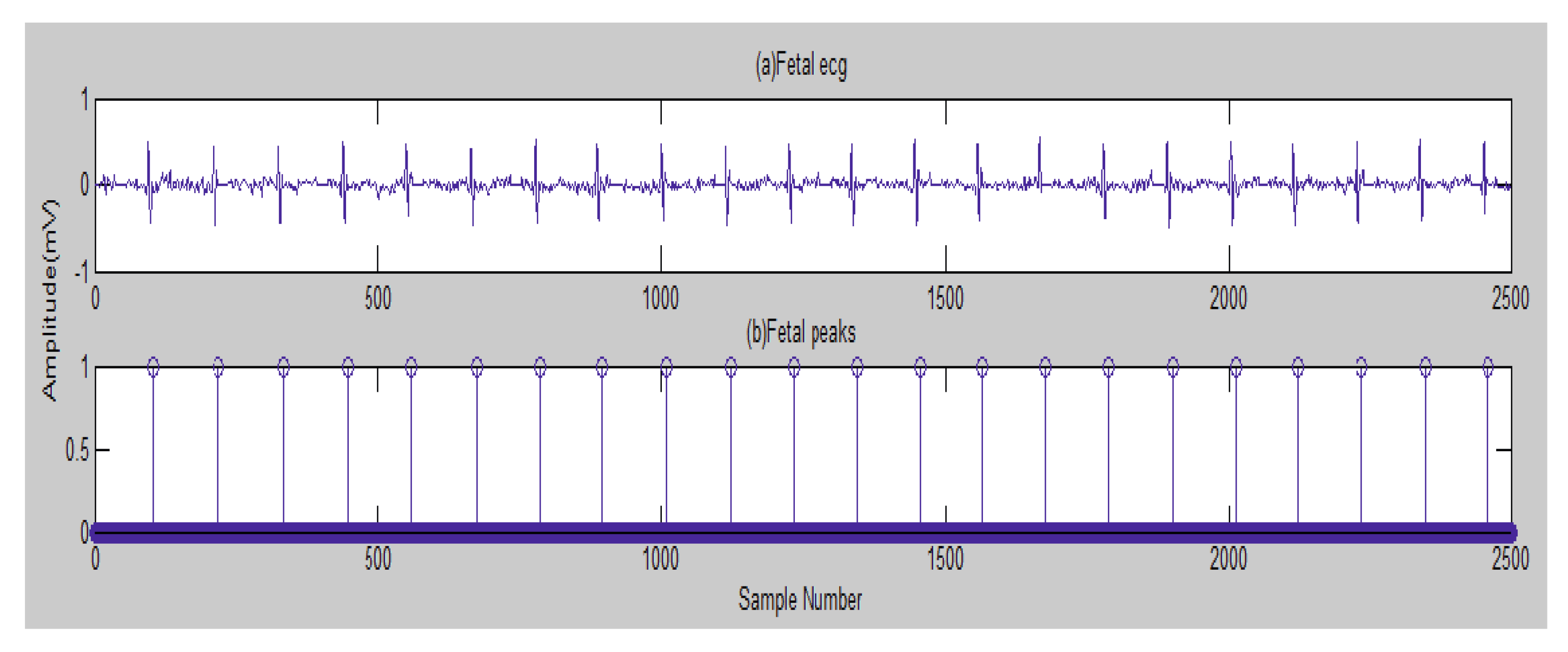
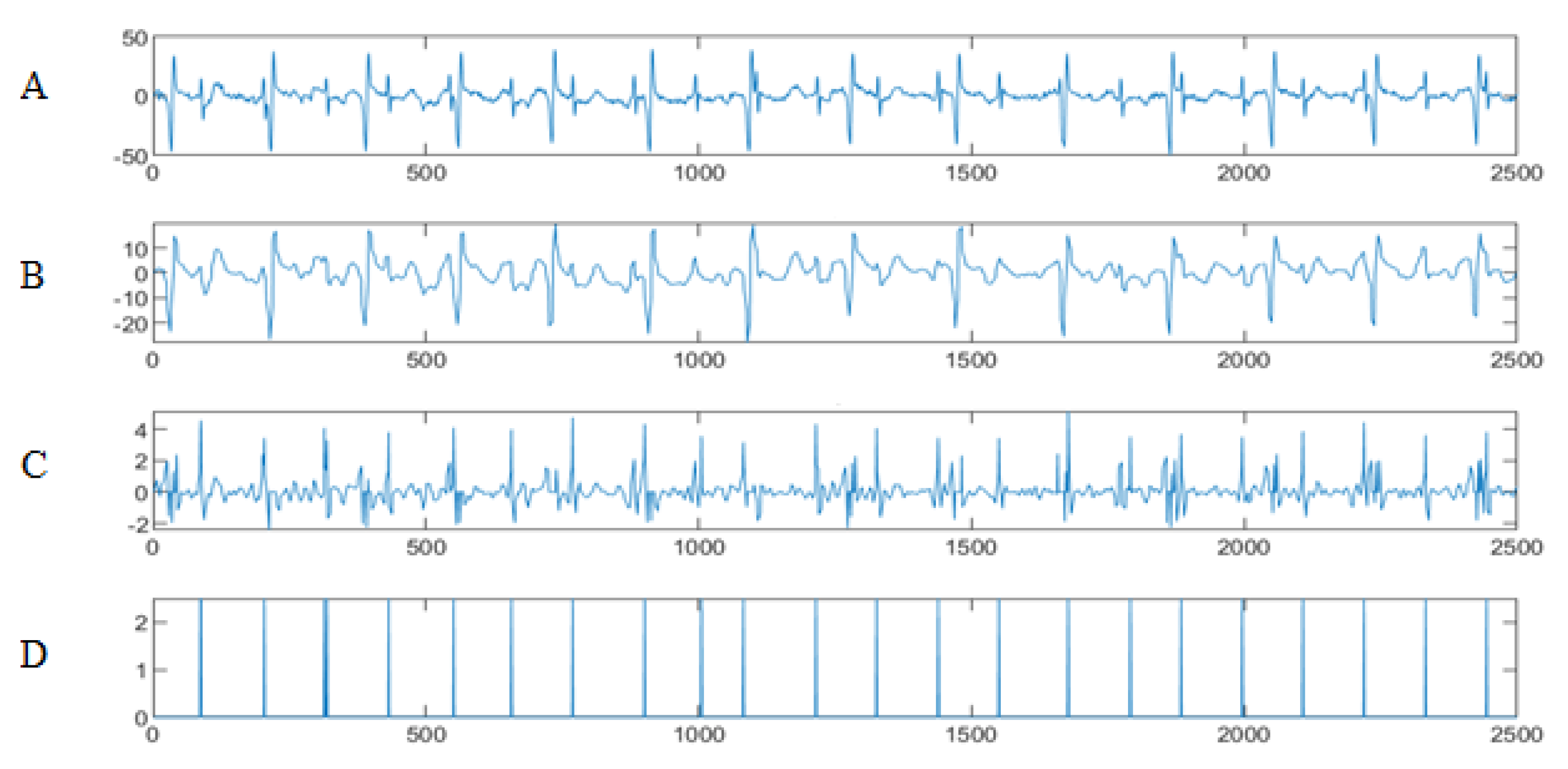
4.3. The FECG Extraction
| Algorithm 1 FECG extraction |
| Input AbdECG Output FECG Begin [Detail1,App1] = Wavelet/multiwavelet decomposition(AbdECG); MECG = Wavelet/multiwavelet reconstruction(App1); [Detail2,App2] = Wavelet/multiwavelet decomposition(MECG); App3 = App1-App2; FECG = Wavelet/multiwavelet reconstruction(App3); Return FECG End |
4.4. Performance Measurements
5. Results
5.1. Data Collection and Bases
5.2. The Processing of DAISY Signals
5.3. The Processing of Cinc Challenge Database
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ECG | Electrocardiogram |
| MECG | Mother electrocardiogram |
| FECG | Fetal electrocardiogram |
| WHO | World Health Organization |
| AbdECG | Abdominal electrocardiogram |
| EKG | Electrocardiography |
| The probability at the level j | |
| Se | Sensitivity |
| PPV | Positive predictive value |
| DAISY | Data base for the Identification of Systems |
| CinC Challenge 2013 | Computing in Cardiology Challenge 2013 |
| R-peaks | Real peaks |
| STFT | Short time Fourier transform |
| QRS | ventricular depolarization curve |
| RR | Interval between two R-peaks |
| FHR | Fetal heart rate |
| QT | The sum of depolarization (QRS) and repolarization (T) |
| SNR | Signal-to-noise ratio |
| R-Wave | Ventricular depolarization |
| HFSCH | Haar-Faber-Schauder |
| TD | Truly diagnosed |
| FP | False positive |
| FN | False negative |
| Approximation of the fetal electrocardiogram at the level J | |
| Approximation of the mother electrocardiogram at the level J | |
| Approximation of a signal S at the level j | |
| Detail component of the fetal electrocardiogram at the level J | |
| Detail component of the mother electrocardiogram at the level J | |
| Detail component of a signal S at the level J | |
| detail coefficient at the level j and the position k | |
| Approximation coefficient at the level j and the position k | |
| The energy of a signal S at the level j | |
| The total energy of a signal S | |
| The entropy of the signal | |
| The entropy of the signal at the level J |
References
- Zegre-Hemsey, J.K.; Garvey, J.L.; Carey, M.G. Cardiac Monitoring in the Emergency Department. Crit. Care Nurs. Clin. N. Am. 2016, 28, 331–345. [Google Scholar] [CrossRef]
- Bensegueni, S. Developpement de Techniques Utilisant les Ondelettes Pour l’Analyse, la Classification et le Traitement du Signal ECG. Ph.D. Thesis, Université des Frères Mentouri, Constantine, Algeria, 2016. [Google Scholar]
- El Tatar, A. Caractérisation et Modélisation des Potentiels Induits par les Commutations des Gradients de Champ Magnétique sur les Signaux Électrophysiologiques en IRM. Ph.D. Thesis, Université de Technologie de Compiègne, Compiègne, France, 2013. [Google Scholar]
- Sende, J. Guide Pratique de l’ECG; De Boeck Secundair: Paris, France, 2003. [Google Scholar]
- Amini, A.; Duncan, J. Pointwise tracking of left-ventricular motion in 3D. In Proceedings of the IEEE Workshop on Visual Motion, Princeton, NJ, USA, 7–9 October 1991. [Google Scholar]
- Jamali, D.F.; Mosayebi, P.; Abrishami Moghadam, H.; Giti, M.; Kermani, S. A Fully 3D system for cardiac wall deformation analysis in MRI data. In Proceedings of the 4th International Conference on Functional Imaging and Modeling of the Heart, Salt Lake City, UT, USA, 7–9 June 2007; pp. 12–21. [Google Scholar]
- Robert, A. Etude de la Forme et du Mouvement du Coeur à partir de Données Lacunaires. Ph.D. Thesis, Ecole Nationale Supérieure des Télécommunications, Paris, France, 1996. [Google Scholar]
- Schneider, J.E. Assessment of global cardiac function. Methods Mol. Biol. 2011, 771, 387–405. [Google Scholar] [PubMed]
- Bianca, C.; Pappalard, F.; Pennisi, M.; Ragusa, M.A. Persistence analysis in a Kolmogorov-type model for cancer-immune system competition. In Proceedings of the AIP Conference, Rhodes, Greece, 21–27 September 2013; Volume 1558, pp. 1797–1800. [Google Scholar]
- Atiya, A.F.; Abdel-Gawad, A.H.; Fayed, H.A. A new Monte-Carlo based exact algorithm for the Gaussian process classification problem. Adv. Math. Models Appl. 2020, 5, 261–288. [Google Scholar]
- Cattani, C. A review on harmonic wavelets and their fractional extension. J. Adv. Eng. Comput. 2018, 2, 224–238. [Google Scholar] [CrossRef]
- Cattani, C. Fractal similarities between the distribution of primes and nucleotides in DNA, Proceedings of the Institute of Mathematics and Mechanics. Natl. Acad. Sci. Azerbaijan 2020, 46, 360–393. [Google Scholar]
- Guido, R.C.; Barbon, S., Jr.; Vieira, L.S.; Sanchez, F.L.; Maciel, C.D.; Pereira, J.C.; Scalassara, P.R.; Fonseca, E.S. Introduction to the discrete shapelet transform and a new paradigm: Joint time-frequency-shape analysis. In Proceedings of the IEEE International Symposium on Circuits and Systems (IEEE ISCAS 2008), Seattle, WA, USA, 18–21 May 2008; Volume 1, pp. 2893–2896. [Google Scholar]
- Singh, R.; Khare, A. Fusion of multimodal medical images using daubechies complex wavelet transform—A multiresolution approach. Inf. Fusion 2014, 19, 49–60. [Google Scholar] [CrossRef]
- Bardinet, E.; Cohen, L.D.; Ayache, N. A parametric deformable model to fit unstructured 3D data. Comput. Vis. Image Underst. 1998, 71, 39–54. [Google Scholar] [CrossRef]
- Cohen, I.; Cohen, D. A hybrid hyperquadric model for 2D and 3D data fitting. Comput. Vis. Image Underst. 1994, 63, 527–541. [Google Scholar] [CrossRef]
- Mäkitalo, M.; Foi, A. Optimal inversion of the anscombe transfotmation in lowcount poisson image denoising. IEEE Trans. Image Process. 2011, 20, 99–109. [Google Scholar] [CrossRef] [PubMed]
- Nicolis, O.; Mateu, J. 2D Anisotropic Wavelet Entropy with an Application to Earthquakes in Chile. Entropy 2015, 17, 4155–4172. [Google Scholar] [CrossRef]
- Cattani, C.; Ciancio, A. On the fractal distribution of primes and prime-indexed primes by the binary image analysis. Phys. A Stat. Mech. Appl. 2016, 460, 222–229. [Google Scholar] [CrossRef]
- Shahriari, M.; Manafian, J. An efficient algorithm for solving the fractional Dirac differential operator. Adv. Math. Models Appl. 2020, 5, 289–297. [Google Scholar]
- Zhao, Y.; Baleanu, D.; Cattani, C.; Cheng, D.F.; Yang, X.J. Local fractional discrete wavelet transform for solving signals on Cantor sets. Math. Probl. Eng. 2013, 2013, 560932. [Google Scholar] [CrossRef]
- Cattani, C. Harmonic wavelet approximation of random, fractal and high frequency signals. Telecommun. Syst. 2010, 43, 207. [Google Scholar] [CrossRef]
- Li, S.; Wu, H.-T. Extract Fetal ECG from Single-Lead Abdominal ECG by De-Shape Short Time Fourier Transform and Nonlocal Median. Front. Appl. Math. Stat. 2017. [Google Scholar] [CrossRef]
- Niknazar, M.; Rivet, B.; Jutten, C. Fetal ECG Extraction by Extended State Kalman Filtering Based on Single-Channel Recordings. IEEE Trans. Biomed. Eng. 2013, 60, 1345–1352. [Google Scholar] [CrossRef]
- Almeida, R.; Gonçalves, H.; Rocha, A.P.; Bernardes, J. A Wavelet-Based Method for Assessing Fetal Cardiac Rhythms from Abdominal ECGs. Comput. Cardiol. 2013, 40, 289–292. [Google Scholar]
- Christov, I.; Simova, I.; Abacherli, R. Cancellation of the Maternal and Extraction of the Fetal ECG in Noninvasive Recordings. Comput. Cardiol. 2013, 40, 153–156. [Google Scholar]
- Di Maria, C.; Duan, W.; Bojarnejad, M.; Pan, F.; King, S.; Zheng, D.; Murray, A.; Langley, P. An Algorithm for the Analysis of Fetal ECGs from 4-channel Non-invasive Abdominal Recordings. Comput. Cardiol. 2013, 40, 305–308. [Google Scholar]
- Fatemi, M.; Niknazar, M.; Sameni, R. A Robust Framework for Noninvasive Extraction of Fetal Electrocardiogram Signals. Comput. Cardiol. 2013, 40, 201–204. [Google Scholar]
- Ghaffari, A.; Atyabi, S.A.; Mollakazemi, M.J.; Niknazar, M.; Niknami, M.; Soleimani, A. PhysioNet/CinC Challenge 2013: A Novel Noninvasive Technique to Recognize Fetal QRS Complexes from Noninvasive Fetal Electrocardiogram Signals. Comput. Cardiol. 2013, 40, 293–296. [Google Scholar]
- Kuzilek, J.; Lhotska, L. Advanced Signal Processing Techniques for Fetal ECG Analysis. Comput. Cardiol. 2013, 40, 177–180. [Google Scholar]
- Lipponen, J.A.; Tarvainen, M.P. Advanced Maternal ECG Removal and Noise Reduction for Application of Fetal QRS Detection. Comput. Cardiol. 2013, 40, 161–164. [Google Scholar]
- Liu, C.; Li, P. Systematic Methods for Fetal Electrocardiographic Analysis: Determining the Fetal Heart Rate, RR Interval and QT Interval. Comput. Cardiol. 2013, 40, 309–312. [Google Scholar]
- Maier, C.; Dickhaus, H. Fetal QRS Detection and RR Interval Measurement in Noninvasively Registered Abdominal ECGs. Comput. Cardiol. 2013, 40, 165–168. [Google Scholar]
- Niknazar, M.; Rivet, B.; Jutten, C. Fetal QRS Complex Detection Based on Three-Way Tensor Decomposition. Comput. Cardiol. 2013, 40, 185–188. [Google Scholar]
- Akhbari, M.; Niknazar, M.; Jutten, C.; Shamsollahi, M.B.; Rivet, B. Fetal Electrocardiogram R-peak Detection using Robust Tensor Decomposition and Extended Kalman Filtering. Comput. Cardiol. 2013, 40, 189–192. [Google Scholar]
- Andreotti, F.; Riedl, M.; Himmelsbach, T.; Wedekind, D.; Zaunseder, S.; Wessel, N.; Malberg, H. Maternal Signal Estimation by Kalman Filtering and Template Adaptation for Fetal Heart Rate Extraction. Comput. Cardiol. 2013, 40, 193–196. [Google Scholar]
- Behar, J.; Oster, J.; Clifford, G.D. Non-Invasive FECG Extraction from a Set of Abdominal Sensors. Comput. Cardiol. 2013, 40, 297–300. [Google Scholar]
- Perlman, O.; Katz, A.; Zigel, Y. Noninvasive Fetal QRS Detection using a Linear Combination of Abdomen ECG Signals. Comput. Cardiol. 2013, 40, 169–172. [Google Scholar]
- Liamedo, M.; Martin-Yebra, A.; Laguna, P.; Martínez, J.P. Noninvasive Fetal ECG Estimation Based on Linear Transformations. Comput. Cardiol. 2013, 40, 285–288. [Google Scholar]
- Lukosevicius, M.; Marozas, V. Noninvasive Fetal QRS Detection Using Echo State Network. Comput. Cardiol. 2013, 40, 205–208. [Google Scholar]
- Petrolis, R.; Krisciukaitis, A. Multi Stage Principal Component Analysis Based Method for Detection of Fetal Heart Beats in Abdominal ECGs. Comput. Cardiol. 2013, 40, 301–304. [Google Scholar]
- Xu-Wilson, M.; Carlson, E.; Cheng, L.; Vairavan, S. Spatial Filtering and Adaptive Rule Based Fetal Heart Rate Extraction from Abdominal Fetal ECG Recordings. Comput. Cardiol. 2013, 40, 197–200. [Google Scholar]
- Plesinger, F.; Jurak, P.; Halamek, J. Extracting the R-Wave Position from an FECG Record using Recognition of Multi-channel Shapes. Comput. Cardiol. 2013, 40, 157–160. [Google Scholar]
- Haghpanahi, M.; Borkholder, D.A. Fetal ECG Extraction from Abdominal Recordings using Array Signal Processing. Comput. Cardiol. 2013, 40, 173–176. [Google Scholar]
- Kropf, M.; Modre-Osprian, R.; Schreier, G.; Hayn, D. Robust Algorithm for Fetal QRS Detection using Non-invasive Maternal Abdomenal ECGs. Comput. Cardiol. 2013, 40, 313–316. [Google Scholar]
- Razavipour, F.; Haghpanahi, M.; Sameni, R. Fetal QRS Complex Detection using Semi-Blind Source Separation Framework. Comput. Cardiol. 2013, 40, 181–184. [Google Scholar]
- Starc, V. Non-invasive Fetal Multilead RR Interval Determination from Maternal Abdominal Recordings: The Physionet/CinC Challenge 2013. Comput. Cardiol. 2013, 40, 317–320. [Google Scholar]
- Mihalef, V.; Ionasec, R.; Wang, Y.; Zheng, Y.; Georgescu, B.; Comaniciu, D. Patient-specific modeling of left heart anatomy, dynamics, and hemodynamics from high resolution 4D CT. In Proceedings of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Rotterdam, The Netherlands, 14–17 April 2010. [Google Scholar]
- Ruben, M.; Jose, L.C.; Susana, H.; Mar, E.; Isabel, R. Fast Technique for Noninvasive Fetal ECG Extraction. IEEE Trans. Biomed. Eng. 2001, 58, 227–230. [Google Scholar]
- Vicente, Z.; Asoke, K.N. Noninvasive Fetal Electrocardiogram Extraction: Blind Separation Versus Adaptive Noise Cancellation. IEEE Trans. Biomed. Eng. 2001, 48, 12–18. [Google Scholar]
- Zhu, Y.; Xenophon, P.; Albert, J.; Sinusas, J.; Duncan, S. Segmentation of the Left Ventricle from Cardiac MR Images Using a Subject-Specific Dynamical Model. IEEE Trans. Med. Imaging 2010, 29, 669–687. [Google Scholar]
- Jallouli, M.; Khelifa, W.B.H.; Mabrouk, A.B.; Mahjoub, M.A. Toward recursive spherical harmonics issued bi-filters: Part II: An associated spherical harmonics entropy for optimal modeling. Soft Comput. 2020, 24, 5231–5243. [Google Scholar] [CrossRef]
- Arfaoui, S.; Ben Mabrouk, A.; Cattani, C. New Type of Gegenbauer-Hermite Monogenic Polynomials and Associated Clifford Wavelets. J. Math. Imaging Vis. 2020, 62, 73–97. [Google Scholar] [CrossRef]
- Arfaoui, S.; Ben Mabrouk, A.; Cattani, C. New Type of Gegenbauer-Jacobi-Hermite Monogenic Polynomials and Associated Continuous Clifford Wavelet Transform. Acta Appl. Math. 2020, 170, 1–35. [Google Scholar] [CrossRef]
- Baspinar, E.; Citti, G.; Sarti, A. A Geometric Model of Multi-scale Orientation Preference Maps via Gabor Functions. J. Math. Imaging Vis. 2018, 60, 900–912. [Google Scholar] [CrossRef]
- Bediaf, H.; Journaux, L.; Cointault, F.; Sabre, R. Détermination de la texture de la feuille de vigne par imagerie. In Orasis, Congrés des Jeunes Chercheurs en Vision par Ordinateur; Centre de Documentation Scientifique, Institut national de l’information gógraphique et forestière: Cluny, France, 2013. [Google Scholar]
- Duits, R.; Felsberg, M.; Granlund, G.; ter Haar Romeny, B. Image Analysis and Reconstruction using a Wavelet Transform Constructed from a Reducible Representation of the Euclidean Motion Group. Int. J. Comput. Vis. 2006, 72, 79–102. [Google Scholar] [CrossRef]
- Ibrahim Mahmoud, M.M.; Ben Mabrouk, A.; Abdallah Hashim, M.H. Wavelet multifractal models for transmembrane proteins’ series. Int. J. Wavelets Multiresolut. Inf. Process. 2016, 14, 1650044. [Google Scholar] [CrossRef]
- Mahbubur Rahman, S.M.; Ahmad, M.O.; Swamy, M.N.S. A New Statistical Detector for DWT-Based Additive Image Watermarking Using the Gauss–Hermite Expansion. IEEE Trans. Image Process. 2009, 18, 1782–1796. [Google Scholar] [CrossRef] [PubMed]
- Mallat, S. A Wavelet Tour of Signal Processing; The Sparse Way; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Keinert, F. Wavelets and multiwavelets. In Studies in Advanced Mathematics; Chapman & Hall/CRC Press: Boca Raton, FL, USA, 2003; Volume 42. [Google Scholar]
- Zhang, J.K.; Davidson, T.N.; Luo, Z.Q.; Wong, K. Design of interpolating biorthogonal multiwavelet systems with compact support. Appl. Comput. Harmon. Anal. 2001, 11, 420–438. [Google Scholar] [CrossRef][Green Version]
- Zemni, M.; Jallouli, M.; Ben Mabrouk, A.; Mahjoub, M.A. Explicit Haar-Schauder multiwavelet filters and algorithms. Part II: Relative entropy-based estimation for optimal modeling of biomedical signals. Int. J. Wavelets Mult. Inf. Process. 2019, 17, 1950038. [Google Scholar] [CrossRef]
- Stankovic, R.S.; Falkowski, B.J. The Haar wavelet transform: Its status and achievements. Comput. Electr. Eng. 2003, 29, 25–44. [Google Scholar] [CrossRef]
- Douzi, H.; Mammass, D.; Nouboud, F. Faber-Schauder Wavelet Transform, Application to Edge Detection and Image Characterization. J. Math. Imaging Vis. 2001, 14, 91–101. [Google Scholar] [CrossRef]
- Antoine, J.-P.; Murenzi, R.; Vandergheynst, P. Directional Wavelets Revisited: Cauchy Wavelets and Symmetry Detection in Patterns. Appl. Comput. Harmon. Anal. 1999, 6, 314–345. [Google Scholar] [CrossRef]
- Antoine, J.-P.; Murenzi, R.; Vandergheynst, P. Two-dimensional directional wavelets in image processing. Int. J. Imaging Syst. Technol. 1996, 7, 152–165. [Google Scholar] [CrossRef]
- Makadia, A.; Daniilidis, K. Direct 3D-rotation estimation from spherical images via a generalized shift theorem. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; pp. 18–20. [Google Scholar]
- Skibbe, H.; Reisert, M. Spherical Tensor Algebra: A Toolkit for 3D Image Processing. J. Math. Imaging Vis. 2017, 58, 349–381. [Google Scholar] [CrossRef]
- Strichartz, R.S. Local harmonic analysis on spheres. J. Funct. Anal. 1988, 77, 403–433. [Google Scholar] [CrossRef][Green Version]
- Alvarez, M.; Sansigre, G. On polynomials with interlacing zeros. In Polynomes Orthogonaux et Applications; Brezinski, C., Ed.; Springer: Berlin, Germany, 1985; pp. 255–258. [Google Scholar]
- Baleanu, D. Wavelet Transforms and Their Recent Applications in Biology and Geoscience; InTech: Rijeka, Croatia, 2012; p. 310. ISBN 978-953-51-0212-0. [Google Scholar]
- Carré, P.; Berthier, W. Color Representation and Processes with Clifford Algebra. In Advanced Color Image Processing and Analysis; Fernandez-Maloigne, C., Ed.; Springer: New York, NY, USA, 2013; pp. 147–179. [Google Scholar]
- Carré, P.; Denis, P.; Fernandez-Maloigne, C. Spatial color image processing using Clifford algebras: Application to color active contour. Signal Image Video Process. 2012, 8, 1357–1372. [Google Scholar] [CrossRef]
- Dian, T.N.; Zainal Arifin, A.; Soelaiman, R. Medical Image Segmentation Using Generalized Gradient Vector Flow and Clifford Geometric Algebra. In Proceedings of the International Conference on Biomedical Engineering, Surabaya, Indonesia, 11 November 2008; p. 5. [Google Scholar]
- Di Claudio, E.D.; Jacovitti, G.; Laurenti, A. On the Inter-Conversion Between Hermite and Laguerre Local Image Expansions. IEEE Trans. Image Process. 2011, 20, 3553–3565. [Google Scholar] [CrossRef]
- Escalante-Ramirez, B. The Hermite transform as an efficient model for local image analysis: An application to medical image fusion. Comput. Electr. Eng. 2008, 34, 99–110. [Google Scholar] [CrossRef]
- Estudillo-Romero, A.; Escalante-Ramirez, B. The Hermite Transform: An Alternative Image Representation Model for Iris Recognition. In Progress in Pattern Recognition, Image Analysis and Applications, Proceedings of the 13th Iberoamerican Congress on Pattern Recognition, CIARP 2008, Havana, Cuba, 9–12 September 2008; Walter, J., Kropatsch, G., Eds.; Lecture Notes in Computer Science 5197; Springer: Berlin/Heidelberg, Germany, 2008; pp. 86–93. [Google Scholar]
- Felsberg, M.; Sommer, G. The monogenic signal. IEEE Trans. Signal Process. 2001, 49, 3136–3144. [Google Scholar] [CrossRef]
- Huang, Z.J.; Huang, G.H.; Cheng, L. Medical Image Segmentation of Blood Vessels Based on Clifford Algebra and Voronoi Diagram. J. Softw. 2018, 13, 361–373. [Google Scholar] [CrossRef]
- Jallouli, M.; Zemni, M.; Ben Mabrouk, A.; Mahjoub, M.A. Toward recursive spherical harmonics-issued bi-filters: Part I: Theoretical framework. Soft Comput. 2019, 23, 10415–10428. [Google Scholar] [CrossRef]
- Khelifa, W.B.; Ben Abdallah, A.; Ghorbel, F. Three dimensional modeling of the left ventricle of the heart using spherical harmonic analysis. In Proceedings of the 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Paris, France, 14–17 May 2008; pp. 1275–1278. [Google Scholar]
- Mohlenkamp, M. A Fast Transform for Spherical Harmonics. Ph.D. Thesis, Yale University, New Haven, CT, USA, May 1997. [Google Scholar]
- Mousa, M.-H. Calcul Efficace et direct des Représentations de Maillages 3D Utilisant les Harmoniques Sphériques. Ph.D. Thesis, Université Claude Bernard, Lyon, France, 2007. [Google Scholar]
- Sau, K.; Basaka, R.K.; Chanda, A. Image Compression based on Block Truncation Coding using Clifford Algebra. International Conference on Computational Intelligence: Modeling Techniques and Applications (CIMTA) 2013. Procedia Technol. 2013, 10, 699–706. [Google Scholar] [CrossRef]
- Shen, L.; Chung, M.K. Large-Scale Modeling of Parametric Surfaces using Spherical Harmonics. In Proceedings of the Third International Symposium on 3D Data Processing, Visualization and Transmission (3DPVT), Chapel Hill, NC, USA, 14–16 June 2006; p. 8. [Google Scholar]
- Soulard, R.; Carré, P. Characterization of color images with multiscale monogenic maxima. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2289–2302. [Google Scholar] [CrossRef] [PubMed]
- Brackx, F.; De Schepper, N.; Sommen, F. The Two-Dimensional Clifford-Fourier Transform. J. Math. Imaging 2006, 26, 5–18. [Google Scholar] [CrossRef]
- Brackx, F.; De Schepper, N.; Sommen, F. Clifford-Hermite and two-dimensional Clifford-Gabor filters for early vision. In Proceedings of the 17th International Conference on the Application of Computer Science and Mathematics in Architecture and Civil Engineering, Bauhaus-Universität, Weimar, Germany, 12–14 July 2006. [Google Scholar]
- Yang, B.; Suk, T.; Dai, M.; Flusser, J. 2D and 3D Image Analysis by Gaussian-Hermite Moments. In Moments and Moment Invariants—Theory and Applications; Papakostas, G.A., Ed.; Science Gate Publishing: Xanthi, Greece, 2014; Volume 1, Chapter 7; pp. 143–173. [Google Scholar]
- Kolmogorov, A.N. On the Shannon theory of infor mation transmission in the case of continuous signals. IRE Trans. Inf. Theory 1956, 2, 102–108. [Google Scholar] [CrossRef]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Fischer, F. Multiresolution analysis for 2D turbulence Part 1: Wavelets vs cosince packets, a comparative study. Discret. Contin. Dyn. Syst. B 2005, 5, 659–686. [Google Scholar] [CrossRef]
- Ruppert-Felsot, J.E.; Praud, O.; Sharon, E.; Swinney, H.L. Extraction of coherent structures in a rotating turbulent flow experiment. Phys. Rev. E 2005, 72, 17. [Google Scholar] [CrossRef] [PubMed]
- Bulusu, K.V.; Plesniak, M.W. Shannon Entropy-Based Wavelet Transform Method for Autonomous Coherent Structure Identification in Fluid Flow Field Data. Entropy 2015, 17, 6617–6642. [Google Scholar] [CrossRef]
- Rosso, O.; Blanco, S.; Yordanova, J.; Kolev, V.; Figliola, A.; Schrrmann, M.; Basar, E. Wavelet entropy: A New Tool for analysis of Short DurationB Electrical Signals. J. Neurosci. Methods 2001, 105, 65–75. [Google Scholar] [CrossRef]
- Varanini, M.; Tartarisco, G.; Billeci, L.; Macerata, A.; Pioggia, G.; Balocchi, R. A Multi-step Approach for Non-invasive Fetal ECG Analysis. Comput. Cardiol. 2013, 40, 281–284. [Google Scholar]
- De Moor, B.L.R. (Ed.) DaISy: Database for the Identification of Systems, Department of Electrical Engineering, ESAT/STADIUS, KU Leuven, Belgium. Available online: http://homes.esat.kuleuven.be/~smc/daisy/ (accessed on 19 April 2021).
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Li, P.; Maria, C.; Zhao, L.; Zhang, H.; Chen, Z. A multi-step method with signal quality assessment and fine-tuning procedure to locate maternal and fetal QRS complexes from abdominal ECG recordings. Physiol. Meas. 2014, 35, 1665. [Google Scholar] [CrossRef]
- Silva, I.; Behar, J.; Sameni, R.; Zhu, T.; Oster, J.; Clifford, G.D.; Moody, G.B. Noninvasive Fetal ECG: The PhysioNet/Computing in Cardiology Challenge 2013. Comput. Cardiol. 2013, 40, 149–152. [Google Scholar]
- Podziemski, P.; Gieraltowski, J. Fetal heart rate discovery: Algorithm for detection of fetal heart rate from noisy, non-invasive fetal ECG recordings. Comput. Cardiol. 2013, 40, 333–336. [Google Scholar]
- Di Marco, L.Y.; Marzo, A.; Frangi, A. Multichannel foetal heartbeat detection by combining source cancellation with expectation-weighted estimation of fiducial points. Comput. Cardiol. 2013, 40, 329–332. [Google Scholar]
- Nair, R.H.; Gini, J.R.; Ramachandran, K.I. A Simplified Approach to Identify the Fetal ECG from AbdECG and to Measure the fHR. In Proceedings of the 7th WACBE World Congress on Bioengineering 2015, Singapore, 6–8 July 2015; Goh, J., Lim, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 52. [Google Scholar] [CrossRef]
- Andreotti, F.; Riedl, M.; Himmelsbach, T.; Wedekind, D.; Wessel, N.; Stepan, H.; Schmieder, C.; Jank, A.; Malberg, H.; Zaunseder, S. Robust fetal ECG extraction and detection from abdominal leads. Physiol. Meas. 2014, 35, 1551. [Google Scholar] [CrossRef] [PubMed]
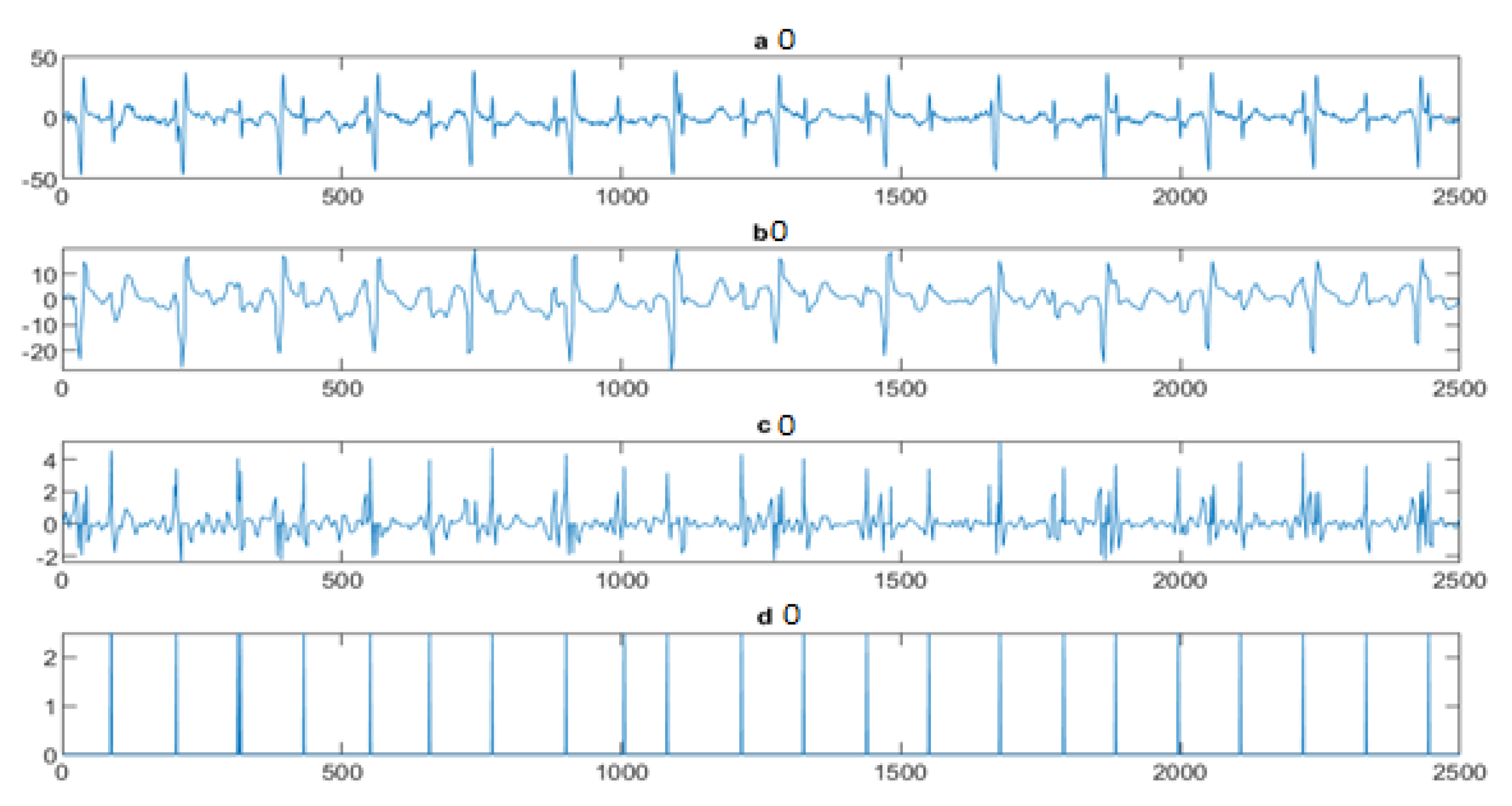
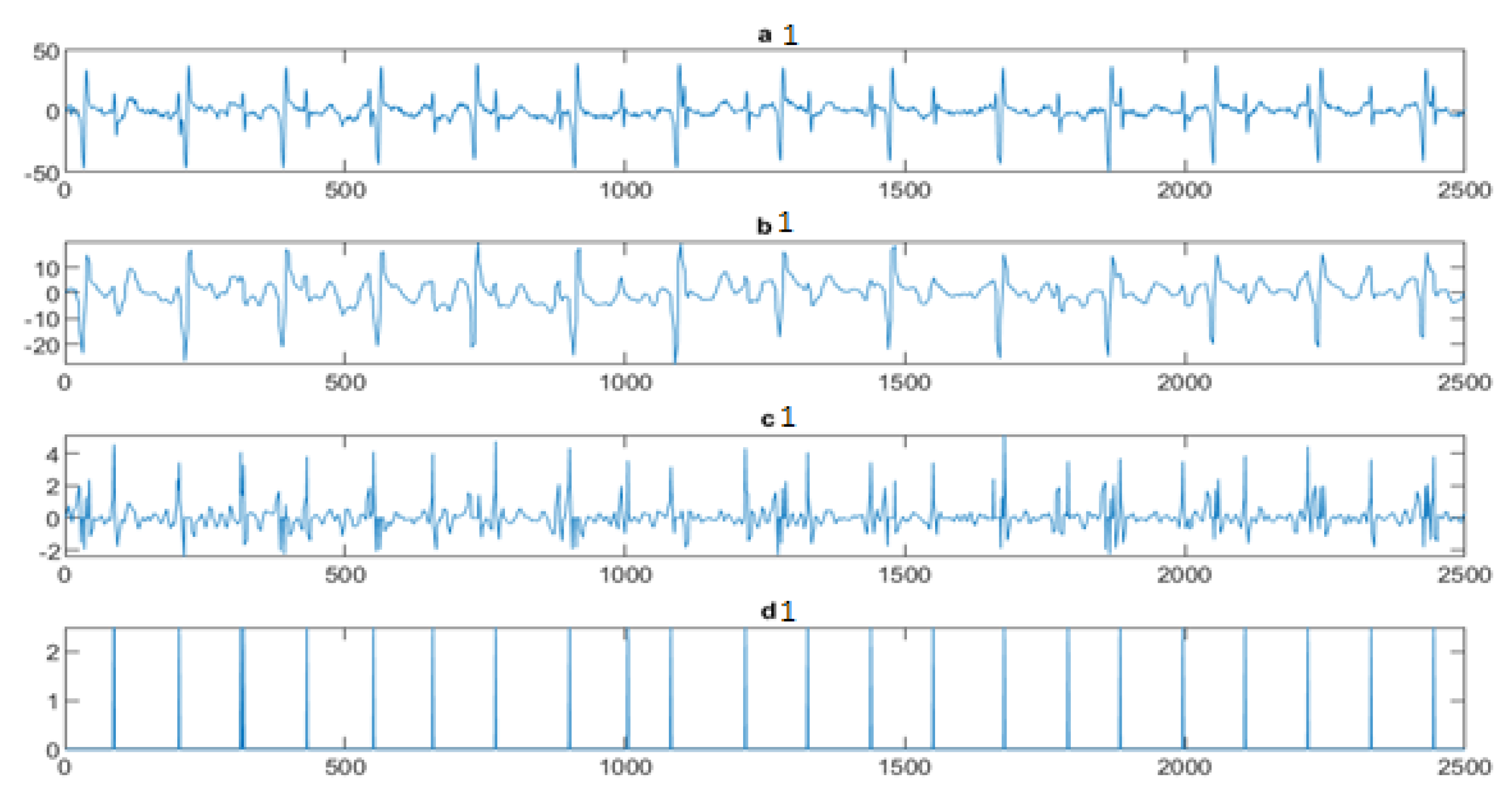

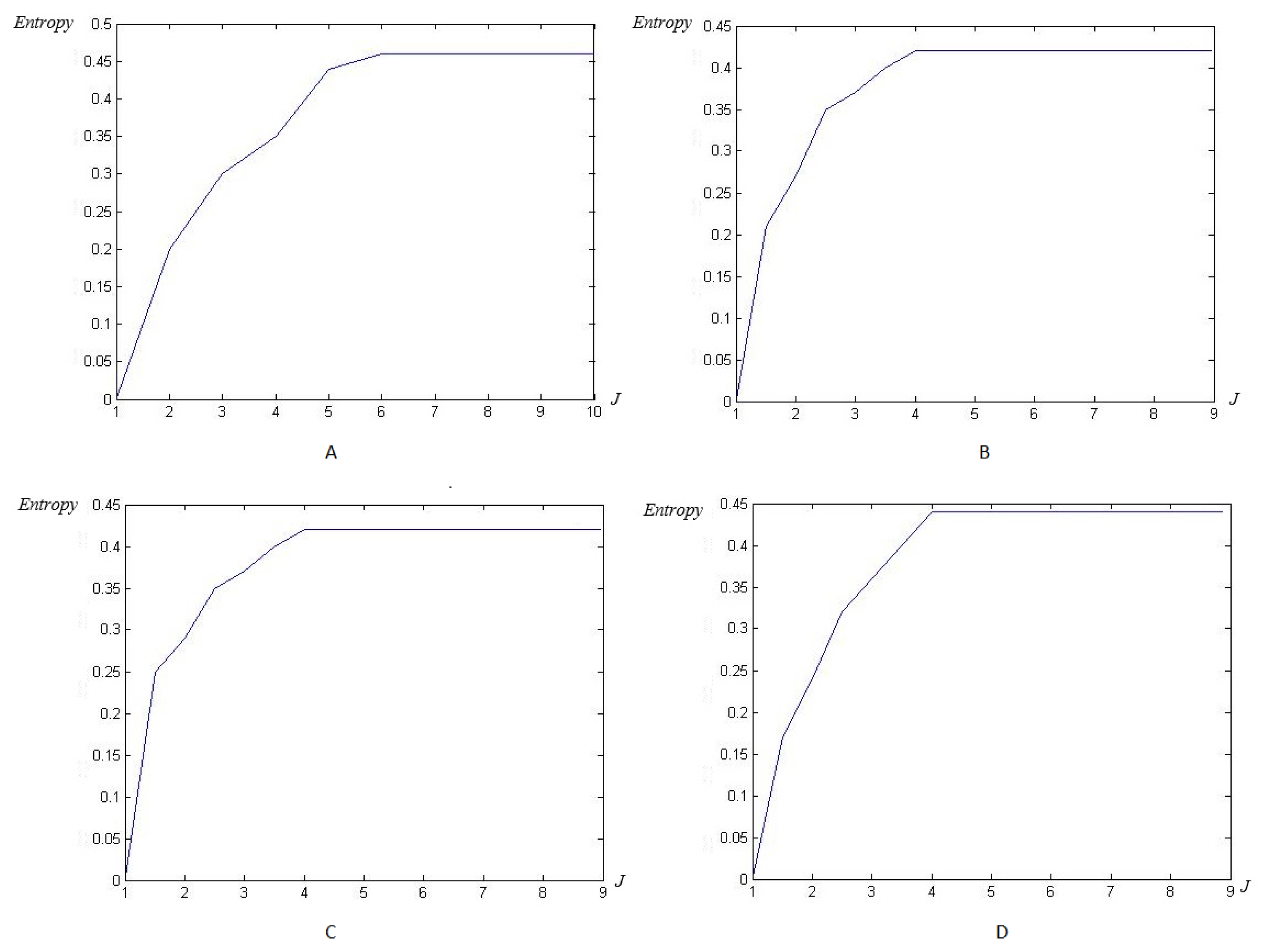
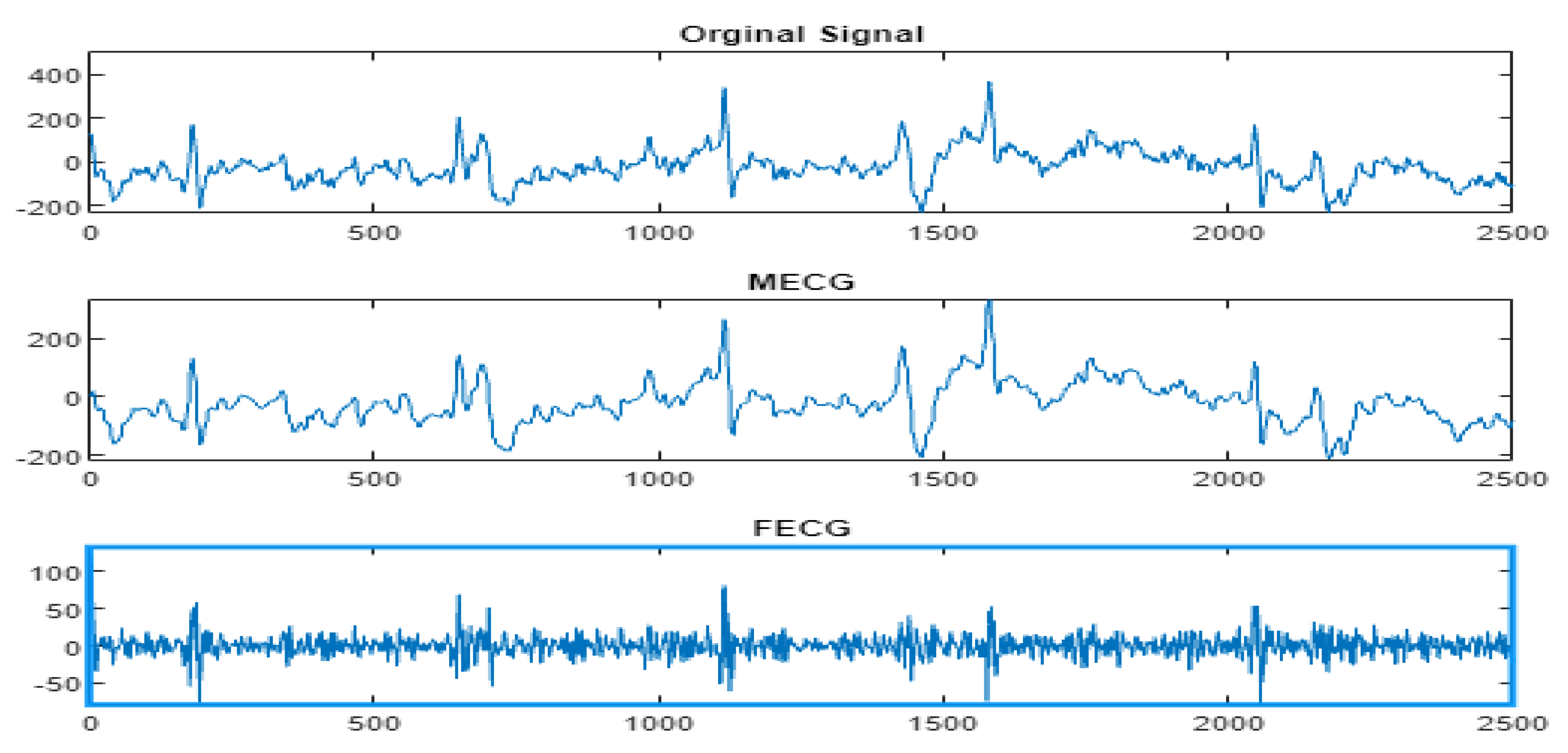


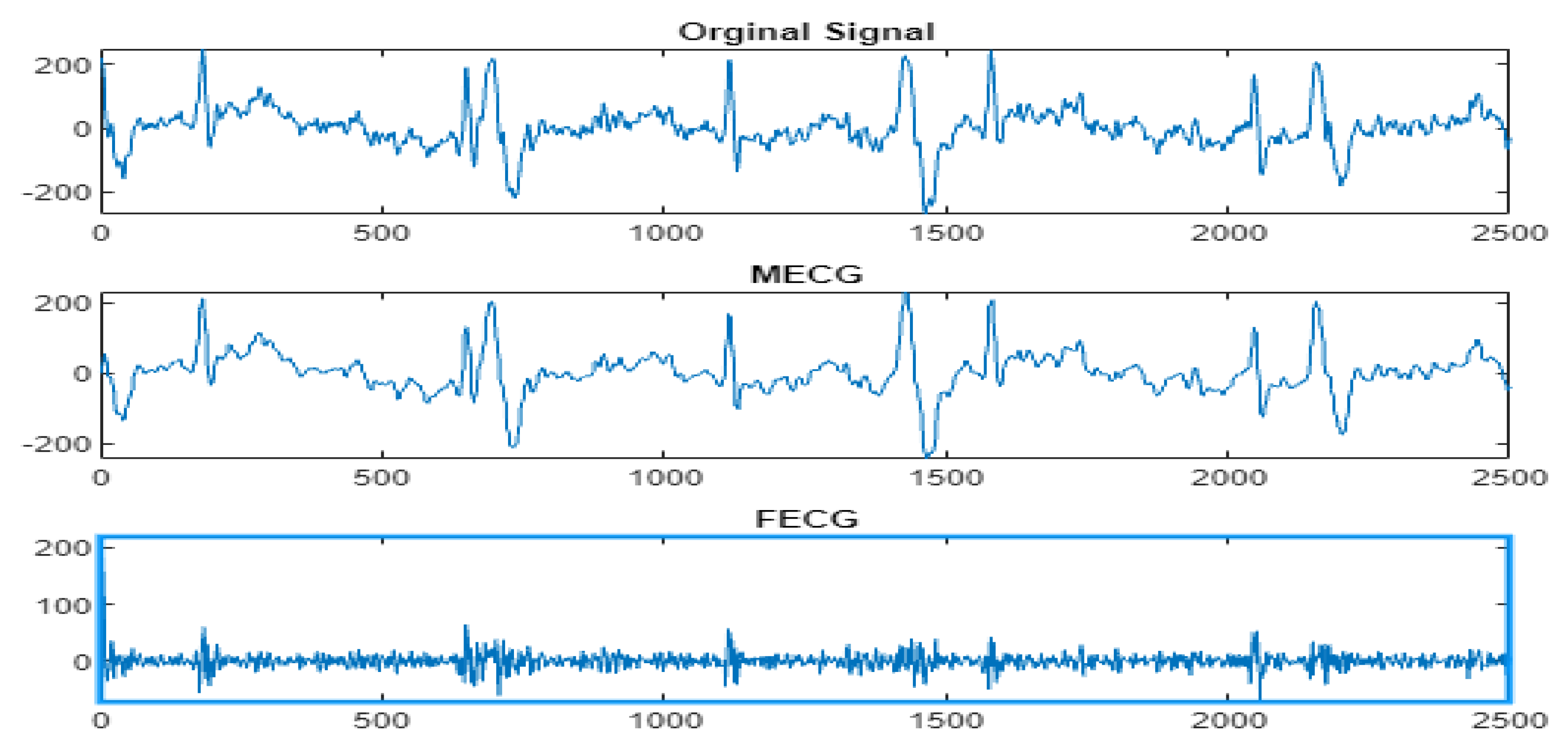
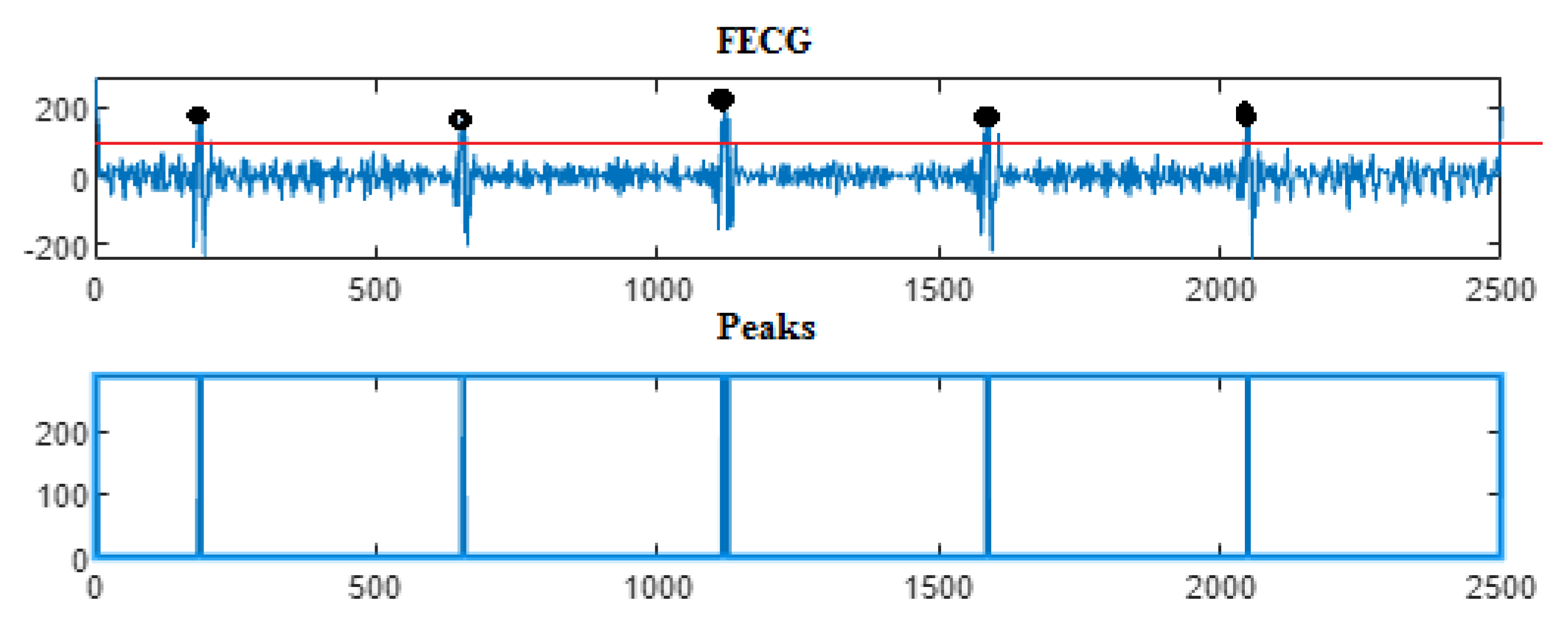
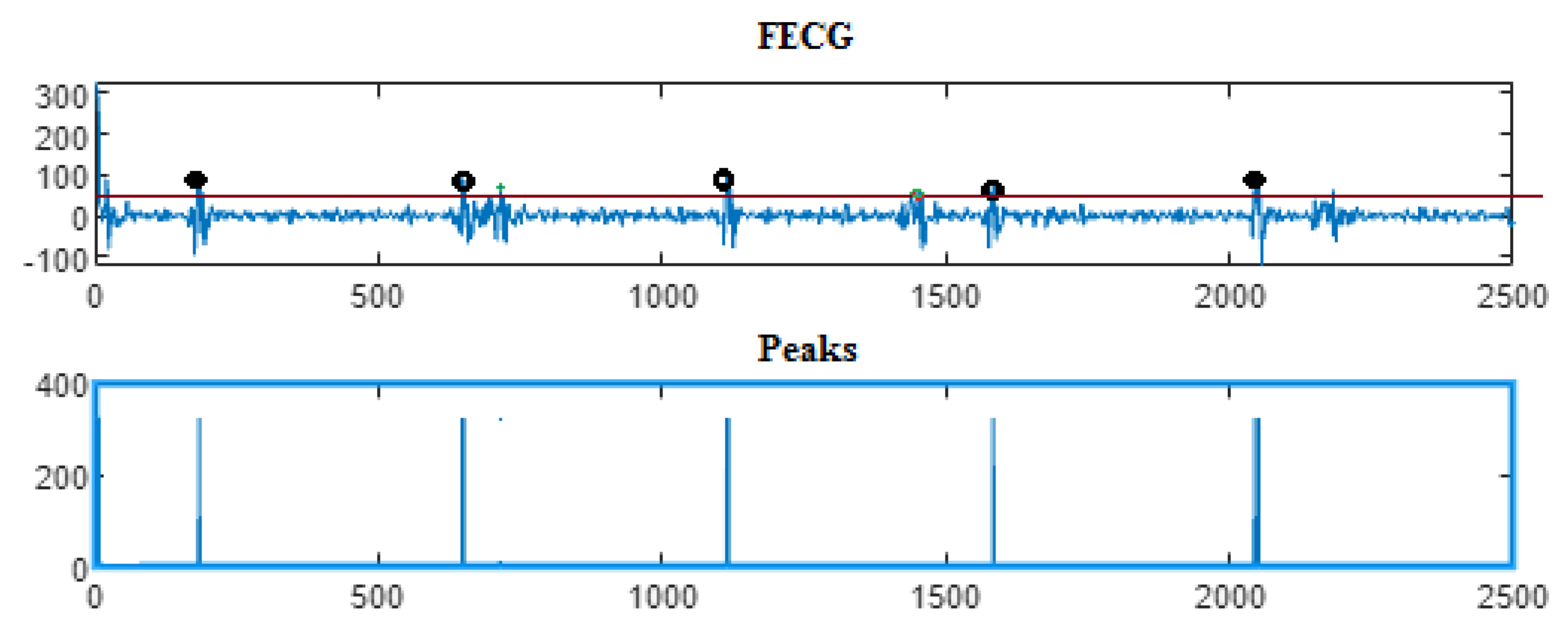
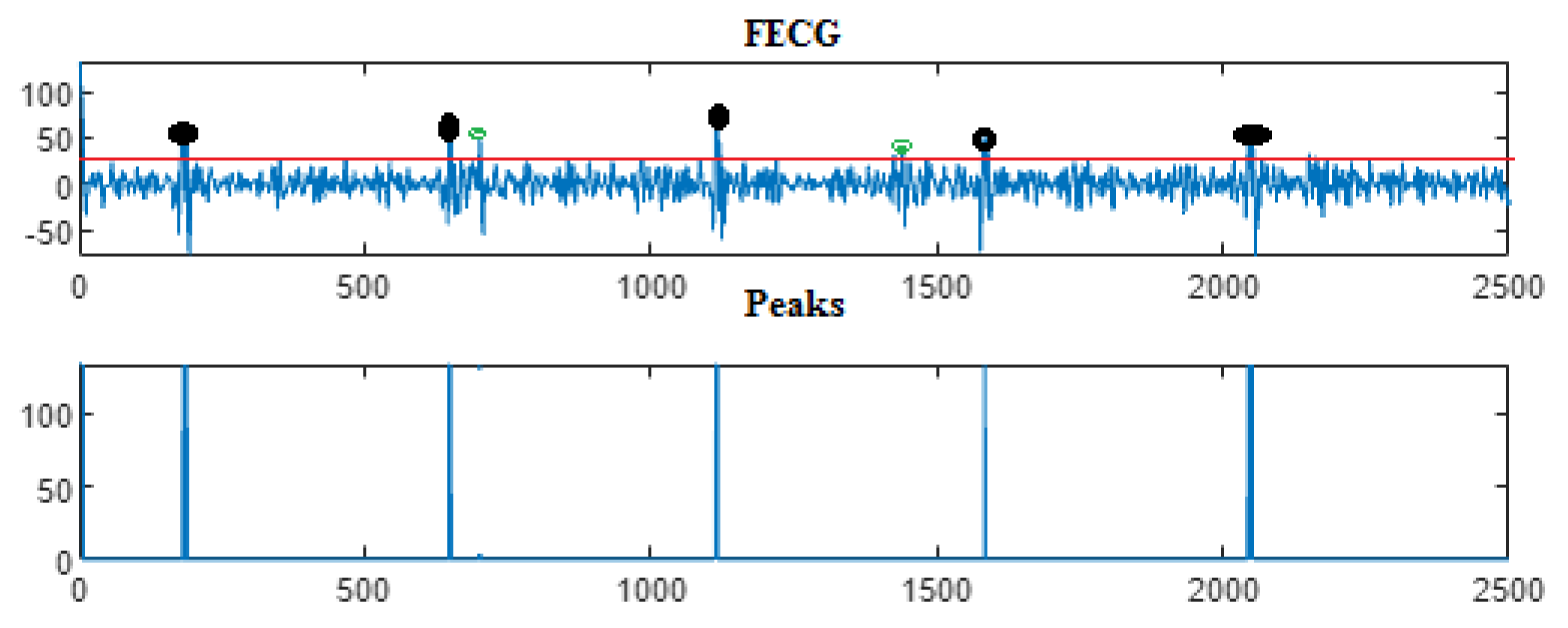
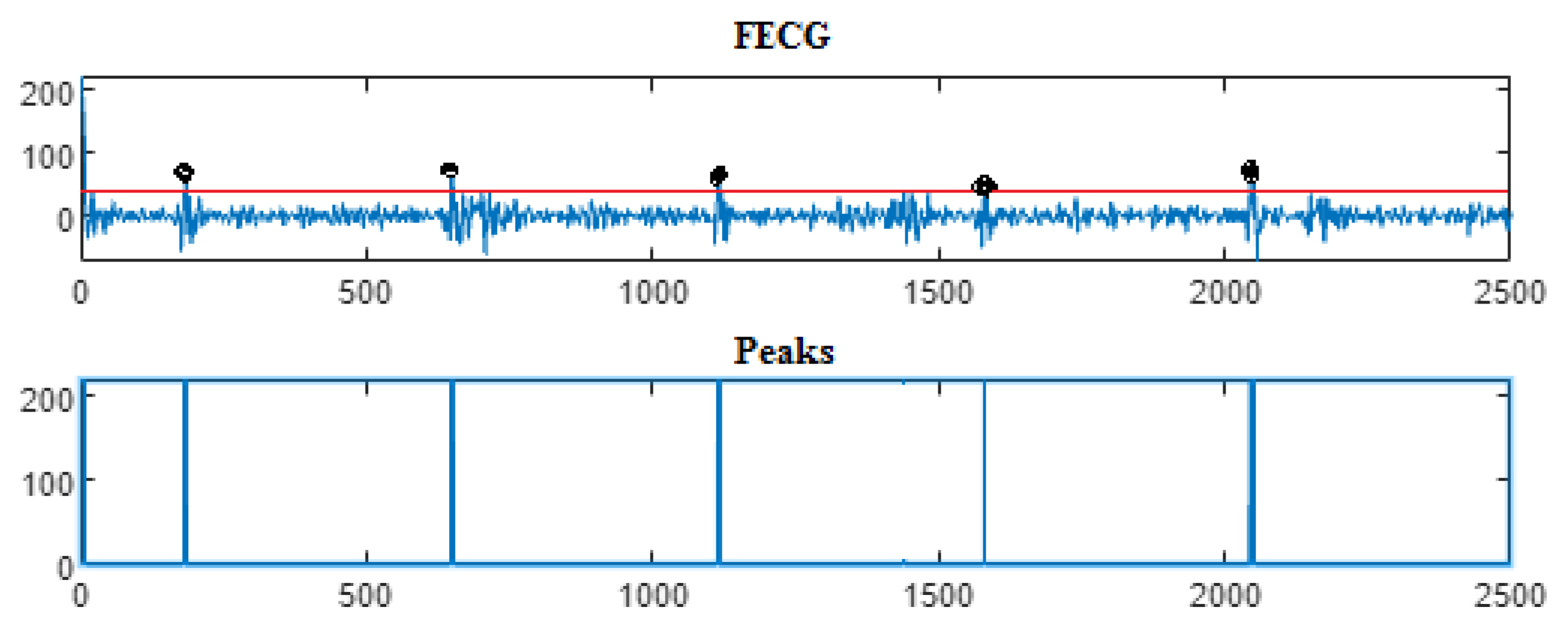
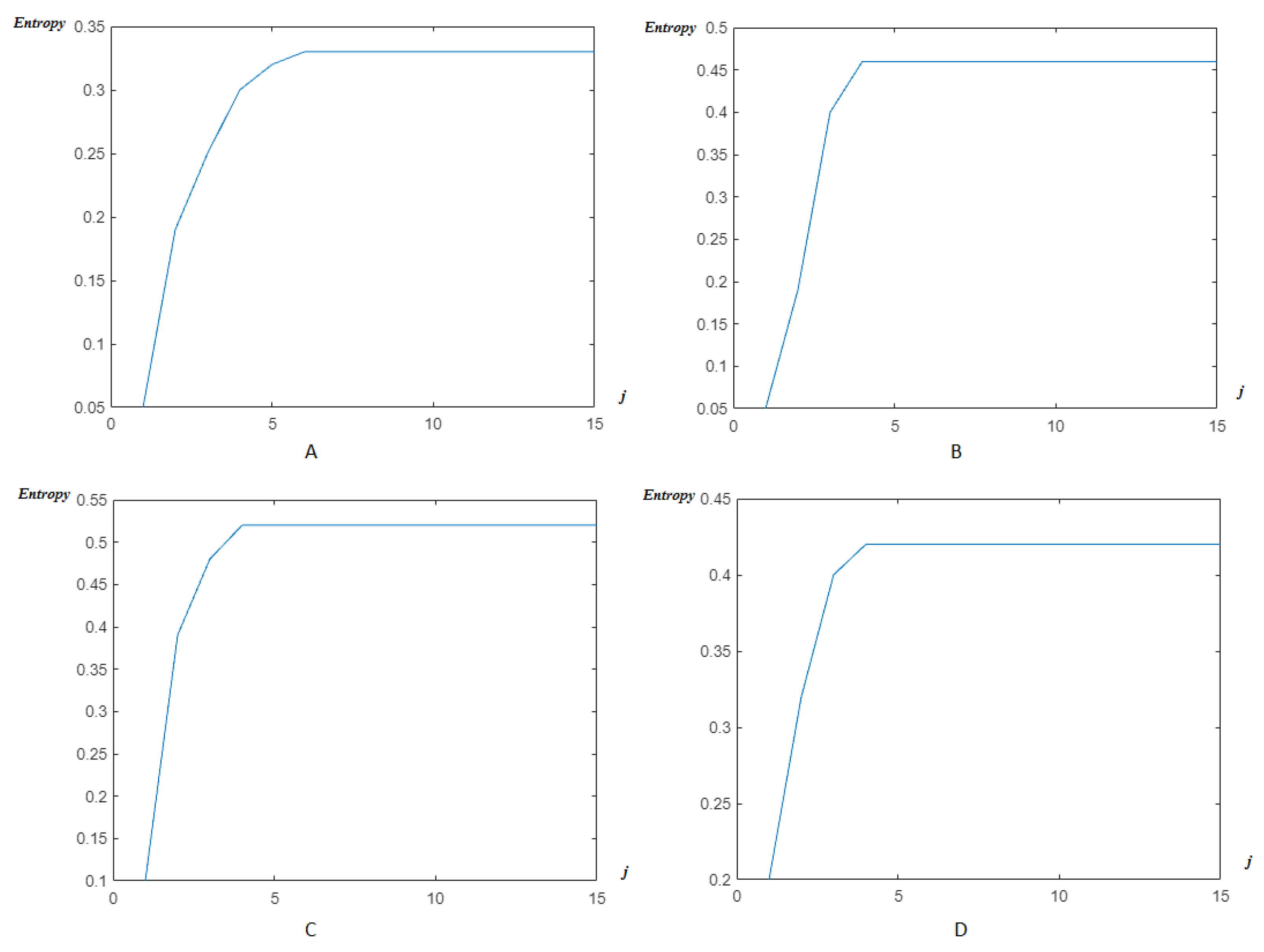
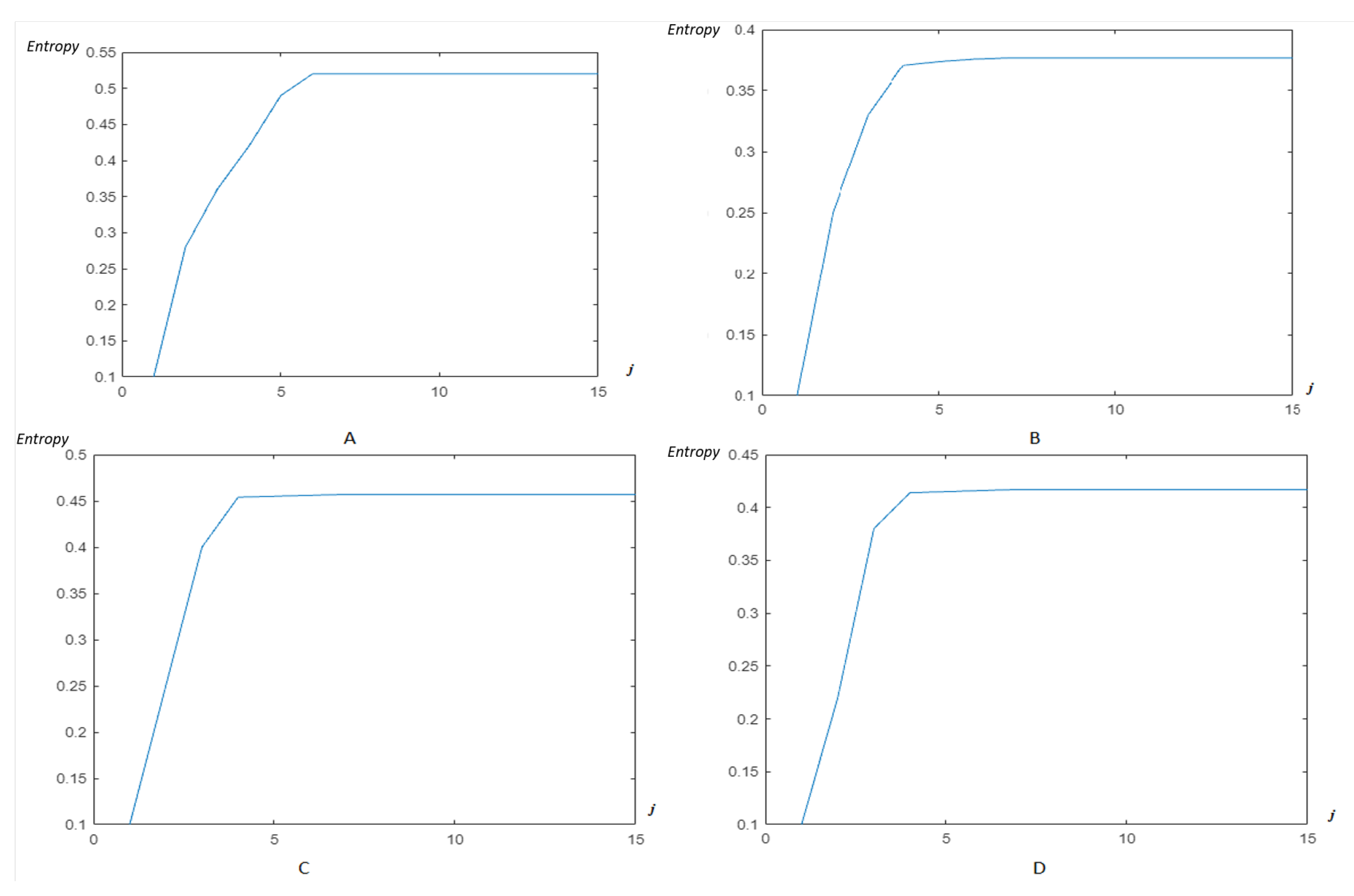
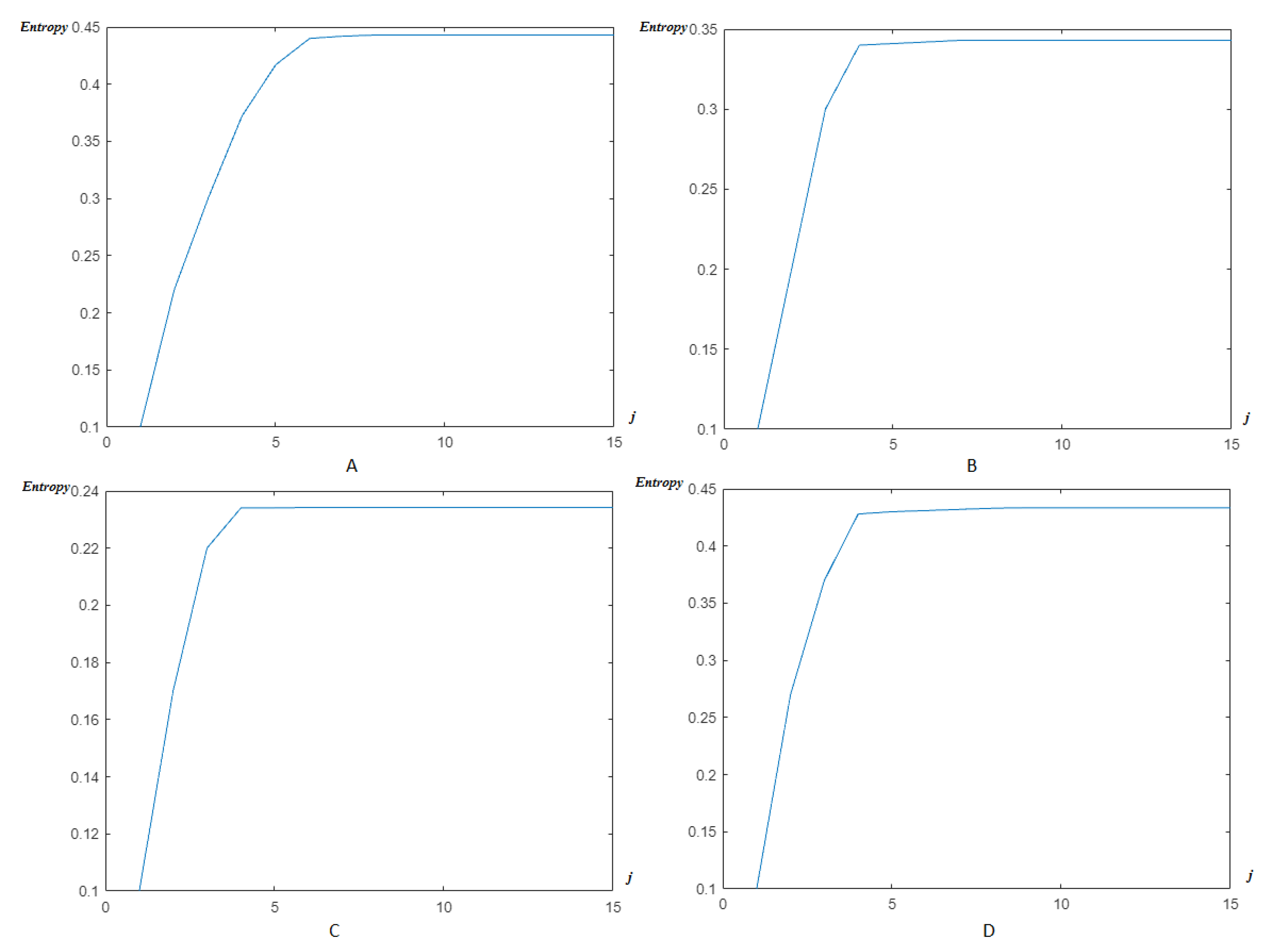
| Ch. No. | Total pks | Pks det in [105] | HFSch Multiwavelet pks det for FECG | pks det | pks det | pks det |
|---|---|---|---|---|---|---|
| 2 | 22 | 22 | 22 | 22 | 22 | 22 |
| 3 | 21 | 21 | 21 | 21 | 21 | 21 |
| 4 | 21 | 22 | 21 | 21 | 21 | 21 |
| Channel Number | Acc [105] | HFSch Multiwavelet Acc for FECG | Acc Using | Acc Using | Acc Using |
|---|---|---|---|---|---|
| 2 | 100 | 100 | 100 | 100 | 100 |
| 3 | 100 | 100 | 100 | 100 | 100 |
| 4 | 86.95 | 100 | 100 | 100 | 100 |
| Channel Number | Sens [105] | HFSch Multiwavelet Sens for FECG | Se Using | Se Using | Se Using |
|---|---|---|---|---|---|
| 2 | 100 | 100 | 100 | 100 | 100 |
| 3 | 100 | 100 | 100 | 100 | 100 |
| 4 | 95.23 | 100 | 100 | 100 | 100 |
| Sig. No. | Total pks | HFSch Multiwavelet pks det | pks det | pks det | pks det |
|---|---|---|---|---|---|
| a12 | 5 | 5 | 5 | 5 | 5 |
| a29 | 5 | 5 | 5 | 5 | 5 |
| a47 | 5 | 5 | 5 | 5 | 5 |
| a59 | 5 | 5 | 5 | 5 | 5 |
| Sig. No. | HFSch Multiwavelet Acc for FECG | Acc Using | Acc Using | Acc Using |
|---|---|---|---|---|
| a12 | 100 | 100 | 100 | 100 |
| a29 | 100 | 100 | 100 | 100 |
| a47 | 100 | 100 | 100 | 100 |
| a59 | 100 | 100 | 100 | 100 |
| Sig. No. | HFSch Multiwavelet Sens for FECG | Se Using | Se Using | Se Using |
|---|---|---|---|---|
| a12 | 100 | 100 | 100 | 100 |
| a29 | 100 | 100 | 100 | 100 |
| a47 | 100 | 100 | 100 | 100 |
| a59 | 100 | 100 | 100 | 100 |
| Database | Accuracy (%) | Se (%) | PPV (%) | |
|---|---|---|---|---|
| DAISY | 100 | 100 | 100 | 100 |
| CinC | 100 | 100 | 100 | 100 |
| Method | TA/[106] | EKS/[106] | SQA + FTM [101] | New Method |
|---|---|---|---|---|
| TP | - | - | 9573 | 10,088 |
| FP | - | - | 639 | 24 |
| FN | - | - | 596 | 81 |
| Accuracy(%) | 88.57 | 98.96 | ||
| Se (%) | 94.13 | 99.76 | ||
| PPV (%) | 93.74 | 99.2 | ||
| 93.9 | 99.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jallouli, M.; Arfaoui, S.; Ben Mabrouk, A.; Cattani, C. Clifford Wavelet Entropy for Fetal ECG Extraction. Entropy 2021, 23, 844. https://doi.org/10.3390/e23070844
Jallouli M, Arfaoui S, Ben Mabrouk A, Cattani C. Clifford Wavelet Entropy for Fetal ECG Extraction. Entropy. 2021; 23(7):844. https://doi.org/10.3390/e23070844
Chicago/Turabian StyleJallouli, Malika, Sabrine Arfaoui, Anouar Ben Mabrouk, and Carlo Cattani. 2021. "Clifford Wavelet Entropy for Fetal ECG Extraction" Entropy 23, no. 7: 844. https://doi.org/10.3390/e23070844
APA StyleJallouli, M., Arfaoui, S., Ben Mabrouk, A., & Cattani, C. (2021). Clifford Wavelet Entropy for Fetal ECG Extraction. Entropy, 23(7), 844. https://doi.org/10.3390/e23070844







