Extended Variational Message Passing for Automated Approximate Bayesian Inference
Abstract
:1. Introduction
2. Problem Statement
Variational Message Passing on Forney-Style Factor Graphs
- Choose a variable from the set .
- Compute the incoming messages.
- Update the posterior.
- Update the local free energy (for performance tracking), i.e., update all terms in that are affected by the update (4):
3. Specification of EVMP Algorithm
3.1. Distribution Types
- (1)
- The standard Exponential Family (EF) of distributions, i.e., the following:where is the base measure, is the sufficient statistics vector, is the natural parameters vector and is the log-partition function.
- (2)
- Distributions that are of the following exponential form:where is a deterministic function. The key characteristic here is that is not recognized as a sufficient statistics vector for any of the standard EF distributions. We call this distribution type a Non-Standard Exponential Family (NEF) distribution. As we show in Section 3.6, this distribution type arises only in backward message calculations.
- (3)
- A List of Weighted Samples (LWS), i.e., the following:
- (4)
- Deterministic relations are represented by delta distributions, i.e., the following:Technically, the equality factor also specifies a deterministic relation between variables.
3.2. Factor Types
3.3. Message Types
3.4. Posterior Types
3.5. Computation of Posteriors
- (1)
- In the case that the colliding forward and backward messages both carry EF distributions with the same sufficient statistics , then computing the posterior simplifies to a summation of natural parameters:In this case, the posterior will also be represented by the EF distribution type. This case corresponds to classical VMP with conjugate factor pairs.
- (2)
- The forward message again carries a standard EF distribution. The backward message carries either an NEF distribution or a non-conjugate EF distribution.
- (a)
- If the forward message is Gaussian, i.e., , we use a Laplace approximation to compute the posterior:
- (b)
- Otherwise ( is not a Gaussian), we use Importance Sampling (IS) to compute the posterior:
- (3)
- The forward message carries an LWS distribution, i.e., the following:and the backward message carries either an EF or NEF distribution. In that case, the posterior computation refers to updating the weights in (see Appendix E):
3.6. Computation of Messages
- (1)
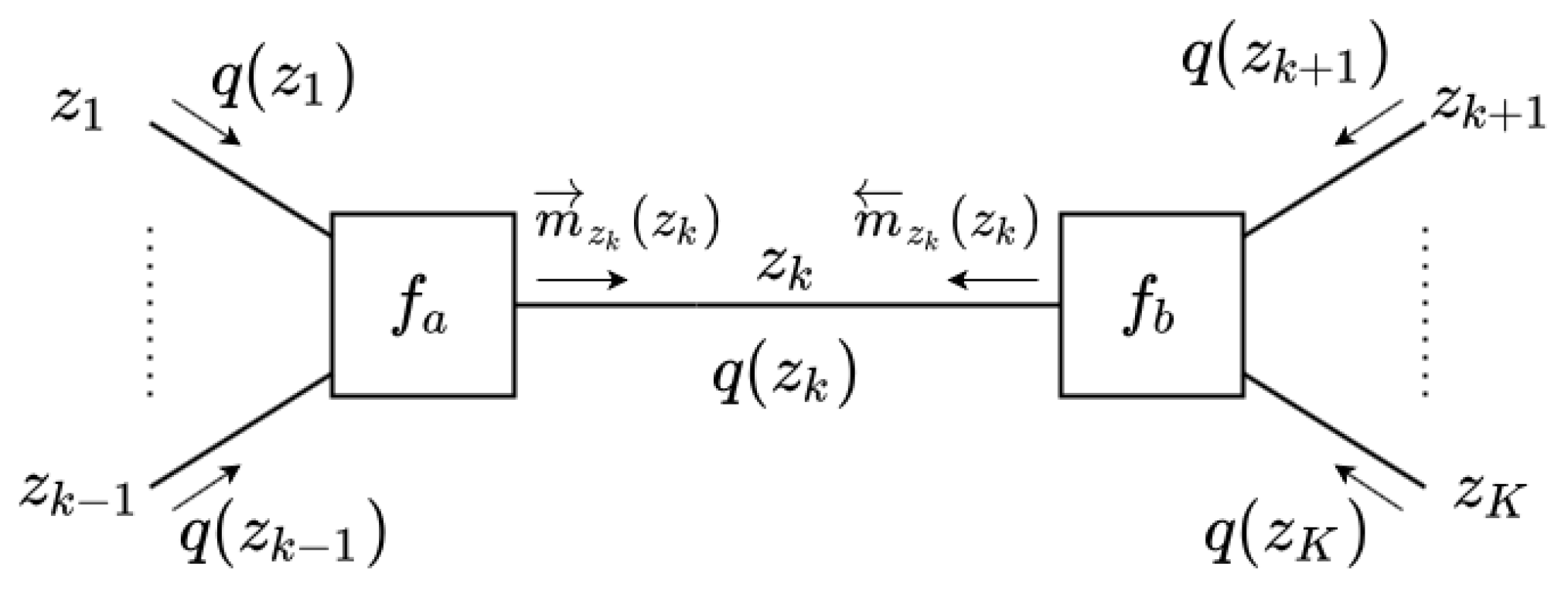
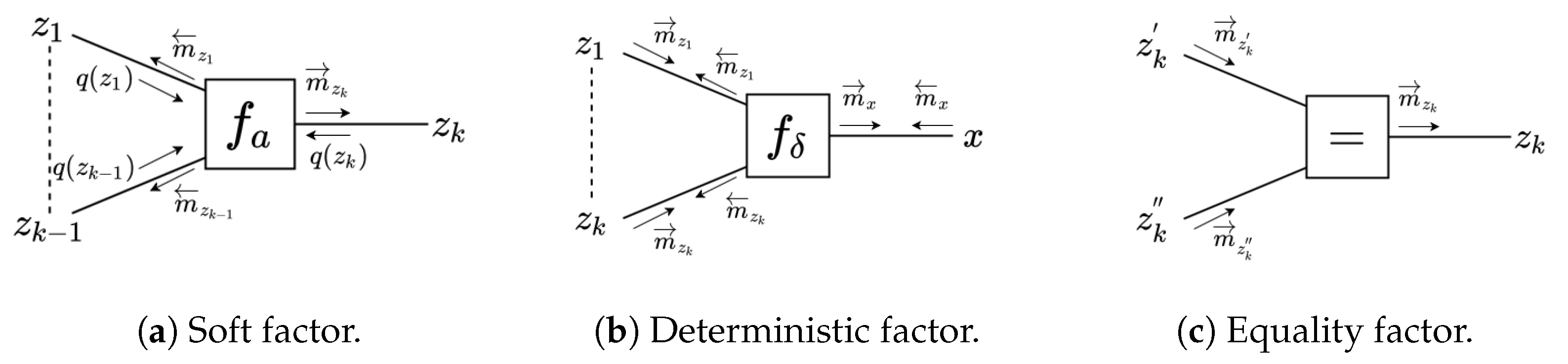
- If factor is a soft factor of the form (see Figure 3a)then the outgoing VMP message to is the following EF-distributed message:If rather (or ) than is the output variable of , i.e., if the following is true:then the outgoing message to is either an EF or an NEF distribution of the following form:In this last expression, we chose to assign a backward arrow to since it is customary to align the message direction with the direction of the factor, which in this case points to .Note that the message calculation rule for requires the computation of expectation , and for we need to compute expectations and . In the update rules to be shown below, we will see these expectations of statistics of z appear over and again. In Section 3.8 we detail how we calculate these expectations and in Appendix A, we further discuss the origins of these expectations.
- (2)
- In the case that is a deterministic factor (see Figure 3b):then the forward message from to x is of LWS type and is calculated as follows:For the computation of the backward message toward , we distinguish two cases:
- (a)
- If all forward incoming messages from the variables are Gaussian, we first use a Laplace approximation to obtain a Gaussian joint posterior ; see Appendix B.1.2 and Appendix B.2.2 for details. Then, we evaluate the posteriors for individual random variables, e.g., . Finally, we send the following Gaussian backward message:
- (b)
- Otherwise (the incoming messages from the variables are not all Gaussian), we use Monte Carlo and send a message to as a NEF distribution:Note that if is a single input deterministic node, i.e., , then the backward message simplifies to (Appendix B.1.1).
- (3)
- The third factor type that leads to a special message computation rule is the equality node; see Figure 3c. The outgoing message from an equality nodeis computed by following the sum–product rule:
3.7. Computation of Free Energy
3.8. Expectations of Statistics
- (1)
- We have two cases when is coded as an EF distribution, i.e.,
- (a)
- If , i.e., the statistic matches with elements of the sufficient statistics vector , then is available in closed form as the gradient of the log-partition function (this is worked out in Appendix A.1.1, see (A14) and (A15)):
- (b)
- Otherwise (), then we evaluatewhere .
- (2)
- In case is represented by a LWS, i.e., the following:then, we evaluate the following:
3.9. Pseudo-Code for the EVMP Algorithm
| Algorithm 1 Extended VMP (Mean-field assumption) |
|
4. Experiments
4.1. Filtering with the Hierarchical Gaussian Filter
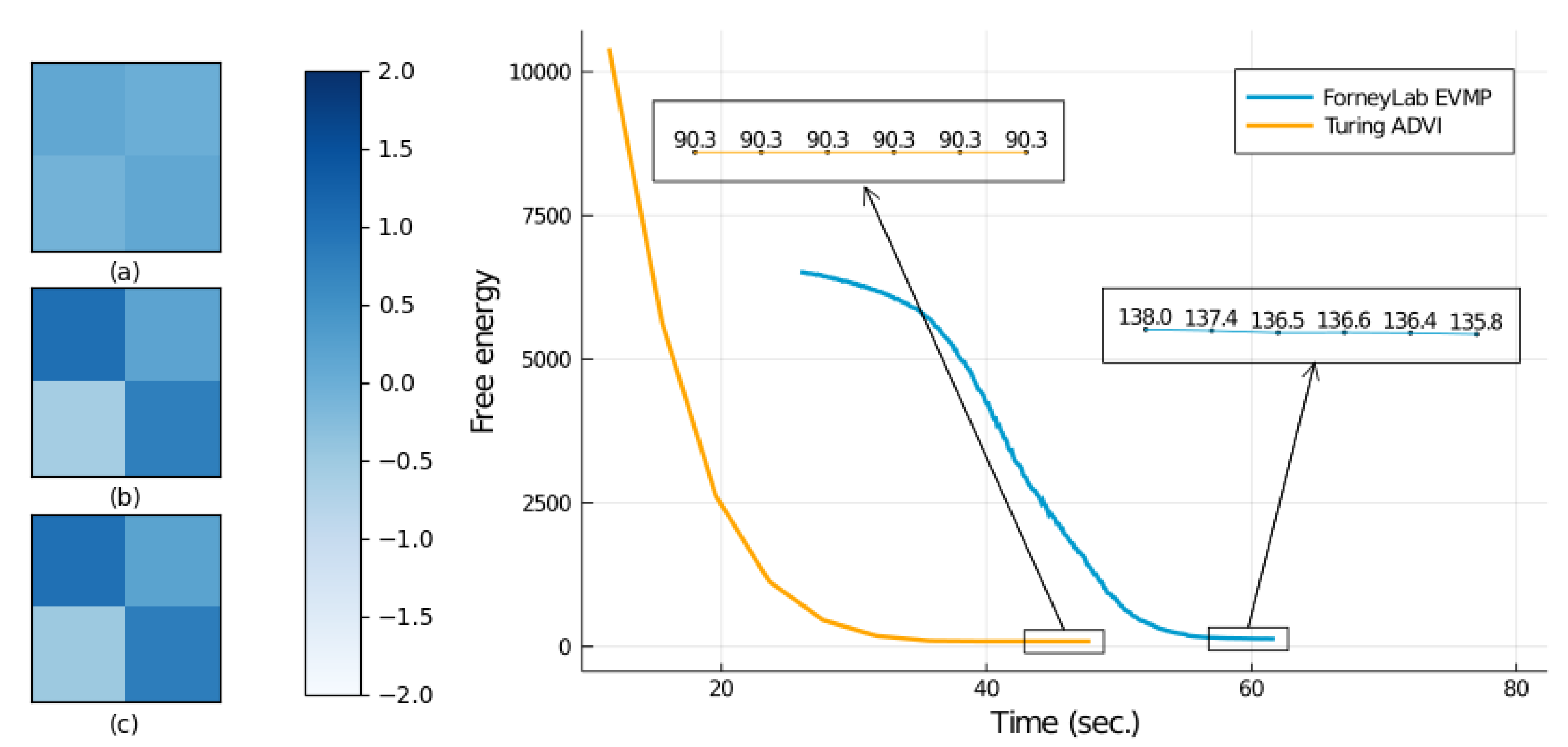
4.2. Parameter Estimation for a Linear Dynamical System
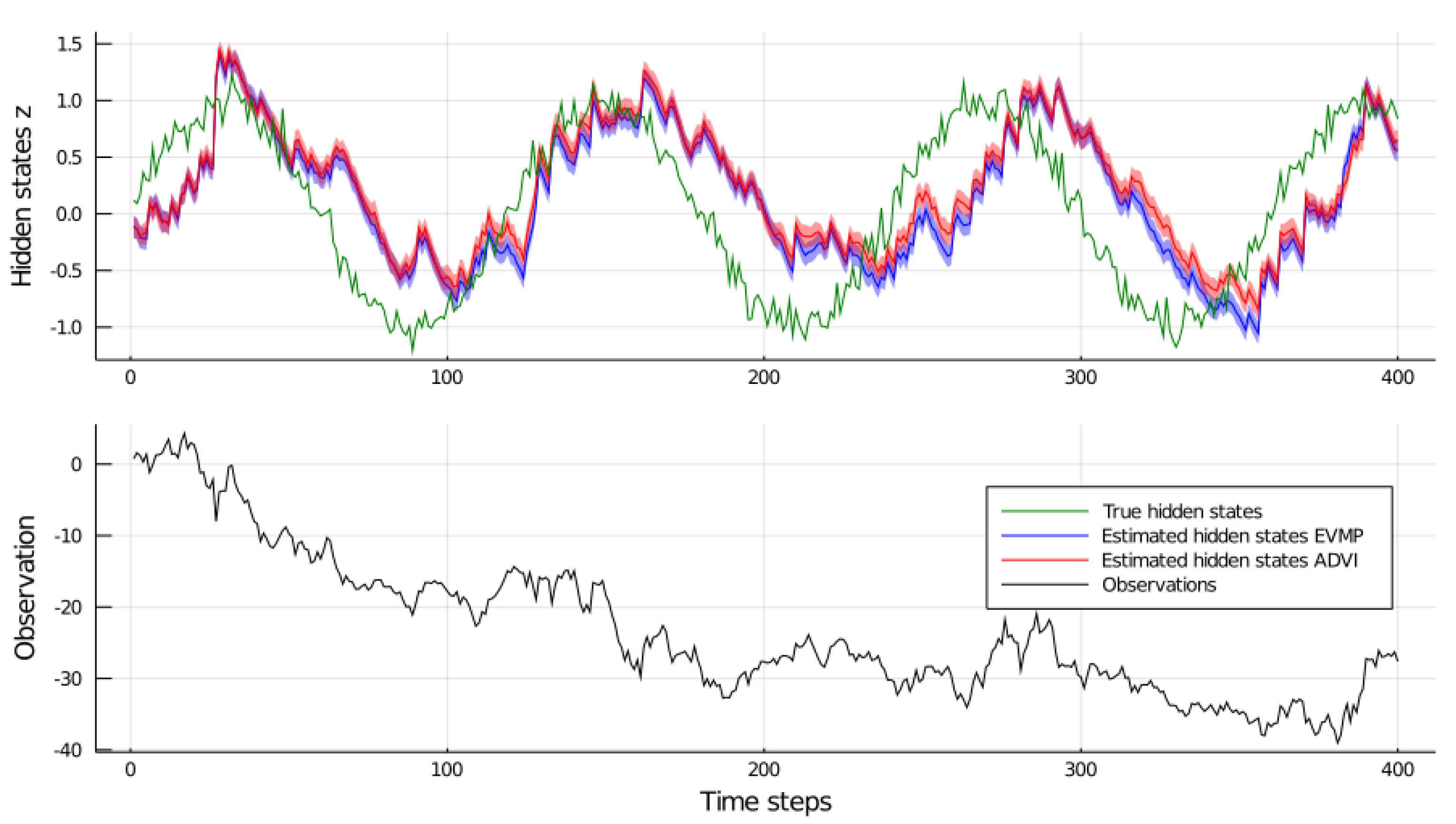
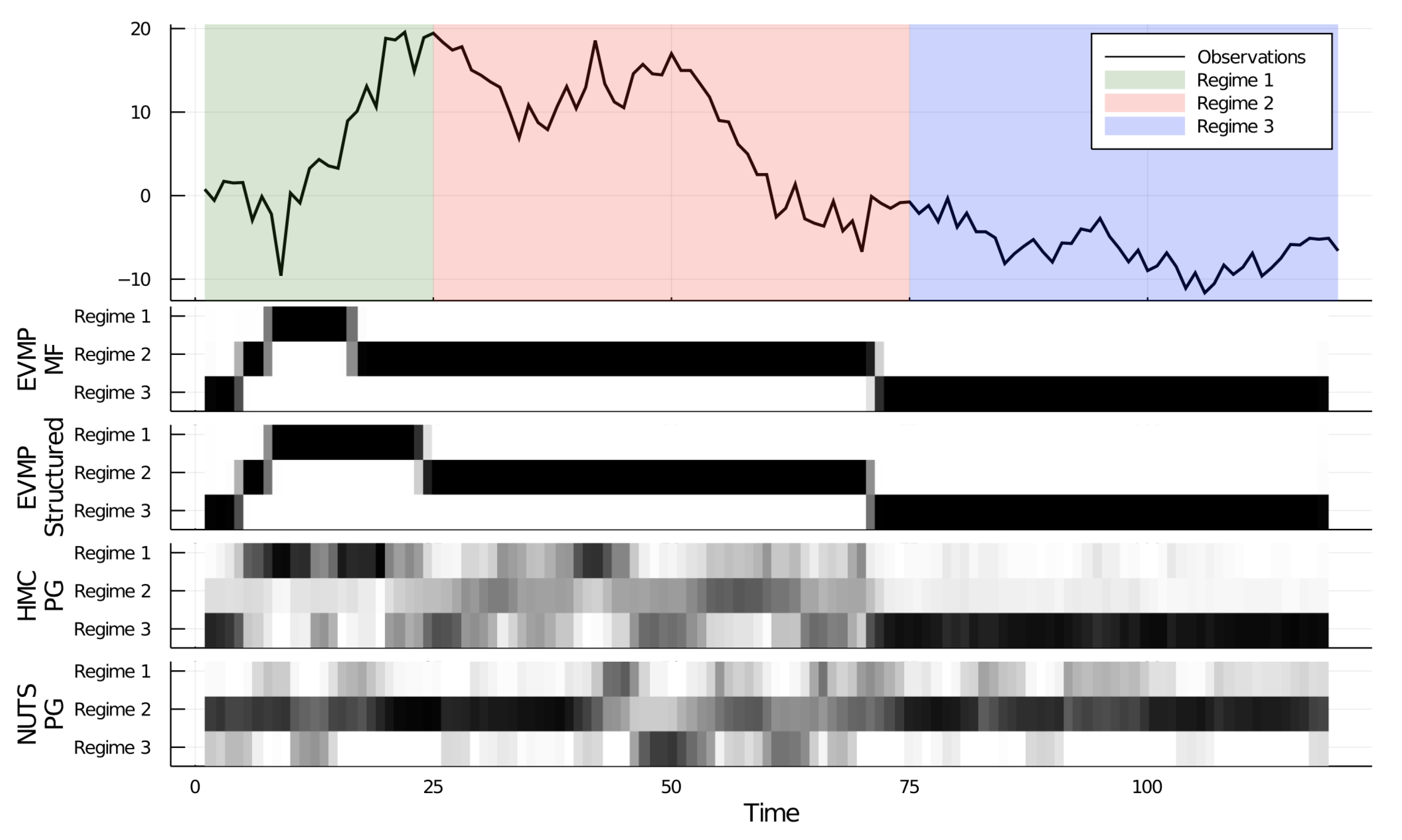
4.3. EVMP for a Switching State Space Model
5. Related Work
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VMP | Variational Message Passing |
| EVMP | Extended Variational Message Passing |
| BP | Belief propagation |
| EP | Expectation propagation |
| FFG | Forney-style Factor Graph |
| EF | Exponential family |
| NEF | Non-standard exponential family |
| LWS | List of Weighted Samples |
| IS | Importance sampling |
| MCMC | Markov Chain Monte Carlo |
| HMC | Hamiltonian Monte Carlo |
| ADVI | Automatic Differentiation Variational Inference |
| PG | Particle Gibbs |
Appendix A. On the Applicability of VMP
- is an element of the exponential family (EF) of distributions, i.e.,In this equation, is a base measure, is a vector of natural (or canonical) parameters, are the sufficient statistics, and is the log-partition function, i.e., . It is always possible to write the log-partition function as a function of natural parameters , such that . Throughout the paper, we sometimes prefer the natural parameter parameterization of the log partition.
- We differentiate a few cases for :
- is also an element of the EF, given by the following:and is a conditionally conjugate pair with for . This (conditional conjugacy) property implies that, given , we can modify in such a way that its sufficient statistics will match the sufficient statistics of . Technically, this means we can rewrite as follows:The crucial element of this rewrite is that both and are written as exponential functions of the same sufficient statistics function . This case leads to the regular VMP update equations, see Appendix A.1.Our Extended VMP does not need this assumption and derives approximate VMP update rules for the following extensions.
- is an element of the EF, but not amenable to the modification given in (A3), i.e., it cannot be written as an exponential function of sufficient statistics . Therefore, is not a conjugate pair with for .
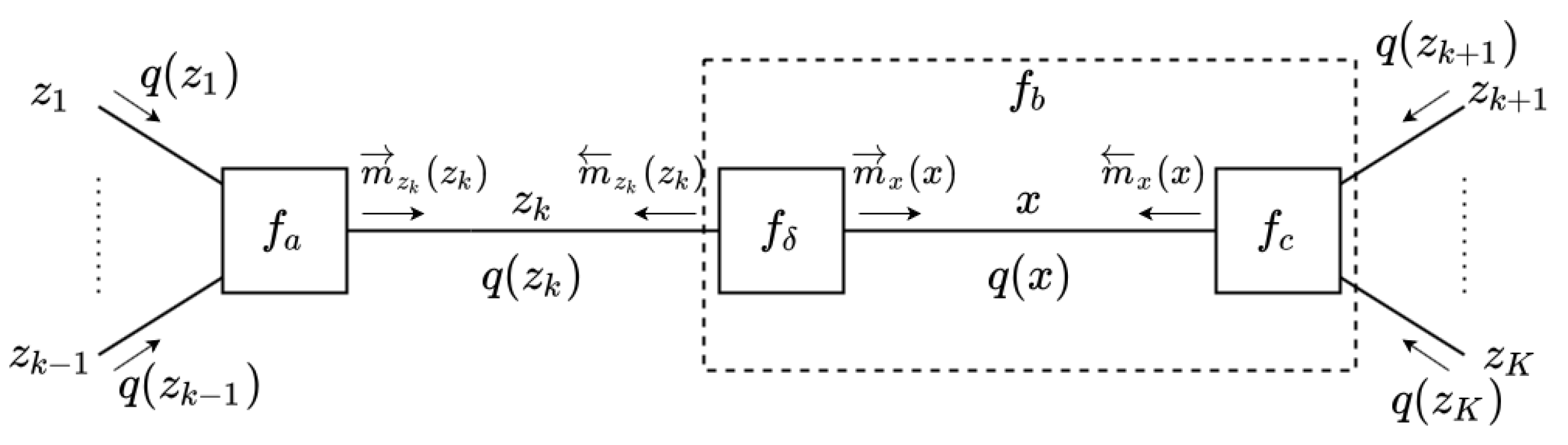
- is a composition of a deterministic node with an EF node, see Figure A1. In particular, in this case can be decomposed as follows:where is a deterministic, possibly nonlinear transformation and is an element of the EF:We assume that the conjugate prior to for random variable x has sufficient statistics vector , and hence (A5) can be modified as follows:where refers to the terms that does not include x.
Appendix A.1. VMP with Conjugate Soft Factor Pairs
Appendix A.1.1. Messages and Posteriors
Appendix A.1.2. Free Energy
Appendix A.2. VMP with Non-Conjugate Soft Factor Pairs
Appendix A.3. VMP with Composite Nodes
Appendix B. Derivation of Extended VMP
Appendix B.1. Deterministic Mappings with Single Inputs
Appendix B.1.1. Non-Gaussian Case
Appendix B.1.2. Gaussian Case

Appendix B.2. Deterministic Mappings with Multiple Inputs
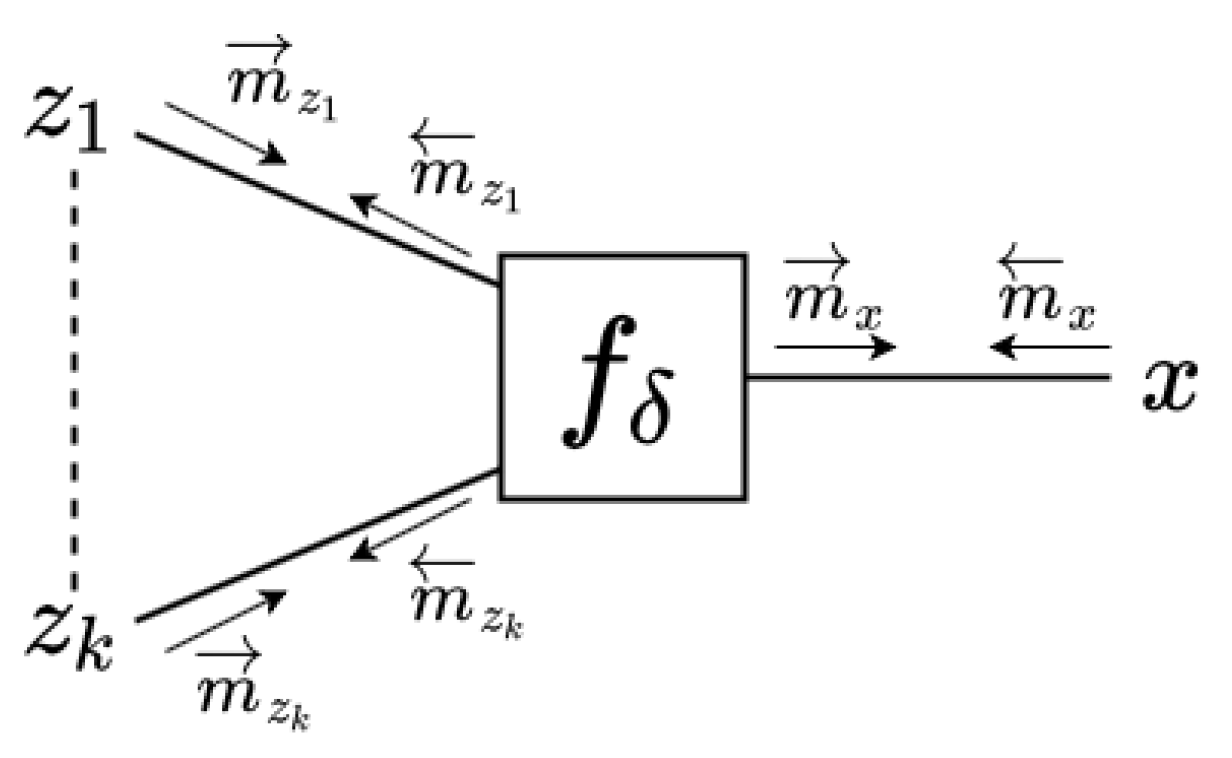
Appendix B.2.1. Monte Carlo Approximation to the Backward Message
Appendix B.2.2. Gaussian Approximation to the Backward Message
Appendix B.3. Non-Conjugate Soft Factor Pairs
- If is a Gaussian message, apply Laplace to approximate with a Gaussian distribution as in (A31a,b).
- Otherwise, use IS as in (A30a,b).
Appendix C. Free Energy Approximation
Appendix D. Implementation Details in ForneyLab
Appendix E. Bonus: Bootstrap Particle Filtering
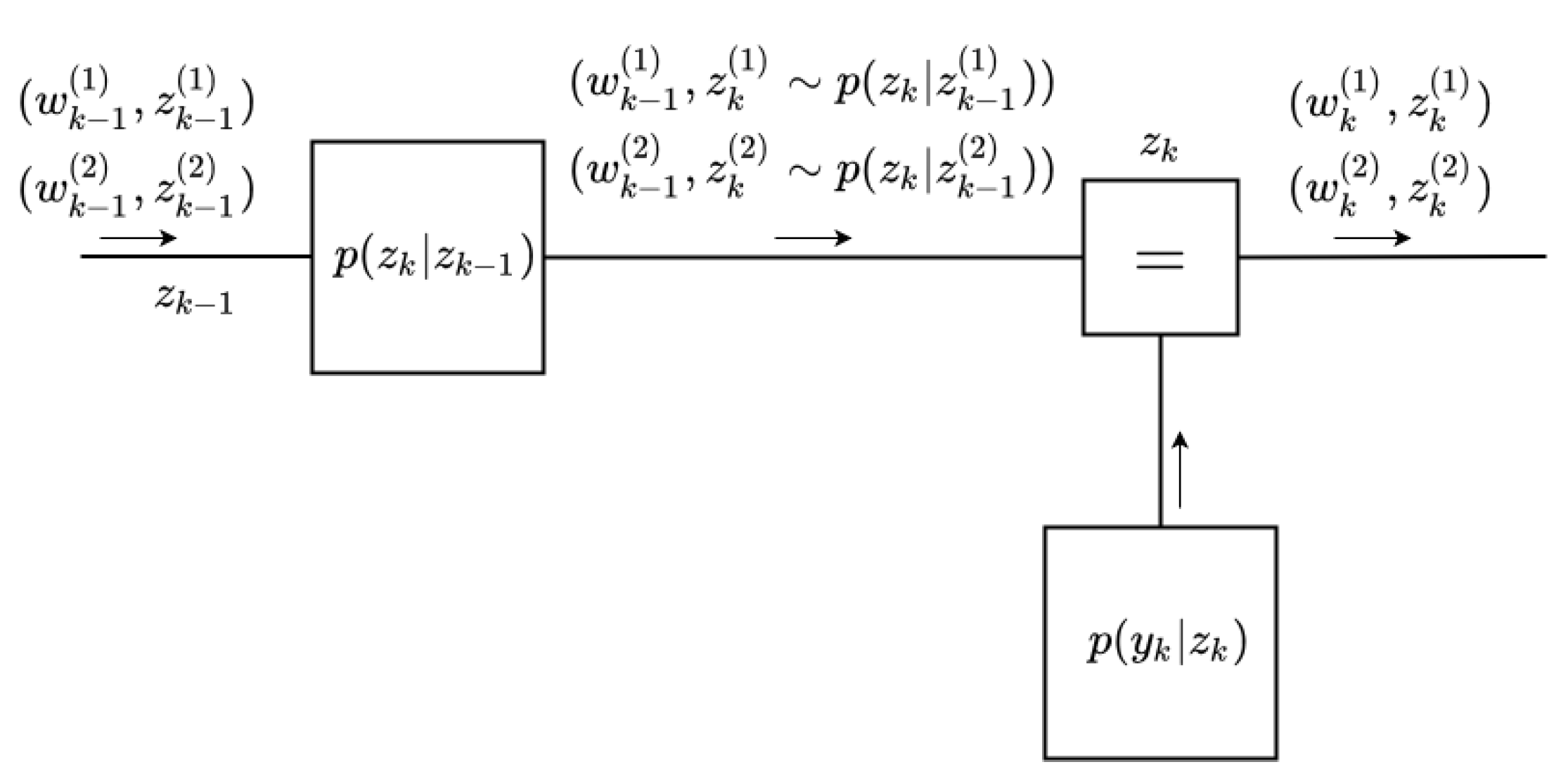
Appendix F. Illustrative Example
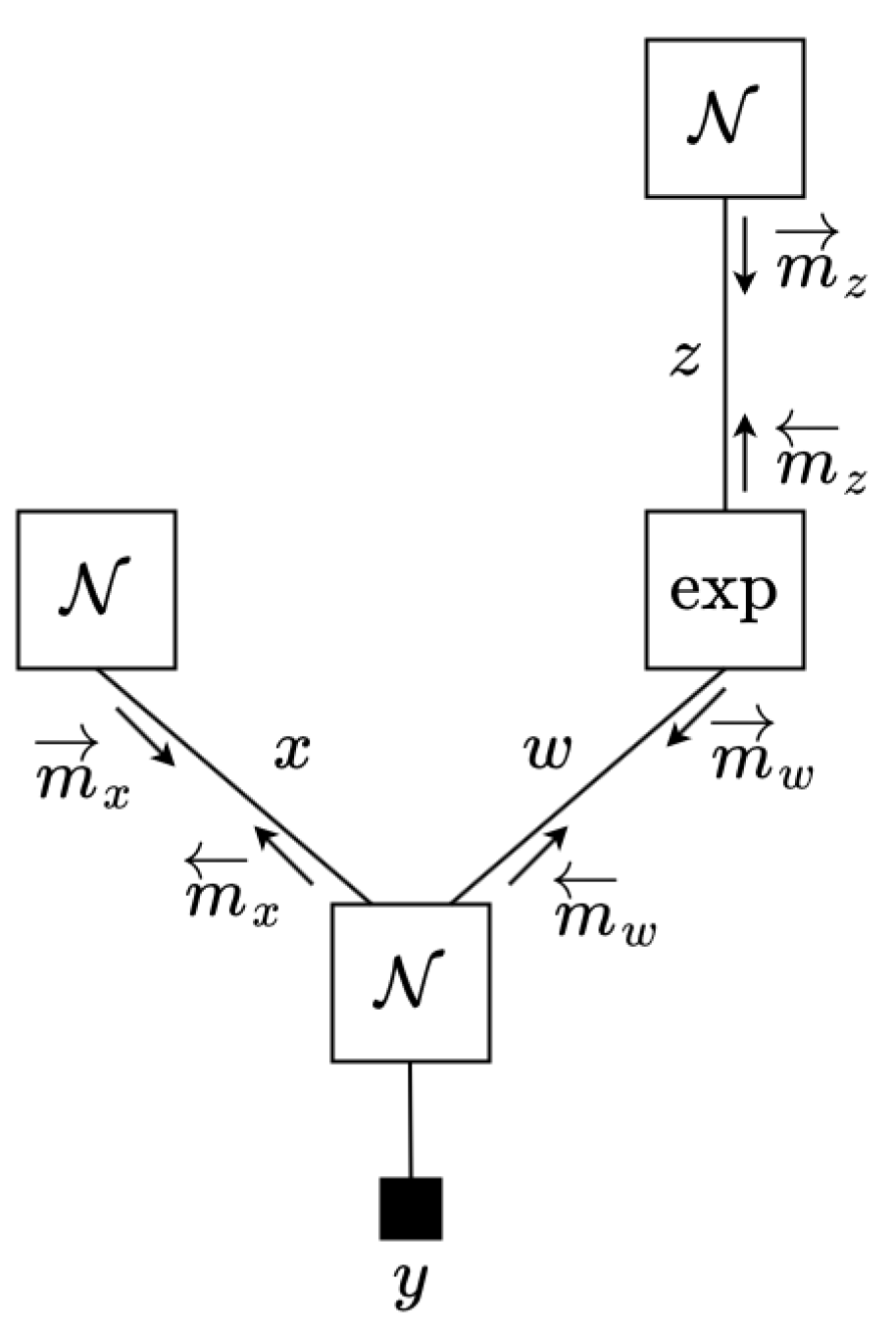
- Initiate , by Normal distributions and by an LWS.
- Repeat until convergence the following three steps:
- -
- Choose w for updating.
- -
- Calculate VMP message by (14). In this case,where is a Gamma distribution with shape and rate .
- -
- Calculate by the following (16):
- -
- Update by Section 3.5 rule (3).
- -
- Choose z for updating.
- -
- Calculate by (18), which is a NEF distribution:
- -
- The forward message is simply the prior:
- -
- Update by Section 3.5 rule (2)(a).
- -
- Choose x for updating.
- -
- Calculate VMP message by (14). In this case,
- -
- The forward message is the prior:
- -
- Update by Section 3.5 rule (1), i.e., the following:
References
- van de Meent, J.W.; Paige, B.; Yang, H.; Wood, F. An Introduction to Probabilistic Programming. arXiv 2018, arXiv:1809.10756. [Google Scholar]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.; Guo, J.; Li, P.; Riddell, A. Stan: A Probabilistic Programming Language. J. Stat. Softw. 2017, 76, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Dillon, J.V.; Langmore, I.; Tran, D.; Brevdo, E.; Vasudevan, S.; Moore, D.; Patton, B.; Alemi, A.; Hoffman, M.; Saurous, R.A. TensorFlow Distributions. arXiv 2017, arXiv:1711.10604. [Google Scholar]
- Bingham, E.; Chen, J.P.; Jankowiak, M.; Obermeyer, F.; Pradhan, N.; Karaletsos, T.; Singh, R.; Szerlip, P.; Horsfall, P.; Goodman, N.D. Pyro: Deep Universal Probabilistic Programming. J. Mach. Learn. Res. 2019, 20, 1–6. [Google Scholar]
- Ge, H.; Xu, K.; Ghahramani, Z. Turing: A Language for Flexible Probabilistic Inference. In International Conference on Artificial Intelligence and Statistics; PMLR, 2018; pp. 1682–1690. [Google Scholar]
- Titsias, M.; Lázaro-Gredilla, M. Doubly stochastic variational Bayes for non-conjugate inference. In International Conference on Machine Learning; PMLR, 2014; pp. 1971–1979. [Google Scholar]
- Minka, T.; Winn, J.; Guiver, J.; Zaykov, Y.; Fabian, D.; Bronskill, J. Infer.NET 0.3. 2018. Available online: https://dotnet.github.io/infer/ (accessed on 25 June 2021).
- Cox, M.; van de Laar, T.; de Vries, B. A factor graph approach to automated design of Bayesian signal processing algorithms. Int. J. Approx. Reason. 2019, 104, 185–204. [Google Scholar] [CrossRef] [Green Version]
- Winn, J.; Bishop, C.M. Variational message passing. J. Mach. Learn. Res. 2005, 6, 661–694. [Google Scholar]
- Dauwels, J. On Variational Message Passing on Factor Graphs. In Proceedings of the IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 2546–2550. [Google Scholar]
- Tokdar, S.T.; Kass, R.E. Importance sampling: A review. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 54–60. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2017, 18, 5595–5637. [Google Scholar]
- Bezanson, J.; Karpinski, S.; Shah, V.B.; Edelman, A. Julia: A fast dynamic language for technical computing. arXiv 2012, arXiv:1209.5145. [Google Scholar]
- Loeliger, H.A.; Dauwels, J.; Hu, J.; Korl, S.; Ping, L.; Kschischang, F.R. The factor graph approach to model-based signal processing. Proc. IEEE 2007, 95, 1295–1322. [Google Scholar] [CrossRef] [Green Version]
- Loeliger, H.A. An introduction to factor graphs. IEEE Signal Process. Mag. 2004, 21, 28–41. [Google Scholar] [CrossRef] [Green Version]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef] [Green Version]
- Dauwels, J.; Korl, S.; Loeliger, H.A. Particle methods as message passing. In Proceedings of the IEEE International Symposium on Information Theory, Seattle, WA, USA, 9–14 July 2006; pp. 2052–2056. [Google Scholar]
- Şenöz, I.; De Vries, B. Online variational message passing in the hierarchical Gaussian filter. In Proceedings of the 2018 IEEE 28th International Workshop on Machine Learning for Signal Processing (MLSP), Aalborg, Denmark, 17–20 September 2018; pp. 1–6. [Google Scholar]
- Mathys, C.D.; Lomakina, E.I.; Daunizeau, J.; Iglesias, S.; Brodersen, K.H.; Friston, K.J.; Stephan, K.E. Uncertainty in perception and the Hierarchical Gaussian Filter. Front. Hum. Neurosci. 2014, 8, 825. [Google Scholar] [CrossRef] [Green Version]
- Kucukelbir, A.; Tran, D.; Ranganath, R.; Gelman, A.; Blei, D.M. Automatic differentiation variational inference. J. Mach. Learn. Res. 2017, 18, 430–474. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Barber, D. Bayesian Reasoning and Machine Learning; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Ghahramani, Z.; Hinton, G.E. Parameter Estimation for Linear Dynamical Systems; Technical Report CRG-TR-92-2; Department of Computer Science, University of Toronto: Toronto, ON, Canada, 1996. [Google Scholar]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, UCL (University College London), London, UK, 2003. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Ghahramani, Z.; Hinton, G.E. Variational learning for switching state-space models. Neural Comput. 2000, 12, 831–864. [Google Scholar] [CrossRef] [PubMed]
- Neal, R.M. MCMC using Hamiltonian dynamics. Handb. Markov Chain Monte Carlo 2011, 2, 113–162. [Google Scholar]
- Betancourt, M. A conceptual introduction to Hamiltonian Monte Carlo. arXiv 2017, arXiv:1701.02434. [Google Scholar]
- Wood, F.; Meent, J.W.; Mansinghka, V. A new approach to probabilistic programming inference. In Artificial Intelligence and Statistics; PMLR, 2014; pp. 1024–1032. [Google Scholar]
- Andrieu, C.; Doucet, A.; Holenstein, R. Particle markov chain monte carlo methods. J. R. Stat. Soc. Ser. B 2010, 72, 269–342. [Google Scholar] [CrossRef] [Green Version]
- De Freitas, N.; Højen-Sørensen, P.; Jordan, M.I.; Russell, S. Variational MCMC. In Proceedings of the Seventeenth Conference on Uncertainty in Artificial Intelligence; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2001; pp. 120–127. [Google Scholar]
- Wexler, Y.; Geiger, D. Importance sampling via variational optimization. In Proceedings of the Twenty-Third Conference on Uncertainty in Artificial Intelligence; AUAI Press: Arlington, VA, USA, 2007; pp. 426–433. [Google Scholar]
- Salimans, T.; Kingma, D.; Welling, M. Markov chain monte carlo and variational inference: Bridging the gap. In International Conference on Machine Learning; PMLR, 2015; pp. 1218–1226. [Google Scholar]
- Ye, L.; Beskos, A.; De Iorio, M.; Hao, J. Monte Carlo co-ordinate ascent variational inference. In Statistics and Computing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–19. [Google Scholar]
- Särkkä, S. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2013; Volume 3. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEEE Proc. Radar Signal Process. 1993, 140, 107–113. [Google Scholar] [CrossRef] [Green Version]
- Frank, A.; Smyth, P.; Ihler, A. Particle-based variational inference for continuous systems. Adv. Neural Inf. Process. Syst. 2009, 22, 826–834. [Google Scholar]
- Ihler, A.; McAllester, D. Particle belief propagation. In Artificial Intelligence and Statistics; PMLR, 2009; pp. 256–263. [Google Scholar]
- Wainwright, M.J.; Jaakkola, T.S.; Willsky, A.S. A new class of upper bounds on the log partition function. IEEE Trans. Inf. Theory 2005, 51, 2313–2335. [Google Scholar] [CrossRef]
- Saeedi, A.; Kulkarni, T.D.; Mansinghka, V.K.; Gershman, S.J. Variational particle approximations. J. Mach. Learn. Res. 2017, 18, 2328–2356. [Google Scholar]
- Raiko, T.; Valpola, H.; Harva, M.; Karhunen, J. Building Blocks for Variational Bayesian Learning of Latent Variable Models. J. Mach. Learn. Res. 2007, 8, 155–201. [Google Scholar]
- Knowles, D.A.; Minka, T. Non-conjugate variational message passing for multinomial and binary regression. Adv. Neural Inf. Process. Syst. 2011, 24, 1701–1709. [Google Scholar]
- Khan, M.; Lin, W. Conjugate-Computation Variational Inference: Converting Variational Inference in Non-Conjugate Models to Inferences in Conjugate Models. In Artificial Intelligence and Statistics; PMLR, 2017; pp. 878–887. [Google Scholar]
- Ranganath, R.; Gerrish, S.; Blei, D. Black box variational inference. In Artificial Intelligence and Statistics; PMLR, 2014; pp. 814–822. [Google Scholar]
- Mackay, D.J.C. Introduction to monte carlo methods. In Learning in Graphical Models; Springer: Berlin/Heidelberg, Germany, 1998; pp. 175–204. [Google Scholar]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: Burlington, MA, USA, 1988. [Google Scholar]
- MacKay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Minka, T.P. Expectation Propagation for approximate Bayesian inference. In Proceedings of the 17th Conference in Uncertainty in Artificial Intelligence; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2001; pp. 362–369. [Google Scholar]
- Vehtari, A.; Gelman, A.; Sivula, T.; Jylänki, P.; Tran, D.; Sahai, S.; Blomstedt, P.; Cunningham, J.P.; Schiminovich, D.; Robert, C.P. Expectation Propagation as a Way of Life: A Framework for Bayesian Inference on Partitioned Data. J. Mach. Learn. Res. 2020, 21, 1–53. [Google Scholar]
- Wainwright, M.J.; Jordan, M.I. Graphical Models, Exponential Families, and Variational Inference. Found. Trends Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Koyama, S.; Castellanos Pérez-Bolde, L.; Shalizi, C.R.; Kass, R.E. Approximate methods for state-space models. J. Am. Stat. Assoc. 2010, 105, 170–180. [Google Scholar] [CrossRef] [Green Version]
- Macke, J.H.; Buesing, L.; Cunningham, J.P.; Yu, B.M.; Shenoy, K.V.; Sahani, M. Empirical models of spiking in neural populations. Adv. Neural Inf. Process. Syst. 2011, 24, 1350–1358. [Google Scholar]
- Smola, A.J.; Vishwanathan, S.; Eskin, E. Laplace propagation. In Proceedings of the 16th International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2004; pp. 441–448. [Google Scholar]
- Acerbi, L. Variational bayesian monte carlo. arXiv 2018, arXiv:1810.05558. [Google Scholar]
- Ajgl, J.; Šimandl, M. Differential entropy estimation by particles. IFAC Proc. Vol. 2011, 44, 11991–11996. [Google Scholar] [CrossRef]
- Revels, J.; Lubin, M.; Papamarkou, T. Forward-Mode Automatic Differentiation in Julia. arXiv 2016, arXiv:1607.07892. [Google Scholar]
- Doucet, A.; de Freitas, N.; Gordon, N. Sequential Monte Carlo Methods in Practice; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
| Algorithm | Run Time (s) |
|---|---|
| EVMP (ForneyLab) | |
| ADVI (Turing) |
| Algorithm | Free Energy | Total Time (s) |
|---|---|---|
| EVMP (ForneyLab) | 135.837 | |
| ADVI (Turing) | 90.285 | |
| NUTS (Turing) | - |
| Algorithm | Free Energy | Total Time (s) |
|---|---|---|
| EVMP (Mean-field) | 283.991 | |
| EVMP (Structured) | 273.596 | |
| HMC-PG (Turing) | - | |
| NUTS-PG (Turing) | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbayrak, S.; Bocharov, I.; de Vries, B. Extended Variational Message Passing for Automated Approximate Bayesian Inference. Entropy 2021, 23, 815. https://doi.org/10.3390/e23070815
Akbayrak S, Bocharov I, de Vries B. Extended Variational Message Passing for Automated Approximate Bayesian Inference. Entropy. 2021; 23(7):815. https://doi.org/10.3390/e23070815
Chicago/Turabian StyleAkbayrak, Semih, Ivan Bocharov, and Bert de Vries. 2021. "Extended Variational Message Passing for Automated Approximate Bayesian Inference" Entropy 23, no. 7: 815. https://doi.org/10.3390/e23070815
APA StyleAkbayrak, S., Bocharov, I., & de Vries, B. (2021). Extended Variational Message Passing for Automated Approximate Bayesian Inference. Entropy, 23(7), 815. https://doi.org/10.3390/e23070815





