Diffusion Model of a Non-Integer Order PIγ Controller with TCP/UDP Streams
Abstract
1. Introduction
2. Background and Related Work
2.1. AQMs Based on the Control Theory Approach
2.2. Diffusion Approximation
3. RED, NLRED and a Non-Integer Order Controllers
4. Diffusion Approximation of the TCP and UDP Network Streams
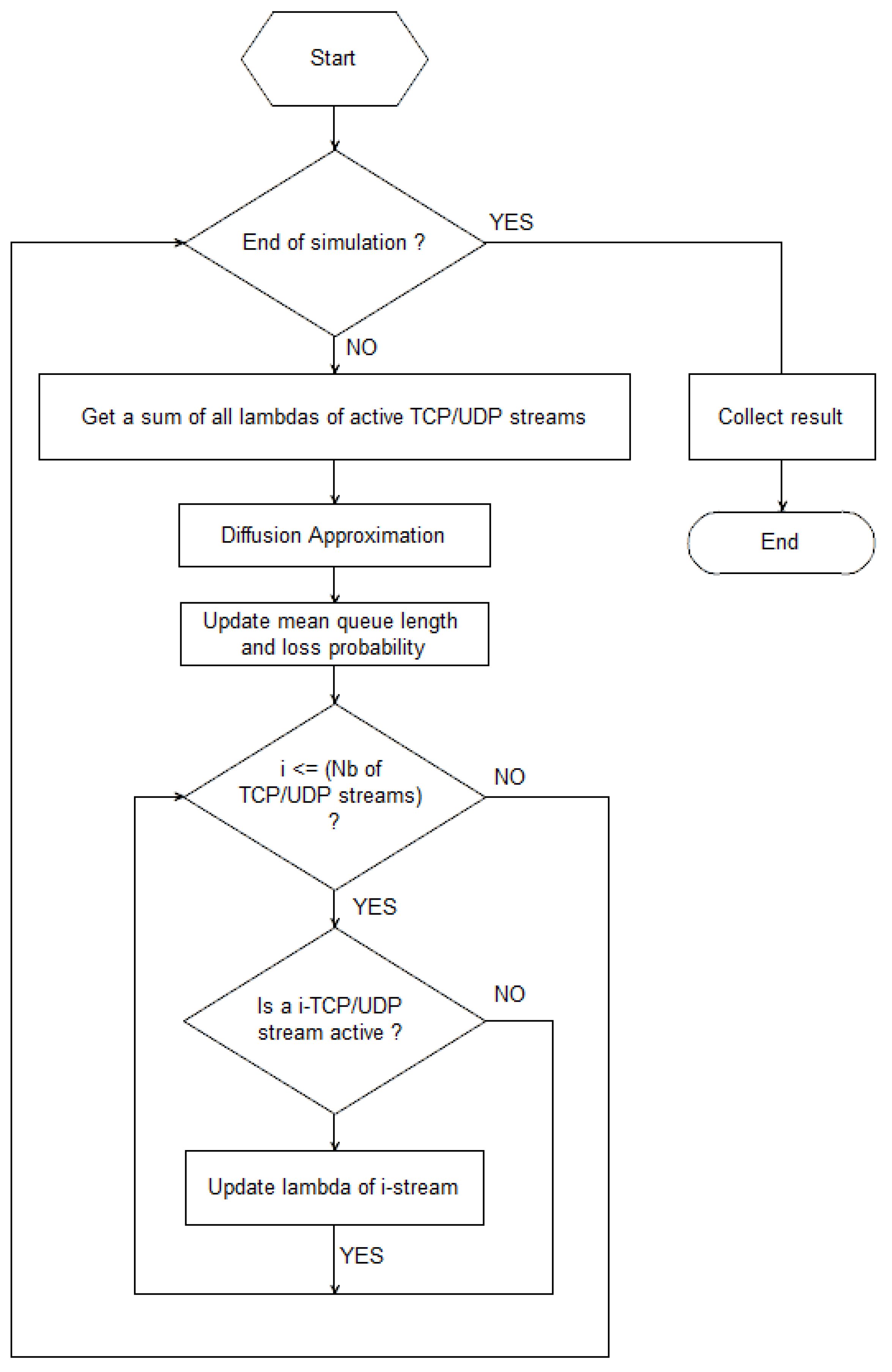
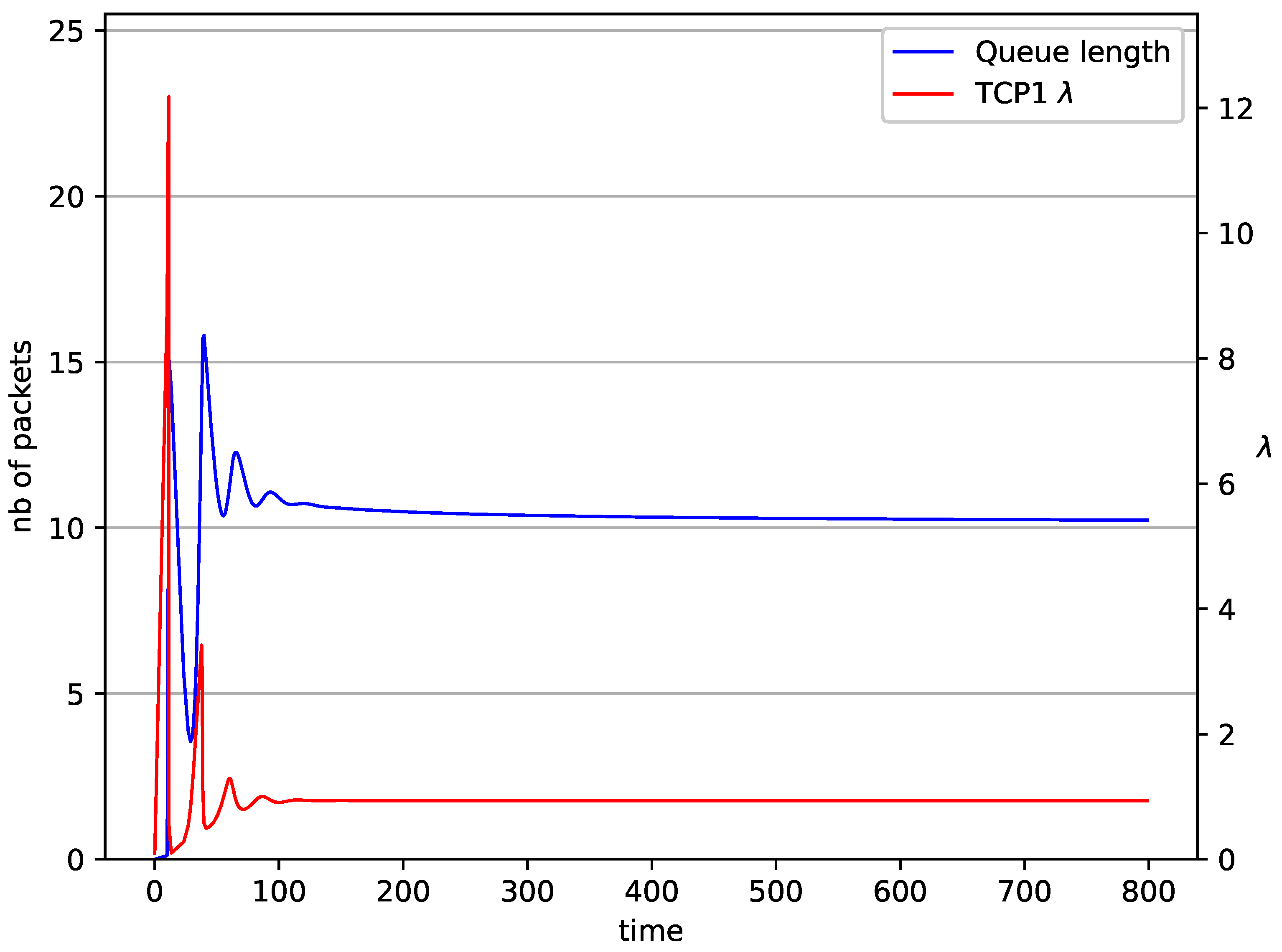
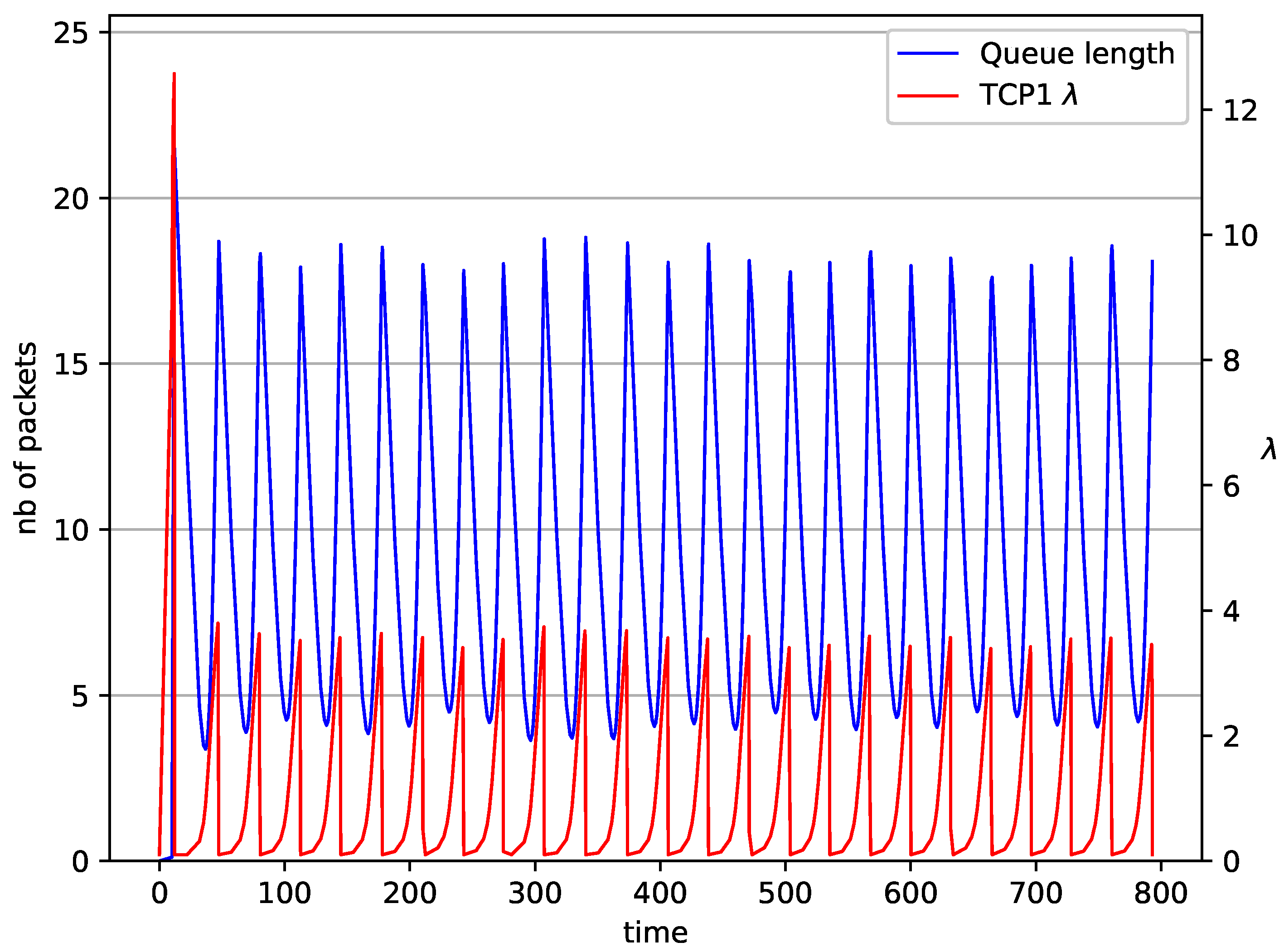
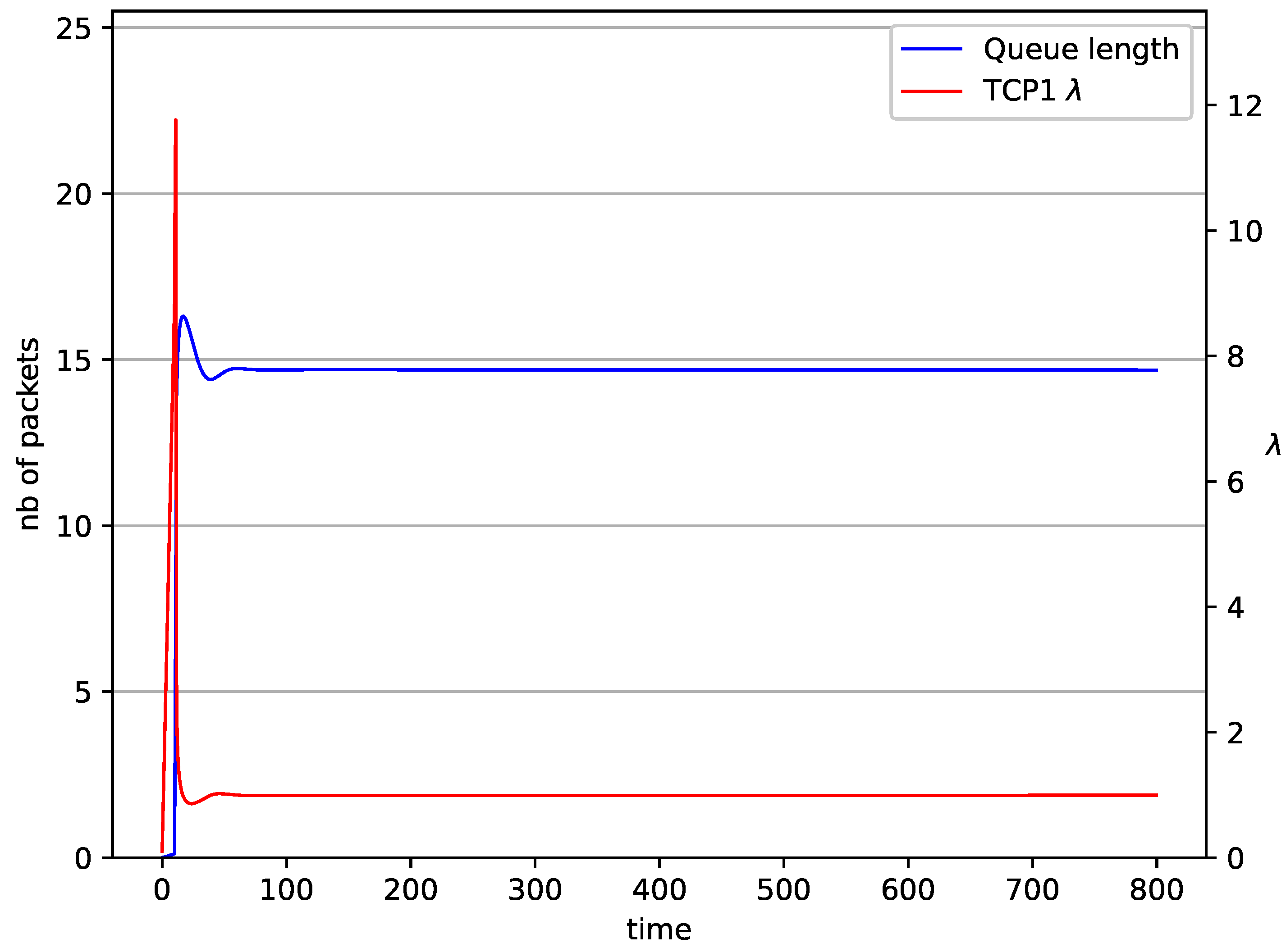
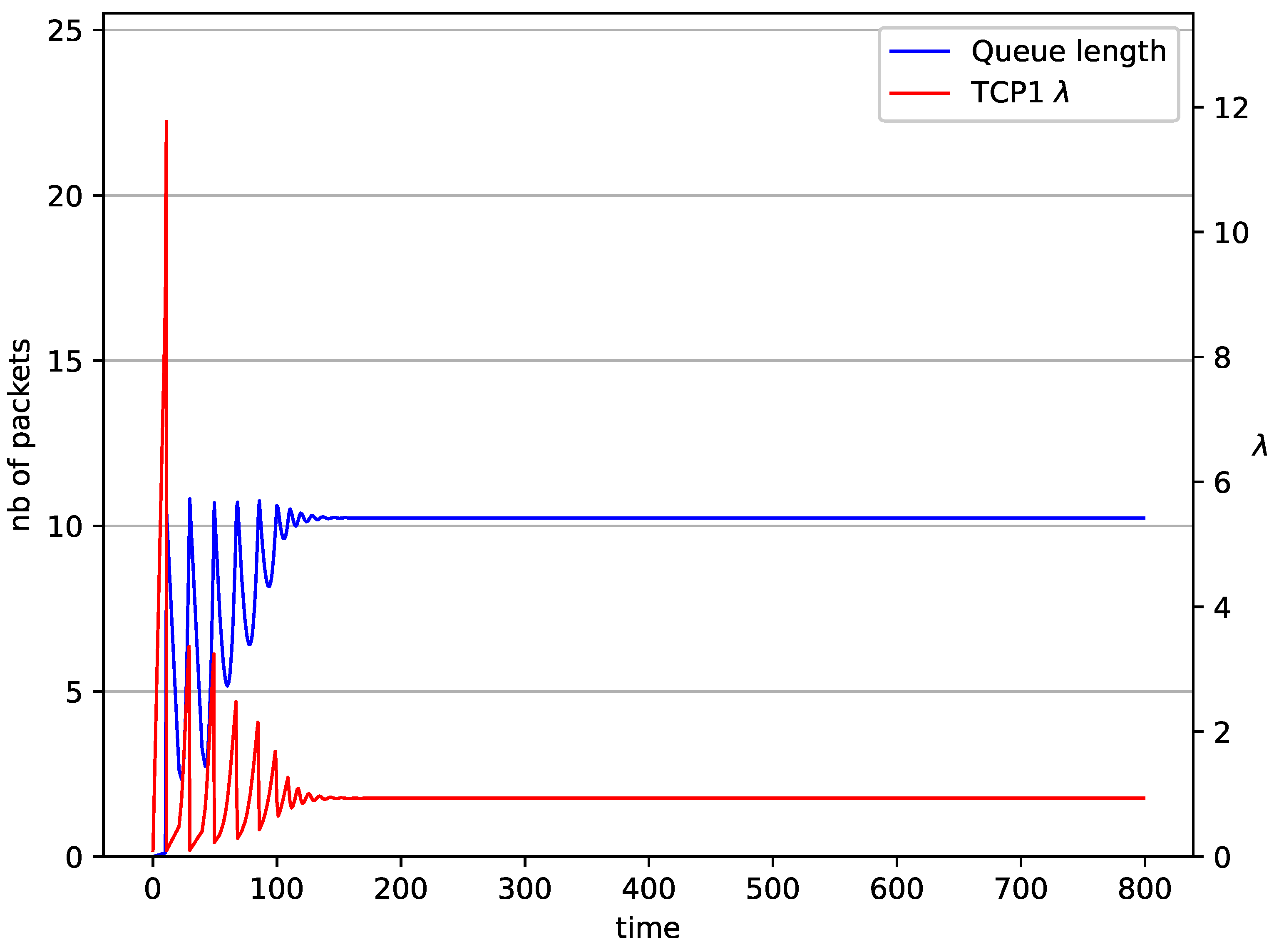
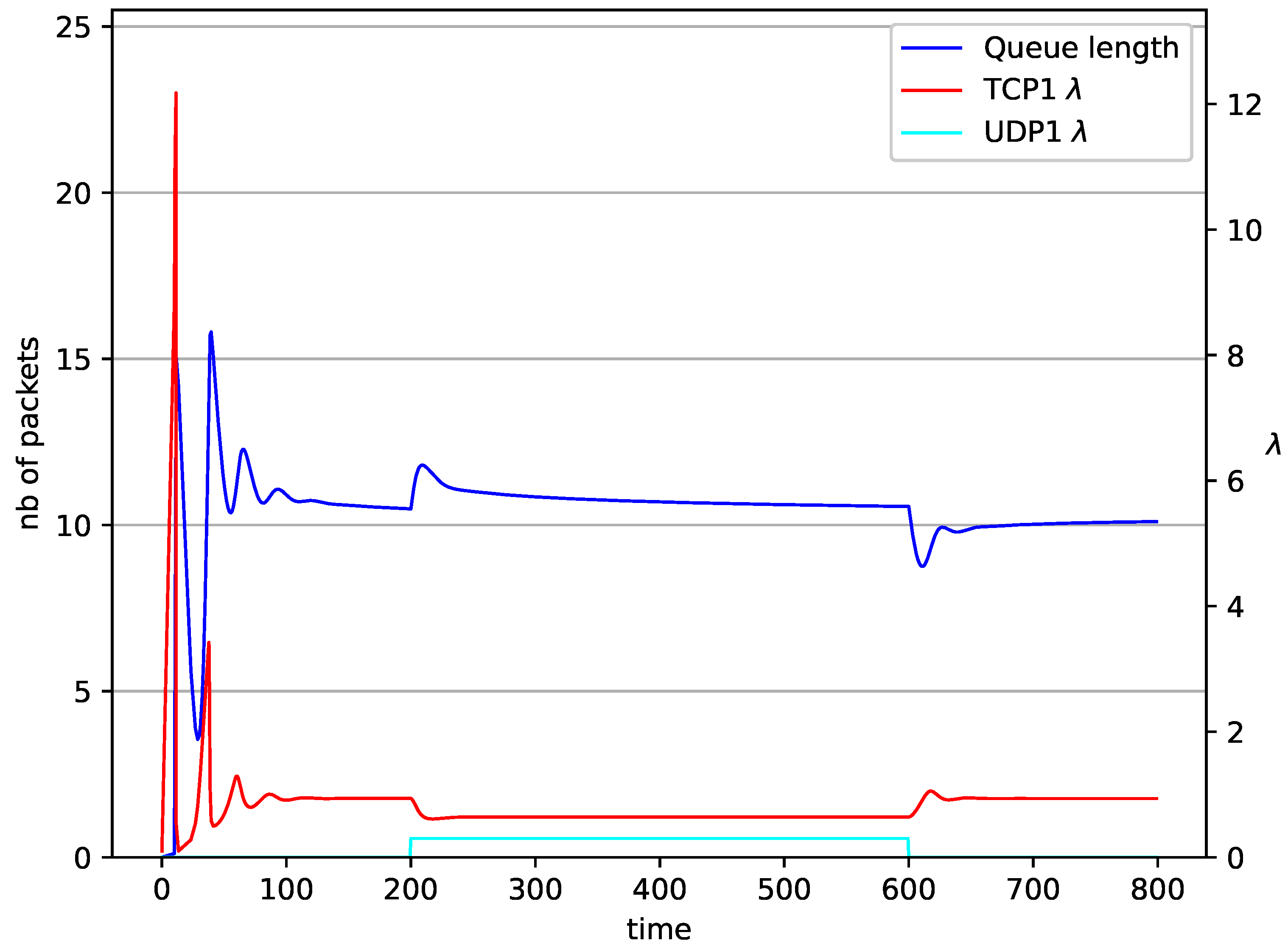
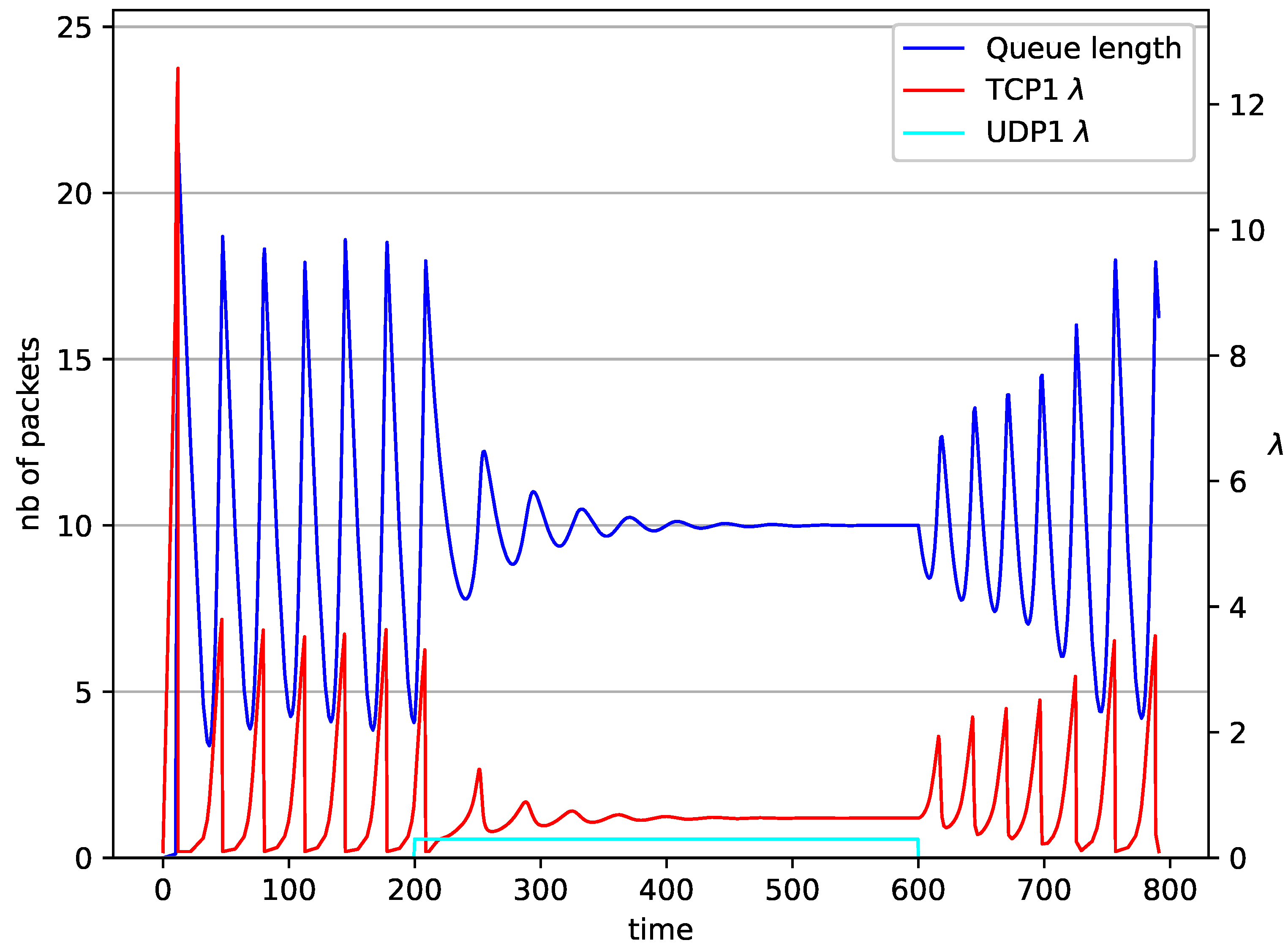
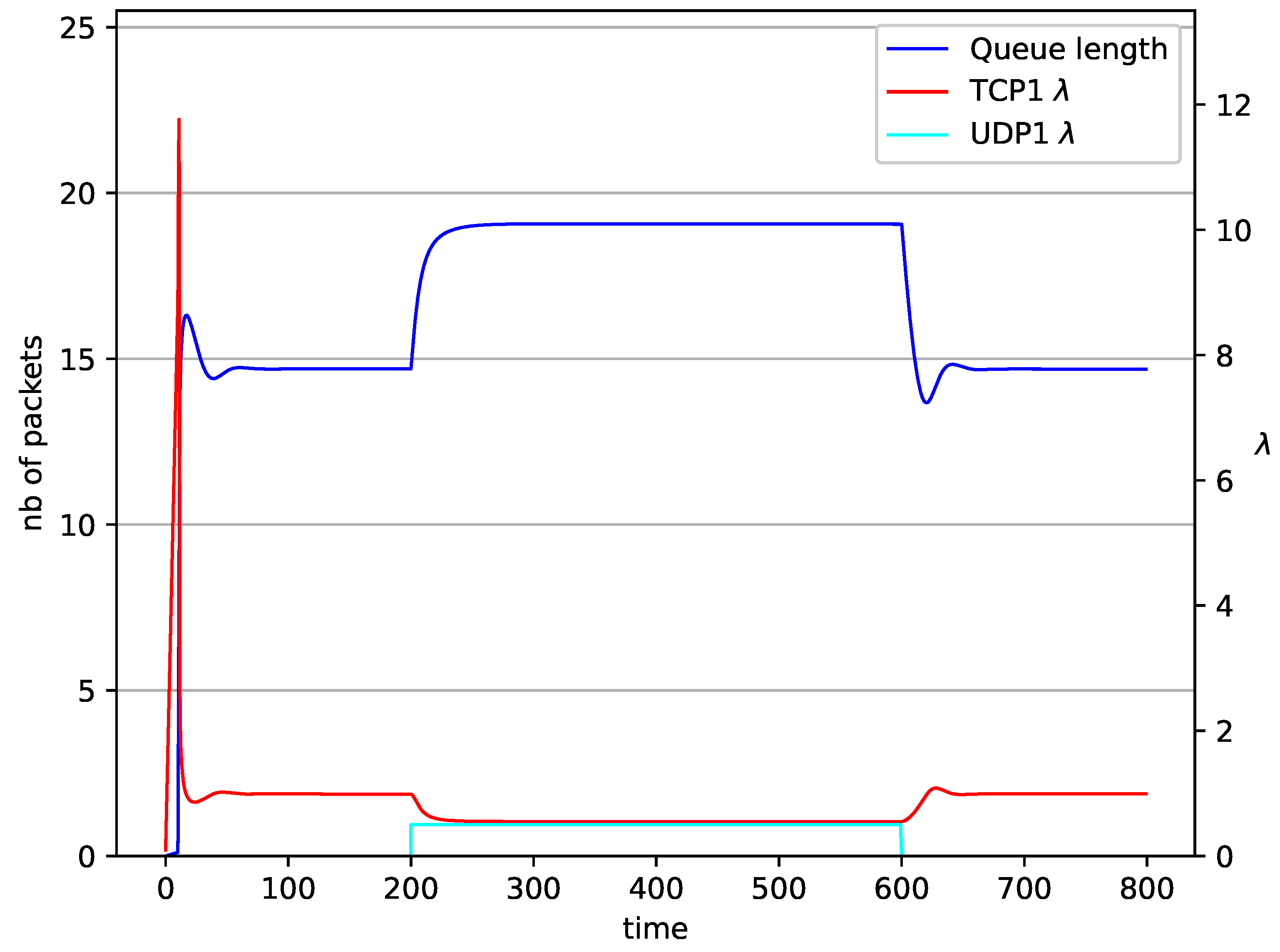
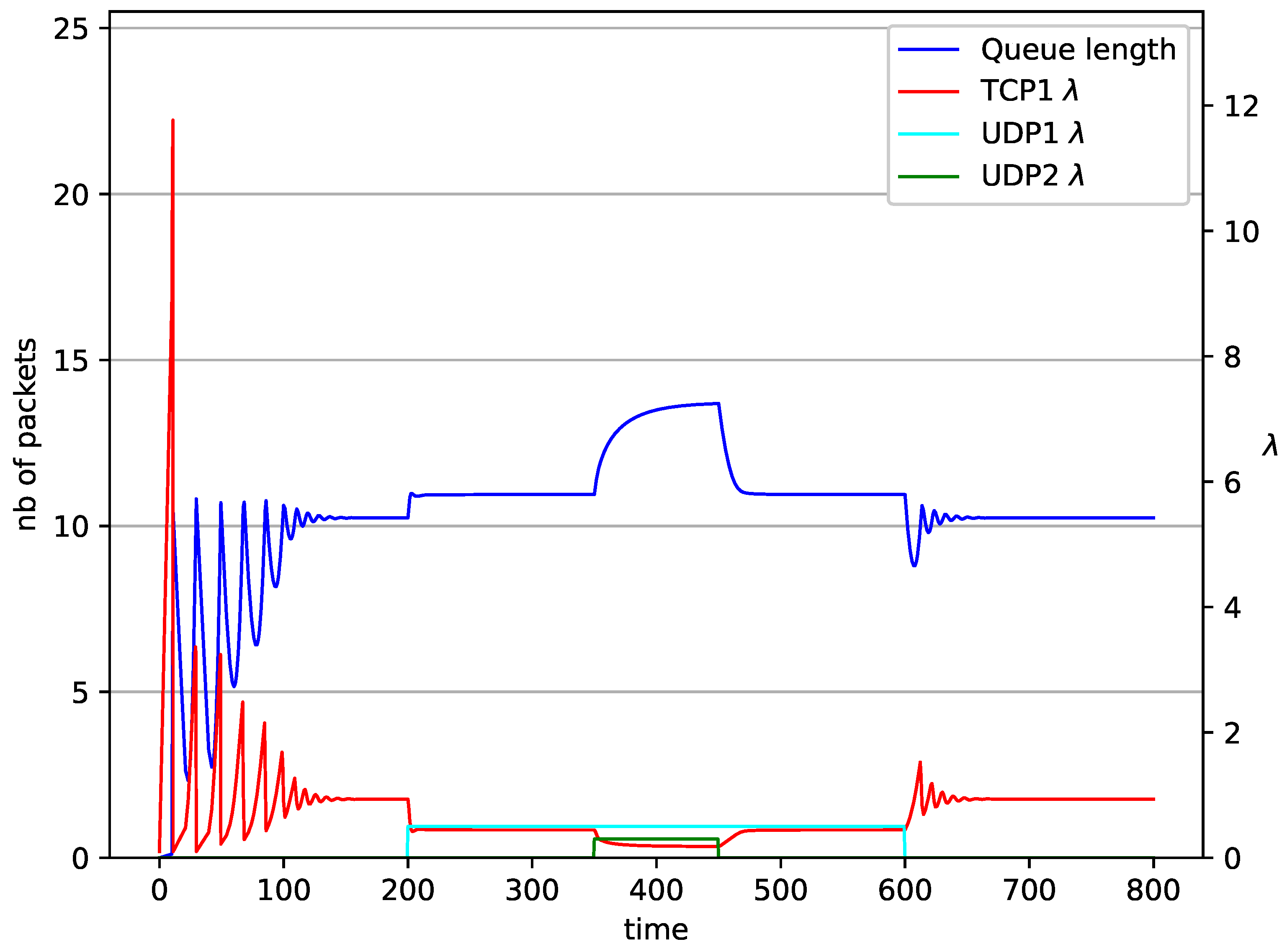
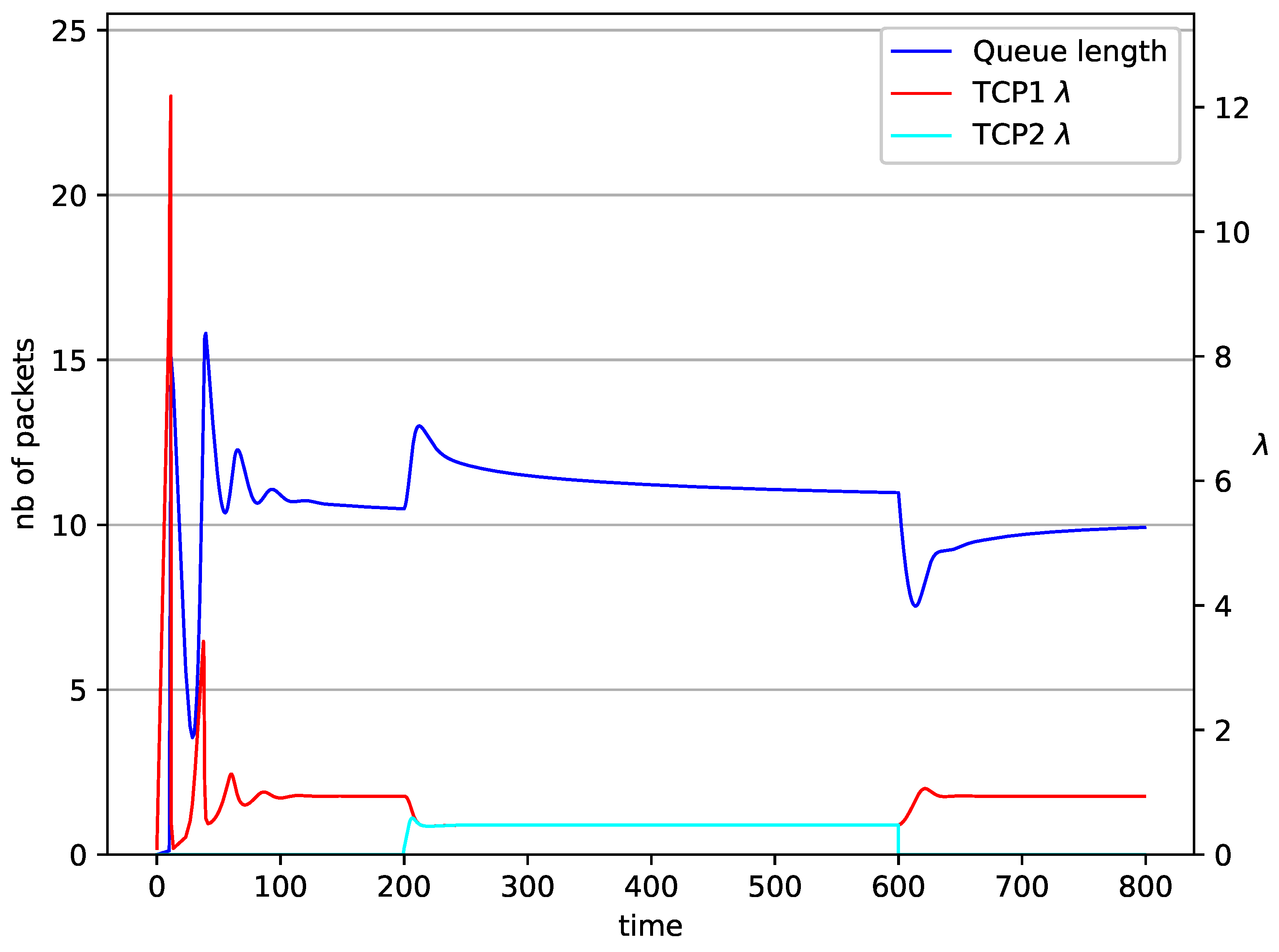
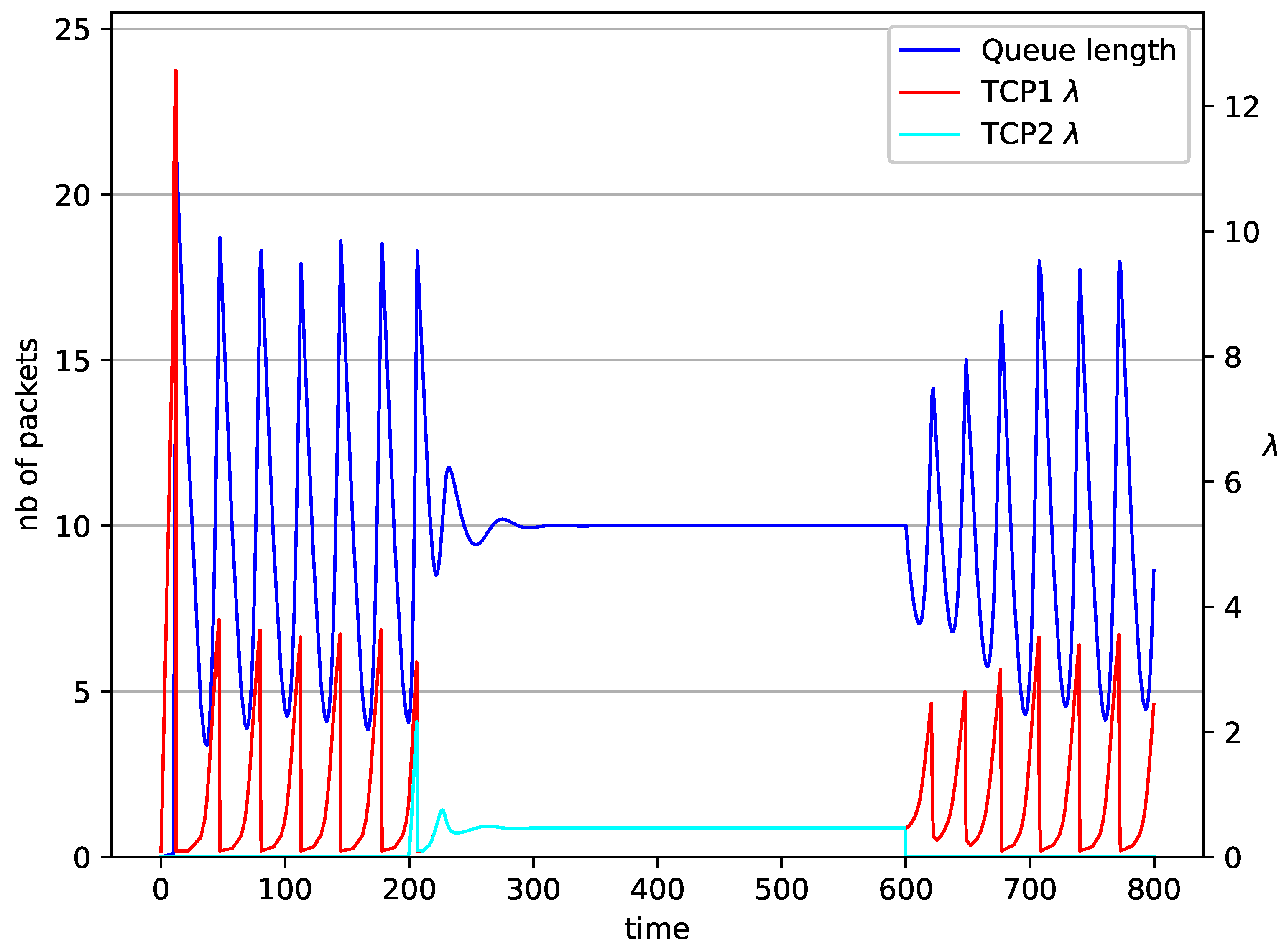
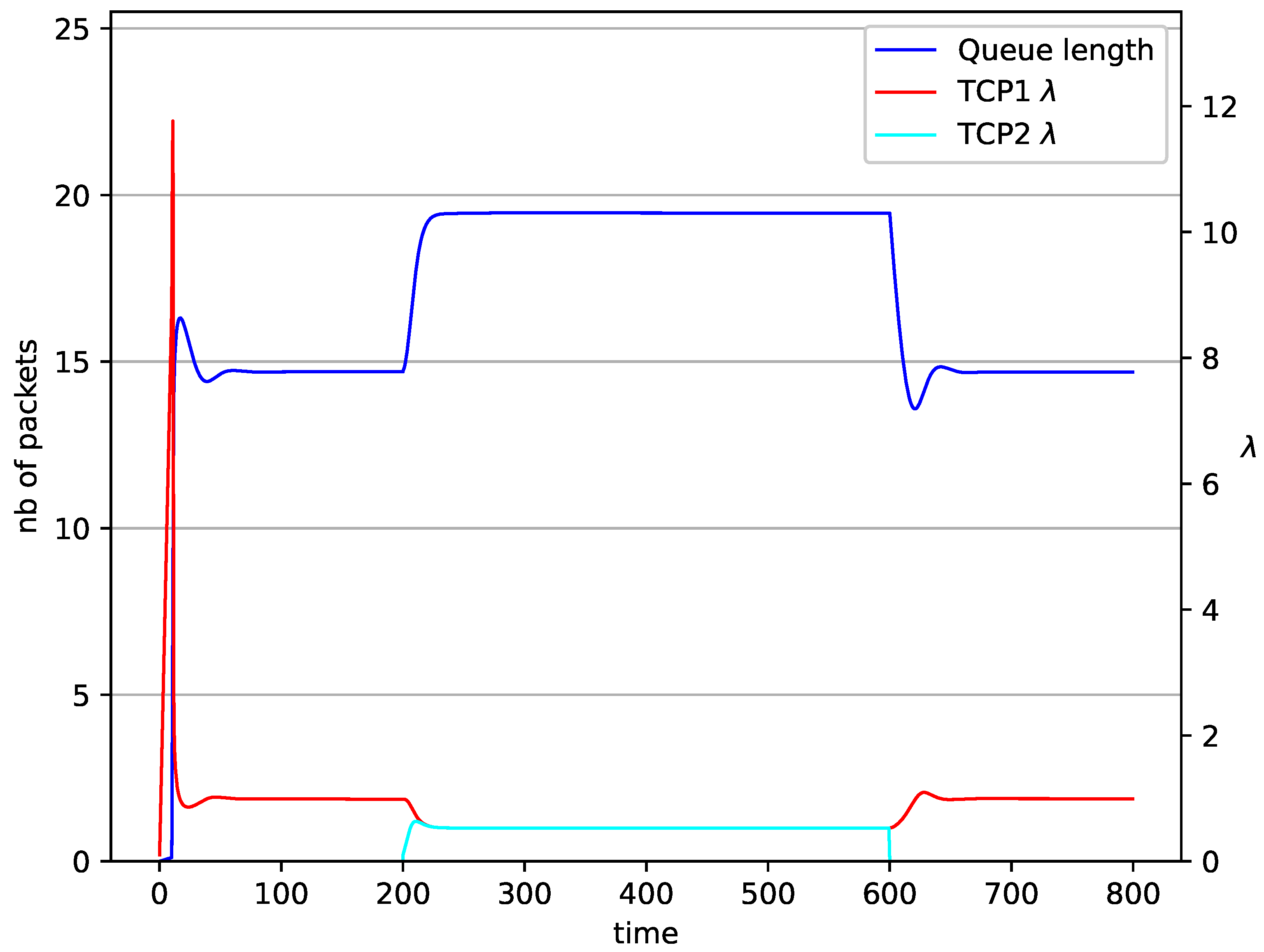
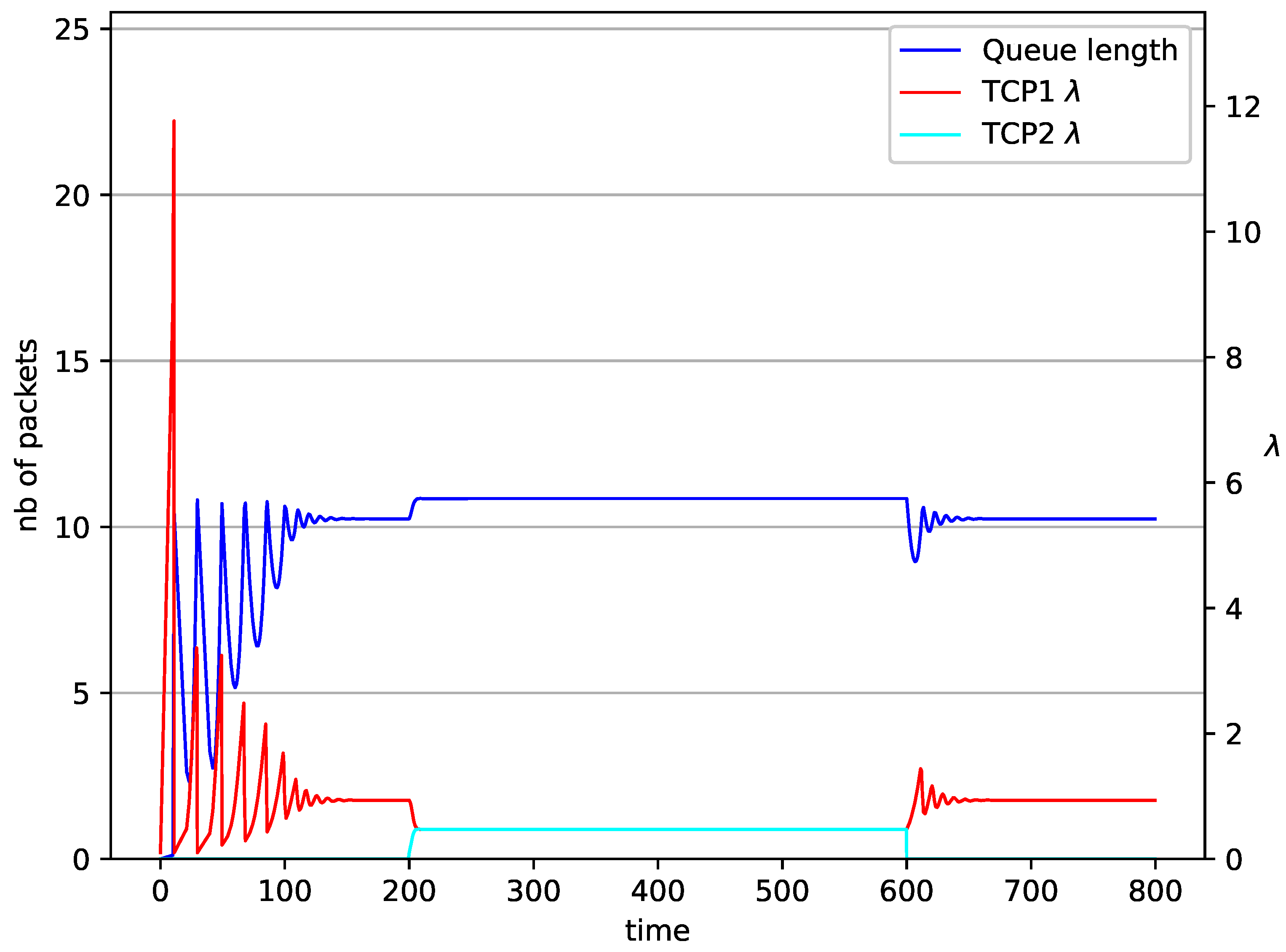
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yue, Z.; Zhang, X.; Ren, Y.; Li, J.; Zhong, Q. The performance evaluation and comparison of TCP-based high-speed transport protocols. In Proceedings of the 2012 IEEE International Conference on Computer Science and Automation Engineering, Beijing, China, 22–24 June 2012; pp. 509–512. [Google Scholar] [CrossRef]
- Chydzinski, A. On the Transient Queue with the Dropping Function. Entropy 2020, 22, 825. [Google Scholar] [CrossRef] [PubMed]
- Grazia, C.A.; Patriciello, N.; Klapez, M.; Casoni, M. A cross-comparison between TCP and AQM algorithms: Which is the best couple for congestion control? In Proceedings of the 14th International Conference on Telecommunications (IEEE ConTEL), Zagreb, Croatia, 28–30 June 2017; pp. 75–82. [Google Scholar]
- Floyd, S.; Jacobson, V. Random Early Detection gateways for congestion avoidance. IEEE/ACM Trans. Netw. 1993, 1, 397–413. [Google Scholar] [CrossRef]
- Feng, C.; Huang, L.; Xu, C.; Chang, Y. Congestion Control Scheme Performance Analysis Based on Nonlinear RED. IEEE Syst. J. 2017, 11, 2247–2254. [Google Scholar] [CrossRef]
- Kahe, G.; Jahangir, A.H. A self-tuning controller for queuing delay regulation in TCP/AQM networks. Telecommun. Syst. 2019, 71, 215–229. [Google Scholar] [CrossRef]
- Feng, W.-C.; Shin, K.G.; Kandlur, D.D.; Saha, D. The BLUE Active Queue Management algorithms. IEEE/ACM Trans. Netw. 2002, 10, 513–528. [Google Scholar] [CrossRef]
- Hu, L.; Kshemkalyani, A.D. HRED: A simple and efficient Active Queue Management algorithm. In Proceedings of the 13th International Conference on Computer Communications and Networks (IEEE Cat. No.04EX969), Chicago, IL, USA, 11–13 October 2004; pp. 387–393. [Google Scholar]
- Long, C.; Zhao, B.; Guan, X.; Yang, J. The Yellow Active Queue Management algorithm. Comput. Netw. 2005, 47, 525–550. [Google Scholar] [CrossRef]
- Kelly, F. Mathematical Modelling of the Internet. In Mathematics Unlimited—2001 and Beyond; Springer: Berlin/Heisenberg, Germany, 2001; pp. 685–702. [Google Scholar]
- Athuraliya, S.; Low, S.H.; Li, V.H.; Yin, Q. REM: Active Queue Management. IEEE Netw. 2001, 15, 48–53. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Y.; Jing, Y. Active Queue Management Algorithm for TCP Networks with Integral Backstepping and Minimax. Int. J. Control Autom. Syst. 2019, 17, 1059–1066. [Google Scholar] [CrossRef]
- Hollot, C.V.; Misra, V.; Towsley, D. Analysis and design of controllers for AQM routers supporting TCP flows. IEEE Trans. Autom. Control 2002, 47, 945–959. [Google Scholar] [CrossRef]
- Shah, P.; Yasmin, S.; Asghar, S.; Qayyum, A.; Hasbullah, H. A Fluid Flow Model for SCTP Traffic over the Internet. In Proceedings of the International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 8–9 October 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Domańska, J.; Domański, A.; Czachórski, T.; Klamka, J. Fluid flow approximation of time-limited TCP/UDP/XCP streams. Bull. Pol. Acad. Sci. Tech. Sci. 2014, 62, 217–225. [Google Scholar] [CrossRef]
- Bonaventura, M.; Castro, R. Fluid-flow and packet-level models of data networks unified under a modular/hierarchical framework: Speedups and simplicity, combined. In Proceedings of the 2018 Winter Simulation Conference (WSC), Gothenburg, Sweden, 9–12 December 2018; pp. 3825–3836. [Google Scholar]
- Domański, A.; Domańska, J.; Czachórski, T.; Klamka, J.; Szyguła, J.; Marek, D. Diffusion Approximation Model of TCP NewReno Congestion Control Mechanism. Springer Nat. Comput. Sci. 2020, 1, 43. [Google Scholar] [CrossRef]
- Unal, H.; Melchor-Aguilar, D.; Ustebay, D.; Niculescu, S.I.; Ozbay, H. Comparison of PI controllers designed for the delay model of TCP/AQM. Comput. Commun. 2013, 36, 1225–1234. [Google Scholar] [CrossRef]
- Fan, Y.; Ren, F.; Lin, C. Design a PID controller for Active Queue Management. In Proceedings of the Eighth IEEE Symposium on Computers and Communications, ISCC 2003, Kemer-Antalya, Turkey, 3 July 2003; Volume 2, pp. 985–990. [Google Scholar]
- Krajewski, W.; Viaro, U. On robust fractional order PI controller for TCP packet flow. In Proceedings of the BOS Coference: Systems and Operational Research, Angers, France, 6–8 March 2014. [Google Scholar]
- Domańska, J.; Domański, A.; Czachórski, T.; Klamka, J. The use of a non-integer order PI controller with an Active Queue Management Mechanism. Int. J. Appl. Math. Comput. Sci. 2016, 26, 777–789. [Google Scholar] [CrossRef]
- Domańska, J.; Domański, A.; Czachórski, T.; Klamka, J. Self-similarity Traffic and AQM Mechanism Based on Non-integer Order PIαDβ Controller. Commun. Comput. Inf. Sci. Springer Int. Publ. 2017, 718, 336–350. [Google Scholar] [CrossRef]
- Domański, A.; Domańska, J.; Czachórski, T.; Klamka, J.; Marek, D.; Szyguła, J. The Influence of the Traffic Self-similarity on the Choice of the Non-integer Order PIα Controller Parameters. Commun. Comput. Inf. Sci. Springer Int. Publ. 2018, 935, 76–83. [Google Scholar] [CrossRef]
- Szyguła, J.; Domański, A.; Domańska, J.; Czachórski, T.; Marek, D.; Klamka, J. AQM Mechanism with Neuron Tuning Parameters. In Intelligent Information and Database Systems; Springer: Berlin/Heisenberg, Germany, 2020; pp. 299–311. [Google Scholar] [CrossRef]
- Marek, D.; Domański, A.; Domańska, J.; Czachórski, T.; Klamka, J.; Szyguła, J. Combined diffusion approximation–simulation model of AQM’s transient behavior. Elsevier Comput. Commun. 2020, 166, 40–48. [Google Scholar] [CrossRef]
- Seferoglu, H.; Modiano, E. TCP-aware backpressure routing and scheduling. In Proceedings of the Information Theory and Applications Workshop (ITA), San Diego, CA, USA, 9–14 February 2014; pp. 1–9. [Google Scholar] [CrossRef]
- Bohloulzadeh, A.; Mehri, R. A Survey on Congestion Control Protocols in Wireless Sensor Networks. Int. J. Wirel. Inf. Netw. 2020, 365–384. [Google Scholar] [CrossRef]
- Athanasopoulou, E.; Bui, L.X.; Ji, T.; Srikant, R.; Stolyar, A. Back-Pressure-Based Packet-by-Packet Adaptive Routing in Communication Networks. IEEE/ACM Trans. Netw. 2013, 21, 244–257. [Google Scholar] [CrossRef]
- Jan, M.A.; Jan, S.; Alam, M.; Akhunzada, A.; Rahman, I. A Comprehensive Analysis of Congestion Control Protocols in Wireless Sensor Networks. Mob. Netw. Appl. 2018, 23, 456–468. [Google Scholar] [CrossRef]
- Misra, V.; Gong, W.; Towsley, D. Fluid-based analysis of network of AQM routers supporting TCP flows with an application to RED. Comput. Commun. Rev. 2000, 30, 151–160. [Google Scholar] [CrossRef]
- Hong, Y.; Yang, O.W.W. Adaptive AQM controllers for IP routers with a heuristic monitor on TCP flows. Int. J. Commun. Syst. 2006, 19, 17–38. [Google Scholar] [CrossRef]
- Sun, J.; Ko, K.; Chen, G.; Chan, S.; Zukerman, M. PD-RED: To improve the performance of RED. IEEE Commun. Lett. 2003, 7, 406–408. [Google Scholar]
- Chen, Y.; Petras, I.; Xue, D. Fractional order control—A tutorial. In Proceedings of the American Control Coference, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar]
- Domańska, J.; Domański, A.; Czachórski, T.; Klamka, J.; Szyguła, J. The AQM Dropping Packet Probability Function Based on Non-integer Order PIαDβ Controller. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heisenberg, Germany, 2019; Volume 496, pp. 36–48. [Google Scholar] [CrossRef]
- Czachórski, T.; Pekergin, F. Diffusion Approximation as a Modelling Tool. In Network Performance Engineering—A Handbook on Convergent Multi-Service Networks and Next Generation Internet, LNCS; Springer: Berlin/Heisenberg, Germany, 2011; Volume 5233, pp. 447–476. [Google Scholar] [CrossRef]
- Czachórski, T.; Grochla, K.; Nycz, T.; Pekergin, F. A diffusion approximation model for wireless networks based on IEEE 802.11 standard. Comput. Commun. 2010, 33, 86–92. [Google Scholar] [CrossRef]
- Nycz, T.; Nycz, M.; Czachórski, T. A Numerical Comparison of Diffusion and Fluid-Flow Approximations Used in Modelling Transient States of TCP/IP Networks. Commun. Comput. Inf. Sci. 2014, 431, 213–222. [Google Scholar]
- Qi, Y.; Ohtsuki, T. QoE-Aware Video Streaming Transmission Optimization Method for Playout Threshold Adjustment in LTE. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–5. [Google Scholar]
- Zhou, K.; Yeung, K.; Li, V. Nonlinear RED: A simple yet efficient Active Queue Management scheme. Comput. Netw. Int. J. Comput. Telecommun. Netw. 2006, 50, 3784–3794. [Google Scholar] [CrossRef]
- Domańska, J.; Augustyn, D.; Domański, A. The choice of optimal 3-rd order polynomial packet dropping function for NLRED in the presence of self-similar traffic. Bull. Pol. Acad. Sci. Tech. Sci. 2012, 60, 779–786. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional order systems and PIλDμ controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Domański, A.; Domańska, J.; Czachórski, T.; Klamka, J.; Marek, D.; Szyguła, J. GPU Accelerated Non-integer Order PIαDβ Controller Used as AQM Mechanism. In Communications in Computer and Information Science; Springer: Berlin/Heisenberg, Germany, 2018; Volume 860, pp. 286–299. [Google Scholar] [CrossRef]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Ciesielski, M.; Leszczynski, J. A Numerical Method for Solution of Ordinary Differential Equations of Fractional Order. In Parallel Processing and Applied Mathematics; Springer: Berlin/Heisenberg, Germany, 2002; Volume 2328, pp. 695–702. [Google Scholar] [CrossRef]
- Newell, G.F. Queues with time-dependent arrival rates. I—The transition through saturation. J. Appl. Probab. 1968, 2, 436–451. [Google Scholar] [CrossRef]
- Gelenbe, E. On Approximate Computer Systems Models. J. ACM 1975, 22, 261–269. [Google Scholar] [CrossRef]
- Gelenbe, E. A Diffusion Model for Packet Travel Time in a Random Multi-hop Medium. ACM Trans. Sens. Netw. (TOSN) 2007, 3, 10. [Google Scholar] [CrossRef]
- Czachórski, T. A method to solve Diffusion Equation with Instantaneous return Processes Acting as Boundary Conditions. Bull. Pol. Acad. Sci. Tech. Sci. 1993, 41, 417–451. [Google Scholar]
- Bonald, T.; May, M.; Bolot, J. Analytic evaluation of RED performance. In Proceedings of the INFOCOM, Tel Aviv, Israel, 26–30 March 2000. [Google Scholar]
- Zheng, B.; Atiquzzaman, M. A Framework to Determine the Optimal Weight Parameter of RED in Next-Generation Internet Routers. Int. J. Commun. Syst. 2008, 21, 987–1008. [Google Scholar] [CrossRef]
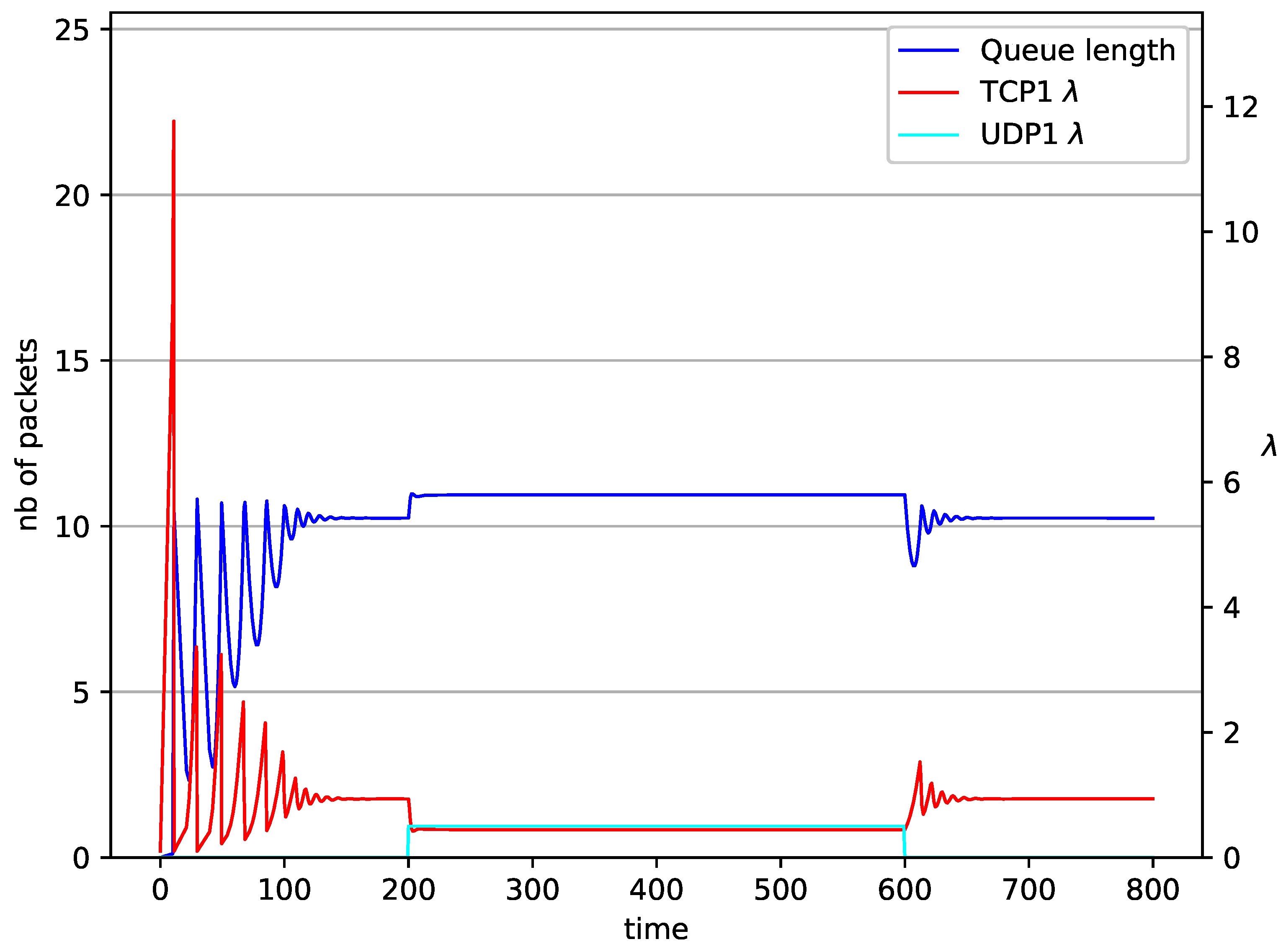
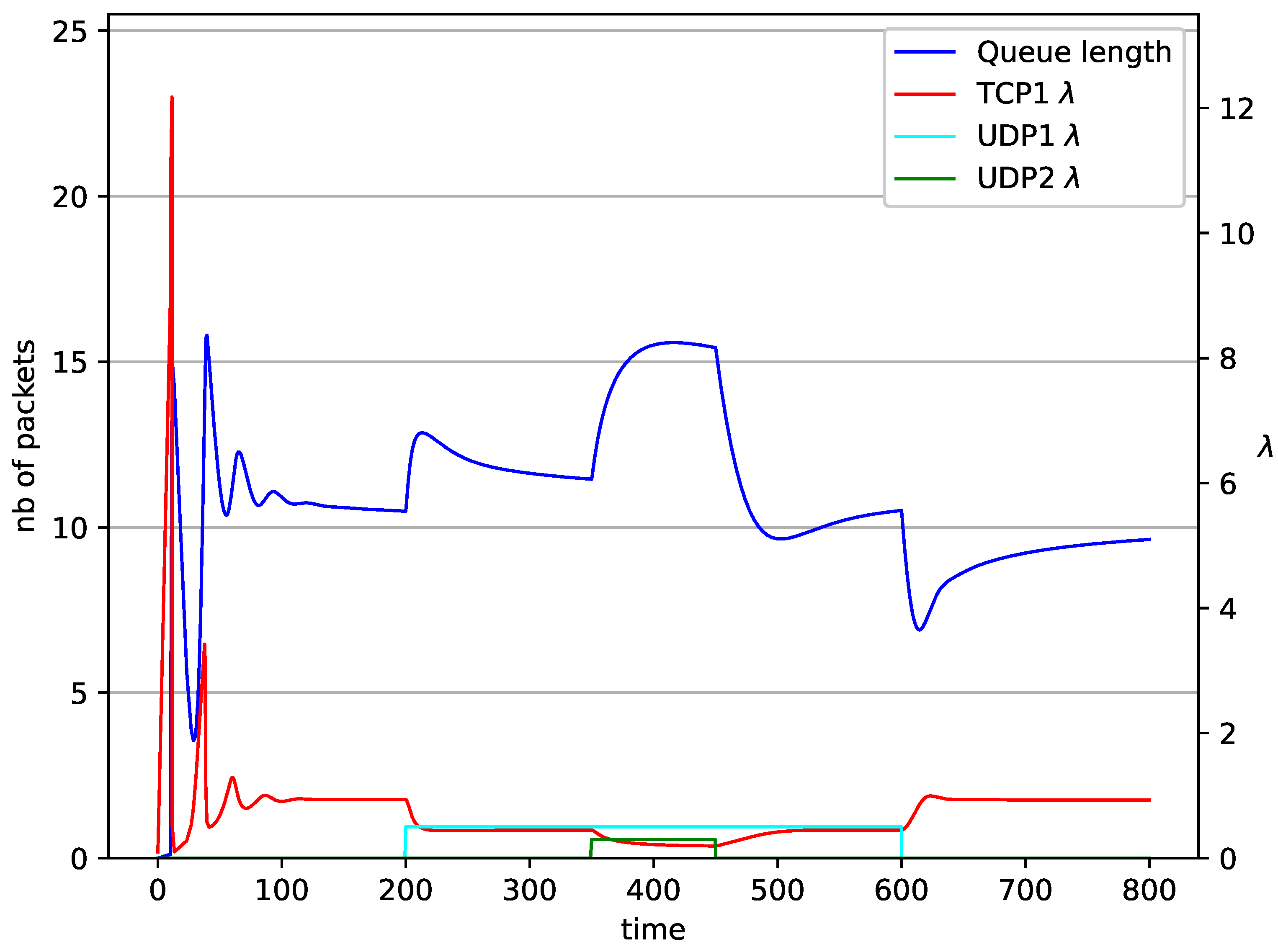
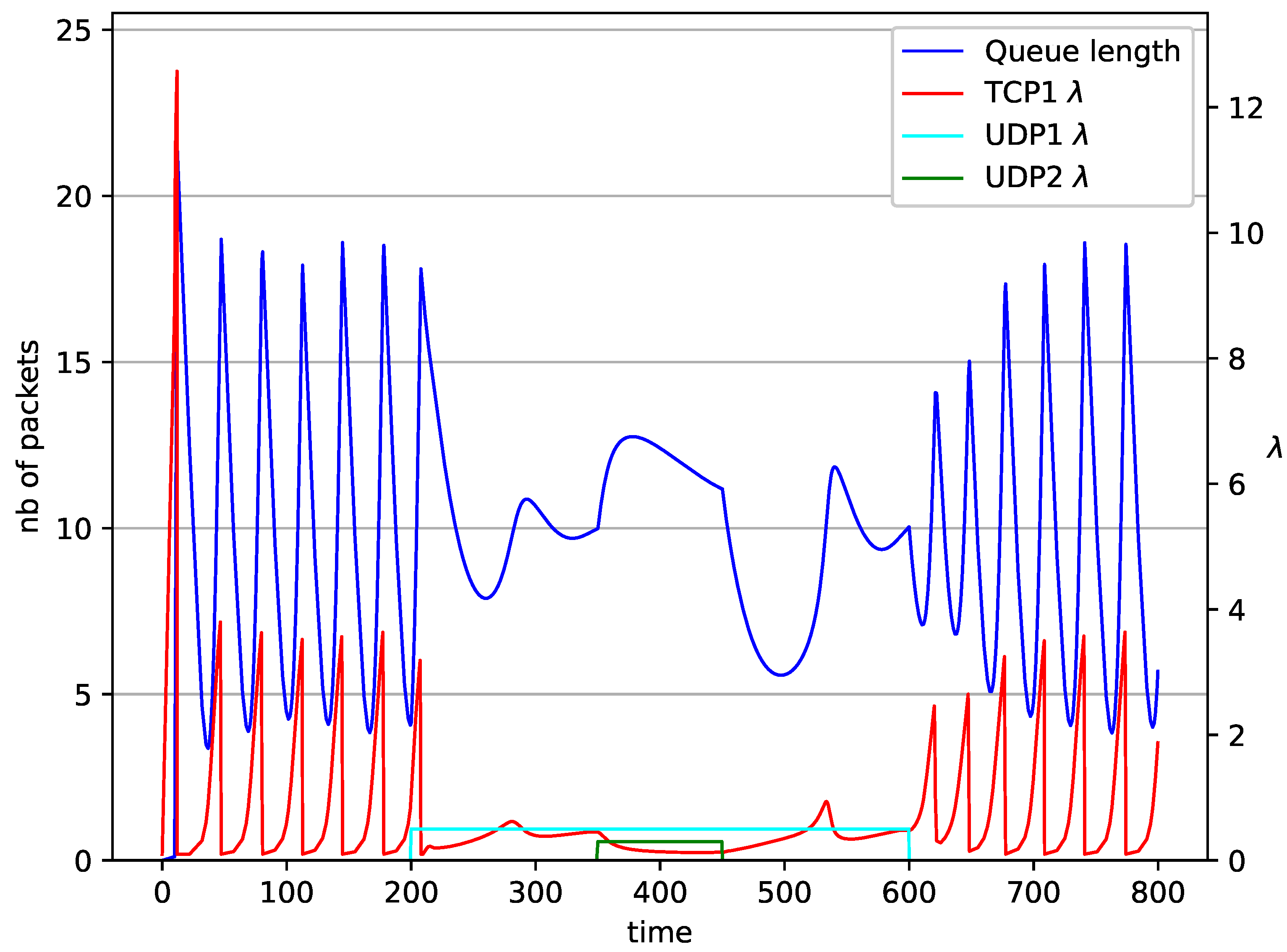
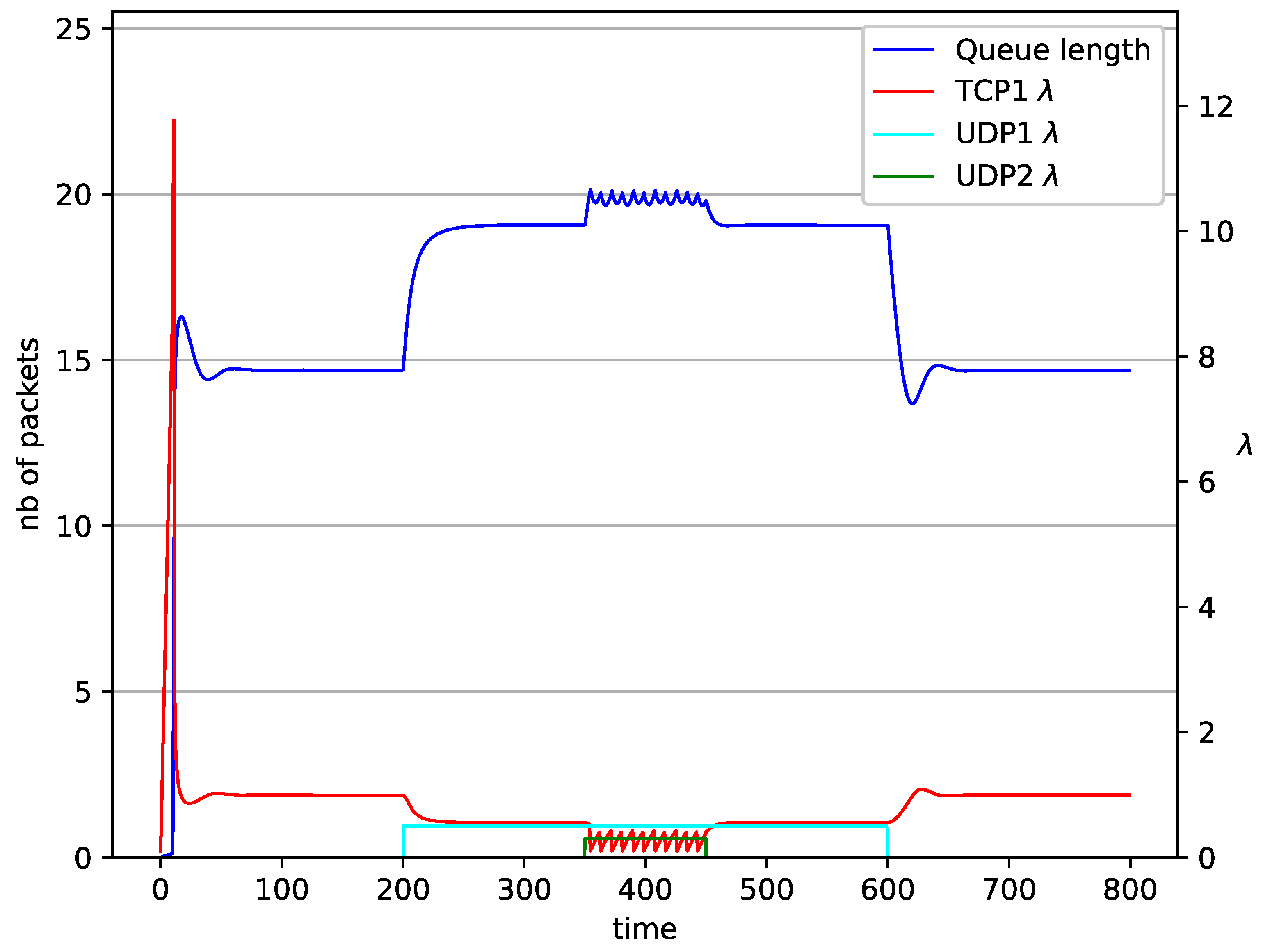
| PI (Simulation) [18] | Study of the TCP/AQM mechanisms based on PI controllers |
| PID (Simulation) [19] | Evaluation of the AQM based on non-integer order PID controller |
| (Fluid-Flow) [20] | First application of non-integer order controller to an AQM strategy |
| (Fluid-Flow/Simulation) [21] | Fluid flow approximation and discrete-event simulation to investigate the influence of the AQM policy based on non-integer order controller on the packet loss probability, the queue length and its variability |
| (Simulation) [22] | Model of AQM mechanism based on non-integer order controller |
| (Simulation) [23] | Finding optimal parameters of the non-integer order controller used as AQM mechanisms. The optimization was made by using the well-known Hooke and Jeeves direct search method applied for minimization of a multivariate score function |
| Adapted (Simulation) [24] | Choice of non-integer order controller parameters based on machine learning algorithms. The controller parameters automatically adjust to network traffic parameters (traffic intensity and self-similarity) |
| TCP (Diffusion) [17] | The diffusion approximation model of the simple TCP traffic. Evaluation (in close loop scenario) of the effectiveness of active queue management (AQM) mechanisms based non-integer order controller |
| TCP (Combined Diffusion and Simulation) [25] | Combined diffusion approximation and simulation model based on non-integer order controller |
| Proportional term | |
| Integral term | |
| Integral order | |
| Error in current slot | |
| Actual queue length | |
| q | Desired queue length |
| Intensity of the input traffic | |
| Intensity of packet processing and dispatching | |
| Variance of interarrival time distribution | |
| Variance of service time distribution | |
| Squared coefficient of variation of interarrival time distribution | |
| Squared coefficient of variation of service time distribution | |
| Diffusion process | |
| Diffusion parameter; is the mean value of changes of during | |
| Diffusion parameter; is the variance of changes of during | |
| Probability density that the process will be in state x at time t, for initial conditions |
| Setpoint | Type of Controller | ||||
|---|---|---|---|---|---|
| 1 | 0.0001 | 0.005 | −0.4 | 10 | non integer order controller |
| 2 | 0.0001 | 0.005 | −1.0 | 10 | classical controller |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marek, D.; Domański, A.; Domańska, J.; Szyguła, J.; Czachórski, T.; Klamka, J. Diffusion Model of a Non-Integer Order PIγ Controller with TCP/UDP Streams. Entropy 2021, 23, 619. https://doi.org/10.3390/e23050619
Marek D, Domański A, Domańska J, Szyguła J, Czachórski T, Klamka J. Diffusion Model of a Non-Integer Order PIγ Controller with TCP/UDP Streams. Entropy. 2021; 23(5):619. https://doi.org/10.3390/e23050619
Chicago/Turabian StyleMarek, Dariusz, Adam Domański, Joanna Domańska, Jakub Szyguła, Tadeusz Czachórski, and Jerzy Klamka. 2021. "Diffusion Model of a Non-Integer Order PIγ Controller with TCP/UDP Streams" Entropy 23, no. 5: 619. https://doi.org/10.3390/e23050619
APA StyleMarek, D., Domański, A., Domańska, J., Szyguła, J., Czachórski, T., & Klamka, J. (2021). Diffusion Model of a Non-Integer Order PIγ Controller with TCP/UDP Streams. Entropy, 23(5), 619. https://doi.org/10.3390/e23050619







