A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0-1 Knapsack Problems
Abstract
1. Introduction
2. Background
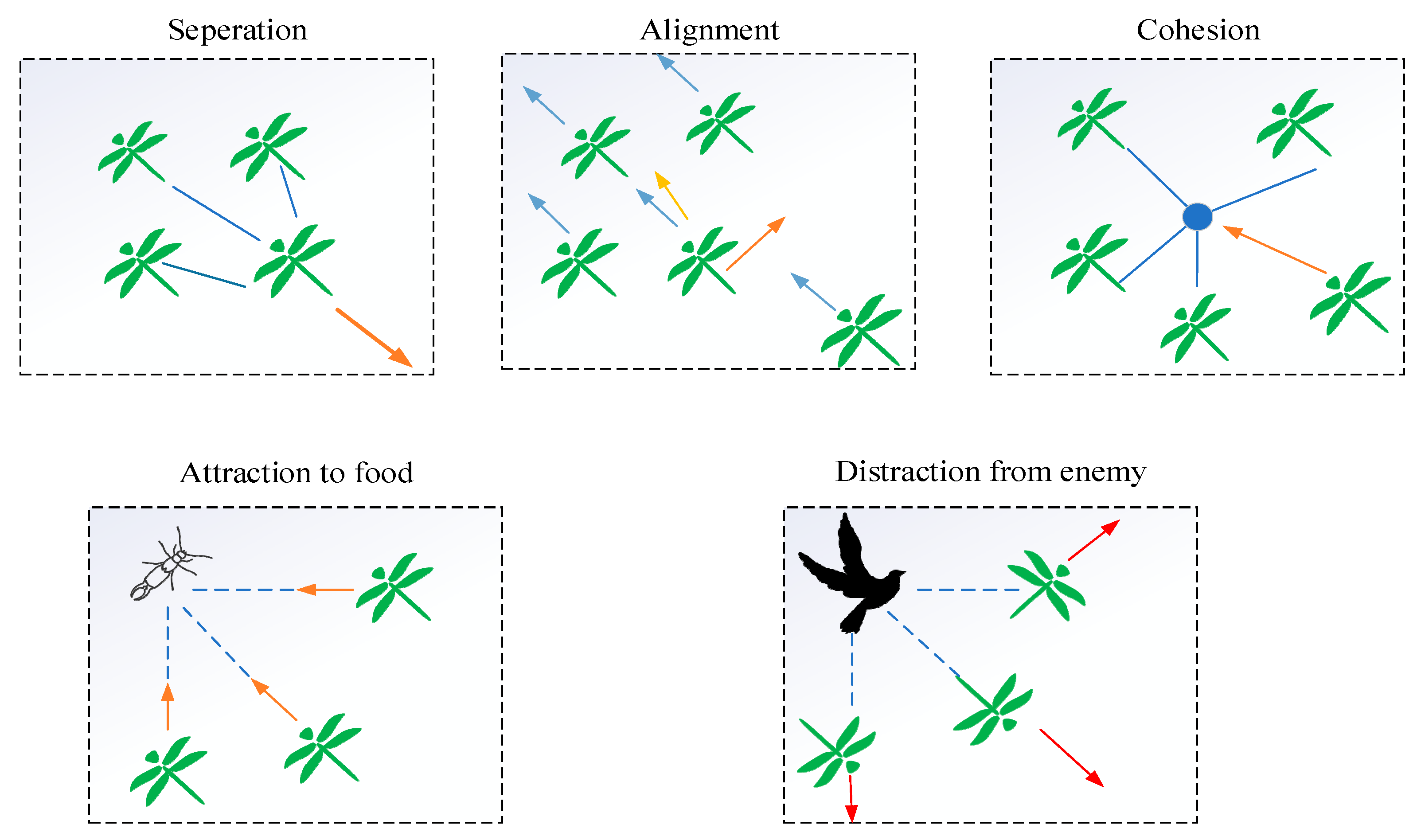
2.1. The Dragonfly Algorithm
2.2. Binary Dragonfly Algorithm
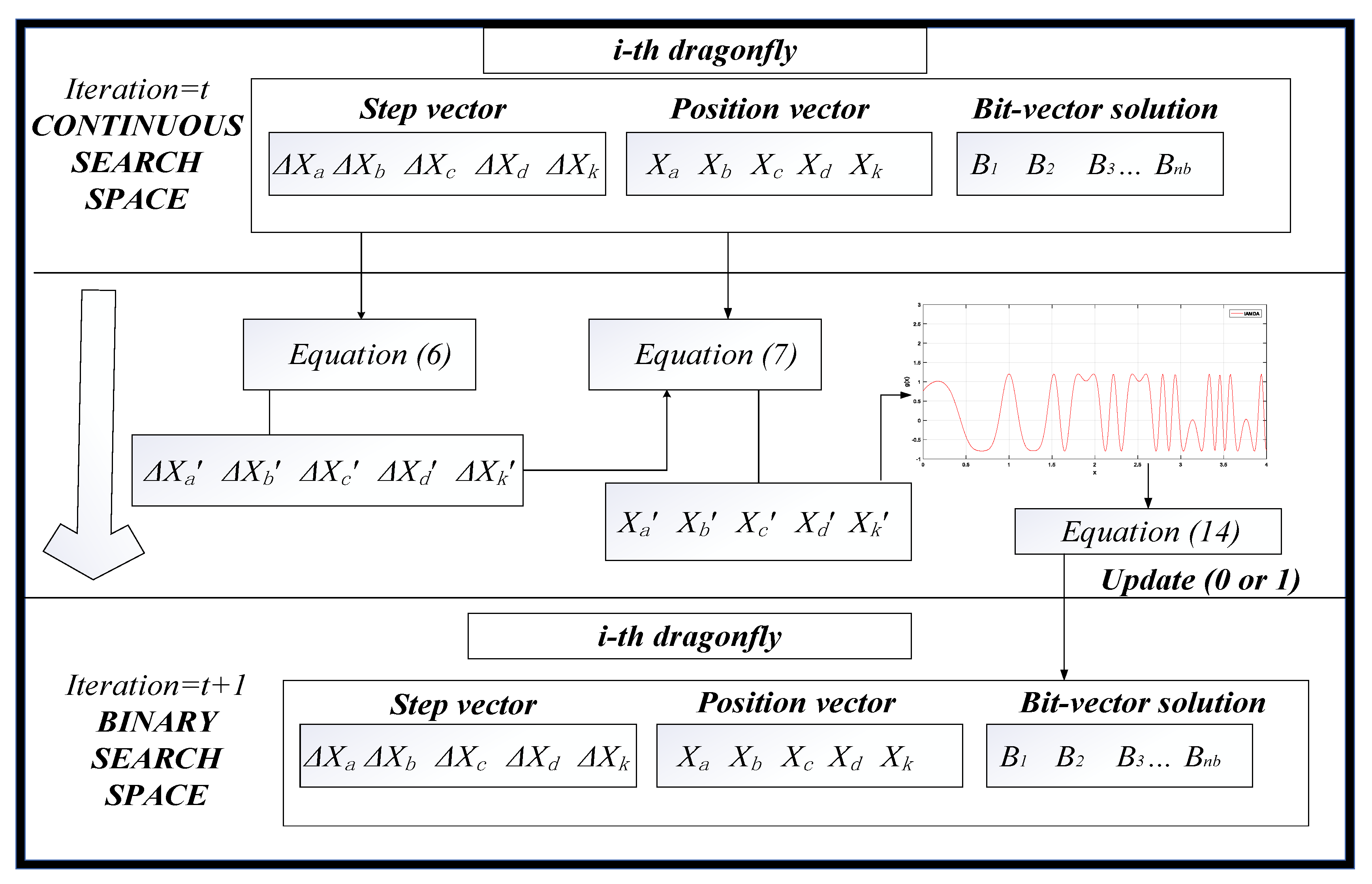
3. Improved Angle Modulated Dragonfly Algorithm (IAMDA)
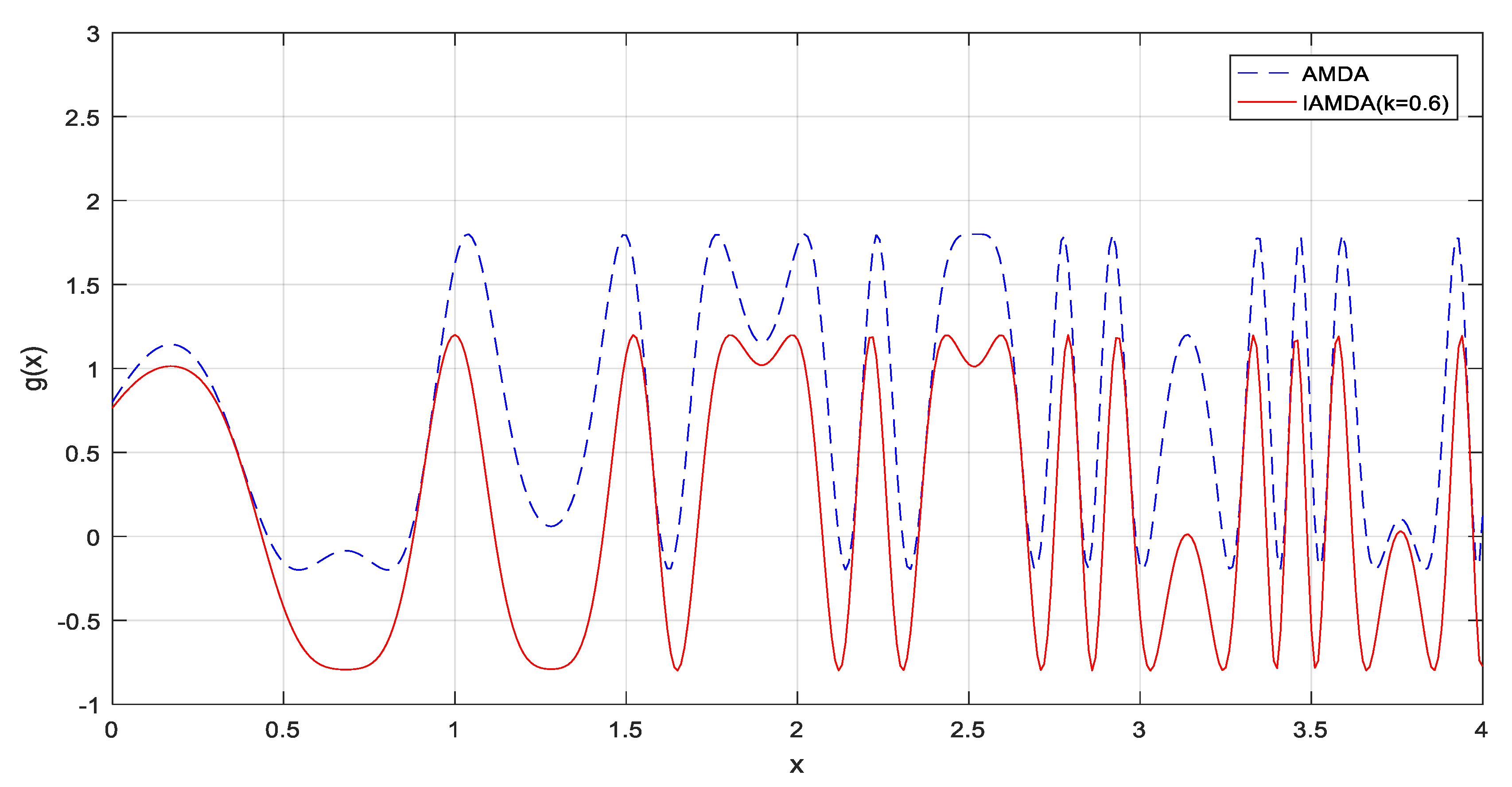
3.1. AMDA
3.2. IAMDA
4. Experimental Results and Discussion
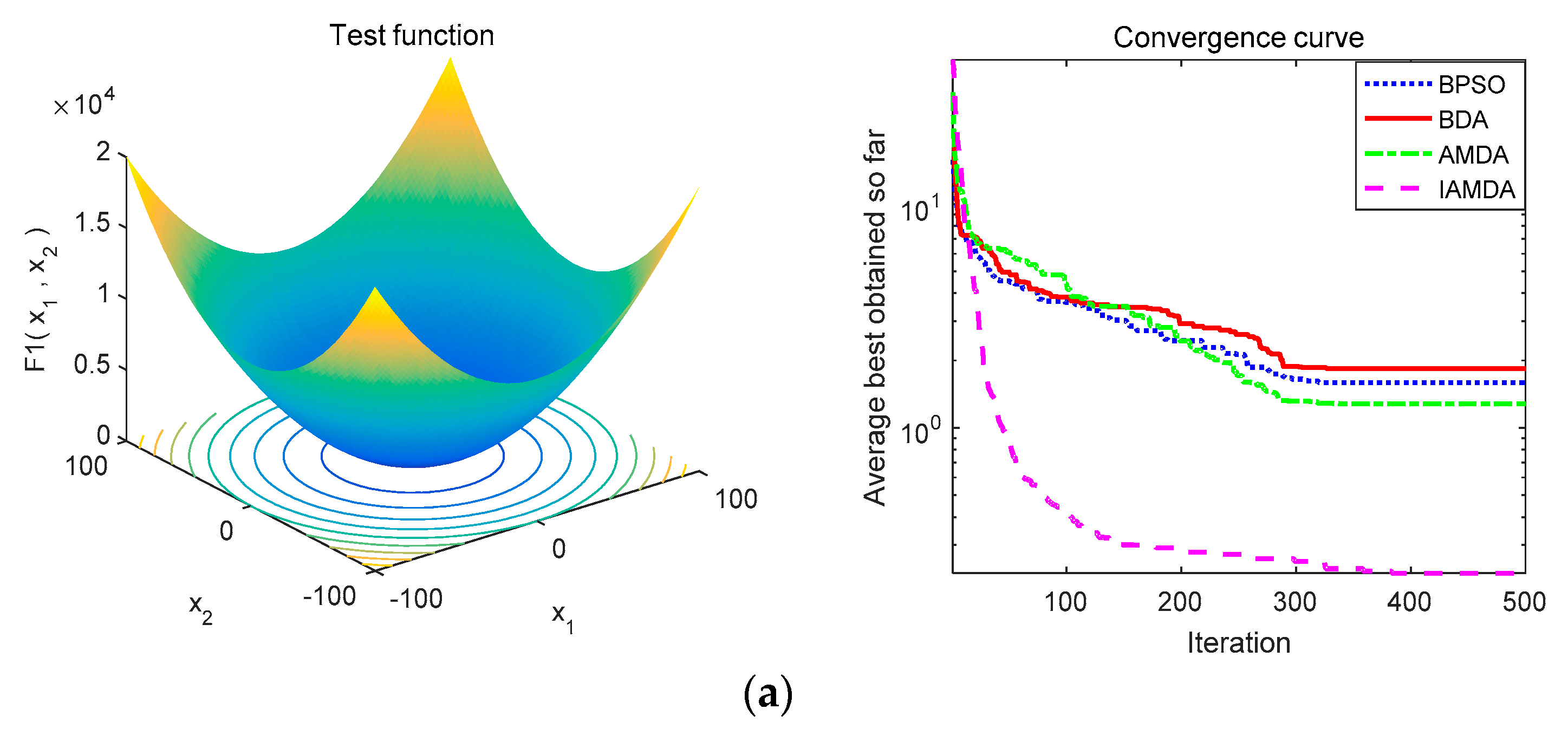
4.1. Test Functions and Parameter Settings
4.2. IAMDA Performance on Unimodal and Multimodal Benchmark Functions
4.3. Zero-One Knapsack Problems
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—part I. Orsa J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—part II. Orsa J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Sampson, J.R. Adaptation in Natural and Artificial Systems (John H. Holland); Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1975. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithm; MIT press: Cambridge, MA, USA, 1998. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Farmer, J.D.; Packard, N.H.; Perelson, A.S. The immune system, adaptation, and machine learning. Phys. D Nonlinear Phenom. 1986, 22, 187–204. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 6 August 2002; pp. 1942–1948. [Google Scholar]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Liu, X.-F.; Zhan, Z.-H.; Deng, J.D.; Li, Y.; Gu, T.; Zhang, J. An energy efficient ant colony system for virtual machine placement in cloud computing. IEEE Trans. Evol. Comput. 2016, 22, 113–128. [Google Scholar] [CrossRef]
- Chen, Z.-G.; Zhan, Z.-H.; Lin, Y.; Gong, Y.-J.; Gu, T.-L.; Zhao, F.; Yuan, H.-Q.; Chen, X.; Li, Q.; Zhang, J. Multiobjective cloud workflow scheduling: A multiple populations ant colony system approach. IEEE Trans. Cybern. 2018, 49, 2912–2926. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly Algorithms for Multimodal Optimization. International Symposium on Stochastic Algorithms; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Li, X. A New Intelligent Optimization-Artificial Fish Swarm Algorithm. Doctor Thesis, Zhejiang University, Zhejiang, China, 2003. [Google Scholar]
- Pan, W.-T. A new fruit fly optimization algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Xu, L.; Jia, H.; Lang, C.; Peng, X.; Sun, K. A novel method for multilevel color image segmentation based on dragonfly algorithm and differential evolution. IEEE Access 2019, 7, 19502–19538. [Google Scholar] [CrossRef]
- Tharwat, A.; Gabel, T.; Hassanien, A.E. Parameter optimization of support vector machine using dragonfly algorithm. In International Conference on Advanced Intelligent Systems and Informatics; Springer: Berlin/Heidelberg, Germany, 2017; pp. 309–319. [Google Scholar]
- Zhang, Z.; Hong, W.-C. Electric load forecasting by complete ensemble empirical mode decomposition adaptive noise and support vector regression with quantum-based dragonfly algorithm. Nonlinear Dyn. 2019, 98, 1107–1136. [Google Scholar] [CrossRef]
- Amroune, M.; Bouktir, T.; Musirin, I. Power system voltage stability assessment using a hybrid approach combining dragonfly optimization algorithm and support vector regression. Arab. J. Sci. Eng. 2018, 43, 3023–3036. [Google Scholar] [CrossRef]
- Sureshkumar, K.; Ponnusamy, V. Power flow management in micro grid through renewable energy sources using a hybrid modified dragonfly algorithm with bat search algorithm. Energy 2019, 181, 1166–1178. [Google Scholar] [CrossRef]
- Suresh, V.; Sreejith, S. Generation dispatch of combined solar thermal systems using dragonfly algorithm. Computing 2017, 99, 59–80. [Google Scholar] [CrossRef]
- Babayigit, B. Synthesis of concentric circular antenna arrays using dragonfly algorithm. Int. J. Electron. 2018, 105, 784–793. [Google Scholar] [CrossRef]
- Hammouri, A.I.; Samra, E.T.A.; Al-Betar, M.A.; Khalil, R.M.; Alasmer, Z.; Kanan, M. A dragonfly algorithm for solving traveling salesman problem. In Proceedings of the 2018 8th IEEE International Conference on Control System, Computing and Engineering (ICCSCE), Penang, Malaysia, 23–25 November 2018; pp. 136–141. [Google Scholar]
- Mafarja, M.M.; Eleyan, D.; Jaber, I.; Hammouri, A.; Mirjalili, S. Binary dragonfly algorithm for feature selection. In Proceedings of the 2017 International Conference on New Trends in Computing Sciences (ICTCS), Amman, Jordan, 11–13 October 2017; pp. 12–17. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4108. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.-S. Binary bat algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Hammouri, A.I.; Mafarja, M.; Al-Betar, M.A.; Awadallah, M.A.; Abu-Doush, I. An improved dragonfly algorithm for feature selection. Knowl. Based Syst. 2020, 203, 106131. [Google Scholar] [CrossRef]
- Proakis, J.G.; Salehi, M.; Zhou, N.; Li, X. Communication Systems Engineering; Prentice Hall New Jersey: Hoboken, NJ, USA, 1994; Volume 2. [Google Scholar]
- Pampara, G.; Franken, N.; Engelbrecht, A. Combining particle swarm optimization with angle modulation to solve binary problems. IEEE Congr. Evol. Comput. 2005, 1, 89–96. [Google Scholar]
- Pampara, G.; Engelbrecht, A.; Franken, N. Binary differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation Vancouver, BC, Canada, 16–21 July 2006; pp. 1873–1879. [Google Scholar]
- Dong, J.; Wang, Z.; Mo, J. A Phase Angle-Modulated Bat Algorithm with Application to Antenna Topology Optimization. Appl. Sci. 2021, 11, 2243. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, Herds, and Schools: A Distributed Behavioral Model. ACM SIGGRAPH Comput Gr. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Too, J.; Abdullah, A.R.; Mohd Saad, N.; Mohd Ali, N.; Tee, W. A New Competitive Binary Grey Wolf Optimizer to Solve the Feature Selection Problem in EMG Signals Classification. Computers 2018, 7, 58. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Tsai, H.C.; Tyan, Y.Y.; Wu, Y.W.; Lin, Y.H. Isolated particle swarm optimization with particle migration and global best adoption. Eng. Optim. 2012, 44, 1405–1424. [Google Scholar] [CrossRef]
- Kashan, M.H.; Kashan, A.H.; Nahavandi, N. A novel differential evolution algorithm for binary optimization. Comput. Optim. Appl. 2013, 55, 481–513. [Google Scholar]
- Yılmaz, S.; Küçüksille, E.U. A new modification approach on bat algorithm for solving optimization problems. Appl. Soft Comput. 2015, 28, 259–275. [Google Scholar] [CrossRef]
- Hu, T.; Kahng, A.B. Linear and Integer Programming Made Easy; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Mavrotas, G.; Diakoulaki, D.; Kourentzis, A. Selection among ranked projects under segmentation, policy and logical constraints. Eur. J. Oper. Res. 2008, 187, 177–192. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, X.-F.; Gong, D.-W. A return-cost-based binary firefly algorithm for feature selection. Inf. Sci. 2017, 418, 561–574. [Google Scholar] [CrossRef]
- Zhang, L.; Shan, L.; Wang, J. Optimal feature selection using distance-based discrete firefly algorithm with mutual information criterion. Neural Comput. Appl. 2017, 28, 2795–2808. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid binary ant lion optimizer with rough set and approximate entropy reducts for feature selection. Soft Comput. 2019, 23, 6249–6265. [Google Scholar] [CrossRef]
- Kulkarni, A.J.; Shabir, H. Solving 0–1 knapsack problem using cohort intelligence algorithm. Int. J. Mach. Learn. Cybern. 2016, 7, 427–441. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, F.-M.; Zhan, R.; Wang, S.; Zhang, C. A binary wolf pack algorithm for solving 0-1 knapsack problem. Syst. Eng. Electron. 2014, 36, 1660–1667. [Google Scholar]
- Zou, D.; Gao, L.; Li, S.; Wu, J. Solving 0–1 knapsack problem by a novel global harmony search algorithm. Appl. Soft Comput. 2011, 11, 1556–1564. [Google Scholar] [CrossRef]




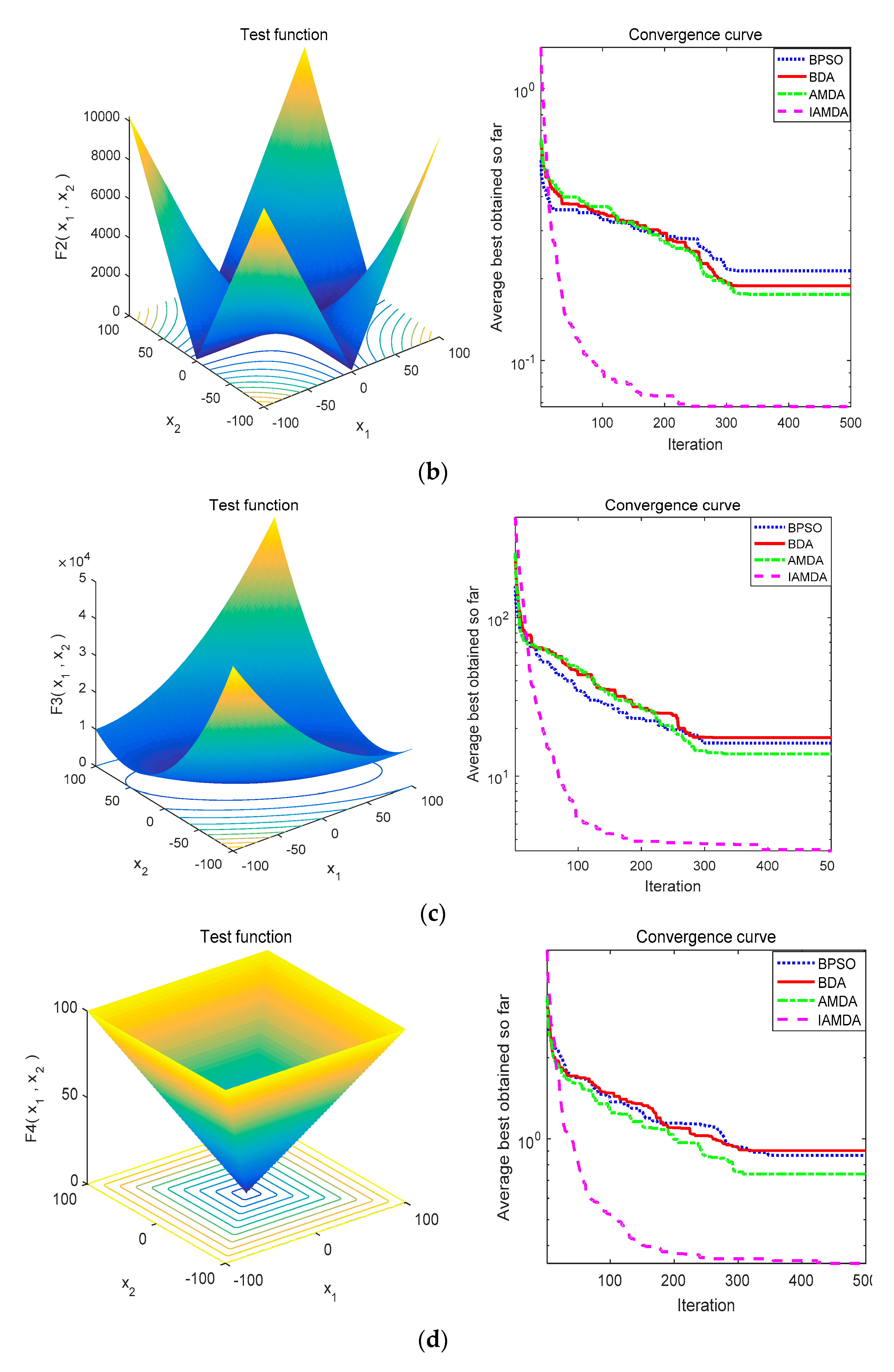
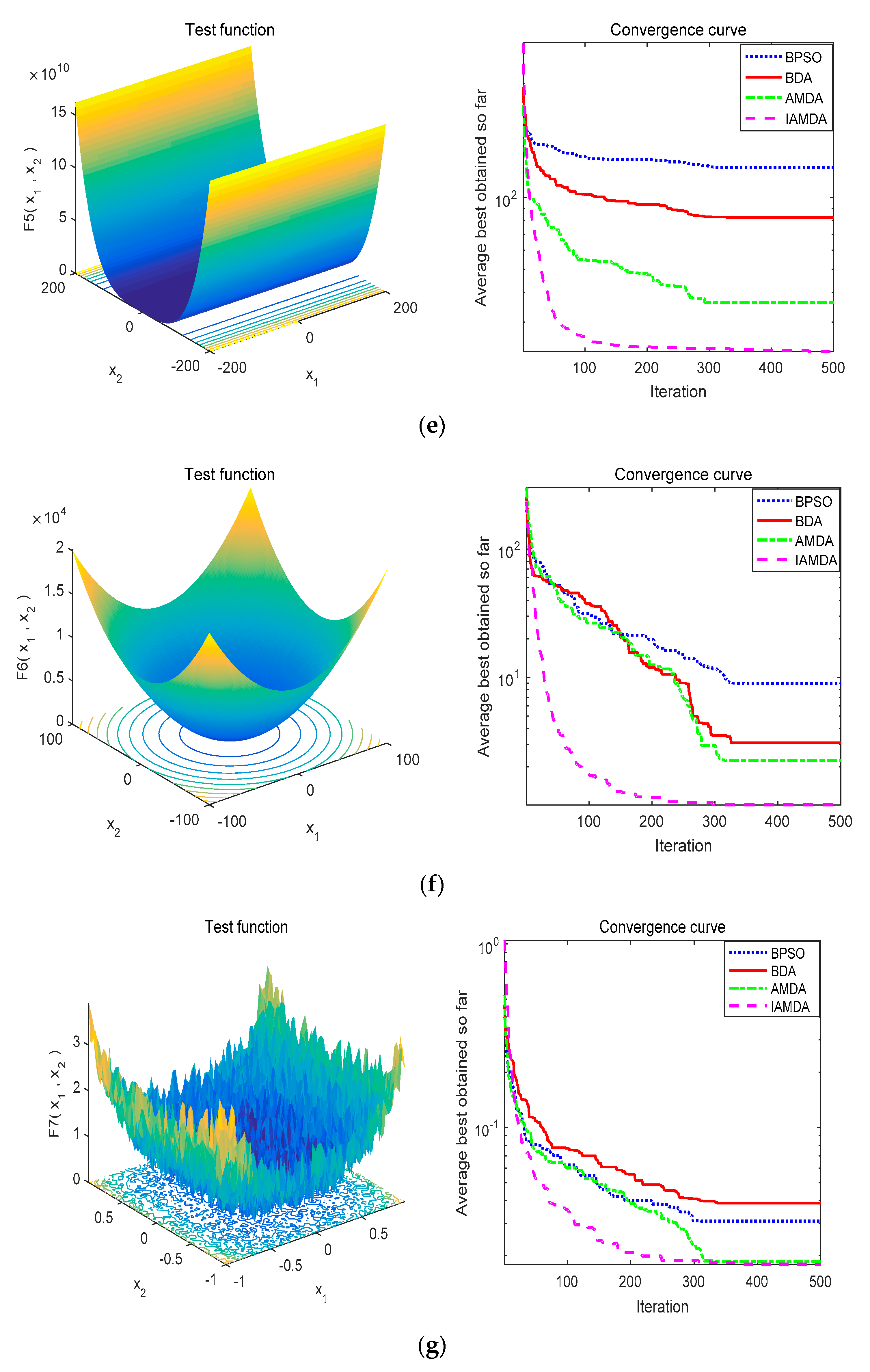
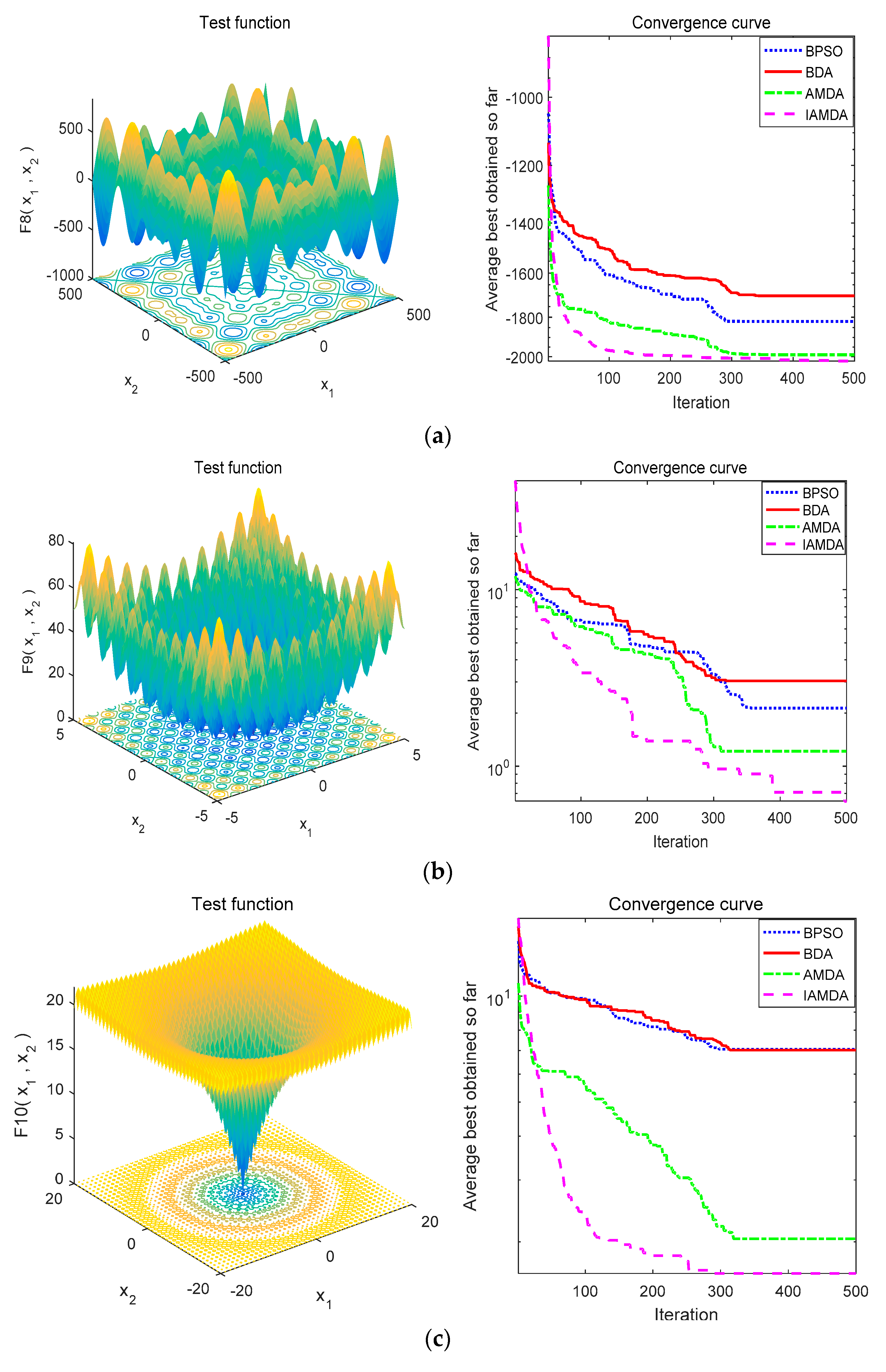
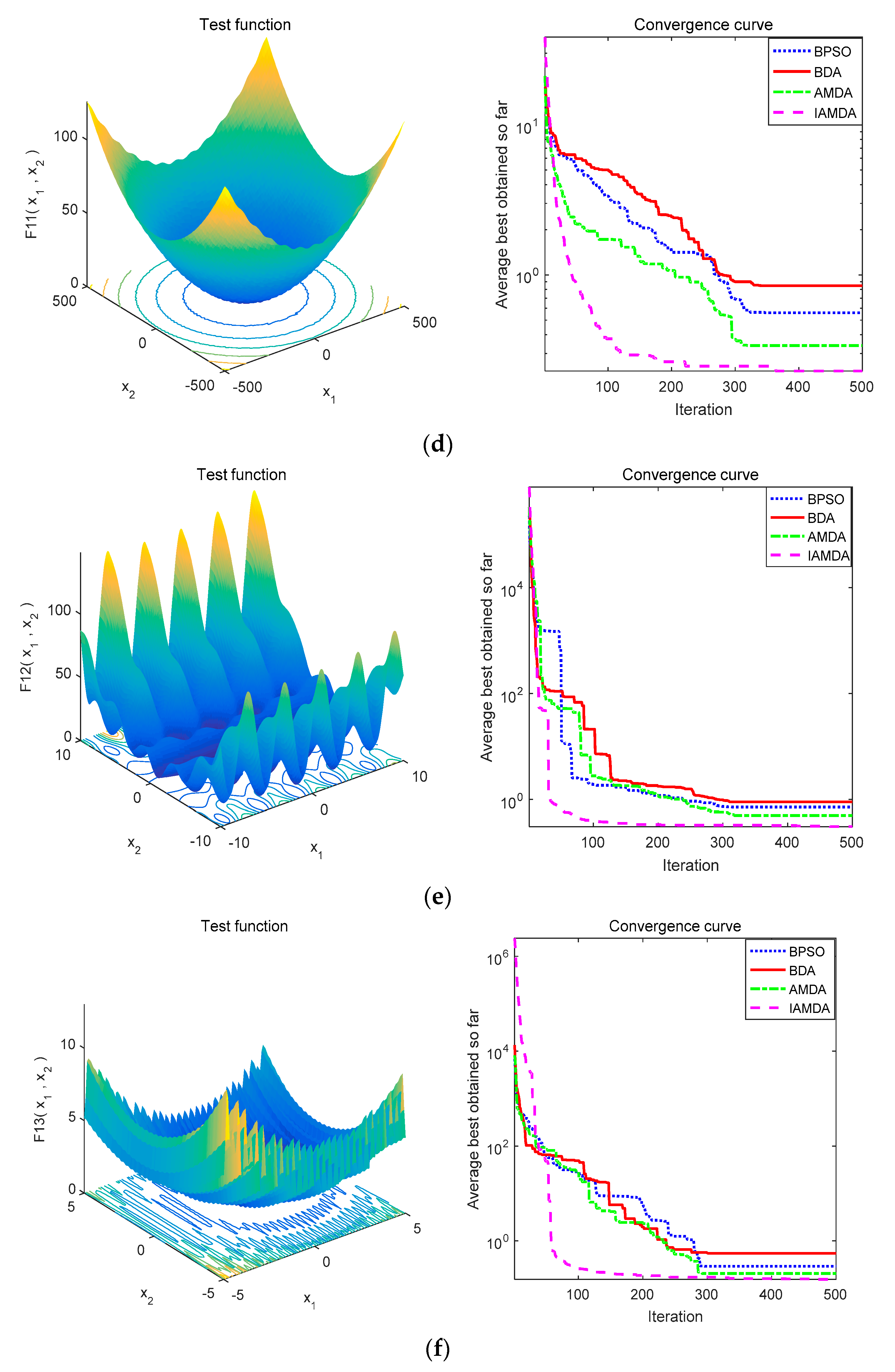

| Algorithms | Parameters | Values |
|---|---|---|
| IAMDA | Number of dragonflies | 30 |
| (a, b, c, d, k) | [−1,1] | |
| Max iteration | 500 | |
| Stopping criterion | Max iteration | |
| AMDA | Number of dragonflies | 30 |
| (a, b, c, d) | [−1,1] | |
| Max iteration | 500 | |
| Stopping criterion | Max iteration | |
| BDA | Number of dragonflies | 30 |
| Max iteration | 500 | |
| Stopping criterion | Max iteration | |
| BPSO | Number of particles | 30 |
| C1, C2 | 2 | |
| w | Decreased linearly from 0.9 to 0.4 | |
| Max velocity | 0.6 | |
| Max iteration | 500 | |
| Stopping criterion | Max iteration |
| Function | Expression | n | Range | fmin |
|---|---|---|---|---|
| Sphere | 5 | [−100,100] | 0 | |
| Schwefel 2.22 | 5 | [−10,10] | 0 | |
| Schwefel 1.2 | 5 | [−100,100] | 0 | |
| Schwefel 2.21 | 5 | [−100,100] | 0 | |
| Rosenbrock | 5 | [−30,30] | 0 | |
| Step | 5 | [−100,100] | 0 | |
| Quartic | 5 | [−1.28,1.28] | 0 |
| Function | Expression | n | Range | fmin |
|---|---|---|---|---|
| Schwefel | 5 | [−500,500] | −418.9829 × 5 | |
| Rastrigrin | 5 | [−5.12,5.12] | 0 | |
| Ackley | 5 | [−32.32] | 0 | |
| Griewank | 5 | [−600,600] | 0 | |
| Penalty# | 5 | [−50,50] | 0 | |
| Penalized 1.2 | 5 | [−50,50] | 0 |
| f | Metric | IAMDA | AMDA | BDA | BPSO |
|---|---|---|---|---|---|
| f1 | Mean | 0.2244 | 1.2797 | 1.8412 | 1.5942 |
| SD | 0.1599 | 0.9732 | 1.6625 | 1.3609 | |
| Med | 0.1510 | 0.6655 | 1.6669 | 1.3278 | |
| Rank | 1 | 2 | 4 | 3 | |
| f2 | Mean | 0.0676 | 0.1751 | 0.1883 | 0.2137 |
| SD | 0.0216 | 0.0913 | 0.1004 | 0.0882 | |
| Med | 0.0585 | 0.1423 | 0.2765 | 0.2702 | |
| Rank | 1 | 2 | 3 | 4 | |
| f3 | Mean | 3.4279 | 15.1108 | 19.8865 | 21.8408 |
| SD | 1.9467 | 14.1566 | 22.7839 | 11.6904 | |
| Med | 2.4599 | 18.7306 | 19.1034 | 23.0999 | |
| Rank | 1 | 2 | 3 | 4 | |
| f4 | Mean | 0.3383 | 0.6840 | 0.8205 | 0.8701 |
| SD | 0.0988 | 0.4461 | 0.3266 | 0.3559 | |
| Med | 0.3446 | 0.6906 | 0.9330 | 0.9568 | |
| Rank | 1 | 2 | 3 | 4 | |
| f5 | Mean | 22.6485 | 36.2572 | 82.5599 | 133.7547 |
| SD | 3.0791 | 10.9330 | 11.4133 | 9.5546 | |
| Med | 20.4659 | 30.0536 | 71.9376 | 124.0569 | |
| Rank | 1 | 2 | 3 | 4 | |
| f6 | Mean | 1.0166 | 2.2309 | 3.0771 | 8.9318 |
| SD | 0.5524 | 11.0604 | 9.7121 | 13.7554 | |
| Med | 1.7111 | 3.6660 | 3.1051 | 11.9169 | |
| Rank | 1 | 2 | 3 | 4 | |
| f7 | Mean | 0.0179 | 0.0186 | 0.0387 | 0.0309 |
| SD | 0.0119 | 0.0156 | 0.0235 | 0.0216 | |
| Med | 0.0163 | 0.0182 | 0.0327 | 0.0335 | |
| Rank | 1 | 2 | 4 | 3 | |
| f8 | Mean | −2.0236e+03 | −1.9898e+03 | −1.7002e+03 | −1.8200e+03 |
| SD | 53.4828 | 170.8601 | 147.8324 | 101.7015 | |
| Med | −2.0207e+03 | −1.8977e+03 | −1.6972e+03 | −1.8307e+03 | |
| Rank | 1 | 2 | 4 | 3 | |
| f9 | Mean | 0.6359 | 1.2144 | 3.0472 | 2.1303 |
| SD | 1.7575 | 5.5272 | 3.7159 | 5.0115 | |
| Med | 0.7802 | 0.8932 | 3.5783 | 2.3890 | |
| Rank | 1 | 2 | 4 | 3 | |
| f10 | Mean | 1.6269 | 2.0406 | 7.0218 | 7.0607 |
| SD | 0.7271 | 2.4153 | 2.5491 | 2.4290 | |
| Med | 1.4469 | 2.3801 | 6.7427 | 7.4276 | |
| Rank | 1 | 2 | 3 | 4 | |
| f11 | Mean | 0.2291 | 0.3381 | 0.8498 | 0.5594 |
| SD | 0.2448 | 1.2435 | 1.6054 | 1.1212 | |
| Med | 0.2821 | 0.4894 | 0.7234 | 0.4527 | |
| Rank | 1 | 2 | 4 | 3 | |
| f12 | Mean | 0.3092 | 0.5014 | 0.8959 | 0.7153 |
| SD | 0.1880 | 0.3313 | 0.5359 | 0.4502 | |
| Med | 0.3947 | 0.4381 | 0.8416 | 0.7652 | |
| Rank | 1 | 2 | 4 | 3 | |
| f13 | Mean | 0.1547 | 0.2057 | 0.5492 | 0.2908 |
| SD | 0.0675 | 0.7528 | 2.2227 | 1.2097 | |
| Med | 0.1654 | 0.2089 | 0.5847 | 0.1755 | |
| Rank | 1 | 2 | 4 | 3 |
| f | AMDA and IAMDA | BDA and IAMDA | BPSO and IAMDA | |||
|---|---|---|---|---|---|---|
| t | Sig. | t | Sig. | t | Sig. | |
| f1 | 9.2046 | IAMDA | 8.3274 | IAMDA | 8.5994 | IAMDA |
| f2 | 9.8566 | IAMDA | 10.1103 | IAMDA | 13.8404 | IAMDA |
| f3 | 7.0330 | IAMDA | 6.1916 | IAMDA | 13.3650 | IAMDA |
| f4 | 6.5086 | IAMDA | 12.1566 | IAMDA | 12.3855 | IAMDA |
| f5 | 10.3097 | IAMDA | 43.5972 | IAMDA | 95.2107 | IAMDA |
| f6 | 0.9433 | N.S. | 1.9721 | IAMDA | 4.9460 | IAMDA |
| f7 | 0.3069 | N.S. | 6.7927 | IAMDA | 4.5347 | IAMDA |
| f | AMDA and IAMDA | BDA and IAMDA | BPSO and IAMDA | |||
|---|---|---|---|---|---|---|
| t | Sig. | t | Sig. | t | Sig. | |
| f8 | 1.9640 | IAMDA | 17.6961 | IAMDA | 15.2422 | IAMDA |
| f9 | 0.8580 | N.S. | 5.0462 | IAMDA | 2.4206 | IAMDA |
| f10 | 1.4109 | N.S. | 17.5076 | IAMDA | 18.4356 | IAMDA |
| f11 | 0.7398 | N.S. | 3.2879 | IAMDA | 2.4759 | IAMDA |
| f12 | 4.3404 | IAMDA | 8.8868 | IAMDA | 7.1604 | IAMDA |
| f13 | 0.5805 | N.S. | 1.9661 | IAMDA | 2.9663 | IAMDA |
| No. | D | Parameter (w, p, C) | Opt |
|---|---|---|---|
| k1 | 10 | w = (95,4,60,32,23,72,80,62,65,46); p = (55,10,47,5,4,50,8,61,85,87); C = 269 | 295 |
| k2 | 20 | w = (92,4,43,83,84,68,92,82,6,44,32,18,56,83,25,96,70,48,14,58); p = (44,46,90,72,91,40,75,35,8,54,78,40,77,15,61,17,75,29,75,63); C = 878 | 1024 |
| k3 | 50 | w = (80,82,85,70,72,70,66,50,55,25,50,55,40,48,59,32,22,60,30, 32,40,38,35,32,25,28,30,22,50,30,45,30,60,50,20,65,20,25,30, 10,20,25,15,10,10,10,4,4,2,1); p = (220,208,198,192,180,180,165,162,160,158,155,130,125, 122,120,118,115,110,105,101,100,100,98,96,95,90,88,82,80,77,75,7,72,70,69,66,65,63,60,58,56,50,30,20,15, 0,8,5,3,1); C = 1000 | 3103 |
| k4 | 80 | w = (40, 27,5,21,51, 16, 42, 18, 52, 28, 57, 34, 44, 43,52,55,53,42, 47, 56,57,44, 16,2, 12, 9, 40, 23, 56, 3, 39,16, 54, 36, 52,5,53, 48, 23, 47, 41, 49, 22, 42, 10, 16, 53, 58, 40, 1,43,56,40,32,44,35, 37, 45, 52, 56, 40, 2, 23,49, 50, 26, 11,35, 32, 34, 58, 6, 52,26,31, 23, 4, 52, 53, 19); p = (199,194,193,191,189,178,174,169,164,164,161,158,157, 154,152,152,149,142,131,125,124,124,124,122,119,116,114,113,111,110,109,100,97,94,91,82,82,81,80,80,80,79,77,76,74, 72, 71, 70, 69,68, 65, 65, 61, 56, 55, 54, 53, 47, 47, 46, 41, 36, 34, 32, 32,30, 29, 29, 26, 25, 23, 22, 20, 11, 10, 9,5,4,3, 1); C = 1173 | 5183 |
| k5 | 100 | w = (54, 95, 36, 18,4, 71,83, 16, 27, 84, 88, 45, 94, 64, 14, 80, 4, 23, 75, 36, 90, 20, 77, 32, 58, 6, 14, 86, 84, 59,71, 21, 30, 22, 96, 49, 81, 48, 37, 28, 6, 84,19,55,88,38,51,52,79,55,70,53,64,99,61,86,1,64,32,60,42,45,34,22,49,37,33,1,78,43,85,24,96,32,99,57,23,8,10,74,59,89,95,40,46,65,6,89,84,83,6,19,45, 59, 26, 13, 8, 26, 5, 9); p = (297, 295, 293, 292, 291, 289, 284, 284, 283, 283, 281, 280, 279, 277, 276, 275, 273,264, 260, 257, 250, 236, 236, 235, 235, 233, 232, 232, 228, 218, 217, 214, 211, 208, 205, 204, 203, 201, 196, 194,193, 193, 192, 191, 190, 187, 187, 184, 184, 184, 181, 179, 176, 173, 172, 171, 160, 128, 123, 114, 113, 107, 105,101, 100, 100, 99, 98, 97, 94, 94, 93, 91, 80, 74, 73, 72, 63, 63, 62, 61, 60, 56, 53, 52, 50, 48, 46, 40, 40, 35, 28, 22,22, 18, 15, 12,11, 6,5); C = 3818; | 15,170 |
| No. | D | C | Total Values |
|---|---|---|---|
| k6 | 200 | 1948.5 | 15,132 |
| k7 | 300 | 2793.5 | 22,498 |
| k8 | 500 | 4863.5 | 37,519 |
| k9 | 800 | 7440.5 | 59,791 |
| k10 | 1000 | 9543.5 | 75,603 |
| k11 | 1200 | 11,267 | 90,291 |
| k12 | 1500 | 14,335 | 111,466 |
| No. | Alg. | Best | Worst | Mean | SD | Time |
|---|---|---|---|---|---|---|
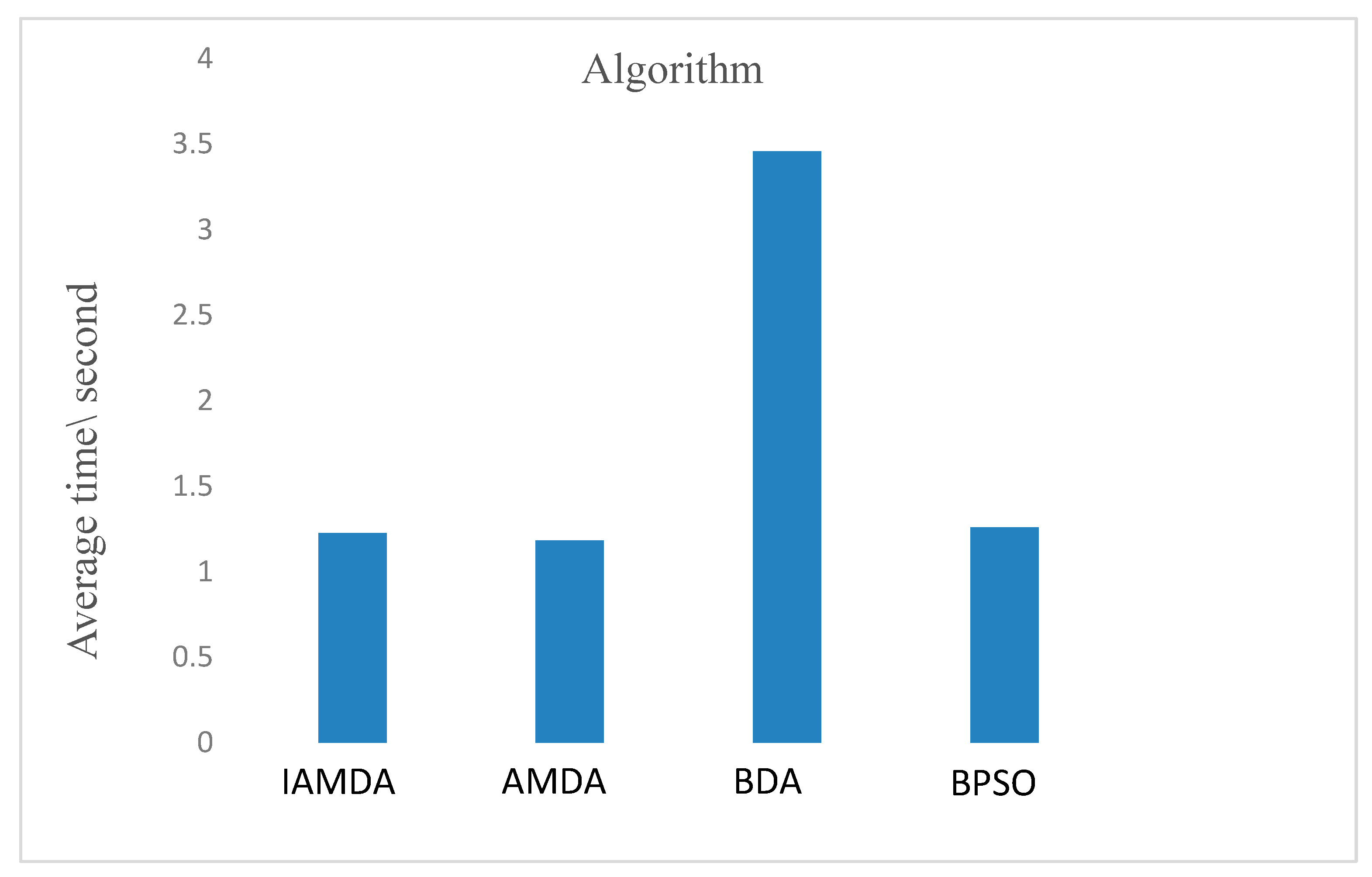
| k1 | IAMDA | 295 | 295 | 295 | 0 | 0.2175 |
| AMDA | 295 | 295 | 295 | 0 | 0.2112 | |
| BDA | 295 | 295 | 295 | 0 | 0.9646 | |
| BPSO | 295 | 295 | 295 | 0 | 0.0389 | |
| k2 | IAMDA | 1024 | 1018 | 1.0231e+03 | 2.1981 | 0.2858 |
| AMDA | 1024 | 1013 | 1.0226e+03 | 3.5452 | 0.2766 | |
| BDA | 1024 | 1018 | 1.0225e+03 | 2.6656 | 1.0450 | |
| BPSO | 1024 | 1024 | 1024 | 0 | 0.0618 | |
| k3 | IAMDA | 3076 | 2991 | 3.0308e+03 | 21.1636 | 0.2863 |
| AMDA | 3064 | 2969 | 3.0367e+03 | 29.6729 | 0.2782 | |
| BDA | 3074 | 2970 | 3.0203e+03 | 30.0559 | 1.0461 | |
| BPSO | 3074 | 2957 | 2.9978e+03 | 26.6114 | 0.1460 | |
| k4 | IAMDA | 4991 | 4763 | 4.9131e+03 | 66.2322 | 0.3929 |
| AMDA | 5090 | 4678 | 4.8918e+03 | 115.7004 | 0.3796 | |
| BDA | 5041 | 4705 | 4.8880e+03 | 105.7243 | 1.2035 | |
| BPSO | 4695 | 4348 | 4.4823e+03 | 99.1591 | 0.2175 | |
| k5 | IAMDA | 14,965 | 14,261 | 1.4631e+04 | 166.4238 | 0.3979 |
| AMDA | 15,010 | 14,155 | 1.4626e+04 | 220.8765 | 0.3803 | |
| BDA | 14,986 | 14,149 | 1.4611e+04 | 208.1295 | 1.2696 | |
| BPSO | 13,986 | 13,324 | 1.3595e+04 | 188.0612 | 0.2488 | |
| k6 | IAMDA | 1.3075e+04 | 1.2300e+04 | 1.2632e+04 | 207.7428 | 0.4770 |
| AMDA | 1.2801e+04 | 1.1921e+04 | 1.2498e+04 | 211.4083 | 0.4631 | |
| BDA | 1.2820e+04 | 1.1501e+04 | 1.2316e+04 | 315.2521 | 1.6793 | |
| BPSO | 1.1640e+04 | 1.0951e+04 | 1.1174e+04 | 213.5035 | 0.6185 | |
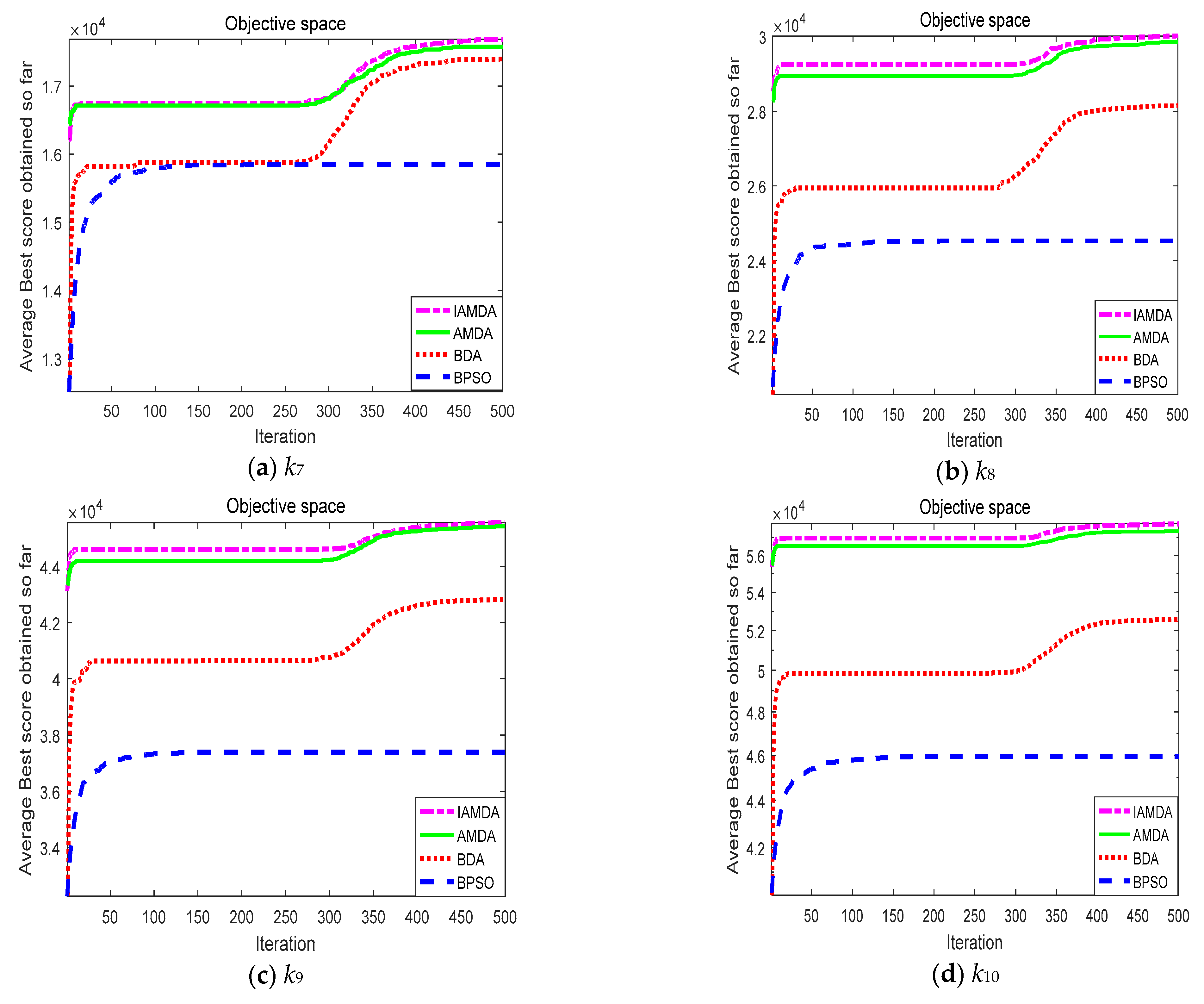
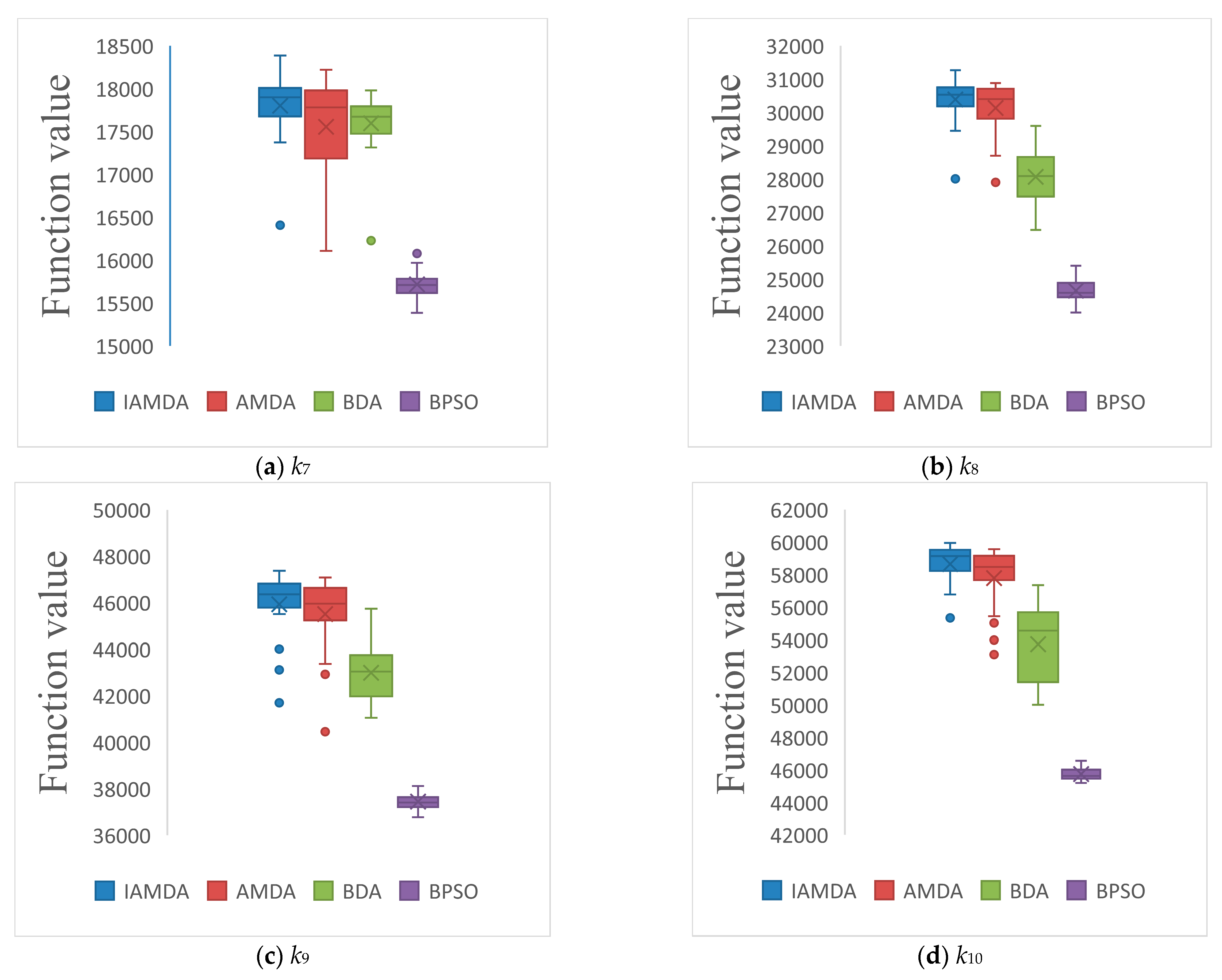
| k7 | IAMDA | 1.8386e+04 | 1.6408e+04 | 1.7800e+04 | 413.3773 | 0.6500 |
| AMDA | 1.8220e+04 | 1.6107e+04 | 1.7595e+04 | 594.7544 | 0.6137 | |
| BDA | 1.7979e+04 | 1.6227e+04 | 1.7554e+04 | 370.3743 | 2.8821 | |
| BPSO | 1.6084e+04 | 1.5385e+04 | 1.5717e+04 | 181.8523 | 0.8482 | |
| k8 | IAMDA | 3.1266e+04 | 2.8010e+04 | 3.0387e+04 | 713.8203 | 0.9952 |
| AMDA | 3.0763e+04 | 2.7902e+04 | 3.0134e+04 | 816.0871 | 0.9457 | |
| BDA | 2.9598e+04 | 2.6478e+04 | 2.8067e+04 | 848.2838 | 3.6978 | |
| BPSO | 2.5404e+04 | 2.3997e+04 | 2.4656e+04 | 328.1345 | 1.3125 | |
| k9 | IAMDA | 4.7364e+04 | 4.1702e+04 | 4.5928e+04 | 1.4190e+03 | 1.7125 |
| AMDA | 4.7078e+04 | 4.0453e+04 | 4.5502e+04 | 1.6564e+03 | 1.7014 | |
| BDA | 4.5734e+04 | 4.1055e+04 | 4.2988e+04 | 1.2721e+03 | 5.3235 | |
| BPSO | 3.8119e+04 | 3.6775e+04 | 3.7448e+04 | 355.7410 | 2.0791 | |
| k10 | IAMDA | 5.9952e+04 | 5.5355e+04 | 5.8646e+04 | 1.3125e+03 | 2.5047 |
| AMDA | 5.9566e+04 | 5.3099e+04 | 5.7783e+04 | 1.8917e+03 | 2.5023 | |
| BDA | 5.7356e+04 | 5.0011e+04 | 5.3727e+04 | 2.3538e+03 | 6.2211 | |
| BPSO | 4.6572e+04 | 4.5209e+04 | 4.5749e+04 | 362.8049 | 2.6863 | |
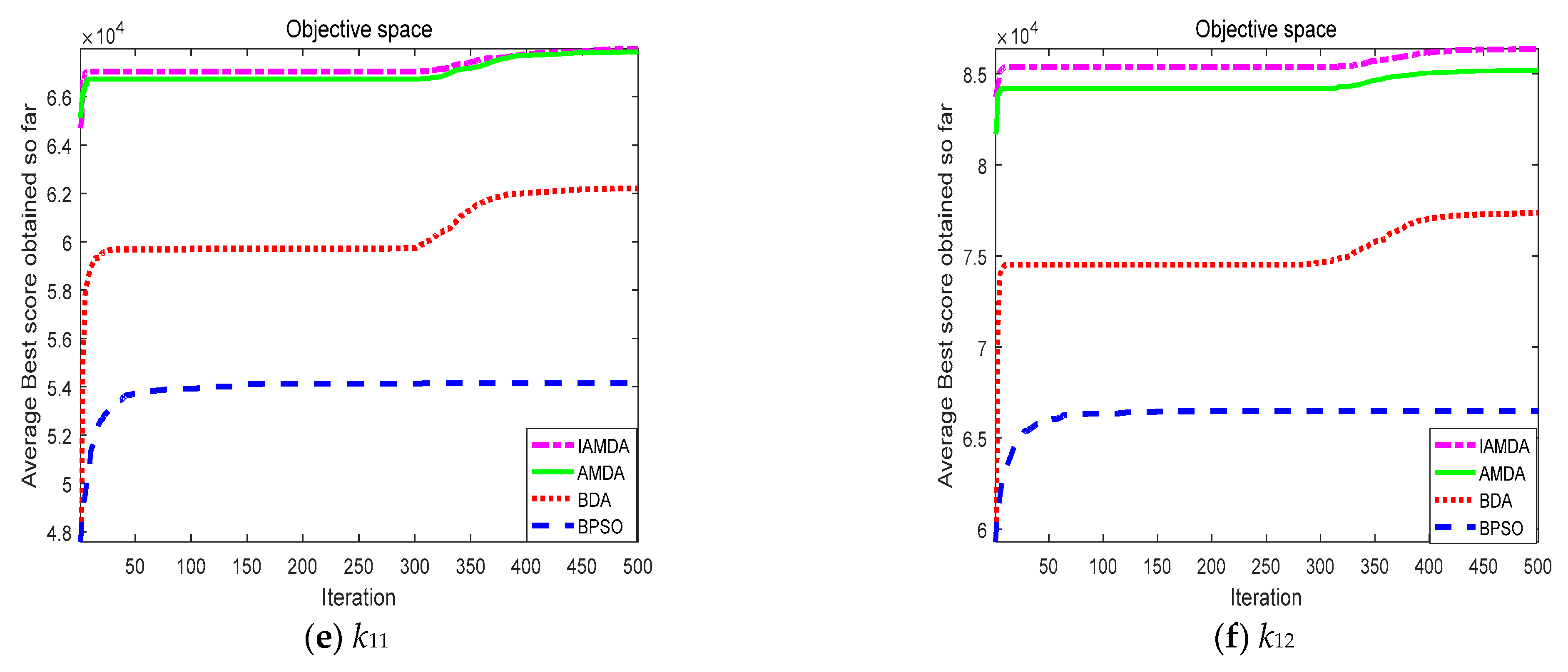
| k11 | IAMDA | 7.1022e+04 | 6.3479e+04 | 6.8977e+04 | 1.9784e+03 | 3.2814 |
| AMDA | 7.0417e+04 | 5.9200e+04 | 6.7161e+04 | 3.0546e+03 | 3.0616 | |
| BDA | 6.7241e+04 | 5.5492e+04 | 6.3396e+04 | 3.0978e+03 | 7.6517 | |
| BPSO | 5.5506e+04 | 5.3168e+04 | 5.4227e+04 | 552.3881 | 3.0838 | |
| k12 | IAMDA | 8.8872e+04 | 8.1067e+04 | 8.7179e+04 | 2.1245e+03 | 3.5053 |
| AMDA | 8.8691e+04 | 7.8917e+04 | 8.6422e+04 | 2.5499e+03 | 3.3711 | |
| BDA | 8.2644e+04 | 6.9772e+04 | 7.6970e+04 | 3.9042e+03 | 8.5147 | |
| BPSO | 6.7097e+04 | 6.5470e+04 | 6.6496e+04 | 648.1773 | 3.7690 |
| f | AMDA and IAMDA | BDA and IAMDA | BPSO and IAMDA | |||
|---|---|---|---|---|---|---|
| t | Sig. | t | Sig. | t | Sig. | |
| k6 | 0.0709 | N.S. | 0.0937 | IAMDA | 6.7956e-08 | IAMDA |
| k7 | 0.2085 | N.S. | 0.0066 | IAMDA | 6.7956e-08 | IAMDA |
| k8 | 0.3793 | N.S. | 4.5390e-07 | IAMDA | 6.7956e-08 | IAMDA |
| k9 | 0.2393 | N.S. | 5.8736e-07 | IAMDA | 6.7956e-08 | IAMDA |
| k10 | 0.0409 | IAMDA | 3.4156e-07 | IAMDA | 6.7956e-08 | IAMDA |
| k11 | 0.0155 | IAMDA | 2.6898e-06 | IAMDA | 6.7956e-08 | IAMDA |
| k12 | 0.1636 | N.S. | 1.2346e-07 | IAMDA | 6.7956e-08 | IAMDA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Shi, R.; Dong, J. A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0-1 Knapsack Problems. Entropy 2021, 23, 598. https://doi.org/10.3390/e23050598
Wang L, Shi R, Dong J. A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0-1 Knapsack Problems. Entropy. 2021; 23(5):598. https://doi.org/10.3390/e23050598
Chicago/Turabian StyleWang, Lin, Ronghua Shi, and Jian Dong. 2021. "A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0-1 Knapsack Problems" Entropy 23, no. 5: 598. https://doi.org/10.3390/e23050598
APA StyleWang, L., Shi, R., & Dong, J. (2021). A Hybridization of Dragonfly Algorithm Optimization and Angle Modulation Mechanism for 0-1 Knapsack Problems. Entropy, 23(5), 598. https://doi.org/10.3390/e23050598







