Electrophysiological Properties from Computations at a Single Voltage: Testing Theory with Stochastic Simulations
Abstract
1. Introduction
2. Theory and Method
2.1. Calculating the Potential of Mean Force
2.2. Calculating I-V Dependence from Simulation at a Single Voltage
2.3. Stochastic Simulations
3. Results and Discussion
3.1. Connection with Molecular Dynamics
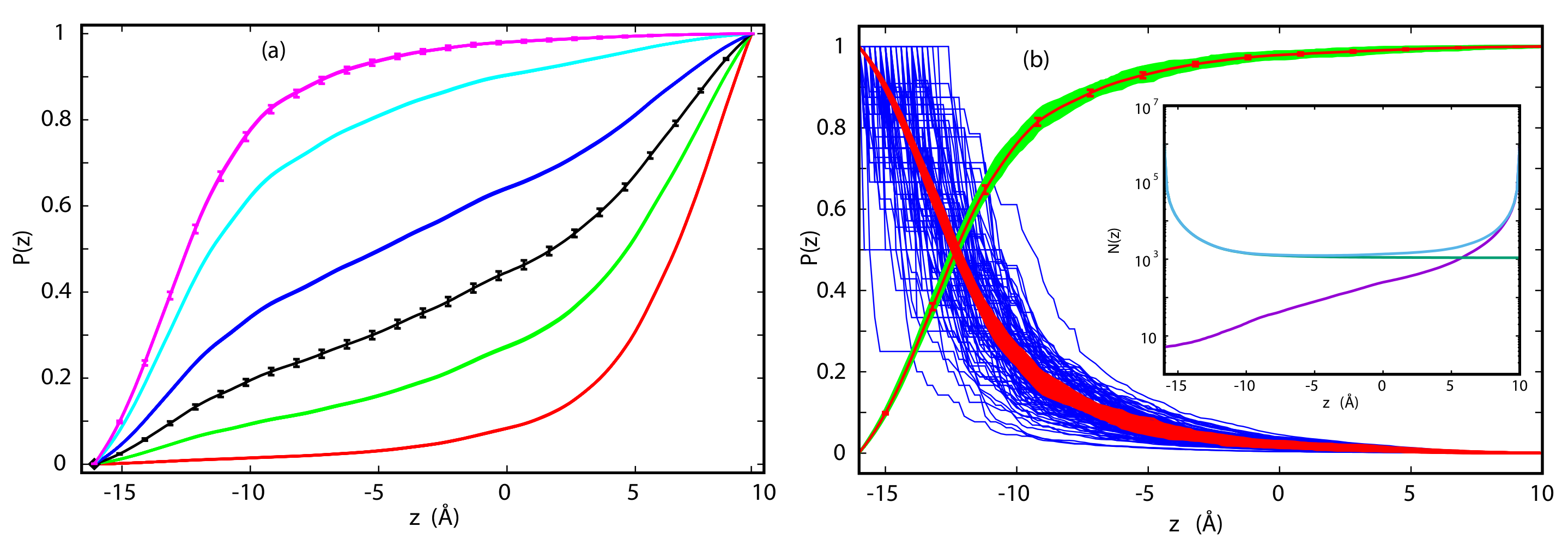
3.2. Committor Probabilities
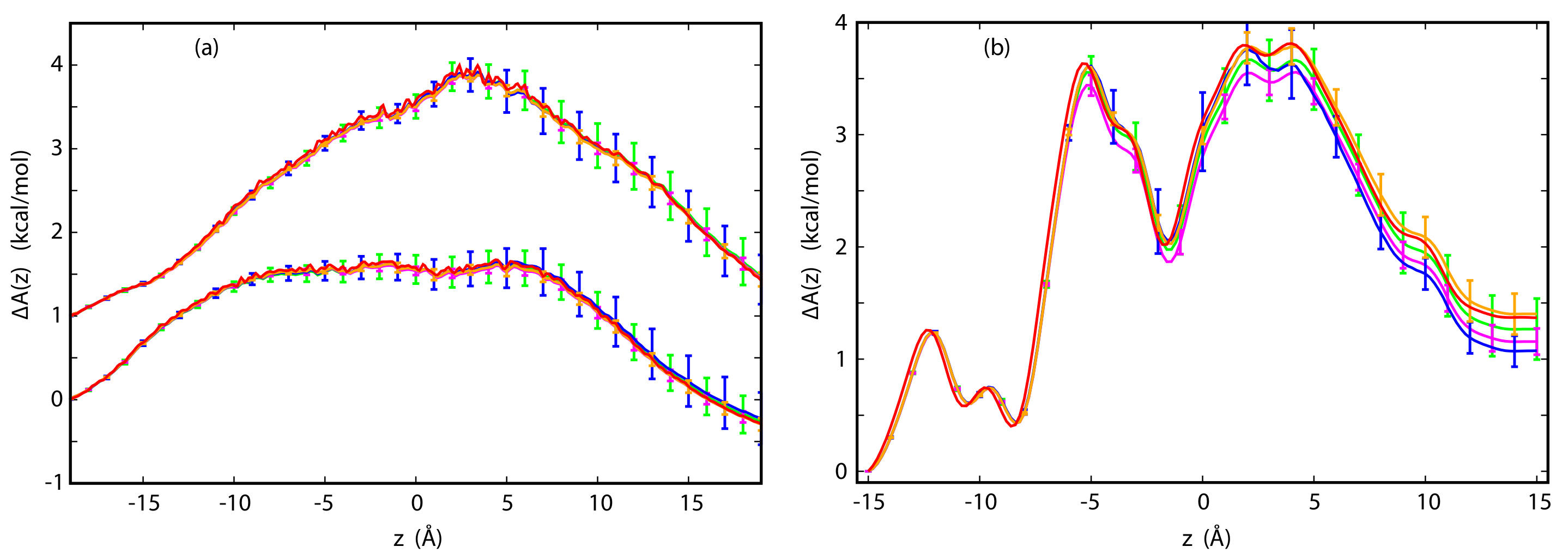
3.3. The Potential of Mean Force
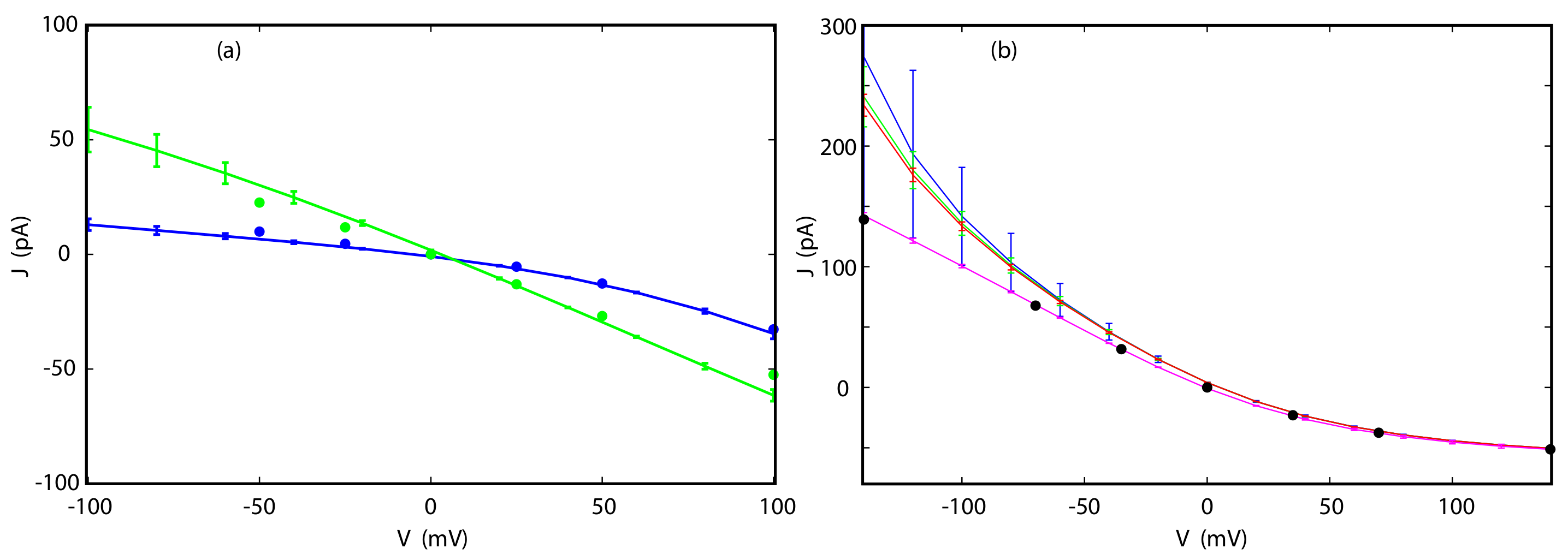
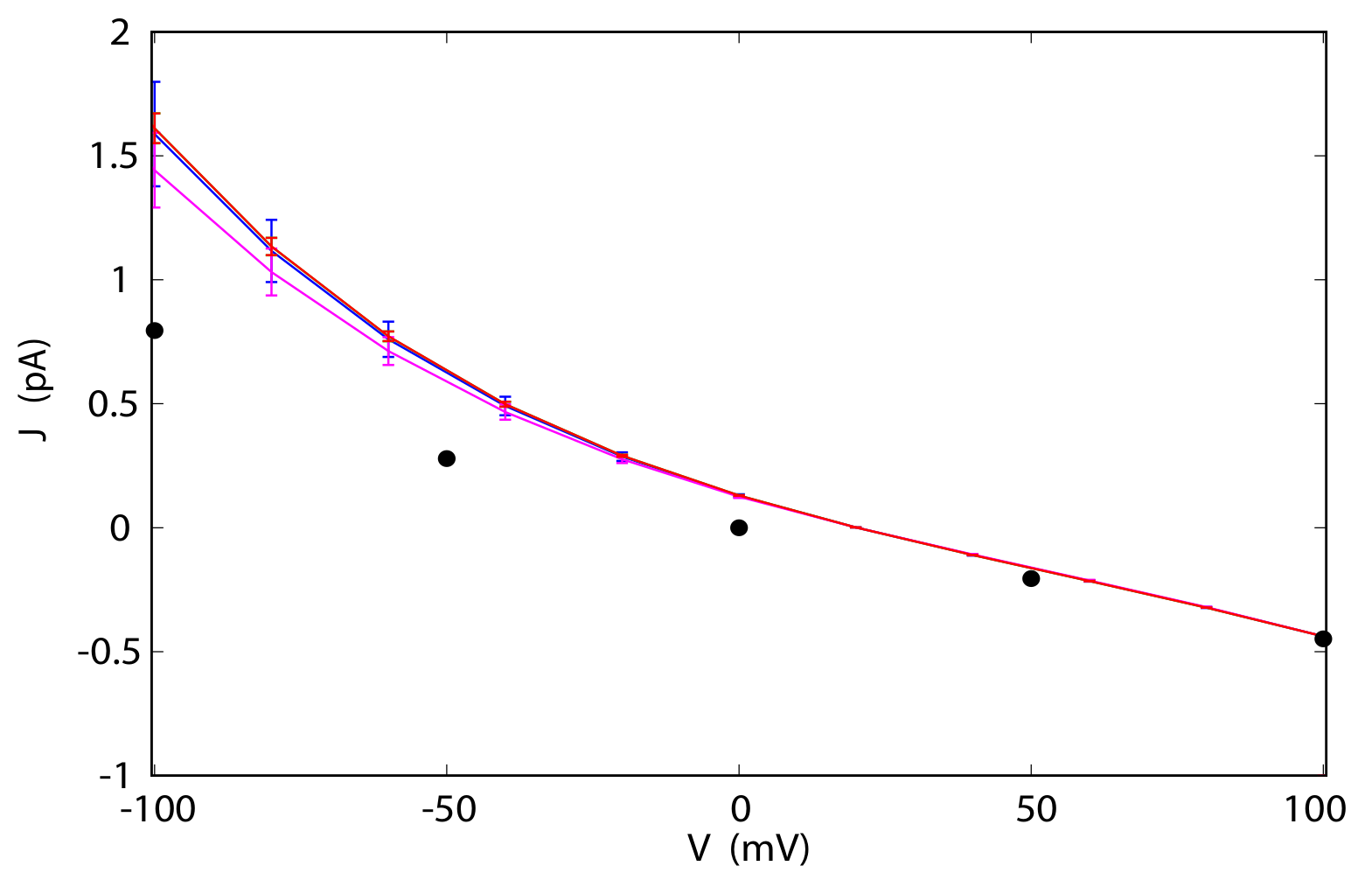
3.4. Current-Voltage Dependence
3.5. Reversal Potential
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| BD | Brownian Dyanmics |
| CPM | Committor Probability Method |
| CWDM | Current-Weighted Density Method |
| ED | electrodiffusion |
| GHK | Goldman Hodgkin Katz (equation) |
| IEEM | Integrated Electrodiffusion Equation Method |
| MD | molecular dynamics |
| PNP | Poisson-Nernst-Planck |
| PMF | potential of mean force |
| TTX | trichotoxin channel |
| WHAM | Weighted Histogram Analysis Method |
References
- Hille, B. Ion Channels of Excitable Membranes, 3rd ed.; Sinauer Associates, Inc.: Sunderland, MA, USA, 2001. [Google Scholar]
- Zheng, J.; Trudeau, M.C. Handbook of Ion Channels; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Kubalski, A.; Martinac, B. Bacterial Ion Channels and Their Eukaryotic Homologs; ASM Press: Washington, DC, USA, 2005. [Google Scholar]
- Bocquet, N.; Nury, H.; Baaden, M.; Le Poupon, C.; Changeux, J.P.; Delarue, M.; Corringer, P.J. X-ray structure of a pentameric ligand-gated ion channel in an apparently open conformation. Nature 2009, 457, 111–114. [Google Scholar] [CrossRef] [PubMed]
- Sakmann, B.; Boheim, G. Alamethicin-induced single channel conductance fluctuations in biological membranes. Nature 1979, 282, 336–339. [Google Scholar] [CrossRef] [PubMed]
- Duclohier, H.; Alder, G.M.; Bashford, C.L.; Bruckner, H.; Chugh, J.K.; Wallace, B.A. Conductance studies on trichotoxin_A50E and implications for channel structure. Biophys. J. 2004, 87, 1705–1710. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Martinac, B. Mechanosensitive ion channels: An evolutionary and scientific tour de force in mechanobiology. Channels 2012, 211–213. [Google Scholar] [CrossRef]
- Bass, R.B.; Strop, P.; Barclay, M.; Rees, D.C. Crystal structure of Escherichia coli MscS, a voltage-modulated and mechanosensitive channel. Science 2002, 298, 1582–1587. [Google Scholar] [CrossRef]
- Panaghie, G.; Purtell, K.; Tai, K.K.; Abbott, G.W. Voltage-dependent C-type inactivation in a constitutively open K+ channel. Biophys. J. 2008, 95, 2759–2778. [Google Scholar] [CrossRef]
- Anstee, Q.M.; Knapp, S.; Maguire, E.P.; Hosie, A.M.; Thomas, P.; Mortensen, M.; Bhome, R.; Martinez, A.; Walker, S.E.; Dixon, C.I.; et al. Mutations in the Gabrb1 gene promote alcohol consumption through increased tonic inhibition. Nat. Commun. 2013, 4, 2816. [Google Scholar] [CrossRef]
- Hou, X.; Outhwaite, I.R.; Pedi, L.; Long, S.B. Cryo-EM structure of the calcium release-activated calcium channel Orai in an open conformation. Elife 2020, 338, 1308–1313. [Google Scholar]
- Ashcroft, F.M. Ion Channels and Disease; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Bagal, S.K.; Brown, A.D.; Cox, P.J.; Omoto, K.; Owen, R.M.; Pryde, D.C.; Sidders, B.; Skerratt, S.E.; Stevens, E.B.; Storer, R.I.; et al. Ion channels as therapeutic targets: A drug discovery perspective. J. Med. Chem. 2013, 56, 593–624. [Google Scholar] [CrossRef]
- Garcia, M.L.; Kaczorowski, G.J. Ion channels find a pathway for therapeutic success. Proc. Natl. Acad. Sci. USA 2016, 113, 5472–5474. [Google Scholar] [CrossRef]
- Aksimentiev, A.; Schulten, K. Imaging α-hemolysin with molecular dynamics: Ionic conductance, osmotic permeability, and the electrostatic potential map. Biophys. J. 2005, 88, 3745–3761. [Google Scholar] [CrossRef]
- Sotomayor, M.; Vásquez, V.; Perozo, E.; Schulten, K. Ion conduction through MscS as determined by electrophysiology and simulation. Biophys. J. 2007, 92, 886–902. [Google Scholar] [CrossRef]
- Pezeshki, S.; Chimerel, C.; Bessonov, A.N.; Winterhalter, M.; Kleinekathöfer, U. Understanding ion conductance on a molecular level: An all-atom modeling of the bacterial porin OmpF. Biophys. J. 2009, 97, 1898–1906. [Google Scholar] [CrossRef]
- Kutzner, C.; Grubmüller, H.; De Groot, B.L.; Zachariae, U. Computational electrophysiology: The molecular dynamics of ion channel permeation and selectivity in atomistic detail. Biophys. J. 2011, 101, 809–817. [Google Scholar] [CrossRef]
- Wilson, M.A.; Wei, C.; Bjelkmar, P.; Wallace, B.A.; Pohorille, A. Molecular dynamics simulation of the antiamoebin ion channel: Linking structure and conductance. Biophys. J. 2011, 100, 2394–2402. [Google Scholar] [CrossRef]
- Zhu, F.; Hummer, G. Theory and simulation of ion conduction in the pentameric GLIC channel. J. Chem. Theory Comput. 2012, 8, 3759–3768. [Google Scholar] [CrossRef]
- Stock, L.; Delemotte, L.; Carnevale, V.; Treptow, W.; Klein, M.L. Conduction in a biological sodium selective channel. J. Phys. Chem. B 2013, 117, 3782–3789. [Google Scholar] [CrossRef]
- Jensen, M.Ø; Jogini, V.; Eastwood, M.P.; Shaw, D.E. Atomic-level simulation of current–voltage relationships in single-file ion channels. J. General Physiol. 2013, 141, 619–632. [Google Scholar] [CrossRef]
- Ulmschneider, M.B.; Bagnéris, C.; McCusker, E.C.; DeCaen, P.G.; Delling, M.; Clapham, D.E.; Ulmschneider, J.P.; Wallace, B.A. Molecular dynamics of ion transport through the open conformation of a bacterial voltage-gated sodium channel. Proc. Natl. Acad. Sci. USA 2013, 110, 6364–6369. [Google Scholar] [CrossRef]
- Wilson, M.A.; Nguyen, T.H.; Pohorille, A. Combining molecular dynamics and an electrodiffusion model to calculate ion channel conductance. J. Chem. Phys. 2014, 141, 22D519. [Google Scholar] [CrossRef]
- Pohorille, A.; Wilson, M.A.; Wei, C. Validity of the electrodiffusion model for calculating conductance of simple ion channels. J. Phys. Chem. B 2017, 121, 3607–3619. [Google Scholar] [CrossRef] [PubMed]
- Callahan, K.M.; Roux, B. Molecular dynamics of ion conduction through the selectivity filter of the NaVAb sodium channel. J. Phys. Chem. B 2018, 122, 10126–10142. [Google Scholar] [CrossRef] [PubMed]
- Flood, E.; Boiteux, C.; Lev, B.; Vorobyov, I.; Allen, T.W. Atomistic Simulations of Membrane Ion Channel Conduction, Gating, and Modulation. Chem. Rev. 2019, 119, 7737–7832. [Google Scholar] [CrossRef] [PubMed]
- Oestringer, B.P.; Bolivar, J.H.; Hensen, M.; Claridge, J.K.; Chipot, C.; Dehez, F.; Holzmann, N.; Zitzmann, N.; Schnell, J.R. Re-evaluating the p7 viroporin structure. Nature 2018, 562, E8–E18. [Google Scholar] [CrossRef] [PubMed]
- Machtens, J.P.; Kortzak, D.; Lansche, C.; Leinenweber, A.; Kilian, P.; Begemann, B.; Zachariae, U.; Ewers, D.; de Groot, B.L.; Briones, R.; et al. Mechanisms of anion conduction by coupled glutamate transporters. Cell 2015, 160, 542–553. [Google Scholar] [CrossRef] [PubMed]
- Roux, B. The membrane potential and its representation by a constant electric field in computer simulations. Biophys. J. 2008, 95, 4205–4216. [Google Scholar] [CrossRef] [PubMed]
- Gumbart, J.; Khalili-Araghi, F.; Sotomayor, M.; Roux, B. Constant electric field simulations of the membrane potential illustrated with simple systems. Biochim. Biophys. Acta 2012, 1818, 294–302. [Google Scholar] [CrossRef]
- Faraudo, J.; Calero, C.; Aguilella-Arzo, M. Ionic partition and transport in multi-ionic channels: A molecular dynamics simulation study of the OmpF bacterial porin. Biophys. J. 2010, 99, 2107–2115. [Google Scholar] [CrossRef]
- Pohorille, A.; Wilson, M.A. Computational Electrophysiology from a Single Molecular Dynamics Simulation and the Electrodiffusion Model. J. Phys. Chem. B 2021, 125, 3132–3144. [Google Scholar] [CrossRef]
- Biró, I.; Pezeshki, S.; Weingart, H.; Winterhalter, M.; Kleinekathöfer, U. Comparing the temperature-dependent conductance of the two structurally similar E. coli porins OmpC and OmpF. Biophys. J. 2010, 98, 1830–1839. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D.E.; Penin, F.; Schulten, K.; Chipot, C. The p7 protein of hepatitis C virus forms structurally plastic, minimalist ion channels. PLoS Comput. Biol. 2012, 8, e1002702. [Google Scholar] [CrossRef] [PubMed]
- Zachariae, U.; Schneider, R.; Briones, R.; Gattin, Z.; Demers, J.P.; Giller, K.; Maier, E.; Zweckstetter, M.; Griesinger, C.; Becker, S.; et al. β-Barrel mobility underlies closure of the voltage-dependent anion channel. Structure 2012, 20, 1540–1549. [Google Scholar] [CrossRef]
- Holzmann, N.; Chipot, C.; Penin, F.; Dehez, F. Assessing the physiological relevance of alternate architectures of the p7 protein of hepatitis C virus in different environments. Bioorgan. Med. Chem. 2016, 24, 4920–4927. [Google Scholar] [CrossRef] [PubMed]
- Wood, M.L.; Freites, J.A.; Tombola, F.; Tobias, D.J. Atomistic modeling of ion conduction through the voltage-sensing domain of the Shaker K+ ion channel. J. Phys. Chem. B 2017, 121, 3804–3812. [Google Scholar] [CrossRef]
- Chen, D.P.; Eisenberg, R.S. Flux, coupling, and selectivity in ionic channels of one conformation. Biophys. J. 1993, 65, 727–746. [Google Scholar] [CrossRef]
- Noskov, S.Y.; Im, W.; Roux, B. Ion permeation through the α-hemolysin channel: Theoretical studies based on Brownian dynamics and Poisson-Nernst-Plank electrodiffusion theory. Biophys. J. 2004, 87, 2299–2309. [Google Scholar] [CrossRef]
- Coalson, R.D.; Kurnikova, M.G. Poisson-Nernst-Planck theory approach to the calculation of current through biological ion channels. IEEE Trans. Nanobiosci. 2005, 4, 81–93. [Google Scholar] [CrossRef]
- Coalson, R.D.; Kurnikova, M.G. Poisson–Nernst–Planck theory of ion permeation through biological channels. In Biological Membrane Ion Channels; Springer: Berlin, Germany, 2007; pp. 449–484. [Google Scholar]
- Liu, J.L.; Eisenberg, B. Poisson-Nernst-Planck–Fermi theory for modeling biological ion channels. J. Chem. Phys. 2014, 141, 12B640_1. [Google Scholar] [CrossRef]
- Liu, J.L.; Eisenberg, B. Molecular mean-field theory of ionic solutions: A Poisson-Nernst-Planck-Bikerman model. Entropy 2020, 22, 550. [Google Scholar] [CrossRef]
- Im, W.; Roux, B. Brownian dynamics simulations of ions channels: A general treatment of electrostatic reaction fields for molecular pores of arbitrary geometry. J. Chem. Phys. 2001, 115, 4850–4861. [Google Scholar] [CrossRef]
- Chung, S.H.; Kuyucak, S. Recent advances in ion channel research. Biochim. Biophys. Acta 2002, 1565, 267–286. [Google Scholar] [CrossRef]
- Chung, S.H.; Allen, T.W.; Kuyucak, S. Conducting-state properties of the KcsA potassium channel from molecular and Brownian dynamics simulations. Biophys. J. 2002, 82, 628–645. [Google Scholar] [CrossRef]
- Chung, S.H.; Krishnamurthy, V. Brownian Dynamics: Simulation for Ion Channel Permeation. In Biological Membrane Ion Channels; Springer: Berlin, Germany, 2007; pp. 507–543. [Google Scholar]
- Berneche, S.; Roux, B. Molecular dynamics of the KcsA K+ channel in a bilayer membrane. Biophys. J. 2000, 78, 2900–2917. [Google Scholar] [CrossRef]
- Köpfer, D.A.; Song, C.; Gruene, T.; Sheldrick, G.M.; Zachariae, U.; de Groot, B.L. Ion permeation in K+ channels occurs by direct Coulomb knock-on. Science 2014, 346, 352–355. [Google Scholar] [CrossRef]
- Allen, T.W.; Andersen, O.S.; Roux, B. Energetics of ion conduction through the gramicidin channel. Proc. Natl. Acad. Sci. USA 2004, 101, 117–122. [Google Scholar] [CrossRef]
- Keener, J.P.; Sneyd, J. Mathematical Physiology; Springer: Berlin, Germany, 1998; Volume 1. [Google Scholar]
- Berneche, S.; Roux, B. Energetics of ion conduction through the K+ channel. Nature 2001, 414, 73–77. [Google Scholar] [CrossRef]
- Furini, S.; Domene, C. On conduction in a bacterial sodium channel. PLoS Comput. Biol. 2012, 8, e1002476. [Google Scholar] [CrossRef]
- Chakrabarti, N.; Ing, C.; Payandeh, J.; Zheng, N.; Catterall, W.A.; Pomès, R. Catalysis of Na+ permeation in the bacterial sodium channel NaVAb. Proc. Natl. Acad. Sci. USA 2013, 110, 11331–11336. [Google Scholar] [CrossRef] [PubMed]
- Boiteux, C.; Vorobyov, I.; Allen, T.W. Ion conduction and conformational flexibility of a bacterial voltage-gated sodium channel. Proc. Natl. Acad. Sci. USA 2014, 111, 3454–3459. [Google Scholar] [CrossRef] [PubMed]
- Harpole, T.J.; Grosman, C. Side-chain conformation at the selectivity filter shapes the permeation free-energy landscape of an ion channel. Proc. Natl. Acad. Sci. USA 2014, 111, E3196–E3205. [Google Scholar] [CrossRef] [PubMed]
- Finol-Urdaneta, R.K.; Wang, Y.; Al-Sabi, A.; Zhao, C.; Noskov, S.Y.; French, R.J. Sodium channel selectivity and conduction: Prokaryotes have devised their own molecular strategy. J. General Physiol. 2014, 143, 157–171. [Google Scholar] [CrossRef]
- Trick, J.L.; Chelvaniththilan, S.; Klesse, G.; Aryal, P.; Wallace, E.J.; Tucker, S.J.; Sansom, M.S. Functional annotation of ion channel structures by molecular simulation. Structure 2016, 24, 2207–2216. [Google Scholar] [CrossRef]
- Flood, E.; Boiteux, C.; Allen, T.W. Selective ion permeation involves complexation with carboxylates and lysine in a model human sodium channel. PLoS Comput. Biol. 2018, 14, e1006398. [Google Scholar] [CrossRef]
- Cottone, G.; Chiodo, L.; Maragliano, L. Thermodynamics and kinetics of ion permeation in wild-type and mutated open active conformation of the human α7 nicotinic receptor. J. Chem. Inf. Model. 2020, 60, 5045–5056. [Google Scholar] [CrossRef]
- Jensen, M.; Borhani, D.W.; Lindorff-Larsen, K.; Maragakis, P.; Jogini, V.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Principles of conduction and hydrophobic gating in K+ channels. Proc. Natl. Acad. Sci. USA 2010, 107, 5833–5838. [Google Scholar] [CrossRef]
- Corry, B.; Thomas, M. Mechanism of ion permeation and selectivity in a voltage gated sodium channel. J. Am. Chem. Soc. 2012, 134, 1840–1846. [Google Scholar] [CrossRef]
- Modi, N.; Bárcena-Uribarri, I.; Bains, M.; Benz, R.; Hancock, R.E.; Kleinekathöfer, U. Role of the central arginine R133 toward the ion selectivity of the phosphate specific channel OprP: Effects of charge and solvation. Biochemistry 2013, 52, 5522–5532. [Google Scholar] [CrossRef]
- Jorgensen, C.; Furini, S.; Domene, C. Energetics of ion permeation in an open-activated TRPV1 channel. Biophys. J. 2016, 111, 1214–1222. [Google Scholar] [CrossRef]
- Polovinkin, L.; Hassaine, G.; Perot, J.; Neumann, E.; Jensen, A.A.; Lefebvre, S.N.; Corringer, P.J.; Neyton, J.; Chipot, C.; Dehez, F.; et al. Conformational transitions of the serotonin 5-HT 3 receptor. Nature 2018, 563, 275–279. [Google Scholar] [CrossRef]
- Klesse, G.; Rao, S.; Tucker, S.J.; Sansom, M.S. Induced polarization in molecular dynamics simulations of the 5-HT3 receptor channel. J. Am. Chem. Soc. 2020, 142, 9415–9427. [Google Scholar] [CrossRef]
- Rao, S.; Klesse, G.; Lynch, C.I.; Tucker, S.J.; Sansom, M.S. Molecular Simulations of Hydrophobic Gating of Pentameric Ligand Gated Ion Channels: Insights into Water and Ions. J. Physic. Chem. B 2021, 125, 981–994. [Google Scholar] [CrossRef]
- OuYang, B.; Xie, S.; Berardi, M.J.; Zhao, X.; Dev, J.; Yu, W.; Sun, B.; Chou, J.J. Unusual architecture of the p7 channel from hepatitis C virus. Nature 2013, 498, 521–525. [Google Scholar] [CrossRef] [PubMed]
- Sauguet, L.; Poitevin, F.; Murail, S.; Van Renterghem, C.; Moraga-Cid, G.; Malherbe, L.; Thompson, A.W.; Koehl, P.; Corringer, P.J.; Baaden, M.; et al. Structural basis for ion permeation mechanism in pentameric ligand-gated ion channels. EMBO J. 2013, 32, 728–741. [Google Scholar] [CrossRef]
- Chipot, C.; Pohorille, A. Free Energy Calculations. Theory and Applications to Chemistry and Biology; Springer: Berlin, Germany, 2007. [Google Scholar]
- Pohorille, A. Free Energy Calculation for Understanding Membrane Receptors. In Computational Biophysics of Membrane Proteins (Theoretical and Computational Chemistry, Band 10); The Royal Society of Chemistry: London, UK, 2017; pp. 59–106. [Google Scholar]
- Furini, S.; Domene, C. Computational studies of transport in ion channels using metadynamics. Biochim. Biophys. Acta 2016, 1858, 1733–1740. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Berendsen, H.J.C. Simulation of water transport through a lipid membrane. J. Phys. Chem. 1994, 98, 4155–4168. [Google Scholar] [CrossRef]
- Hummer, G. Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations. New J. Phys. 2005, 7, 34. [Google Scholar] [CrossRef]
- Peter, C.; Hummer, G. Ion transport through membrane-spanning nanopores studied by molecular dynamics simulations and continuum electrostatics calculations. Biophys. J. 2005, 89, 2222–2234. [Google Scholar] [CrossRef] [PubMed]
- Comer, J.; Chipot, C.; González-Nilo, F.D. Calculating position-dependent diffusivity in biased molecular dynamics simulations. J. Chem. Theory Comput. 2013, 9, 876–882. [Google Scholar] [CrossRef]
- Hummer, G. From transition paths to transition states and rate coefficients. J. Chem. Phys. 2004, 120, 516–523. [Google Scholar] [CrossRef]
- Weinan, E.; Vanden-Eijnden, E. Transition-path theory and path-finding algorithms for the study of rare events. Ann. Rev. Phys. Chem. 2010, 61, 391–420. [Google Scholar]
- Elber, R.; Bello-Rivas, J.M.; Ma, P.; Cardenas, A.E.; Fathizadeh, A. Calculating iso-committor surfaces as optimal reaction coordinates with milestoning. Entropy 2017, 19, 219. [Google Scholar] [CrossRef]
- Berezhkovskii, A.M.; Szabo, A. Committors, first-passage times, fluxes, Markov states, milestones, and all that. J. Chem. Phys. 2019, 150, 054106. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Pieprzyk, S.; Heyes, D.M.; Brańka, A.C. Spatially dependent diffusion coefficient as a model for pH sensitive microgel particles in microchannels. Biomicrofluidics 2016, 10, 054118. [Google Scholar] [CrossRef]
- Huber, G.A.; McCammon, J.A. Brownian Dynamics Simulations of Biological Molecules. Trends Chem. 2019, 1, 727–738. [Google Scholar] [CrossRef]
- Pratt, L.R. A statistical method for identifying transition states in high dimensional problems. J. Chem. Phys. 1986, 85, 5045–5048. [Google Scholar] [CrossRef]
- Gennis, R.B. Biomembranes: Molecular Structure and Function; Springer: New York, NY, USA, 1989. [Google Scholar]
- Parsegian, V.A. Energy of an Ion crossing a Low Dielectric Membrane: Solutions to Four Relevant Electrostatic Problems. Nature 1969, 221, 844–846. [Google Scholar] [CrossRef]
- Neumcke, B.; Läuger, P. Nonlinear electrical effects in lipid bilayer membranes. II. Biophys. J. 1969, 9, 1160–1170. [Google Scholar] [CrossRef]
- Montserret, R.; Saint, N.; Vanbelle, C.; Salvay, A.G.; Simorre, J.P.; Ebel, C.; Sapay, N.; Renisio, J.G.; Bockmann, A.; Steinmann, E.; et al. NMR structure and ion channel activity of the p7 protein from hepatitis C virus. J. Biol. Chem. 2010, 285, 31446–31461. [Google Scholar] [CrossRef]
- Khalili-Araghi, F.; Ziervogel, B.; Gumbart, J.C.; Roux, B. Molecular dynamics simulations of membrane proteins under asymmetric ionic concentrations. J. Gen. Physiol. 2013, 142, 465–475. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, M.A.; Pohorille, A. Electrophysiological Properties from Computations at a Single Voltage: Testing Theory with Stochastic Simulations. Entropy 2021, 23, 571. https://doi.org/10.3390/e23050571
Wilson MA, Pohorille A. Electrophysiological Properties from Computations at a Single Voltage: Testing Theory with Stochastic Simulations. Entropy. 2021; 23(5):571. https://doi.org/10.3390/e23050571
Chicago/Turabian StyleWilson, Michael A., and Andrew Pohorille. 2021. "Electrophysiological Properties from Computations at a Single Voltage: Testing Theory with Stochastic Simulations" Entropy 23, no. 5: 571. https://doi.org/10.3390/e23050571
APA StyleWilson, M. A., & Pohorille, A. (2021). Electrophysiological Properties from Computations at a Single Voltage: Testing Theory with Stochastic Simulations. Entropy, 23(5), 571. https://doi.org/10.3390/e23050571





