Mesoscale Simulation of Bacterial Chromosome and Cytoplasmic Nanoparticles in Confinement
Abstract
1. Introduction
2. Simulation Models and Methods
3. Results and Discussion
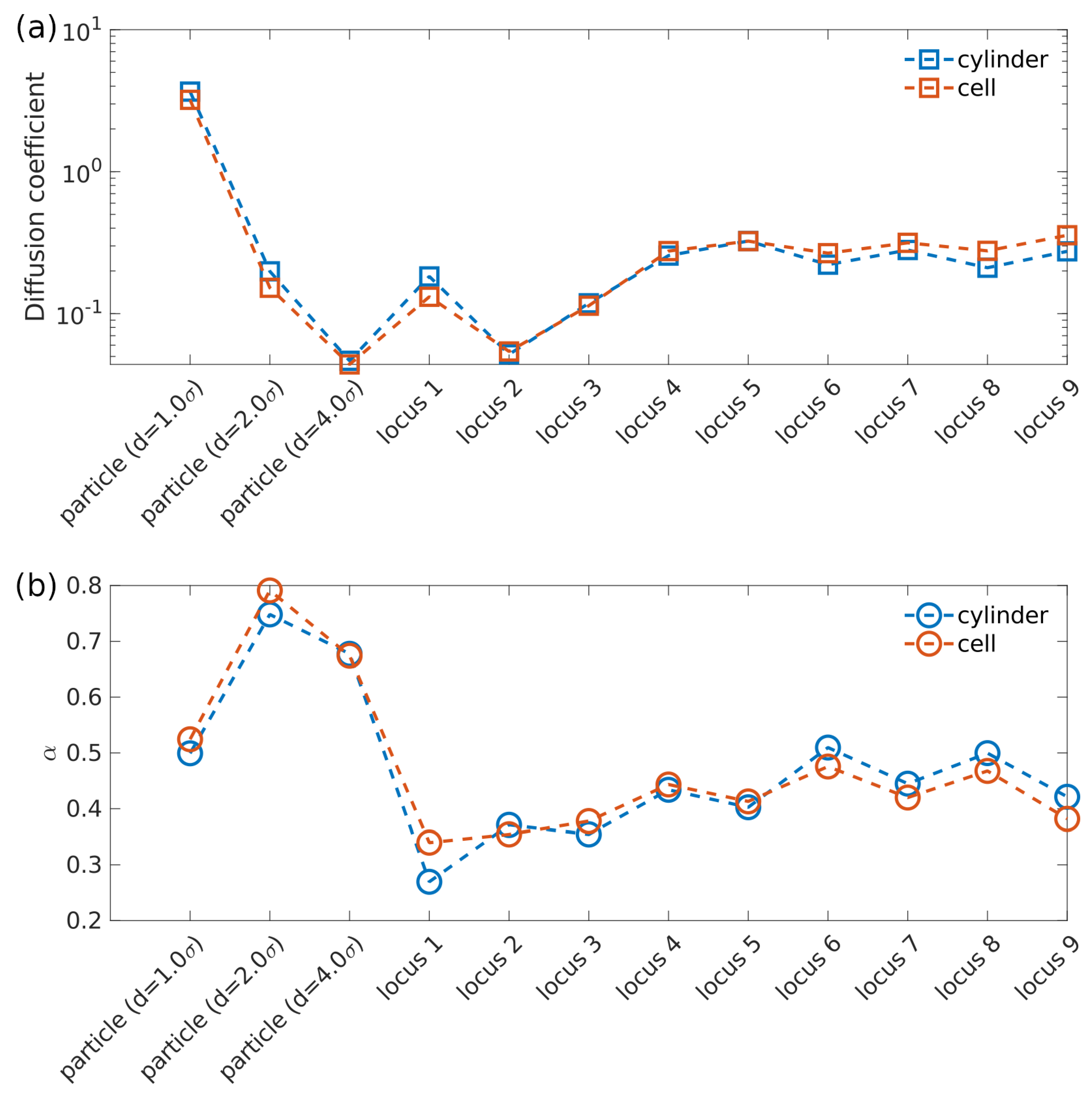
3.1. Subdiffusion of Cytoplasmic Particle and Chromosomal Loci in Uncompressed Cell
3.2. Cell Wall Geometry Effects: Cylinder vs. Ellipsoid
3.3. Density Effects on Subdiffusion of Cytoplasmic Particles and Loci
3.4. Subdiffusion of Cytoplasmic Particles and Loci in Compressed Cell
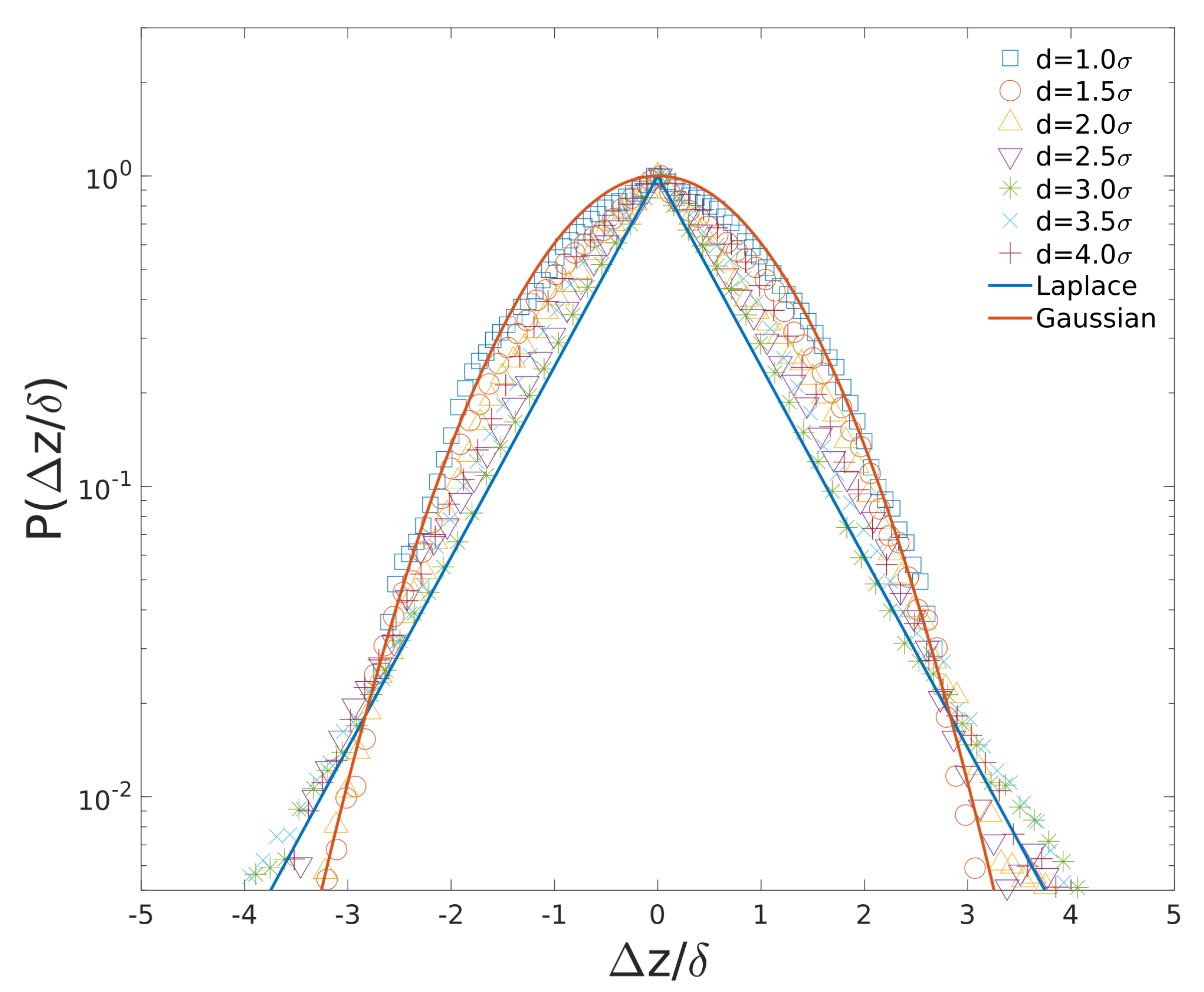
3.5. Non-Gaussian Subdiffusion of Cytoplasmic Particles and Loci
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marenduzzo, D.; Micheletti, C.; Orlandini, E. Biopolymer organization upon confinement. J. Phys. Condens. Matter 2010, 22, 283102. [Google Scholar] [CrossRef]
- Benza, V.G.; Bassetti, B.; Dorfman, K.D.; Scolari, V.F.; Bromek, K.; Cicuta, P.; Lagomarsino, M.C. Physical descriptions of the bacterial nucleoid at large scales, and their biological implications. Rep. Prog. Phys. 2012, 75, 076602. [Google Scholar] [CrossRef] [PubMed]
- Weber, S.C.; Spakowitz, A.J.; Theriot, J.A. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys. Rev. Lett. 2010, 104, 27–30. [Google Scholar] [CrossRef]
- Javer, A.; Long, Z.; Nugent, E.; Grisi, M.; Siriwatwetchakul, K.; Dorfman, K.D.; Cicuta, P.; Cosentino Lagomarsino, M. Short-time movement of E. coli chromosomal loci depends on coordinate and subcellular localization. Nat. Commun. 2013, 4, 3003. [Google Scholar] [CrossRef] [PubMed]
- Javer, A.; Kuwada, N.J.; Long, Z.; Benza, V.G.; Dorfman, K.D.; Wiggins, P.A.; Cicuta, P.; Lagomarsino, M.C. Persistent super-diffusive motion of Escherichia coli chromosomal loci. Nat. Commun. 2014, 5, 3854. [Google Scholar] [CrossRef][Green Version]
- Weber, S.C.; Theriot, J.A.; Spakowitz, A.J. Subdiffusive motion of a polymer composed of subdiffusive monomers. Phys. Rev. E 2010, 82, 011913. [Google Scholar] [CrossRef] [PubMed]
- Lampo, T.J.; Stylianidou, S.; Backlund, M.P.; Wiggins, P.A.; Spakowitz, A.J. Cytoplasmic RNA-Protein Particles Exhibit Non-Gaussian Subdiffusive Behavior. Biophys. J. 2017, 112, 532–542. [Google Scholar] [CrossRef]
- Parry, B.R.; Surovtsev, I.V.; Cabeen, M.T.; O’Hern, C.S.; Dufresne, E.R.; Jacobs-Wagner, C. The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell 2014, 156, 183–194. [Google Scholar] [CrossRef]
- Swain, P.; Mulder, B.M.; Chaudhuri, D. Confinement and crowding control the morphology and dynamics of a model bacterial chromosome. Soft Matter 2019, 15, 2677–2687. [Google Scholar] [CrossRef]
- Okumus, B.; Landgraf, D.; Lai, G.C.; Bakhsi, S.; Arias-Castro, J.C.; Yildiz, S.; Huh, D.; Fernandez-Lopez, R.; Peterson, C.N.; Toprak, E.; et al. Mechanical slowing-down of cytoplasmic diffusion allows in vivo counting of proteins in individual cells. Nat. Commun. 2016, 7, 11641. [Google Scholar] [CrossRef]
- Yu, S.; Dorfman, K.D.; Sheats, J.; Sclavi, B.; Cosentino Lagomarsino, M.; Cicuta, P. Subdiffusion of loci and cytoplasmic particles are different in compressed Escherichia coli cells. Commun. Biol. 2018, 1, 176. [Google Scholar] [CrossRef]
- Si, F.; Li, B.; Margolin, W.; Sun, S.X. Bacterial growth and form under mechanical compression. Sci. Rep. 2015, 5, 11367. [Google Scholar] [CrossRef] [PubMed]
- Männik, J.; Driessen, R.; Galajda, P.; Keymer, J.E.; Dekker, C. Bacterial growth and motility in sub-micron constrictions. Proc. Natl. Acad. Sci. USA 2009, 106, 14861–14866. [Google Scholar] [CrossRef] [PubMed]
- Yu, I.; Mori, T.; Ando, T.; Harada, R.; Jung, J.; Sugita, Y.; Feig, M. Biomolecular interactions modulate macromolecular structure and dynamics in atomistic model of a bacterial cytoplasm. ELife 2016, 5, e19274. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- Pereira, M.C.F.; Brackley, C.A.; Lintuvuori, J.S.; Marenduzzo, D.; Orlandini, E. Entropic elasticity and dynamics of the bacterial chromosome: A simulation study. J. Chem. Phys. 2017, 147, 044908. [Google Scholar] [CrossRef]
- Woldringh, C.L.; Jun, S.; Wong, W.P.; Sandler, S.J.; Halvorsen, K.; Ha, B.-Y.; Pelletier, J.; Paparcone, R. Physical manipulation of the Escherichia coli chromosome reveals its soft nature. Proc. Natl. Acad. Sci. USA 2012, 109, E2649–E2656. [Google Scholar]
- Mondal, J.; Bratton, B.P.; Li, Y.; Yethiraj, A.; Weisshaar, J.C. Entropy-based mechanism of ribosome-nucleoid segregation in E. coli cells. Biophys. J. 2011, 100, 2605–2613. [Google Scholar] [CrossRef]
- Kim, J.; Jeon, C.; Jeong, H.; Jung, Y.; Ha, B.Y. A polymer in a crowded and confined space: Effects of crowder size and poly-dispersity. Soft Matter 2015, 11, 1877–1888. [Google Scholar] [CrossRef]
- Jun, S.; Mulder, B. Entropy-driven spatial organization of highly confined polymers: Lessons for the bacterial chromosome. Proc. Natl. Acad. Sci. USA 2006, 103, 12388–12393. [Google Scholar] [CrossRef]
- Shendruk, T.N.; Bertrand, M.; De Haan, H.W.; Harden, J.L.; Slater, G.W. Simulating the entropic collapse of coarse-grained chromosomes. Biophys. J. 2015, 108, 810–820. [Google Scholar] [CrossRef]
- Kang, H.; Pincus, P.A.; Hyeon, C.; Thirumalai, D. Effects of macromolecular crowding on the collapse of biopolymers. Phys. Rev. Lett. 2015, 114, 068303. [Google Scholar] [CrossRef] [PubMed]
- Jeon, C.; Jung, Y.; Ha, B.Y. A ring-polymer model shows how macromolecular crowding controls chromosome-arm organization in Escherichia coli. Sci. Rep. 2017, 7, 11896. [Google Scholar] [CrossRef] [PubMed]
- Pierro, M.D.; Potoyan, D.A.; Wolynes, P.G.; Onuchic, J.N. Anomalous diffusion, spatial coherence, and viscoelasticity from the energy landscape of human chromosomes. Proc. Natl. Acad. Sci. USA 2018, 115, 7753–7758. [Google Scholar] [CrossRef] [PubMed]
- Ando, T.; Skolnick, J. Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc. Natl. Acad. Sci. USA 2010, 107, 18457–18462. [Google Scholar] [CrossRef]
- Miyaguchi, T. Reduction of self-diffusion coefficient in a coarse-grained model of cytoplasm. Phys. Rev. Res. 2020, 2, 013279. [Google Scholar] [CrossRef]
- Chaudhuri, D.; Mulder, B.M. Spontaneous helicity of a polymer with side loops confined to a cylinder. Phys. Rev. Lett. 2012, 108, 268305. [Google Scholar] [CrossRef]
- Chaudhuri, D.; Mulder, B.M. Molecular dynamics simulation of a feather-boa model of a bacterial chromosome. Methods Mol. Biol. 2018, 1837, 403–415. [Google Scholar]
- Spakowitz, A.J. Transient Anomalous Diffusion in a Heterogeneous Environment. Front. Phys. 2019, 7, 119. [Google Scholar] [CrossRef]
- Grebenkov, D.S.; Metzler, R.; Oshanin, G. Towards a full quantitative description of single-molecule reaction kinetics in biological cells. Phys. Chem. Chem. Phys. 2018, 20, 16393–16401. [Google Scholar] [CrossRef]
- Chubynsky, M.V.; Slater, G.W. Diffusing diffusivity: A model for anomalous, yet Brownian, diffusion. Phys. Rev. Lett. 2014, 113, 098302. [Google Scholar] [CrossRef] [PubMed]
- Jain, R.; Sebastian, K.L. Diffusing diffusivity: A new derivation and comparison with simulations. J. Chem. Sci. 2017, 129, 929–937. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Ha, B.-Y.; Jung, Y. Polymers under confinement: Single polymers, how they interact, and as model chromosomes. Soft Matter 2015, 11, 2333–2352. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, D.; Mulder, B. Size and shape of excluded volume polymers confined between parallel plates. Phys. Rev. E 2011, 83, 031803. [Google Scholar] [CrossRef] [PubMed]
- Reiss, P.; Fritsche, M.; Heermann, D.W. Looped star polymers show conformational transition from spherical to flat toroidal shapes. Phys. Rev. E 2011, 84, 051910. [Google Scholar] [CrossRef]
- Deng, Y.; Sun, M.; Shaevitz, J.W. Direct measurement of cell wall stress stiffening and turgor pressure in live bacterial cells. Phys. Rev. Lett. 2011, 107, 158101. [Google Scholar] [CrossRef]
- Zhu, Y.; Mohapatra, S.; Weisshaar, J.C. Rigidification of the Escherichia coli cytoplasm by the human antimicrobial peptide LL-37 revealed by superresolution fluorescence microscopy. Proc. Natl. Acad. Sci. USA 2019, 116, 1017–1026. [Google Scholar] [CrossRef]
- Fodor, É.; Guo, M.; Gov, N.S.; Visco, P.; Weitz, D.A.; van Wijland, F. Activity-driven fluctuations in living cells. EPL 2015, 110, 48005. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Wu, J.; Meng, X.; Chu, R.; Li, X.; Wu, G. Mesoscale Simulation of Bacterial Chromosome and Cytoplasmic Nanoparticles in Confinement. Entropy 2021, 23, 542. https://doi.org/10.3390/e23050542
Yu S, Wu J, Meng X, Chu R, Li X, Wu G. Mesoscale Simulation of Bacterial Chromosome and Cytoplasmic Nanoparticles in Confinement. Entropy. 2021; 23(5):542. https://doi.org/10.3390/e23050542
Chicago/Turabian StyleYu, Shi, Jiaxin Wu, Xianliang Meng, Ruizhi Chu, Xiao Li, and Guoguang Wu. 2021. "Mesoscale Simulation of Bacterial Chromosome and Cytoplasmic Nanoparticles in Confinement" Entropy 23, no. 5: 542. https://doi.org/10.3390/e23050542
APA StyleYu, S., Wu, J., Meng, X., Chu, R., Li, X., & Wu, G. (2021). Mesoscale Simulation of Bacterial Chromosome and Cytoplasmic Nanoparticles in Confinement. Entropy, 23(5), 542. https://doi.org/10.3390/e23050542






