Industry 4.0 Quantum Strategic Organizational Design Configurations. The Case of 3 Qubits: One Reports to Two
Abstract
1. Introduction
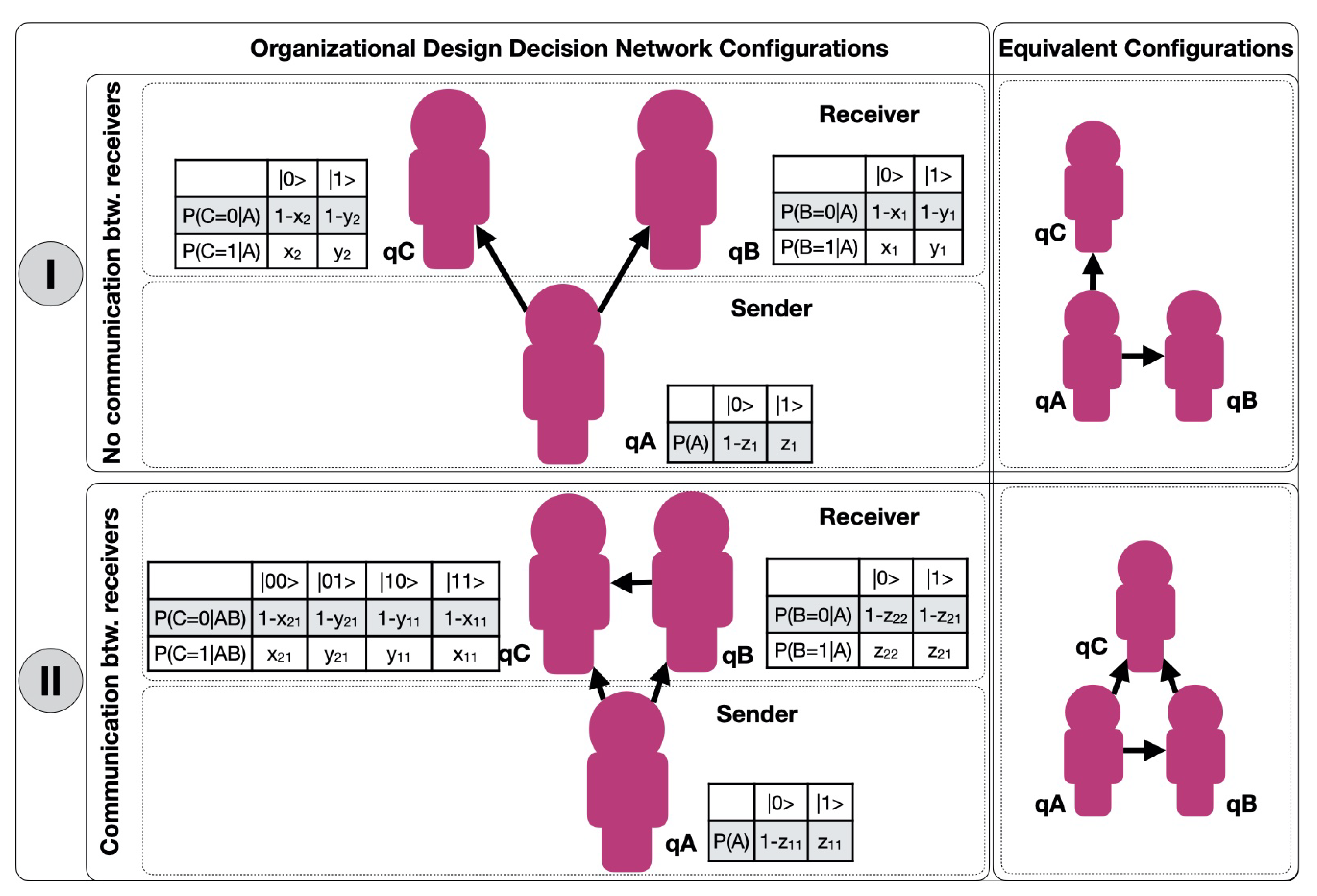
2. QSOD Circuits–3 Qubit Organizational Design Configurations–One Reports to Two
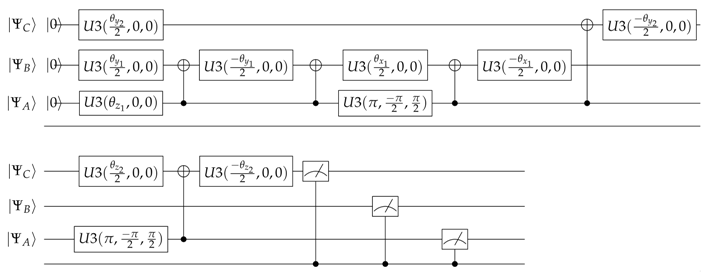
2.1. Quantum Circuit–Case I–Agents B and C Have No Communication between Each Other
| . |
- . Probability of alignment of node A.
- . Probability of no–alignment of node B conditioned to the state of alignment of node A.
- . Probability of no–alignment of node B conditioned to the state of no–alignment of node A.
- . Probability of no–alignment of node C conditioned to the state of alignment of node A.
- . Probability of no–alignment of node C conditioned to the state of no–alignment of node A.
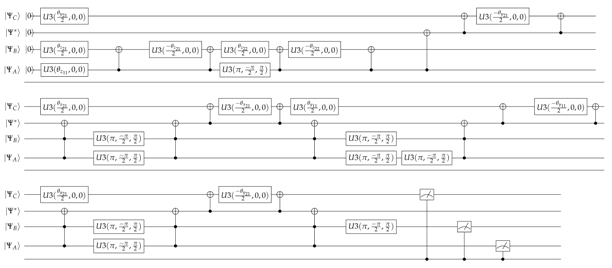
2.2. Quantum Circuit–Case II–Agents B and C Have Communication between Each Other
| . |
- . Probability of alignment of node A.
- . Probability of no–alignment of node B conditioned to the state of no–alignment of node A.
- . Probability of no–alignment of node B conditioned to the state of alignment of node A.
- . Probability of no–alignment of node C conditioned to the state of the waveform .
- . Probability of no–alignment of node C conditioned to the state of the waveform .
- . Probability of no–alignment of node C conditioned to the state of the waveform .
- . Probability of no–alignment of node C conditioned to the state of the waveform .
3. Case Study
3.1. Simulation–Case I–Agents B and C Have No Communication between Each Other
3.2. Simulation–Case II–Agents B and C Have Communication between Each Other
4. Discussion
4.1. Discussion–Case I–Agents B and C Have No Communication between Each Other
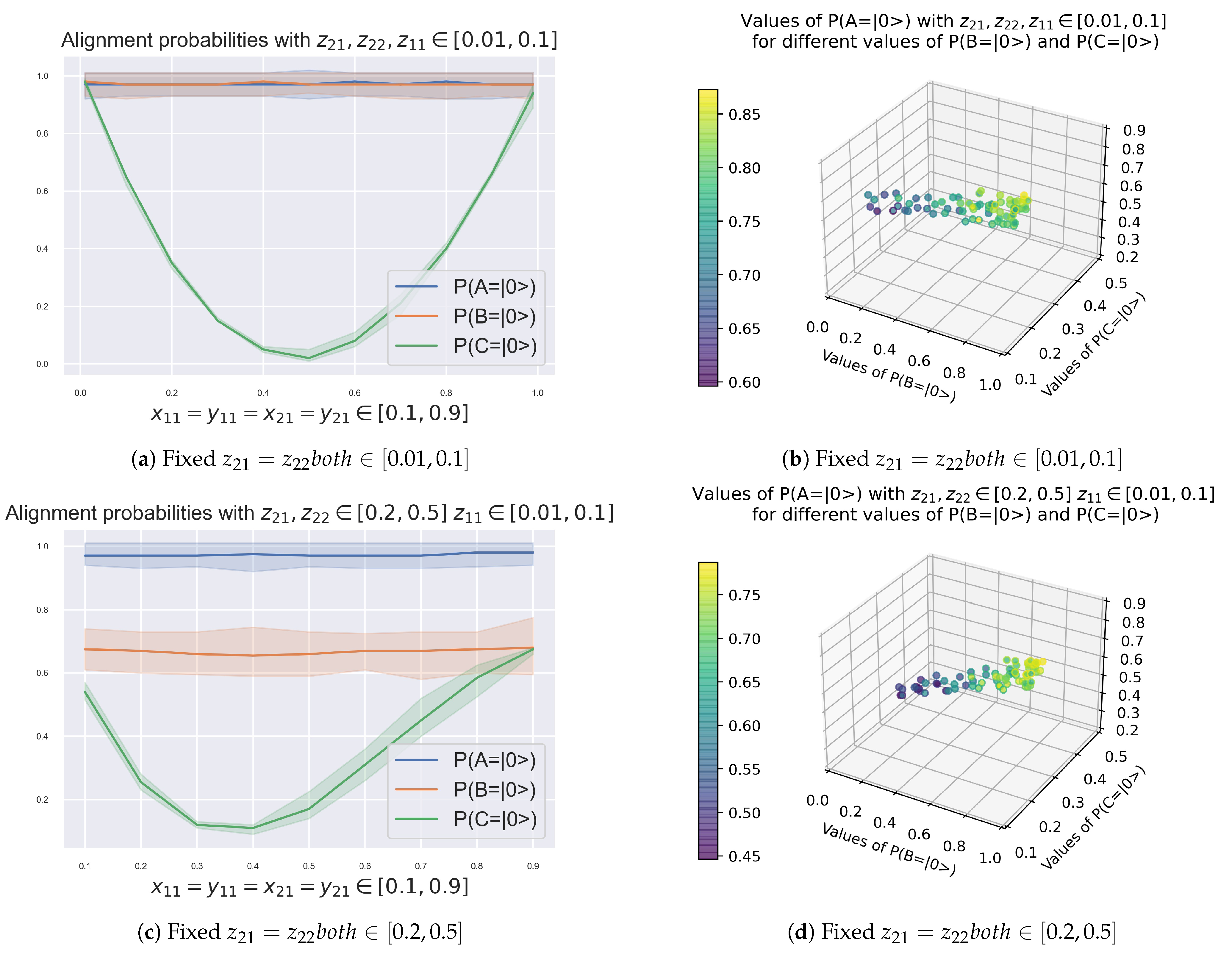
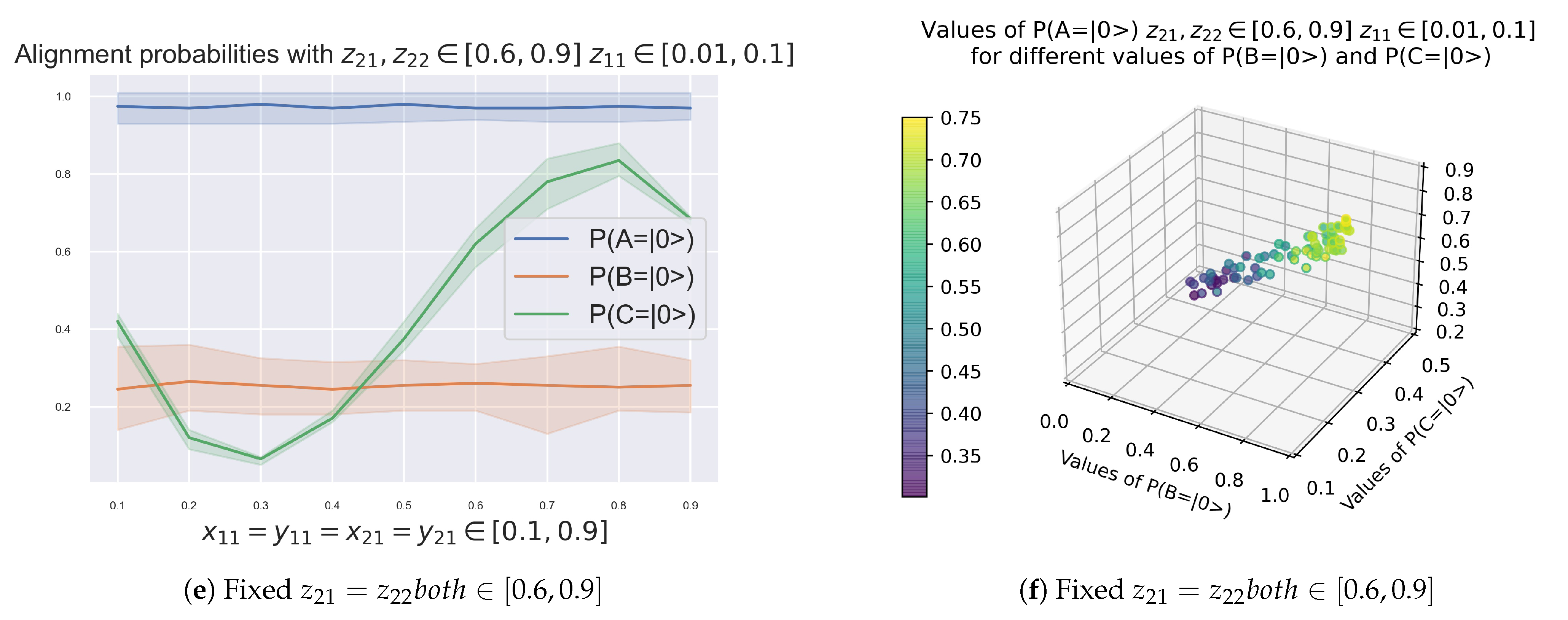
- R1. Agents B and C have an antagonistic alignment probability. The two never have a high probability of alignment simultaneously. In Figure 2 we can see how, for both high and low values of alignment for node A, or respectively, the alignment probabilities of agents B and C have a negative correlation. When one of the two has high alignment probabilities, the other has low ones.
- R2. Agents B and C only agree by chance. In Figure 2 we can see how, as agent A approaches its random alignment probability of 50%, the alignment probabilities of B and C become homogeneous until reaching the 50% value as well.
- R3. Quantum phase transition with 90% alignment probability of node A. The representations of Figure 3 are particular cases of the general solution of Figure 2. In both we can observe a sharp change of slope of the regression between the alignment probabilities of B and C. This clearly indicates a quantum phase change at the point where the probability of non–alignment of agent A is 10%, . In more detail, the observed results show:
- -
- As shown in Figure 3, if the alignment probability of A is very high, (or ), and the probability that B and C are in non–alignment, provided that A is in non–alignment, are equal, , then the alignment probability of C is very low and does not vary with the alignment probability of B;
- -
- As shown in Figure 3, if the alignment probability of A is not high, , and the probability that B and C are in non–alignment, provided that A is in non–alignment, are equal, , then the alignment probability of B and C present a positive correlation.
4.2. Discussion–Case II–Agents B and C Have Communication between Each Other
- R5. Agents B and C interchange energy. Lowering the probability of alignment of node B, , which can be understood as its energy, while maintaining , shows how behaves with changing . The curves shown quantify this interaction.
5. Conclusions, Limitations and Further Steps
5.1. Conclusions–Case I–Agents B and C Have No Communication between Each Other
5.2. Conclusions–Case II–Agents B and C Have Communication between Each Other
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| QSOD | Quantum Strategic Organizational Design |
| KPI | Key Performance Indicators |
References
- Grant, R.M. Organization Structure and Management Systems: The Fundamentals of Strategy Implementation. In Contemporary Strategy Analysis, 7th ed.; John Wiley & Sons: Chichester, UK, 2010; pp. 174–206. [Google Scholar]
- Villalba-Diez, J.; Ordieres-Mere, J.; Chudzick, H.; Lopez-Rojo, P. NEMAWASHI: Attaining Value Stream alignment within Complex Organizational Networks. Procedia CIRP 2015, 37, 134–139. [Google Scholar] [CrossRef]
- Tennant, C.; Roberts, P. Hoshin Kanri: Implementing the Catchball Process. Long Range Plan. 2001, 34, 287–308. [Google Scholar] [CrossRef]
- Cattani, G.; Ferriani, S.; Negro, G.; Perretti, F. The Structure of Consensus: Network Ties, Legitimation, and Exit Rates of U.S. Feature Film Producer Organizations. Adm. Sci. Q. 2008, 53, 145–182. [Google Scholar] [CrossRef]
- Cross, R.; Singer, J.; Colella, S.; Thomas, R.; Silverstone, Y. The Organizational Network Fieldbook: Best Practices, Techniques and Exercises to Drive Organizational Innovation and Performance, 1st ed.; Jossey-Bass: San Francisco, CA, USA, 2010. [Google Scholar]
- Burton, R.M.; Øbel, B.; Håkonsson, D.D. Organizational Design: A Step-by-Step Approach, 3rd ed.; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Barabási, A.-L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Powell, T.C. Organizational alignment as competitive advantage. Strateg. Manag. J. 1992, 13, 119–134. [Google Scholar] [CrossRef]
- Sender, S.W. Systematic agreement: A theory of organizational alignment. Hum. Resour. Dev. Q. 1997, 8, 23–40. [Google Scholar] [CrossRef]
- Ravi, K.; Maheshkumar, P.J.; Stephen, J.P. Organizational alignment and performance: Past, present and future. Manag. Decis. 2007, 45, 503–517. [Google Scholar] [CrossRef]
- Bryan, A.; Arnold, M.; Lisa, E.; Barratt, M.A. Organizational alignment and supply chain governance structure: Introduction and construct validation. Int. J. Logist. Manag. 2009, 20, 169–186. [Google Scholar] [CrossRef]
- Sousa, H.P.; do Prado Leite, J.C.S. Modeling Organizational Alignment. In Conceptual Modeling; Yu, E., Dobbie, G., Jarke, M., Purao, S., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 407–414. [Google Scholar]
- Javier, C.F.; Bo, E.; Javier, R.; Egren, M. Alignment of resources, actors and contexts for value creation: Bringing knowledge management into service-dominant logic. Int. J. Q. Serv. Sci. 2019, 11, 424–438. [Google Scholar] [CrossRef]
- Yung-Chang, H.; Ming-Ho, W. How organizational structure and strategic alignment influence new product success. Manag. Decis. 2020, 58, 182–200. [Google Scholar] [CrossRef]
- Gyongyosi, L.; Imre, S. A Survey on quantum computing technology. Comput. Sci. Rev. 2019, 31, 51–71. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the STOC ’96, Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996. [Google Scholar]
- Nielsen, T.D.; Jensen, F.V. Bayesian Networks and Decision Graphs, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Villalba-Diez, J.; Zheng, X. Quantum Strategic Organizational Design: Alignment in Industry 4.0 Complex-Networked Cyber-Physical Lean Management Systems. Sensors 2020, 20, 5856. [Google Scholar] [CrossRef] [PubMed]
- Villalba-Diez, J.; Benito, R.M.; Losada, J.C. Industry 4.0 Quantum Strategic Organizational Design Configurations. The Case of Two Qubits: One Reports to One. Sensors 2020, 20, 6977. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Piattini, M.; Peterssen, G.; Pérez-Castillo, R. Quantum Computing: A New Software Engineering Golden Age. SIGSOFT Softw. Eng. Notes 2020, 45, 12–14. [Google Scholar] [CrossRef]
- Villalba-Diez, J.; Ordieres-Mere, J. Improving manufacturing operational performance by standardizing process management. Trans. Eng. Manag. 2015, 62, 351–360. [Google Scholar] [CrossRef]
- Villalba-Diez, J.; Ordieres-Meré, J.; Nuber, G. The HOSHIN KANRI TREE. Cross-Plant Lean Shopfloor Management. In The 5th Conference on Learning Factories 2015; Elsevier: Bochum, Germanny, 2015. [Google Scholar] [CrossRef]
- Jimenez, P.; Villalba-Diez, J.; Ordieres-Meré, J. HOSHIN KANRI Visualization with Neo4j. Empowering Leaders to Operationalize Lean Structural Networks. In PROCEDIA CIRP; Elsevier: Athens, Greece, 2016; Volume 55, pp. 284–289. [Google Scholar] [CrossRef]
- Villalba-Diez, J.; Ordieres-Mere, J. Strategic Lean Organizational Design: Towards Lean World-Small World Configurations through Discrete Dynamic Organizational Motifs. Math. Probl. Eng. 2016, 2016, 1825410. [Google Scholar] [CrossRef]
- Villalba-Diez, J. The HOSHIN KANRI FOREST. Lean Strategic Organizational Design, 1st ed.; CRC Press; Taylor and Francis Group LLC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Villalba-Diez, J. The Lean Brain Theory. Complex Networked Lean Strategic Organizational Design; CRC Press; Taylor and Francis Group LLC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Villalba-Diez, J.; Ordieres-Mere, J.; Molina, M.; Rossner, M.; Lay, M. Lean dendrochronology: Complexity reduction by representation of kpi dynamics looking at strategic organizational design. Manag. Prod. Eng. Rev. 2018, 9, 3–9. [Google Scholar] [CrossRef]
- Ordieres-Mere, J.; Villalba-Diez, J.; Zheng, X. Challenges and Opportunities for Publishing IIoT Data in Manufacturing as a Service Business. Procedia Manuf. 2019, 39, 185–193. [Google Scholar] [CrossRef]
- Sun, S.; Zheng, X.; Villalba-Díez, J.; Ordieres-Meré, J. Data Handling in Industry 4.0: Interoperability Based on Distributed Ledger Technology. Sensors 2020, 20, 3046. [Google Scholar] [CrossRef] [PubMed]
- Mosseri, R.; Dandoloff, R. Geometry of entangled states, Bloch spheres and Hopf fibrations. J. Phys. A Math. Gen. 2001, 34, 10243–10252. [Google Scholar] [CrossRef]
- van Rossum, G. Python Tutorial; Technical Report CS-R9526; Centrum voor Wiskunde en Informatica (CWI): Amsterdam, The Newtherland, 1995. [Google Scholar]
- Wille, R.; Meter, R.V.; Naveh, Y. IBM’s Qiskit Tool Chain: Working with and Developing for Real Quantum Computers. In Proceedings of the 2019 Design, Automation Test in Europe Conference Exhibition (DATE), Florence, Italy, 25–29 March 2019; pp. 1234–1240, ISSN 1558-1101. [Google Scholar] [CrossRef]



| Qubit | Interpretation | Equation |
|---|---|---|
| The probability of qubit to be in not–alignment translates into the rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of to be in the state translates into rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of to be in the state translates into rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of to be in the state translates into rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of to be in the state translates into rotation angle . |
| Qubit | Interpretation | Equation |
|---|---|---|
| The probability of qubit to be in not–alignment translates into the rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of to be in the state translates into rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of to be in the state translates into rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of the waveform to be in the state translates into rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of the waveform to be in the state translates into rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of the waveform to be in the state translates into rotation angle . | ||
| The conditional probability of qubit to be in not–alignment depending on the probability of the waveform to be in the state translates into rotation angle . | ||
| The ancilla qubit is a support qubit and as such is not subject to any conditional probability rotation. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villalba-Diez, J.; Losada, J.C.; Benito, R.M.; González-Marcos, A. Industry 4.0 Quantum Strategic Organizational Design Configurations. The Case of 3 Qubits: One Reports to Two. Entropy 2021, 23, 374. https://doi.org/10.3390/e23030374
Villalba-Diez J, Losada JC, Benito RM, González-Marcos A. Industry 4.0 Quantum Strategic Organizational Design Configurations. The Case of 3 Qubits: One Reports to Two. Entropy. 2021; 23(3):374. https://doi.org/10.3390/e23030374
Chicago/Turabian StyleVillalba-Diez, Javier, Juan Carlos Losada, Rosa María Benito, and Ana González-Marcos. 2021. "Industry 4.0 Quantum Strategic Organizational Design Configurations. The Case of 3 Qubits: One Reports to Two" Entropy 23, no. 3: 374. https://doi.org/10.3390/e23030374
APA StyleVillalba-Diez, J., Losada, J. C., Benito, R. M., & González-Marcos, A. (2021). Industry 4.0 Quantum Strategic Organizational Design Configurations. The Case of 3 Qubits: One Reports to Two. Entropy, 23(3), 374. https://doi.org/10.3390/e23030374








