Abstract
The seismo-electrical coupling is critical to understand the mechanism of geoelectrical precursors to earthquakes. A novel seismo-electrical model, called Chen–Ouillon–Sornette (COS) model, has been developed by combining the Burridge–Knopoff spring-block system with the mechanisms of stress-activated charge carriers (i.e., electrons and holes) and pressure-stimulated currents. Such a model, thus, can simulate fracture-induced electrical signals at a laboratory scale or earthquake-related geoelectrical signals at a geological scale. In this study, by using information measures of time series analysis, we attempt to understand the influence of diverse electrical conditions on the characteristics of the simulated electrical signals with the COS model. We employ the Fisher–Shannon method to investigate the temporal dynamics of the COS model. The result showed that the electrical parameters of the COS model, particularly for the capacitance and inductance, affect the levels of the order/disorder in the electrical time series. Compared to the field observations, we infer that the underground electrical condition has become larger capacitance or smaller inductance in seismogenic processes. Accordingly, this study may provide a better understanding of the mechanical–electrical coupling of the earth’s crust.
1. Introduction
Earthquake prediction and forecasting has been vigorously debated; so far, scientists have developed no practical methodology [1,2,3,4,5,6]. Nevertheless, numerous research groups have reported a variety of earthquake precursors in different times and places. Such precursors include radon emissions [7,8], hydrological changes [9,10], electromagnetic signals [4,5,6,11,12,13]. Particularly, electromagnetic phenomena before earthquakes are the most promising candidate [14]. Hence, understanding precursory indicators and their generation mechanisms of preseismic electromagnetic phenomena is critical, as it may help to achieve short-term earthquake forecasts [15,16,17,18,19,20,21,22,23].
At present, the precursory mechanisms are still argumentative owing to undecided seismo-electromagnetic theories, inconsistent precursory phenomena, and shortage of objectively testable models [24,25,26,27]. Despite these reasons, scientists have significantly observed several electromagnetic anomalies within a few days or weeks before large seismic events [28,29,30,31,32] and proposed various relevant mechanisms, including solid-state physics, piezoelectric effects, electrokinetic effects, contact electrification [33,34,35,36,37,38,39,40,41,42,43,44,45]. Modeling earthquake-related geoelectrical signals, however, is still very tough, particularly for preseismic ones. Certain models [42,43,44,45] have solely simulated co-seismic electromagnetic phenomena rather than preseismic electromagnetic signals.
Recently, Chen et al. [46] have developed a seismo-electrical model to simulate electrical signals regarding rock fracturing and frictional sliding. This model combines a spring-block system [47,48,49,50,51] with the concepts of stress-activated charge carriers (i.e., electrons and holes) [34,35,36] and pressure-stimulated currents [39,40,52,53,54]. The spring-block system, originally proposed by Burridge and Knopoff in 1967 [47], can simulate stick-slip events and reproduce power-law frequency-size distributions [55,56] in a single fault or rupture zones [49,51,57]. On the other hand, the mechanisms of the stress-activated charge carriers and the pressure-stimulated currents can well justify the generation and transportation of electrical charges in seismogenic processes. As for pressure-stimulated currents, Varotsos et al. [58] also provided a useful review of a pressure-stimulated currents model proposed in the 1980s and explained that this model is compatible with experimental results deduced recently by independent research groups. After the combination, the seismo-electrical model, named Chen–Ouillon–Sornette (COS), can thus mimic fracture-induced electrical signals at a laboratory scale [40,59,60] and earthquake-related geoelectrical signals at a geological scale [18,32]. It also reproduces polar-like electromagnetic pulses that are usually observed before earthquakes [61,62,63,64,65].
Despite the self-consistent COS model, its simulated electrical signals have still uncovered properties. In this study, we simulate electrical signals through the COS model under different electrical conditions and analyze their informational properties by using the Fisher–Shannon (FS) method. In this way, we can investigate the impact of the electrical parameters of the COS model on the simulated signals. Comparing the results obtained here to the field observations, we suggest a possible evolution of underground electrical conditions during a seismogenic process. Figuring out the characteristics of the temporal organizations and structures in such simulated signals may help us to deduce the features of geoelectrical signals in real situations.
2. COS Seismo-Electrical Model
Within a coupled mechanical–electrical system, Chen et al. [46] have developed a fully self-consistent COS model that combines the generation of ruptures within a Burridge–Knopoff spring-block model [47,48,49,50] with the nucleation and propagation of electric pulses within an RLC-type circuit. The COS model has a theoretical framework for simulating and analyzing earthquake-related geoelectrical signals and successfully reproduces unipolar-like pulses that often precede large seismic events [61,62,63,64,65]. Moreover, it sheds some light on preseismic electromagnetic phenomena, such as variations of statistical moments [12,13,32] and transitions of power-law exponents in power spectra [19,66,67].
Let us start with a one-dimensional COS model [46,48], as illustrated in Figure 1. For its mechanical part, we consider that a loading plate pulls a linear chain on a rough surface at a velocity . This chain has N blocks of identical mass m; in the meantime, a spring with stiffness links the loading plate to each block, and a spring with stiffness links the adjacent blocks. Through the rough surface, all blocks are subject to friction forces. Hence, the static stability condition on the k-th block gives the following equation:
where is the resulting spring force, is the maximum static friction force between the k-th block and the surface, and is the position of the k-th block relative to the loading plate. During strain accumulation caused by the loading plate motion, all blocks are unmoving relative to the surface and have the same increment of position relative to the loading plate, which can be shown as:
When the resulting spring force on the k-th block exceeds its maximum static friction, the block starts to slide. Its governing equation of the dynamic sliding gives the following equation:
where is the dynamic friction force acting on the k-th block, satisfying . The moving of one block may destabilize the other blocks, thus forming a multiblock sliding event. Suppose that the velocity of a moving block is nonzero or the resulting force of this block still exceeds its maximum static friction, then this block continues to slide according to Equation (3); otherwise, this block sticks to the surface owing to Equation (1).
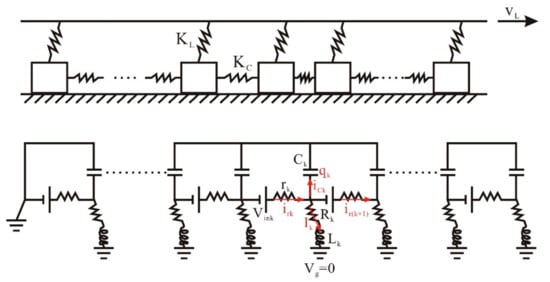
Figure 1.
Schematic diagram of the Chen–Ouillon–Sornette (COS) seismo-electrical model (originated from Chen et al. [46]. For the spring-block system, is the velocity of the loading plate; and are the spring stiffness. For the RLC-type circuit, r and c are the block resistance and capacitance, respectively; R and L are the earth resistance and inductance surrounding the blocks, respectively; q is the stored electrical charge in one block; , , and I are the currents; is the stress-induced voltage. Subscript k means the index of the blocks. is the grounding voltage and set to be 0 V by convention.
Regarding the mechanical–electrical relationship in crustal materials, scientists have reported that the rock voltage is related to the stress gradient and a stressed rock can serve as a battery [35,68,69,70,71]. Hence, the stress-induced voltage in a rock is a function of stress, coupling the mechanical part with the electrical part in the crustal system. Here, we simply defined the stress-induced voltage on the k-th block as follows:
where is the stress-induced voltage; is the stress, equivalent to the resulting spring force in Equation (1); is a conversion constant to convert stress to voltage [35,36,72]; is the polarization direction of the k-th block, meaning that positive holes flow from higher stressed regions to lower stressed ones [70]; is randomly assigned to ±1 when .
As for the model’s electrical part, each block is characterized by a resistor with resistance r and a capacitor with capacitance c, which are affected by electrolyte concentrations, water content, porosity, and so on [73,74,75,76,77]. Depending on the applied stresses, the block capacitor can store or release electricity. Additionally, each block is electrically grounded because of its embedment in the earth’s crust; hence, the grounded current I passes through a grounded resistor with resistance R and a grounded inductor with inductance L. The grounded resistance plays an ambient resistance to the blocks, and the grounded inductance relates with the permeability of rock minerals and the ability to transform magnetic energies through electrical currents.
According to the above-mentioned architecture, we can derive the governing equations of the electrical part in the crust within an RLC-type circuit (Figure 1). First of all, Kirchhoff’s voltage law on the k-th block gives the following:
where and are the block resistance and capacitance, respectively; is the current passing through the block resistor; is the charge stored in the block. Secondly, the current–charge relation on the k-th block gives the following:
where is the current passing through the block capacitor. Thirdly, Kirchhoff’s law for the current flowing towards the neighboring blocks and the ground gives the following:
where is the current flowing toward the ground. Finally, the voltage balance on the k-th block concerned with the earth terminal (i.e., the RL component) gives the following:
where and are the grounded resistance and inductance, respectively. Besides, the resulting voltage of the mechanical–electrical coupling system was written as:
Such a simulated voltage can be analog to self-potential signals measured in real fields (e.g., in a fault zone). In other words, the equations simulate fractured-induced electrical signals or earthquake-related geoelectrical signals.
For convenience’ sake, the above equations are nondimensionalized by introducing the suitable variables as follows:
The variables in Equations (10) and (11) are used for the mechanical and electrical parts of the COS model, respectively. Hence, the equations of the mechanical part can be written as:
On the other hand, the equations of the electrical part can be described as:
These nondimensional equations enable us to investigate the relationships between the electrical parameters and the time series of the simulated voltages.
To elucidate the process of how the simulated voltages are generated in the coupled mechanical–electrical system, Figure 2 shows the flowchart of the COS model. Based on Equations (12)–(14), we first solve the block displacement of the spring-block system. Subsequently, we calculate the stress of each block based on Equation (12). Then, we calculated the stress-induced voltage by using Equation (15). Given the obtained stress-induced voltage, we can solve the variables of charges and currents in Equations (16)–(19). Finally, we obtained the simulated voltages of the spring-block system through Equation (20).
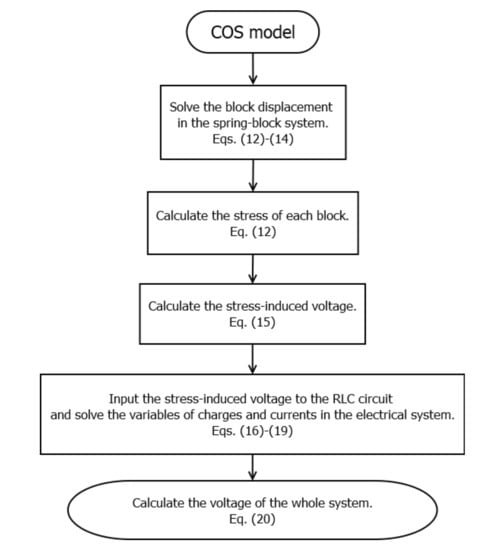
Figure 2.
Flowchart of the COS seismo-electrical model.
In this study, we set to be 128, to be 30, to be 1.5, and was randomly assigned between 1 and 3.5 for each block. In addition, we set diverse values to , , and to investigate the influence of changing the electrical parameters on the temporal dynamics of the simulated voltages . For instance, Figure 3a,b shows the time series and its power spectral density (PSD), respectively, of the voltages simulated under the parameters of , , and . We observed that such time series were similar to real ones (e.g., in comparison to those in Figure 2 in [78] at a laboratory scale and those in Figure 2 in [79] at a geological scale). In Figure 3b, the PSD of the simulated voltages conforms to the noise with the power-law scaling of ; the scaling for geoelectrical signals usually ranges from 1 to 2 [66,67,79]. Therefore, the COS model can reproduce pulse-like behaviors in the time domain and the scaling behavior in the frequency domain.
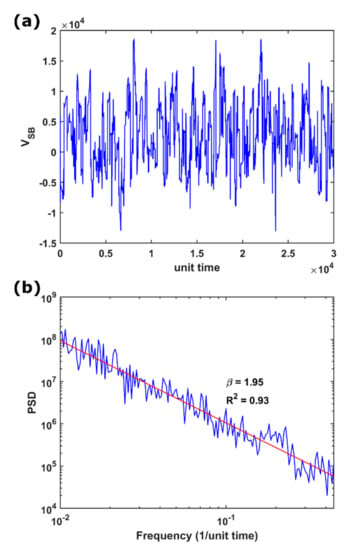
Figure 3.
(a) Time series of the voltages simulated under the electrical parameters of , , and . (b) Power spectral density (PSD) of the time series in (a). The red line represents the fitting of the noise with the scaling of and the R-squared of 0.93.
3. FS Method
To get information regarding the temporal dynamics of the simulated voltages, we employed the well-known FS method. Fisher developed a measure, in terms of probability density functions (PDFs), to discuss the loss of data information [80]. On the other hand, Shannon introduced the concept of information entropy to data communication for investigating how well data from the source can be losslessly compressed onto a perfectly noiseless channel [81]. The FS method jointly uses the Fisher information measure and the Shannon information entropy, which are efficient statistical indices for studying the dynamics of complex nonstationary time series and the change of physical systems [82,83,84,85,86,87]. For example, the FS method is utilized for portraying the temporal evolution of physical processes, suggesting the direction of decreasing accuracy for the determination of the mean value of a physical parameter [83].
Moreover, scientists have used the FS method and studied various complex geophysical and environmental phenomena to reveal informational properties of the mechanisms governing their temporal dynamics [88,89,90,91,92] and detect precursors of catastrophic events [93,94,95,96,97]. For example, Telesca and Lovallo analyzed hourly wind speed time series at several heights above the ground level, finding that the FS informational properties of the wind data are height-dependent [90]. Furthermore, Telesca et al. applied the FS method to discriminate between tsunamigenic and nontsunamigenic earthquake seismograms, suggesting that this method may efficiently speed up the tsunami warning time [91]. Therefore, the FS method is regarded as an efficient data exploration tool.
Now, let us introduce the relevant Fisher and Shannon quantities. Assuming that is the PDF of variable , its Fisher information measure can be written as:
and its Shannon entropy can be described as:
Comparing Equation (21) with Equation (22), the major difference between the integrands is a squared derivative of . Thus, the Fisher information offers a local measure of the concentration of the PDFs, whereas the Shannon entropy gives a global measure [83,84]. The Shannon entropy is nonnegative for discrete distributions and can take any real positive and negative values for continuous distributions. To avoid the difficulty arising with negative information measures, we used the Shannon entropy power instead of the entropy and obtained the following equation:
Applying both and satisfies the “isoperimetric inequality”, a lower bound to the FS product of ≥, where is the dimension of the space of the variable [98]. Such an isoperimetric inequality indicates that the Fisher information measure and the Shannon entropy power are intrinsically linked to each other; hence, the dynamics of complex time series can be characterized by using the two measures jointly in the FS information plane. The product can be considered as a statistical measure of complexity [99,100]. The “isocomplexity line” separates the FS plane into two parts, and the distance of a signal point to this line can quantify the degree of the signal complexity.
The estimation of the FS quantities depends on the calculation of a PDF. A rough approximation of the unknown PDF is given by the histogram. Nevertheless, we can smoothly and robustly estimate the PDF utilizing the kernel density estimator technique [101,102] that approximates as:
where is the bandwidth and is the number of data. The kernel function is a continuous nonnegative and symmetric function satisfying the two following conditions:
Here, we employed a Gaussian kernel with zero mean and unit variance [103,104], so that was estimated as:
where the bandwidth is estimated through an optimization process, described in Telesca and Lovallo [105].
4. Results
To understand the temporal dynamics of the COS model, we investigated several time series of voltages simulated under diverse electrical conditions. Figure 4 lists the quantities of the resistance, capacitance, and inductance used in the simulation. In our strategy, we simulated 10 sets of the realizations of the voltage time series for each parameter set; each time series was simulated with random initial conditions of block positions. For each time series, we estimated its Fisher information measure and Shannon entropy power . Then, we compared the behaviors of the two indicators by fixing two parameters among capacitance, resistance, and inductance and varying the remaining one.
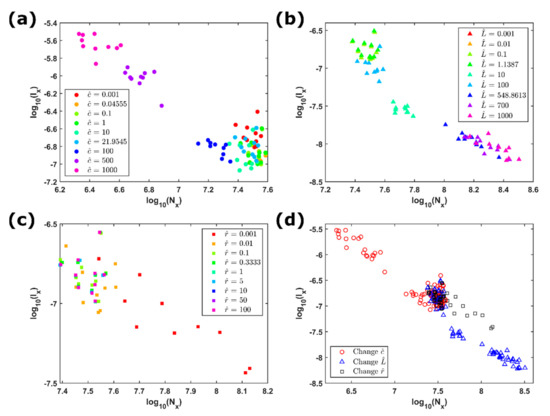
Figure 4.
Fisher–Shannon (FS) information plane of the simulated voltages: (a) the voltages simulated through the COS model for and , while increasing from 0.001 to 1000. Each case has 10 simulations with different initial block positions; (b) the voltages with the fixed parameters and and the increase of from 0.001 to 1000; (c) the voltages with the fixed parameters and and the increase of from 0.001 to 100; (d) FS information plane for all cases from (a) to (c). Red circles represent the simulations of changing , blue triangles changing , and black squares changing .
At the beginning, we researched the effect of the capacitance on the voltage time series. Figure 4a displays the FS indices on the information plane for the voltages simulated by assigning and and increasing from 0.001 to 1000. The distribution of the FS indices has a trend that the values of the two indices with a larger capacitance fall in the region of higher and lower . This means that the temporal dynamics of the voltage time series is characterized by higher local order and lower global disorder with the increasing quantity of the capacitance, particularly for . As for the effect of the inductance, Figure 4b presents the FS information plane for the voltages simulated by fixing and and increasing from 0.001 to 1000. A clear pattern is visible: when the inductance increases, increases and decreases, indicating a tendency to lose the order and augment the uncertainty at both local and global scales with the increase of the inductance. In terms of the resistance, Figure 4c shows the FS information plane for the voltages simulated by fixing and and increasing from 0.001 to 100. We observed a discrimination that the FS indices with the lowest resistance () distinguish from the indices of all the other resistances and spread in the area of larger . This indicated that for the lowest resistance the signals are characterized by the large uncertainty or disorder.
To sum up, Figure 4d shows the FS indices of all the simulated voltages on the same information plane. Generally speaking, three clusters can be identified. First, the voltages simulated with occupy mostly the area of larger and smaller ; second, the voltages simulated with occupy the area of smaller and larger ; third, the voltages simulated by changing occupy the area between the two previous clusters, mixing with those of changing smaller than 500 and of changing smaller than 500. Those results suggested that the levels of the local and global orders of the simulated voltages mainly depend on the quantities of the capacitance and inductance rather than resistance. We note, in this study, that the FS information planes show the results with fixed values of five for any two electrical parameters in all the simulations. When changing the fixed values of the electrical parameters, the quantities and change. However, the tendencies obtained here keep preserved, i.e., the increase of the order with increasing the capacitance and the increase of the disorder with increasing the inductance.
Besides, we defined a statistical measure of complexity, which can be expressed as the product of Fisher information measure and Shannon entropy power () [100]. The statistical complexity represents a combined effect of both local and global factors, offering an evaluation of the organization, structure, and correlation in a system or time series. Figure 5 shows the complexity versus the capacitance (Figure 5a), inductance (Figure 5b), and resistance (Figure 5c). All the results showed that . First, we observed that the complexity versus the capacitance shows the lowest value of around 3 when . As for the inductance, the complexity exhibits two regimes separated by , showing that the mean value is around 5.5 when whereas that is mostly 2 when . In terms of the resistance, the complexity changes insignificantly with , most of which show a mean value of five.
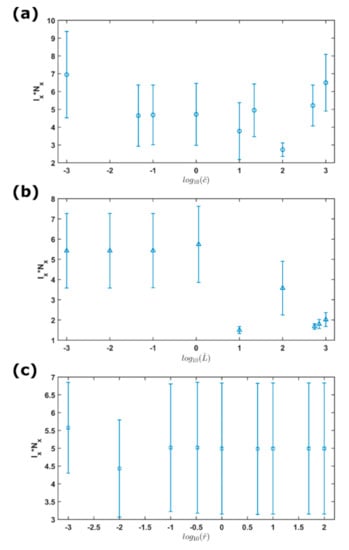
Figure 5.
Complexity () for the simulations of changing (a), changing (b), and changing (c). Each vertical line represents the mean value within one standard error.
5. Discussion and Conclusions
In this study, we investigated the FS information of the voltages simulated through the diverse electrical conditions of the COS seismo-electrical model. According to the simulation results, the quantities of the capacitance and inductance affect the levels of the local and global orders of the simulated voltages, while the changes of the resistance mostly do not affect their informational properties. In this section, we discussed the dependence of the electrical conditions on the organization and structure of the simulated voltages.
Establishing the seismo-electrical model, Chen et al. [46] have derived its analytical solutions for the single-block architecture, showing that the three electrical parameters (resistance, capacitance, and inductance) impact on the waveform of the charge Green function (see Equations (19)–(21) and Figure 2 in [46]). According to the different quantities of the electrical parameters, one sliding event generates the diversity of voltage time series. The generated voltages are featured by two predominant factors: decay time and amplitude. The decay time is controlled by the resistance, capacitance, and inductance, while the amplitude is dominated by the resistance and is reversely proportional to the resistance. The voltage time series generated by the present sliding event is fluctuated with the voltages generated by the past sliding events. Particularly when the decay time of the voltage time series is longer than the interevent time of two consecutive sliding events, the resulting voltage time series become more disordered. On the other hand, as mentioned above, the small amplitudes of the voltages can be due to the large resistance. Such small amplitudes lead to a concentrated distribution of its voltage time series. This concentrated distribution results in large and small , indicating an ordered state [87]. Even if the decay time is longer than the interevent time, the voltage time series show less disorder owing to the superposition of small amplitudes of the voltages generated by the sliding events. Hence, the dynamics (the state of disorder) of the simulated voltages is seriously affected by the electrical parameters owing to the length of the decay time and the amplitude of the voltage.
From the perspective of physics, the capacitance of a capacitor is the ratio of the magnitude of the stored charge to the magnitude of the voltage across the capacitor:
We rewrote Equation (27) in a differential form:
Based on Equation (28), we understand that the capacitance tends to resist the change of voltages. Given a small change of the electric charges, increasing the capacitance reduces the change of the voltages. Hence, the voltages simulated with larger capacitance show the localization of the time series, leading to the state of order (i.e., higher and lower ). On the other hand, the voltage across an inductor of inductance is proportional to the time rate of change of the current flowing through it, as follows:
We observed the form of Equation (29) and figured out that the inductance tends to amplify voltage changes. When the rate of current change is subject to a slight fluctuation in time, a larger inductance leads to a larger voltage variation. Therefore, increasing the inductance of the COS model exhibits a scattered distribution of the simulated voltages, leading to a disordered state of the time series (i.e., lower and higher ). Understanding the effects of the electrical parameters helps us to identify the electrical signals in real situations. As a result, the COS model contributes to a deeper understanding of the mechanical–electrical coupling of the crustal system.
In field observations, several studies have applied the FS method to investigate the relationship between geoelectrical signals and seismic events [93,94,95,96,97]. For instance, Potirakis et al. investigated the electromagnetic signals before, during, and after strong earthquakes through the FS method [96]. They found that the higher level of the order in the electromagnetic signals precedes the earthquake occurrences, indicating that the FS method reliably distinguishes the candidate electromagnetic precursors from noises. The geoelectrical signals preceding the seismic events seem to exhibit higher organized and ordered states, which can be simulated with larger capacitance or smaller inductance in the COS model. Combining the field observations with the results in this study, we reasonably infer that the electrical properties of the earth’s crust have become larger capacitance or smaller inductance in the seismogenic processes. Several possible explanations may be provided for such a variation. The electrical characteristics of the crust are affected by rock composition, porosity, fluid permeability, permittivity, and so forth [17,33,44]. For instance, during an earthquake preparation, dielectric crystals may be polarized towards a preferred orientation under tectonic stresses [17,58]; hence, the permittivity increases. In electromagnetism, the capacitance is proportional to the permittivity. This suggests that highly organized electrical structures due to seismogenic processes generate highly ordered geoelectrical signals with larger Fisher information and smaller Shannon entropy.
In conclusion, the results obtained in this study might not only gain insights into a better understanding of the complexity of the mechanical–electrical mechanisms in the earth’s crust but also be useful for developing the detection of preseismic electromagnetic signals. Despite this, some possibilities remain for future work that follows the present study. The COS model used is currently a one-dimension case and can be further developed into a two-dimension architecture. In this way, the characteristics of the simulated voltages are expected to approach those of real geoelectrical signals. Moreover, besides the information measures, it is worth exploring more properties of the COS model through other methodologies, for example, natural time analysis [106,107,108,109,110]. The results of such studies will be reported elsewhere.
Author Contributions
Conceptualization, H.-J.C. and L.T.; methodology, H.-J.C. and L.T.; model simulation, H.-J.C.; data analysis, L.T. and M.L.; writing and visualization, H.-J.C.; review, L.T. and C.-C.C.; supervision, C.-C.C.; funding acquisition, L.T. and C.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are openly available in Mendeley Data at http://dx.doi.org/10.17632/x9k4ypjrmj.1. We accessed the data on 27 August 2020.
Acknowledgments
We thank the cooperative research project between Taiwan and Italy supported by Taiwan’s Ministry of Science and Technology (107-2911-I-008-503 and 108-2911-I-008-501) and by National Research of Council of Italy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jordan, T.H.; Chen, Y.-T.; Gasparini, P.; Madariaga, R.; Main, I.; Marzocchi, W.; Papadopoulos, G.; Sobolev, G.; Yamaoka, K.; Zschau, J. Operational Earthquake Forecasting: State of Knowledge and Guidelines for Utilization. Ann. Geophys. 2011, 54, 316–391. [Google Scholar] [CrossRef]
- Wyss, M. Why is earthquake prediction research not progressing faster? Tectonophysics 2001, 338, 217–223. [Google Scholar] [CrossRef]
- Geller, R.J. Earthquake prediction: A critical review. Geophys. J. Int. 1997, 131, 425–450. [Google Scholar] [CrossRef]
- Uyeda, S. VAN method of short-term earthquake prediction shows promise. Eos Trans. Am. Geophys. Union 1998, 79, 573–580. [Google Scholar] [CrossRef]
- Varotsos, P.; Eftaxias, K.; Vallianatos, F.; Lazaridou, M. Basic principles for evaluating an earthquake prediction method. Geophys. Res. Lett. 1996, 23, 1295–1298. [Google Scholar] [CrossRef]
- Lighthill, S.J. A Critical Review of Van: Earthquake Prediction from Seismic Electrical Signals; World Scientific: Singapore, 1996; ISBN 978-981-4499-44-6. [Google Scholar]
- Fu, C.-C.; Walia, V.; Yang, T.F.; Lee, L.-C.; Liu, T.-K.; Chen, C.-H.; Kumar, A.; Lin, S.-J.; Lai, T.-H.; Wen, K.-L. Preseismic anomalies in soil-gas radon associated with 2016 M 6.6 Meinong earthquake, Southern Taiwan. Terr. Atmos. Ocean. Sci. 2017, 28, 787–798. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Panagiotaras, D.; Cantzos, D.; Yannakopoulos, P.; Nomicos, C.; Stonham, J. Radon-222: A Po-tential Short-Term Earthquake Precursor. J. Earth Sci. Clim. Chang. 2015, 6, 1. [Google Scholar]
- Chien, S.-H.J.; Chi, W.-C.; Ke, C.-C. Precursory and coseismic groundwater temperature perturbation: An example from Taiwan. J. Hydrol. 2020, 582, 124457. [Google Scholar] [CrossRef]
- Chen, C.-H.; Tang, C.-C.; Cheng, K.-C.; Wang, C.-H.; Wen, S.; Lin, C.-H.; Wen, Y.-Y.; Meng, G.; Yeh, T.-K.; Jan, J.C.; et al. Groundwater–strain coupling before the 1999 M w 7.6 Taiwan Chi-Chi earthquake. J. Hydrol. 2015, 524, 378–384. [Google Scholar] [CrossRef]
- Hattori, K. ULF Geomagnetic Changes Associated with Large Earthquakes. Terr. Atmos. Ocean. Sci. 2004, 15, 329–360. [Google Scholar] [CrossRef]
- Chen, H.-J.; Chen, C.-C. Testing the correlations between anomalies of statistical indexes of the geoelectric system and earthquakes. Nat. Hazards 2016, 84, 877–895. [Google Scholar] [CrossRef]
- Chen, H.-J.; Chen, C.-C.; Ouillon, G.; Sornette, D. Using Skewness and Kurtosis of Geoelectric Fields to Forecast the 2016/2/6, ML6.6 Meinong, Taiwan Earthquake. Terr. Atmos. Ocean. Sci. 2017, 28, 745–761. [Google Scholar] [CrossRef]
- Hayakawa, M.; Sandhu, A.; Okada, H. Earthquake Prediction with Electromagnetic Phenomena. AIP Conf. Proc. 2016, 1709, 020002. [Google Scholar] [CrossRef]
- Morgounov, V.; Malzev, S. A multiple fracture model of pre-seismic electromagnetic phenomena. Tectonophysics 2007, 431, 61–72. [Google Scholar] [CrossRef]
- Eftaxias, K.; Contoyiannis, Y.; Balasis, G.; Karamanos, K.; Kopanas, J.; Antonopoulos, G.; Koulouras, G.; Nomicos, C. Evidence of fractional-Brownian-motion-type asperity model for earthquake generation in candidate pre-seismic electromagnetic emissions. Nat. Hazards Earth Syst. Sci. 2008, 8, 657–669. [Google Scholar] [CrossRef]
- Huang, Q. Rethinking earthquake-related DC-ULF electromagnetic phenomena: Towards a physics-based approach. Nat. Hazards Earth Syst. Sci. 2011, 11, 2941–2949. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Nomicos, C.; Stonham, J.; Cantzos, D.; Yannakopoulos, P.; Kottou, S. Electromagnetic Pre-earthquake Precursors: Mechanisms, Data and Models-A Review. J. Earth Sci. Clim. Chang. 2015, 6, 11. [Google Scholar] [CrossRef]
- Eftaxias, K.; Kapiris, P.; Polygiannakis, J.; Peratzakis, A.; Kopanas, J.; Antonopoulos, G.; Rigas, D. Experience of short term earthquake precursors with VLF–VHF electromagnetic emissions. Nat. Hazards Earth Syst. Sci. 2003, 3, 217–228. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hobara, Y. Current status of seismo-electromagnetics for short-term earthquake prediction. Geomat. Nat. Hazards Risk 2010, 1, 115–155. [Google Scholar] [CrossRef]
- Schekotov, A.; Chebrov, D.; Hayakawa, M.; Belyaev, G.; Berseneva, N. Short-term earthquake prediction in Kamchatka using low-frequency magnetic fields. Nat. Hazards 2020, 100, 735–755. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Seismic Electric Signals: An additional fact showing their physical interconnection with seismicity. Tectonophysics 2013, 589, 116–125. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Long-range correlations in the electric signals that precede rupture: Further investigations. Phys. Rev. E 2003, 67, 021109. [Google Scholar] [CrossRef]
- Tzanis, A.; Vallianatos, F.; Gruszow, S. Identification and discrimination of transient electrical earthquake precursors: Fact, fiction and some possibilities. Phys. Earth Planet. Inter. 2000, 121, 223–248. [Google Scholar] [CrossRef]
- Eftaxias, K.; Kapiris, P.; Polygiannakis, J.; Bogris, N.; Kopanas, J.; Antonopoulos, G.; Peratzakis, A.; Hadjicontis, V. Signature of pending earthquake from electromagnetic anomalies. Geophys. Res. Lett. 2001, 28, 3321–3324. [Google Scholar] [CrossRef]
- Pham, V.N.; Geller, R.J. Comment on “Signature of pending earthquake from electromagnetic anomalies” by K. Eftaxias et al. Geophys. Res. Lett. 2002, 29, 18-1–18-2. [Google Scholar] [CrossRef]
- Park, S.K.; Dalrymple, W.; Larsen, J.C. The 2004 Parkfield earthquake: Test of the electromagnetic precursor hypothesis. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Chen, Y.-I.; Huang, C.-S.; Liu, J.-Y. Statistical evidences of seismo-ionospheric precursors applying receiver operating characteristic (ROC) curve on the GPS total electron content in China. J. Asian Earth Sci. 2015, 114, 393–402. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Zhuang, J.; Chen, C.-H.; Liu, J.-Y.; Yoshida, S. Evaluation of ULF seismo-magnetic phenomena in Kakioka, Japan by using Molchan’s error diagram. Geophys. J. Int. 2017, 208, 482–490. [Google Scholar] [CrossRef]
- Sarlis, N.V. Statistical Significance of Earth’s Electric and Magnetic Field Variations Preceding Earthquakes in Greece and Japan Revisited. Entropy 2018, 20, 561. [Google Scholar] [CrossRef]
- Chen, H.-J.; Chen, C.-C.; Ouillon, G.; Sornette, D. A paradigm for developing earthquake probability forecasts based on geoelectric data. Eur. Phys. J. Spec. Top. 2021, 230, 381–407. [Google Scholar] [CrossRef]
- Eccles, D.; Sammonds, P.R.; Clint, O.C. Laboratory studies of electrical potential during rock failure. Int. J. Rock Mech. Min. Sci. 2005, 42, 933–949. [Google Scholar] [CrossRef]
- Freund, F. Toward a unified solid state theory for pre-earthquake signals. Acta Geophys. 2010, 58, 719–766. [Google Scholar] [CrossRef]
- Takeuchi, A.; Lau, B.W.S.; Freund, F.T. Current and surface potential induced by stress-activated positive holes in igneous rocks. Phys. Chem. Earth Parts A B C 2006, 31, 240–247. [Google Scholar] [CrossRef]
- Takeuchi, A.; Nagao, T. Activation of hole charge carriers and generation of electromotive force in gabbro blocks subjected to nonuniform loading. J. Geophys. Res. Solid Earth 2013, 118, 915–925. [Google Scholar] [CrossRef]
- Rabinovitch, A.; Frid, V.; Bahat, D. Surface oscillations—A possible source of fracture induced electromagnetic radiation. Tectonophysics 2007, 431, 15–21. [Google Scholar] [CrossRef]
- Vallianatos, F.; Tzanis, A. Electric current generation associated with the deformation rate of a solid: Preseismic and coseismic signals. Phys. Chem. Earth 1998, 23, 933–938. [Google Scholar] [CrossRef]
- Vallianatos, F.; Triantis, D.; Tzanis, A.; Anastasiadis, C.; Stavrakas, I. Electric earthquake precursors: From laboratory results to field observations. Phys. Chem. Earth Parts A B C 2004, 29, 339–351. [Google Scholar] [CrossRef]
- Vallianatos, F.; Triantis, D. Scaling in Pressure Stimulated Currents related with rock fracture. Phys. A Stat. Mech. Its Appl. 2008, 387, 4940–4946. [Google Scholar] [CrossRef]
- Yoshida, S.; Uyeshima, M.; Nakatani, M. Electric potential changes associated with slip failure of granite: Preseismic and coseismic signals. J. Geophys. Res. Solid Earth 1997, 102, 14883–14897. [Google Scholar] [CrossRef]
- Revil, A.; Jardani, A. Seismoelectric response of heavy oil reservoirs: Theory and numerical modelling. Geophys. J. Int. 2010, 180, 781–797. [Google Scholar] [CrossRef]
- Zhu, Z.; Toksöz, M.N. Experimental measurements of the streaming potential and seismoelectric conversion in Berea sandstone. Geophys. Prospect. 2012, 61, 688–700. [Google Scholar] [CrossRef]
- Huang, Q.; Ren, H.; Zhang, D.; Chen, Y.J. Medium effect on the characteristics of the coupled seismic and electromagnetic signals. Proc. Jpn. Acad. Ser. B 2015, 91, 17–24. [Google Scholar] [CrossRef]
- Ren, H.; Huang, Q.; Chen, X. Numerical simulation of seismo-electromagnetic fields associated with a fault in a porous medium. Geophys. J. Int. 2016, 206, 205–220. [Google Scholar] [CrossRef]
- Chen, H.-J.; Chen, C.-C.; Ouillon, G.; Sornette, D. Coupled mechano-electrokinetic Burridge-Knopoff model of fault sliding events and transient geoelectric signals. Eur. Phys. J. Spec. Top. 2021, 230, 67–84. [Google Scholar] [CrossRef]
- Burridge, R.; Knopoff, L. Model and Theoretical Seismicity. Bull. Seismol. Soc. Am. 1967, 57, 341–371. [Google Scholar]
- Abaimov, S.G.; Turcotte, D.L.; Shcherbakov, R.; Rundle, J.B. Recurrence and interoccurrence behavior of self-organized complex phenomena. Nonlinear Process. Geophys. 2007, 14, 455–464. [Google Scholar] [CrossRef]
- Brown, S.R.; Scholz, C.H.; Rundle, J.B. A simplified spring-block model of earthquakes. Geophys. Res. Lett. 1991, 18, 215–218. [Google Scholar] [CrossRef]
- Carlson, J.M. Two-dimensional model of a fault. Phys. Rev. A 1991, 44, 6226–6232. [Google Scholar] [CrossRef]
- Pelletier, J.D. Spring-Block Models of Seismicity: Review and Analysis of a Structurally Heterogeneous Model Coupled to a Viscous Asthenosphere. In Geocomplexity and the Physics of Earthquakes; Rundle, J.B., Turcotte, D.L., Klein, W., Eds.; American Geophysical Union (AGU): Washington, DC, USA, 2000; pp. 27–42. ISBN 978-1-118-66837-5. [Google Scholar]
- Varotsos, P.; Alexopoulos, K.; Nomicos, K. Comments on the Pressure Variation of the Gibbs Energy for Bound and Unbound Defects. Phys. Status Solidi 1982, 111, 581–590. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations of the electric field of the earth preceding earthquakes. II. determination of epicenter and magnitude. Tectonophysics 1984, 110, 99–125. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on seismic electric signals, II. Tectonophysics 1993, 224, 1–37. [Google Scholar] [CrossRef]
- Gutenberg, B.A.; Richter, C.F. Seismicity of the Earth and Related Phenomena, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 1954. [Google Scholar]
- Hainzl, S.; Zöller, G.; Kurths, J. Similar power laws for foreshock and aftershock sequences in a spring-block model for earthquakes. J. Geophys. Res. Solid Earth 1999, 104, 7243–7253. [Google Scholar] [CrossRef]
- Ruff, L.J. Asperity distributions and large earthquake occurrence in subduction zones. Tectonophysics 1992, 211, 61–83. [Google Scholar] [CrossRef][Green Version]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Phenomena preceding major earthquakes interconnected through a physical model. Ann. Geophys. 2019, 37, 315–324. [Google Scholar] [CrossRef]
- Mavromatou, C.; Hadjicontis, V.; Ninos, D.; Mastrogiannis, D.; Eftaxias, K.; Hadjicontis, E. Understanding the fracture phenomena in inhomogeneous rock samples and ionic crystals, by monitoring the electromagnetic emission during their deformation. Phys. Chem. Earth Parts A B C 2004, 29, 353–357. [Google Scholar] [CrossRef]
- Yang, C.; Liu, S.; Liu, J.; Yang, H.; Xie, J. Characteristics of self-potential of coal samples under uniaxial compression. J. Appl. Geophys. 2019, 168, 1–11. [Google Scholar] [CrossRef]
- Nenovski, P. Underground current impulses as a possible source of unipolar magnetic pulses. Acta Geod. Geophys. 2018, 53, 555–577. [Google Scholar] [CrossRef]
- Scoville, J.T.; Heraud, J.; Freund, F. Pre-earthquake magnetic pulses. Nat. Hazards Earth Syst. Sci. 2015, 15, 1873–1880. [Google Scholar] [CrossRef]
- Bleier, T.; Dunson, C.; Maniscalco, M.; Bryant, N.; Bambery, R.; Freund, F. Investigation of ULF magnetic pulsations, air conductivity changes, and infra red signatures associated with the 30 October Alum Rock M5.4 earthquake. Nat. Hazards Earth Syst. Sci. 2009, 9, 585–603. [Google Scholar] [CrossRef]
- Bleier, T.; Dunson, C.; Alvarez, C.; Freund, F.; Dahlgren, R. Correlation of pre-earthquake electromagnetic signals with laboratory and field rock experiments. Nat. Hazards Earth Syst. Sci. 2010, 10, 1965–1975. [Google Scholar] [CrossRef]
- Bleier, T.; Dunson, C.; Roth, S.; Heraud, J.; Lira, A.; Freund, F.; Dahlgren, R.; Bambery, R.; Bryant, N.; Liu, J.Y.; et al. Ground-based and space-based electromagnetic monitoring for pre-earthquake signals. In Earthquake Prediction Studies: Seismo Electromagnetics; Hayakawa, M., Ed.; TERRAPUB: Tokyo, Japan, 2013; pp. 113–127. ISBN 978-4-88704-163-9. [Google Scholar]
- Ramírez-Rojas, A.; Pavía-Miller, C.; Angulo-Brown, F. Statistical behavior of the spectral exponent and the correlation time of electric self-potential time series associated to the Ms=7.4 14 September 1995 earthquake in Mexico. Phys. Chem. Earth Parts A B C 2004, 29, 305–312. [Google Scholar] [CrossRef]
- Petraki, E.; Nikolopoulos, D.; Chaldeos, Y.; Koulouras, G.; Nomicos, C.; Yannakopoulos, P.H.; Kottou, S.; Stonham, J. Fractal evolution of MHz electromagnetic signals prior to earthquakes: Results collected in Greece during 2009. Geomat. Nat. Hazards Risk 2016, 7, 550–564. [Google Scholar] [CrossRef][Green Version]
- Archer, J.W.; Dobbs, M.R.; Aydin, A.; Reeves, H.J.; Prance, R.J. Measurement and correlation of acoustic emissions and pressure stimulated voltages in rock using an electric potential sensor. Int. J. Rock Mech. Min. Sci. 2016, 89, 26–33. [Google Scholar] [CrossRef]
- Freund, F. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Freund, F.T. Pre-earthquake signals—Part I: Deviatoric stresses turn rocks into a source of electric currents. Nat. Hazards Earth Syst. Sci. 2007, 7, 535–541. [Google Scholar] [CrossRef]
- Freund, F.T. Pre-earthquake signals—Part II: Flow of battery currents in the crust. Nat. Hazards Earth Syst. Sci. 2007, 7, 543–548. [Google Scholar] [CrossRef]
- Takeuchi, A.; Aydan, Ö.; Sayanagi, K.; Nagao, T. Generation of electromotive force in igneous rocks subjected to non-uniform loading. Earthq. Sci. 2011, 24, 593–600. [Google Scholar] [CrossRef][Green Version]
- Theimer, B.D.; Nobes, D.C.; Warner, B.G. A study of the geoelectrical properties of peatlands and their influence on ground-penetrating radar surveying1. Geophys. Prospect. 1994, 42, 179–209. [Google Scholar] [CrossRef]
- Jouniaux, L.; Pozzi, J.-P. Permeability dependence of streaming potential in rocks for various fluid conductivities. Geophys. Res. Lett. 1995, 22, 485–488. [Google Scholar] [CrossRef]
- Knight, R.J.; Nur, A. The dielectric constant of sandstones, 60 kHz to 4 MHz. Geophysics 1987, 52, 644–654. [Google Scholar] [CrossRef]
- Niu, Q.; Zhang, C.; Prasad, M. A Framework for Pore-Scale Simulation of Effective Electrical Conductivity and Permittivity of Porous Media in the Frequency Range from 1 mHz to 1 GHz. J. Geophys. Res. Solid Earth 2020, 125. [Google Scholar] [CrossRef]
- Porretta, R.; Bianchi, F. Profiles of Relative Permittivity and Electrical Conductivity from Unsaturated Soil Water Content Models. Ann. Geophys. 2016, 59, 0320. [Google Scholar] [CrossRef]
- Cartwright-Taylor, A.; Vallianatos, F.; Sammonds, P. Superstatistical view of stress-induced electric current fluctuations in rocks. Phys. A Stat. Mech. Its Appl. 2014, 414, 368–377. [Google Scholar] [CrossRef]
- Chen, H.-J.; Ye, Z.-K.; Chiu, C.-Y.; Telesca, L.; Chen, C.-C.; Chang, W.-L. Self-Potential Ambient Noise and Spectral Relationship with Urbanization, Seismicity, and Strain Rate Revealed via the Taiwan Geoelectric Monitoring Network. J. Geophys. Res. Solid Earth 2020, 125. [Google Scholar] [CrossRef]
- Fisher, R.A. Theory of Statistical Estimation. Math. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Vignat, C.; Bercher, J.-F. Analysis of signals in the Fisher–Shannon information plane. Phys. Lett. A 2003, 312, 27–33. [Google Scholar] [CrossRef]
- Frieden, B.R. Fisher information, disorder, and the equilibrium distributions of physics. Phys. Rev. A 1990, 41, 4265–4276. [Google Scholar] [CrossRef] [PubMed]
- Frieden, B.R.; Soffer, B.H. Lagrangians of physics and the game of Fisher-information transfer. Phys. Rev. E 1995, 52, 2274–2286. [Google Scholar] [CrossRef]
- Martin, M.; Perez, J.; Plastino, A. Fisher information and nonlinear dynamics. Phys. A Stat. Mech. Its Appl. 2001, 291, 523–532. [Google Scholar] [CrossRef]
- Sen, K.D.; Antolín, J.; Angulo, J.C. Fisher-Shannon analysis of ionization processes and isoelectronic series. Phys. Rev. A 2007, 76, 032502. [Google Scholar] [CrossRef]
- Baravalle, R.; Rosso, O.A.; Montani, F. Causal Shannon–Fisher Characterization of Motor/Imagery Movements in EEG. Entropy 2018, 20, 660. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L.; Lovallo, M. Analysis of the time dynamics in wind records by means of multifractal detrended fluctuation analysis and the Fisher–Shannon information plane. J. Stat. Mech. Theory Exp. 2011, 2011, P07001. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Hsu, H.-L.; Chen, C.-C. Analysis of dynamics in magnetotelluric data by using the Fisher–Shannon method. Phys. A Stat. Mech. Its Appl. 2011, 390, 1350–1355. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M. Fisher-Shannon Analysis of Wind Records. Int. J. Energy Stat. 2013, 1, 281–290. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Chamoli, A.; Dimri, V.P.; Srivastava, K. Fisher–Shannon analysis of seismograms of tsunamigenic and non-tsunamigenic earthquakes. Phys. A Stat. Mech. Its Appl. 2013, 392, 3424–3429. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Romano, G.; Konstantinou, K.I.; Hsu, H.-L.; Chen, C.-C. Using the informational Fisher–Shannon method to investigate the influence of long-term deformation processes on geoelectrical signals: An example from the Taiwan orogeny. Phys. A Stat. Mech. Its Appl. 2014, 414, 340–351. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Ramírez-Rojas, A.; Angulo-Brown, F. A nonlinear strategy to reveal seismic precursory signatures in earthquake-related self-potential signals. Phys. A Stat. Mech. Its Appl. 2009, 388, 2036–2040. [Google Scholar] [CrossRef]
- Telesca, L.; Lovallo, M.; Carniel, R. Time-dependent Fisher Information Measure of volcanic tremor before the 5 April 2003 paroxysm at Stromboli volcano, Italy. J. Volcanol. Geotherm. Res. 2010, 195, 78–82. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Minadakis, G.; Eftaxias, K. Analysis of electromagnetic pre-seismic emissions using Fisher information and Tsallis entropy. Phys. A Stat. Mech. Its Appl. 2012, 391, 300–306. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Minadakis, G.; Nomicos, C.D.; Eftaxias, K. A multidisciplinary analysis for traces of the last state of earthquake generation in preseismic electromagnetic emissions. Nat. Hazards Earth Syst. Sci. 2011, 11, 2859–2879. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V.; Lovallo, M. Fisher Information Analysis of earthquake-related geoelectrical signals. Nat. Hazards Earth Syst. Sci. 2005, 5, 561–564. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Angulo, J.C.; Antolín, J.; Dehesa, J.S.; López-Rosa, S.; Flores-Gallegos, N. Analysis of complexity measures and information planes of selected molecules in position and momentum spaces. Phys. Chem. Chem. Phys. 2010, 12, 7108–7116. [Google Scholar] [CrossRef] [PubMed]
- Romera, E.; Dehesa, J.S. The Fisher–Shannon information plane, an electron correlation tool. J. Chem. Phys. 2004, 120, 8906–8912. [Google Scholar] [CrossRef]
- Angulo, J.C.; Antolín, J.; Sen, K.D. Fisher–Shannon plane and statistical complexity of atoms. Phys. Lett. A 2008, 372, 670–674. [Google Scholar] [CrossRef]
- Janicki, A.; Weron, A. Simulation and Chaotic Behavior of Alpha-Stable Stochastic Processes; Chapman & Hall/CRC Pure and Applied Mathematics; CRC Press: Boca Raton, FL, USA, 1993; ISBN 978-0-8247-8882-7. [Google Scholar]
- Devroye, L. A Course in Density Estimation; Progress in Probability; Birkhäuser Boston Inc.: Cambridge, MA, USA, 1987; ISBN 978-0-8176-3365-3. [Google Scholar]
- Troudi, M.; Alimi, A.M.; Saoudi, S. Analytical Plug-in Method for Kernel Density Estimator Applied to Genetic Neutrality Study. Eurasip J. Adv. Signal Process. 2008, 2008, 739082. [Google Scholar] [CrossRef]
- Raykar, V.C.; Duraiswami, R. Fast optimal bandwidth selection for kernel density estimation. In Proceedings of the 2006 SIAM International Conference on Data Mining, Bethesda, MD, USA, 20–22 April 2006; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006; pp. 524–528. [Google Scholar]
- Telesca, L.; Lovallo, M. On the performance of Fisher Information Measure and Shannon entropy estimators. Phys. A Stat. Mech. Its Appl. 2017, 484, 569–576. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Karadimitrakis, A.; Eftaxias, K. Natural time analysis of critical phenomena: The case of pre-fracture electromagnetic emissions. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 023117. [Google Scholar] [CrossRef]
- Ramirezrojas, A.; Telesca, L.; Angulo-Brown, F. Entropy of geoelectrical time series in the natural time domain. Nat. Hazards Earth Syst. Sci. 2011, 11, 219–225. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Skordas, E.; Sarlis, N.; Lazaridou, M.S. Fluctuations, under time reversal, of the natural time and the entropy distinguish similar looking electric signals of different dynamics. J. Appl. Phys. 2008, 103, 14906. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Study of the temporal correlations in the magnitude time series before major earthquakes in Japan. J. Geophys. Res. Space Phys. 2014, 119, 9192–9206. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Order parameter fluctuations of seismicity in natural time before and after mainshocks. EPL Europhys. Lett. 2010, 91, 59001. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).