Onset of the Mach Reflection of Zel’dovich–von Neumann–Döring Detonations
Abstract
1. Introduction
2. Problem Formulation and Numerical Details
3. Results and Discussion
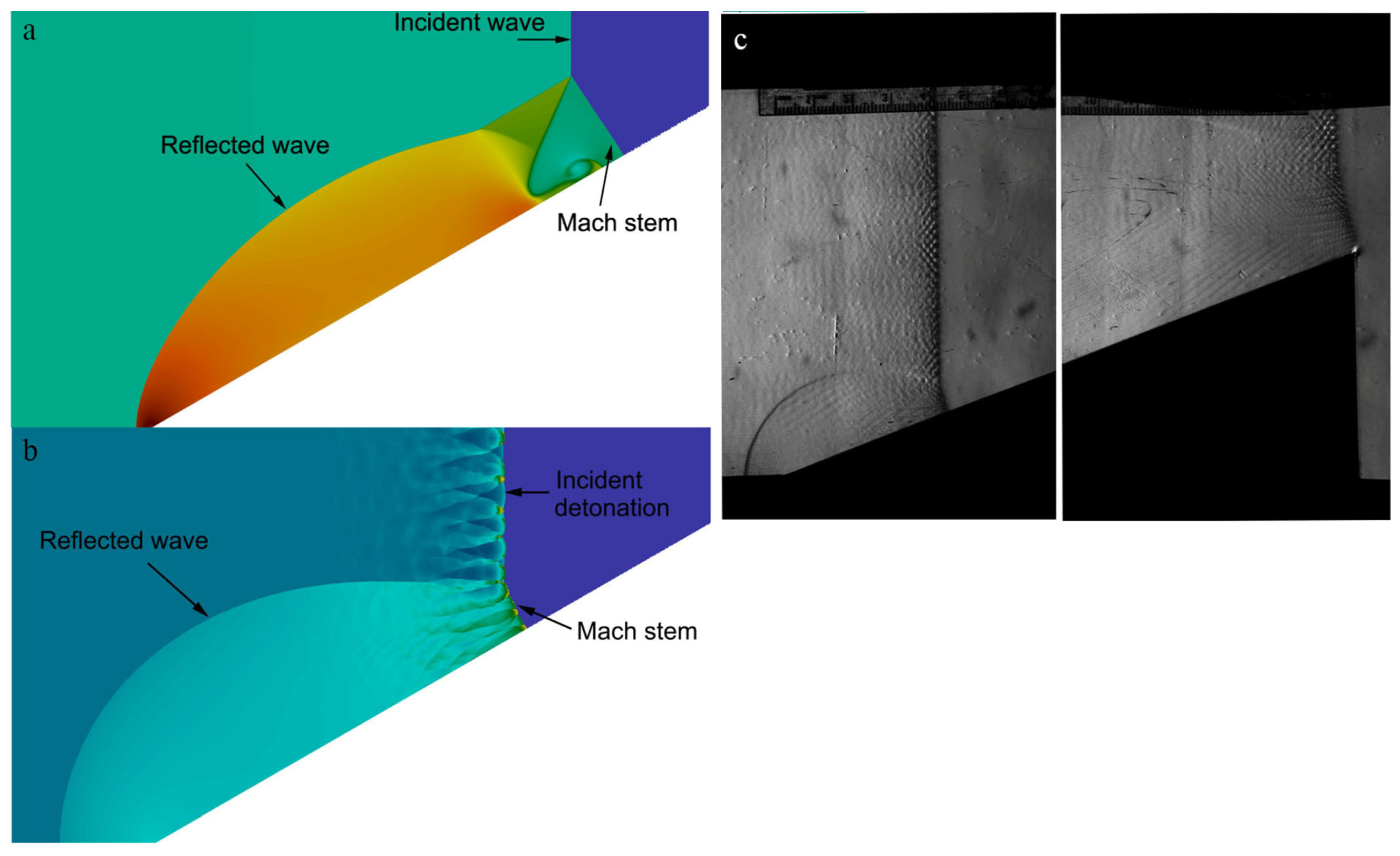
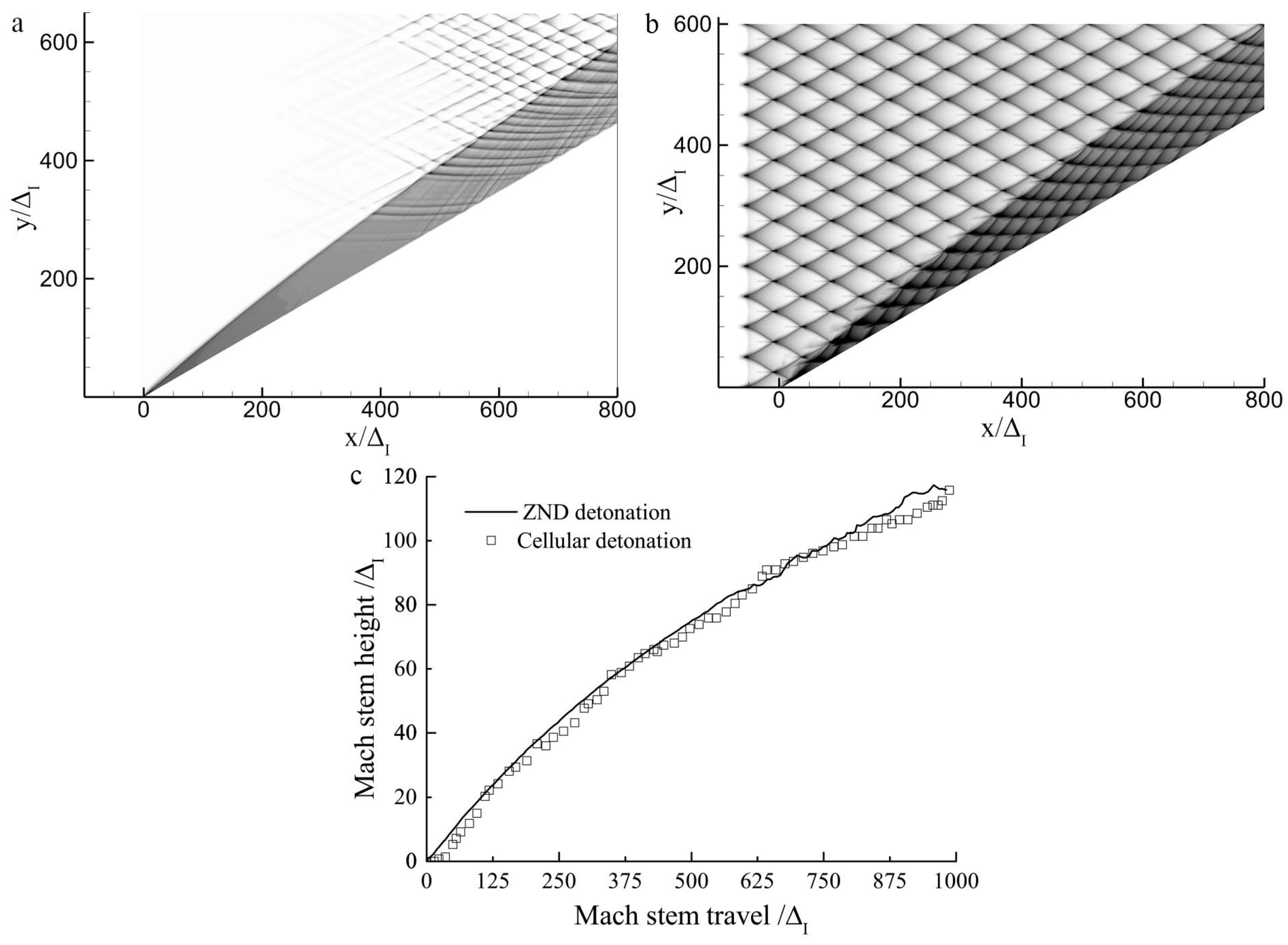
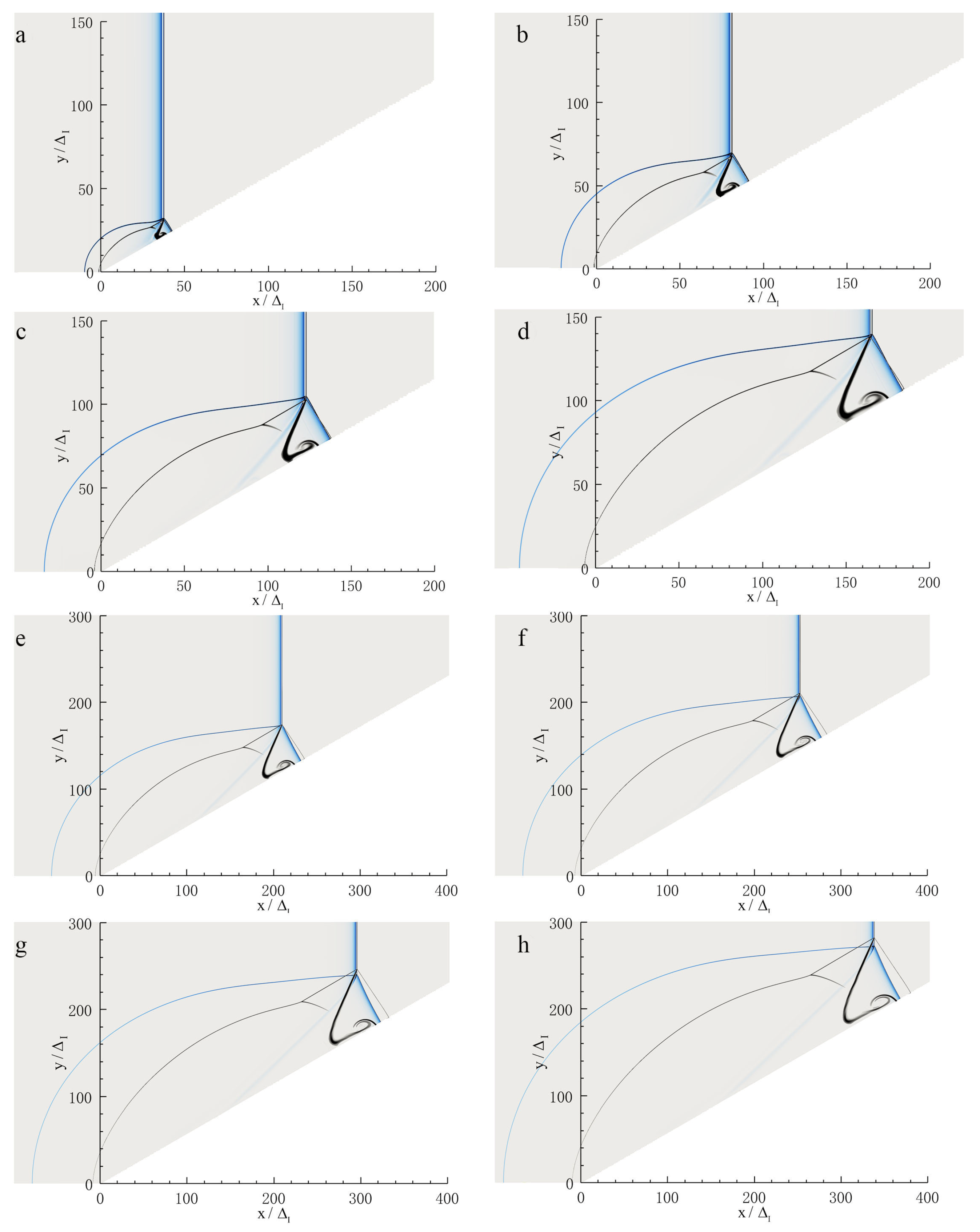
3.1. The Overall Behavior of the Mach Reflection of Detonations on a Wedge
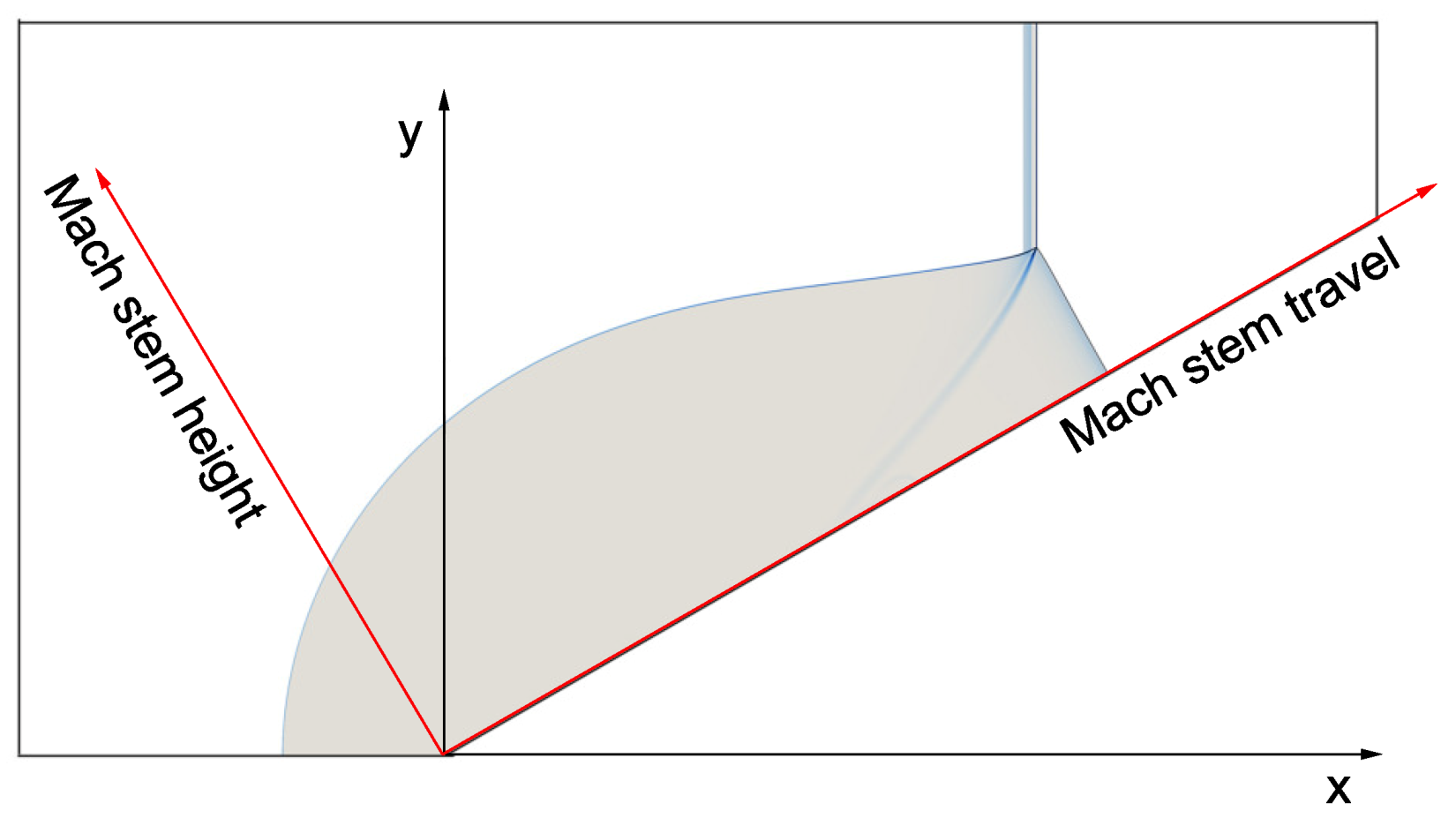
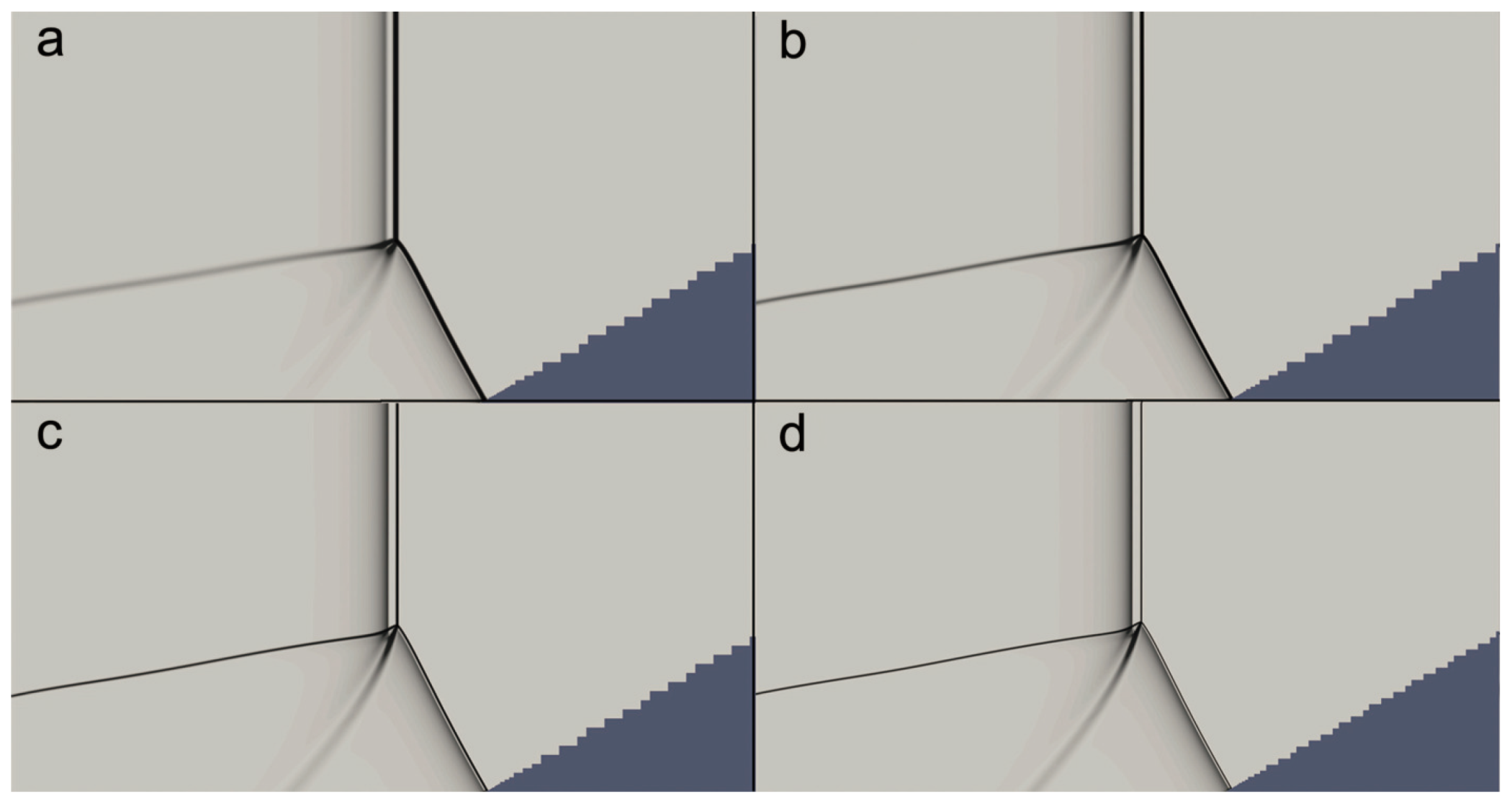
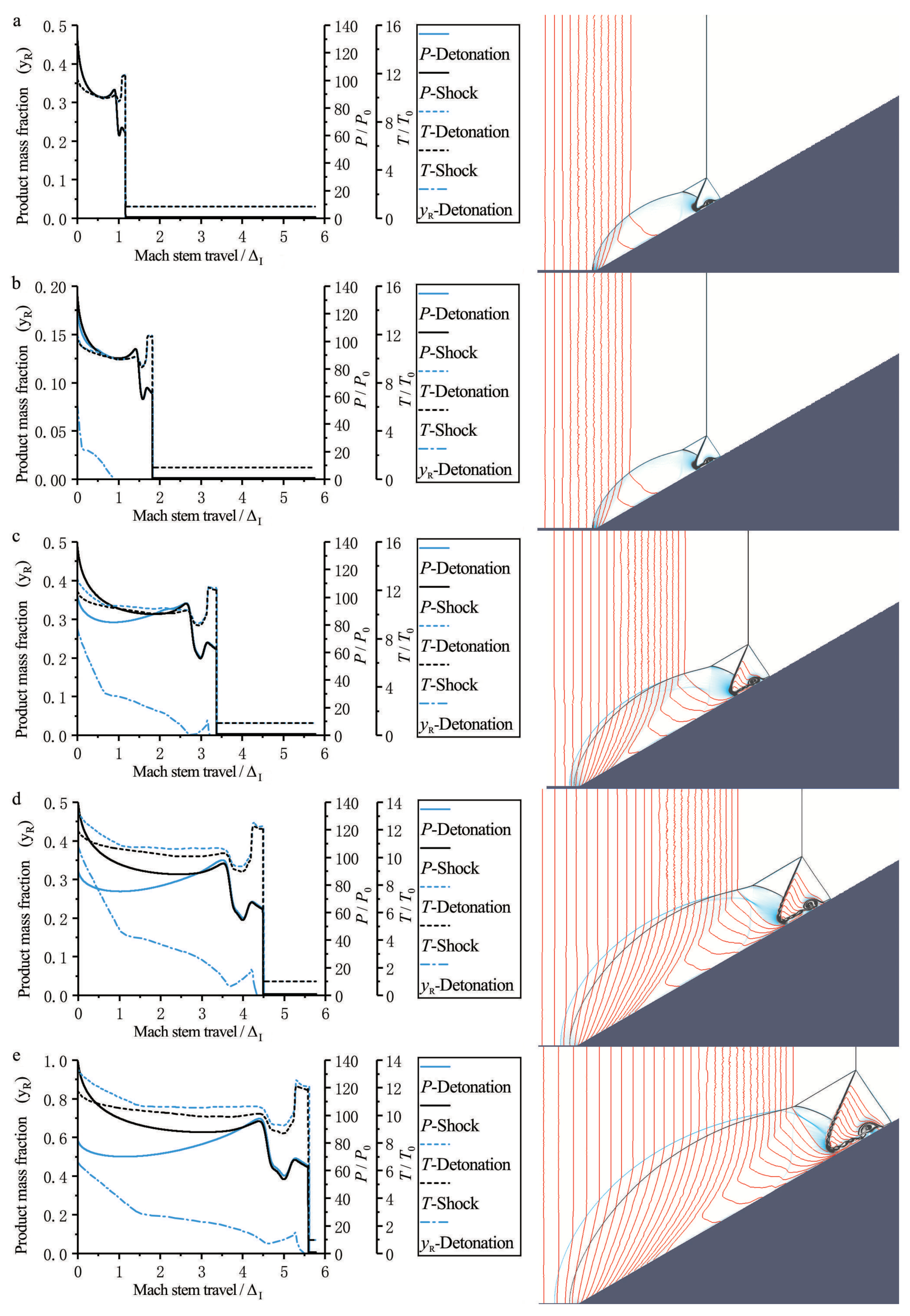
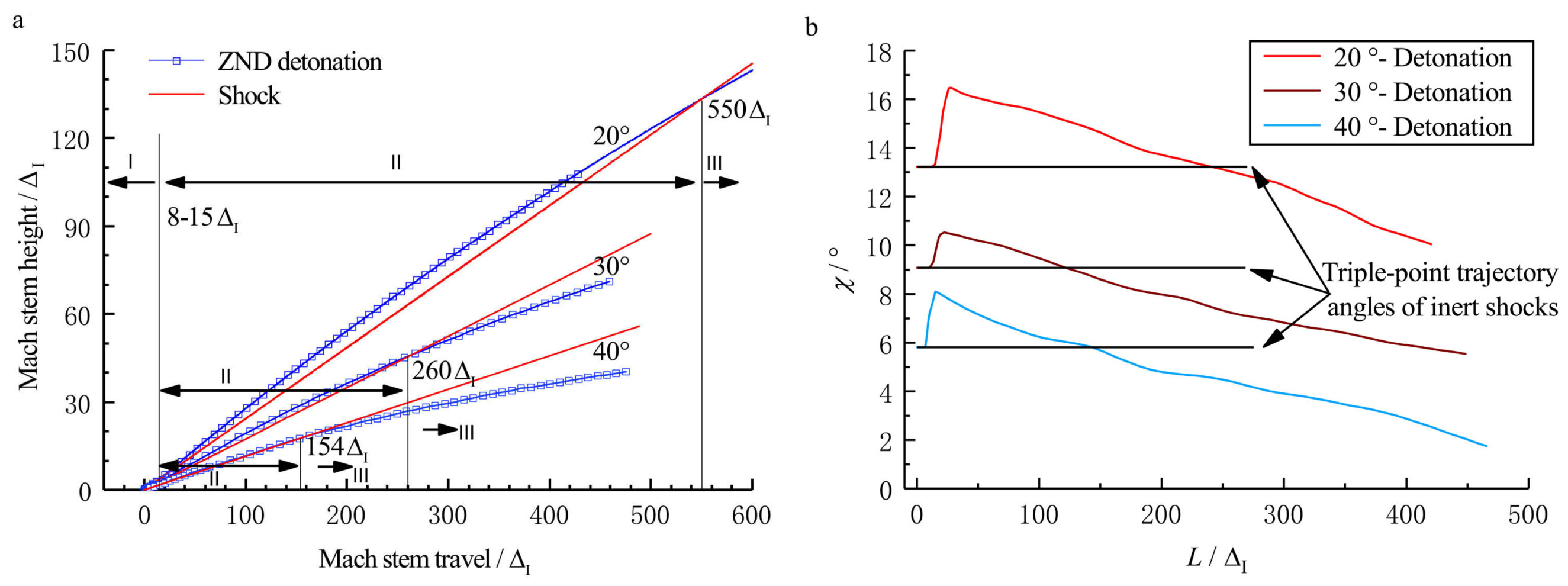
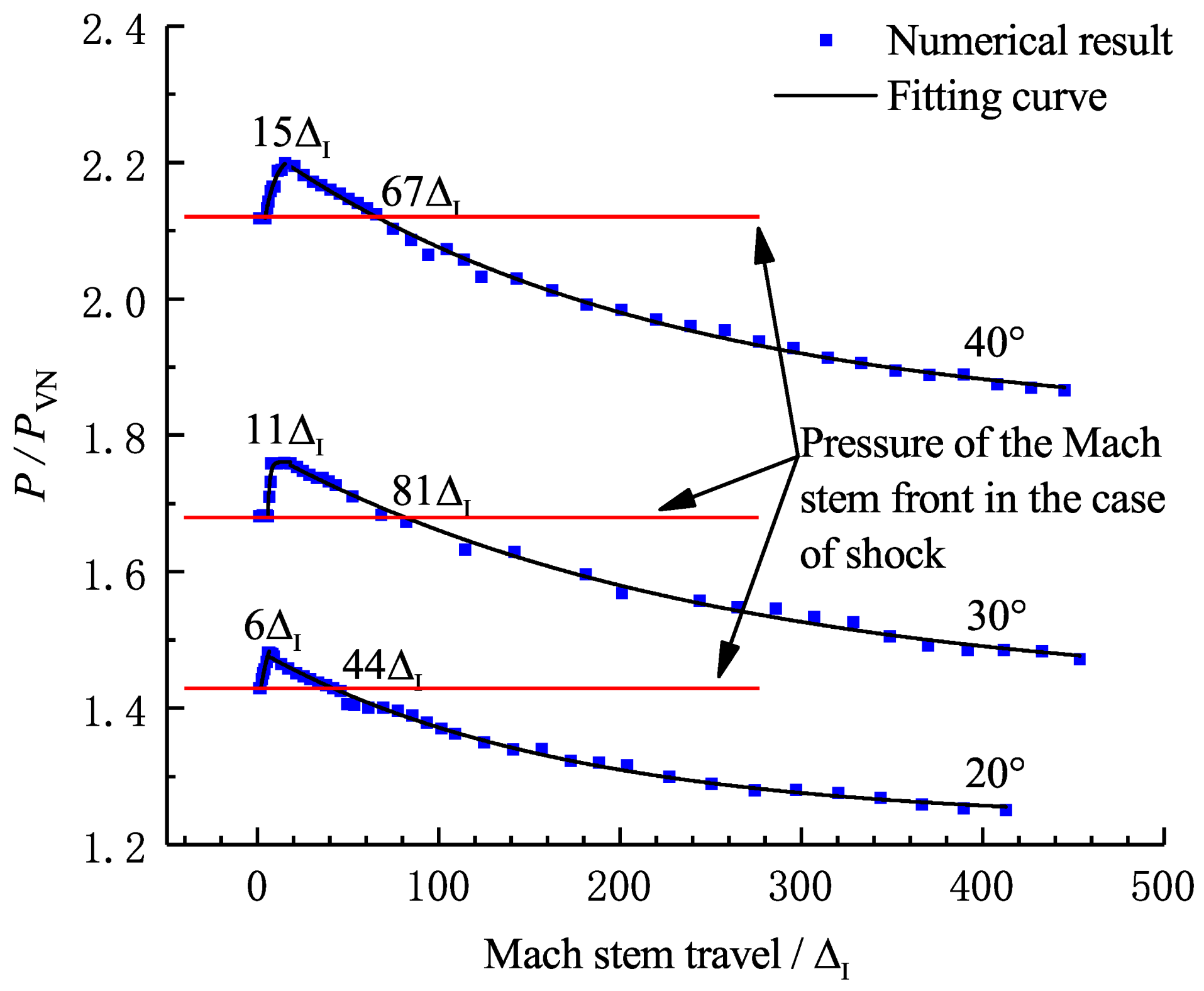
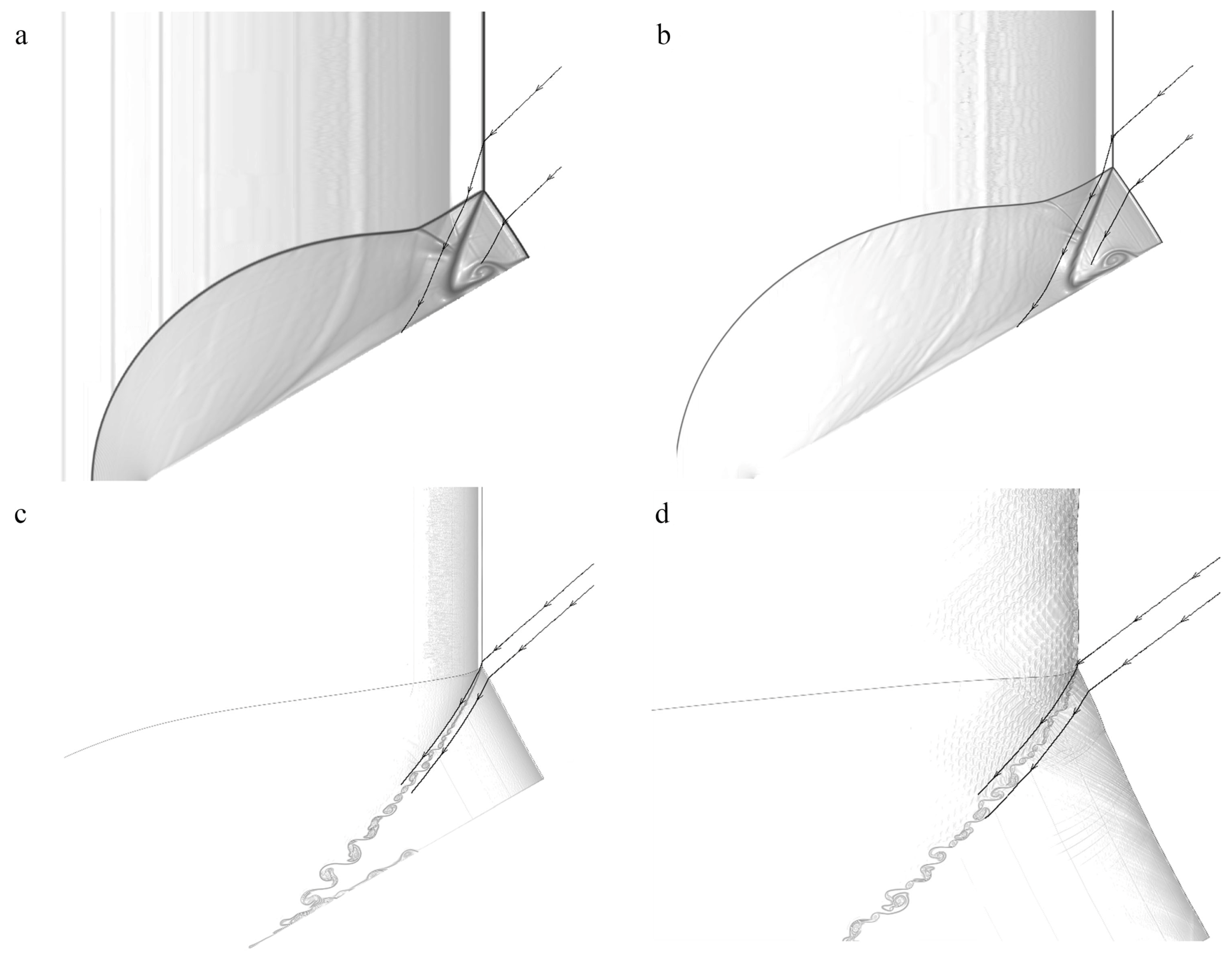
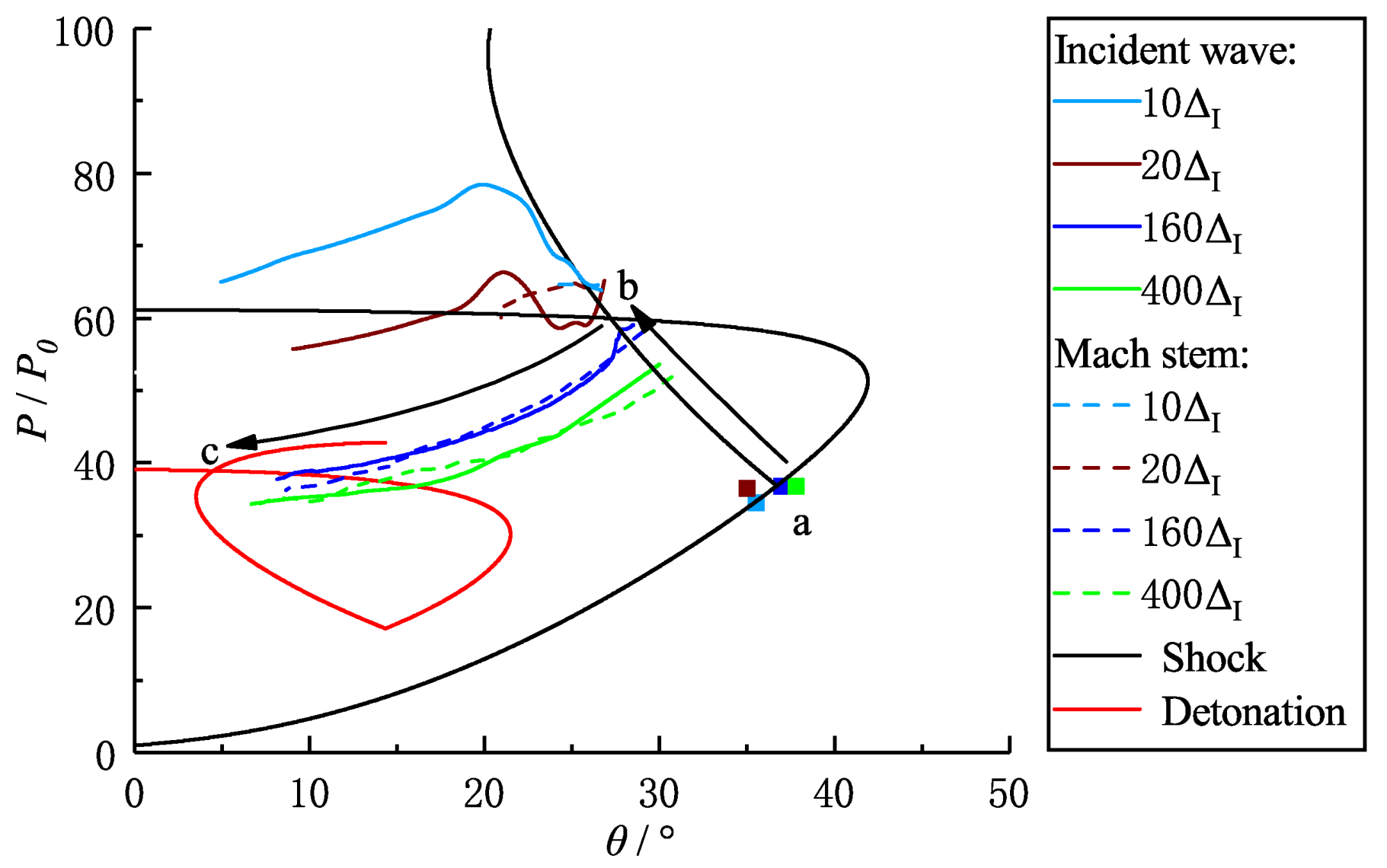
3.2. Evolution of the Mach Reflection Configuration
3.2.1.
3.2.2.
3.2.3.
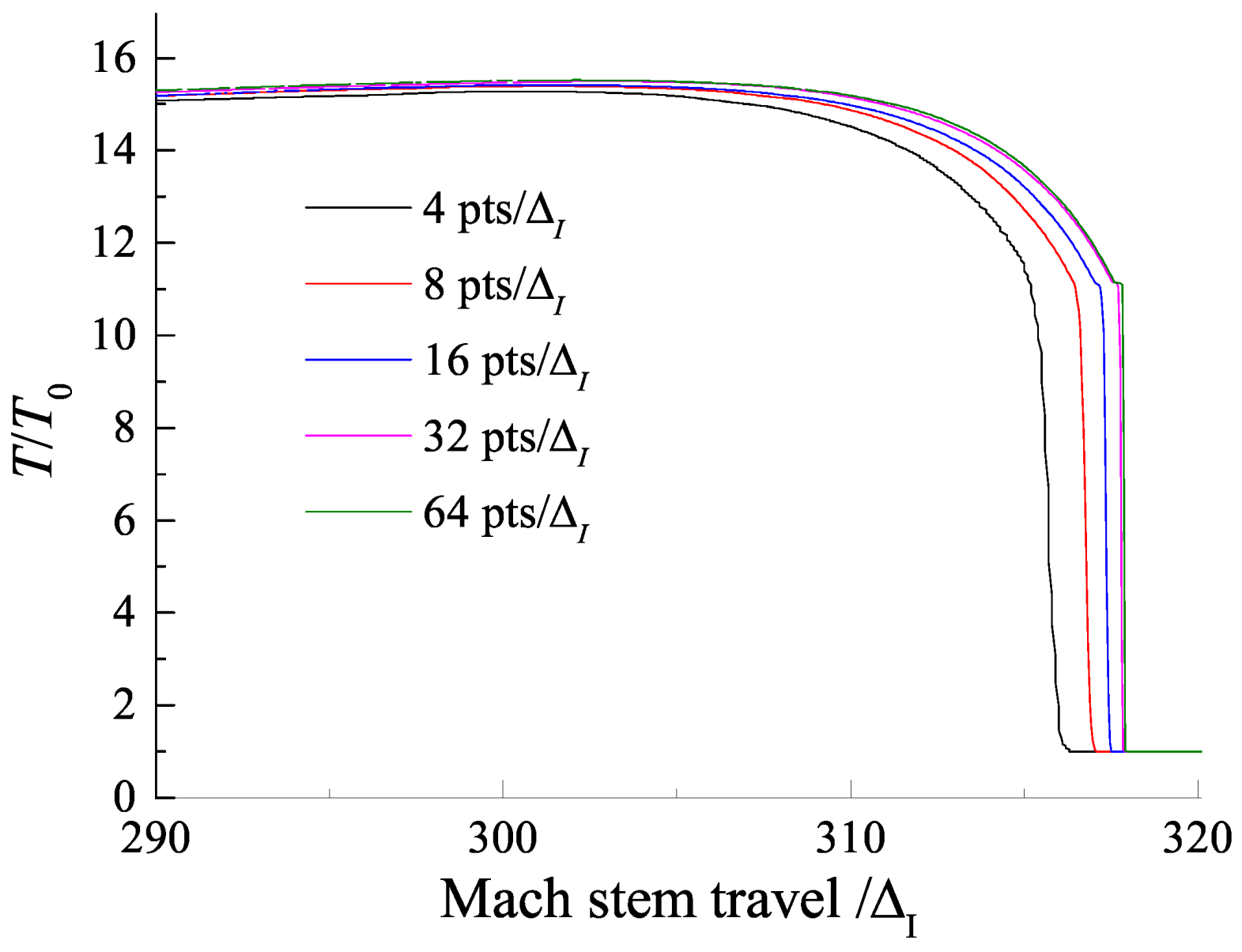
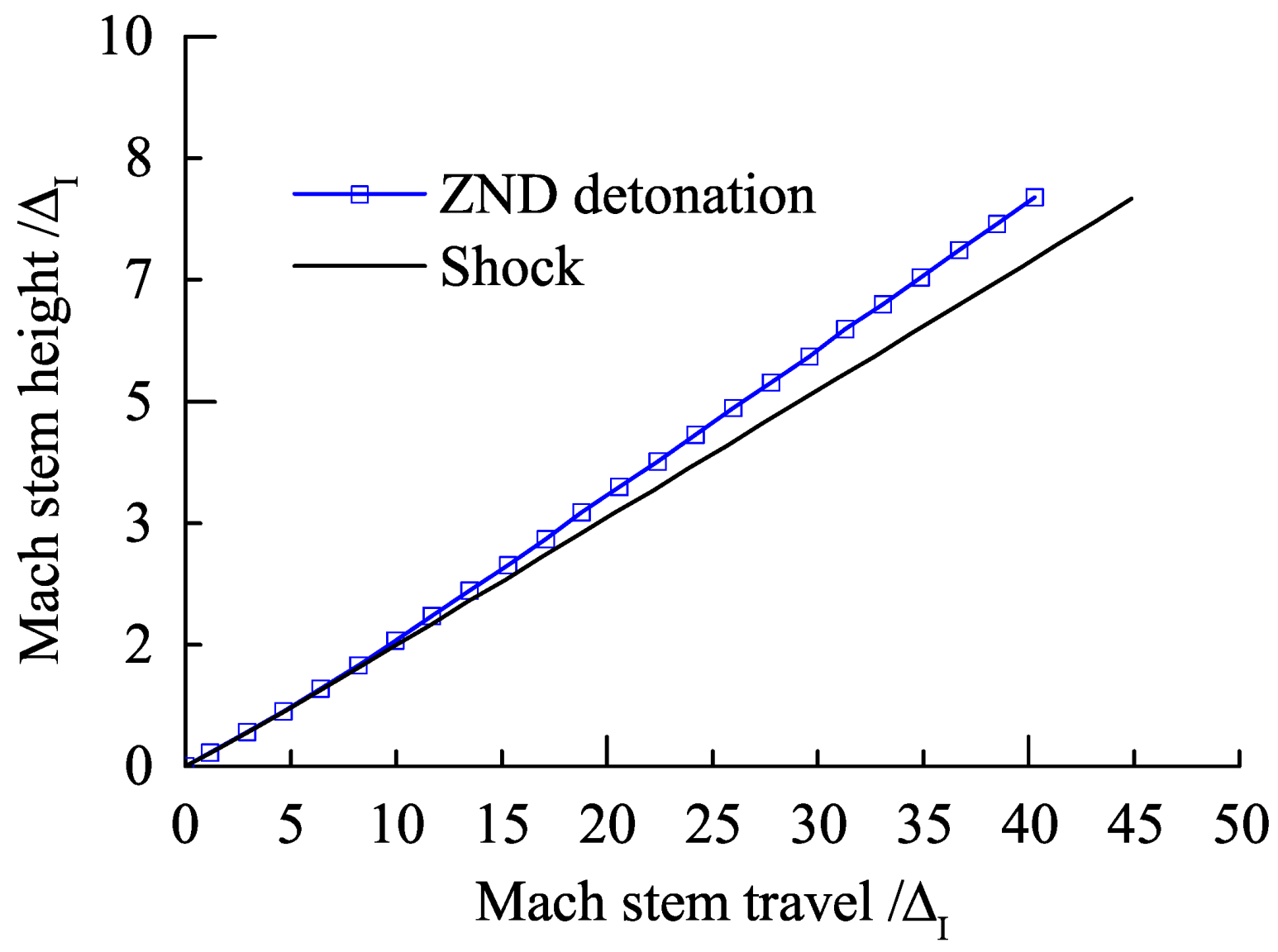
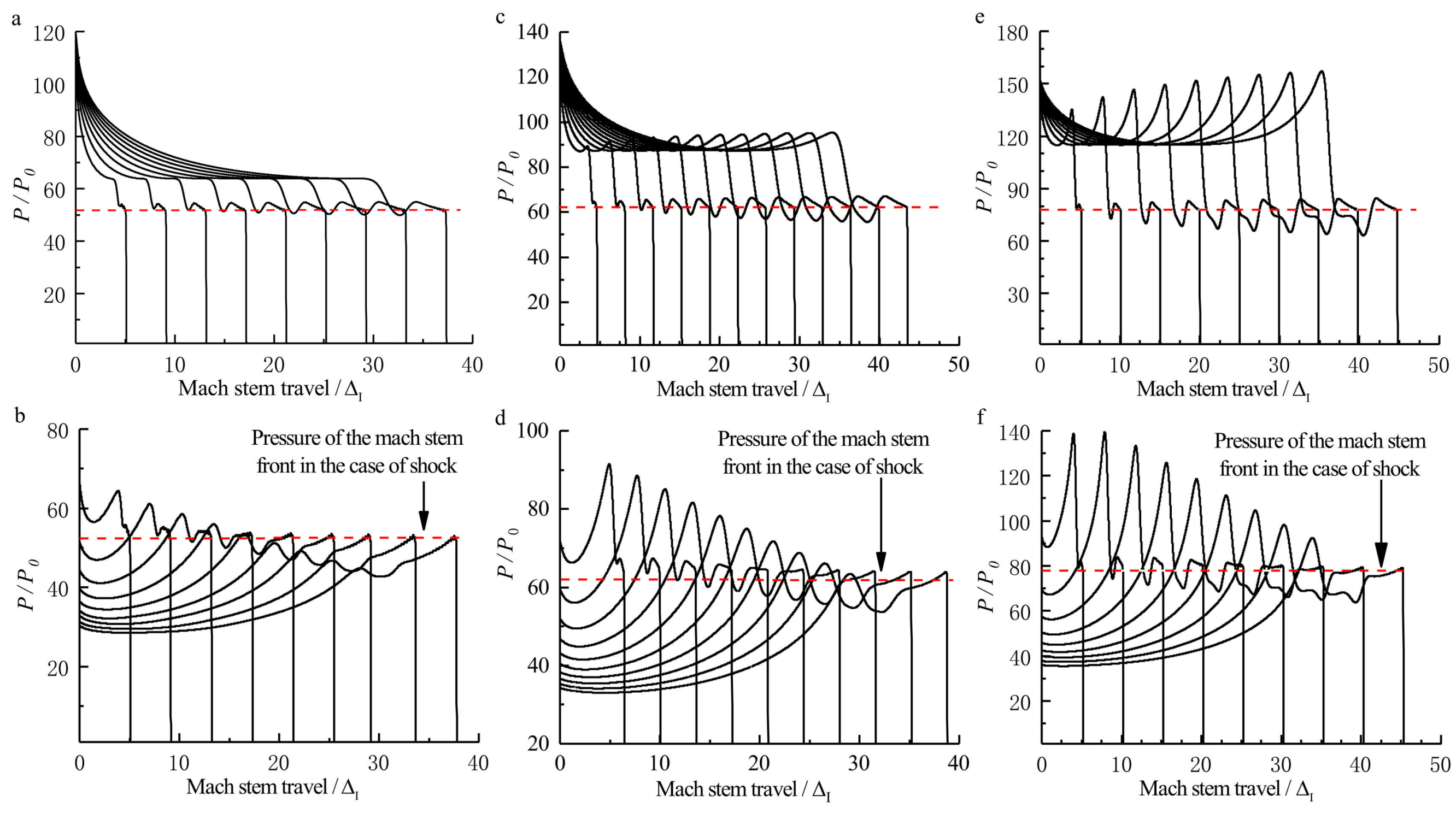
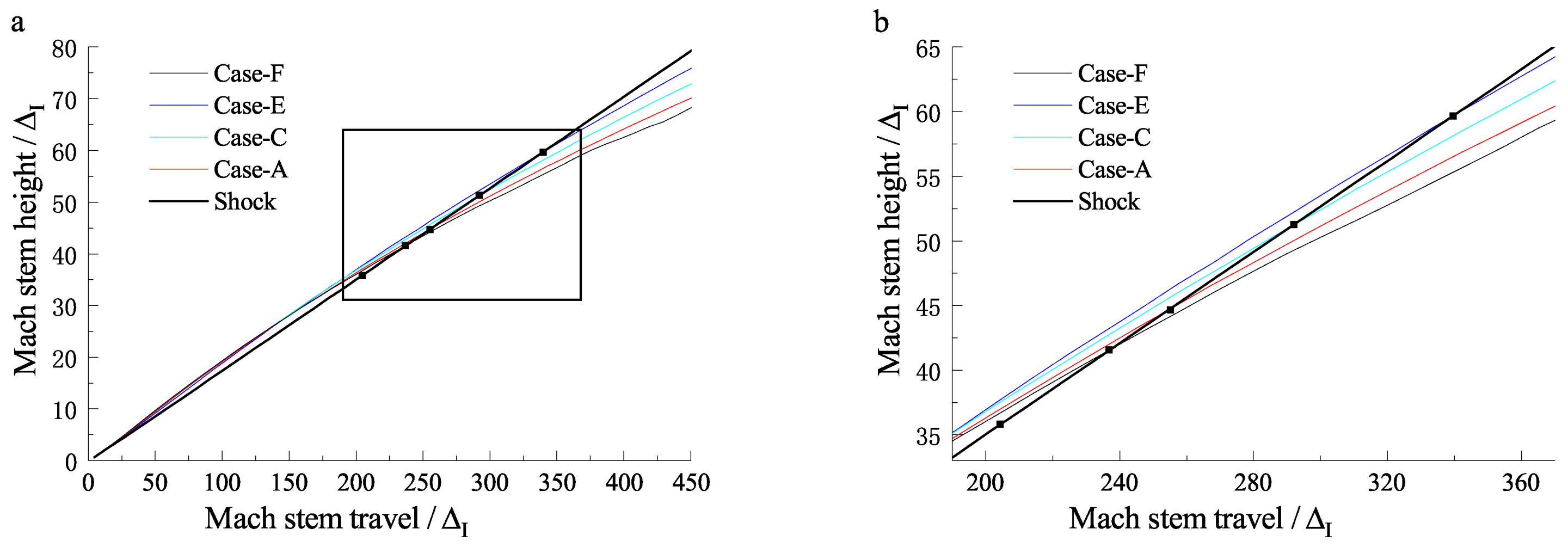
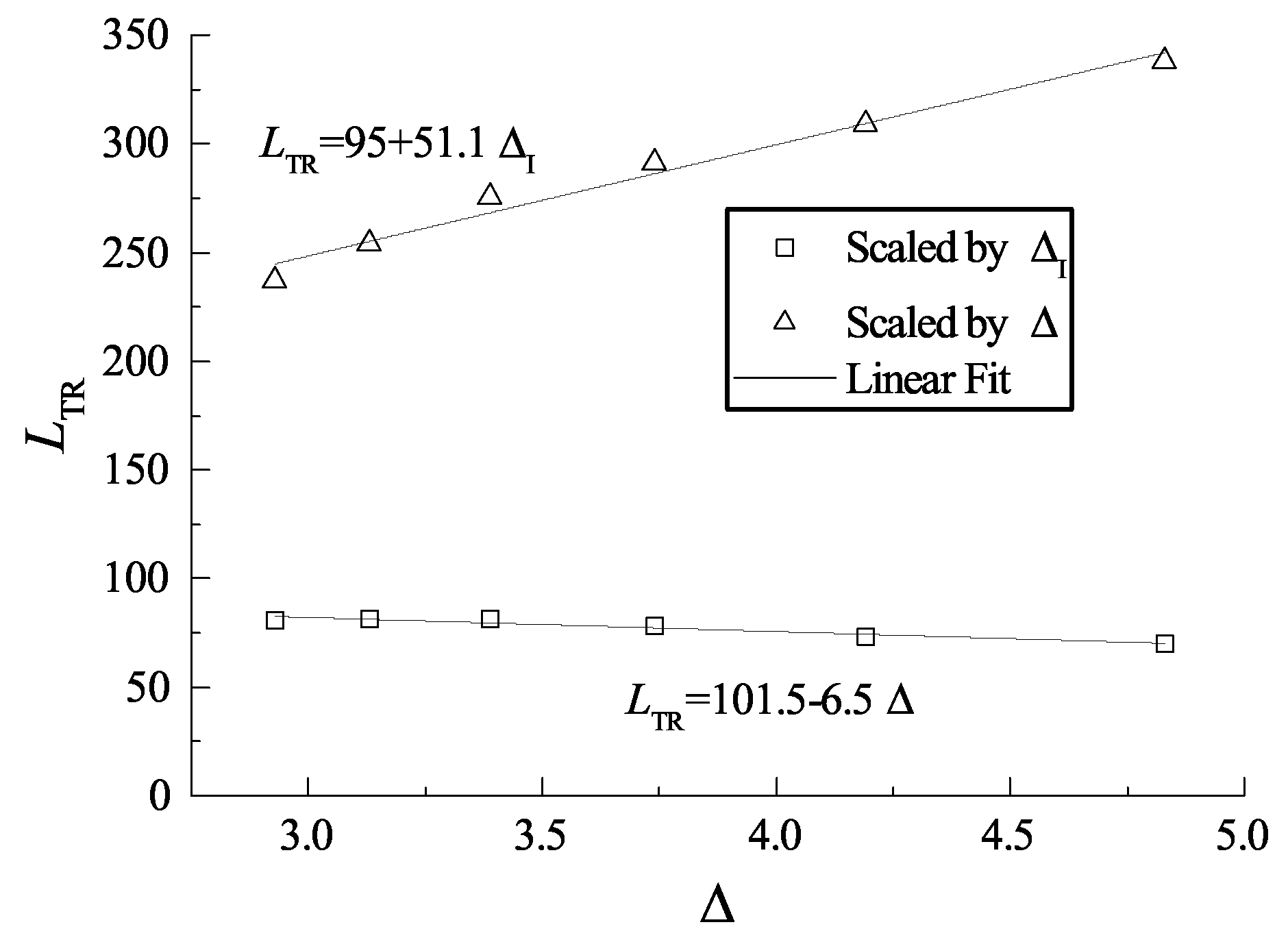
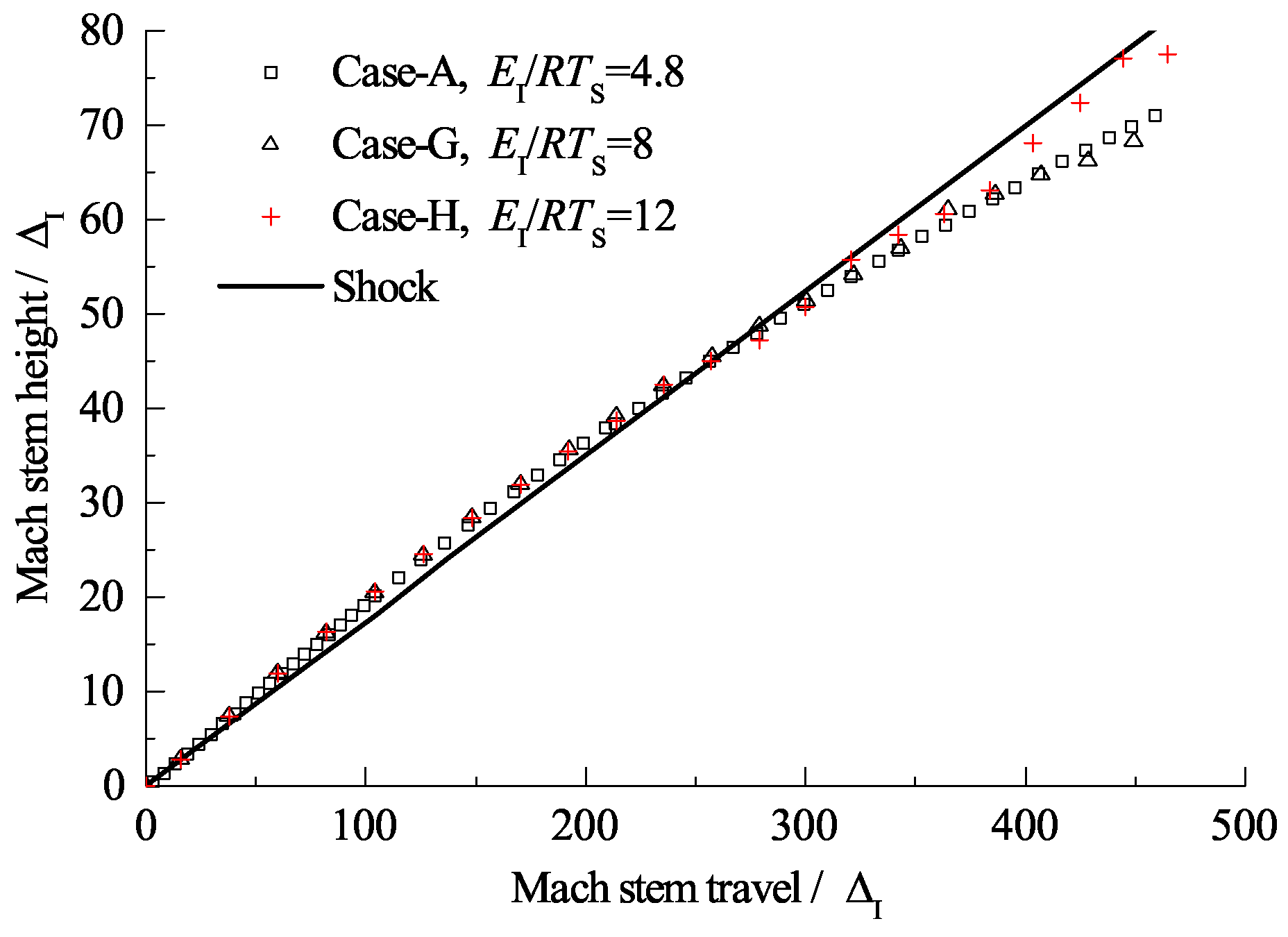
3.3. Length Scale Effect
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Cell size | |
| , , | Induction length, reaction length, detonation thickness |
| Mach number of the Chapman–Jouguet detonation wave | |
| wedge angle | |
| , , | Initial pressure, initial temperature, initial density |
| , | von Neumann pressure and temperature |
| von Neumann pressure | |
| , | Induction and reaction rate constants |
| , | Induction and reaction activation energies |
| , | Induction and reaction progress parameters |
| Q | Heat release |
| R | Gas constant |
| Specific heat ratio | |
| L | Distance of the Mach stem travel |
| Subscripts | |
| w | wedge |
| I | Induction |
| R | Reaction |
| CJ | Chapman–Jouguet |
| ZND | Zeldovich–von Neumann–Döring |
References
- Ning, J.; Chen, L. Fuzzy interface treatment in Eulerian method. Sci. China Ser. E Eng. Mater. Sci. 2004, 47, 550–568. [Google Scholar] [CrossRef]
- Ma, T.; Wang, J.; Ning, J. A hybrid VOF and PIC multi-material interface treatment method and its application in the penetration. Sci. China-Phys. Mech. Astron. 2010, 53, 209–217. [Google Scholar] [CrossRef]
- Ning, J.; Ma, T.; Fei, G. Multi-Material Eulerian Method and Parallel Computation for 3D Explosion and Impact Problems. Int. J. Comp. Meth-Sing 2014, 11, 1350079. [Google Scholar] [CrossRef]
- Ben-Dor, G. Shock Wave Reflection Phenomena, 2nd ed.; Springer: New York, NY, USA, 2007; pp. 7–14. [Google Scholar]
- Hornung, H. Regular and Mach reflection of shock waves. Annu. Rev. Fluid. Mech. 1986, 18, 33–58. [Google Scholar] [CrossRef]
- von Neumann, J. Collected Works; Pergamon Press: Oxford, UK, 1961. [Google Scholar]
- Ong, R. On the Interaction of a Chapman-Jouguet Detonation Wave with a Wedge. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1955; pp. 33–58. [Google Scholar]
- Akbar, R. Mach Reflection of Gaseous Detonations. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 1997. [Google Scholar]
- Li, H.; Ben-Dor, G.; Grönig, H. Head injuries in the newborn and infant. AIAA J. 1997, 35, 1712–1720. [Google Scholar] [CrossRef]
- Shepherd, J.; Schultz, E.; Akbar, R. Detonation diffraction. In Proceedings of the 22nd International Colloquium on the Dynamics of Explosions and Reactive Systems, Minsk, Belarus, 27–31 July 2009. [Google Scholar]
- Meltzer, J.; Shepherd, J.E.; Akbar, R.; Sabet, A. Mach reflection of detonation waves. In AIAA Progress in Astronautics and Aeronautics: Dynamic Aspects of Detonations; Kuhl, A.L., Ed.; AIAA: Reston, VA, USA, 1993; pp. 78–94. [Google Scholar]
- Fortin, Y.; Liu, J.; Lee, J.H.S. Mach reflection of cellular detonations. Combust. Flame 2015, 162, 819–824. [Google Scholar] [CrossRef]
- Li, J.; Ning, J.; Lee, J.H.S. Mach reflection of a ZND detonation wave. Shock Waves 2015, 25, 293–304. [Google Scholar] [CrossRef]
- Trotsyuk, A.V. Numerical study of the reflection of detonation waves from a wedge. Combust. Explos. Shock 1999, 35, 690–697. [Google Scholar] [CrossRef]
- Sandeman, J.; Leitch, A.; Hornung, H. The influence of relaxation on transition to Mach reflection in pseudosteady flow. In Shock Tubes and Waves, Proceedings of the 12th International Symposium, Jerusalem, Israel, 16–19 July 1979; Magnes Press: Jerusalem, Israel, 1979. [Google Scholar]
- Short, M.; Sharpe, G.J. Pulsating instability of detonations with a two-step chain-branching reaction model: Theory and numerics. Combust. Theor. Model. 2003, 7, 401–416. [Google Scholar] [CrossRef]
- Ng, H.D.; Radulescu, M.I.; Higgins, A.J.; Nikiforakis, N.; Lee, J.H.S. Numerical investigation of the instability for one-dimensional chapman-jouguet detonations with chain-branching kinetics. Theor. Model. 2003, 9, 385–401. [Google Scholar] [CrossRef]
- Hornung, H.G.; Oertel, H.; Sandeman, R.J. Transition to mach reflexion of shock waves in steady and pseudosteady flow with and without relaxation. J. Fluid. Mech. 1979, 90, 541–560. [Google Scholar] [CrossRef]
- Ziegler, J.L. Simulations of Compressible, Diffusive, Reactive Flows with Detailed Chemistry Using a High-Order Hybrid WENO-CD Scheme. Ph.D. Thesis, Caltech, Pasadena, CA, USA, 2012. [Google Scholar]
- Radulescu, M.I.; Papi, A.; Quirk, J.; Mach, J.; Mach, P.; Maxwell, B.M. The origin of shock bifurcations in cellular detonations. In Proceedings of the 22nd International Colloquium on the Dynamics of Explosions and Reactive Systems, Minsk, Belarus, 27–31 July 2009. [Google Scholar]
- Reynolds, W.C. The Element Potential Method for Chemical Equilibrium Analysis: Implementation in the Interactive Program STANJAN. Tech. Rep. 1986, 94305. [Google Scholar]
- Wang, C.; Guo, C. On the influence of low initial pressure and detonation stochastic nature on Mach reflection of gaseous detonation waves. Shock Waves 2014, 24, 467–477. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, D.; Liu, K. Numerical study on critical wedge angle of cellular detonation reflections. Chin. Phys. Lett. 2010, 27, 024701. [Google Scholar]
- Guo, C.; Zhang, D.; Xie, W. The Mach reflection of a detonation based on soot track measurements. Combust. Flame 2001, 127, 2051–2058. [Google Scholar]
- Hu, Z.; Jiang, Z. Wave dynamic processes in cellular detonation reflection from wedges. Acta Mech. Sin. 2007, 23, 33–41. [Google Scholar] [CrossRef]
- Li, J.; Lee, J.H.S. Numerical simulation of Mach reflection of cellular detonations. Shock Waves 2016, 26, 673–682. [Google Scholar] [CrossRef]
- Konnov, A.A.; Sharpe, G.J. Detailed Reaction Mechanism for Small Hydrocarbons Combustion. Release 0.4. 2000. Available online: http://homepages.vub.ac.be/~akonnov/ (accessed on 1 March 2021).
- Lee, J.H.S. The Detonation Phenomenon; Cambridge University Press: Cambridge, UK, 2008; Chapters 7–14. [Google Scholar]
- Wang, X.; Ma, T.; Ning, J. A Pseudo Arc-Length Method for Numerical Simulation of Shock Waves. Chin. Phys. Lett. 2014, 31, 030201. [Google Scholar] [CrossRef]
- Wang, X.; Ma, T.; Ren, H.; Ning, J. A local pseudo arc-length method for hyperbolic conservation laws. Acta Mech. Sin. 2014, 30, 956–965. [Google Scholar] [CrossRef]
- Deterding, R. Parallel Adaptive Simulation of Multi-Dimensional Detonation Structures. Ph.D. Thesis, Brandenburgische Technische Universität Cottbus, Cottbus, Germany, 2003. [Google Scholar]
- Berger, M.J.; Colella, P. Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 1989, 82, 64–84. [Google Scholar] [CrossRef]
- Zel’dovich, Y.B.; Librovich, V.B.; Makhviladze, G.M.; Sivashinsky, G.I. On the development of detonation in nonuniformly preheated gas. Acta. Astronaut. 1970, 15, 313–321. [Google Scholar]
- Oran, E.S.; Khokhlov, A.M. Deflagrations, hot spots, and the transition to detonation. Philos. Trans. R. Soc. B 1999, 357, 3539–3551. [Google Scholar] [CrossRef]
- Gu, X.J.; Emerson, D.R.; Bradley, D. Modes of reaction front propagation from hot spots. Combust. Flame 2003, 133, 63–74. [Google Scholar] [CrossRef]
- Nikiforakis, N.; Clarke, J.F. Quasi-Steady Structures in the Two-Dimensional Initiation of Detonations. Porc. R. Soc. A Math. Phys. 1996, 452, 2023–2042. [Google Scholar]

| (/kg/s) | (/kg/s) | (mm) | (mm) | (mm) | |||
|---|---|---|---|---|---|---|---|
| Case-A | 4.8 | 1.0 | 0.1 | 0.213 | 0.313 | ||
| Case-B | 4.8 | 1.0 | 0.1 | 0.239 | 0.339 | ||
| Case-C | 4.8 | 1.0 | 0.1 | 0.274 | 0.374 | ||
| Case-D | 4.8 | 1.0 | 0.1 | 0.319 | 0.419 | ||
| Case-E | 4.8 | 1.0 | 0.1 | 0.383 | 0.483 | ||
| Case-F | 4.8 | 1.0 | 0.1 | 0.193 | 0.293 | ||
| Case-G | 8.0 | 1.0 | 0.1 | 0.213 | 0.313 | ||
| Case-H | 12.0 | 1.0 | 0.1 | 0.213 | 0.313 |
| Model Parameters | Value | Unit |
|---|---|---|
| R | 218.79 | ·K |
| 50 | kPa | |
| 295 | K | |
| 0.775 | kg/ | |
| 19.7 | ||
| 1.44 | ||
| 5.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, T.; Ren, H.; Li, J. Onset of the Mach Reflection of Zel’dovich–von Neumann–Döring Detonations. Entropy 2021, 23, 314. https://doi.org/10.3390/e23030314
Jing T, Ren H, Li J. Onset of the Mach Reflection of Zel’dovich–von Neumann–Döring Detonations. Entropy. 2021; 23(3):314. https://doi.org/10.3390/e23030314
Chicago/Turabian StyleJing, Tianyu, Huilan Ren, and Jian Li. 2021. "Onset of the Mach Reflection of Zel’dovich–von Neumann–Döring Detonations" Entropy 23, no. 3: 314. https://doi.org/10.3390/e23030314
APA StyleJing, T., Ren, H., & Li, J. (2021). Onset of the Mach Reflection of Zel’dovich–von Neumann–Döring Detonations. Entropy, 23(3), 314. https://doi.org/10.3390/e23030314







