Entropy-Regularized Optimal Transport on Multivariate Normal and q-normal Distributions
Abstract
1. Introduction
- Normal distributions are the simplest and best-studied probability distributions, and thus, it is useful to examine the regularization theoretically in order to infer results for other distributions. In particular, we will partly answer the questions “How much do entropy constraints affect the results?” and “What does it mean to constrain by the entropy?’’ for the simplest cases. Furthermore, as a first step in constructing a theory for more general probability distributions, in Section 4, we propose a generalization to multivariate q-normal distributions.
- Because normal distributions are the limit distributions in asymptotic theories using the central limit theorem, studying normal distributions is necessary for the asymptotic theory of regularized Wasserstein distances and estimators computed by them. Moreover, it was proposed to use the entropy-regularized Wasserstein distance to compute a lower bound of the generalization error for a variational autoencoder [29]. The study of the asymptotic behavior of such bounds is one of the expected applications of our results.
- Though this has not yet been proven theoretically, we suspect that entropy regularization is efficient not only for computational reasons, such as the use of the Sinkhorn algorithm, but also in the sense of efficiency in statistical inference. Such a phenomenon can be found in some existing studies, including [33]. Such statistical efficiency is confirmed by some experiments in Section 6.
2. Preliminary
3. Entropy-Regularized Optimal Transport between Multivariate Normal Distributions
- (i)
- is minimized by and
- (ii)
- is maximized by ,
4. Extension to Tsallis Entropy Regularization
5. Entropy-Regularized Kantorovich Estimator
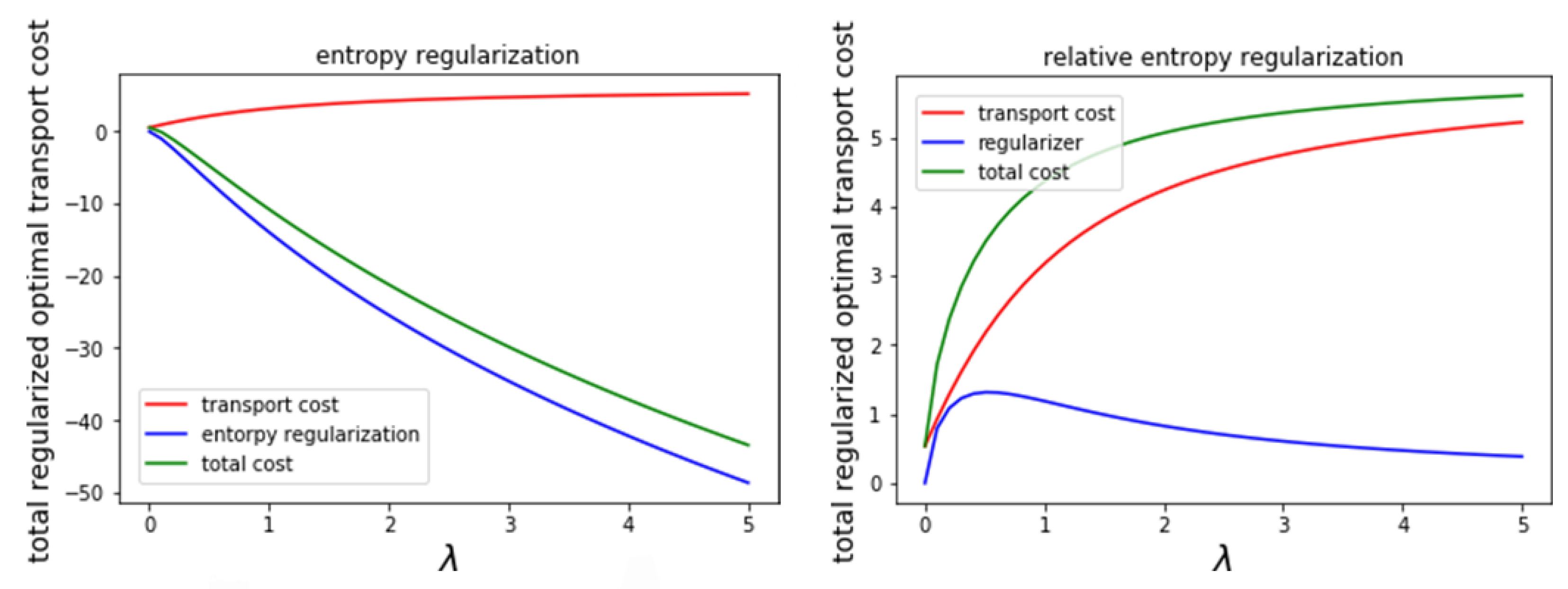
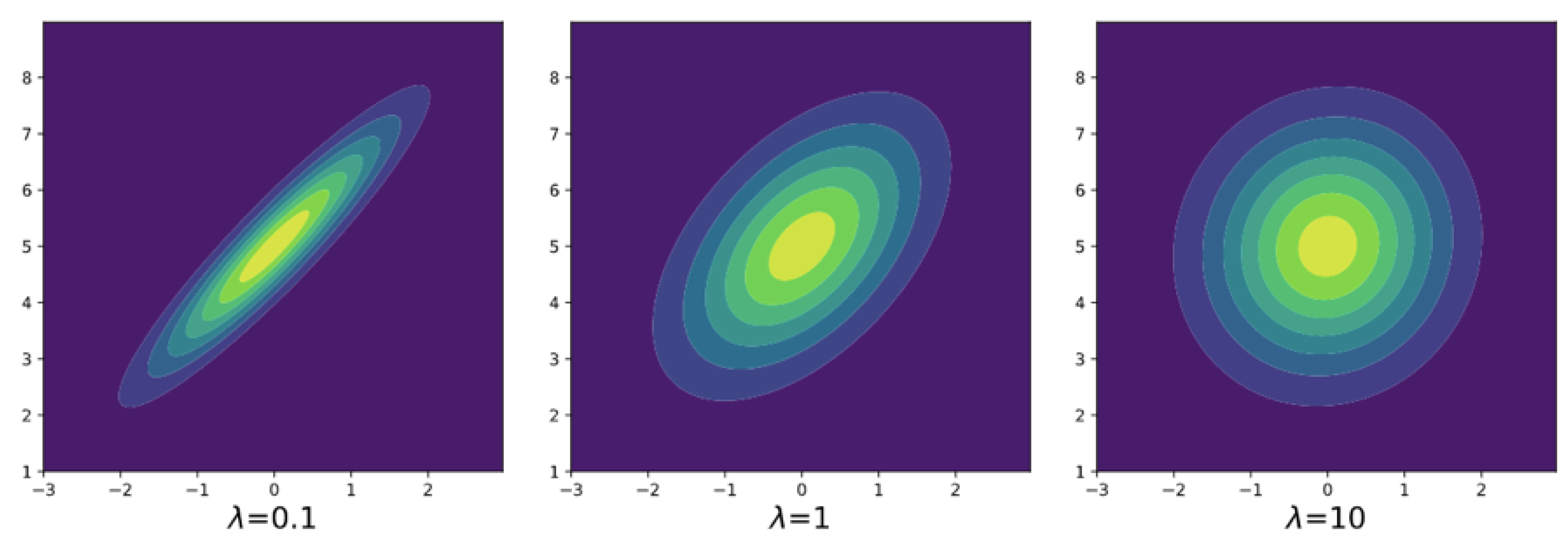
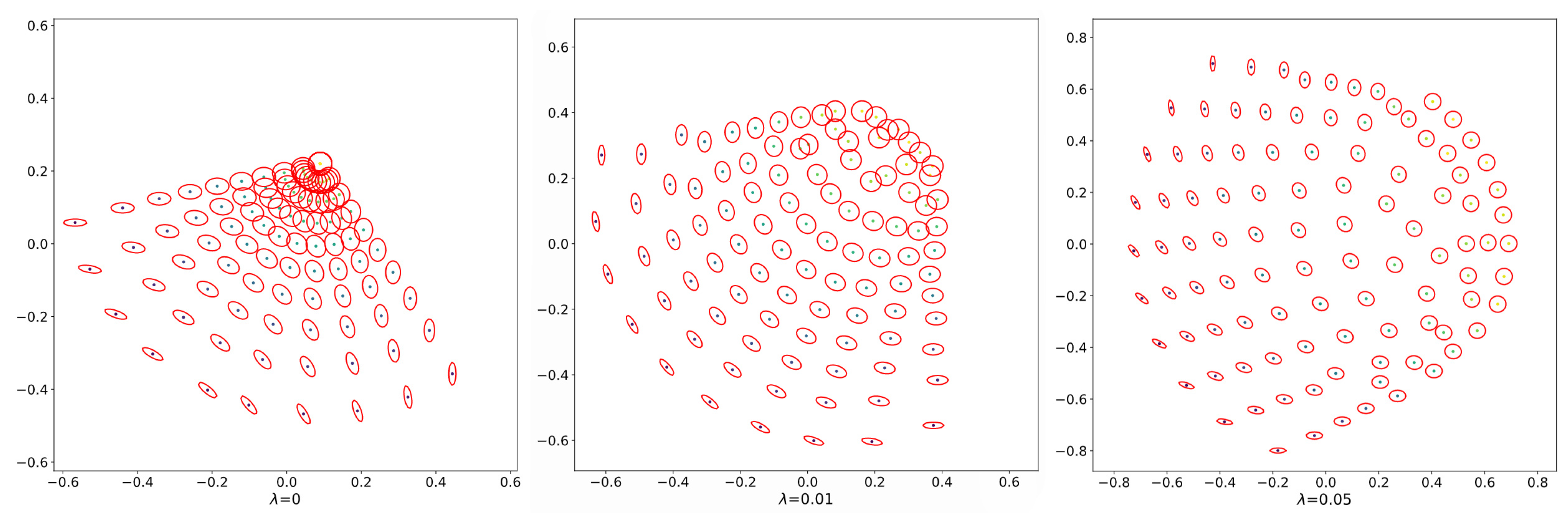
6. Numerical Experiments
6.1. Estimation of Covariance Matrices
- 1.
- Obtain a random sample of size 60 (or 120) from and its sample covariance matrix .
- 2.
- Obtain the entropy-regularized minimum Kantorovich estimator of obtained in Step 1.
- 3.
- Compute the prediction error between and the entropy-regularized minimum Kantorovich estimator of
- 4.
- Repeat the above steps 1000 times and obtain a confidence interval of the prediction error.
6.2. Estimation of the Wasserstein Barycenter
- 1.
- Obtain a random sample of size 60 (or 120) from and its sample covariance matrix .
- 2.
- Repeat Step 1 three times, and obtain .
- 3.
- Obtain the barycenter of .
- 4.
- Compute the prediction error between and the barycenter obtained in step 3.
- 5.
- Repeat the above steps 100 times and obtain a confidence interval of the prediction error.
6.3. Gradient Descent on
6.4. Approximate the Matrix Square Root
| Algorithm 1 Gradient descent on the manifold of positive definite matrices. |
|
| Algorithm 2: Newton–Schulz method. |
|
7. Conclusions and Future Work
- We obtain the explicit form of entropy-regularized optimal transport between two multivariate normal distributions and derived Corollaries 1 and 2, which clarified the properties of optimal coupling. Furthermore, we demonstrate experimentally how entropy regularization affects the Wasserstein distance, the optimal coupling, and the geometric structure of multivariate normal distributions. Overall, the properties of optimal coupling were revealed both theoretically and experimentally. We expect that the explicit formula can be a replacement for the existing methodology using the (nonregularized) Wasserstein distance between normal distributions (for example, [4,5]).
- Theorem 2 derives the explicit form of the optimal coupling of the Tsallis entropy-regularized optimal transport between multivariate q-normal distributions. The optimal coupling of the Tsallis entropy-regularized optimal transport between multivariate q-normal distributions is also a multivariate q-normal distribution, and the obtained result has an analogy to that of the normal distribution. We believe that this result can be extended to other elliptical distribution families.
- The entropy-regularized Kantorovich estimator of a probability measure in is the convolution of a multivariate normal distribution and its own density function. Our experiments show that both the entropy-regularized Kantorovich estimator and the Wasserstein barycenter of multivariate normal distributions outperform the maximum likelihood estimator in the prediction error for adequately selected in a high dimensionality and small sample setting. As future work, we want to show the efficiency of entropy regularization using real data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Villani, C. Optimal Transport: Old and New; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 338. [Google Scholar]
- Rubner, Y.; Tomasi, C.; Guibas, L.J. The Earth Mover’s Distance as a metric for Image Retrieval. Int. J. Comput. Vis. 2000, 40, 99–121. [Google Scholar] [CrossRef]
- Solomon, J.; De Goes, F.; Peyré, G.; Cuturi, M.; Butscher, A.; Nguyen, A.; Du, T.; Guibas, L. Convolutional Wasserstein Distances: Efficient optimal transportation on geometric domains. ACM Trans. Graph. TOG 2015, 34, 1–11. [Google Scholar] [CrossRef]
- Muzellec, B.; Cuturi, M. Generalizing point embeddings using the Wasserstein space of elliptical distributions. In Advances in Neural Information Processing Systems; ACM: New York, NY, USA, 2018; pp. 10237–10248. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs trained by a two time-scale update rule converge to a local nash equilibrium. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 214–223. [Google Scholar]
- Nitanda, A.; Suzuki, T. Gradient layer: Enhancing the convergence of adversarial training for generative models. In Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, Playa Blanca, Spain, 9–11 April 2018; Volume 84, pp. 1008–1016. [Google Scholar]
- Sonoda, S.; Murata, N. Transportation analysis of denoising autoencoders: A novel method for analyzing deep neural networks. arXiv 2017, arXiv:1712.04145. [Google Scholar]
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
- Cuturi, M. Sinkhorn distances: Lightspeed computation of optimal transport. In Advances in Neural Information Processing Systems; ACM: New York, NY, USA, 2013; pp. 2292–2300. [Google Scholar]
- Sinkhorn, R.; Knopp, P. Concerning nonnegative matrices and doubly stochastic matrices. Pac. J. Math. 1967, 21, 343–348. [Google Scholar] [CrossRef]
- Lin, T.; Ho, N.; Jordan, M.I. On the efficiency of the Sinkhorn and Greenkhorn algorithms and their acceleration for optimal transport. arXiv 2019, arXiv:1906.01437. [Google Scholar]
- Lee, Y.T.; Sidford, A. Path finding methods for linear programming: Solving linear programs in o (vrank) iterations and faster algorithms for maximum flow. In Proceedings of the 2014 IEEE 55th Annual Symposium on Foundations of Computer Science, Philadelphia, PA, USA, 18–21 October 2014; pp. 424–433. [Google Scholar]
- Dvurechensky, P.; Gasnikov, A.; Kroshnin, A. Computational optimal transport: Complexity by accelerated gradient descent is better than by Sinkhorn’s algorithm. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1367–1376. [Google Scholar]
- Aude, G.; Cuturi, M.; Peyré, G.; Bach, F. Stochastic optimization for large-scale optimal transport. arXiv 2016, arXiv:1605.08527. [Google Scholar]
- Altschuler, J.; Weed, J.; Rigollet, P. Near-linear time approximation algorithms for optimal transport via Sinkhorn iteration. arXiv 2017, arXiv:1705.09634. [Google Scholar]
- Blondel, M.; Seguy, V.; Rolet, A. Smooth and sparse optimal transport. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Playa Blanca, Spain, 9–11 April 2018; pp. 880–889. [Google Scholar]
- Cuturi, M.; Peyré, G. A smoothed dual approach for variational Wasserstein problems. SIAM J. Imaging Sci. 2016, 9, 320–343. [Google Scholar] [CrossRef]
- Lin, T.; Ho, N.; Jordan, M. On efficient optimal transport: An analysis of greedy and accelerated mirror descent algorithms. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 3982–3991. [Google Scholar]
- Allen-Zhu, Z.; Li, Y.; Oliveira, R.; Wigderson, A. Much faster algorithms for matrix scaling. In Proceedings of the 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS), Berkeley, CA, USA, 15–17 October 2017; pp. 890–901. [Google Scholar]
- Cohen, M.B.; Madry, A.; Tsipras, D.; Vladu, A. Matrix scaling and balancing via box constrained Newton’s method and interior point methods. In Proceedings of the 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS), Berkeley, CA, USA, 15–17 October 2017; pp. 902–913. [Google Scholar]
- Blanchet, J.; Jambulapati, A.; Kent, C.; Sidford, A. Towards optimal running times for optimal transport. arXiv 2018, arXiv:1810.07717. [Google Scholar]
- Quanrud, K. Approximating optimal transport with linear programs. arXiv 2018, arXiv:1810.05957. [Google Scholar]
- Frogner, C.; Zhang, C.; Mobahi, H.; Araya, M.; Poggio, T.A. Learning with a Wasserstein loss. In Advances in Neural Information Processing Systems; ACM: New York, NY, USA, 2015; pp. 2053–2061. [Google Scholar]
- Courty, N.; Flamary, R.; Tuia, D.; Rakotomamonjy, A. Optimal transport for domain adaptation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1853–1865. [Google Scholar] [CrossRef]
- Lei, J. Convergence and concentration of empirical measures under Wasserstein distance in unbounded functional spaces. Bernoulli 2020, 26, 767–798. [Google Scholar] [CrossRef]
- Mena, G.; Niles-Weed, J. Statistical bounds for entropic optimal transport: Sample complexity and the central limit theorem. In Advances in Neural Information Processing Systems; ACM: New York, NY, USA, 2019; pp. 4543–4553. [Google Scholar]
- Rigollet, P.; Weed, J. Entropic optimal transport is maximum-likelihood deconvolution. Comptes Rendus Math. 2018, 356, 1228–1235. [Google Scholar] [CrossRef]
- Balaji, Y.; Hassani, H.; Chellappa, R.; Feizi, S. Entropic GANs meet VAEs: A Statistical Approach to Compute Sample Likelihoods in GANs. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 414–423. [Google Scholar]
- Amari, S.I.; Karakida, R.; Oizumi, M. Information geometry connecting Wasserstein distance and Kullback–Leibler divergence via the entropy-relaxed transportation problem. Inf. Geom. 2018, 1, 13–37. [Google Scholar] [CrossRef]
- Dowson, D.; Landau, B. The Fréchet distance between multivariate normal distributions. J. Multivar. Anal. 1982, 12, 450–455. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Amari, S.I.; Karakida, R.; Oizumi, M.; Cuturi, M. Information geometry for regularized optimal transport and barycenters of patterns. Neural Comput. 2019, 31, 827–848. [Google Scholar] [CrossRef]
- Janati, H.; Muzellec, B.; Peyré, G.; Cuturi, M. Entropic optimal transport between (unbalanced) Gaussian measures has a closed form. In Advances in Neural Information Processing Systems; ACM: New York, NY, USA, 2020. [Google Scholar]
- Mallasto, A.; Gerolin, A.; Minh, H.Q. Entropy-Regularized 2-Wasserstein Distance between Gaussian Measures. arXiv 2020, arXiv:2006.03416. [Google Scholar]
- Peyré, G.; Cuturi, M. Computational optimal transport. Found. Trends® Mach. Learn. 2019, 11, 355–607. [Google Scholar] [CrossRef]
- Monge, G. Mémoire sur la Théorie des Déblais et des Remblais; Histoire de l’Académie Royale des Sciences de Paris: Paris, France, 1781. [Google Scholar]
- Kantorovich, L.V. On the translocation of masses. Proc. USSR Acad. Sci. 1942, 37, 199–201. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Mardia, K.V. Characterizations of directional distributions. In A Modern Course on Statistical Distributions in Scientific Work; Springer: Berlin/Heidelberg, Germany, 1975; pp. 365–385. [Google Scholar]
- Petersen, K.; Pedersen, M. The Matrix Cookbook; Technical University of Denmark: Lyngby, Denmark, 2008; Volume 15. [Google Scholar]
- Takatsu, A. Wasserstein geometry of Gaussian measures. Osaka J. Math. 2011, 48, 1005–1026. [Google Scholar]
- Kruskal, J.B. Nonmetric multidimensional scaling: A numerical method. Psychometrika 1964, 29, 115–129. [Google Scholar] [CrossRef]
- Bhatia, R. Positive Definite Matrices; Princeton University Press: Princeton, NJ, USA, 2009; Volume 24. [Google Scholar]
- Hiai, F.; Petz, D. Introduction to Matrix Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications; Springer: Berlin/Heidelberg, Germany, 1979; Volume 143. [Google Scholar]
- Markham, D.; Miszczak, J.A.; Puchała, Z.; Życzkowski, K. Quantum state discrimination: A geometric approach. Phys. Rev. A 2008, 77, 42–111. [Google Scholar] [CrossRef]
- Costa, J.; Hero, A.; Vignat, C. On solutions to multivariate maximum α-entropy problems. In International Workshop on Energy Minimization Methods in Computer Vision and Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2003; pp. 211–226. [Google Scholar]
- Naudts, J. Generalised Thermostatistics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kotz, S.; Nadarajah, S. Multivariate t-Distributions and their Applications; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Clason, C.; Lorenz, D.A.; Mahler, H.; Wirth, B. Entropic regularization of continuous optimal transport problems. J. Math. Anal. Appl. 2021, 494, 124432. [Google Scholar] [CrossRef]
- Agueh, M.; Carlier, G. Barycenters in the Wasserstein space. SIAM J. Math. Anal. 2011, 43, 904–924. [Google Scholar] [CrossRef]
- Jeuris, B.; Vandebril, R.; Vandereycken, B. A survey and comparison of contemporary algorithms for computing the matrix geometric mean. Electron. Trans. Numer. Anal. 2012, 39, 379–402. [Google Scholar]
- Higham, N.J. Newton’s method for the matrix square root. Math. Comput. 1986, 46, 537–549. [Google Scholar]
| 0(MLE) | 0.062 | 1.346 | 10.69 |
| 0.01 | 0.051 | 1.242 | 8.973 |
| 0.1 | 0.104 | 0.841 | 4.180 |
| 0.5 | 0.647 | 0.931 | 3.093 |
| 1.0 | 1.166 | 1.670 | 5.075 |
| 0(MLE) | 0.024 | 0.490 | 2.810 |
| 0.01 | 0.020 | 0.459 | 2.528 |
| 0.1 | 0.101 | 0.397 | 1.700 |
| 0.5 | 0.659 | 0.875 | 2.833 |
| 1.0 | 1.180 | 1.730 | 5.124 |
| 0 | 0.455 | 1.318 | 4.875 |
| 0.001 | 0.429 | 1.318 | 4.887 |
| 0.01 | 0.434 | 1.344 | 4.551 |
| 0.025 | 0.780 | 1.456 | 5.710 |
| 0.005 | 1.047 | 1.537 | 7.570 |
| 0 | 0.154 | 1.303 | 5.091 |
| 0.001 | 0.212 | 1.305 | 5.072 |
| 0.01 | 0.306 | 1.328 | 5.274 |
| 0.025 | 0.671 | 1.337 | 5.851 |
| 0.005 | 1.109 | 1.603 | 8.072 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, Q.; Kobayashi, K. Entropy-Regularized Optimal Transport on Multivariate Normal and q-normal Distributions. Entropy 2021, 23, 302. https://doi.org/10.3390/e23030302
Tong Q, Kobayashi K. Entropy-Regularized Optimal Transport on Multivariate Normal and q-normal Distributions. Entropy. 2021; 23(3):302. https://doi.org/10.3390/e23030302
Chicago/Turabian StyleTong, Qijun, and Kei Kobayashi. 2021. "Entropy-Regularized Optimal Transport on Multivariate Normal and q-normal Distributions" Entropy 23, no. 3: 302. https://doi.org/10.3390/e23030302
APA StyleTong, Q., & Kobayashi, K. (2021). Entropy-Regularized Optimal Transport on Multivariate Normal and q-normal Distributions. Entropy, 23(3), 302. https://doi.org/10.3390/e23030302





