Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture
Abstract
1. Introduction
2. Theoretical Background
3. Specimens
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sammonds, P.R.; Meredith, P.G.; Main, I.G. Role of pore fluids in the generation of seismic precursors to shear fracture. Nature 1992, 359, 228–230. [Google Scholar] [CrossRef]
- Shiotani, T. Evaluation of progressive failure using AE sources and improved b-value on slope model tests. Prog. Acoust. Emiss. VII JSNDI 1994, 7, 529–534. [Google Scholar]
- Colombo, I.S.; Main, I.G.; Forde, M.C. Assessing Damage of Reinforced Concrete Beam Using “b-value” Analysis of Acoustic Emission Signals. J. Mater. Civ. Eng. 2003, 15, 280–286. [Google Scholar] [CrossRef]
- Triantis, D.; Kourkoulis, S.K. An Alternative Approach for Representing the Data Provided by the Acoustic Emission Technique. Rock Mech. Rock Eng. 2018, 51, 2433–2438. [Google Scholar] [CrossRef]
- Loukidis, A.; Pasiou, E.D.; Sarlis, N.V.; Triantis, D. Fracture analysis of typical construction materials in natural time. Phys. A Stat. Mech. Appl. 2019, 123831. [Google Scholar] [CrossRef]
- Ohtsu, M.; Uchida, M.; Okamoto, T.; Yuyama, S. Damage Assessment of Reinforced Concrete Beams Qualified by Acoustic Emission. ACI Struct. J. 2002, 99. [Google Scholar] [CrossRef]
- Holford, K.M. Acoustic Emission in Structural Health Monitoring. Key Eng. Mater. 2009, 413–414, 15–28. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Ganniari-Papageorgiou, E.; Mentzini, M. Dionysos marble beams under bending: A contribution towards understanding the fracture of the Parthenon architraves. Eng. Geol. 2010, 115, 246–256. [Google Scholar] [CrossRef]
- Lacidogna, G.; Manuello, A.; Niccolini, G.; Carpinteri, A. Acoustic emission monitoring of Italian historical buildings and the case study of the Athena temple in Syracuse. Archit. Sci. Rev. 2015, 58, 290–299. [Google Scholar] [CrossRef]
- Main, I.; Meredith, P.; Jones, C. A reinterpretation of the precursory seismic b-value anomaly from fracture mechanics. Geophys. J. Int. 1989, 96, 131–138. [Google Scholar] [CrossRef]
- Shiotani, T.; Yuyama, S.; Li, Z.W.; Ohtsu, M. Application of AE improved b-value to quantitative evaluation of fracture process in concrete materials. J. Acoust. Emiss. 2001, 19, 118–133. [Google Scholar]
- Rao, M.V.M.S.; Lakshmi, K.J.P. Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture. Curr. Sci. 2005, 89, 1577–1582. [Google Scholar]
- Sagar, R.V.; Prasad, B.K.R.; Kumar, S.S. An experimental study on cracking evolution in concrete and cement mortar by the b-value analysis of acoustic emission technique. Cem. Concr. Res. 2012, 42, 1094–1104. [Google Scholar] [CrossRef]
- Hirata, T. Omori’s Power Law aftershock sequences of microfracturing in rock fracture experiment. J. Geophys. Res. Solid Earth 1987, 92, 6215–6221. [Google Scholar] [CrossRef]
- Meredith, P.G.; Main, I.G.; Jones, C. Temporal variations in seismicity during quasi-static and dynamic rock failure. Tectonophysics 1990, 175, 249–268. [Google Scholar] [CrossRef]
- Cox, S.J.D.; Meredith, P.G. Microcrack formation and material softening in rock measured by monitoring acoustic emissions. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 11–24. [Google Scholar] [CrossRef]
- Benson, P.M.; Vinciguerra, S.; Meredith, P.G.; Young, R.P. Laboratory Simulation of Volcano Seismicity. Science 2008, 322, 249. [Google Scholar] [CrossRef] [PubMed]
- Jiaying, C.; Xudong, Z.; Linmei, Y.; Fenng, W. The vacancy defects and oxygen atoms occupation effects on mechanical and electronic properties of Mo5Si3 silicides. Commun. Theor. Phys. 2021. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, T.; Ma, H.; Li, D.; Ying, C.; Liu, C.; Wang, F. A first principles investigation on the influence of transition-metal elements on the structural, mechanical, and anisotropic properties of CaM2Al20 intermetallics. J. Mol. Graph. Model. 2020, 96, 107509. [Google Scholar] [CrossRef]
- Mai, Z.; Zhang, X.; Liu, Y.; Yu, H.; Wang, F. Insight into the structure dependence on physical properties of the high temperature ceramics TaB2 boride. Vacuum 2020, 177, 109427. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Baldovin, F.; Cerbino, R.; Pierobon, P. Introduction to Nonextensive Statistical Mechanics and Thermodynamics. Phys. Complex Syst. 2003, 155, 229–252. [Google Scholar]
- Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics -an overview after 20 years. Braz. J. Phys. 2009, 39, 337–356. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Tsallis, C.; Brigatti, E. Nonextensive statistical mechanics: A brief introduction. Contin. Mech. Thermodyn. 2004, 16, 223–235. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Law for the distance between successive earthquakes. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Scale-free statistics of time interval between successive earthquakes. Phys. A Stat. Mech. Appl. 2005, 350, 588–596. [Google Scholar] [CrossRef]
- Hasumi, T. Interoccurrence time statistics in the two-dimensional Burridge-Knopoff earthquake model. Phys. Rev. E 2007, 76, 026117. [Google Scholar] [CrossRef] [PubMed]
- Darooneh, A.H.; Dadashinia, C. Analysis of the spatial and temporal distributions between successive earthquakes: Nonextensive statistical mechanics viewpoint. Phys. A Stat. Mech. Appl. 2008, 387, 3647–3654. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Is plate tectonics a case of non-extensive thermodynamics? Phys. A Stat. Mech. Appl. 2010, 389, 4989–4993. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Nonextensivity and natural time: The case of seismicity. Phys. Rev. E 2010, 82, 021110. [Google Scholar] [CrossRef] [PubMed]
- Vallianatos, F.; Sammonds, P. A non-extensive statistics of the fault-population at the Valles Marineris extensional province, Mars. Tectonophysics 2011, 509, 50–54. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G.; Tzanis, A. Evidence of non-extensivity in the seismicity observed during the 2011-2012 unrest at the Santorini volcanic complex, Greece. Nat. Hazards Earth Syst. Sci. 2013, 13, 177–185. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran–Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 2013, 590, 52–58. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Non-extensive and natural time analysis of seismicity before the Mw6.4, October 12, 2013 earthquake in the South West segment of the Hellenic Arc. Phys. A Stat. Mech. Appl. 2014, 414, 163–173. [Google Scholar] [CrossRef]
- Vallianatos, F.; Benson, P.; Meredith, P.; Sammonds, P. Experimental evidence of a non-extensive statistical physics behaviour of fracture in triaxially deformed Etna basalt using acoustic emissions. EPL (Europhys. Lett.) 2012, 97, 58002. [Google Scholar] [CrossRef]
- Stergiopoulos, C.; Stavrakas, I.; Hloupis, G.; Triantis, D.; Vallianatos, F. Electrical and Acoustic Emissions in cement mortar beams subjected to mechanical loading up to fracture. Eng. Fail. Anal. 2013, 35, 454–461. [Google Scholar] [CrossRef]
- Stavrakas, I.; Triantis, D.; Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I. Acoustic Emission Analysis of Cement Mortar Specimens During Three Point Bending Tests. Lat. Am. J. Solids Struct. 2016, 13, 2283–2297. [Google Scholar] [CrossRef]
- Saltas, V.; Vallianatos, F.; Triantis, D.; Stavrakas, I. 8—Complexity in Laboratory Seismology: From Electrical and Acoustic Emissions to Fracture. In Complexity of Seismic Time Series; Chelidze, T., Vallianatos, F., Telesca, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 239–273. [Google Scholar] [CrossRef]
- Saltas, V.; Vallianatos, F.; Triantis, D.; Koumoudeli, T.; Stavrakas, I. Non-extensive statistical analysis of acoustic emissions series recorded during the uniaxial compression of brittle rocks. Phys. A Stat. Mech. Appl. 2019, 528, 121498. [Google Scholar] [CrossRef]
- Greco, A.; Tsallis, C.; Rapisarda, A.; Pluchino, A.; Fichera, G.; Contrafatto, L. Acoustic emissions in compression of building materials: Q-statistics enables the anticipation of the breakdown point. Eur. Phys. J. Spec. Top. 2020, 229, 841–849. [Google Scholar] [CrossRef]
- Loukidis, A.; Triantis, D.; Stavrakas, I. Non-Extensive Statistical Analysis of Acoustic Emissions Recorded in Marble and Cement Mortar Specimens Under Mechanical Load Until Fracture. Entropy 2020, 22, 1115. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Exadaktylos, G.E.; Vardoulakis, I. U-Notched Dionysos-Pentelicon Marble Beams in Three Point Bending: The Effect of Nonlinearity, Anisotropy and Microstructure. Int. J. Fract. 1999, 98, 369–392. [Google Scholar] [CrossRef]
- Exadaktylos, G.E.; Vardoulakis, I.; Kourkoulis, S.K. Influence of nonlinearity and double elasticity on flexure of rock beams–II. Characterization of Dionysos marble. Int. J. Solids Struct. 2001, 38, 4119–4145. [Google Scholar] [CrossRef]
- Perdikatsis, V.; Kritsotakis, K.; Markopoulos, T.; Laskaridis, K. Petrography, Fabric and Properties. In Fracture and Failure of Natural Building Stones: Applications in the Restoration of Ancient Monuments; Kourkoulis, S.K., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 497–515. [Google Scholar] [CrossRef]
- Young, J.F. Portland Cements. In Encyclopedia of Materials: Science and Technology; Buschow, K.H.J., Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2001; pp. 7768–7773. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D. Mechanical response of notched marble beams under bending versus acoustic emissions and electric activity. J. Theor. Appl. Mech. 2018, 56, 523–547. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D. Notched marble plates under tension: Detecting prefailure indicators and predicting entrance to the “critical stage”. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 776–786. [Google Scholar] [CrossRef]
- Markides, C.F.; Pasiou, E.D.; Kourkoulis, S.K. A preliminary study on the potentialities of the Circular Semi-Ring test. Procedia Struct. Integr. 2018, 9, 108–115. [Google Scholar] [CrossRef]
- Loukidis, A.; Pasiou, E.D.; Sarlis, N.V.; Triantis, D. Similarity of fluctuations of acoustic emissions in natural time. Procedia Struct. Integr. 2020, 25, 195–200. [Google Scholar] [CrossRef]
- Stergiopoulos, C.; Stavrakas, I.; Triantis, D.; Vallianatos, F.; Stonham, J. Predicting fracture of mortar beams under three-point bending using non-extensive statistical modeling of electric emissions. Phys. A Stat. Mech. Appl. 2015, 419, 603–611. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; Dover Publications, Inc.: New York, NY, USA, 1965. [Google Scholar]
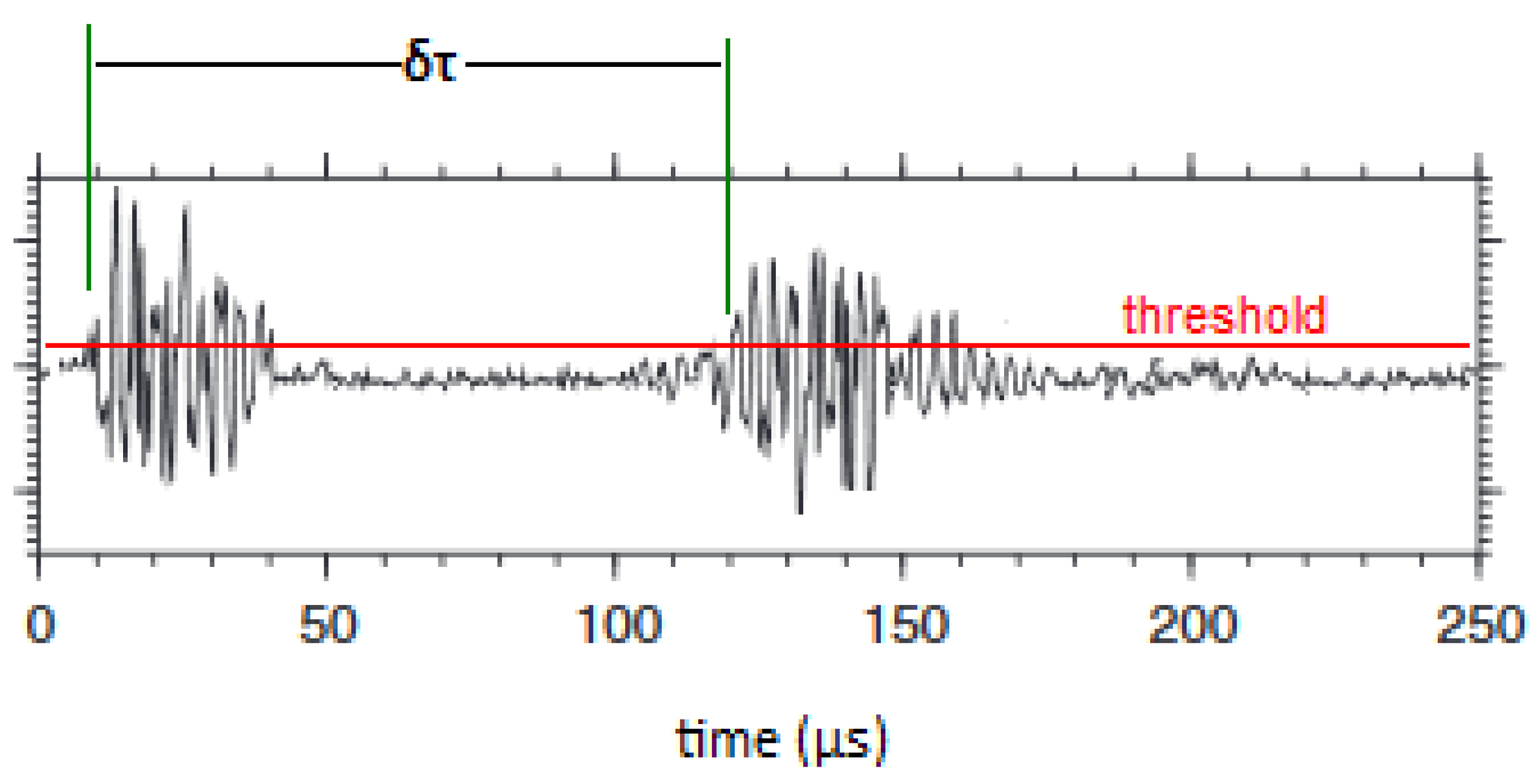
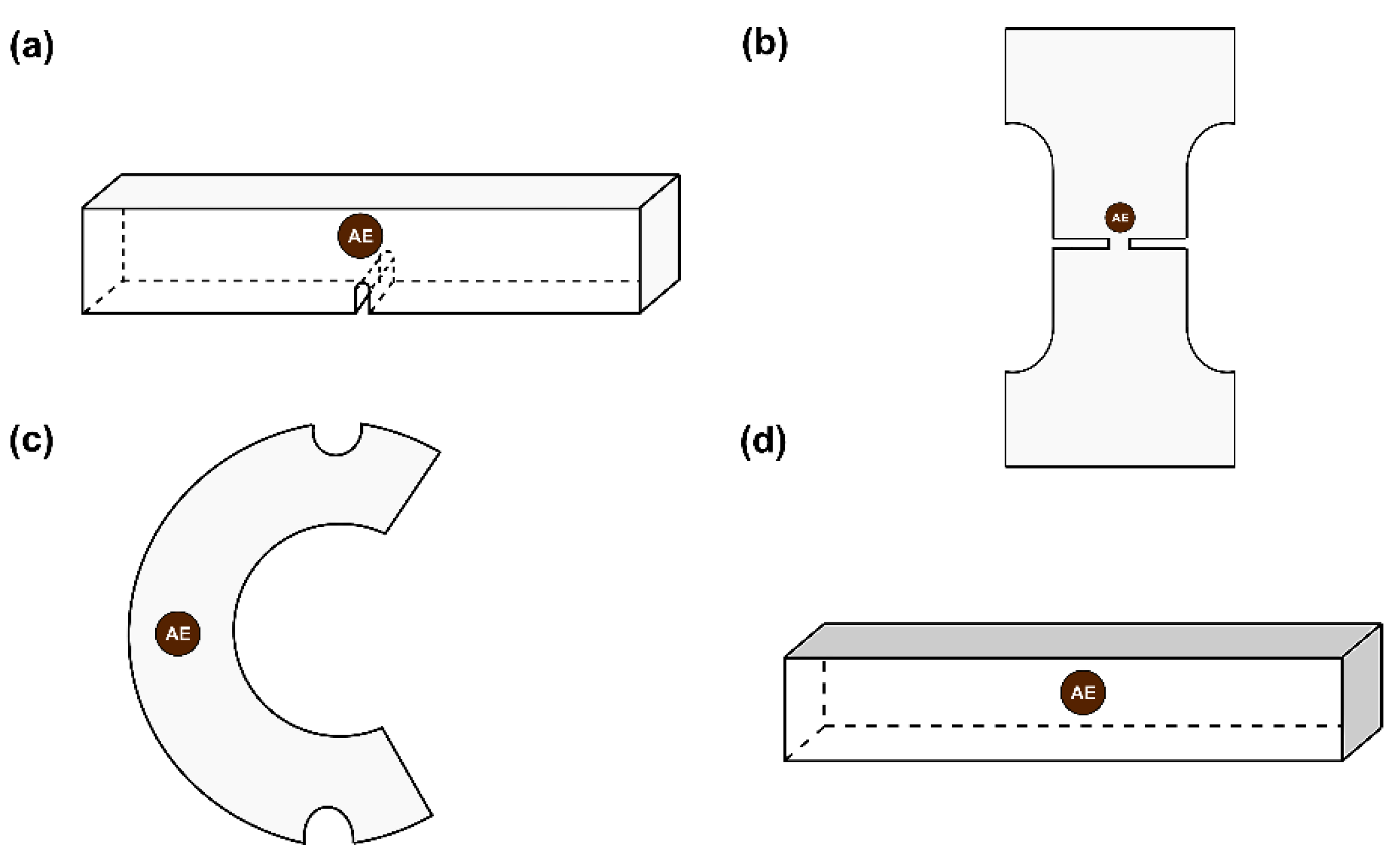
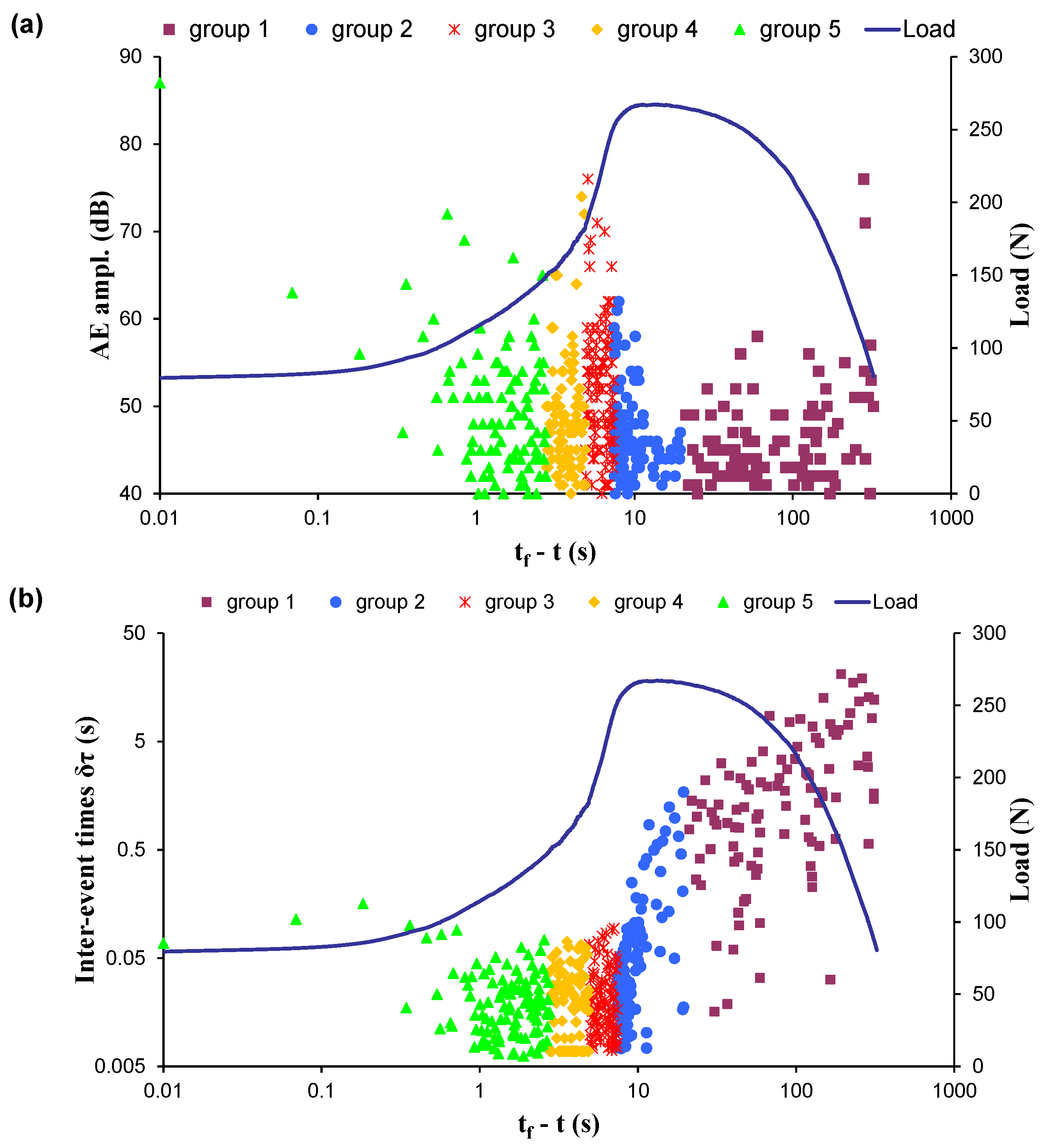
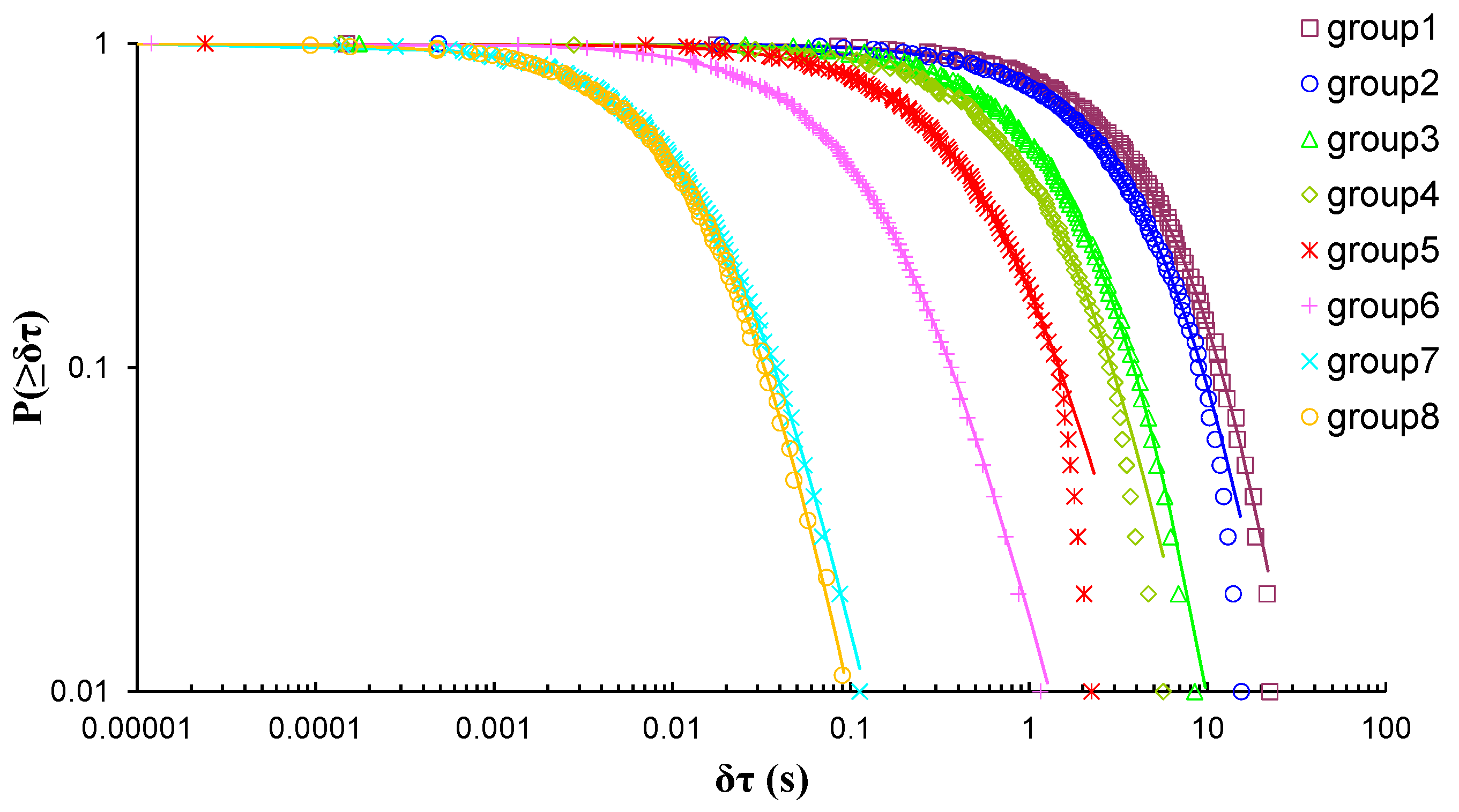
| Experiment | Loading Protocol | Material | Total AE Hits |
|---|---|---|---|
| 1 | Three-point bending | Marble | 790 |
| 2 | Direct tension | “ | 574 |
| 3 | Diametral compression | “ | 507 |
| 4 | Three-point bending | Cement mortar | 549 |
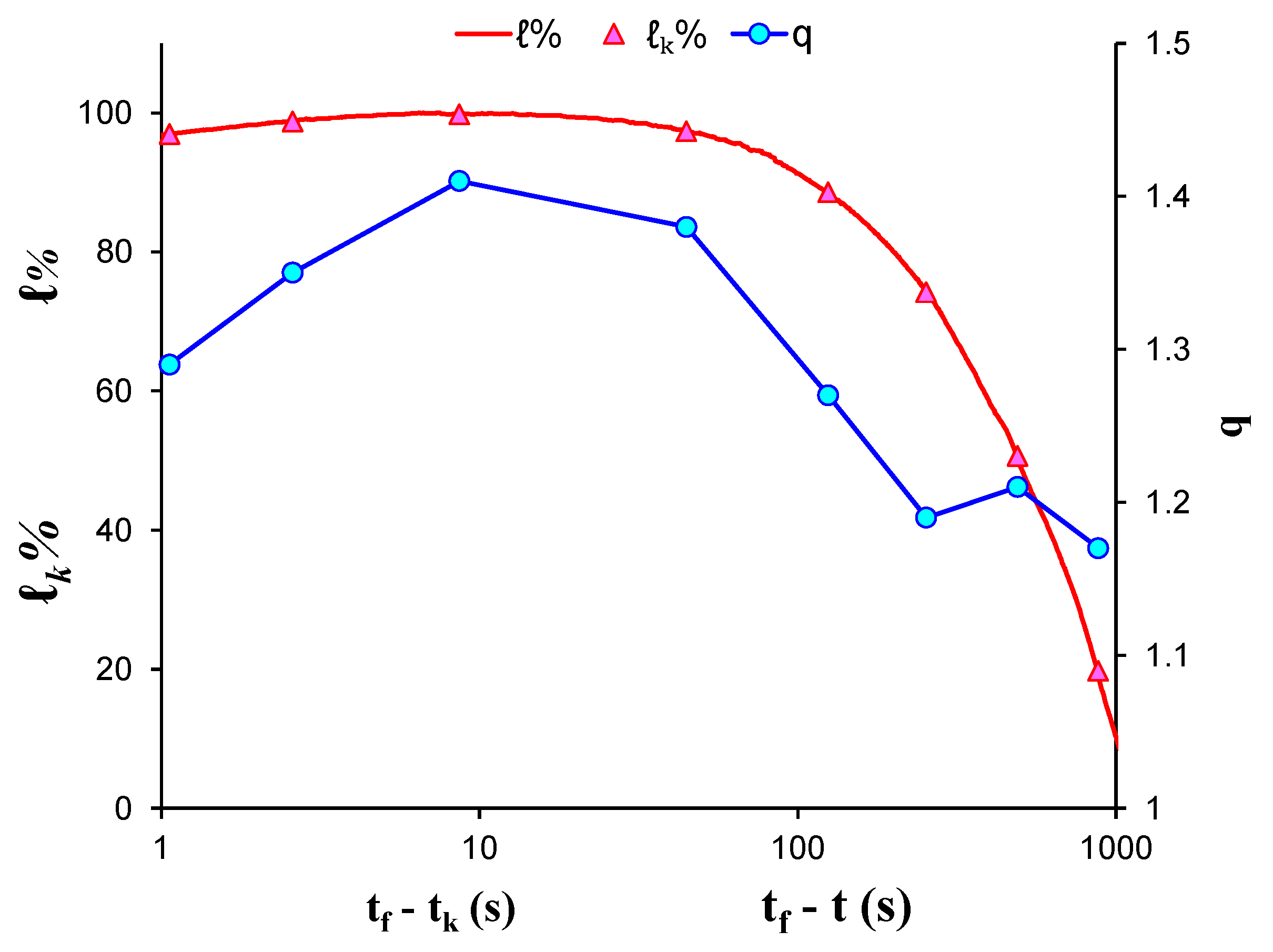
| AE Hit Group | (%) | ||||
|---|---|---|---|---|---|
| 1 | 881.12 | 1.17 | 0.24 | 4.167 | 19.8 |
| 2 | 490.93 | 1.21 | 0.32 | 3.125 | 50.7 |
| 3 | 253.75 | 1.19 | 0.75 | 1.333 | 74.2 |
| 4 | 124.65 | 1.27 | 1.10 | 0.909 | 88.5 |
| 5 | 44.70 | 1.38 | 2.50 | 0.400 | 97.3 |
| 6 | 8.65 | 1.41 | 10.50 | 0.095 | 99.8 |
| 7 | 2.59 | 1.35 | 94.90 | 0.011 | 98.7 |
| 8 | 1.06 | 1.29 | 100.10 | 0.010 | 96.9 |
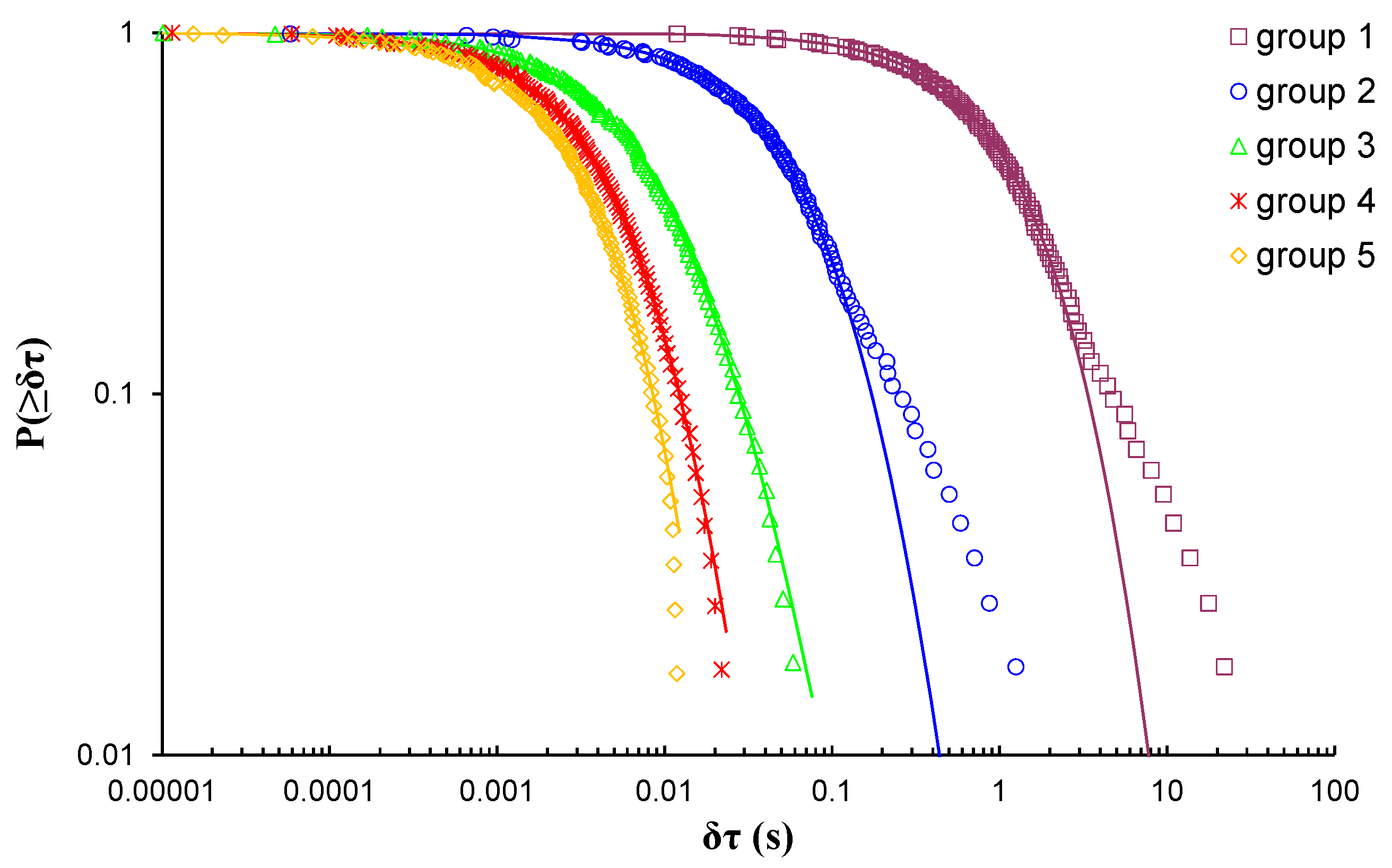
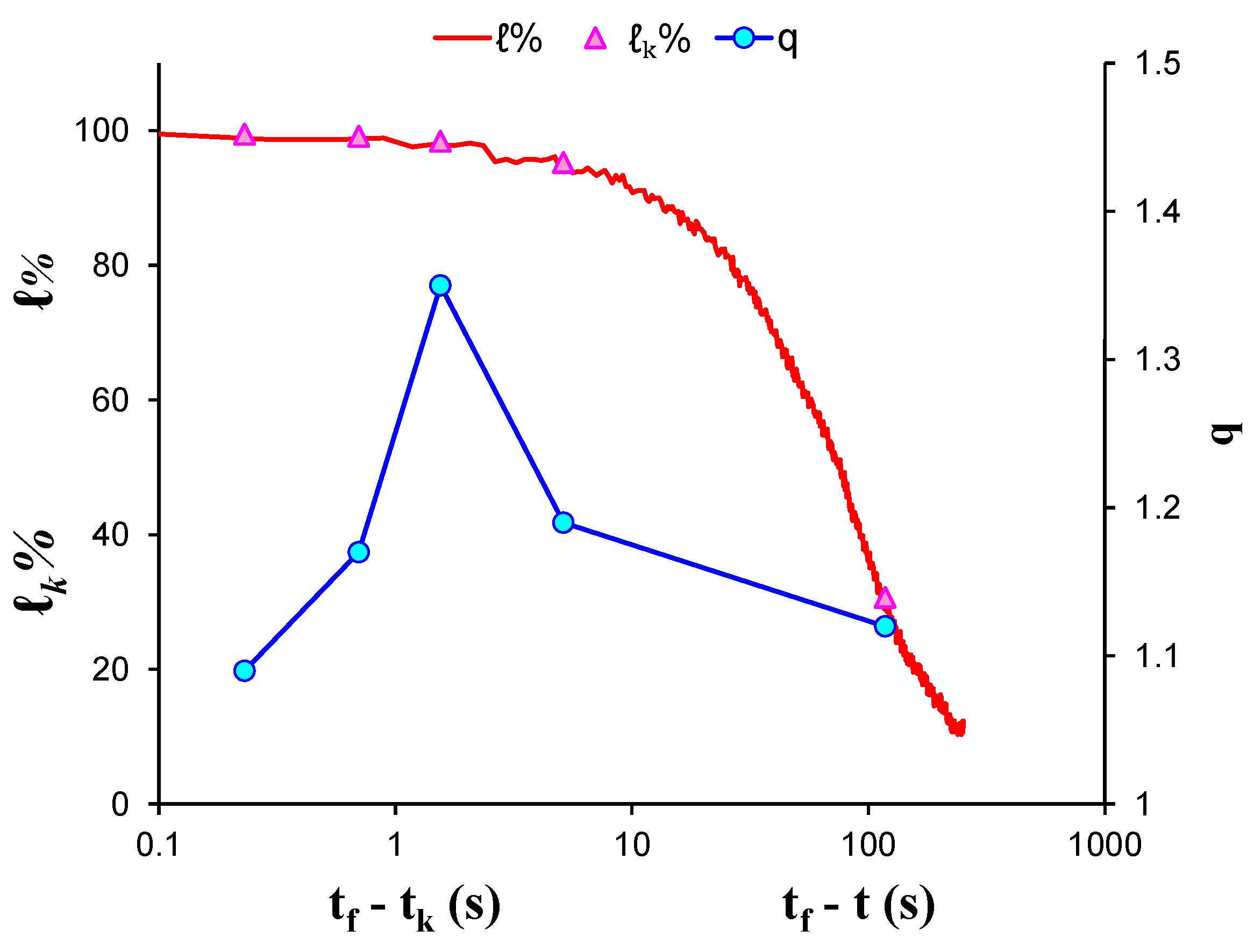
| AE Hit Group | q | (%) | |||
|---|---|---|---|---|---|
| 1 | 117.8 | 1.12 | 0.79 | 1.2658 | 30.7% |
| 2 | 5.13 | 1.19 | 16.8 | 0.0595 | 95.3% |
| 3 | 1.55 | 1.35 | 127.8 | 0.0078 | 98.4% |
| 4 | 0.70 | 1.17 | 230.2 | 0.0043 | 99.2% |
| 5 | 0.23 | 1.09 | 300.5 | 0.0033 | 99.6% |
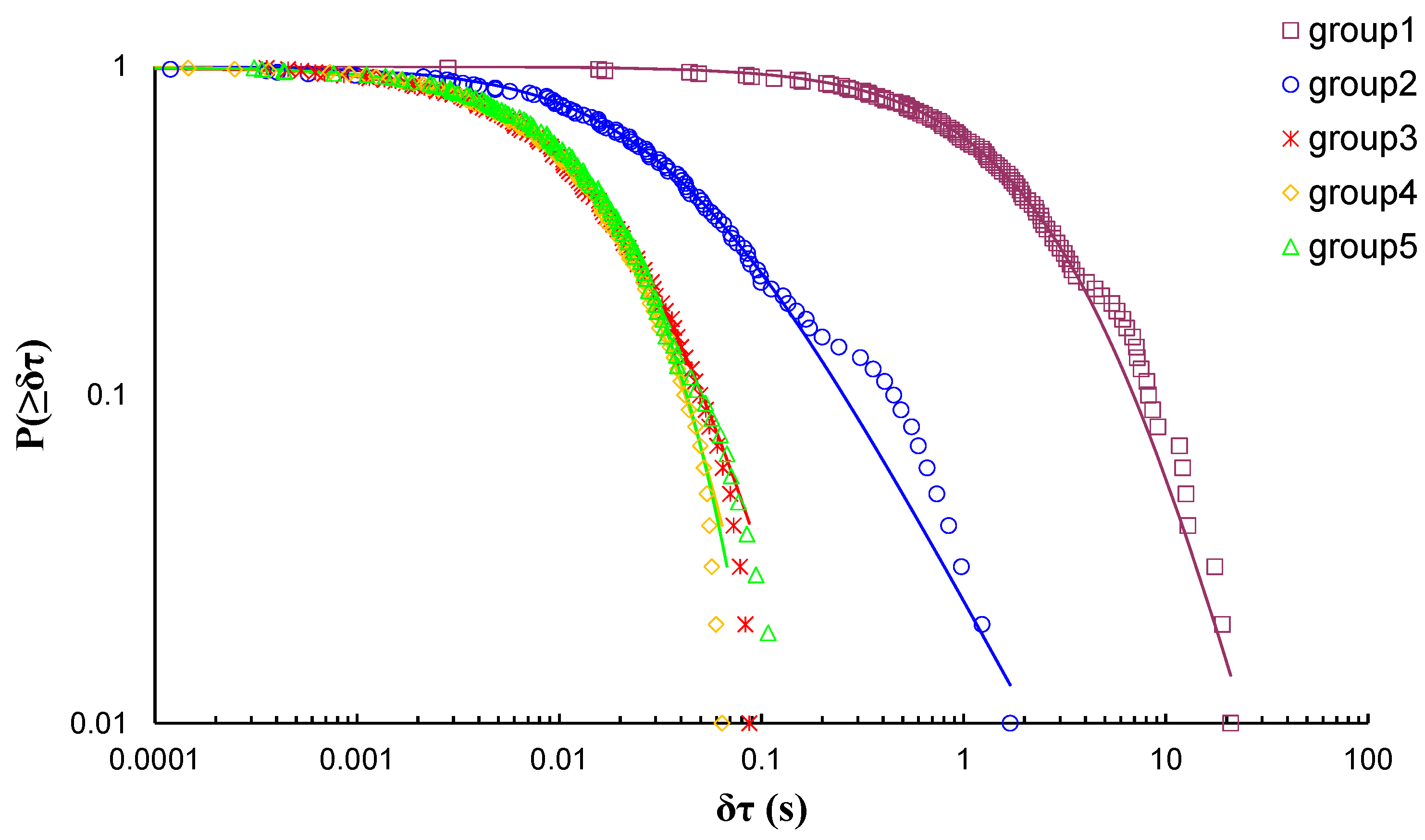
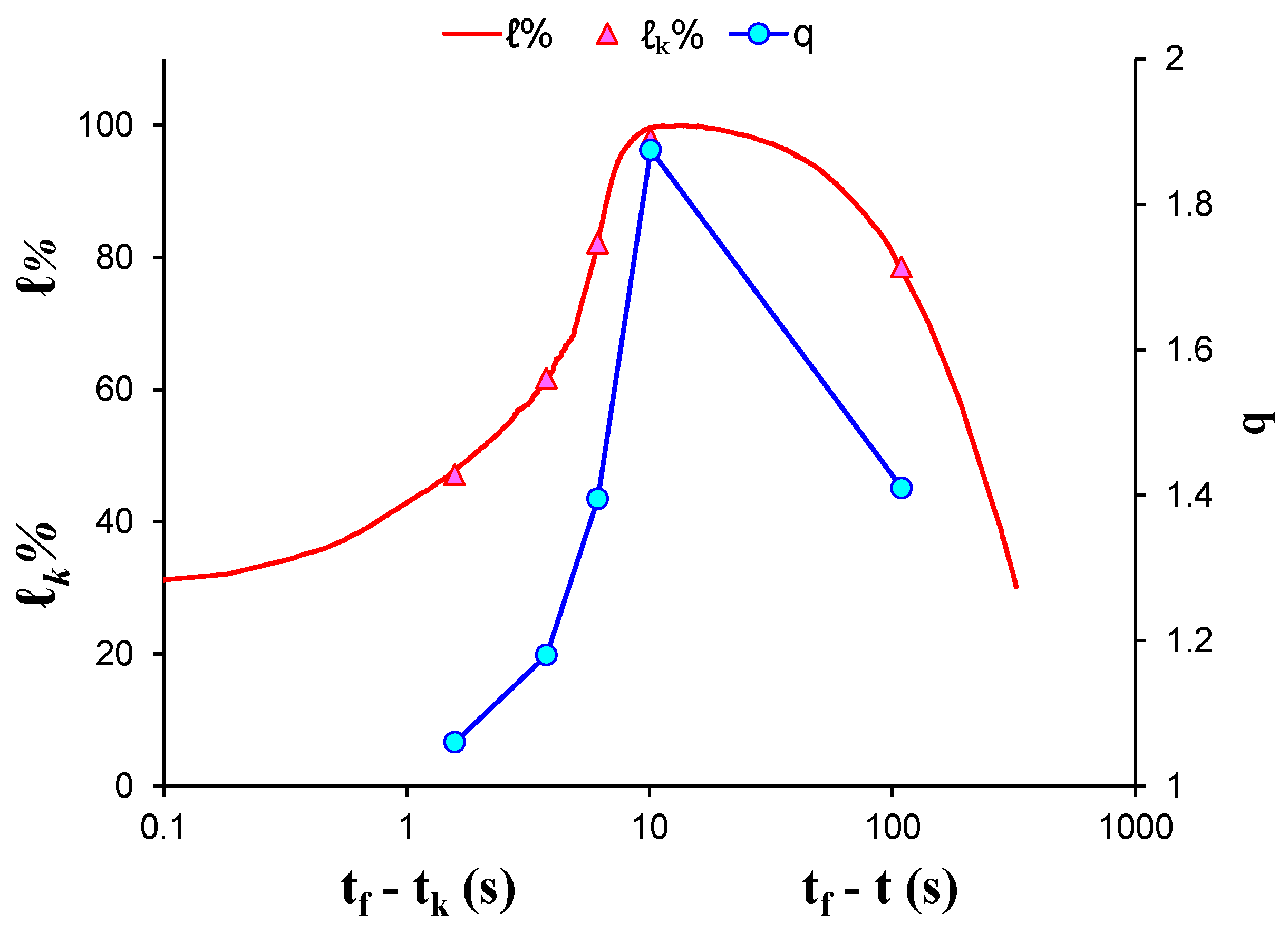
| AE Hit Group | q | ||||
|---|---|---|---|---|---|
| 1 | 109.27 | 1.41 | 0.55 | 1.803 | 78.5% |
| 2 | 10.12 | 1.88 | 29.26 | 0.034 | 98.0% |
| 3 | 6.12 | 1.40 | 74.00 | 0.014 | 82.1% |
| 4 | 3.77 | 1.18 | 68.11 | 0.015 | 61.7% |
| 5 | 1.58 | 1.06 | 57.78 | 0.017 | 47.1% |
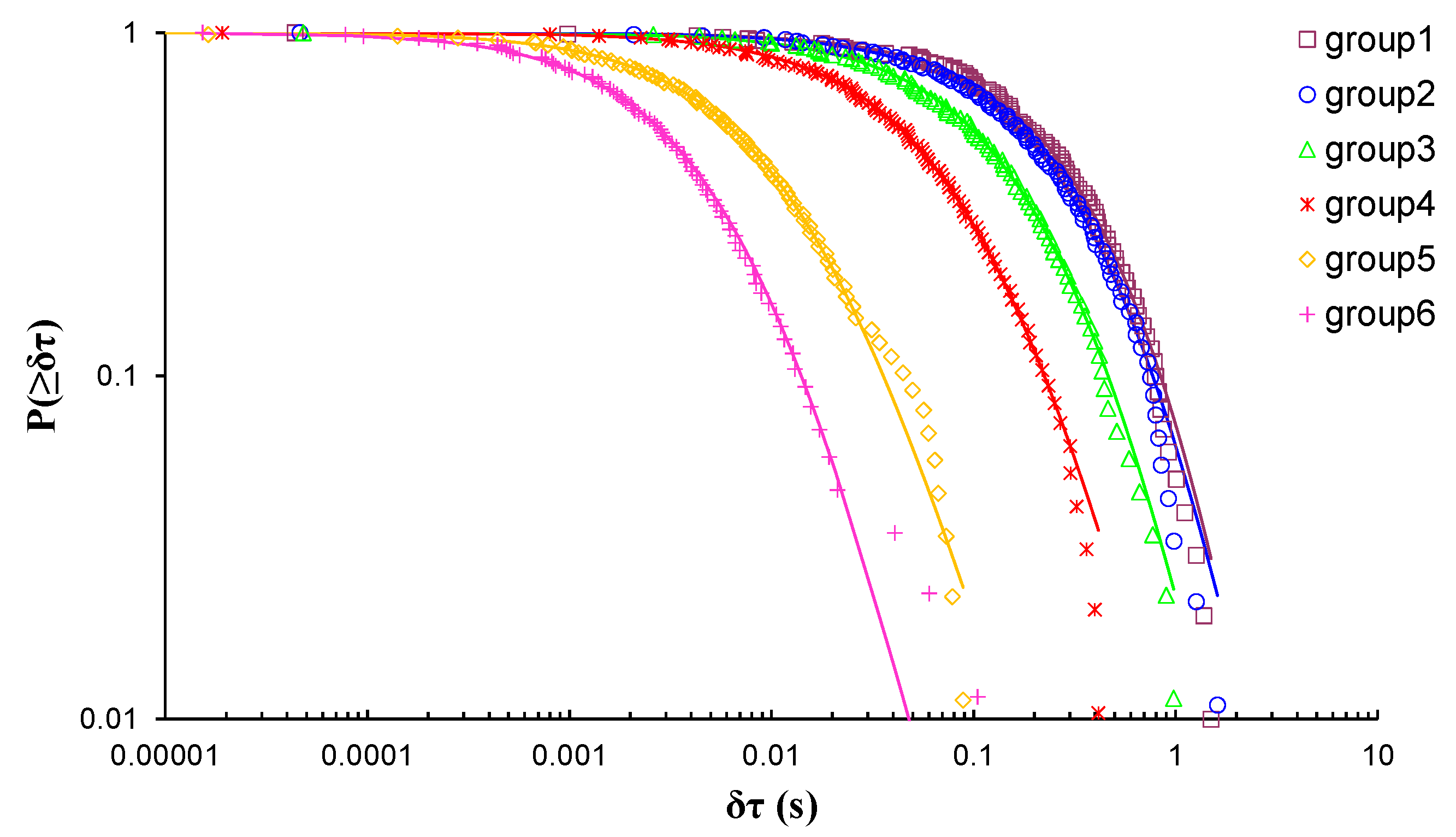
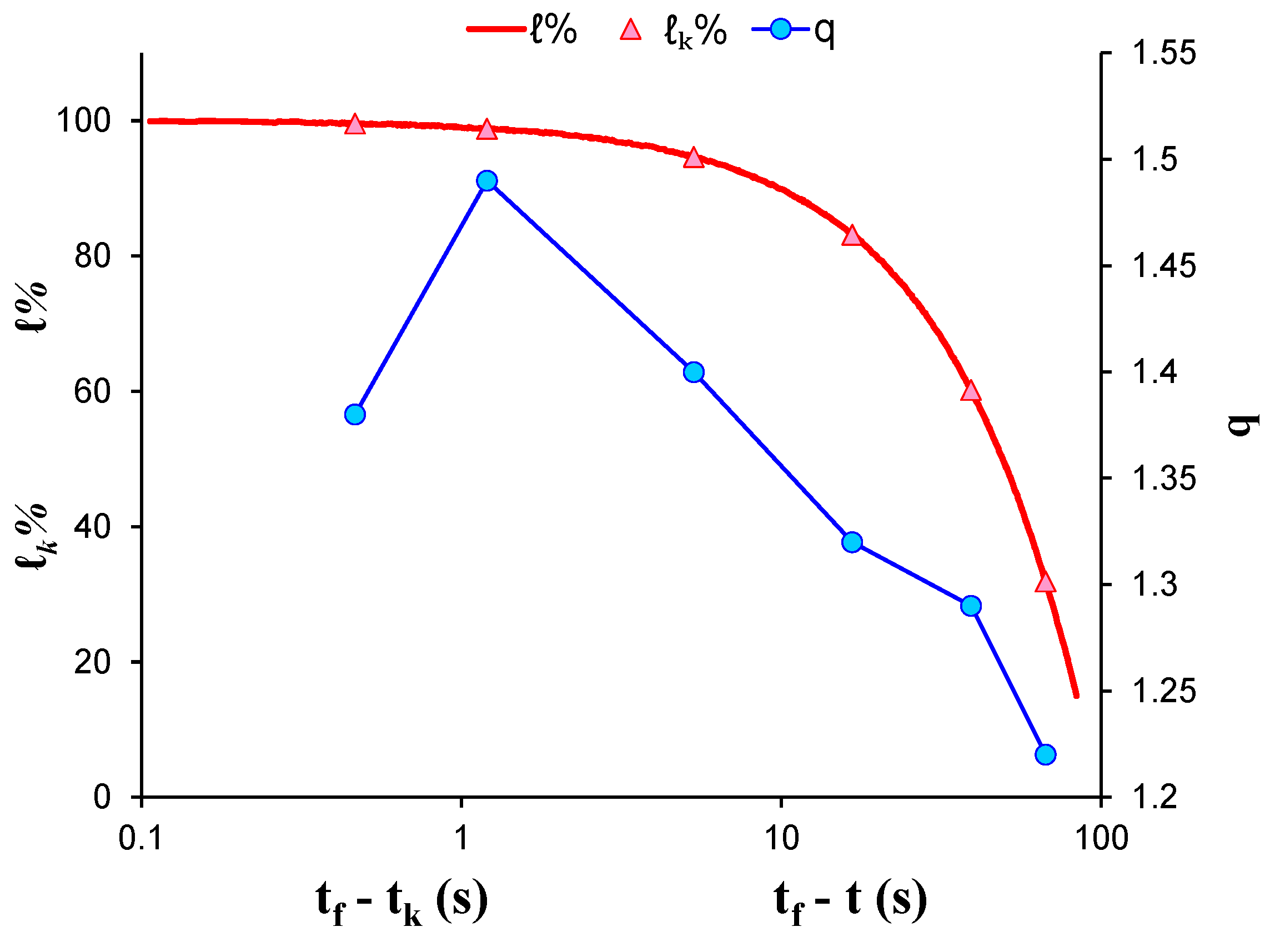
| AE Hit Group | (s) | q | |||
|---|---|---|---|---|---|
| 1 | 67.07 | 1.22 | 3.56 | 0.2809 | 31.9% |
| 2 | 39.22 | 1.29 | 4.25 | 0.2352 | 60.2% |
| 3 | 16.68 | 1.32 | 7.34 | 0.1362 | 83.2% |
| 4 | 5.33 | 1.40 | 16.86 | 0.0593 | 94.6% |
| 5 | 1.20 | 1.49 | 119.4 | 0.0084 | 98.8% |
| 6 | 0.47 | 1.38 | 262.4 | 0.0038 | 99.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loukidis, A.; Triantis, D.; Stavrakas, I. Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture. Entropy 2021, 23, 276. https://doi.org/10.3390/e23030276
Loukidis A, Triantis D, Stavrakas I. Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture. Entropy. 2021; 23(3):276. https://doi.org/10.3390/e23030276
Chicago/Turabian StyleLoukidis, Andronikos, Dimos Triantis, and Ilias Stavrakas. 2021. "Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture" Entropy 23, no. 3: 276. https://doi.org/10.3390/e23030276
APA StyleLoukidis, A., Triantis, D., & Stavrakas, I. (2021). Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture. Entropy, 23(3), 276. https://doi.org/10.3390/e23030276







