A Neural Network MCMC Sampler That Maximizes Proposal Entropy
Abstract
:1. Introduction
- 1.
- Here, we employed the entropy-based objective in a neural network MCMC sampler for optimizing exploration speed. To build the model, we designed a novel flexible proposal distribution wherein the optimization of the entropy objective is tractable.
- 2.
- Inspired by the HMC and the L2HMC [10] algorithm, the proposed sampler uses a special architecture that utilizes the gradient of the target distribution to aid sampling.
- 3.
- We demonstrate a significant improvement in sampling efficiency over previous techniques, sometimes by an order of magnitude. We also demonstrate energy-based model training with the proposed sampler and demonstrate higher exploration and higher resultant sample quality.
2. Preliminaries: MCMC Methods from Vanilla to Learned
3. A Gradient-Based Sampler with Tractable Proposal Probability
3.1. Proposal Model and How to Use Gradient Information
3.2. Model Formulation
3.3. Optimizing the Proposal Entropy Objective
4. Related Work: Other Samplers Inspired by HMC
5. Experimental Result
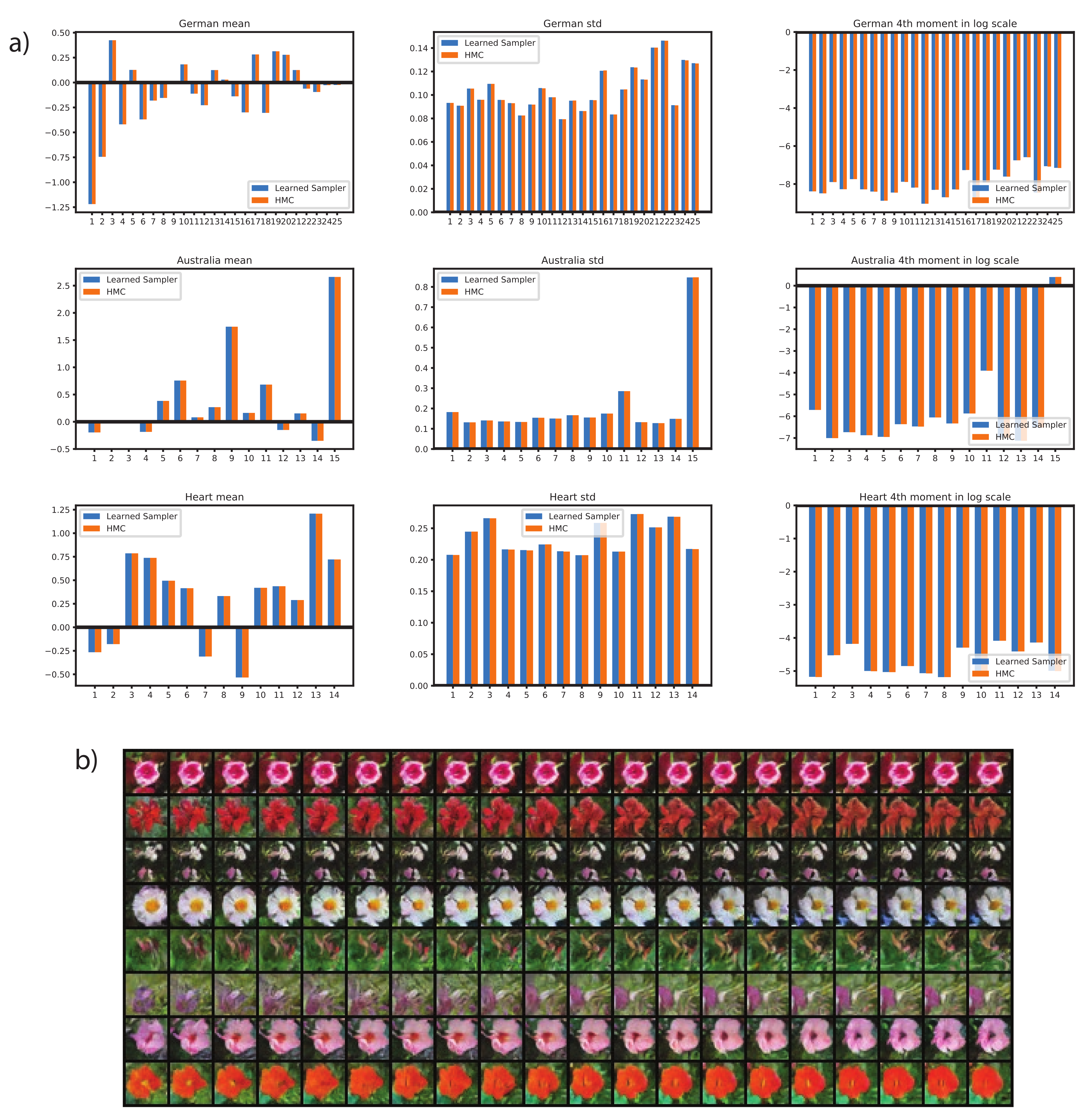
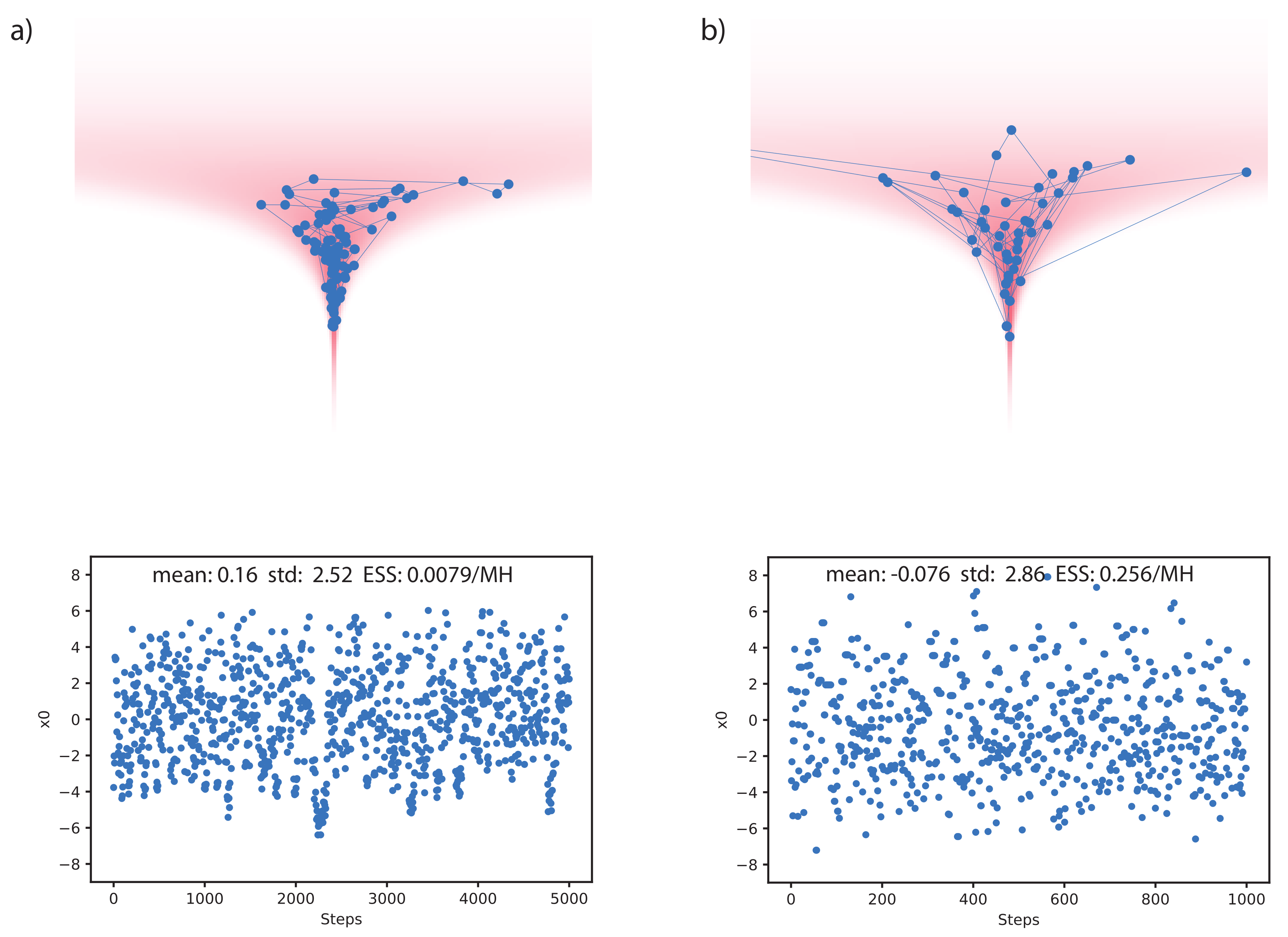
5.1. Synthetic Dataset and Bayesian Logistic Regression
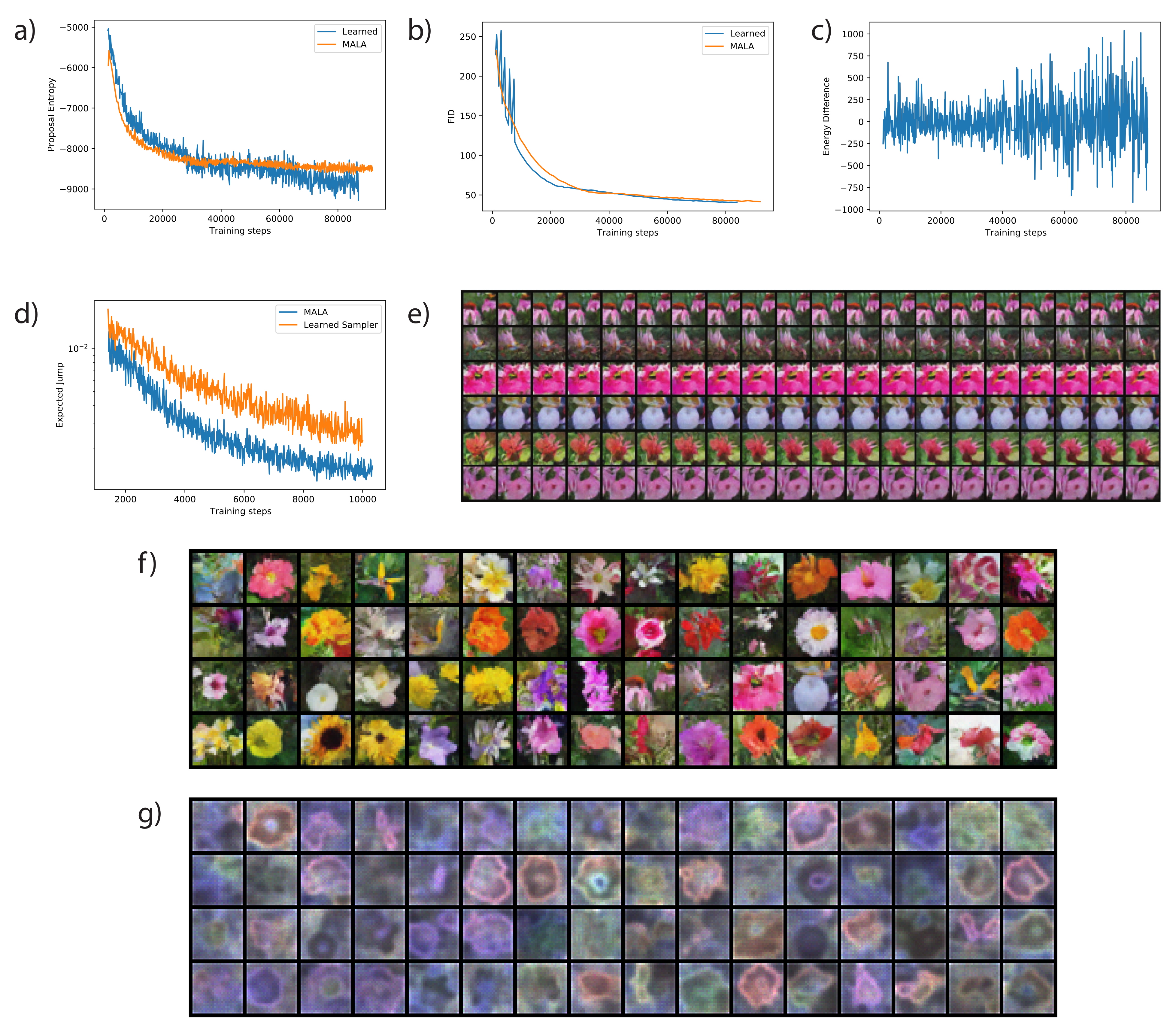
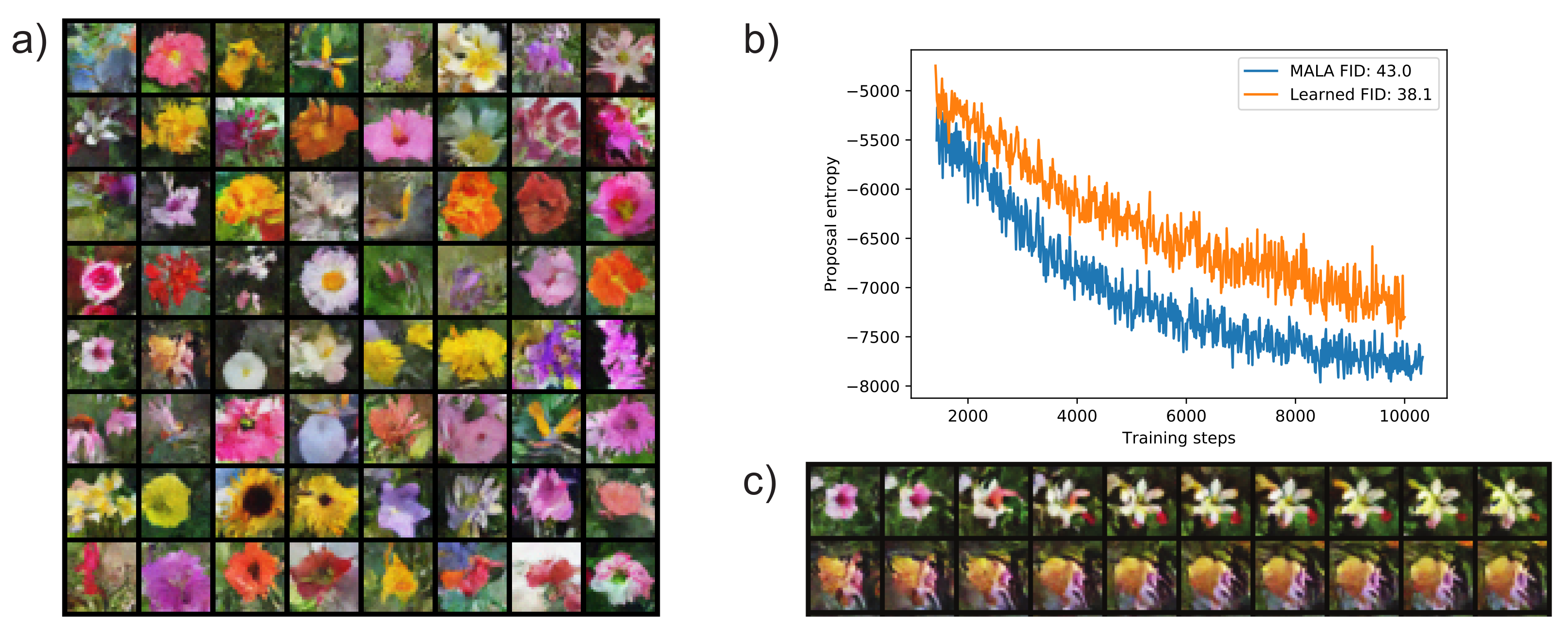
5.2. Training a Convergent Deep Energy-Based Model
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| MCMC | Markov Chain Monte Carlo |
| HMC | Hamiltonian Monte Carlo |
| EBM | Energy-based Model |
| MALA | Metropolis-Adjusted Langevin Algorithm |
| FID | Fréchet Inception Distance |
| GAN | Generative Adversarial Network |
| ESS | Effective Sample Size |
| MH | Metropolis-Hastings |
| A-NICE-MC | Adversarial Nonlinear Independent Component Estimation Monte Carlo |
| L2HMC | Learn to HMC |
| NFLMC | Normalizing Flow Langevine Monte Carlo |
| RealNVP | Real-Valued Non-Volume-Preserving flow |
Appendix A
Appendix A.1. Ablation Study: Effect of Gradient Information
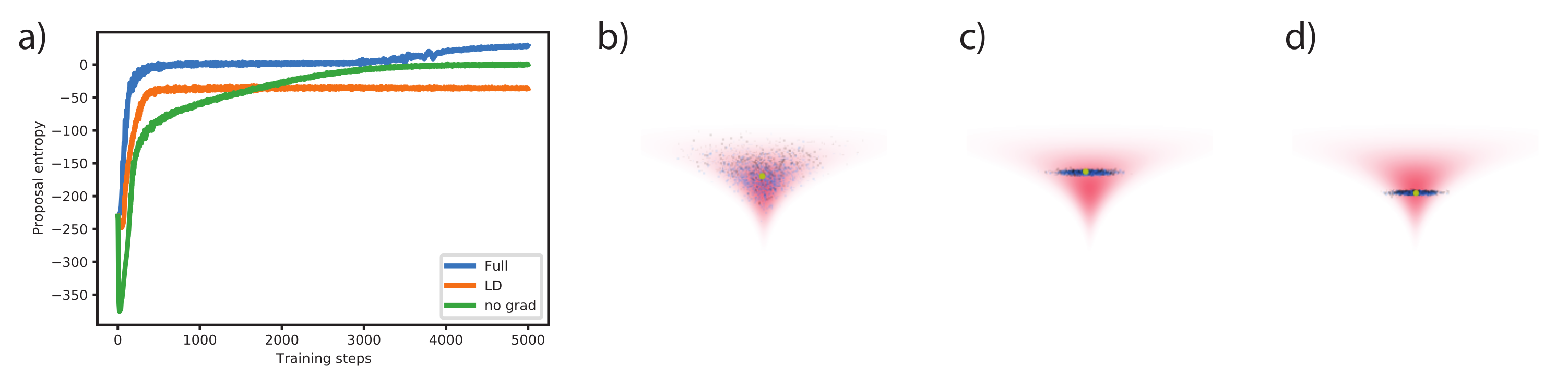
Appendix A.2. Experimental Details
| Width | Steps | AR | LR | Min LR | |
|---|---|---|---|---|---|
| 50d ICG | 256 | 1 | 0.9 | ||
| 2d SCG | 32 | 1 | 0.9 | ||
| 100d Funnel-1 | 512 | 3 | 0.7 | ||
| 20d Funnel-3 | 1024 | 4 | 0.6 | ||
| German | 128 | 1 | 0.7 | ||
| Australian | 128 | 1 | 0.8 | ||
| Heart | 128 | 1 | 0.9 |
Appendix A.3. Additional Experimental Results
| Dataset (Measure) | HMC | Ours |
|---|---|---|
| German (ESS/s) | 772.7 | 3651 |
| Australian (ESS/s) | 127.2 | 3433 |
| Heart (ESS/s) | 997.1 | 4235 |

References
- Noé, F.; Olsson, S.; Köhler, J.; Wu, H. Boltzmann generators: Sampling equilibrium states of many-body systems with deep learning. Science 2019, 365, eaaw1147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nijkamp, E.; Hill, M.; Han, T.; Zhu, S.C.; Wu, Y.N. On the Anatomy of MCMC-based Maximum Likelihood Learning of Energy-Based Models. In Proceedings of the Conference on Artificial Intelligence (AAAI), New York, NY, USA, 7–12 February 2019. [Google Scholar]
- Neal, R.M. Probabilistic Inference Using Markov Chain Monte Carlo Methods; Department of Computer Science, University of Toronto: Toronto, ON, Canada, 1993. [Google Scholar]
- Neal, R.M. MCMC using Hamiltonian dynamics. Handb. Markov Chain Monte Carlo 2011, 2, 2. [Google Scholar]
- Radivojević, T.; Akhmatskaya, E. Modified Hamiltonian Monte Carlo for Bayesian Inference. Stat. Comput. 2020, 30, 377–404. [Google Scholar] [CrossRef] [Green Version]
- Beskos, A.; Pillai, N.; Roberts, G.; Sanz-Serna, J.M.; Stuart, A. Optimal tuning of the hybrid Monte Carlo algorithm. Bernoulli 2013, 19, 1501–1534. [Google Scholar] [CrossRef]
- Betancourt, M.; Byrne, S.; Livingstone, S.; Girolami, M. The geometric foundations of hamiltonian monte carlo. Bernoulli 2017, 23, 2257–2298. [Google Scholar] [CrossRef]
- Girolami, M.; Calderhead, B. Riemann manifold langevin and hamiltonian monte carlo methods. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2011, 73, 123–214. [Google Scholar] [CrossRef]
- Song, J.; Zhao, S.; Ermon, S. A-nice-mc: Adversarial training for mcmc. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5140–5150. [Google Scholar]
- Levy, D.; Hoffman, M.D.; Sohl-Dickstein, J. Generalizing Hamiltonian Monte Carlo with Neural Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Gu, M.; Sun, S.; Liu, Y. Dynamical Sampling with Langevin Normalization Flows. Entropy 2019, 21, 1096. [Google Scholar] [CrossRef] [Green Version]
- Hoffman, M.; Sountsov, P.; Dillon, J.V.; Langmore, I.; Tran, D.; Vasudevan, S. Neutra-lizing bad geometry in hamiltonian monte carlo using neural transport. arXiv 2019, arXiv:1903.03704. [Google Scholar]
- Nijkamp, E.; Gao, R.; Sountsov, P.; Vasudevan, S.; Pang, B.; Zhu, S.C.; Wu, Y.N. Learning Energy-based Model with Flow-based Backbone by Neural Transport MCMC. arXiv 2020, arXiv:2006.06897. [Google Scholar]
- Titsias, M.; Dellaportas, P. Gradient-based Adaptive Markov Chain Monte Carlo. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 15730–15739. [Google Scholar]
- Hastings, W. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Sohl-Dickstein, J.; Mudigonda, M.; DeWeese, M.R. Hamiltonian Monte Carlo without detailed balance. arXiv 2014, arXiv:1409.5191. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using real nvp. arXiv 2016, arXiv:1605.08803. [Google Scholar]
- Kobyzev, I.; Prince, S.; Brubaker, M.A. Normalizing flows: Introduction and ideas. arXiv 2019, arXiv:1908.09257. [Google Scholar]
- Papamakarios, G.; Nalisnick, E.; Rezende, D.J.; Mohamed, S.; Lakshminarayanan, B. Normalizing flows for probabilistic modeling and inference. arXiv 2019, arXiv:1912.02762. [Google Scholar]
- Spanbauer, S.; Freer, C.; Mansinghka, V. Deep Involutive Generative Models for Neural MCMC. arXiv 2020, arXiv:2006.15167. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. Nice: Non-linear independent components estimation. arXiv 2014, arXiv:1410.8516. [Google Scholar]
- Marzouk, Y.; Moselhy, T.; Parno, M.; Spantini, A. An introduction to sampling via measure transport. arXiv 2016, arXiv:1602.05023. [Google Scholar]
- Langmore, I.; Dikovsky, M.; Geraedts, S.; Norgaard, P.; Von Behren, R. A Condition Number for Hamiltonian Monte Carlo. arXiv 2019, arXiv:1905.09813. [Google Scholar]
- Salimans, T.; Kingma, D.; Welling, M. Markov chain monte carlo and variational inference: Bridging the gap. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 1218–1226. [Google Scholar]
- Zhang, Y.; Hernández-Lobato, J.M.; Ghahramani, Z. Ergodic measure preserving flows. arXiv 2018, arXiv:1805.10377. [Google Scholar]
- Postorino, M.N.; Versaci, M. A geometric fuzzy-based approach for airport clustering. Adv. Fuzzy Syst. 2014, 2014, 201243. [Google Scholar] [CrossRef] [Green Version]
- Tkachenko, R.; Izonin, I.; Kryvinska, N.; Dronyuk, I.; Zub, K. An approach towards increasing prediction accuracy for the recovery of missing IoT data based on the GRNN-SGTM ensemble. Sensors 2020, 20, 2625. [Google Scholar] [CrossRef]
- Neklyudov, K.; Egorov, E.; Shvechikov, P.; Vetrov, D. Metropolis-hastings view on variational inference and adversarial training. arXiv 2018, arXiv:1810.07151. [Google Scholar]
- Thin, A.; Kotelevskii, N.; Durmus, A.; Panov, M.; Moulines, E. Metropolized Flow: From Invertible Flow to MCMC. In Proceedings of the ICML Workshop on Invertible Neural Networks, Normalizing Flows, and Explicit Likelihood Models, 12–18 July 2020. virtual event. [Google Scholar]
- Pasarica, C.; Gelman, A. Adaptively scaling the Metropolis algorithm using expected squared jumped distance. Stat. Sin. 2010, 20, 343–364. [Google Scholar]
- Poole, B.; Ozair, S.; Oord, A.V.d.; Alemi, A.A.; Tucker, G. On variational bounds of mutual information. arXiv 2019, arXiv:1905.06922. [Google Scholar]
- Song, J.; Ermon, S. Understanding the limitations of variational mutual information estimators. arXiv 2019, arXiv:1910.06222. [Google Scholar]
- Neal, R.M. Slice sampling. Ann. Stat. 2003, 31, 705–741. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Gelman, A. The No-U-Turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Betancourt, M. A general metric for Riemannian manifold Hamiltonian Monte Carlo. In Lecture Notes in Computer Science, Proceedings of the International Conference on Geometric Science of Information, Paris, France, 28–30 August 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 327–334. [Google Scholar]
- Xie, J.; Lu, Y.; Zhu, S.C.; Wu, Y. A theory of generative convnet. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2635–2644. [Google Scholar]
- Du, Y.; Mordatch, I. Implicit generation and generalization in energy-based models. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Tieleman, T. Training restricted Boltzmann machines using approximations to the likelihood gradient. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1064–1071. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6626–6637. [Google Scholar]
- Hoffman, M.D. Learning deep latent Gaussian models with Markov chain Monte Carlo. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 1510–1519. [Google Scholar]
- Che, T.; Zhang, R.; Sohl-Dickstein, J.; Larochelle, H.; Paull, L.; Cao, Y.; Bengio, Y. Your GAN is Secretly an Energy-based Model and You Should use Discriminator Driven Latent Sampling. arXiv 2020, arXiv:2003.06060. [Google Scholar]
- Yu, L.; Song, Y.; Song, J.; Ermon, S. Training Deep Energy-Based Models with f-Divergence Minimization. In Proceedings of the International Conference on Machine Learning, Virtual Event, Vienna, Austria, 12–18 July 2020. [Google Scholar]
- Grathwohl, W.; Wang, K.C.; Jacobsen, J.H.; Duvenaud, D.; Norouzi, M.; Swersky, K. Your classifier is secretly an energy based model and you should treat it like one. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]

| Dataset (Measure) | L2HMC | Ours | |
|---|---|---|---|
| 50d ICG (ESS/MH) | 0.783 | 0.86 | |
| 2d SCG (ESS/MH) | 0.497 | 0.89 | |
| 50d ICG (ESS/grad) | |||
| 2d SCG (ESS/grad) | |||
| Dataset (Measure) | Neutra | Ours | |
| Funnel-1 (ESS/grad) | |||
| Funnel-1 (ESS/grad) | |||
| Dataset (Measure) | A-NICE-MC | NFLMC | Ours |
| German (ESS/5k) | 926.49 | 1176.8 | 3150 |
| Australian (ESS/5k) | 1015.75 | 1586.4 | 2950 |
| Heart (ESS/5k) | 1251.16 | 2000 | 3600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, Y.; Sommer, F.T. A Neural Network MCMC Sampler That Maximizes Proposal Entropy. Entropy 2021, 23, 269. https://doi.org/10.3390/e23030269
Li Z, Chen Y, Sommer FT. A Neural Network MCMC Sampler That Maximizes Proposal Entropy. Entropy. 2021; 23(3):269. https://doi.org/10.3390/e23030269
Chicago/Turabian StyleLi, Zengyi, Yubei Chen, and Friedrich T. Sommer. 2021. "A Neural Network MCMC Sampler That Maximizes Proposal Entropy" Entropy 23, no. 3: 269. https://doi.org/10.3390/e23030269
APA StyleLi, Z., Chen, Y., & Sommer, F. T. (2021). A Neural Network MCMC Sampler That Maximizes Proposal Entropy. Entropy, 23(3), 269. https://doi.org/10.3390/e23030269






