Toward Accelerated Training of Parallel Support Vector Machines Based on Voronoi Diagrams
Abstract
1. Introduction
2. Related Works
2.1. Support Vector Machines
2.2. Ensemble Learning
2.3. Voronoi Diagrams
3. pSVM Algorithm
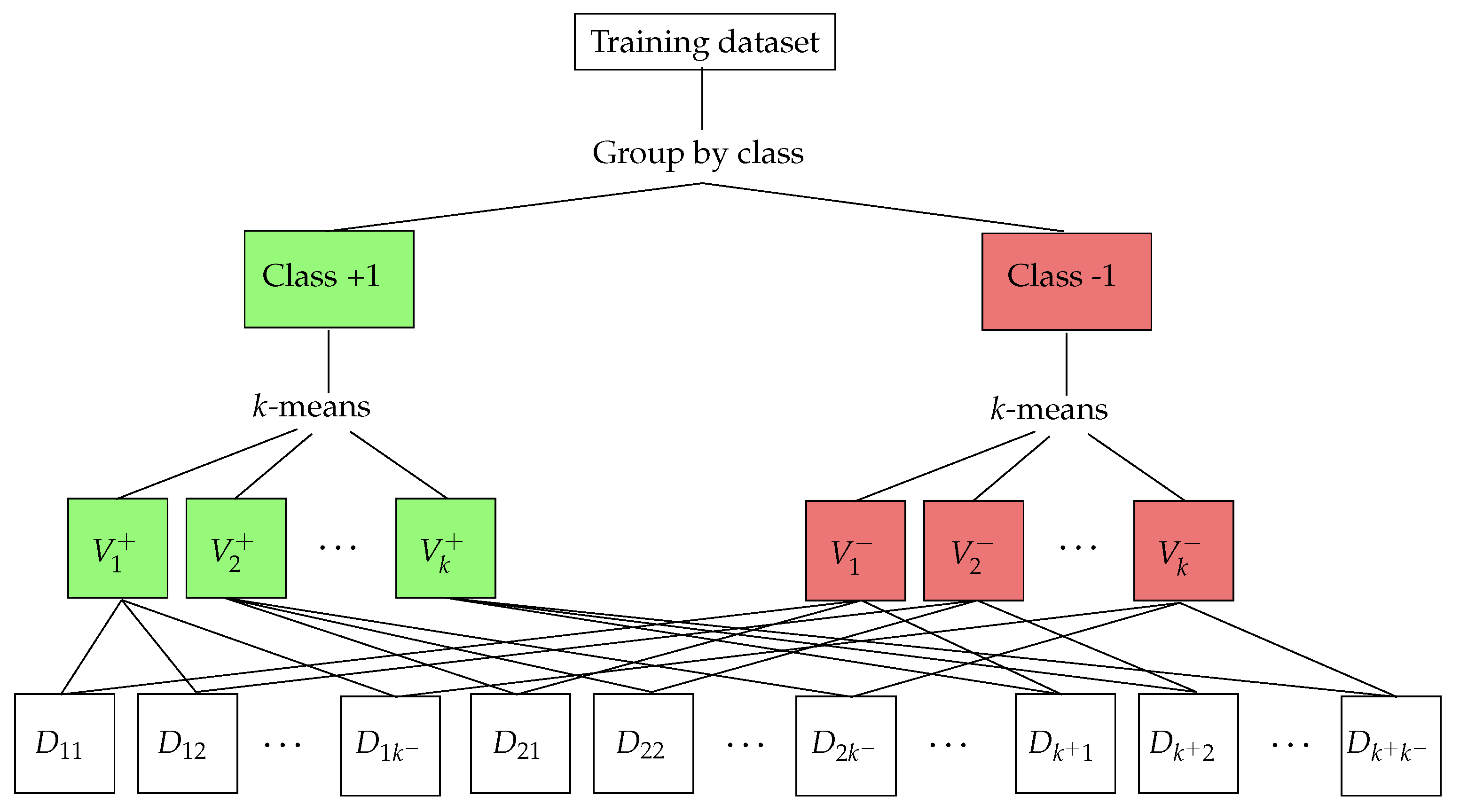
3.1. Data Partitioning
3.2. Training
Learning Strategy of Each Sub-SVM
| Algorithm 1: pSVM training algorithm. |
Data: , , ; N: number of nodes; Result: S (set of Voronoi regions pairs); (ensemble of SVM);
|
3.3. Classification
| Algorithm 2: pSVM classification algorithm. |
 |
3.4. Computational Complexity
4. Experimental Results
4.1. One Region with Two Partially Overlapping Classes
Results
- Single SVM, ensemble, and pSVM with no limit of iterations;
- Single SVM, ensemble, and pSVM with a limit of 10 iterations;
- Single SVM, ensemble, and pSVM with a limit of 1 iteration.
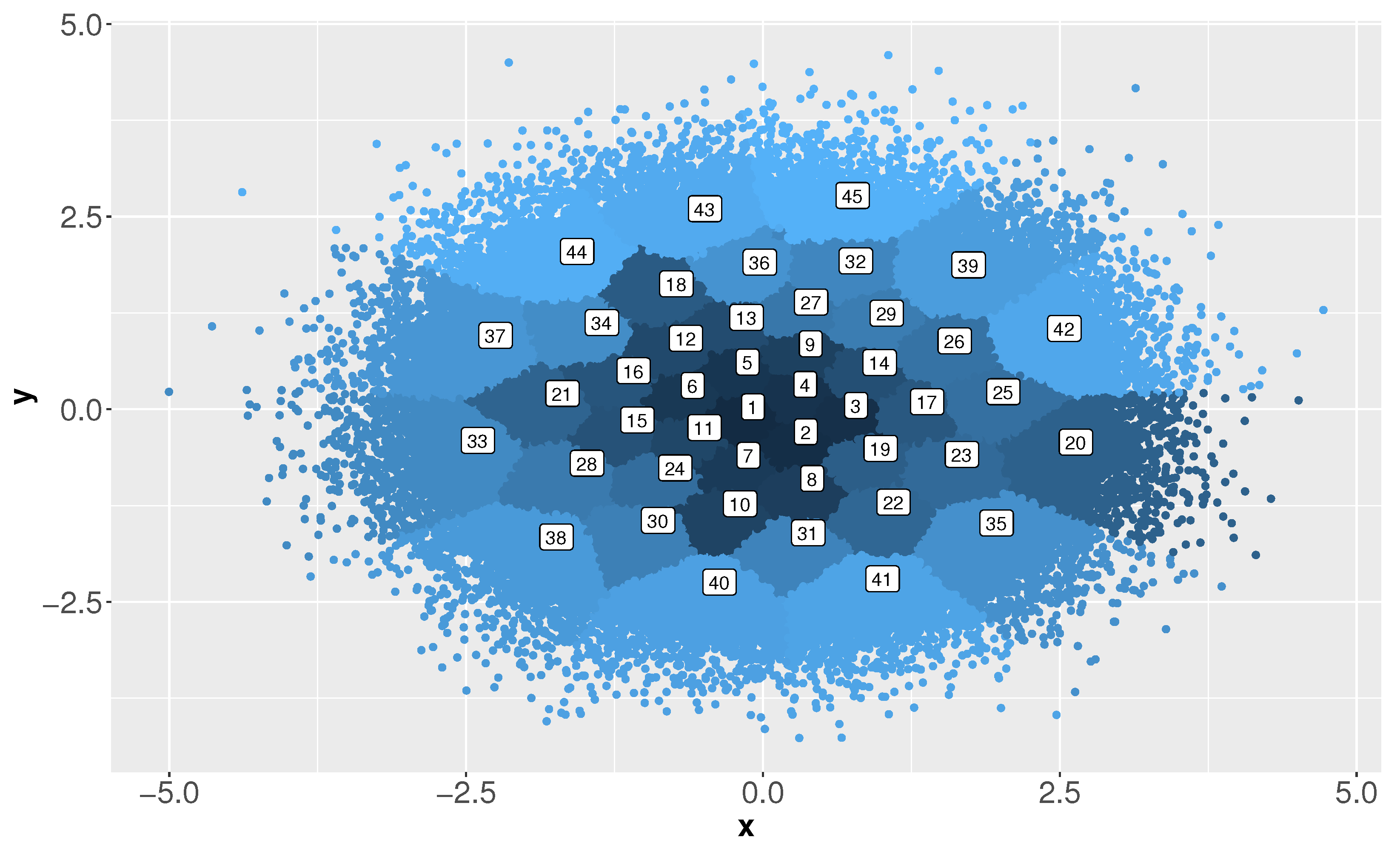
4.2. Eight Multi-Dimensional Regions with Two Partially Overlapping Classes
Results
4.3. A Numerical Estimation of Training Time
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- LeCun, Y.; Boser, B.E.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.E.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; Adaptive Computation and Machine Learning Series; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Clarkson, K.L. Algorithms for Closest-Point Problems (Computational Geometry). Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1985. [Google Scholar]
- Graf, H.P.; Cosatto, E.; Bottou, L.; Durdanovic, I.; Vapnik, V. Parallel Support Vector Machines: The Cascade SVM. In Proceedings of the Advances in Neural Information Processing Systems 17 [Neural Information Processing Systems, NIPS 2004, Vancouver, BC, Canada, 13–18 December 2004; pp. 521–528. [Google Scholar]
- Chang, E.Y. PSVM: Parallelizing Support Vector Machines on Distributed Computers. In Foundations of Large-Scale Multimedia Information Management and Retrieval: Mathematics of Perception; Springer: Berlin/Heidelberg, Germany, 2011; pp. 213–230. [Google Scholar] [CrossRef]
- Caruana, G.; Li, M.; Qi, M. A MapReduce based parallel SVM for large scale spam filtering. In Proceedings of the 2011 Eighth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Shanghai, China, 26–28 July 2011; Volume 4, pp. 2659–2662. [Google Scholar]
- Arampatzis, T.; Lygeros, J.; Manesis, S. A Survey of Applications of Wireless Sensors and Wireless Sensor Networks. In Proceedings of the 2005 IEEE International Symposium on, Mediterrean Conference on Control and Automation Intelligent Control, Limassol, Cyprus, 27–29 June 2005; pp. 719–724. [Google Scholar] [CrossRef]
- da Silva, A.P.R.; Martins, M.H.T.; Rocha, B.P.S.; Loureiro, A.A.F.; Ruiz, L.B.; Wong, H.C. Decentralized intrusion detection in wireless sensor networks. In Proceedings of the Q2SWinet’05—Proceedings of the First ACM Workshop on Q2S and Security for Wireless and Mobile Networks, Montreal, QC, Canada, 13 October 2005; Boukerche, A., de Araujo, R.B., Eds.; ACM: New York, NY, USA, 2005; pp. 16–23. [Google Scholar] [CrossRef]
- Han, Z.; Gao, R.X.; Fan, Z. Occupancy and indoor environment quality sensing for smart buildings. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference Proceedings, Graz, Austria, 13–16 May 2012; pp. 882–887. [Google Scholar] [CrossRef]
- Ko, J.; Lim, J.H.; Chen, Y.; Musvaloiu-E, R.; Terzis, A.; Masson, G.M.; Gao, T.; Destler, W.; Selavo, L.; Dutton, R.P. MEDiSN: Medical emergency detection in sensor networks. ACM Trans. Embed. Comput. Syst. 2010, 10, 11:1–11:29. [Google Scholar] [CrossRef]
- Wan, S.; Zhao, Y.; Wang, T.; Gu, Z.; Abbasi, Q.H.; Choo, K.R. Multi-dimensional data indexing and range query processing via Voronoi diagram for internet of things. Future Gener. Comput. Syst. 2019, 91, 382–391. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. Reine Angew. Math. (Crelles J.) 1908, 1908, 198–287. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Breiman, L. Some Infinity Theory for Predictor Ensembles. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.87.5037&rep=rep1&type=pdf (accessed on 29 November 2021).
- Hu, Z.; Cai, Y.; Li, Y.; Xu, X. Support vector machine based ensemble classifier. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 745–749. [Google Scholar]
- Donta, P.K.; Amgoth, T.; Annavarapu, C.S.R. Machine learning algorithms for wireless sensor networks: A survey. Inf. Fusion 2019, 49, 1–25. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Fischetti, M. Fast training of Support Vector Machines with Gaussian kernel. Discret. Optim. 2016, 22, 183–194. [Google Scholar] [CrossRef]
- Moguerza, J.M.; Muñoz, A. Support Vector Machines with applications. Stat. Sci. 2006, 21, 322–336. [Google Scholar] [CrossRef]
- Zheng, B.; Yoon, S.W.; Lam, S.S. Breast cancer diagnosis based on feature extraction using a hybrid of K-means and support vector machine algorithms. Expert Syst. Appl. 2014, 41, 1476–1482. [Google Scholar] [CrossRef]
- Alfaro, C.; Cano-Montero, J.; Gómez, J.; Moguerza, J.M.; Ortega, F. A multi-stage method for content classification and opinion mining on weblog comments. Ann. Oper. Res. 2016, 236, 197–213. [Google Scholar] [CrossRef]
- Wu, L.C.; Kuo, C.; Loza, J.; Kurt, M.; Laksari, K.; Yanez, L.Z.; Senif, D.; Anderson, S.C.; Miller, L.E.; Urban, J.E.; et al. Detection of American football head impacts using biomechanical features and support vector machine classification. Sci. Rep. 2017, 8, 1–14. [Google Scholar] [CrossRef]
- Zidi, S.; Moulahi, T.; Alaya, B. Fault detection in wireless sensor networks through SVM classifier. IEEE Sensors J. 2017, 18, 340–347. [Google Scholar] [CrossRef]
- Osuna, E.; Freund, R.; Girosi, F. An improved training algorithm for Support Vector Machines. In Proceedings of the Neural networks for signal processing VII. Proceedings of the 1997 IEEE Signal Processing Society Workshop, Amelia Island, FL, USA, 24–26 September 1997; pp. 276–285. [Google Scholar]
- Joachims, T. Making Large-Scale SVM Learning Practical. Available online: https://www.cs.cornell.edu/people/tj/publications/joachims_99a.pdf (accessed on 29 November 2021).
- Platt, J.C. Using Analytic QP and Sparseness to Speed Training of Support Vector Machines. In Advances in Neural Information Processing Systems 11, NIPS Conference, Denver, CO, USA, 30 November–5 December 1998; Kearns, M.J., Solla, S.A., Cohn, D.A., Eds.; The MIT Press: Cambridge, MA, USA, 1998; pp. 557–563. [Google Scholar]
- Nandan, M.; Khargonekar, P.P.; Talathi, S.S. Fast SVM training using approximate extreme points. J. Mach. Learn. Res. 2014, 15, 59–98. [Google Scholar]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms, 2nd ed. Available online: https://www.wiley.com/en-in/Combining+Pattern+Classifiers%3A+Methods+and+Algorithms%2C+2nd+Edition-p-9781118315231 (accessed on 29 November 2021).
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Kang, M.; Ahn, J.; Lee, K. Opinion mining using ensemble text hidden Markov models for text classification. Expert Syst. Appl. 2018, 94, 218–227. [Google Scholar] [CrossRef]
- Deng, L.; Platt, J. Ensemble deep learning for speech recognition. Available online: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/EnsembleDL_submitted.pdf (accessed on 29 November 2021).
- Zvarevashe, K.; Olugbara, O. Ensemble learning of hybrid acoustic features for speech emotion recognition. Algorithms 2020, 13, 70. [Google Scholar] [CrossRef]
- Araque, O.; Corcuera-Platas, I.; Sánchez-Rada, J.F.; Iglesias, C.A. Enhancing deep learning sentiment analysis with ensemble techniques in social applications. Expert Syst. Appl. 2017, 77, 236–246. [Google Scholar] [CrossRef]
- Liu, B.; Li, C.C.; Yan, K. DeepSVM-fold: Protein fold recognition by combining Support Vector Machines and pairwise sequence similarity scores generated by deep learning networks. Briefings Bioinform. 2020, 21, 1733–1741. [Google Scholar] [CrossRef] [PubMed]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. Super ensemble learning for daily streamflow forecasting: Large-scale demonstration and comparison with multiple machine learning algorithms. Neural Comput. Appl. 2021, 33, 3053–3068. [Google Scholar] [CrossRef]
- de Almeida, R.; Goh, Y.M.; Monfared, R.; Steiner, M.T.A.; West, A. An ensemble based on neural networks with random weights for online data stream regression. Soft Comput. 2020, 24, 9835–9855. [Google Scholar] [CrossRef]
- El Hindi, K.; AlSalman, H.; Qasem, S.; Al Ahmadi, S. Building an ensemble of fine-tuned naive Bayesian classifiers for text classification. Entropy 2018, 20, 857. [Google Scholar] [CrossRef]
- Maudes, J.; Rodríguez, J.J.; García-Osorio, C.; García-Pedrajas, N. Random feature weights for decision tree ensemble construction. Inf. Fusion 2012, 13, 20–30. [Google Scholar] [CrossRef]
- Gu, J.; Wang, L.; Wang, H.; Wang, S. A novel approach to intrusion detection using SVM ensemble with feature augmentation. Comput. Secur. 2019, 86, 53–62. [Google Scholar] [CrossRef]
- Huang, M.W.; Chen, C.W.; Lin, W.C.; Ke, S.W.; Tsai, C.F. SVM and SVM ensembles in breast cancer prediction. PLoS ONE 2017, 12, e0161501. [Google Scholar] [CrossRef]
- Boots, B.; Okabe, A.; Sugihara, K. Spatial tessellations. Geogr. Inf. Syst. 1999, 1, 503–526. [Google Scholar]
- Du, Q.; Faber, V.; Gunzburger, M. Centroidal Voronoi tessellations: Applications and algorithms. SIAM Rev. 1999, 41, 637–676. [Google Scholar] [CrossRef]
- Wang, P.; González, M.C.; Menezes, R.; Barabási, A.L. Understanding the spread of malicious mobile-phone programs and their damage potential. Int. J. Inf. Secur. 2013, 12, 383–392. [Google Scholar] [CrossRef][Green Version]
- Hartigan, J.A. Clustering Algorithms; John Wiley & Sons, Inc.: Chichester, UK, 1975. [Google Scholar]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice Hall; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Preparata, F.P.; Shamos, M.I. Computational Geometry: An Introduction; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Albers, G.; Guibas, L.J.; Mitchell, J.S.; Roos, T. Voronoi diagrams of moving points. Int. J. Comput. Geom. Appl. 1998, 8, 365–379. [Google Scholar] [CrossRef]
- Berchtold, S.; Ertl, B.; Keim, D.A.; Kriegel, H.P.; Seidl, T. Fast nearest neighbor search in high-dimensional space. In Proceedings of the 14th International Conference on Data Engineering, Orlando, FL, USA, 23–27 February 1998; pp. 209–218. [Google Scholar]
- Zheng, A.; Bian, S.; Chaudhry, E.; Chang, J.; Haron, H.; You, L.; Zhang, J.J. Voronoi diagram and Monte-Carlo simulation based finite element optimization for cost-effective 3D printing. J. Comput. Sci. 2021, 50, 101301. [Google Scholar] [CrossRef]
- Haker, S.; Angenent, S.; Tannenbaum, A.; Kikinis, R.; Sapiro, G.; Halle, M. Conformal surface parameterization for texture mapping. IEEE Trans. Vis. Comput. Graph. 2000, 6, 181–189. [Google Scholar] [CrossRef]
- Lopes, A.; Fonseca, S.; Lese, R.; Baca, A. Using voronoi diagrams to describe tactical behaviour in invasive team sports: An application in basketball. Cuad. Psicol. Deporte 2015, 15, 123–130. [Google Scholar] [CrossRef]
- Ayawli, B.B.K.; Mei, X.; Shen, M.; Appiah, A.Y.; Kyeremeh, F. Mobile robot path planning in dynamic environment using Voronoi diagram and computation geometry technique. IEEE Access 2019, 7, 86026–86040. [Google Scholar] [CrossRef]
- Young, W.A.; Nykl, S.L.; Weckman, G.R.; Chelberg, D.M. Using Voronoi diagrams to improve classification performances when modeling imbalanced datasets. Neural Comput. Appl. 2015, 26, 1041–1054. [Google Scholar] [CrossRef]
- Silva, E.J.; Zanchettin, C. A voronoi diagram based classifier for multiclass imbalanced data sets. In Proceedings of the 2016 5th Brazilian Conference on Intelligent Systems (BRACIS), Recife, Brazil, 9–12 October 2016; pp. 109–114. [Google Scholar]
- de Carvalho, A.M.; Prati, R.C. DTO-SMOTE: Delaunay Tessellation Oversampling for Imbalanced Data Sets. Information 2020, 11, 557. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Sugar, C.A.; James, G.M. Finding the number of clusters in a dataset: An information-theoretic approach. J. Am. Stat. Assoc. 2003, 98, 750–763. [Google Scholar] [CrossRef]
- Masud, M.A.; Huang, J.Z.; Wei, C.; Wang, J.; Khan, I.; Zhong, M. I-nice: A new approach for identifying the number of clusters and initial cluster centres. Inf. Sci. 2018, 466, 129–151. [Google Scholar] [CrossRef]
- Sturges, H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Krebel, U.G. Pairwise classification and Support Vector Machines. Available online: https://dl.acm.org/doi/10.5555/299094.299108 (accessed on 29 November 2021).
- Bordes, A.; Ertekin, S.; Weston, J.; Botton, L.; Cristianini, N. Fast kernel classifiers with online and active learning. J. Mach. Learn. Res. 2005, 6, 1579–1619. [Google Scholar]
- Aloise, D.; Deshpande, A.; Hansen, P.; Popat, P. NP-hardness of Euclidean sum-of-squares clustering. Mach. Learn. 2009, 75, 245–248. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Kim, H.C.; Pang, S.; Je, H.M.; Kim, D.; Bang, S.Y. Constructing support vector machine ensemble. Pattern Recognit. 2003, 36, 2757–2767. [Google Scholar] [CrossRef]



| Iterations | SVM (Linear Kernel) | SVM (RBF Kernel) | Ensemble (Linear Kernel) | Ensemble (RBF Kernel) | pSVM (Linear Kernel) | pSVM (RBF Kernel) |
|---|---|---|---|---|---|---|
| No limit | () | () | () | () | () | () |
| 10 | () | () | () | () | () | () |
| 1 | () | () | () | () | () | () |
| Iterations | SVM | SVM | Ensemble | Ensemble | pSVM | pSVM | |
|---|---|---|---|---|---|---|---|
| (Linear Kernel) | (RBF Kernel) | (Linear Kernel) | (RBF Kernel) | (Linear Kernel) | (RBF Kernel) | ||
| No limit | 1 | () | () | () | () | () | () |
| 7 | - | - | () | () | () | () | |
| 15 | - | - | () | () | () | () | |
| 10 | 1 | () | () | () | () | () | () |
| 7 | - | - | () | () | () | () | |
| 15 | - | - | () | () | () | () | |
| 1 | 1 | () | () | () | () | () | () |
| 7 | - | - | () | () | () | () | |
| 15 | - | - | () | () | () | () |
| Iterations | SVM (Linear Kernel) | SVM (RBF Kernel) | Nodes | Ensemble (Linear Kernel) | Ensemble (RBF Kernel) | pSVM (Linear Kernel) | pSVM (RBF Kernel) |
|---|---|---|---|---|---|---|---|
| 4 | () | () | () | () | |||
| No limit | () | () | 9 | () | () | () | () |
| 16 | () | () | () | () | |||
| 4 | () | () | () | () | |||
| 10 | () | () | 9 | () | () | () | () |
| 16 | () | () | () | () | |||
| 4 | () | () | () | () | |||
| 1 | () | () | 9 | () | () | () | () |
| 16 | () | () | () | () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfaro, C.; Gomez, J.; Moguerza, J.M.; Castillo, J.; Martinez, J.I. Toward Accelerated Training of Parallel Support Vector Machines Based on Voronoi Diagrams. Entropy 2021, 23, 1605. https://doi.org/10.3390/e23121605
Alfaro C, Gomez J, Moguerza JM, Castillo J, Martinez JI. Toward Accelerated Training of Parallel Support Vector Machines Based on Voronoi Diagrams. Entropy. 2021; 23(12):1605. https://doi.org/10.3390/e23121605
Chicago/Turabian StyleAlfaro, Cesar, Javier Gomez, Javier M. Moguerza, Javier Castillo, and Jose I. Martinez. 2021. "Toward Accelerated Training of Parallel Support Vector Machines Based on Voronoi Diagrams" Entropy 23, no. 12: 1605. https://doi.org/10.3390/e23121605
APA StyleAlfaro, C., Gomez, J., Moguerza, J. M., Castillo, J., & Martinez, J. I. (2021). Toward Accelerated Training of Parallel Support Vector Machines Based on Voronoi Diagrams. Entropy, 23(12), 1605. https://doi.org/10.3390/e23121605






