Cryptanalysis of a New Chaotic Image Encryption Technique Based on Multiple Discrete Dynamical Maps

Abstract

Recently, a new chaotic image encryption technique was proposed based on multiple discrete dynamic maps. The authors claim that the scheme can provide excellent privacy for traditional digital images. However, in order to minimize the computational cost, the encryption scheme adopts one-round encryption and a traditional permutation–diffusion structure. Through cryptanalysis, there is no strong correlation between the key and the plain image, which leads to the collapse of cryptosystem. Based on this, two methods of chosen-plaintext attacks are proposed in this paper. The two methods require 3 pairs and 258 pairs of plain and cipher images, respectively, to break the original encryption system. The simulation results show the effectiveness of the two schemes.

1. Introduction

In this era of big data, information security has always been a sensitive topic [1]. Image files as one of the most typical multimedia information will inevitably pass through unstable and unsafe channels, and probably resulting in information leakage. Criminals intercept important information by certain technical means to change and transmit it at will, causing a series of information security problems [2]. Over the years, a large number of researchers have proposed a variety of image encryption ideas and strived to solve the security of image transmission. Among them, chaos-based methods are more suitable for image encryption than DES [3] and AES [4] because of the characteristics of pseudo-randomness and sensitivity. Therefore, chaos-based image encryption schemes have sprung up owing to the researchers who are investing a lot of time and effort in this field [5,6,7,8,9,10,11,12].

So far, many chaos-based image encryption schemes have been based on the permutation–diffusion structure proposed by Fridrich [13]. However, some encryption schemes [14,15,16,17,18] are insecure, which have been cracked by some researchers with known/chosen-ciphertext attacks or known/chosen-plaintext attacks [19,20,21,22,23]. Hu et al. in [17] found security vulnerabilities in the scheme [24] and carried out cryptanalysis and improvement. In the improved scheme, different secret keys were proposed to eliminate vulnerabilities in two rounds of diffusion. However, this scheme was still cracked by Li et al. in [25], who found a linear relationship of diffusion and used chosen-plaintext attacks. These broken encryption schemes are problematic because the key is fixed—it cannot be adapted to different plain images. At this point, the plain/cipher images can be constructed. The generated plain/cipher is then used to infer the key. To overcome this shortcoming, Hsiao et al. in [26] proposed a color image encryption scheme that uses the sum of plain image pixels to enhance the secret key space. The sum of its pixels (Mod 256) is set as the basic parameter of chaotic sequence. Since the sum of its pixels (Mod 256) has 256 possibilities, it can be exhaustively listed and calculated for correlation analysis. Having found the most relevant image among 256 plain/cipher images, this scheme was cracked by Fan et al. in [27] with a chosen-plaintext attack. However, the broken encryption scheme exposed some features of the plain image due to the low-level key space and square image limitations. The attacker uses the number of key matrices and the range of pixel values in encryption to successfully crack the cryptosystem through correlation analysis. In [28], an image encryption algorithm based on improved Henon mapping is proposed to encrypt images through shift transformation and diffusion. This scheme was effectively cracked by Zhou et al. in [29] using 257 plaintext images, and if boundary pixels were not taken into account, two plaintext images were required to achieve effectively attack. Mondal et al. in [30] proposed a new 2D chaotic mapping. The encryption scheme first scrambles the pixel position and then changes the pixel position by diffusion. Li et al. in [31] found three security vulnerabilities in this scheme, and successfully cracked them by using a chosen-plaintext attack. Although these schemes involve multiple rounds of encryption with a high level of time complexity, they are all based on the permutation–diffusion structure, and the key is independent of the plain image. Therefore, the attacker can first eliminate the diffusion effect of the cipher image and observe the different characteristics leaked in the encryption stage, and then verify possible solutions to break the stages of multiple rounds of permutation and diffusion.

Recently, Majid in [32] proposed a new chaotic image encryption technique based on multiple discrete dynamical maps. It uses three chaotic maps to generate random sequences, and in order to save time, it only uses one round of encryption to achieve confusion and diffusion. The scheme can be divided into two parts: pixel permutation and pixel diffusion. This scheme involves one round of encryption based on a permutation–diffusion structure, which has been analyzed and studied by many researchers [33,34]. We conducted cryptanalysis on the encryption scheme and then proposed related attack methods to crack it. In this paper, we have used two methods of chosen-plaintext attack, both of which can destroy diffusion and permutation transformation, and successfully attacked the original encryption scheme. The rest of the paper is organized as follows: Section 2 summarizes Majid’s scheme [30]; Section 3 proposes two kinds of chosen-plaintext attacks and carries out simulation experiments; the final section simply summarizes the whole paper.

2. Overview of Majid’s Encryption Scheme

Majid et al. designed an original image encryption scheme, which used one-round encryption to provide better confidentiality. This encryption scheme is divided into five main steps: image sub-blocking, permutation within blocks, permutation between blocks, the first diffusion, and the second diffusion.

2.1. Chaotic Maps of the Original Cipher Scheme

A two-dimensional Henon chaotic map has good chaotic behavior, and its mathematical expression is presented as follows:

$$x_{n+1}=1-a{x}_n+y_n,$$

(1)

$$y_{n+1}=b{x}_n,$$

(2)

where x₀ and y₀ are the initial parameters of the chaotic map, and x₀ = 1.61001, y₀ = 2.9996, a = 1.7085, b = 0.32032.

A circle chaotic map has good chaotic behavior, and its mathematical expression is as follows:

$${\theta }_{n+1}=\mathrm{mod}({\theta }_n+\mathsf{\Omega }-\frac{K}{2\pi }\sin (2\pi ({\theta }_n)),1),$$

(3)

where θ₀ = 0.4, Ω = 0.4, K is a constant.

A Duffing chaotic map also has good chaotic behavior. Its mathematical expression is as follows:

$$x_{n+1}=y_n,$$

(4)

$$y_{n+1}=-b{x}_n+a{y}_n-y_n{}^3,$$

(5)

where x₀ = −1.5, y₀ = 1.5, a = 2.738, b = 0.1534.

2.2. Majid’s Encryption Scheme

The specific steps are as follows:

Step 1 

Input a 256 × 256 × 3 plain image, divide it into three channels, and then separate the single-channel image into 32 × 32 blocks.

Step 2 

Generate a chaotic sequence using a two-dimensional Henon chaotic map and perform pixel permutation within blocks of each channel in order.

Step 3 

Perform random permutation between blocks of each channel orderly.

Step 4 

Use a circle chaotic map to execute the first diffusion for each channel.

Step 5 

Use a Duffing chaotic map to execute the second diffusion for each channel.

3. Cryptanalysis

This section mainly introduces the preparation work and two schemes to eliminate the diffusion effect and obtain equivalent displacement mapping. The feasibility of the two schemes is verified by simulation experiments.

3.1. Preparations

Proposition 1.

For the encryption scheme of the permutation–diffusion structure, using the all-zero image can break the diffusion transform to obtain the equivalent diffusion matrix.

Proof. 

Assuming that the plain image of 256 × 256 × 3 is P_i, the permutation transformation expression is defined as:

$$S=F_i(P_i),$$

(6)

where F_i(.) is the permutation transform of the image, S is the permutation-only image of plain image P_i. During the permutation transformation, the pixel value P_i(i, j) in the plain image only corresponds to the pixel value S(i, j) in the permutation-only image of row i and column j.

The expression of image diffusion transformation is as follows:

$$D=S\oplus D_i,$$

(7)

where ⊕ is the XOR operation, D_i is the diffusion matrix, and D is the image after diffusion transformation. Finally, the cipher image C_i corresponding to the plain image P_i is obtained as shown in Equation (8).

$$C_i=F_i\left(P_i\right)\oplus D_i=S\oplus D_i.$$

(8)

The permutation phase will not change the original pixel value of the image but simply changes the pixel position of the previous image. A plain image of all zero pixels is still with all zero pixels after permutation. Then, one will obtain the cipher image C₀ from the all-zero image P₀ after the diffusion step.

$$C_0=F_i\left(P_0\right)\oplus D_i=P_0\oplus D_i=D_i.$$

(9)

It can be seen that after a round of permutation and diffusion of all-zero image P₀, the cipher image C₀ obtained at this time is exactly equal to diffusion matrix D_i. Then, the permutation-only image S can be obtained by XOR operation in Equation (10).

$$C_i\oplus C_0=S\oplus D_i\oplus D_i=S.$$

(10)

□

Proposition 2.

Two diffusions on a permutation-only image S can be linearly transformed into one diffusion.

Proof. 

$$C_i(i,j)=S(i,j)\oplus D_1(i,j)\oplus D_2(i,j),$$

(11)

where D₁ is the first diffusion matrix and D₂ is the second diffusion matrix.

At this time, according to the reversible operation of XOR, the XOR result of the next two matrices is calculated firstly as follows:

$$D_i(i,j)=D_1(i,j)\oplus D_2(i,j).$$

(12)

Finally, the pixel value of D_i(i, j) is obtained and XOR operation is performed with the pixel value of S(i, j).

$$C_i(i,j)=S(i,j)\oplus D_i(i,j).$$

(13)

Then,

$$C_i=S\oplus D_i.$$

(14)

□

Proposition 3.

Suppose a plain image is denoted by P₁, and P₂ is obtained by changing n pixels of image P₁. Then, P₁ and P₂ are encrypted to obtain the cipher images C₁ and C₂. So, C₁ and C₂ will have n different pixel values. The pixel value of each position in the plain image is one-to-one mapped to the pixel value of a certain position in the cipher image, that is, there is a mapping relationship between them.

Proof. 

The encryption process for plain image P₁ is as follows:

$$\{\begin{array}{l}{S}_1(i^{\prime },j^{\prime })=F_2(F_1(P_1(i,j)))\\ C_1(i^{\prime },j^{\prime })=S_1(i^{\prime },j^{\prime })\oplus K_1(i^{\prime },j^{\prime })\oplus K_2(i^{\prime },j^{\prime })\end{array},$$

(15)

where F₁ is the first intra-block pixel displacement and F₂ is the second inter-block displacement. Image S₁ represents the permutation-only image after two permutations, K₁ is the diffusion XOR matrix for the first time, and K₂ is the diffusion XOR matrix for the second time. Position (i′, j′) is the transposition of Position (i, j).

The encryption process for plain image P₂ is as follows:

$$\{\begin{array}{l}{S}_2(i^{\prime },j^{\prime })=F_2(F_1(P_2(i,j)))\\ C_2(i^{\prime },j^{\prime })=S_2(i^{\prime },j^{\prime })\oplus K_1(i^{\prime },j^{\prime })\oplus K_2(i^{\prime },j^{\prime })\end{array}.$$

(16)

According to proposition 2, image S₁ and S₂ after two diffusions can be considered equivalent to those being processed by one linearly transformed diffusion.

$$\{\begin{array}{l}{S}_1(i^{\prime },j^{\prime })=F_2(F_1(P_1(i,j)))\\ C_1(i^{\prime },j^{\prime })=S_1(i^{\prime },j^{\prime })\oplus K(i^{\prime },j^{\prime })\end{array},$$

(17)

$$\{\begin{array}{l}{S}_2(i^{\prime },j^{\prime })=F_2(F_1(P_2(i,j)))\\ C_2(i^{\prime },j^{\prime })=S_2(i^{\prime },j^{\prime })\oplus K(i^{\prime },j^{\prime })\end{array},$$

(18)

where K (i′, j′) is the XOR result of K₁ (i′, j′) and K₂ (i′, j′).

Since the permutation rules for P₁ and P₂ are the same, the permutation positions for P₁ and P₂ are the same. Now, assuming that the number of different pixel values n = 1, there is only one different pixel value at (i″, j″) between P₁ and P₂. Therefore, in XOR, all pixels at the same positions will have the same values, except the one at (i″, j″).

$$\{\begin{array}{l}{C}_1(i^{″},j^{″})=S_1(i^{″},j^{″})\oplus K(i^{″},j^{″})\\ C_2(i^{″},j^{″})=S_2(i^{″},j^{″})\oplus K(i^{″},j^{″})\end{array}.$$

(19)

Then,

$$C_1(i^{″},j^{″})\ne C_2(i^{″},j^{″}).$$

(20)

Change the pixel values of P₁(1,1) and P₁(1,2) to obtain image P′.

$$\{\begin{array}{c}{P}^{\prime }(1,1)=\mathrm{mod}(P_1(1,1)+1256)\\ P^{\prime }(1,2)=\mathrm{mod}(P_1(1,2)-1256)\end{array}.$$

(21)

Change the pixel values of P₁(1,1) and P₁(1,3) to obtain image P″.

$$\{\begin{array}{c}{P}^{″}(1,1)=\mathrm{mod}(P_1(1,1)+1256)\\ P^{″}(1,3)=\mathrm{mod}(P_1(1,3)-1256)\end{array}.$$

(22)

The image P′ is encrypted to obtain the cipher image C₅₁, and the image P″ is encrypted to obtain the cipher image C₅₂. There are two different pixels between C₁ and C₅₁.

$$C_{56}=C_1\oplus C_{51}.$$

(23)

In this case, C₅₆ has two non-zero values, the positions of the two non-zero values are represented by (X₁₁, Y₁₁) and (X₁₂, Y₁₂), where X represents the row and Y represents the column. These two non-zero values are the encrypted positions of P′ (1,1) and P′ (1,2).

There are two different pixels between C₁ and C₅₂.

$$C_{57}=C_1\oplus C_{52}.$$

(24)

In this case, C₅₇ has two non-zero values, the positions of the two non-zero values are represented by (X₁₃, Y₁₃) and (X₁₄, Y₁₄). These two non-zero values are the encrypted positions of P″ (1,1) and P″ (1,3).

So, (X₁₁, Y₁₁) is the same position as (X₁₃, Y₁₃), and (X₁₂, Y₁₂) is different from (X₁₄, Y₁₄). The comparison between C₅₁ and C₅₂ shows that there is only one pixel difference. □

3.2. Elimination of Diffusion Effect

3.2.1. Method 1

In the original encryption scheme, a 256 × 256 × 3 plain image P was used, which was divided into three channel images: ${\mathbf{P}}_{\mathrm{R}}={\left\{P_R\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{P}}_{\mathrm{G}}={\left\{P_G\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{P}}_{\mathrm{B}}={\left\{P_B\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. Three channels are encrypted to obtain ${\mathbf{C}}_{\mathrm{R}}={\left\{C_R\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{C}}_{\mathrm{G}}={\left\{C_G\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{C}}_{\mathrm{B}}={\left\{C_B\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. The color cipher image C is obtained by merging the three channels. The original encryption scheme is expressed as follows:

$$\{\begin{array}{l}{\mathbf{C}}_{\mathrm{R}}(i,j)=F_2\left(F_1\right({\mathbf{P}}_{\mathrm{R}}(i,j)))\oplus K_1(i,j)\oplus K_2(i,j)\\ {\mathbf{C}}_{\mathrm{G}}(i,j)=F_2\left(F_1\right({\mathbf{P}}_{\mathrm{G}}(i,j)))\oplus K_1(i,j)\oplus K_3(i,j)\\ {\mathbf{C}}_{\mathrm{B}}(i,j)=F_2\left(F_1\right({\mathbf{P}}_{\mathrm{B}}(i,j)))\oplus K_1(i,j)\oplus K_4(i,j)\end{array},$$

(25)

where F₁ is the first intra-block pixel permutation and F₂ is the second inter-block permutation. In the original encryption scheme, the same permutation matrices F₁ and F₂ were used for the three channels. Matrix K₁ is the same matrix used for the first diffusion of the three channels, while K₂, K₃, and K₄ are the same for the second diffusion of the three channels.

Since the original scheme used different diffusion matrices for P_R, P_G and P_B, it is necessary to consider the matrices used in the two diffusions. According to proposition 2, two diffusion matrices are transformed into one diffusion matrix for XOR operation.

$$\{\begin{array}{l}{\mathbf{C}}_{\mathrm{R}}(i,j)=F_2\left(F_1\right({\mathbf{P}}_{\mathrm{R}}(i,j)))\oplus K_{12}(i,j)\\ {\mathbf{C}}_{\mathrm{G}}(i,j)=F_2\left(F_1\right({\mathbf{P}}_{\mathrm{G}}(i,j)))\oplus K_{13}(i,j)\\ {\mathbf{C}}_{\mathrm{B}}(i,j)=F_2\left(F_1\right({\mathbf{P}}_{\mathrm{B}}(i,j)))\oplus K_{14}(i,j)\end{array},$$

(26)

where K₁₂ is the XOR matrix of K₁ and K₂, K₁₃ is the XOR matrix of K₁ and K₃, and K₁₄ is the XOR matrix of K₁ and K₄.

As shown in Figure 1, the position of the plain image is still one-to-one mapped to a certain position of the second permutation-only image. So, the two permutation matrices F₁ and F₂ can be linearly transformed into a permutation matrix F, as shown in the following formula:

$$\{\begin{array}{l}{\mathbf{C}}_{\mathrm{R}}(i,j)=F\left({\mathbf{P}}_{\mathrm{R}}\right(i,j))\oplus K_{12}(i,j)\\ {\mathbf{C}}_{\mathrm{G}}(i,j)=F\left({\mathbf{P}}_{\mathrm{G}}\right(i,j))\oplus K_{13}(i,j)\\ {\mathbf{C}}_{\mathrm{B}}(i,j)=F\left({\mathbf{P}}_{\mathrm{B}}\right(i,j))\oplus K_{14}(i,j)\end{array}.$$

(27)

Then, we can construct an all-zero image P₀ of size 256 × 256 × 3 and use the all-zero matrix to obtain the diffusion matrix. The constructed all-zero image P₀ is shown as follows:

$${\mathbf{P}}_0={\left[\begin{array}{ccc}0& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\end{array}\right]}_{256\times 256\times 3}.$$

(28)

We divide the image P₀ into three channels ${\mathbf{P}}_0^R={\left\{P_0^R\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{P}}_0^G$ = ${\left\{P_0^G\right(i, j)\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{P}}_0^B$ = ${\left\{P_0^B\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. After encryption, the cipher images of three channel are ${\mathbf{C}}_0^R={\left\{C_0^R\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{C}}_0^G={\left\{C_0^G\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{C}}_0^B={\left\{C_0^B\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. The three channel images ${\mathbf{C}}_0^R$, ${\mathbf{C}}_0^G$ and ${\mathbf{C}}_0^B$ are merged into the color cipher image C₀.

$$\{\begin{array}{l}{\mathbf{C}}_0^R(i,j)=F\left({\mathbf{P}}_0^R\right(i,j\left)\right)\oplus K_{12}(i,j)\\ {\mathbf{C}}_0^G(i,j)=F\left({\mathbf{P}}_0^G\right(i,j\left)\right)\oplus K_{13}(i,j)\\ {\mathbf{C}}_0^B(i,j)=F\left({\mathbf{P}}_0^B\right(i,j\left)\right)\oplus K_{14}(i,j)\end{array}.$$

(29)

An all-zero matrix is still an all-zero zero matrix after permutation. As follows, Equation (29) can be transformed into Equation (30).

$$\{\begin{array}{l}{\mathbf{C}}_0^R(i,j)={\mathbf{P}}_0^R(i,j)\oplus K_{12}(i,j)\\ {\mathbf{C}}_0^G(i,j)={\mathbf{P}}_0^G(i,j)\oplus K_{13}(i,j)\\ {\mathbf{C}}_0^B(i,j)={\mathbf{P}}_0^B(i,j)\oplus K_{14}(i,j)\end{array}.$$

(30)

According to proposition 1, three diffusion matrices K₁₂, K₁₃ and K₁₄ can be obtained.

$$\{\begin{array}{l}{\mathbf{C}}_0^R(i,j)=K_{12}(i,j)\\ {\mathbf{C}}_0^G(i,j)=K_{13}(i,j)\\ {\mathbf{C}}_0^B(i,j)=K_{14}(i,j)\end{array}.$$

(31)

The process of obtaining three diffusion matrices is shown in Figure 2. The all-zero image P₀ is encrypted to obtain the merged cipher image C₀. The three channel images ${\mathbf{C}}_0^R$, ${\mathbf{C}}_0^G$ and ${\mathbf{C}}_0^B$ of cipher image C₀ can be transformed into three diffusion matrices K₁₂, K₁₃ and K₁₄.

In method 1, the obtained diffusion matrix is used to eliminate the diffusion effect, and the main steps are described as follows:

Step 1 

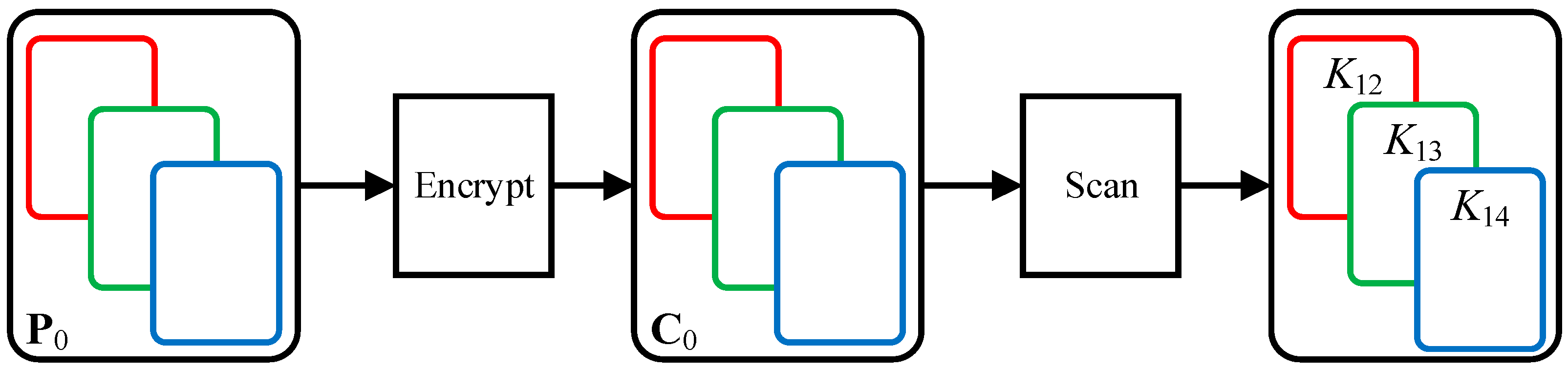
Construct an all-zero image P₀ with 256 × 256 × 3, and the influence of two permutations is eliminated by the all-zero matrix.

Step 2 

Three equivalent diffusion matrices, K₁₂, K₁₃, and K₁₄, are obtained.

Step 3 

Then, permutation-only images can be obtained through Equation (32). In the cipher image C, the red channel image C_R XOR diffusion matrix K₁₂ is permutation-only image S_R, the green channel image C_G XOR diffusion matrix K₁₃ is permutation-only image S_G, and the red channel image C_B XOR diffusion matrix K₁₄ is permutation-only image S_B. Three channel images, S_R, S_G, and S_B, are merged to obtain color permutation-only image S.

$$\{\begin{array}{l}{\mathbf{S}}_{\mathrm{R}}(i,j)={\mathbf{C}}_{\mathrm{R}}(i,j)\oplus K_{12}(i,j)\\ {\mathbf{S}}_{\mathrm{G}}(i,j)={\mathbf{C}}_{\mathrm{G}}(i,j)\oplus K_{13}(i,j)\\ {\mathbf{S}}_{\mathrm{B}}(i,j)={\mathbf{C}}_{\mathrm{B}}(i,j)\oplus K_{14}(i,j)\end{array}.$$

(32)

Figure 3 shows the experiments of method 1. Figure 3(a1) is a plain image and Figure 3(a2) is the cipher image of Figure 3(a1). Figure 3(a3) is a permutation-only image of Figure 3(a2). Figure 3(b1–b3) are permutation-only images from the three channels of Figure 3(a2).

3.2.2. Method 2

In method 2, We can construct 256 plain image ${\left\{\mathbf{P}x\right\}}_{x=0}^{255}$. The plain images ${\left\{\mathbf{P}x\right\}}_{x=0}^{255}$ are encrypted to obtain the cipher images ${\left\{\mathbf{C}x\right\}}_{x=0}^{255}$. The three channel images of the cipher image ${\left\{\mathbf{C}x\right\}}_{x=0}^{255}$ are ${\left\{\mathbf{C}rx\right\}}_{x=0}^{255}$, ${\left\{\mathbf{C}gx\right\}}_{x=0}^{255}$ and ${\left\{\mathbf{C}bx\right\}}_{x=0}^{255}$. The plain image ${\left\{\mathbf{P}x\right\}}_{x=0}^{255}$ is constructed as shown in Equation (33).

$${\mathbf{P}}_x={\left[\begin{array}{cccc}x& x& \cdots & x\\ x& x& \cdots & x\\ ⋮& ⋮& \ddots & ⋮\\ x& x& x& x\end{array}\right]}_{256\times 256\times 3},$$

(33)

where x = 0, 1, 2, …, 255. The x value in the plain image ${\left\{\mathbf{P}x\right\}}_{x=0}^{255}$ changes from 0 to 255.

Thus, 256 different plain images ${\left\{\mathbf{P}x\right\}}_{x=0}^{255}$ are encrypted to obtain 256 different cipher images ${\left\{\mathbf{C}x\right\}}_{x=0}^{255}$. If all the (i, j)th pixels of plain images ${\left\{\mathbf{P}x\right\}}_{x=0}^{255}$ are used to form a vector X = ${\left\{x\right\}}_{x=0}^{255}$, each of the elements of X are different. According to proposition 3, the encrypted cipher image of the plain image always has a unique corresponding position, and each element is mapped one-to-one. So, a given pixel in the target cipher image needs to be decrypted, then the pixel value of the cipher image can be compared with the pixel value at the same position in 256 different cipher images ${\left\{\mathbf{C}x\right\}}_{x=0}^{255}$. For a given cipher image C, the three channel images are C_R, C_G, and C_B. Through Equations (34) and (35), the permutation-only images ${\mathbf{S}}_{\mathrm{R}}={\left\{S_R\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{S}}_{\mathrm{G}}={\left\{S_G\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{S}}_{\mathrm{B}}={\left\{S_B\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ of three channels are retrieved.

$$\{\begin{array}{c}{\mathbf{C}}_{\mathrm{R}}(i,j)=\mathbf{C}{r}_x(i,j)\\ {\mathbf{C}}_{\mathrm{G}}(i,j)=\mathbf{C}{g}_x(i,j)\\ {\mathbf{C}}_{\mathrm{B}}(i,j)=\mathbf{C}{b}_x(i,j)\end{array},$$

(34)

$$\{\begin{array}{c}{\mathbf{S}}_{\mathrm{R}}(i,j)=x\\ {\mathbf{S}}_{\mathrm{G}}(i,j)=x\\ {\mathbf{S}}_{\mathrm{B}}(i,j)=x\end{array}.$$

(35)

Figure 4 shows the process of eliminating the diffusion effect, where the color permutation-only image S of color cipher image C is successfully obtained. Here, S is the combined image of three channel images S_R, S_G, and S_B. Figure 5 shows the experiment of method 2, where Figure 5(a1) is a plain image, Figure 5(a2) is the cipher image of Figure 5(a1), Figure 5(a3) is the permutation-only image of Figure 5(a2), and Figure 5(b1–b3) are permutation-only images from the three channels of Figure 5(a2).

3.3. Obtain Equivalent Permutation Mapping

In the previous section, the effects of diffusion can be eliminated by means of methods 1 and 2. In this way, we can obtain a permutation-only image of all the cipher images.

In this section, the substitution matrices F₁ and F₂ used in P_R, P_G and P_B in the original encryption scheme are the same. Two permutation matrices, F₁ and F₂, can be linearly transformed into one permutation matrix, F, so the permutation matrix F of each of the three channels is universal.

Cryptanalysis is used in [34] to obtain equivalent permutation matrices on the basis of a permutation-only image. Therefore, we can construct the chosen-plaintext image to obtain the corresponding equivalent permutation mapping F′, so that we can eliminate the influence of two permutations and the plain image P can be restored.

Based on Lemma 1 in [35], equivalent permutation mapping can be revealed by n pairs of plain/cipher images.

$$n\ge \lceil {\log }_g(MN)\rceil ,$$

(36)

where g is the gray level of the image and M and N are the rows and columns of the plain image. In the original encryption scheme, 256 × 256 × 3 plain image is used, which is divided into three 256 × 256 channels for permutation transformation.

The size of each channel is 256 × 256, which is a total of 65,536 pixel values. Therefore, g = 256, M = 256, N = 256, n pairs of plain/cipher images can be obtained from Equation (37).

$$2=\lceil {\log }_{256}(256\times 256)\rceil .$$

(37)

By calculating n = 2, the corresponding equivalent permutation map F′ can be solved by using two pairs of plain/cipher images.

The three channel images P_R, P_G, and P_B are stretched into column vectors, which can be expanded to a two-digit representation in base 256.

$$\mathbf{A}={\left[\begin{array}{ccccc}(0)(0)& (0)(1)& (0)(2)& \cdots & (0)(255)\\ (1)(0)& (1)(1)& (1)(2)& \cdots & (1)(255)\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ (254)(0)& (254)(1)& (254)(2)& \cdots & (254)(255)\\ (255)(0)& (255)(1)& (255)(2)& \cdots & (255)(255)\end{array}\right]}_{256\times 256\times 3},$$

(38)

where the element (a1) (a2) corresponds to 256 × a1 + a2 of A. The chosen-plaintext image A is divided into two bitplane images, A₁ and A₂. Then, A₁ and A₂ are used to construct 2 pairs of plain/cipher images.

$${\mathbf{A}}_1={\left[\begin{array}{ccccc}0& 1& 2& \cdots & 255\\ 0& 1& 2& \cdots & 255\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 1& 2& \cdots & 255\\ 0& 1& 2& \cdots & 255\end{array}\right]}_{256\times 256\times 3},$$

(39)

$${\mathbf{A}}_2={\left[\begin{array}{ccccc}0& 0& 0& \cdots & 0\\ 1& 1& 1& \cdots & 1\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 254& 254& 254& \cdots & 254\\ 255& 255& 255& \cdots & 255\end{array}\right]}_{256\times 256\times 3}.$$

(40)

Two cipher images C_A1 and C_A2 are obtained by encrypting two plain images, A₁ and A₂. Plain image A₁ is divided into three channel images: ${\mathbf{A}}_{r1}={\left\{A_{r1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{A}}_{g1}={\left\{A_{g1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{A}}_{b1}={\left\{A_{b1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. Plain image A₂ is divided into three channel images: ${\mathbf{A}}_{r2}={\left\{A_{r2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{A}}_{g2}={\left\{A_{g2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{A}}_{b2}={\left\{A_{b2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. The cipher image C_A1 is divided into three channel images: ${\mathbf{C}}_{r1}={\left\{C_{r1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{C}}_{g1}={\left\{C_{g1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{C}}_{b1}={\left\{C_{b1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. The cipher image C_A2 is divided into three channel images: ${\mathbf{C}}_{r2}={\left\{C_{r2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{C}}_{g2}={\left\{C_{g2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{C}}_{b2}={\left\{C_{b2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. After the Equation (41) transformation, the red channel images A_r1 and A_r2 are transformed into matrices ${\mathbf{P}}_{r1}={\left\{P_{r1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$. Transforming the green channels A_g1 and A_g2 into matrices ${\mathbf{P}}_{g1}={\left\{P_{g1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, the blue channel images A_b1 and A_b2 are transformed into a matrix ${\mathbf{P}}_{b1}={\left\{P_{b1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$.

$$\{\begin{array}{c}{\mathbf{P}}_{r1}=256\times {\mathbf{A}}_{r2}+{\mathbf{A}}_{r1}\\ {\mathbf{P}}_{g1}=256\times {\mathbf{A}}_{g2}+{\mathbf{A}}_{g1}\\ {\mathbf{P}}_{b1}=256\times {\mathbf{A}}_{b2}+{\mathbf{A}}_{b1}\end{array}.$$

(41)

By method 1 or 2, the permutation-only images ${\mathbf{S}}_{r1}={\left\{S_{r1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{S}}_{g1}={\left\{S_{g1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{S}}_{b1}={\left\{S_{b1}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ of C_r1, C_g1 and C_b1 are obtained, and permutation-only images ${\mathbf{S}}_{r2}={\left\{S_{r2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$, ${\mathbf{S}}_{g2}={\left\{S_{g2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ and ${\mathbf{S}}_{b2}={\left\{S_{b2}\right(i, j\left)\right\}}_{i=1, j=1}^{256,256}$ of C_r2, C_g2 and C_b2 are obtained.

$$\{\begin{array}{c}{\mathbf{S}}_r=256\times {\mathbf{S}}_{r2}+{\mathbf{S}}_{r1}\\ {\mathbf{S}}_g=256\times {\mathbf{S}}_{g2}+{\mathbf{S}}_{g1}\\ {\mathbf{S}}_b=256\times {\mathbf{S}}_{b2}+{\mathbf{S}}_{b1}\end{array}.$$

(42)

Then, it can be observed that all elements in image S_r are the permutation order of image P_r1, all elements in image S_g are the permutation order of image P_g1, and all elements in image S_b are the permutation order of image P_b1. We know that the permutation matrices of the three channels are the same, and any of the three channels are stretched row by row to form a vector ${\mathbf{F}}^{\prime }={\left\{F^{\prime }\right(i\left)\right\}}_{i=1}^{\mathrm{66,256}}$. Therefore, F′ is an equivalent permutation mapping.

Figure 6 shows the flow to obtain this equivalent permutation mapping F′. The main steps of equivalent permutation mapping are described as follows:

Step 1 

Two plain images A₁ and A₂ were encrypted to obtain two cipher images: C_A1 and C_A2. The cipher image C_A1 is divided into three channel images: C_r1, C_g1, and C_b1. The cipher image C_A2 is divided into three channel images: C_r2, C_g2, and C_b2.

Step 2 

By using method 1 or 2, the permutation-only images S_r1, S_g1, and S_b1 of C_r1, C_g1, and C_b1 are obtained first, and after that, the permutation-only images S_r2, S_g2, and S_b2 of C_r2, C_g2, and C_b2 are obtained.

Method 1

(i) Three equivalent diffusion matrices, K₁₂, K₁₃, and K₁₄, are known. The red channel image C_r1 is XORed with the diffusion matrix K₁₂ of the cipher image C_A1 to obtain the permutation-only image S_r1. The green channel image C_g1 is XORed with the diffusion matrix K₁₃ to obtain the permutation-only image S_g1, and the blue channel image C_b1 is XORed with the diffusion matrix K₁₄ to obtain the permutation-only image S_b1.

$$\{\begin{array}{l}{\mathbf{S}}_{r1}(i,j)={\mathbf{C}}_{r1}(i,j)\oplus K_{12}(i,j)\\ {\mathbf{S}}_{g1}(i,j)={\mathbf{C}}_{g1}(i,j)\oplus K_{13}(i,j)\\ {\mathbf{S}}_{b1}(i,j)={\mathbf{C}}_{b1}(i,j)\oplus K_{14}(i,j)\end{array}.$$

(43)

(ii) The red channel image C_r2 is XORed with the diffusion matrix K₁₂ of the cipher image C_A2 to obtain the permutation-only image S_r2. The green channel image C_g2 is XORed with the diffusion matrix K₁₃ to obtain the permutation-only image S_g2, and the blue channel image C_b2 is XORed with the diffusion matrix K₁₄ to obtain the permutation-only image S_b2.

$$\{\begin{array}{l}{\mathbf{S}}_{r2}(i,j)={\mathbf{C}}_{r2}(i,j)\oplus K_{12}(i,j)\\ {\mathbf{S}}_{g2}(i,j)={\mathbf{C}}_{g2}(i,j)\oplus K_{13}(i,j)\\ {\mathbf{S}}_{b2}(i,j)={\mathbf{C}}_{b2}(i,j)\oplus K_{14}(i,j)\end{array}.$$

(44)

Method 2

(i) The cipher image C_A1 is divided into three channel images: C_r1, C_g1, and C_b1. The permutation-only images S_r1, S_g1, and S_b1 of the three channel images are retrieved by Equations (45) and (46).

$$\{\begin{array}{c}{\mathbf{C}}_{r1}(i,j)=\mathbf{C}{r}_x(i,j)\\ {\mathbf{C}}_{g1}(i,j)=\mathbf{C}{g}_x(i,j)\\ {\mathbf{C}}_{b1}(i,j)=\mathbf{C}{b}_x(i,j)\end{array},$$

(45)

$$\{\begin{array}{c}{\mathbf{S}}_{r1}(i,j)=x\\ {\mathbf{S}}_{g1}(i,j)=x\\ {\mathbf{S}}_{b1}(i,j)=x\end{array}.$$

(46)

(ii) The cipher image C_A2 is divided into three channel images: C_r2, C_g2 and C_b2. The permutation-only images S_r2, S_g2, and S_b2 of the three channel images are retrieved by Equations (47) and (48).

$$\{\begin{array}{c}{\mathbf{C}}_{r2}(i,j)=\mathbf{C}{r}_x(i,j)\\ {\mathbf{C}}_{g2}(i,j)=\mathbf{C}{g}_x(i,j)\\ {\mathbf{C}}_{b2}(i,j)=\mathbf{C}{b}_x(i,j)\end{array},$$

(47)

$$\{\begin{array}{c}{\mathbf{S}}_{r2}(i,j)=x\\ {\mathbf{S}}_{g2}(i,j)=x\\ {\mathbf{S}}_{b2}(i,j)=x\end{array}.$$

(48)

Step 3 

Image S_r, S_g and S_b are obtained from Equation (42). Any of the three channel images are stretched row by row to form ${\mathbf{F}}^{\prime }={\left\{F^{\prime }\right(i\left)\right\}}_{i=1}^{\mathrm{66,256}}$. Therefore, F′ is an equivalent permutation mapping.

Figure 7 shows the permutation-only images of the constructed plain images A₁ and A₂, where the first column is the plain images A₁ and A₂, the second column is the encrypted images of the first column, and the third, fourth, and fifth columns are permutation-only images of the three channels retrieved from the second column. Since the permutation maps of the three channels in the original encryption scheme are the same, the permutation-only images of the three channels are the same.

3.4. Summary of the Attack Strategy

In this section, we provide a detailed overview of the attack process in methods 1 and 2.

3.4.1. Detailed Process of Method 1

Step 1 

Based on propositions 1 and 2, the three equivalent diffusion matrices K₁₂, K₁₃ and K₁₄ are obtained from the all-zero image (shown in Figure 2) as described in Section 3.2.1. The diffusion effect is eliminated through the known matrices K₁₂, K₁₃ and K₁₄. Then the permutation-only images of the three channel images C_R, C_G and C_B are obtained through the three matrices as shown in the sub-steps (shown in Figure 3).

Sub-Steps 

The red channel image C_R XORing equivalent diffusion matrix K₁₂ is the permutation-only image S_R, the green channel image C_G XORing diffusion matrix K₁₃ is the permutation-only image S_G, and the red channel image C_B XORing diffusion matrix K₁₄ is the permutation-only image S_B.

Step 2 

The equivalent permutation mapping F′ can be obtained from 2 pairs of plain/cipher images (shown in Figure 6) in Section 3.3. The detailed sub-steps are as follows:

Sub-Step 1  

Two plain images A₁ and A₂ were encrypted to obtain two cipher images C_A1 and C_A2. The cipher image C_A1 is divided into three channel images C_r1, C_g1 and C_b1. The cipher image C_A2 is divided into three channel images C_r2, C_g2 and C_b2.

Sub-Step 2  

Based on Section 3.2.1, the permutation-only images S_r1, S_g1 and S_b1 of C_r1, C_g1 and C_b1 were obtained, and the permutation-only images S_r2, S_g2 and S_b2 of C_r2, C_g2 and C_b2 were obtained (shown in Figure 7).

Sub-Step 3  

S_r, S_g and S_b are obtained from Equation (42). All the three channels are stretched row by row to form an equivalent permutation mapping F′.

Step 3 

Invoke Algorithm 1 to obtain deciphered images P_R, P_G and P_B. Merge the three channel images for obtaining image P.

Algorithm 1 Obtain the decrypted image P.

Decryptimg P = De_Img(Sr, SG, Sb, F′)

1: w = 0;

2: for i from 1 to 256

3:   for j from 1 to 256

4:   [r1, c1] ← find(F′ = w);

5:   d_r(i, j) ← Sr(r1, c1);

6:   d_g(i, j) ← Sg(r1, c1);

7:   d_b(i, j) ← Sb(r1, c1);

8:   w + 1 ← w;

9:  end

10: end

11: P ← d_r, d_g, d_b //Merge three channels

3.4.2. Detailed Process of Method 2

Step 1 

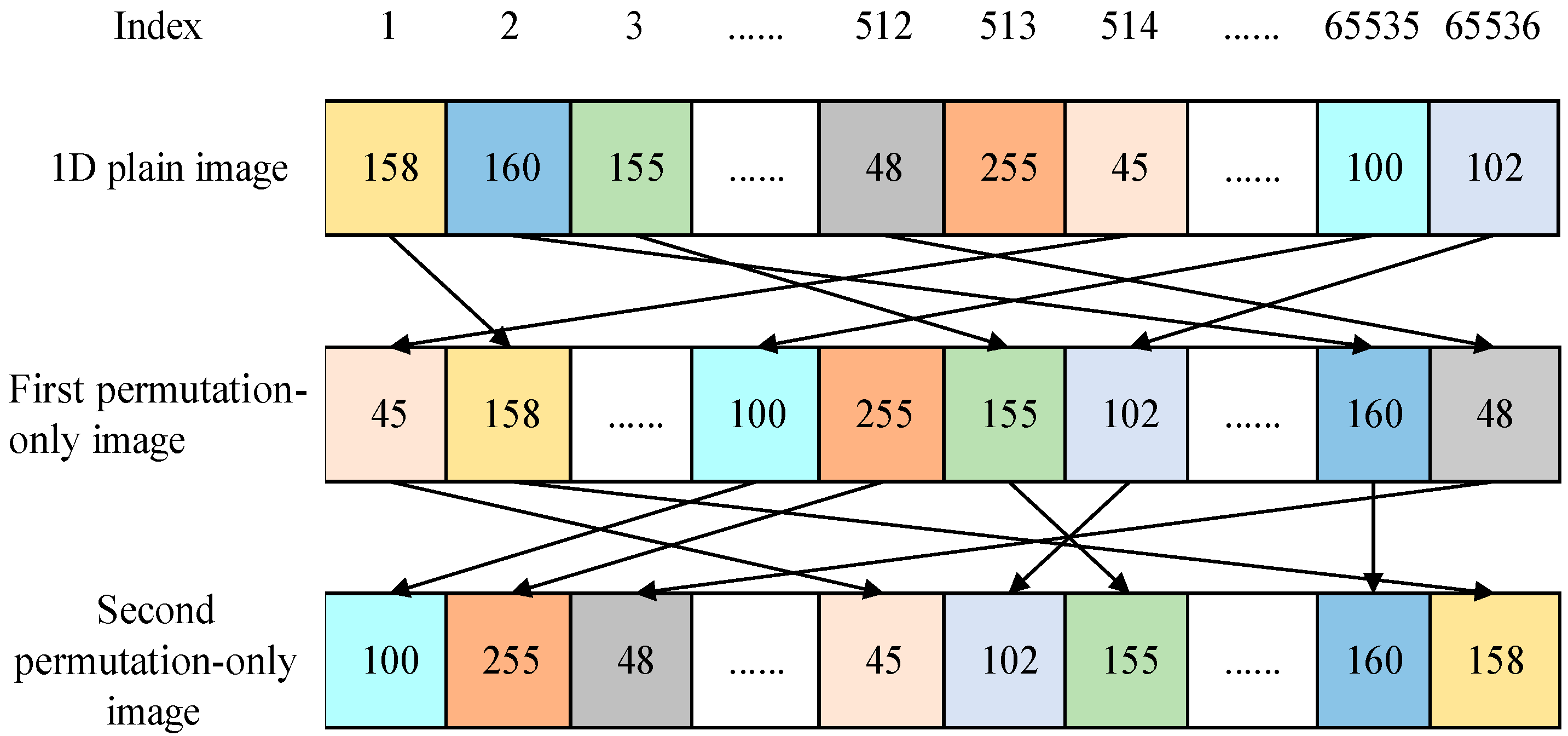
Based on proposition 3, one can construct 256 different plain images ${\left\{{\mathbf{P}}_x\right\}}_{x=0}^{255}$ and encrypt them to obtain 256 different cipher images ${\left\{{\mathbf{C}}_x\right\}}_{x=0}^{255}$ (shown in Figure 4) in Section 3.2.2. For the three channel images C_R, C_G and C_B of the given cipher image C. Equations (34) and (35) are used to eliminate the diffusion effect. The permutation-only images S_R, S_G and S_B of the three channels are retrieved (shown in Figure 5).

Step 2  

The equivalent permutation mapping F′ can be obtained from 2 pairs of plain/cipher images (shown in Figure 6) as described in Section 3.3. The detailed sub-steps are the same as the three sub-steps of step 2 in Section 3.4.1.

Step 3  

Invoke Algorithm 1 to obtain deciphered images P_R, P_G and P_B. Then, image P is obtained by merging the three channel images.

3.5. Simulation Experiment

3.5.1. Computational Complexity Analysis

In our cryptanalysis, method 1 used three chosen plain images to attack the original encryption scheme, one all-zero image to obtain the diffusion matrix and two chosen plain images to obtain the equivalent permutation mapping. For a cipher image with a size of 256 × 256 × 3, the data complexity is O (3 × 256 × 256 × 3), which is close to O (2²³). Method 2 used 258 chosen plain images to attack the original encryption scheme. A total of 256 chosen plain images were used to eliminate the diffusion effect, and 2 chosen plain images were used to obtain the equivalent permutation mapping. Similarly, for a cipher image with a size of 256 × 256 × 3, the data complexity is O (258 × 256 × 256 × 3), which is close to O (2²⁶). More remarkably, method 1 is faster, but method 2 can break the diffusion phase of Majid’s encryption scheme more subtly.

3.5.2. Experimental Results

The simulation experiment was performed on a personal computer (Intel Core i5-10210U 2.11 GHz CPU, 16 GB). All experiments were carried out using MATLAB R2020a. In the simulation experiments, we used the same initial values as the Majid’s scheme. The two attack methods are identical in the steps of obtaining equivalent permutation mapping F′ but different in the steps of eliminating diffusion effect. We implemented these two attack methods using some different experimental images for accuracy. It can be found from

Table 1. Execution time (seconds).

Image	Image Size	Encryption	Deciphering
			Method 1	Method 2
Lena	256 × 256 × 3	1.191755	9.057486	235.661488
Pepper	256 × 256 × 3	1.083255	8.445166	233.262743
Sailboat	256 × 256 × 3	1.058173	8.273460	233.330141

that the two methods will cause time differences due to different computational complexity, and different images will also cause time differences in different attack processes. However, the two solutions we proposed are sufficient in terms of real-time requirements.

The simulation results of the two attack methods in this paper are shown in Figure 8. Figure 8(a1,b1,c1) are the images of “Lena”, “Sailboat”, and “Pepper”. They are encrypted by the original cryptosystem as plain images, and the encrypted images are shown in Figure 8(a2,b2,c2). Then, we can execute two attack methods, respectively. The encrypted image can be restored to permutation-only images first, and then the decrypted image, as shown in column 3, column 4, and column 5 in Figure 8. Figure 8(a6,b6,c6) show the combined images of the three channels, that is, the recovered decrypted images. After comparison, we find that the decrypted image is consistent with the plain image, which confirms the feasibility of our attack methods.

4. Conclusions

In this paper, we cryptanalyzed a new chaotic image encryption technique based on multiple discrete dynamic maps, which adopts one-round encryption and permutation–diffusion structure. (1) The permutation–diffusion structure of one-round execution is found to be insecure because the cipher image generated by the all-zero image is the same as the diffusion matrix of the XOR phase. (2) The original encryption scheme’s secret key is irrelevant to the plain image, leading to the successful attack of the two proposed methods. The simulation results show that both of our methods are feasible.

In view of the original encryption scheme, we put forward some reasonable suggestions. (1) There should be strong correlation between the key and the plain image. (2) Multiple rounds of encryption should be adopted since it is difficult to avoid security problems with only one round of encryption. (3) Add nonlinear substitution phase to the encryption scheme as appropriate. (4) For the diffusion stage, some pixels in the plain image should be fused to complicate the diffusion, so as to avoid obtaining the diffusion matrix directly.