Performances of Transcritical Power Cycles with CO2-Based Mixtures for the Waste Heat Recovery of ICE
Abstract
:1. Introduction
1.1. Background
1.2. ORC
1.3. Transcritical Power Cycle with CO2
1.4. Transcritical Power Cycle with CO2-Based Mixture
1.5. Purpose of This Work
2. Cycle Layout
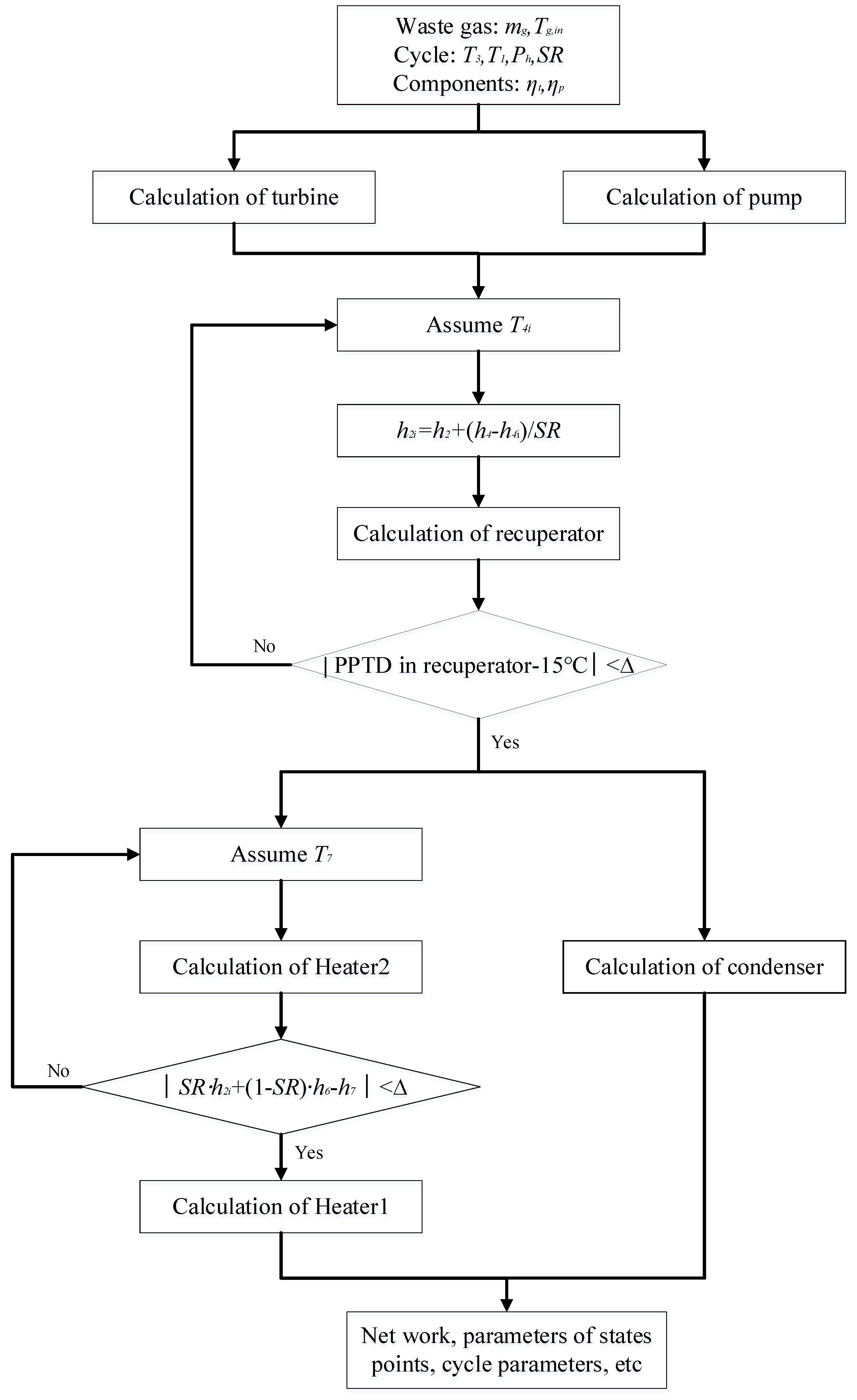
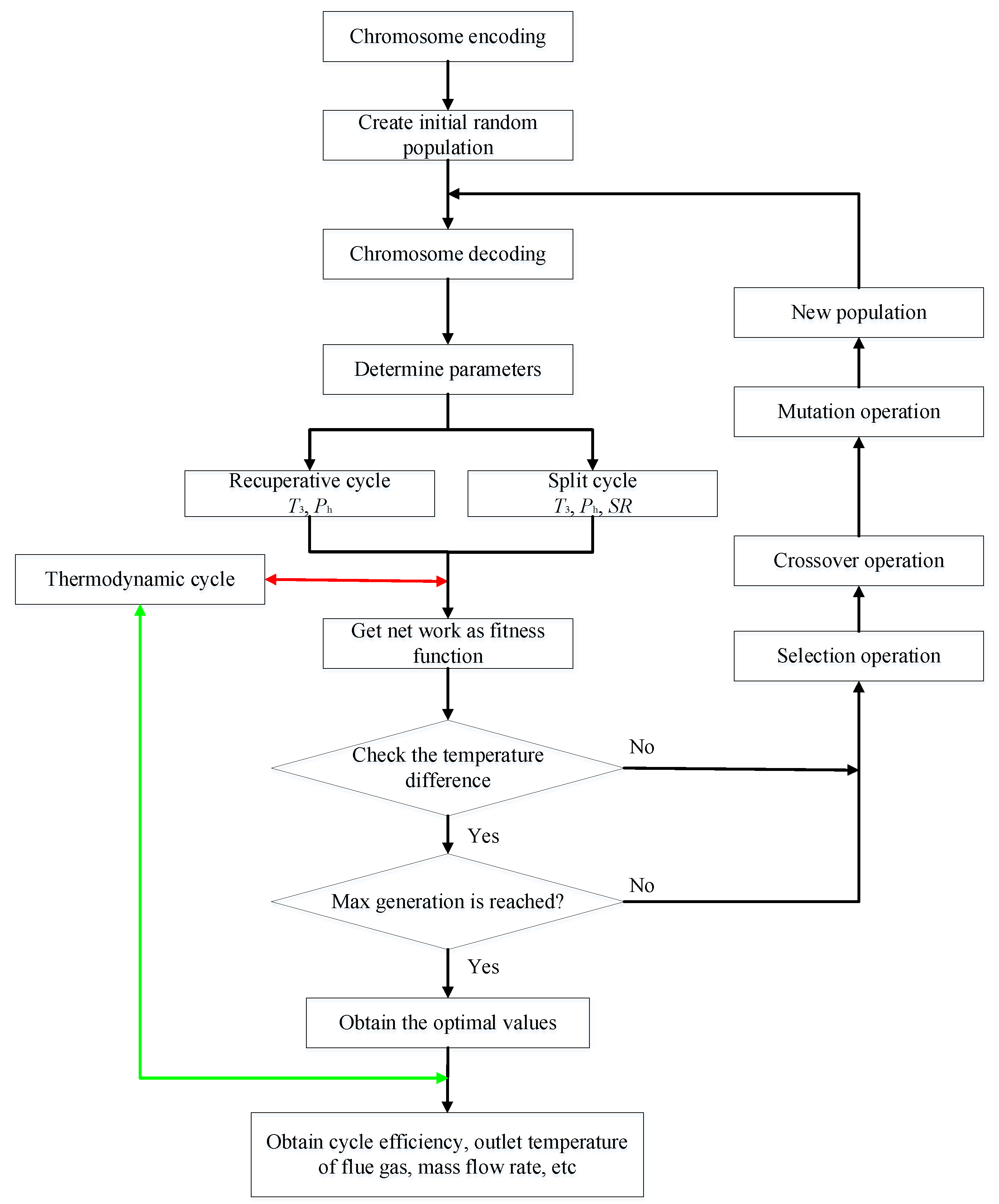
3. Thermodynamic Modeling and Optimization
3.1. Thermodynamic Modeling
3.2. GA Optimization
4. Cycle conditions and Organic Fluid Selections
5. Results and Discussion
5.1. Cycle Analysis and Performance Comparison
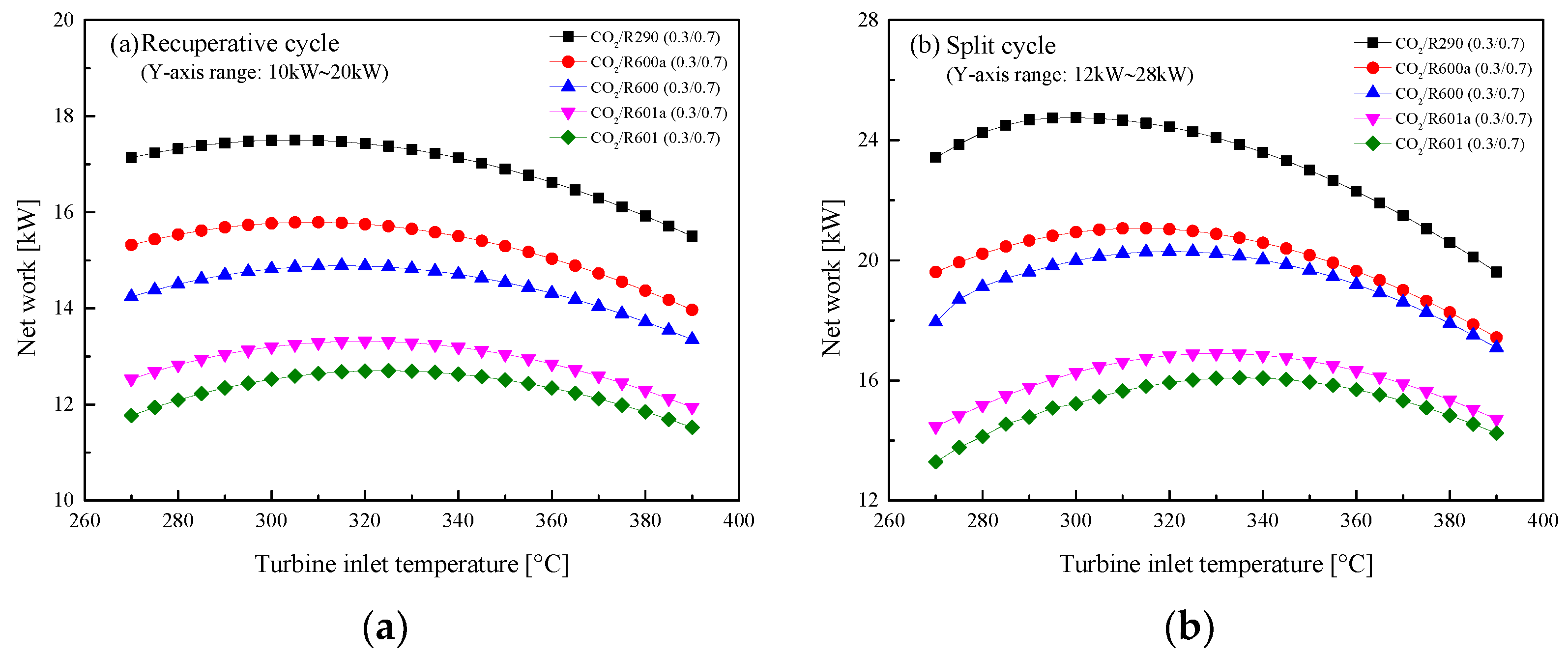
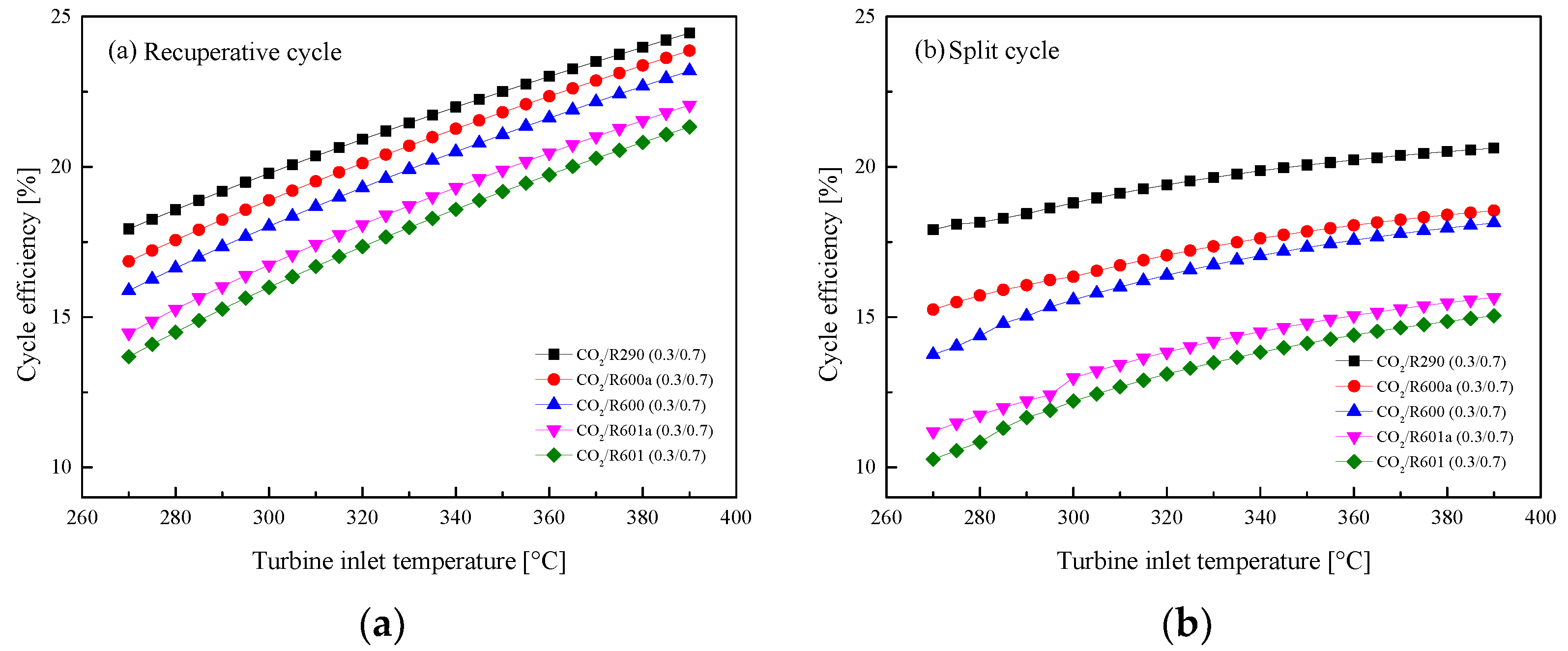
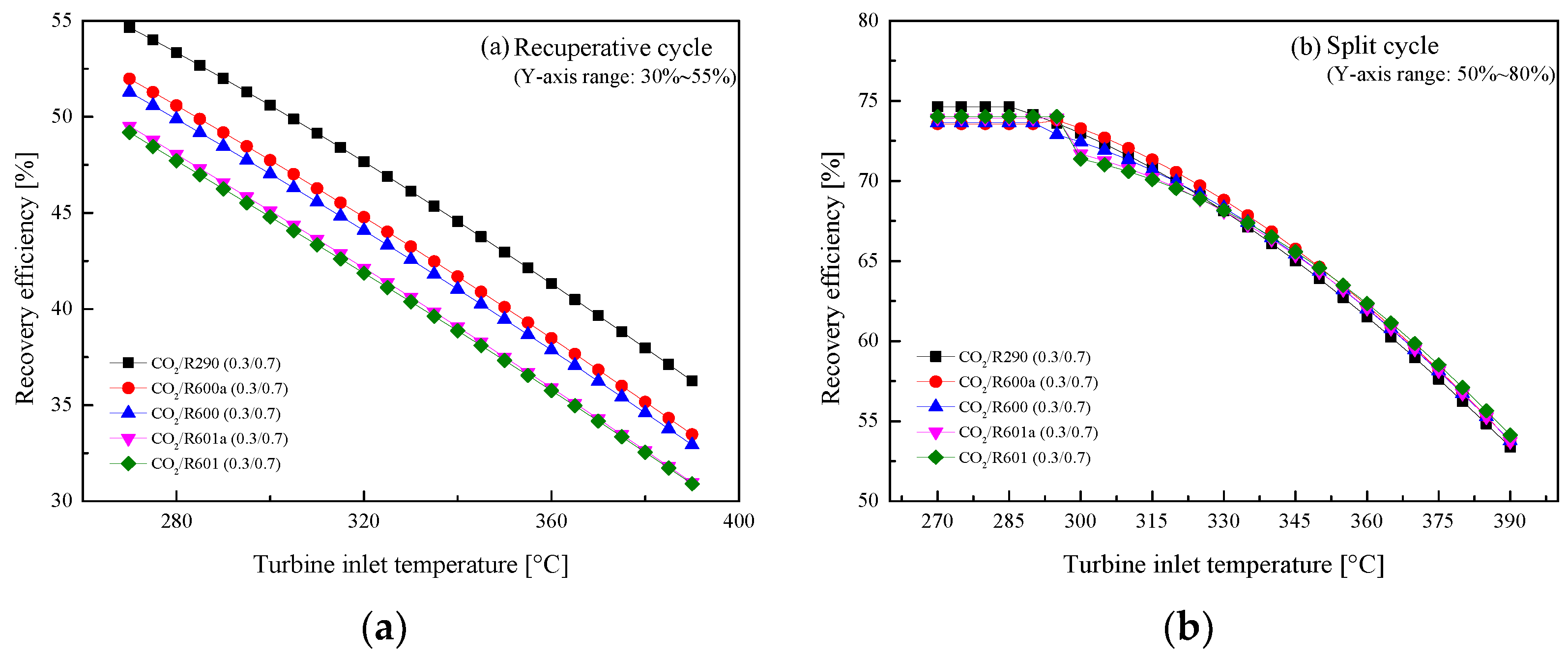
5.2. Effects of Key System Parameters
5.2.1. Effect of Turbine Inlet Temperature
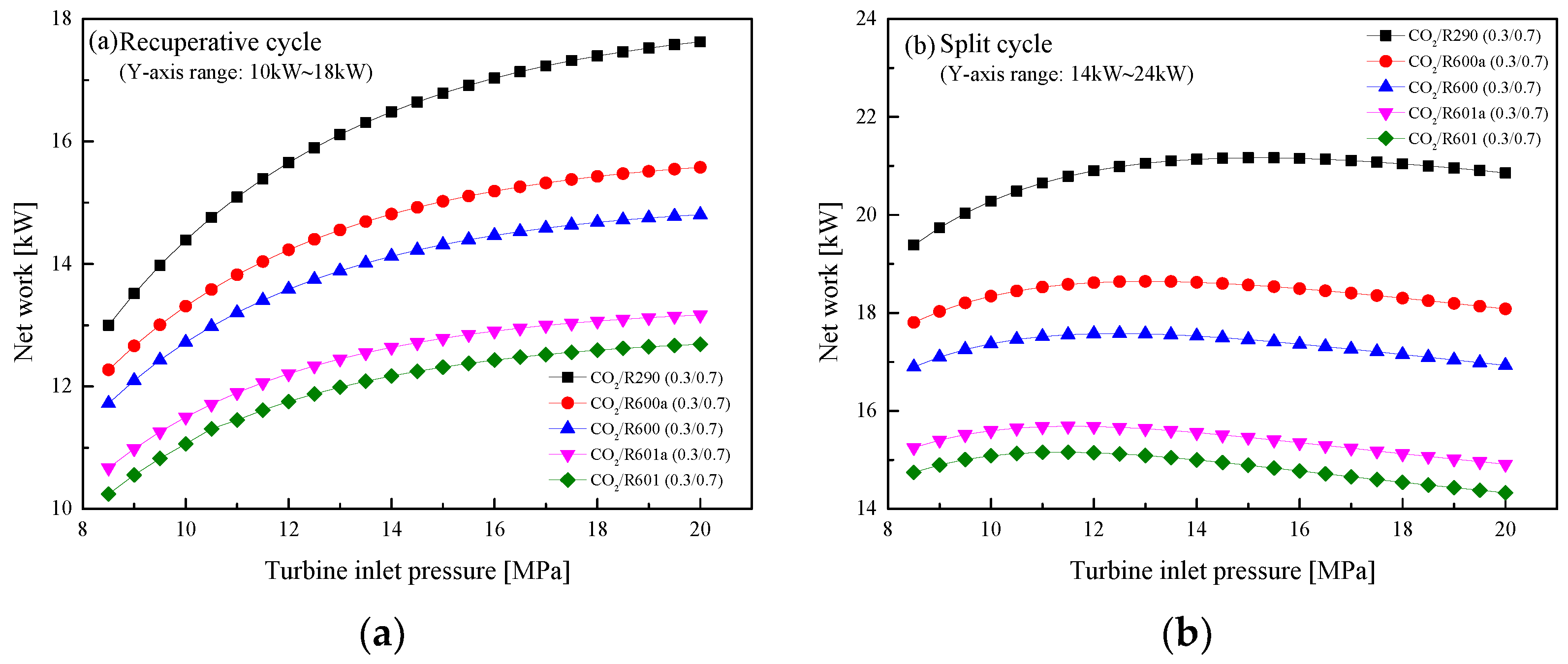
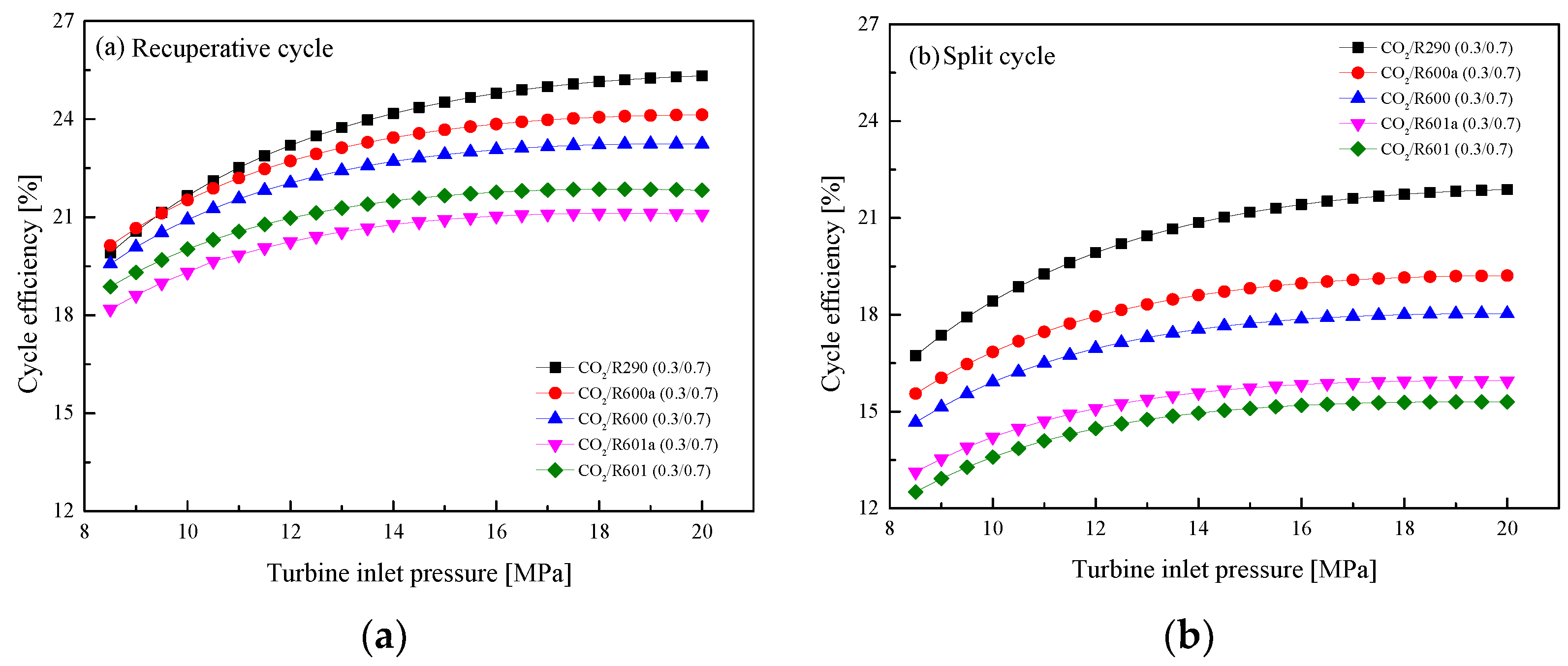
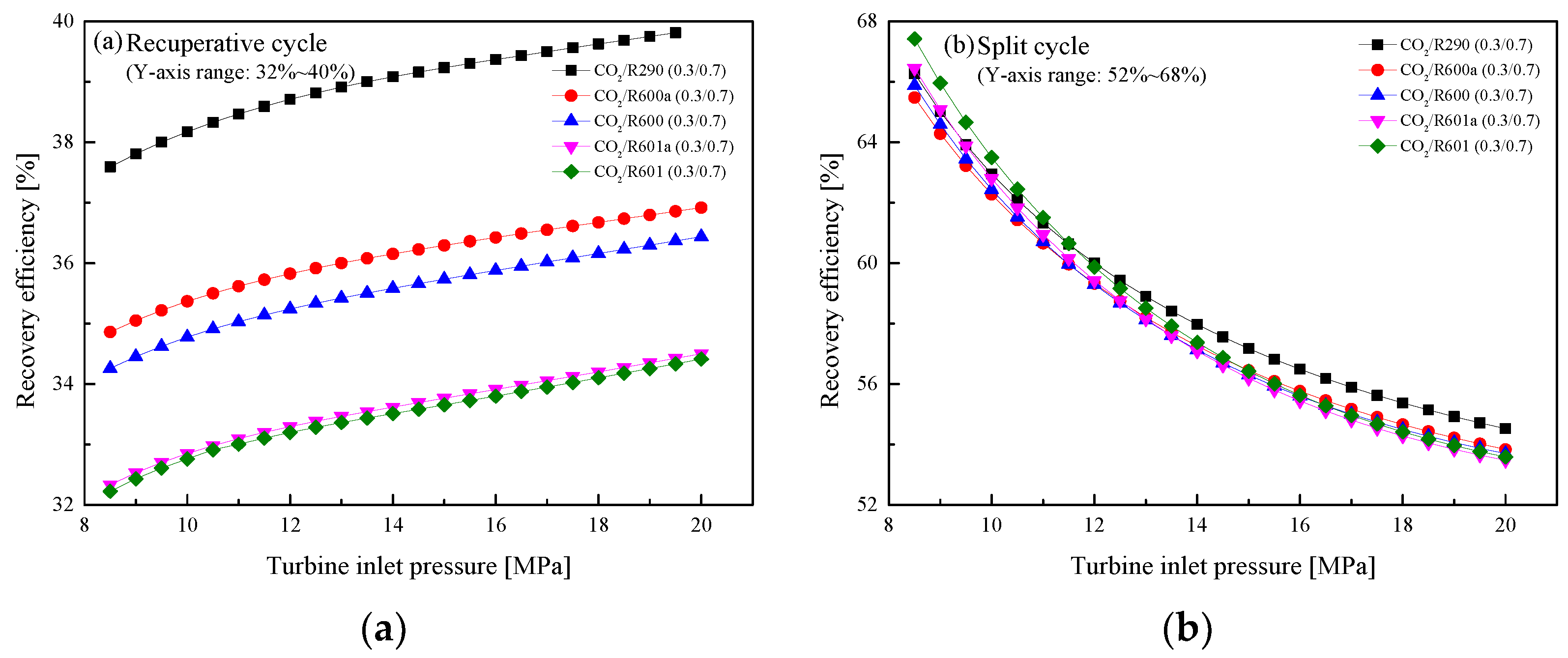
5.2.2. Effect of Turbine Inlet Pressure
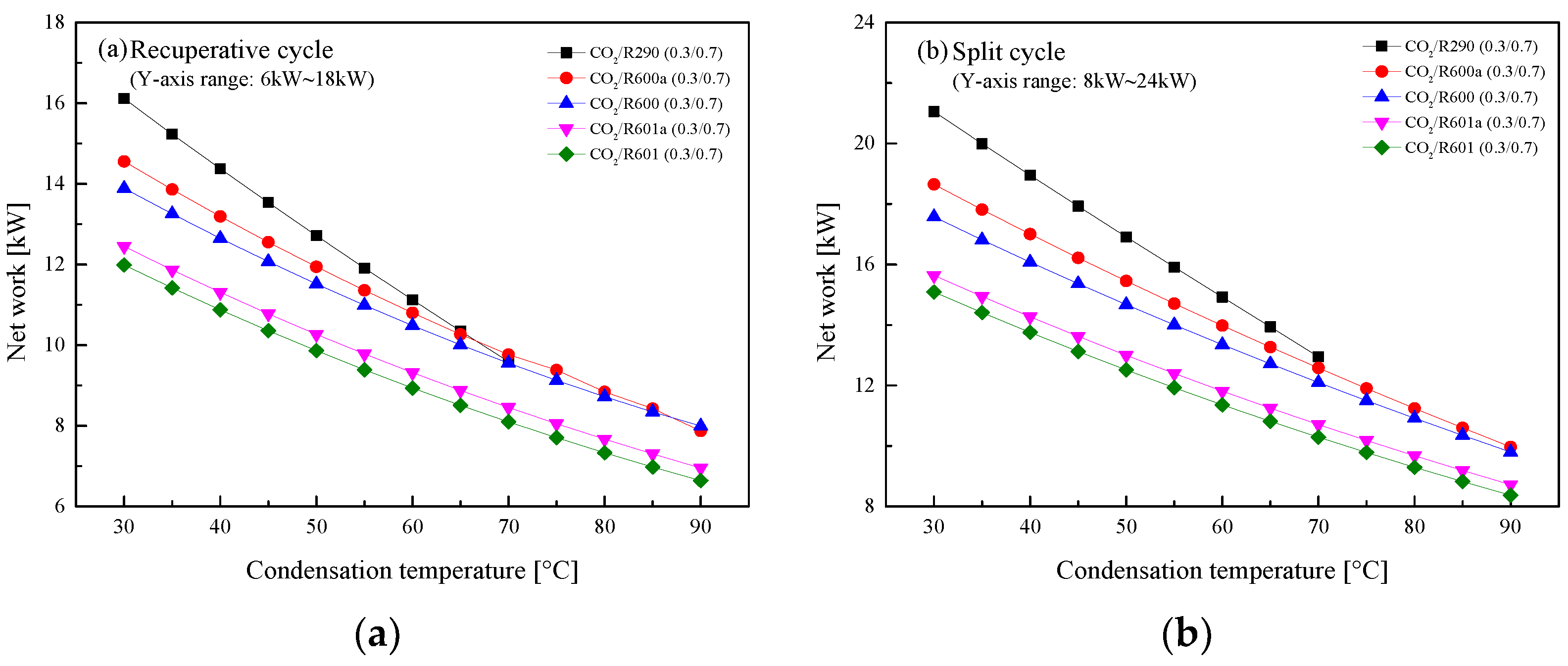
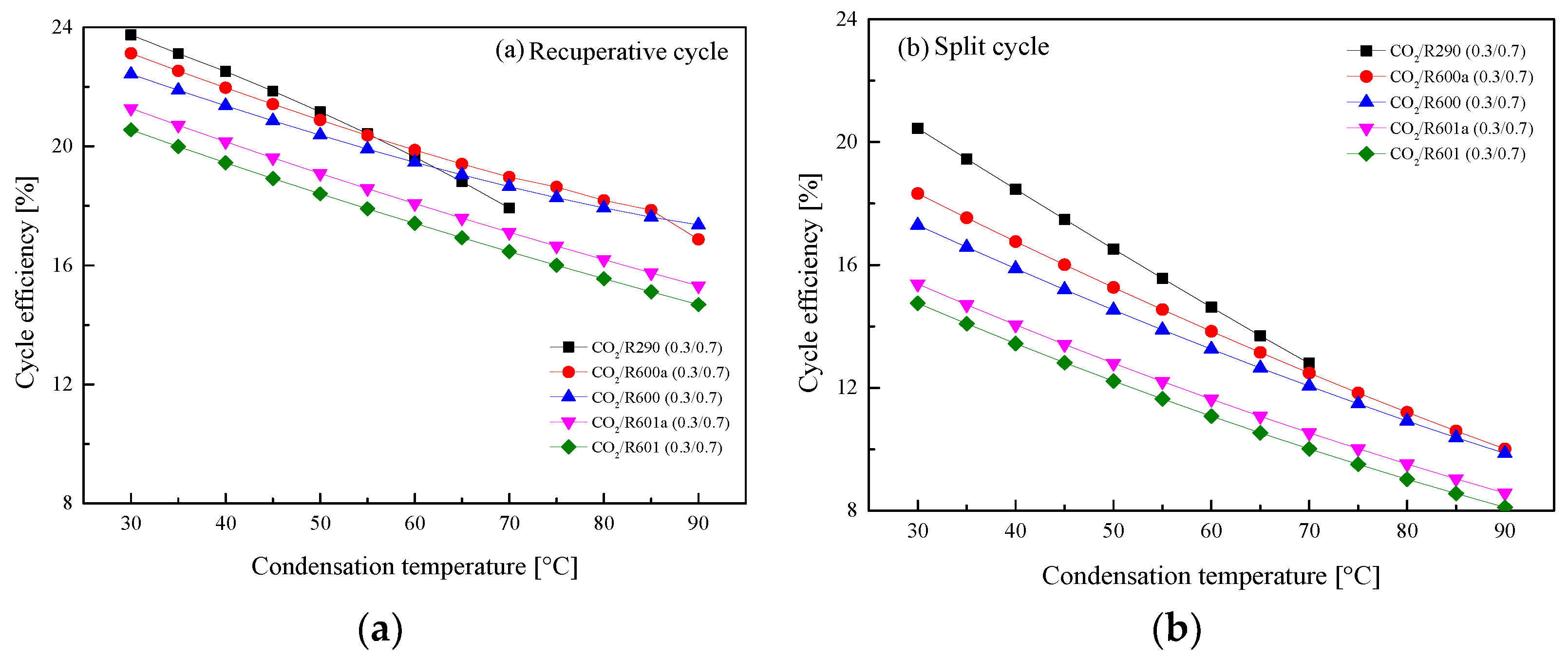
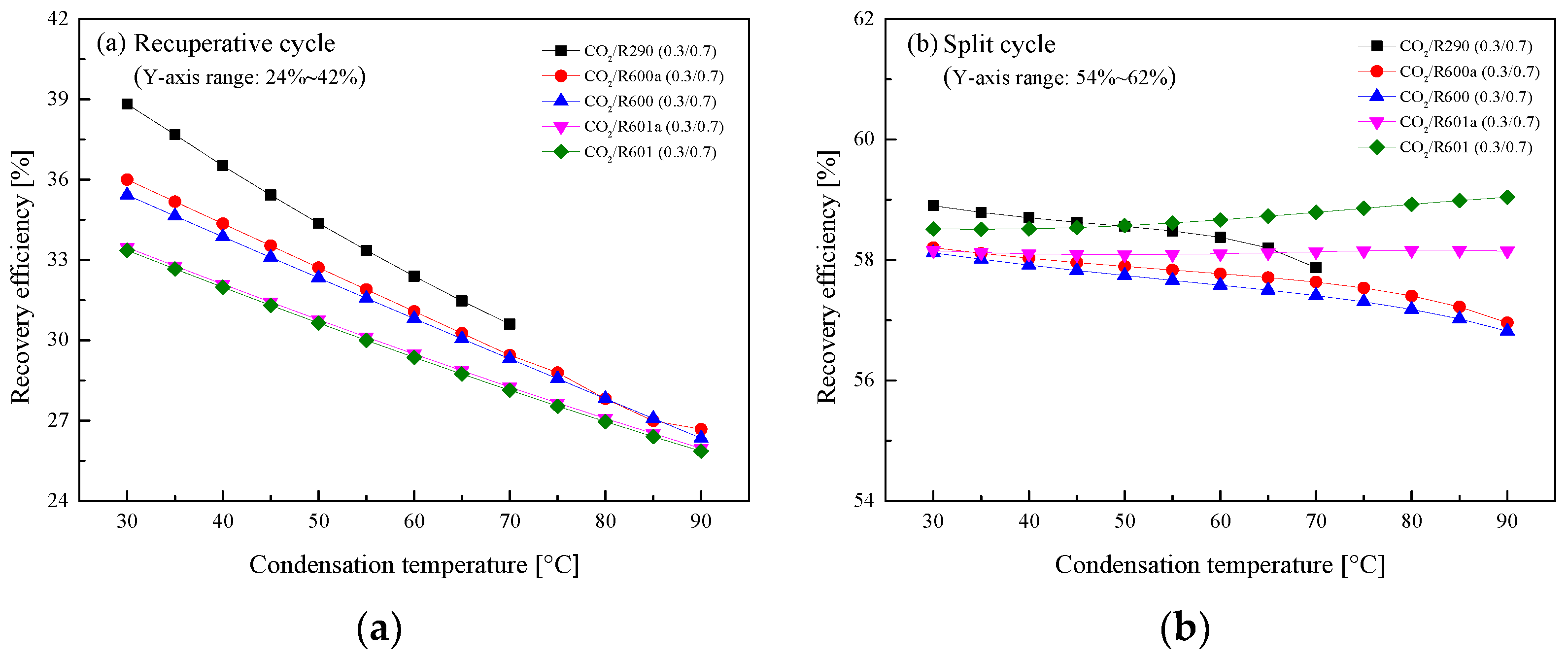
5.2.3. Effect of Condensation Temperature
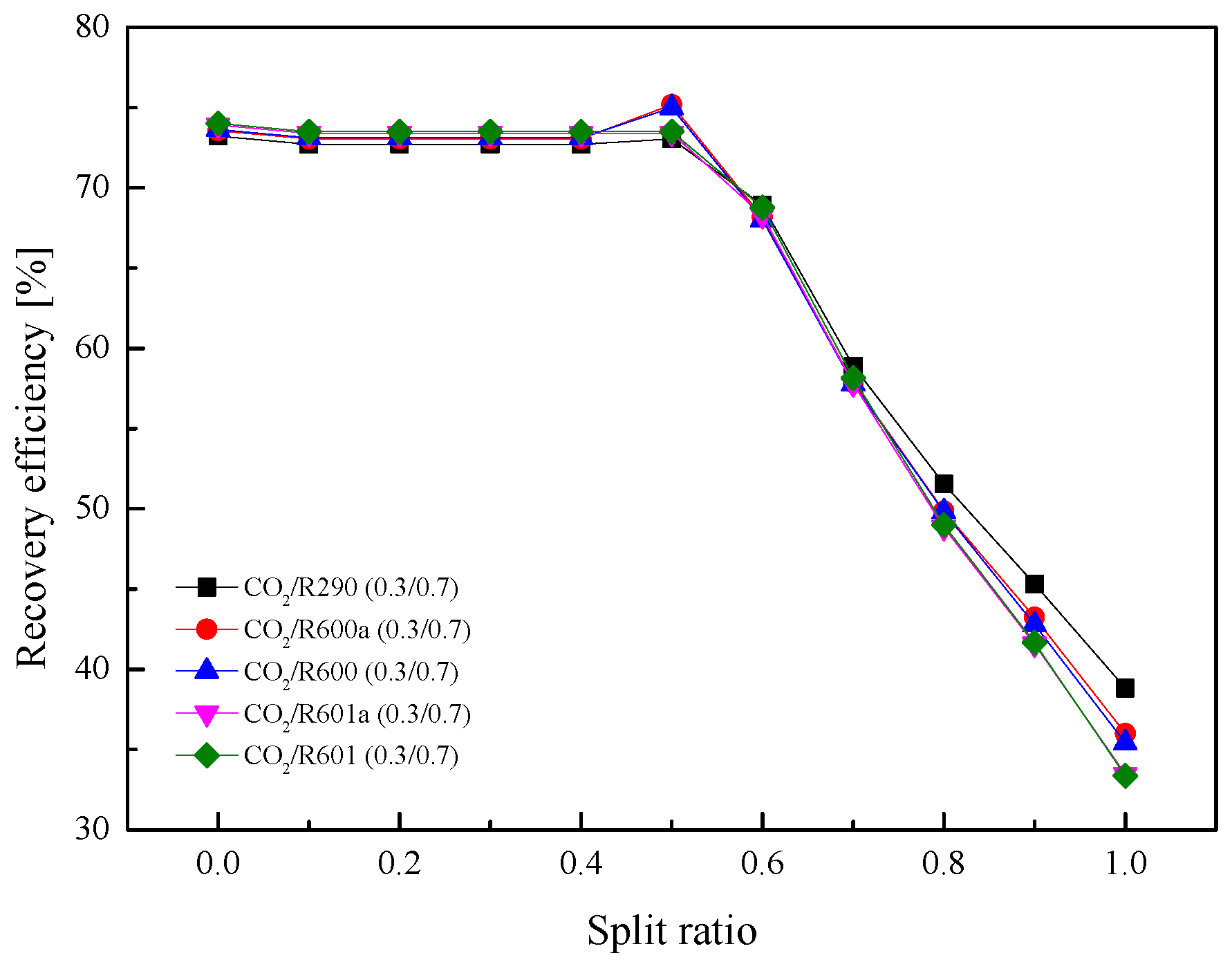
5.2.4. Effect of Split Ratio
5.3. Parametric Optimization
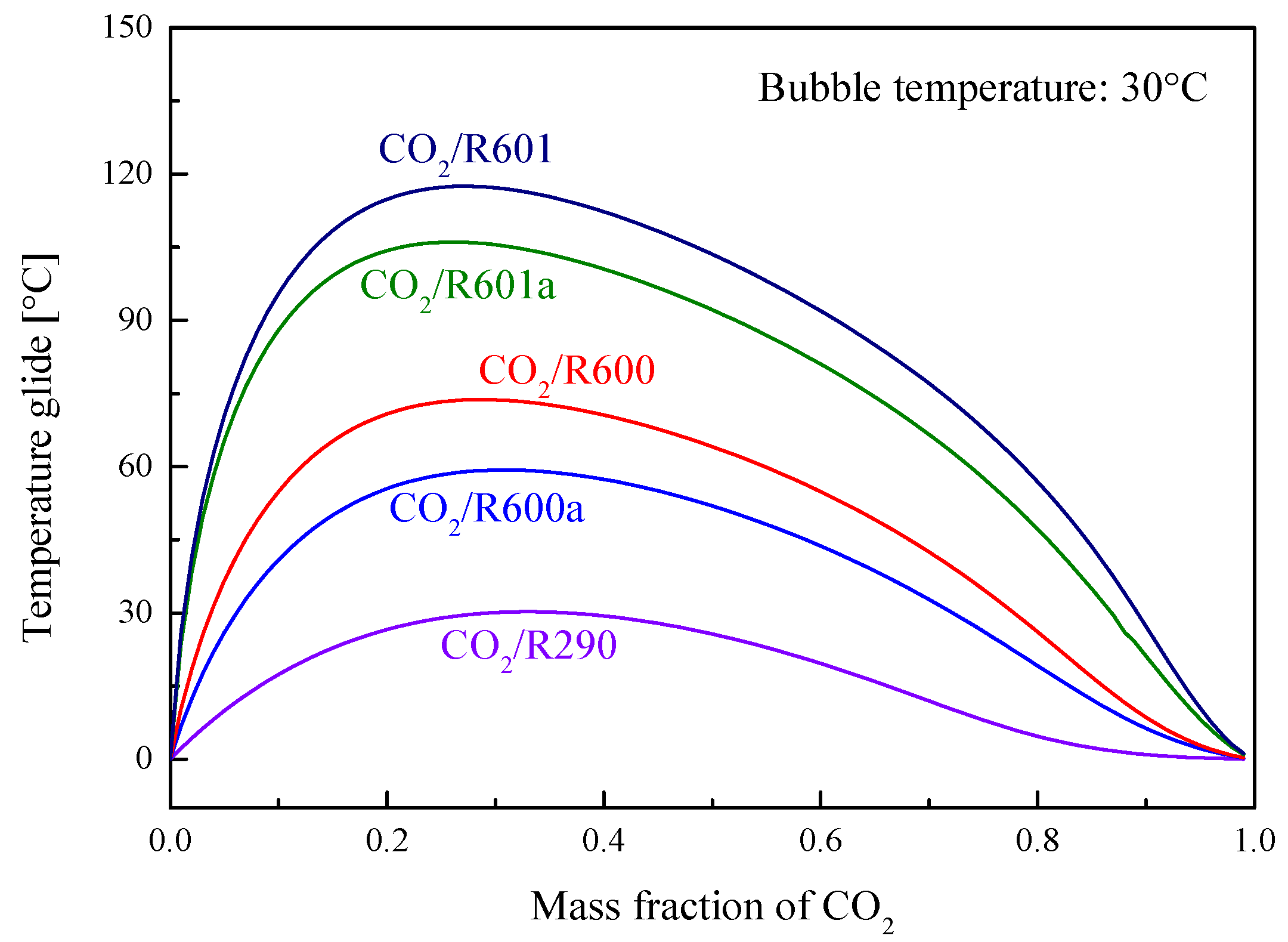
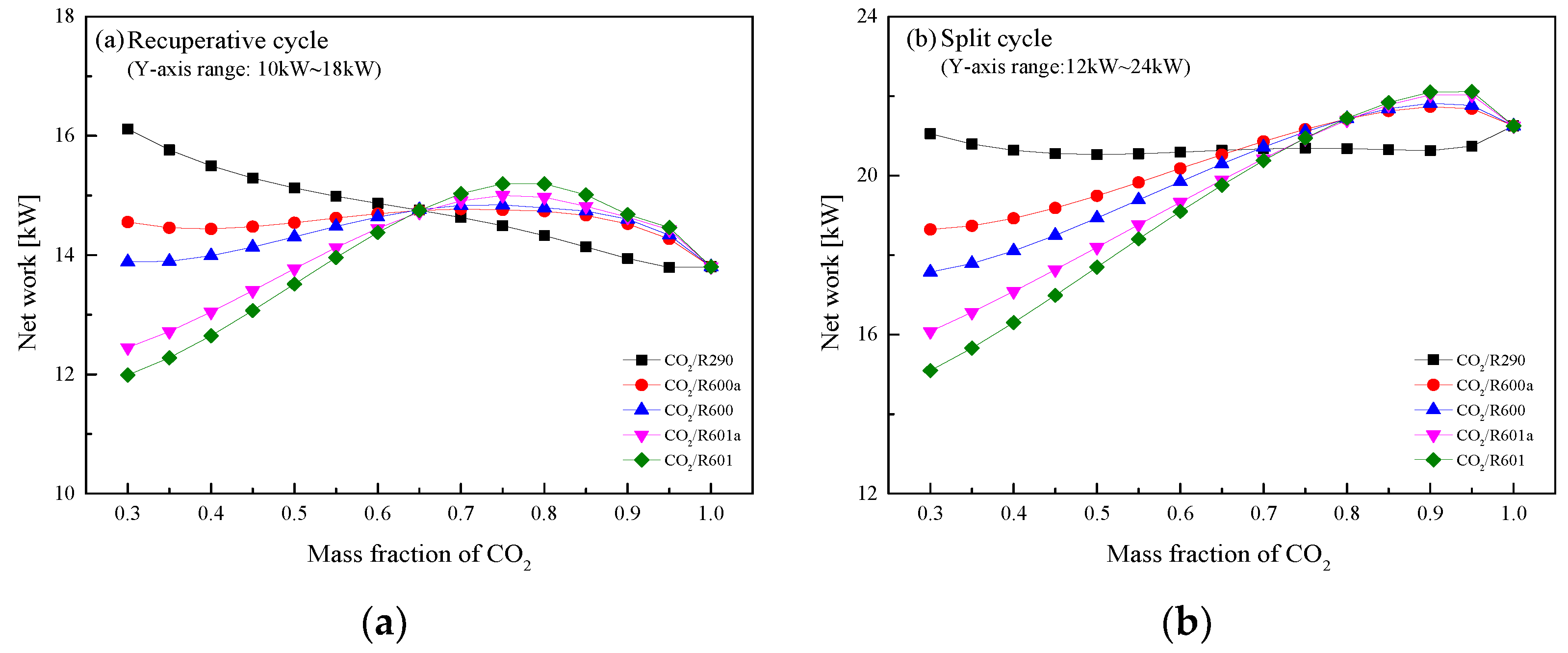
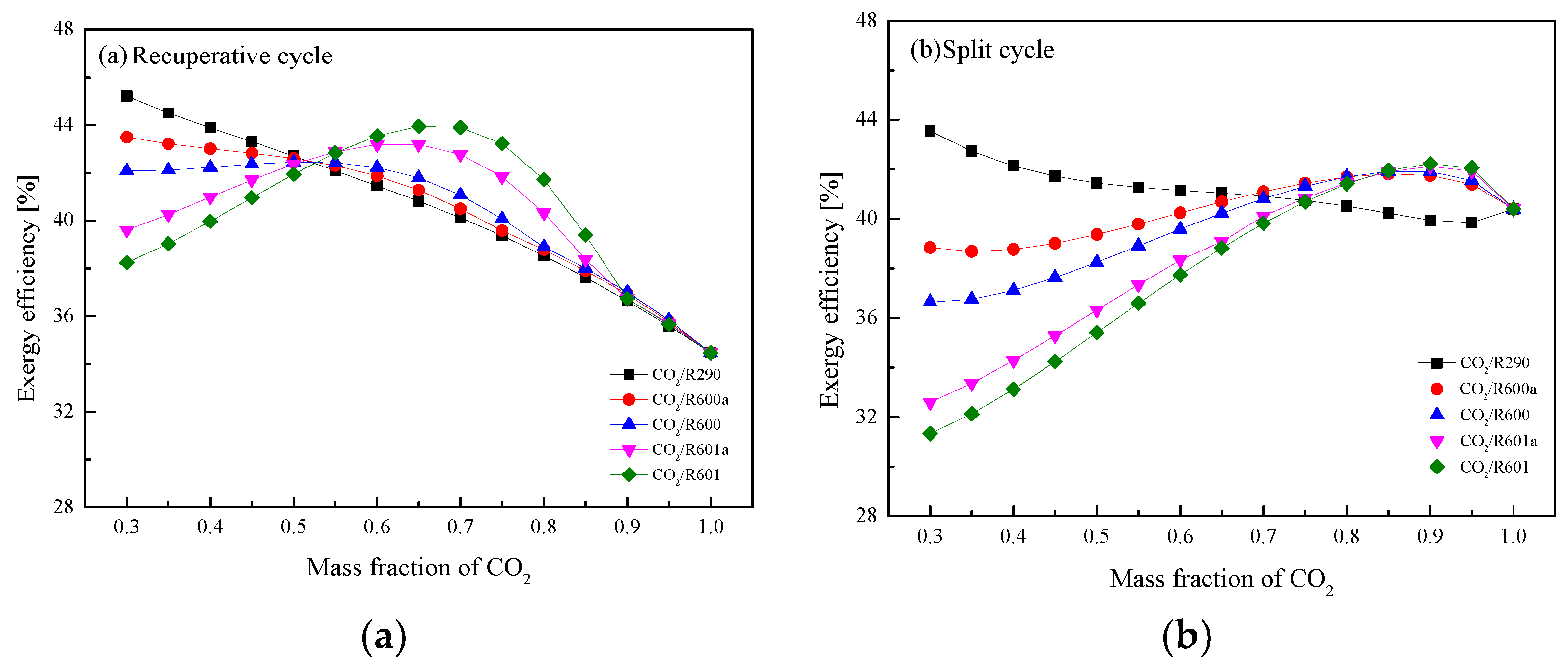
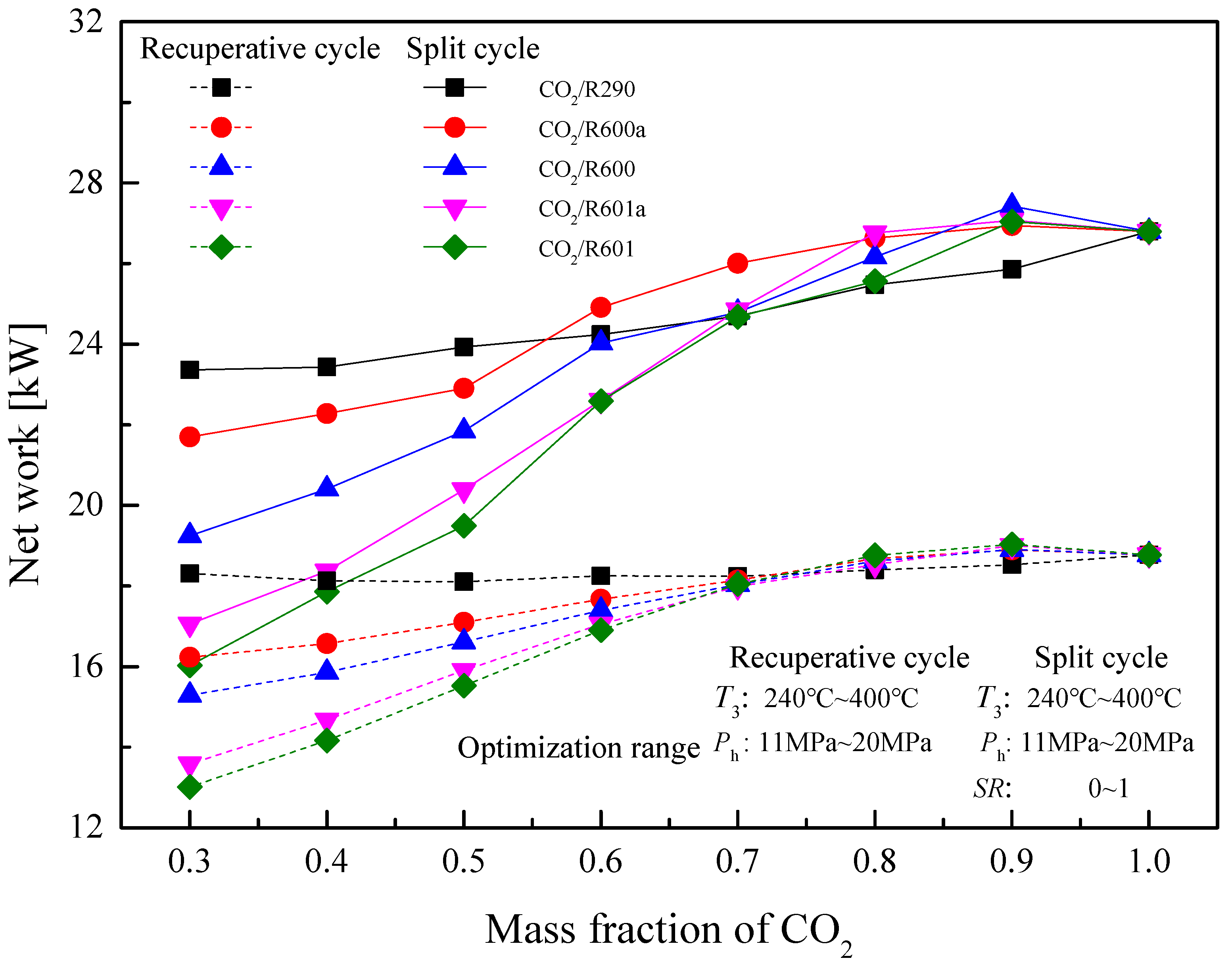
5.4. Performance Comparison at Different CO2 Mass Fractions
5.4.1. Design Conditions
5.4.2. Optimization Conditions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviation
| cp | Specific heat (kJ/(kg·K)) |
| I | Exergy destruction rate (kW) |
| W | Power (kW) |
| e | The specific exergy of flow at any state point (kW/kg) |
| SR | Split ratio |
| E | Exergy (kW) |
| Q | Heat transfer rate (kW) |
| h | Specific enthalpy (kJ/kg) |
| m | Mass flow rate (kg/s) |
| P | Pressure (MPa) |
| s | Entropy (kJ/(kg·K)) |
| T | Temperature (°C) |
| η | Efficiency (%) |
| Δ | Difference |
| ICE | Internal combustion engine |
| ORC | Organic Rankine cycle |
| GA | Genetic algorithm |
| PPTD | Pinch point temperature difference |
| GWP | Global warming potential |
| ODP | Ozone depletion potential |
| p | Pump |
| f | Mixture fluid |
| i | A state point of cycle |
| Re | Recuperator |
| g | Exhaust gas |
| in | Inlet temperature of exhaust gas |
| mid | Outlet temperature of Heater1 |
| out | Outlet temperature of Heater2 |
| con | Condenser |
| t | Turbine |
| L | Turbine out pressure |
| net | Net work |
| b | Normal boiling point |
| c | Critical state |
| h | Turbine inlet pressure |
| r | Recovery efficiency |
| th | Cycle efficiency |
| ex | Exergy |
| total | Total heat absorbed by the system |
Appendix A
| State Point | P(MPa) | T (°C) | s(kJ/(kg·K)) | h(kJ/kg) |
|---|---|---|---|---|
| 1 | 3.27 | 30.00 | 1.40 | 294.91 |
| 2 | 13.00 | 40.98 | 1.42 | 317.50 |
| 2i | 13.00 | 238.35 | 2.82 | 885.51 |
| 3 | 13.00 | 375.00 | 3.44 | 1238.91 |
| 4 | 3.27 | 316.68 | 3.51 | 1132.41 |
| 4i | 3.27 | 59.45 | 2.25 | 564.41 |
| State Point | P(MPa) | T (°C) | s(kJ/kg·K) | h(kJ/kg) |
|---|---|---|---|---|
| 1 | 3.27 | 30.00 | 1.40 | 294.91 |
| 2 | 13.00 | 40.98 | 1.42 | 317.50 |
| 2i | 13.00 | 301.68 | 3.12 | 1047.50 |
| 3 | 13.00 | 375.00 | 3.44 | 1238.91 |
| 4 | 3.27 | 316.68 | 3.51 | 1132.41 |
| 4i | 3.27 | 80.09 | 2.41 | 6214.14 |
| 5 | 13.00 | 40.98 | 1.42 | 3175.04 |
| 6 | 13.00 | 301.68 | 3.12 | 1047.50 |
| 7 | 13.00 | 301.68 | 3.12 | 1047.50 |
References
- Al Moussawi, H.; Fardoun, F.; Louahlia, H. Selection based on differences between cogeneration and trigeneration in various prime mover technologies. Renew. Sustain. Energy Rev. 2017, 74, 491–511. [Google Scholar] [CrossRef]
- Peng, Y.; Lin, X.; Liu, J.; Su, W.; Zhou, N. Machine learning prediction of ORC performance based on properties of working fluid. Appl. Therm. Eng. 2021, 195, 117184. [Google Scholar] [CrossRef]
- Peng, Y.; Su, W.; Zhou, N.; Zhao, L. How to evaluate the performance of sub-critical organic rankine cycle from key properties of working fluids by group contribution methods? Energy Convers. Manag. 2020, 221, 113204. [Google Scholar] [CrossRef]
- Lin, X.; Chen, C.; Yu, A.; Yin, L.; Su, W. Performance comparison of advanced transcritical power cycles with high-temperature working fluids for the engine waste heat recovery. Energies 2021, 14, 5886. [Google Scholar] [CrossRef]
- Zhao, M.; Wei, M.; Song, P.; Liu, Z.; Tian, G. Performance evaluation of a diesel engine integrated with ORC system. Appl. Therm. Eng. 2017, 115, 221–228. [Google Scholar] [CrossRef] [Green Version]
- Uusitalo, A.; Turunen-Saaresti, T.; Honkatukia, J.; Dhanasegaran, R. Experimental study of small scale and high expansion ratio ORC for recovering high temperature waste heat. Energy 2020, 208, 118321. [Google Scholar] [CrossRef]
- Hua, T.; Shu, G.; Wei, H.; Liang, X.; Liu, U. Fluids and parameters optimization for the organic Rankine cycles (ORCs) used in exhaust heat recovery of Internal Combustion Engine (ICE). Energy 2012, 47, 125–136. [Google Scholar]
- Mohammadkhani, F.; Yari, M. A 0D model for diesel engine simulation and employing a transcritical dual loop Organic Rankine Cycle (ORC) for waste heat recovery from its exhaust and coolant: Thermodynamic and economic analysis. Appl. Therm. Eng. 2019, 150, 329–347. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Peng, Z.; Shu, G. A review of researches on thermal exhaust heat recovery with Rankine cycle. Renew. Sustain. Energy Rev. 2011, 15, 2862–2871. [Google Scholar] [CrossRef]
- Yu, A.; Su, W.; Lin, X.; Zhou, N. Recent trends of supercritical CO2 Brayton cycle: Bibliometric analysis and research review. Nucl. Eng. Technol. 2021, 53, 699–714. [Google Scholar] [CrossRef]
- Li, X.; Shu, G.; Tian, H.; Shi, L.; Li, D.; Wang, Y. Preliminary dynamic tests of a CO2 transcritical power cycle for waste heat recovery from diesel engine. Energy Procedia 2017, 142, 1238–1243. [Google Scholar] [CrossRef]
- Shi, L.; Shu, G.; Tian, H.; Chang, L.; Huang, G.; Chen, T. Experimental investigations on a CO2-based Transcritical Power Cycle (CTPC) for waste heat recovery of diesel engine. Energy Procedia 2017, 129, 955–962. [Google Scholar] [CrossRef]
- Ll, A.; Hua, T.A.; Peng, L.A.; Ls, B.; Gs, A. Optimization of CO2 Transcritical Power Cycle (CTPC) for engine waste heat recovery based on split concept. Energy 2021, 229, 120718. [Google Scholar]
- Li, L.; Ge, Y.; Luo, X.; Tassou, S.A. Experimental investigation on power generation with low grade waste heat and CO2 transcritical power cycle. Energy Procedia 2017, 123, 297–304. [Google Scholar] [CrossRef]
- Baik, Y.-J.; Kim, M.; Chang, K.C.; Kim, S.J. Power-based performance comparison between carbon dioxide and R125 transcritical cycles for a low-grade heat source. Appl. Energy 2011, 88, 892–898. [Google Scholar] [CrossRef]
- Li, X.; Shu, G.; Tian, H.; Huang, G.; Liu, P.; Wang, X.; Shi, L. Experimental comparison of dynamic responses of CO2 transcritical power cycle systems used for engine waste heat recovery. Energy Convers. Manag. 2018, 161, 254–265. [Google Scholar] [CrossRef]
- Yu, A.; Su, W.; Zhao, L.; Lin, X.; Zhou, N.; Sciubba, E. New knowledge on the performance of supercritical brayton cycle with CO2 -based mixtures. Energies 2020, 13, 1741. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.C.; Liaw, H.J.; Wang, T.C.; Lin, C.Y. Carbon dioxide dilution effect on flammability limits for hydrocarbons. J. Hazard. Mater. 2009, 163, 795–803. [Google Scholar] [CrossRef]
- Zabetakis, M.G. Flammability Characteristics of Combustible Gases and Vapors; Bureau of Mines: Washington, DC, USA, 1965. [Google Scholar]
- Dai, B.; Li, M.; Ma, Y. Thermodynamic analysis of carbon dioxide blends with low GWP (global warming potential) working fluids-based transcritical Rankine cycles for low-grade heat energy recovery. Energy 2014, 64, 942–952. [Google Scholar] [CrossRef]
- Wu, C.; Wang, S.S.; Jiang, X.; Li, J. Thermodynamic analysis and performance optimization of transcritical power cycles using CO2-based binary zeotropic mixtures as working fluids for geothermal power plants. Appl. Therm. Eng. 2017, 115, 292–304. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Rahman, M.M.; Stefanakos, E.K. Energetic and exergetic analysis of CO2- and R32-based transcritical Rankine cycles for low-grade heat conversion. Appl. Energy 2011, 88, 2802–2808. [Google Scholar] [CrossRef]
- Shu, G.; Yu, Z.; Tian, H.; Liu, P.; Xu, Z. Potential of the transcritical Rankine cycle using CO2-based binary zeotropic mixtures for engine’s waste heat recovery. Energy Convers. Manag. 2018, 174, 668–685. [Google Scholar] [CrossRef]
- Shu, G.; Wang, R.; Tian, H.; Wang, X.; Xu, Z. Dynamic performance of the transcritical power cycle using CO2-based binary zeotropic mixtures for truck engine waste heat recovery. Energy 2019, 194, 116825. [Google Scholar] [CrossRef]
- Wang, R.; Shu, G.; Wang, X.; Tian, H.; Cai, J. Dynamic performance and control strategy of CO2-mixture transcritical power cycle for heavy-duty diesel engine waste-heat recovery. Energy Convers. Manag. 2020, 205, 112389. [Google Scholar] [CrossRef]
- Liu, P.; Shu, G.; Tian, H. How to approach optimal practical Organic Rankine cycle (OP-ORC) by configuration modification for diesel engine waste heat recovery. Energy 2019, 174, 543–552. [Google Scholar] [CrossRef]
- Grelet, V.; Reiche, T.; Lemort, V.; Nadri, M.; Dufour, P. Transient performance evaluation of waste heat recovery rankine cycle based system for heavy duty trucks. Appl. Energy 2016, 165, 878–892. [Google Scholar] [CrossRef]
- Yu, S.C.; Chen, L.; Zhao, Y.; Li, H.X.; Zhang, X.R. Thermodynamic analysis of representative power generation cycles for low-to-medium temperature applications. Int. J. Energy Res. 2015, 39, 84–97. [Google Scholar] [CrossRef]
- Shu, G.; Shi, L.; Tian, H.; Li, X.; Huang, G.; Chang, L. An improved CO2-based transcritical Rankine cycle (CTRC) used for engine waste heat recovery. Appl. Energy 2016, 176, 171–182. [Google Scholar] [CrossRef]
- Zhang, R.; Su, W.; Lin, X.; Zhou, N.; Zhao, L. Thermodynamic analysis and parametric optimization of a novel S-CO2 power cycle for the waste heat recovery of internal combustion engines. Energy 2020, 209, 118484. [Google Scholar] [CrossRef]
- Su, W.; Hwang, Y.; Deng, S.; Zhao, L.; Zhao, D. Thermodynamic performance comparison of Organic Rankine Cycle between zeotropic mixtures and pure fluids under open heat source. Energy Convers. Manag. 2018, 165, 720–737. [Google Scholar] [CrossRef]
- Xi, H.; Li, M.J.; He, Y.L.; Tao, W.Q. A graphical criterion for working fluid selection and thermodynamic system comparison in waste heat recovery. Appl. Therm. Eng. 2015, 89, 772–782. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; Mclinden, M.O. NIST Standard ReferenceDatabase 23: Reference Fluid Thermodynamic and Transport Properties-REFPROP, 9.0; NIST NSRDS: Gaithersburg, MD, USA, 2010. [Google Scholar]

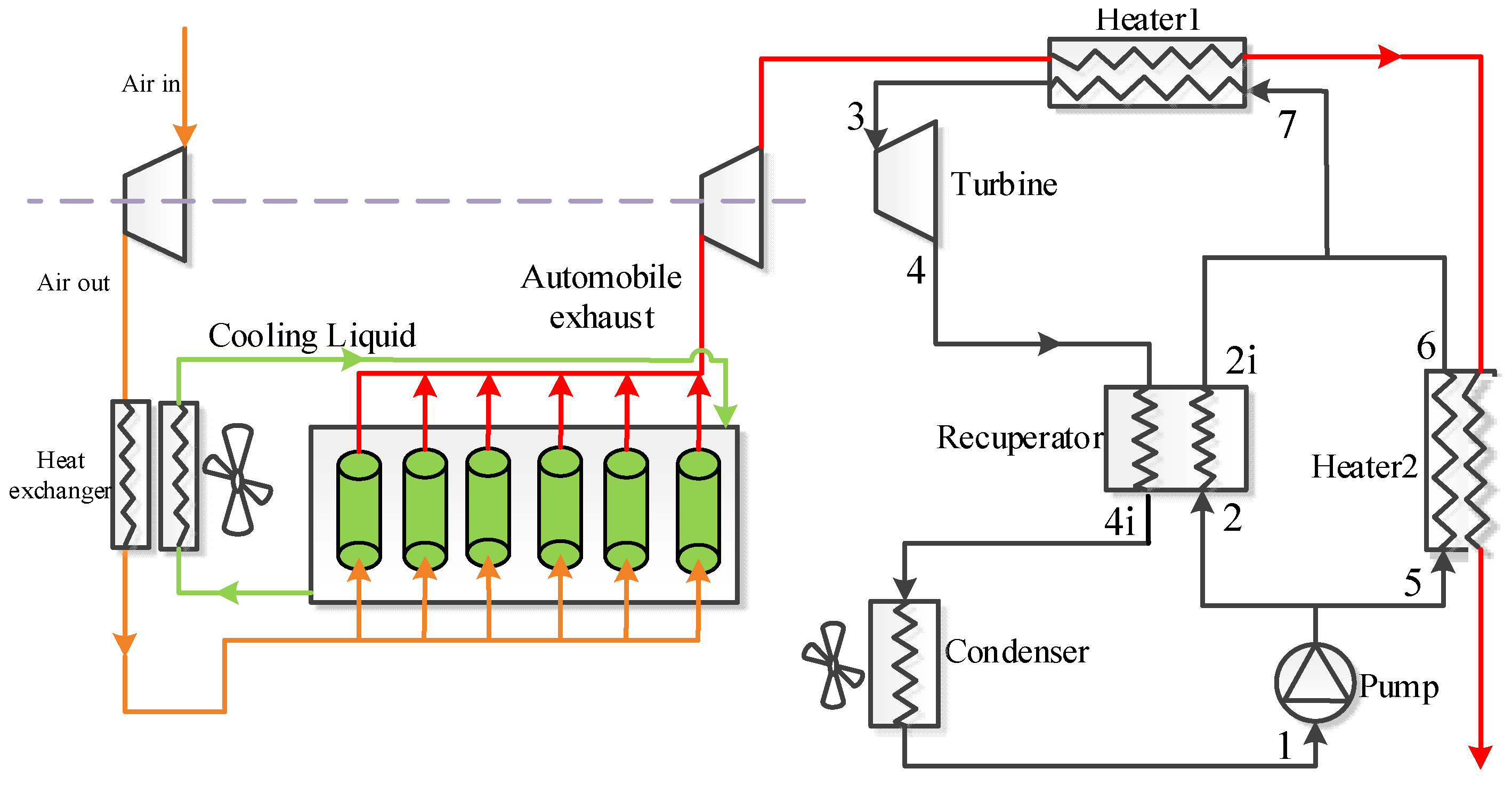
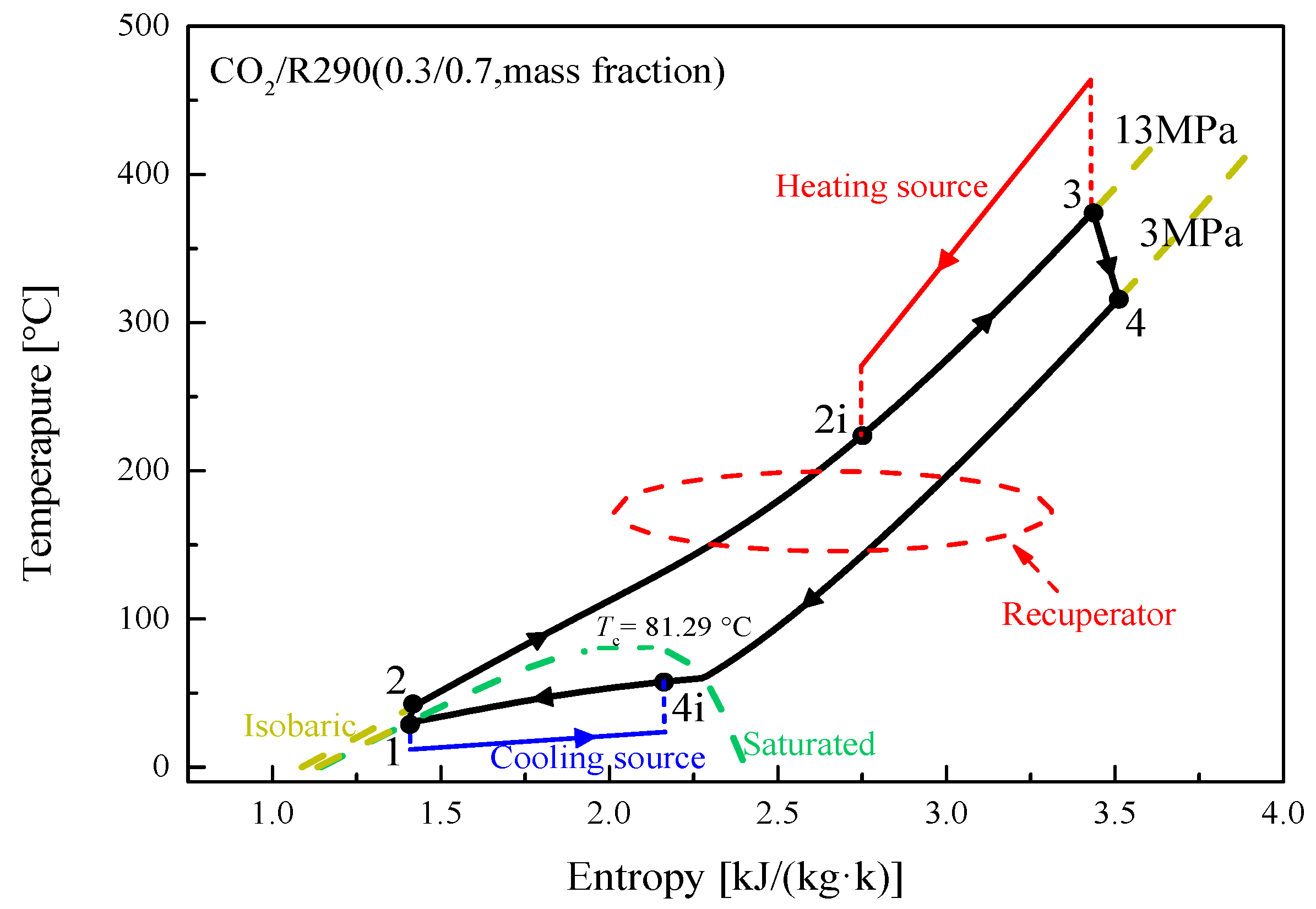
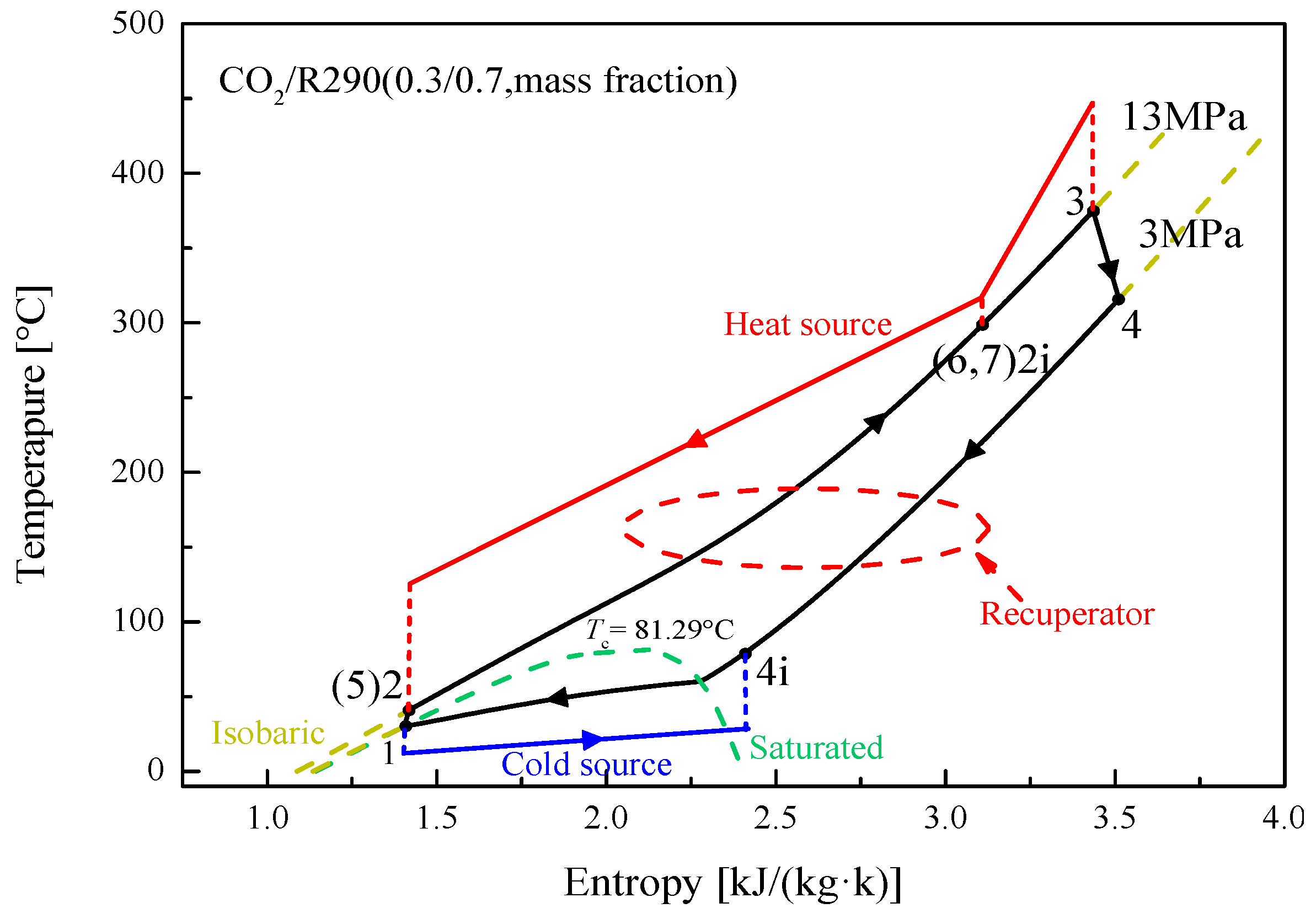
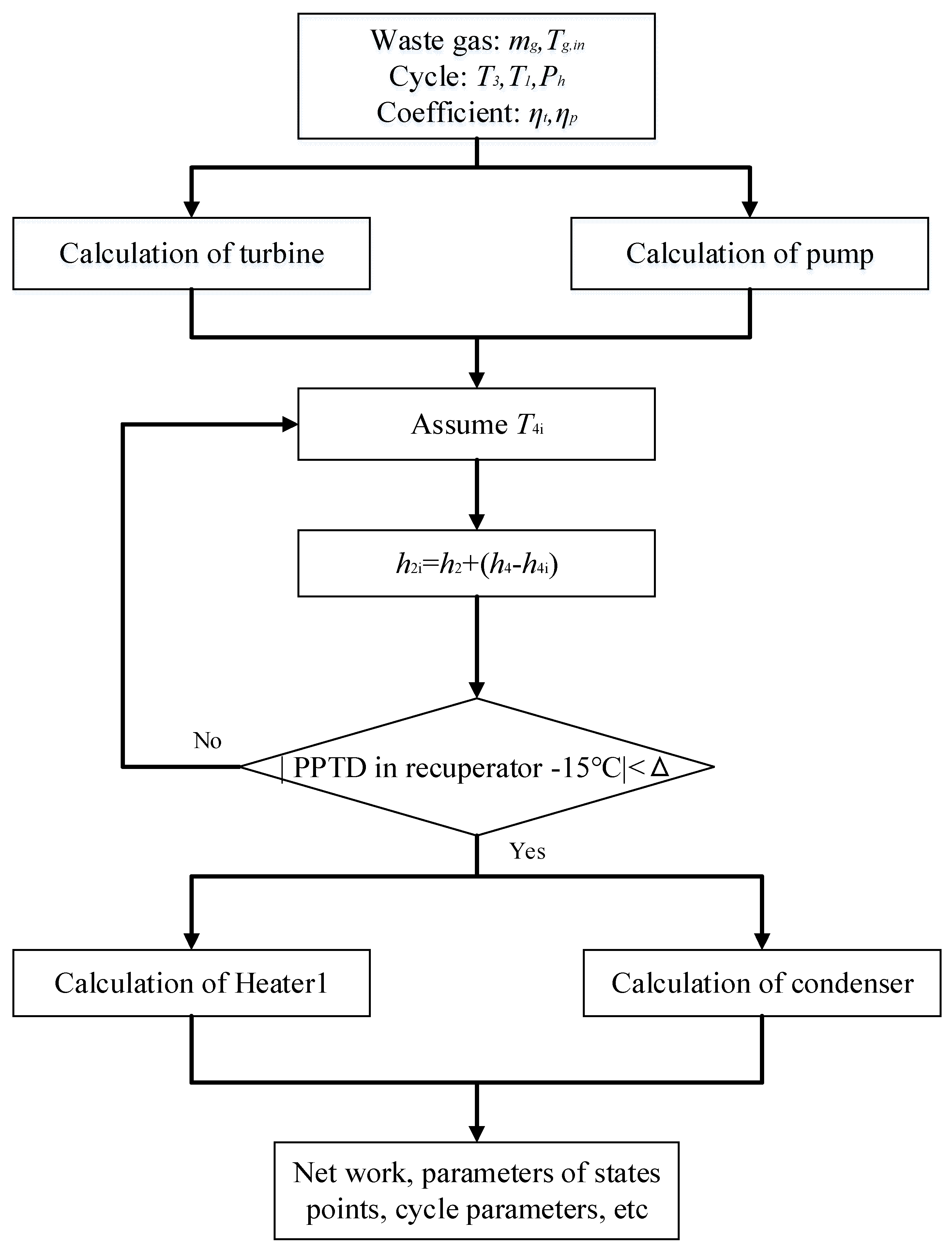


| Components | Recuperative Cycle | Split Cycle |
|---|---|---|
| Pump | ||
| Turbine | ||
| Condenser | ||
| Heater1 | ||
| Recuperator | ||
| Heater2 | --- | |
| Components | Recuperative Cycle | Split Cycle |
|---|---|---|
| Pump | ||
| Turbine | ||
| Condenser | ||
| Heater1 | ||
| Recuperator | ||
| Heater2 | --- | |
| Parameters | Values | Exhaust Gas Components | Values |
|---|---|---|---|
| Fuel combustion energy (kW) | 561.61 | CO2 (%) | 9.1 |
| Rated power (kW) | 236.50 | O2 (%) | 9.3 |
| Rated speed (rpm) | 1694 | H2O (%) | 7.4 |
| Rated torque (N·m) | 1333 | N2 (%) | 74.2 |
| Temperature of exhaust gas (°C) | 466 | ||
| Mass flow of exhaust gas (kg/s) | 0.278 | ||
| Exhaust gas pressure (MPa) | 0.10 |
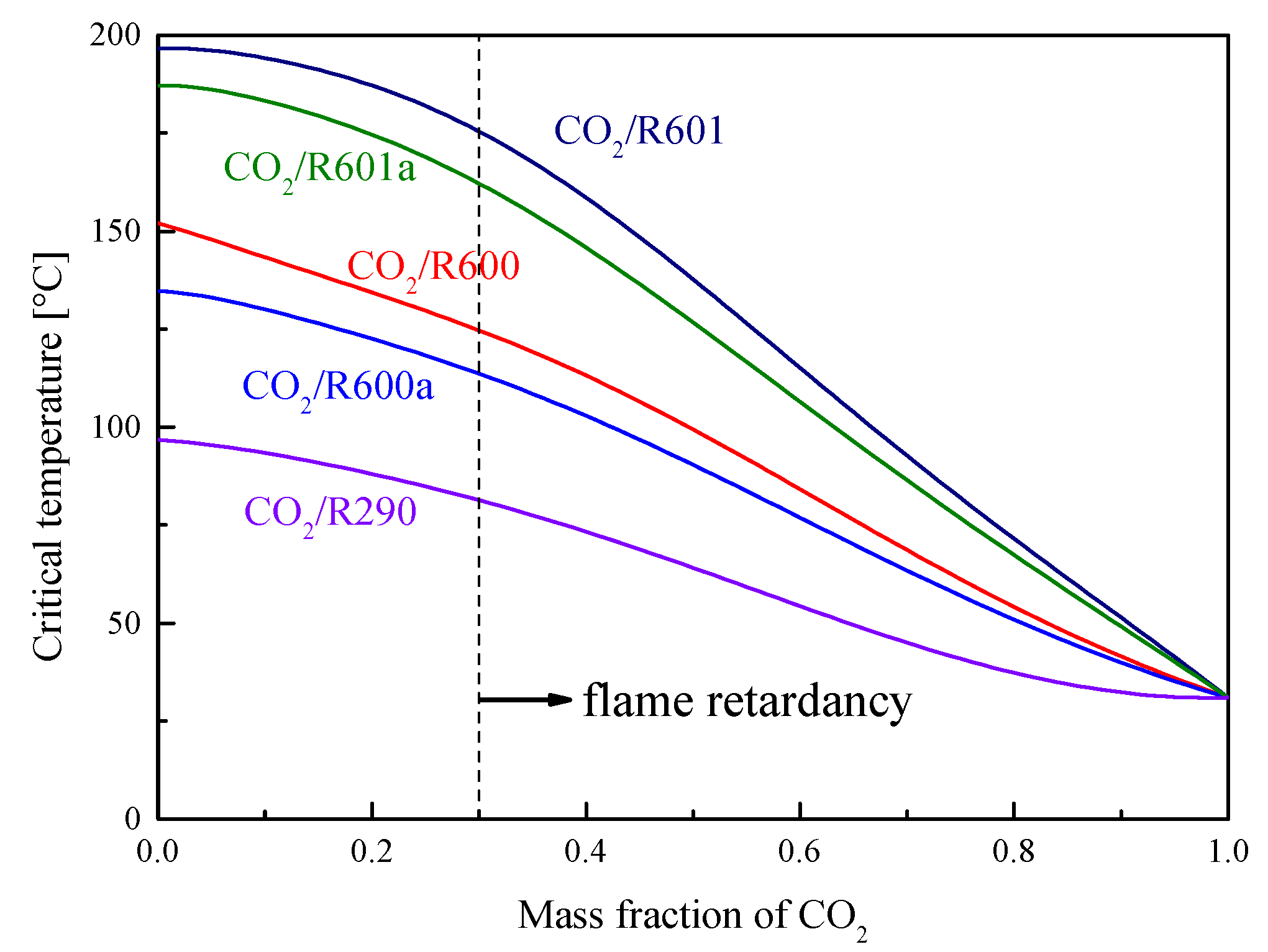
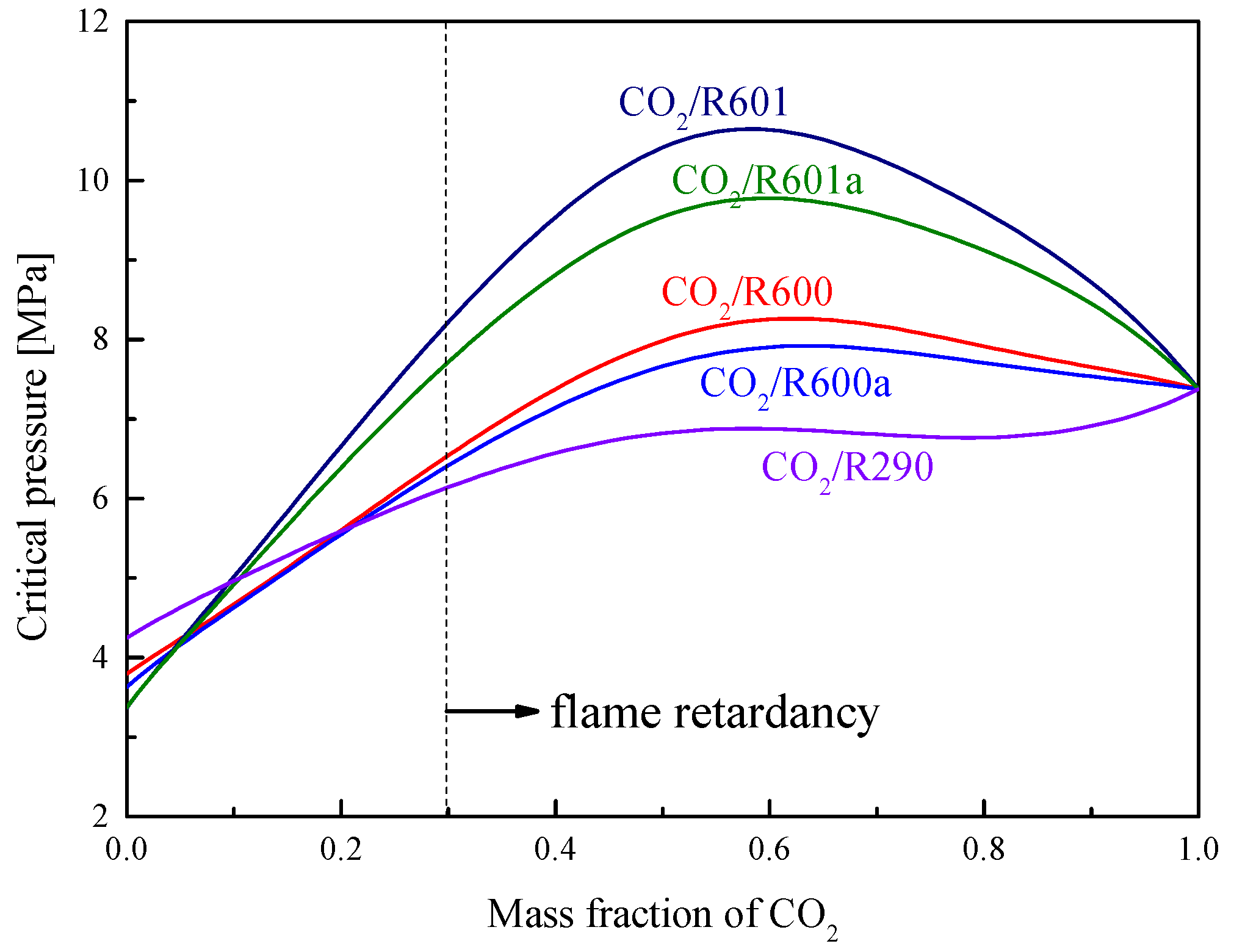
| Fluids | Molecular Mass (g/mol) | Tb (°C) | Tc (°C) | Pc (MPa) |
|---|---|---|---|---|
| CO2 | 44.01 | −78.4 | 31.1 | 7.38 |
| R290 | 44.1 | −42.1 | 96.7 | 4.25 |
| R600a | 58.12 | −11.7 | 134..7 | 3.63 |
| R600 | 58.12 | −0.5 | 152.0 | 3.80 |
| R601a | 72.15 | 27.83 | 187.2 | 3.38 |
| R601 | 72.15 | 36.06 | 196.55 | 3.37 |
| Design Parameters | Set Value | Range of Variation |
|---|---|---|
| Condensation bubble temperature (°C) | 30 | 30–90 |
| Turbine inlet temperature (°C) | 375 | 270–390 |
| Turbine inlet pressure (MPa) | 13 | 8.5–20 |
| Ambient temperature (°C) | 25 | — |
| Ambient pressure (MPa) | 0.1 | — |
| PPTD in Heater1 (°C) | 15 | — |
| PPTD in Heater2 (°C) | 15 | — |
| PPTD in recuperator (°C) | 15 | — |
| Pump efficiency | 0.8 | — |
| Turbine efficiency | 0.7 | — |
| Split ratio | 0.7 | 0–1 |
| Mass fraction of CO2 | 0.3 | 0.3–1 |
| Parameters | CO2/R290 | CO2/R601a | CO2/R601 | CO2/R600a | CO2/R600 |
|---|---|---|---|---|---|
| Mass fraction of CO2 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Tmid (°C) | 253.35 | 283.34 | 283.92 | 269.16 | 272.39 |
| PL (MPa) | 3.27 | 2.95 | 3.06 | 2.88 | 3.00 |
| mf (kg/s) | 0.19 | 0.20 | 0.20 | 0.20 | 0.20 |
| QHeater1 (kW) | 67.86 | 58.51 | 58.33 | 62.94 | 61.93 |
| QRe (kW) | 109.07 | 125.86 | 127.40 | 116.08 | 118.54 |
| Wt (kW) | 20.45 | 16.34 | 15.68 | 18.76 | 18.16 |
| Wp (kW) | 4.34 | 3.89 | 3.69 | 4.21 | 4.28 |
| Wnet (kW) | 16.11 | 12.45 | 11.99 | 14.55 | 13.89 |
| ηth (%) | 23.74 | 21.28 | 20.55 | 23.12 | 22.42 |
| ηr (%) | 38.82 | 33.46 | 33.36 | 36.00 | 35.42 |
| Parameters | CO2/R290 | CO2/R601a | CO2/R601 | CO2/R600a | CO2/R600 |
|---|---|---|---|---|---|
| Mass fraction of CO2 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| Tout (°C) | 139.00 | 143.29 | 141.22 | 143.00 | 143.50 |
| Tmid (°C) | 316.68 | 323.12 | 323.25 | 319.67 | 319.05 |
| PL (MPa) | 3.27 | 2.95 | 3.06 | 2.88 | 3.00 |
| mf (kg/s) | 0.25 | 0.25 | 0.25 | 0.25 | 0.25 |
| QHeater1 (kW) | 48.03 | 45.99 | 45.95 | 47.08 | 47.28 |
| QHeater2 (kW) | 54.95 | 55.68 | 56.35 | 54.68 | 54.33 |
| QRe (kW) | 128.22 | 129.92 | 131.49 | 127.59 | 126.77 |
| Wt (kW) | 26.72 | 20.53 | 19.74 | 24.04 | 22.99 |
| Wp (kW) | 5.67 | 4.89 | 4.65 | 5.39 | 5.41 |
| Wnet (kW) | 21.05 | 15.64 | 15.09 | 18.65 | 17.57 |
| ηth (%) | 20.44 | 15.38 | 14.75 | 18.32 | 17.29 |
| ηr (%) | 58.90 | 58.15 | 58.51 | 58.21 | 58.12 |
| Parameters | CO2/R290 | CO2/R600a | CO2/R600 | CO2/R601a | CO2/R601 |
|---|---|---|---|---|---|
| Mass fraction of CO2 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
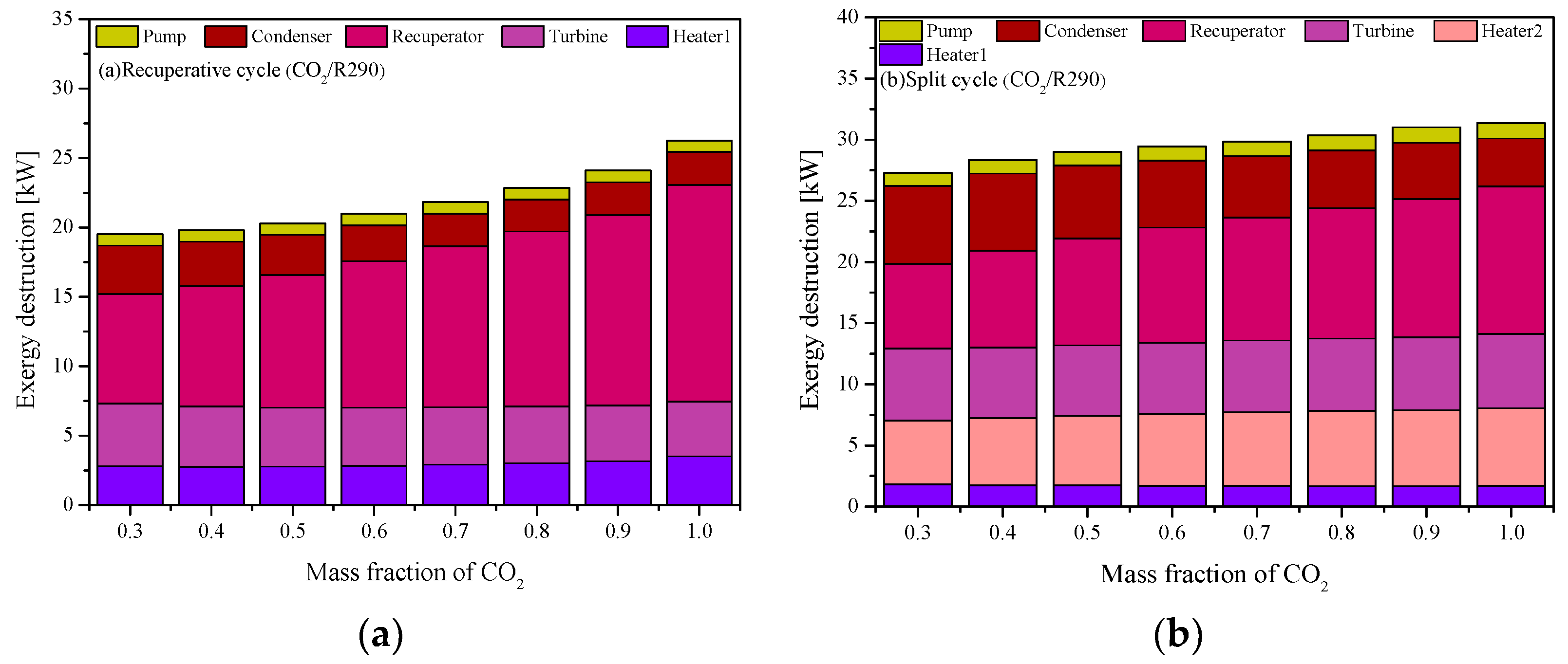
| IHeater1 (kW) | 2.80 | 2.55 | 2.50 | 2.33 | 2.33 |
| It (kW) | 4.50 | 4.10 | 3.98 | 3.54 | 3.40 |
| IRe (kW) | 7.91 | 6.90 | 6.82 | 7.30 | 7.66 |
| Icon (kW) | 3.48 | 4.54 | 4.99 | 5.06 | 5.26 |
| Ip (kW) | 0.83 | 0.81 | 0.82 | 0.75 | 0.71 |
| Itotal (kW) | 19.52 | 18.90 | 19.11 | 18.98 | 19.36 |
| ηex (%) | 45.22 | 43.50 | 42.08 | 39.61 | 38.24 |
| Parameters | CO2/R290 | CO2/R600a | CO2/R600 | CO2/R601a | CO2/R601 |
|---|---|---|---|---|---|
| Mass fraction of CO2 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| IHeater1 (kW) | 1.81 | 1.77 | 1.78 | 1.73 | 1.73 |
| IHeater2 (kW) | 5.22 | 5.00 | 4.94 | 4.90 | 4.87 |
| It (kW) | 5.89 | 5.26 | 5.03 | 4.45 | 4.28 |
| IRe (kW) | 6.94 | 6.94 | 6.87 | 7.69 | 7.96 |
| Icon (kW) | 6.35 | 9.35 | 10.73 | 12.63 | 13.33 |
| Ip (kW) | 1.08 | 1.03 | 1.04 | 0.94 | 0.90 |
| Itotal (kW) | 27.29 | 29.35 | 30.38 | 32.34 | 33.06 |
| ηex (%) | 43.55 | 38.85 | 36.65 | 32.60 | 31.34 |
| Parameters | CO2/R290 | CO2/R600a | CO2/R600 | CO2/R601a | CO2/R601 |
|---|---|---|---|---|---|
| Mass fraction of CO2 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| T1 (°C) | 30 | 30 | 30 | 30 | 30 |
| T3 (°C) | 322.94 | 325.57 | 333.80 | 334.03 | 341.40 |
| Ph (MPa) | 19.51 | 19.47 | 19.23 | 19.42 | 19.42 |
| Tmid (°C) | 204.67 | 221.72 | 230.05 | 247.47 | 248.24 |
| PL (MPa) | 3.27 | 2.88 | 3.00 | 2.95 | 3.06 |
| mf (kg/s) | 0.23 | 0.24 | 0.23 | 0.23 | 0.23 |
| QHeater1 (kW) | 82.91 | 77.66 | 75.09 | 69.69 | 69.45 |
| QRe (kW) | 87.62 | 98.24 | 101.85 | 110.86 | 112.00 |
| Wt (kW) | 26.76 | 24.42 | 23.34 | 20.79 | 19.88 |
| Wp (kW) | 8.43 | 8.18 | 8.06 | 7.21 | 6.86 |
| Wnet (kW) | 18.33 | 16.24 | 15.29 | 13.58 | 13.01 |
| ηth (%) | 22.10 | 20.91 | 20.36 | 19.49 | 18.73 |
| ηr (%) | 47.42 | 44.42 | 42.95 | 39.86 | 39.72 |
| Parameters | CO2/R290 | CO2/R600a | CO2/R600 | CO2/R601a | CO2/R601 |
|---|---|---|---|---|---|
| Mass fraction of CO2 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| T1 (°C) | 30 | 30 | 30 | 30 | 30 |
| T3 (°C) | 344.68 | 309.09 | 320.86 | 330.29 | 334.36 |
| Ph (MPa) | 12.01 | 11.47 | 13.31 | 12.51 | 13.2 |
| SR | 0.67 | 0.78 | 0.66 | 0.74 | 0.63 |
| Tmid (°C) | 289.47 | 256.53 | 261.17 | 277.49 | 279.40 |
| Tout (°C) | 62.83 | 100.57 | 54.18 | 107.44 | 51.40 |
| PL (MPa) | 3.27 | 2.88 | 3.00 | 2.95 | 3.06 |
| mf (kg/s) | 0.31 | 0.38 | 0.33 | 0.33 | 0.31 |
| QHeater1 (kW) | 56.59 | 66.88 | 65.43 | 60.34 | 59.74 |
| QHeater2 (kW) | 69.37 | 47.73 | 63.12 | 52.20 | 69.64 |
| QRe (kW) | 140.84 | 169.23 | 122.53 | 148.56 | 121.00 |
| Wt (kW) | 29.78 | 28.63 | 26.55 | 23.08 | 21.84 |
| Wp (kW) | 6.40 | 6.93 | 7.30 | 6.03 | 5.81 |
| Wnet (kW) | 23.37 | 21.70 | 19.25 | 17.06 | 16.03 |
| ηth (%) | 18.56 | 18.93 | 14.97 | 15.16 | 12.39 |
| ηr (%) | 72.04 | 65.55 | 73.53 | 64.37 | 74.00 |
| Fluids | Parameters | Mass Fraction of CO2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 1.00 | ||
| CO2/R290 | T3 (°C) | 322.94 | 320.69 | 320.45 | 324.33 | 323.66 | 332.79 | 339.31 | 353.74 |
| Ph (MPa) | 19.51 | 19.34 | 19.09 | 19.68 | 19.08 | 20.00 | 19.70 | 19.86 | |
| Wnet (kW) | 18.33 | 18.13 | 18.11 | 18.25 | 18.24 | 18.40 | 18.33 | 18.77 | |
| CO2/R600a | T3 (°C) | 325.57 | 324.15 | 320.56 | 321.40 | 323.95 | 332.19 | 339.29 | 353.74 |
| Ph (MPa) | 19.47 | 19.17 | 18.96 | 19.17 | 19.23 | 19.86 | 19.67 | 19.86 | |
| Wnet (kW) | 16.24 | 16.57 | 17.10 | 17.67 | 18.15 | 18.68 | 18.90 | 18.77 | |
| CO2/R600 | T3 (°C) | 333.80 | 329.38 | 324.45 | 323.27 | 326.42 | 333.90 | 333.90 | 353.74 |
| Ph (MPa) | 19.23 | 19.38 | 18.91 | 19.07 | 19.22 | 19.87 | 19.66 | 19.86 | |
| Wnet (kW) | 15.29 | 15.86 | 16.61 | 17.39 | 18.04 | 18.62 | 18.90 | 18.77 | |
| CO2/R601a | T3 (°C) | 334.03 | 331.62 | 327.22 | 316.92 | 322.50 | 330.65 | 342.74 | 353.74 |
| Ph (MPa) | 19.42 | 19.79 | 19.14 | 19.90 | 19.32 | 19.56 | 19.71 | 19.86 | |
| Wnet (kW) | 13.58 | 14.68 | 15.90 | 17.05 | 17.99 | 18.53 | 19.00 | 18.77 | |
| CO2/R601 | T3 (°C) | 341.40 | 333.92 | 326.84 | 326.39 | 326.58 | 318.00 | 344.03 | 353.74 |
| Ph (MPa) | 19.42 | 19.36 | 19.02 | 19.46 | 19.42 | 19.63 | 19.32 | 19.86 | |
| Wnet (kW) | 13.01 | 14.16 | 15.52 | 16.91 | 18.05 | 18.76 | 19.04 | 18.77 | |
| Fluids | Parameters | Mass Fraction of CO2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 | 1.00 | ||
| CO2/R290 | T3 (°C) | 344.68 | 338.32 | 330.55 | 361.19 | 324.35 | 323.84 | 319.98 | 321.57 |
| Ph (MPa) | 12.01 | 12.39 | 14.48 | 17.31 | 12.84 | 15.70 | 15.98 | 17.16 | |
| SR | 0.67 | 0.73 | 0.69 | 0.61 | 0.71 | 0.70 | 0.68 | 0.62 | |
| Wnet (kW) | 23.36 | 23.43 | 23.93 | 24.24 | 24.70 | 25.48 | 25.86 | 26.80 | |
| CO2/R600a | T3 (°C) | 309.09 | 299.37 | 312.38 | 283.43 | 299.38 | 308.87 | 320.43 | 321.57 |
| Ph (MPa) | 11.47 | 12.37 | 14.05 | 12.46 | 13.99 | 16.38 | 16.54 | 17.16 | |
| SR | 0.78 | 0.79 | 0.68 | 0.79 | 0.74 | 0.68 | 0.63 | 0.62 | |
| Wnet (kW) | 21.70 | 22.28 | 22.91 | 24.91 | 26.01 | 26.63 | 26.95 | 26.80 | |
| CO2/R600 | T3 (°C) | 320.86 | 314.91 | 321.25 | 290.38 | 303.92 | 316.46 | 313.22 | 321.57 |
| Ph (MPa) | 13.31 | 13.57 | 13.56 | 12.60 | 15.90 | 14.61 | 15.33 | 17.16 | |
| SR | 0.66 | 0.75 | 0.67 | 0.72 | 0.71 | 0.66 | 0.66 | 0.62 | |
| Wnet (kW) | 19.25 | 20.41 | 21.84 | 24.03 | 24.79 | 26.17 | 27.43 | 26.80 | |
| CO2/R601a | T3 (°C) | 330.30 | 336.88 | 320.03 | 285.92 | 306.95 | 286.34 | 321.87 | 321.57 |
| Ph (MPa) | 12.51 | 14.13 | 14.83 | 14.13 | 13.66 | 14.07 | 14.78 | 17.16 | |
| SR | 0.74 | 0.66 | 0.74 | 0.74 | 0.69 | 0.76 | 0.66 | 0.62 | |
| Wnet (kW) | 17.06 | 18.37 | 20.39 | 22.61 | 24.85 | 26.76 | 27.07 | 26.80 | |
| CO2/R601 | T3 (°C) | 334.36 | 327.62 | 341.49 | 310.13 | 300.58 | 312.56 | 324.49 | 321.57 |
| Ph (MPa) | 13.20 | 13.71 | 14.89 | 13.38 | 14.19 | 13.56 | 17.10 | 17.16 | |
| SR | 0.63 | 0.76 | 0.68 | 0.73 | 0.73 | 0.64 | 0.63 | 0.62 | |
| Wnet (kW) | 16.03 | 17.86 | 19.49 | 22.59 | 24.68 | 25.56 | 27.04 | 26.80 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yu, A.; Lin, X.; Su, W.; Ou, S. Performances of Transcritical Power Cycles with CO2-Based Mixtures for the Waste Heat Recovery of ICE. Entropy 2021, 23, 1551. https://doi.org/10.3390/e23111551
Liu J, Yu A, Lin X, Su W, Ou S. Performances of Transcritical Power Cycles with CO2-Based Mixtures for the Waste Heat Recovery of ICE. Entropy. 2021; 23(11):1551. https://doi.org/10.3390/e23111551
Chicago/Turabian StyleLiu, Jinghang, Aofang Yu, Xinxing Lin, Wen Su, and Shaoduan Ou. 2021. "Performances of Transcritical Power Cycles with CO2-Based Mixtures for the Waste Heat Recovery of ICE" Entropy 23, no. 11: 1551. https://doi.org/10.3390/e23111551
APA StyleLiu, J., Yu, A., Lin, X., Su, W., & Ou, S. (2021). Performances of Transcritical Power Cycles with CO2-Based Mixtures for the Waste Heat Recovery of ICE. Entropy, 23(11), 1551. https://doi.org/10.3390/e23111551






