Entanglement-Structured LSTM Boosts Chaotic Time Series Forecasting
Abstract
:1. Introduction
2. Recurrent Architecture and Tensorization
2.1. Formalism of LSTM Architecture
2.2. Tensorized State Propagation
2.3. Many-Body Entanglement Structures
2.3.1. MPS
2.3.2. MERA
2.3.3. Scaling Behavior of EE
3. Theoretical Analysis
3.1. Expressive Power
3.2. Worst-Case Bound by EE
4. Results
4.1. Comparison of LSTM-Based Architectures
4.1.1. Lorenz System
4.1.2. Logistic Map
4.2. Comparison with Statistical/ML Models
Gauss Iterated Map
4.3. Comparison with LSTM-MERA Alternatives
Thomas’ Cyclically Symmetric System
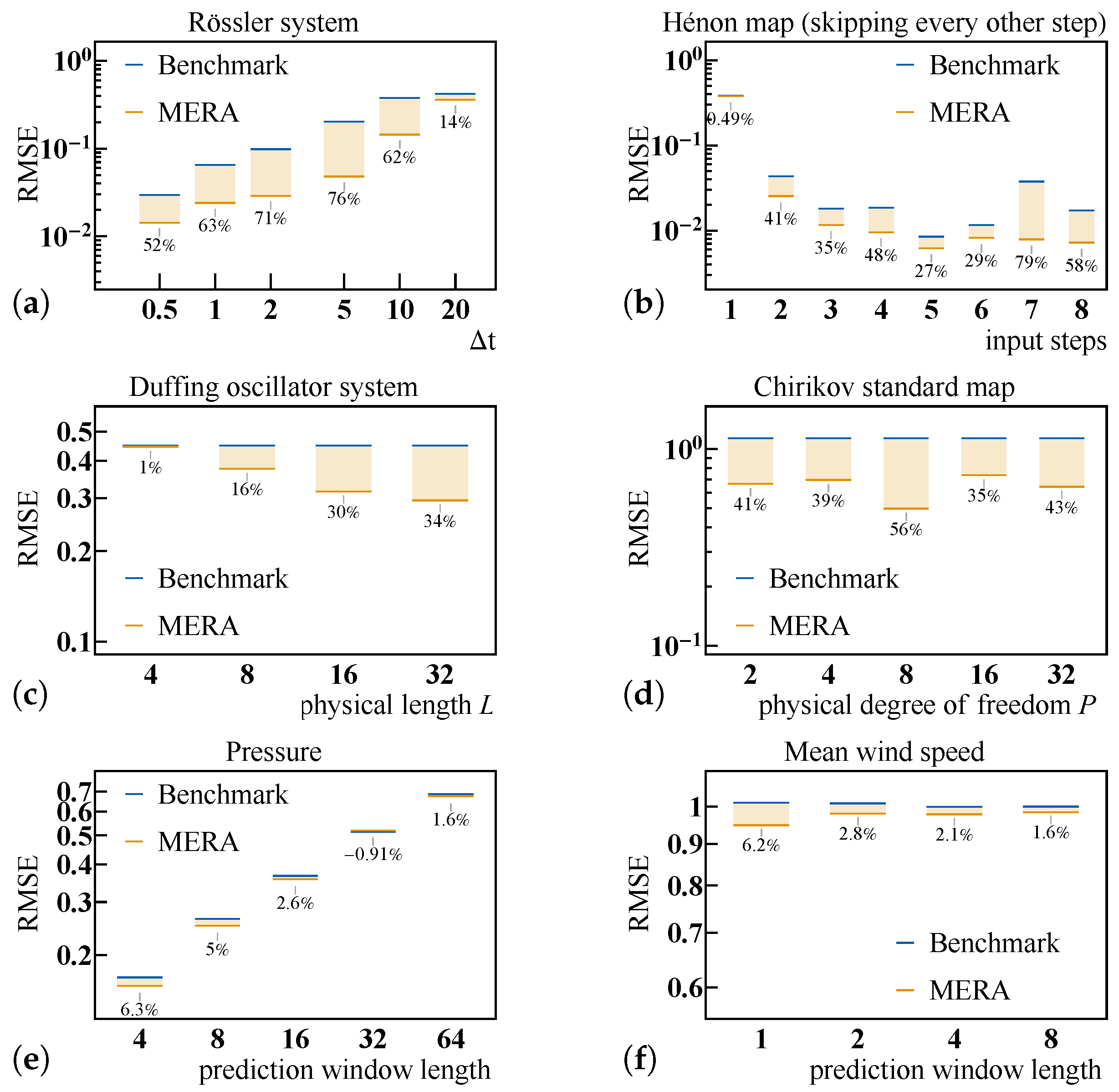
4.4. Generalization and Parameter Dependence of LSTM-MERA
4.4.1. Rössler System
4.4.2. Hénon Map
4.4.3. Duffing Oscillator System
4.4.4. Chirikov Standard Map
4.4.5. Real-World Data: Weather Forecasting
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| NN | Neural Network |
| RNN | Recurrent Neural Network |
| LSTM | Long Short Term Memory |
| HO- | Higher-Order- |
| HOT- | Higher-Order-Tensorized- |
| MPS | Matrix Product State |
| MERA | Multiscale Entanglement Renormalization Ansatz |
| EE | Entanglement Entropy |
| DOF | Degree Of Freedom |
| RMSE | Root Mean Squared Error |
| ARMA | Auto-Regressive Moving Average |
| GBT | Gradient Boosted Trees |
| HMM | Hidden Markov Models |
Appendix A. Variants of LSTM-MERA
Appendix A.1. Translational Symmetry
Appendix A.2. Dilational Symmetry
Appendix A.3. Normalization/Unitarity
Appendix B. Common LSTM Architectures
Appendix B.1. HO- and HOT-RNN/LSTM
Appendix C. Preparation of Time Series Datasets
Appendix C.1. Discrete-Time Maps
| Logistic | Gauss | Hénon | Chirikov | |
|---|---|---|---|---|
| Dimension | 1 | 1 | 1 | 2 |
| Parameters | ||||
| Initial condition | ||||
| (training) | ||||
| Initial condition | ||||
| (testing) | ||||
| – | – |
Appendix C.2. Continuous-Time Dynamical Systems
| Lorentz | Thomas | Rössler | Duffing | |
|---|---|---|---|---|
| Dimension | 3 | 3 | 3 | 1 |
| Parameters | ||||
| Initial condition | ||||
| 0 | 0 | 0 | 0 | |
Appendix C.3. Real-World Time Series: Weather
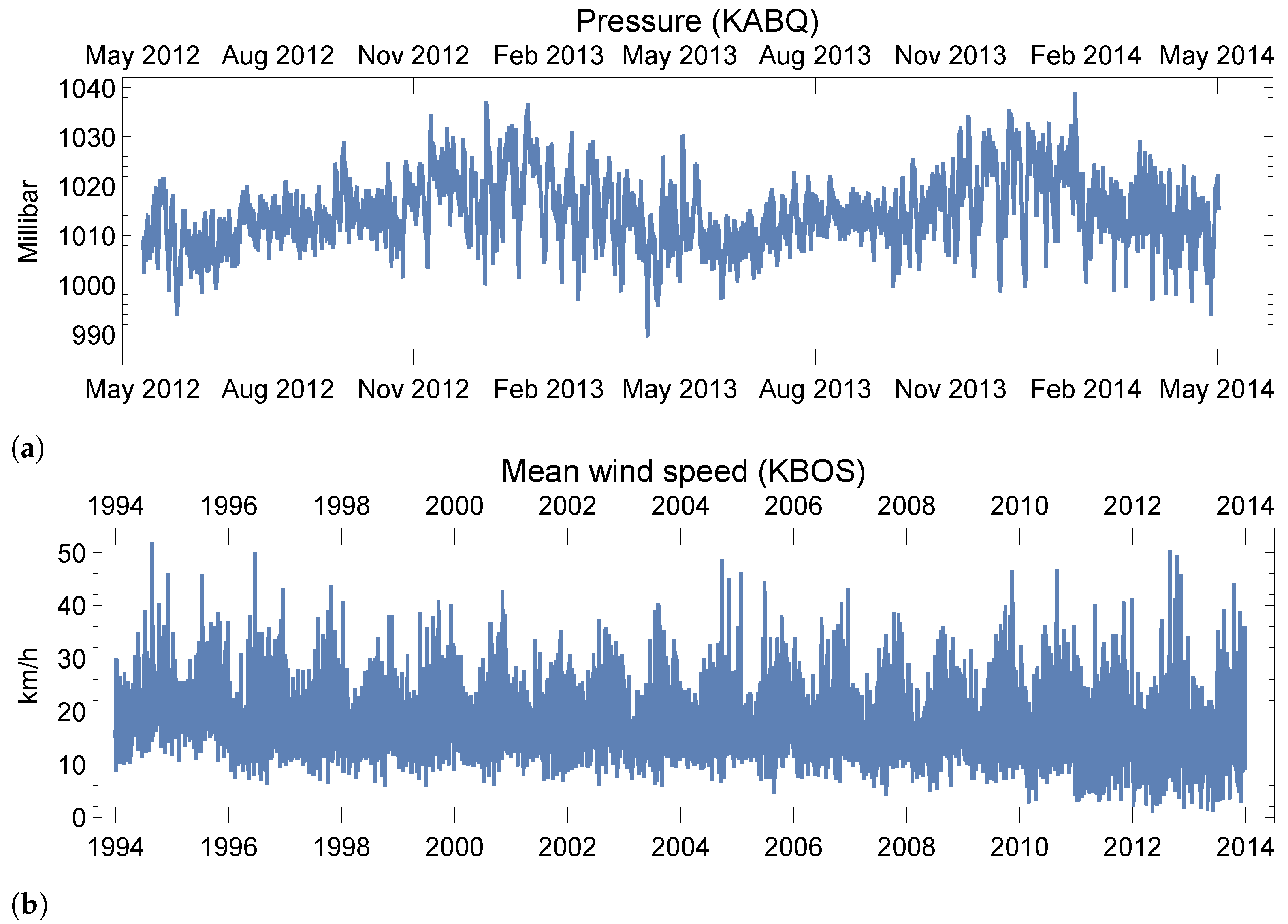
| Pressure | Mean Wind Speed | |
|---|---|---|
| Location | ICAO:KABQ | ICAO:KBOS |
| Span | 05/01/2012–05/01/2014 | 05/01/1994–05/01/2014 |
| Frequency | 8 min | 1 day |
| Total length | 22,426 | 7299 |
References
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and machine learning forecasting methods: Concerns and ways forward. PLoS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, Y.; Anick, P.; Hong, P.; Xue, N. Temporal relation discovery between events and temporal expressions identified in clinical narrative. J. Biomed. Inform. 2013, 46, S48–S53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Rabiner, L.; Juang, B. An introduction to hidden Markov models. IEEE ASSP Mag. 1986, 3, 4–16. [Google Scholar] [CrossRef]
- Hong, P.; Huang, T.S. Automatic temporal pattern extraction and association. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; Volume 2, pp. II–2005–II–2008. [Google Scholar]
- Ahmed, N.K.; Atiya, A.F.; Gayar, N.E.; El-Shishiny, H. An empirical comparison of machine learning models for time series forecasting. Econom. Rev. 2010, 29, 594–621. [Google Scholar] [CrossRef]
- Osogami, T.; Kajino, H.; Sekiyama, T. Bidirectional learning for time-series models with hidden units. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2711–2720. [Google Scholar]
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Conditional time series forecasting with convolutional neural networks. arXiv 2018, arXiv:1703.04691v5. [Google Scholar]
- Ding, D.; Zhang, M.; Pan, X.; Yang, M.; He, X. Modeling extreme events in time series prediction. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1114–1122. [Google Scholar]
- Bar-Yam, Y. Dynamics Of Complex Systems (Studies in Nonlinearity); CRC Press: New York, NY, USA, 1999. [Google Scholar]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2342–2350. [Google Scholar]
- Giles, C.L.; Sun, G.Z.; Chen, H.H.; Lee, Y.C.; Chen, D. Higher order recurrent networks and grammatical inference. Proceedings of Neural Information Processing Systems, Denver, CO, USA, 27–30 November 1989; pp. 380–387. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Soltani, R.; Jiang, H. Higher order recurrent neural networks. arXiv 2016, arXiv:1605.00064. [Google Scholar]
- Haruna, T.; Nakajima, K. Optimal short-term memory before the edge of chaos in driven random recurrent networks. Phys. Rev. E 2019, 100, 062312. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Lai, C.H. Optimal machine intelligence near the edge of chaos. arXiv 2019, arXiv:1909.05176. [Google Scholar]
- Kuo, J.M.; Principle, J.C.; de Vries, B. Prediction of chaotic time series using recurrent neural networks. In Proceedings of the Neural Networks for Signal Processing II Proceedings of the 1992 IEEE Workshop, Helsingoer, Denmark, 31 Augest–2 September 1992; pp. 436–443. [Google Scholar]
- Zhang, J.S.; Xiao, X.C. Predicting chaotic time series using recurrent neural network. Chinese Phys. Lett. 2000, 17, 88–90. [Google Scholar] [CrossRef]
- Han, M.; Xi, J.; Xu, S.; Yin, F.L. Prediction of chaotic time series based on the recurrent predictor neural network. IEEE Trans. Signal Process. 2004, 52, 3409–3416. [Google Scholar] [CrossRef]
- Ma, Q.L.; Zheng, Q.L.; Peng, H.; Zhong, T.W.; Xu, L.Q. Chaotic time series prediction based on evolving recurrent neural networks. In Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007; Volume 6, pp. 3496–3500. [Google Scholar]
- Domino, K. The use of the Hurst exponent to predict changes in trends on the Warsaw stock exchange. Phys. A 2011, 390, 98–109. [Google Scholar] [CrossRef]
- Li, Q.; Lin, R. A new approach for chaotic time series prediction using recurrent neural network. Math. Probl. Eng. 2016, 2016, 3542898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vlachas, P.R.; Byeon, W.; Wan, Z.Y.; Sapsis, T.P.; Koumoutsakos, P. Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks. Proc. R. Soc. A 2018, 474, 20170844. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Domino, K. Multivariate cumulants in outlier detection for financial data analysis. Phys. A 2020, 558, 124995. [Google Scholar] [CrossRef]
- Yang, Y.; Krompass, D.; Tresp, V. Tensor-train recurrent neural networks for video classification. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3891–3900. [Google Scholar]
- Schlag, I.; Schmidhuber, J. Learning to reason with third order tensor products. In Proceedings of the Neural Information Processing Systems 2018, Montreal, QC, Canada, 3–8 December 2018; Volume 31, pp. 9981–9993. [Google Scholar]
- Yu, R.; Zheng, S.; Anandkumar, A.; Yue, Y. Long-term forecasting using higher order tensor RNNs. arXiv 2019, arXiv:1711.00073v3. [Google Scholar]
- Raissi, M. Deep hidden physics models: Deep learning of nonlinear partial differential equations. J. Mach. Learn. Res. 2018, 19, 1–24. [Google Scholar]
- Pathak, J.; Hunt, B.; Girvan, M.; Lu, Z.; Ott, E. Model-free prediction of large spatiotemporally chaotic systems from data: A reservoir computing approach. Phys. Rev. Lett. 2018, 120, 024102. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Lai, Y.C. Model-free prediction of spatiotemporal dynamical systems with recurrent neural networks: Role of network spectral radius. Phys. Rev. Res. 2019, 1, 033056. [Google Scholar] [CrossRef] [Green Version]
- Qi, D.; Majda, A.J. Using machine learning to predict extreme events in complex systems. Proc. Natl. Acad. Sci. USA 2020, 117, 52–59. [Google Scholar] [CrossRef] [Green Version]
- Graves, A. Generating sequences with recurrent neural networks. arXiv 2014, arXiv:1308.0850v5. [Google Scholar]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef] [Green Version]
- Eisert, J.; Cramer, M.; Plenio, M.B. Colloquium: Area laws for the entanglement entropy. Rev. Mod. Phys. 2010, 82, 277–306. [Google Scholar] [CrossRef] [Green Version]
- Vidal, G. Class of quantum many-body states that can be efficiently simulated. Phys. Rev. Lett. 2008, 101, 110501. [Google Scholar] [CrossRef] [Green Version]
- Verstraete, F.; Cirac, J.I. Matrix product states represent ground states faithfully. Phys. Rev. B 2006, 73, 094423. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.H. Entanglement entropy of target functions for image classification and convolutional neural network. arXiv 2017, arXiv:1710.05520. [Google Scholar]
- Khrulkov, V.; Novikov, A.; Oseledets, I.V. Expressive power of recurrent neural networks. In Proceedings of the 6th International Conference on Learning Representations (ICLR 2018), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Bhatia, A.S.; Saggi, M.K.; Kumar, A.; Jain, S. Matrix product state based quantum classifier. Neural Comput. 2019, 31, 1499–1517. [Google Scholar] [CrossRef]
- Jia, Z.A.; Wei, L.; Wu, Y.C.; Guo, G.C.; Guo, G.P. Entanglement area law for shallow and deep quantum neural network states. New J. Phys. 2020, 22, 053022. [Google Scholar] [CrossRef]
- Bigoni, D.; Engsig-Karup, A.P.; Marzouk, Y.M. Spectral tensor-train decomposition. SIAM J. Sci. Comput. 2016, 38, A2405–A2439. [Google Scholar] [CrossRef] [Green Version]
- Grasedyck, L. Hierarchical singular value decomposition of tensors. SIAM J. Matrix Anal. Appl. 2010, 31, 2029–2054. [Google Scholar] [CrossRef] [Green Version]
- Canuto, C.; Quarteroni, A. Approximation results for orthogonal polynomials in Sobolev spaces. Math. Comput. 1982, 38, 67–86. [Google Scholar] [CrossRef]
- Dehmamy, N.; Barabási, A.L.; Yu, R. Understanding the representation power of graph neural networks in learning graph topology. arXiv 2019, arXiv:1907.05008. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Yang, T. Entanglement-Structured LSTM Boosts Chaotic Time Series Forecasting. Entropy 2021, 23, 1491. https://doi.org/10.3390/e23111491
Meng X, Yang T. Entanglement-Structured LSTM Boosts Chaotic Time Series Forecasting. Entropy. 2021; 23(11):1491. https://doi.org/10.3390/e23111491
Chicago/Turabian StyleMeng, Xiangyi, and Tong Yang. 2021. "Entanglement-Structured LSTM Boosts Chaotic Time Series Forecasting" Entropy 23, no. 11: 1491. https://doi.org/10.3390/e23111491
APA StyleMeng, X., & Yang, T. (2021). Entanglement-Structured LSTM Boosts Chaotic Time Series Forecasting. Entropy, 23(11), 1491. https://doi.org/10.3390/e23111491






