Dynamic Event-Triggered Predictive Control for Interval Type-2 Fuzzy Systems with Imperfect Premise Matching
Abstract
:1. Introduction
- A novel IT2 fuzzy model is proposed, which unifies the dynamic ETM and the predictive control method in a framework to compensate the negative effect of network packet loss. Unlike the traditional T-S fuzzy model [27], it does not require the membership function be known by bounding it.
- A method of designing the dynamic event-triggered predictive controller containing global membership boundary information is provided to deal with imperfect premise mathing. Unlike the networked parallel distributed compensation method [28], it does not require the controller to have the same premise variables as the studied T-S fuzzy system by the imperfect premise matching method.
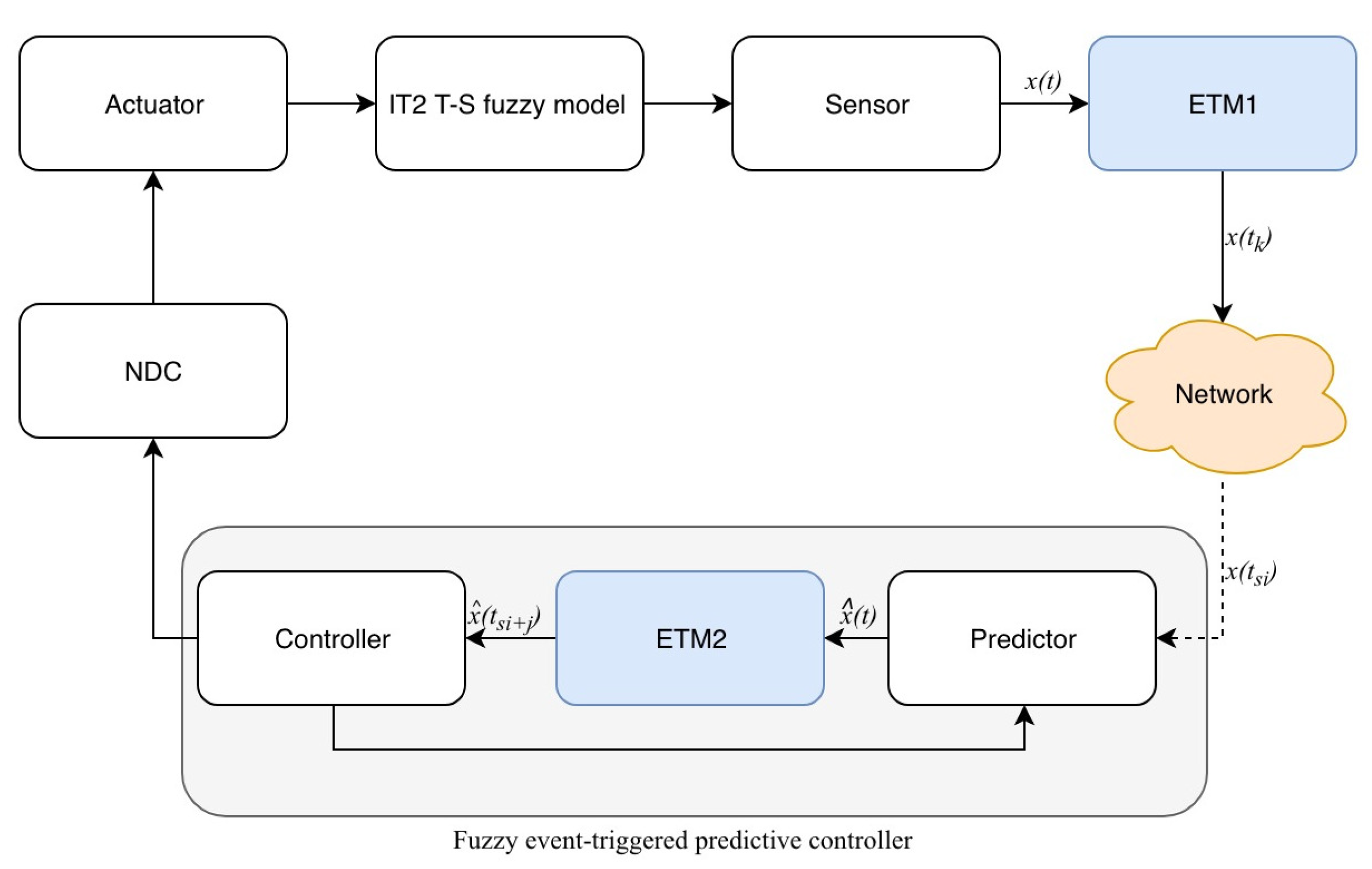
2. System Description
2.1. IT2 Fuzzy Model
2.2. Dynamic ETM
2.3. FETPC under Premise Matching
2.4. Model of Networked T-S Fuzzy Systems
3. Main Results
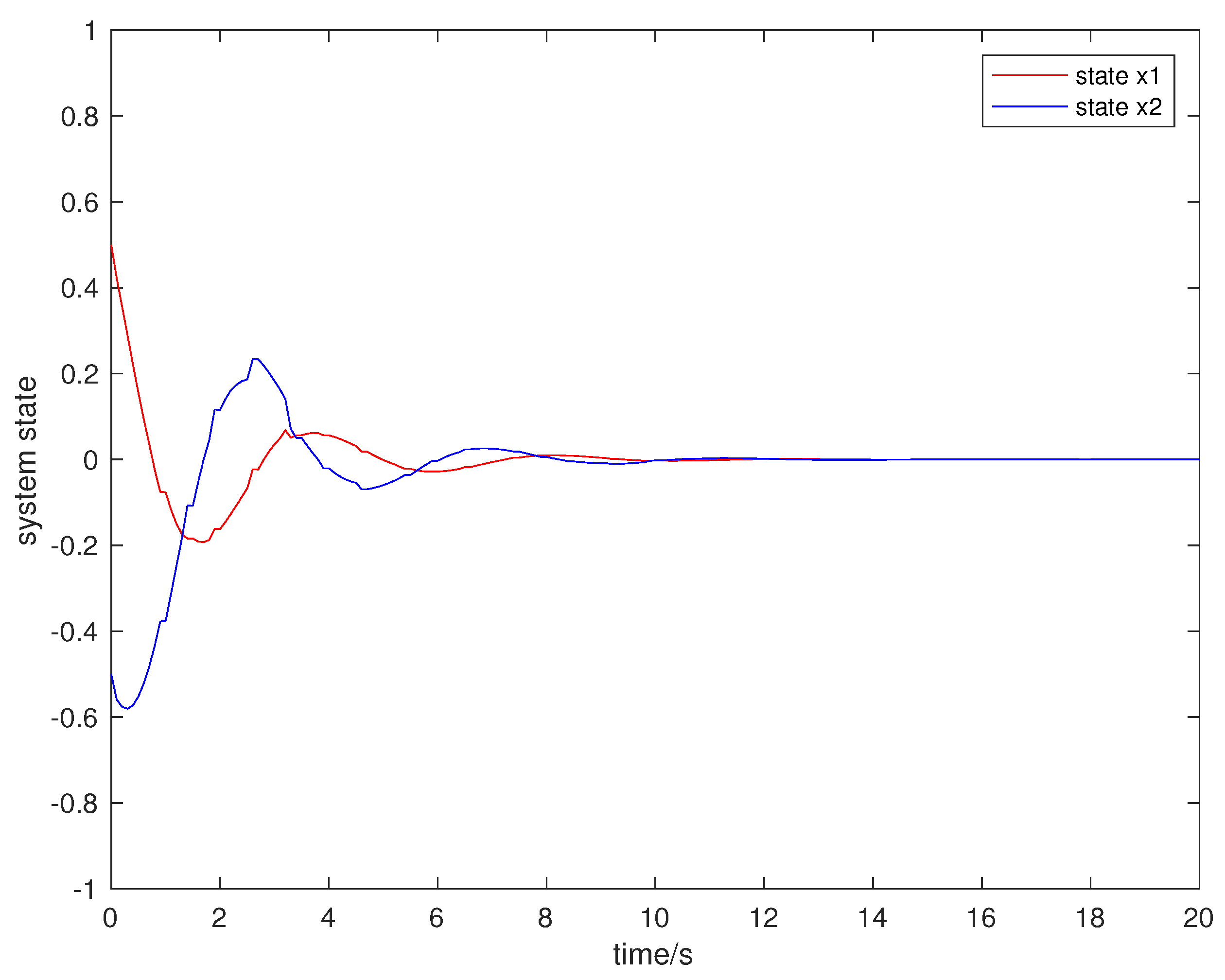
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.M.; Han, Q.L. Networked control stystems: A survey of trends and techniques. IEEE/CAA J. Autom. Sin. 2020, 7, 1–17. [Google Scholar]
- Zhang, X.M.; Han, Q.L. Survey on Recent Advances in Networked Control Systems. IEEE Trans. Ind. Inform. 2016, 12, 1740–1752. [Google Scholar] [CrossRef]
- Martin, S.; Martin, H. A stability criterion for networked control systems with packetized transmissions. IEEE Control Syst. Lett. 2021, 5, 911–916. [Google Scholar]
- Morrison, M.; Kutz, J.N. Nonlinear control of networked dynamical systems. IEEE Trans. Netw. Sci. Eng. 2021, 8, 174–189. [Google Scholar] [CrossRef] [PubMed]
- Yin, Z.P.; Yu, K.M.; Wang, Y.Z. Robust control algorithm and simulation of networked control systems. Comput. Commun. 2020, 157, 394–401. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, H.J.; Jiang, T.Y. Fault detection for nonlinear networked control systems with stochastic interval delay characterisation. Int. J. Syst. Sci. 2012, 43, 952–960. [Google Scholar] [CrossRef]
- Gao, L.; Li, F.; Fu, J. Output-based decentralised event-triggered dissipative control of NCSs under aperiodic DoS attacks. Int. J. Syst. Sci. 2021, 52, 1–17. [Google Scholar] [CrossRef]
- Liu, D.; Yang, G.J.; Er, M.J. Event-triggered control for T-S fuzzy systems under asynchronous network communications. IEEE Trans. Fuzzy Syst. 2020, 28, 390–399. [Google Scholar] [CrossRef]
- Lechappe, V.; Moulay, E.; Plestan, F.; Han, Q.L. Discrete predictor-based event-triggered control of networked control systems. Automatica. 2019, 107, 281–288. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.H.; Mu, X.W. Event-triggered control for networked nonlinear semi-Markovian jump systems with randomly occurring uncertainties and transmission delay. Inf. Sci. 2019, 487, 84–96. [Google Scholar] [CrossRef]
- Tang, X.M.; Deng, L.; Qu, H. Predictive control for networked interval type-2 T-S fuzzy system via an event-triggered dynamic output feedback scheme. IEEE Trans. Fuzzy Syst. 2019, 27, 1573–1586. [Google Scholar] [CrossRef]
- Ning, Z.K.; Yu, J.Y.; Pan, Y.N.; Li, H.Y. Adaptive event-triggered fault detection for fuzzy stochastic systems with missing measurements. IEEE Trans. Fuzzy Syst. 2018, 26, 2201–2212. [Google Scholar] [CrossRef]
- Zhang, L.C.; Liang, H.J.; Sun, Y.H.; Ahn, C.K. Adaptive event-triggered fault detection scheme for semi-Markovian jump systems with output quantization. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 51, 2370–2381. [Google Scholar] [CrossRef]
- Chen, M.; Sun, J.; Karimi, H.R. Input-output finite-time generalized dissipative filter of discrete time-varying systems with quantization and adaptive event-triggered mechanism. IEEE Trans. Cybern. 2020, 50, 5061–5073. [Google Scholar] [CrossRef]
- Ge, X.H.; Han, Q.L.; Wang, Z.D. A dynamic event-triggered transmission scheme for distributed set-membership estimation over wireless sensor networks. IEEE Trans. Cybern. 2019, 49, 171–183. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhu, Q. Adaptive fuzzy event-triggered control for nonstrict-feedback switched stochastic nonlinear systems with state constraints. Int. J. Syst. Sci. 2021, 52, 2889–2903. [Google Scholar] [CrossRef]
- Guo, X.G.; Fan, X.; Ahn, C.K. Adaptive event-triggered fault detection for interval type-2 T-S fuzzy systems with sensor saturation. IEEE Trans. Fuzzy Syst. 2020, 29, 2310–2321. [Google Scholar] [CrossRef]
- Zhang, Z.N.; Su, S.F.; Niu, Y.G. Dynamic event-triggered control for interval type-2 fuzzy systems under fading channel. IEEE Trans. Cybern. 2021, 110, 53–62. [Google Scholar] [CrossRef]
- Peng, C.; Wu, M.; Xie, X.P.; Wang, Y.L. Event-triggered predictive control for networked nonlinear systems with imperfect premise matching. IEEE Trans. Fuzzy Syst. 2018, 26, 2797–2806. [Google Scholar] [CrossRef]
- Deng, Y.R.; Yin, X.X.; Hu, S.L. Event-triggered predictive control for networked control systems with DoS attacks. Inf. Sci. 2021, 542, 71–91. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; Yang, H.L.; Zhong, S.M. An improved fuzzy event-triggered asynchronous dissipative control to T-S FMJSs with nonperiodic sampled data. IEEE Trans. Fuzzy Syst. 2020, 29, 2926–2937. [Google Scholar] [CrossRef]
- Ma, H.; Li, H.Y.; Liang, H.J.; Dong, G.W. Adaptive fuzzy event-triggered control for stochastic nonlinear systems with full state constraints and actuator faults. IEEE Trans. Fuzzy Syst. 2019, 27, 1063–1076. [Google Scholar] [CrossRef]
- Aslam, M.S.; Chen, Z.R. Observer-based dissipative output feedback control for network T-S fuzzy systems under time delays with mismatch premise. Nonlinear Dyn. 2019, 95, 2923–2941. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, K.P.; Dian, S.Y. Security control of interval type-2 fuzzy system with two-terminal deception attacks under premise mismatch. Nonlinear Dyn. 2020, 102, 431–453. [Google Scholar] [CrossRef]
- Li, Z.C.; Yan, H.C.; Zhang, H.; Lam, H.K.; Wang, M. Aperiodic sampled-data-based control for interval type-2 fuzzy systems via refined adaptive event-triggered communication scheme. IEEE Trans. Fuzzy Syst. 2021, 29, 310–321. [Google Scholar] [CrossRef]
- Chen, M.; Lam, H.K.; Xiao, B.; Xuan, C.B. Membership-function-dependent control design and stability analysis of interval type-2 sampled-data fuzzy-model-based control system. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Jiang, B.P.; Karimi, H.R.; Kao, Y.G.; Gao, C.C. Takagi-Sugeno model based event-triggered fuzzy sliding-mode control of networked control systems with semi-markovian switchings. IEEE Trans. Fuzzy Syst. 2020, 28, 673–683. [Google Scholar] [CrossRef]
- Peng, C.; Yue, D.; Fei, M. Relaxed stability and stabilization conditions of networked fuzzy control systems subject to asynchronous grades of membership. IEEE Trans. Fuzzy Syst. 2014, 22, 1101–1112. [Google Scholar] [CrossRef]
- Cao, Y.Y.; Lin, Z.L. Robust stability analysis and fuzzy-scheduling control for nonlinear systems subject to actuator saturation. IEEE Trans. Fuzzy Syst. 2003, 11, 57–67. [Google Scholar]
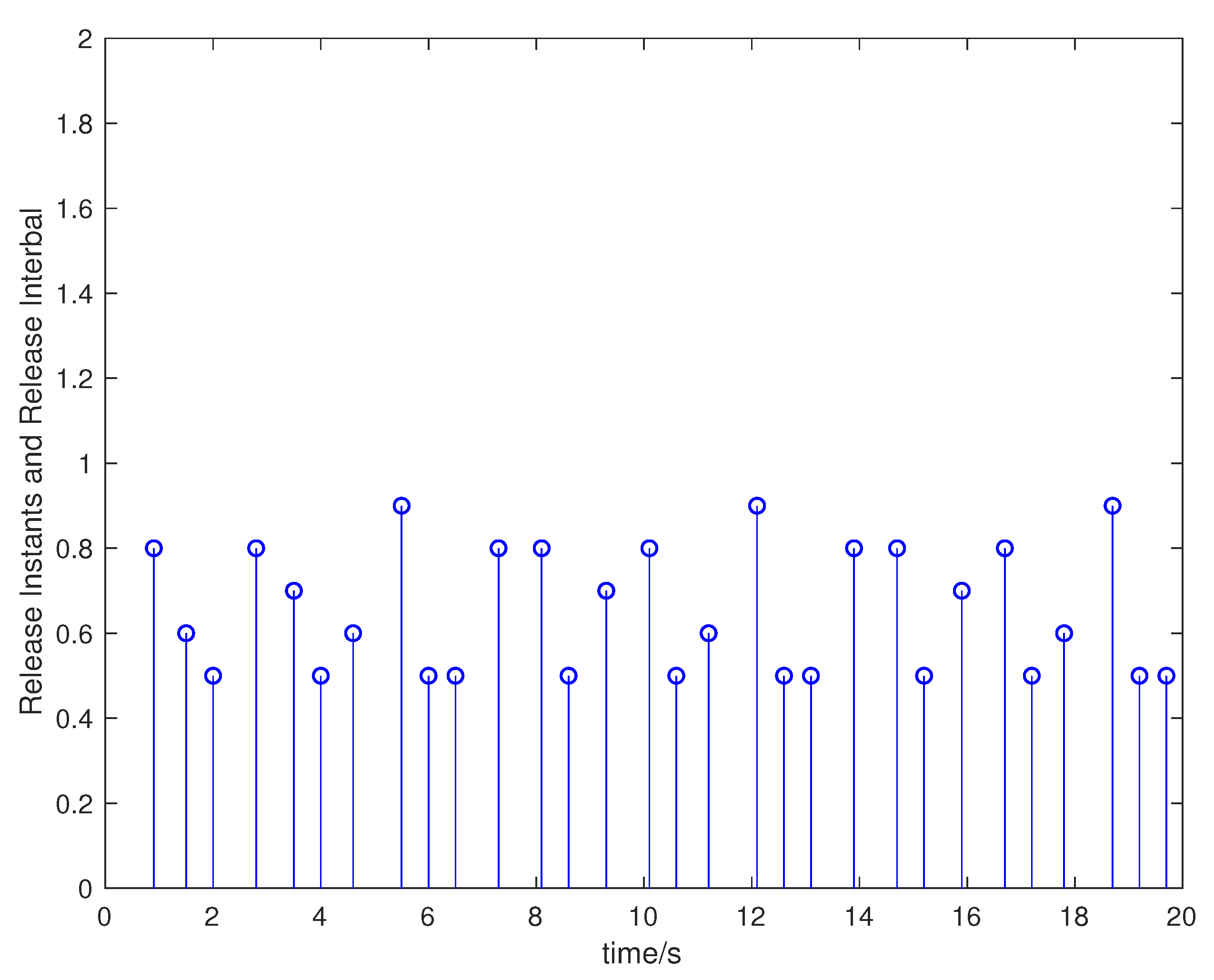

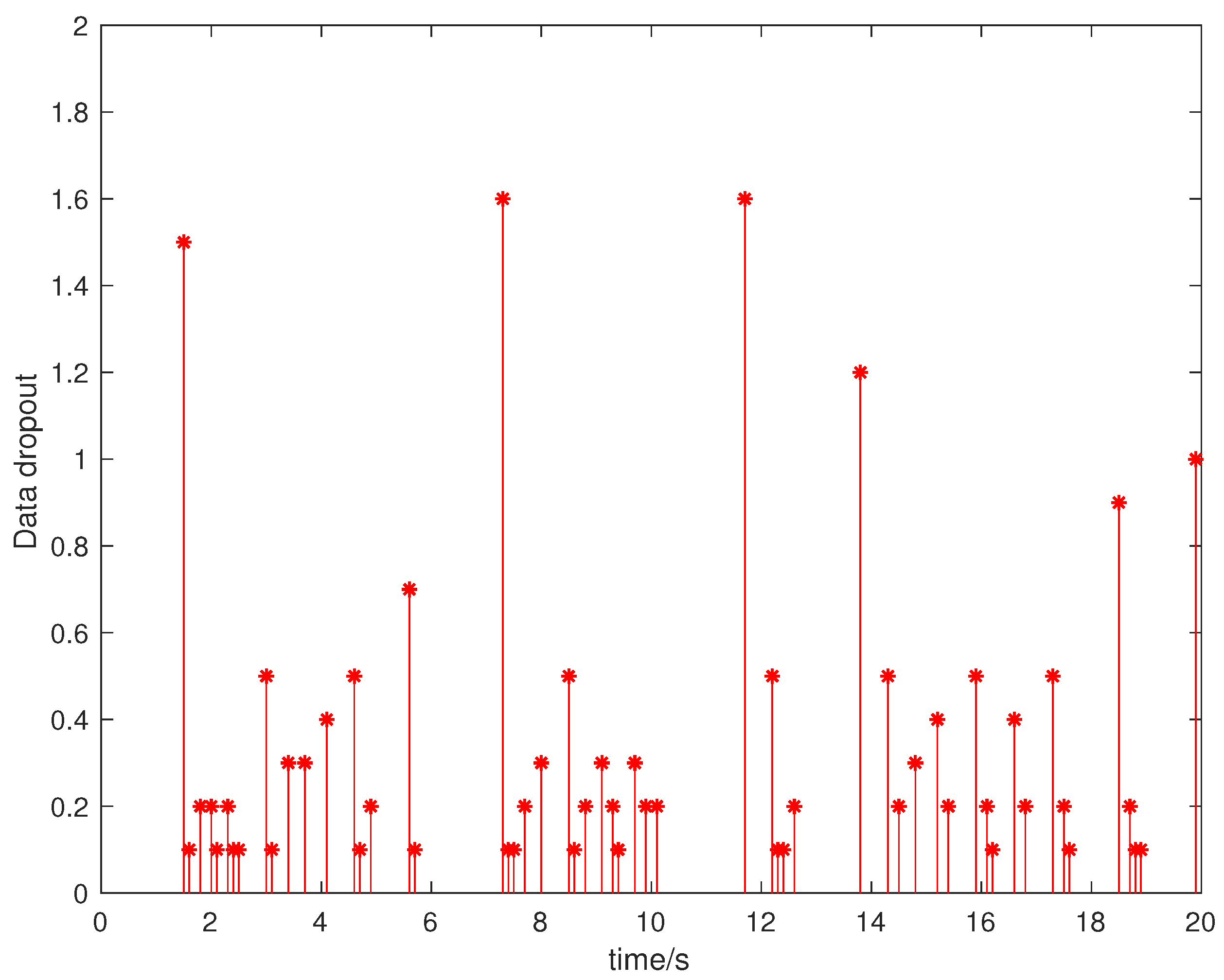
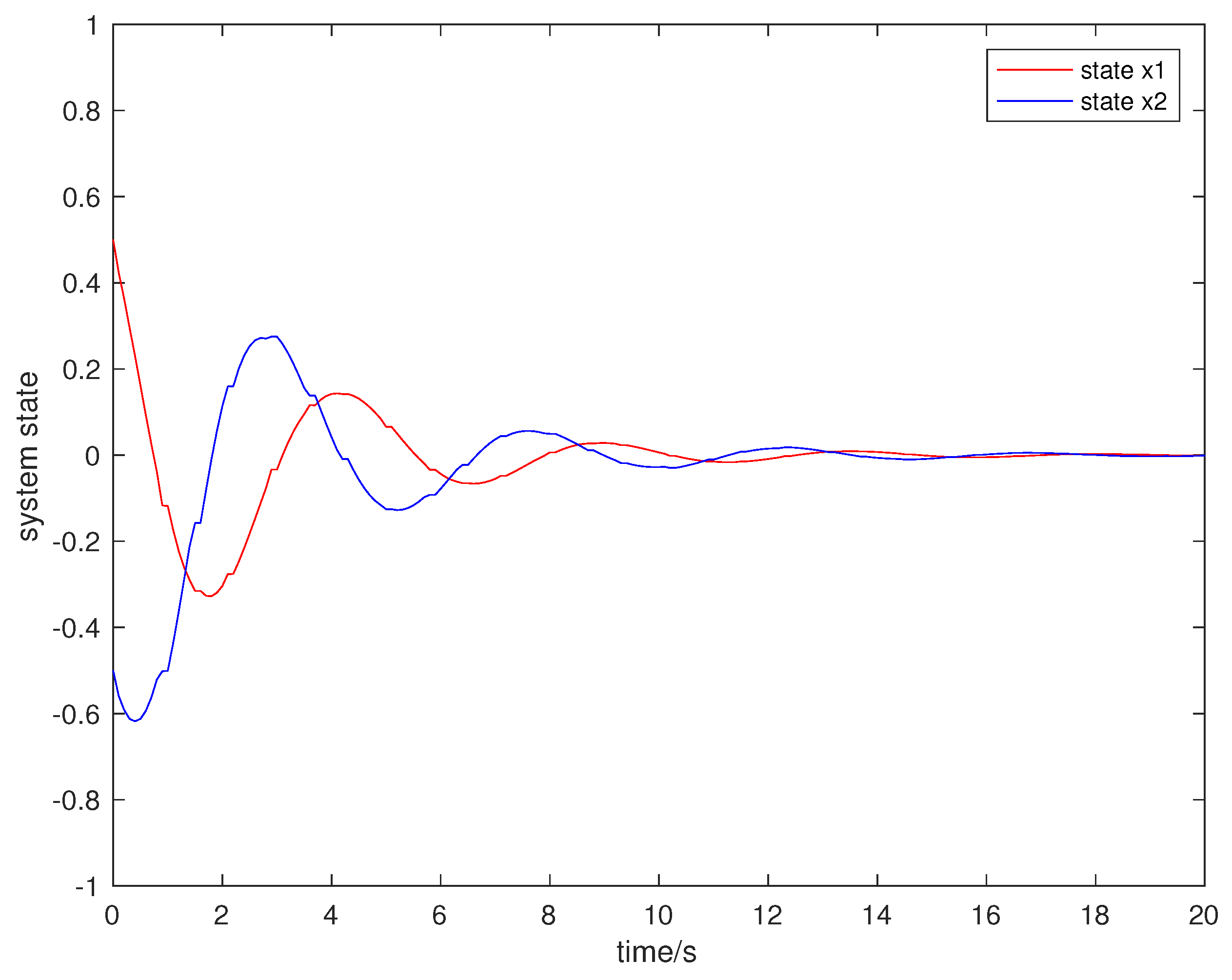
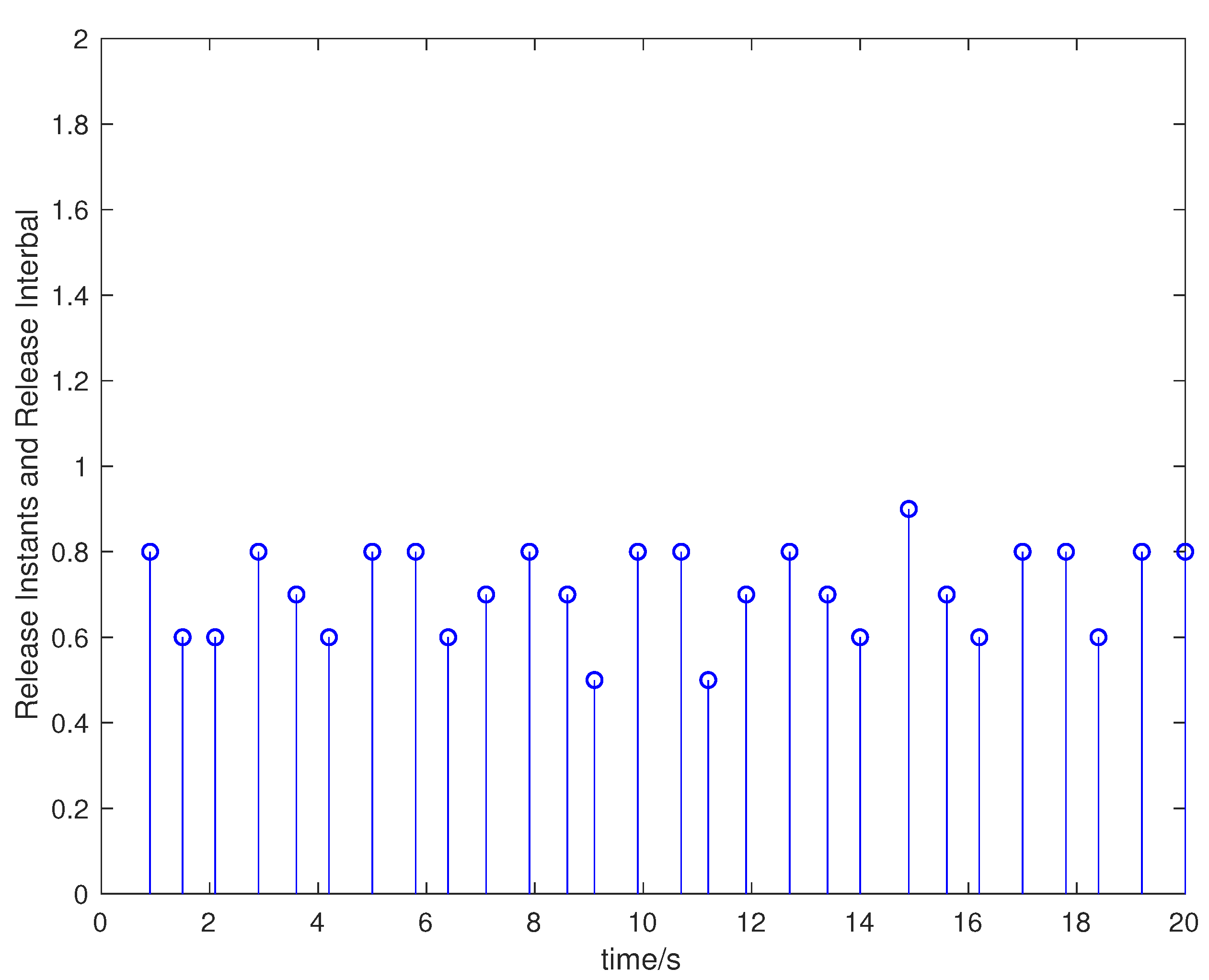
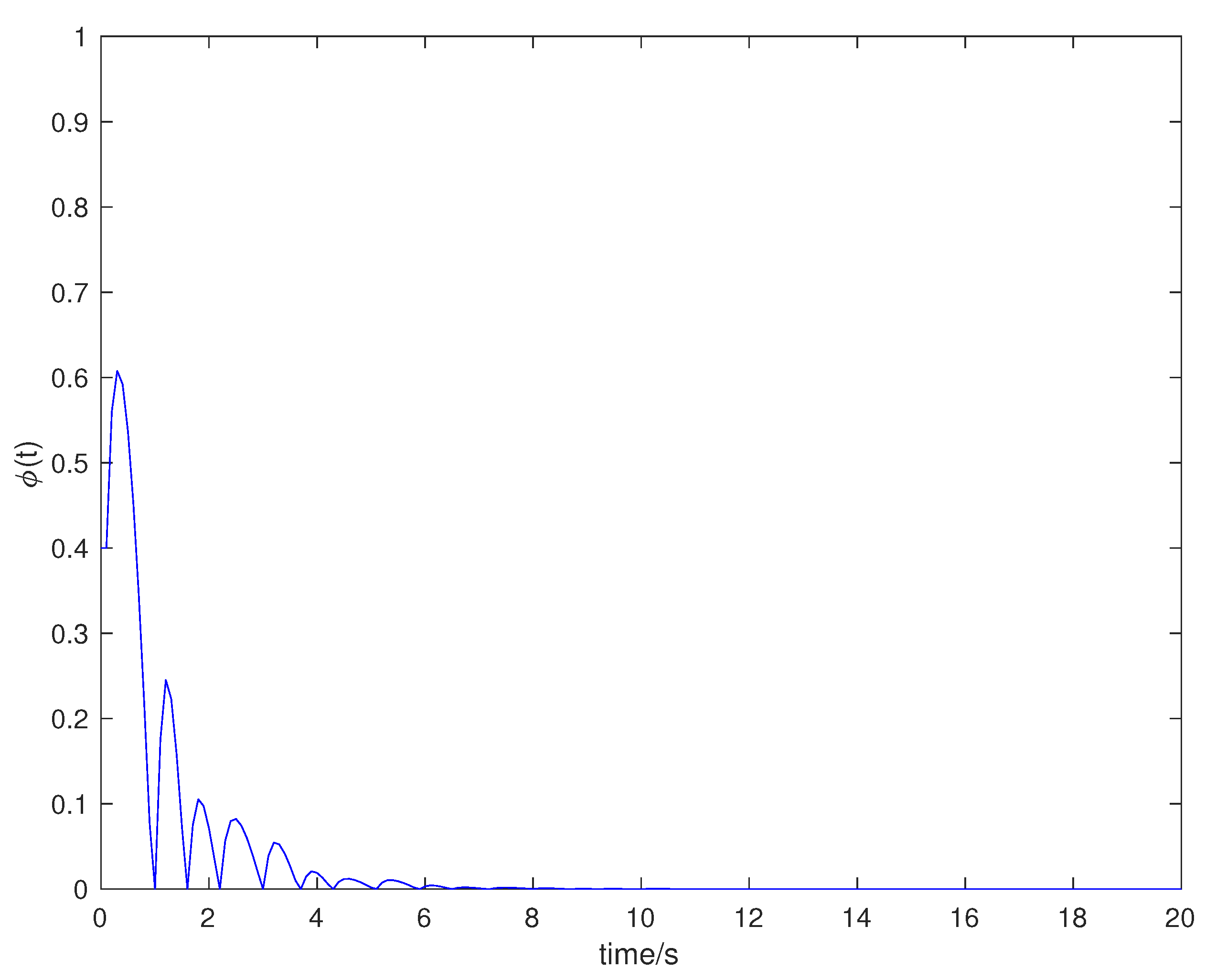
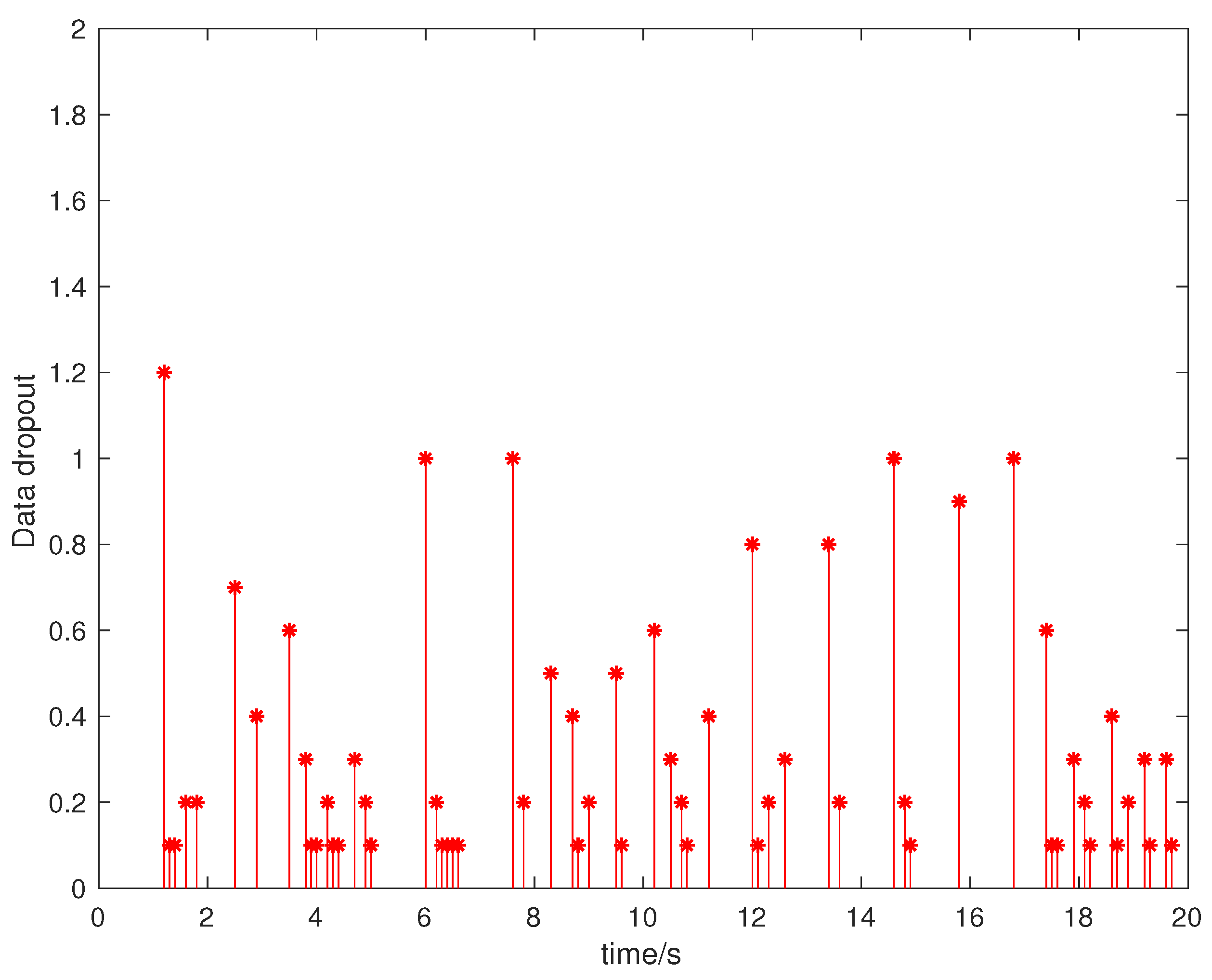
| ETM | Frequency | The Sampling Period |
|---|---|---|
| dynamic ETM in case 1 | 27 | 200 |
| static ETM in case 1 | 52 | 200 |
| dynamic ETM in case 2 | 30 | 200 |
| static ETM in case 2 | 56 | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Cao, J.; Chen, J.; Hu, A.; Zhang, J.; Hu, M. Dynamic Event-Triggered Predictive Control for Interval Type-2 Fuzzy Systems with Imperfect Premise Matching. Entropy 2021, 23, 1452. https://doi.org/10.3390/e23111452
Zhou J, Cao J, Chen J, Hu A, Zhang J, Hu M. Dynamic Event-Triggered Predictive Control for Interval Type-2 Fuzzy Systems with Imperfect Premise Matching. Entropy. 2021; 23(11):1452. https://doi.org/10.3390/e23111452
Chicago/Turabian StyleZhou, Jingfeng, Jianming Cao, Jing Chen, Aihua Hu, Jingxiang Zhang, and Manfeng Hu. 2021. "Dynamic Event-Triggered Predictive Control for Interval Type-2 Fuzzy Systems with Imperfect Premise Matching" Entropy 23, no. 11: 1452. https://doi.org/10.3390/e23111452
APA StyleZhou, J., Cao, J., Chen, J., Hu, A., Zhang, J., & Hu, M. (2021). Dynamic Event-Triggered Predictive Control for Interval Type-2 Fuzzy Systems with Imperfect Premise Matching. Entropy, 23(11), 1452. https://doi.org/10.3390/e23111452






