Trading Imbalance in Chinese Stock Market—A High-Frequency View
Abstract
1. Introduction
2. Methods and Materials
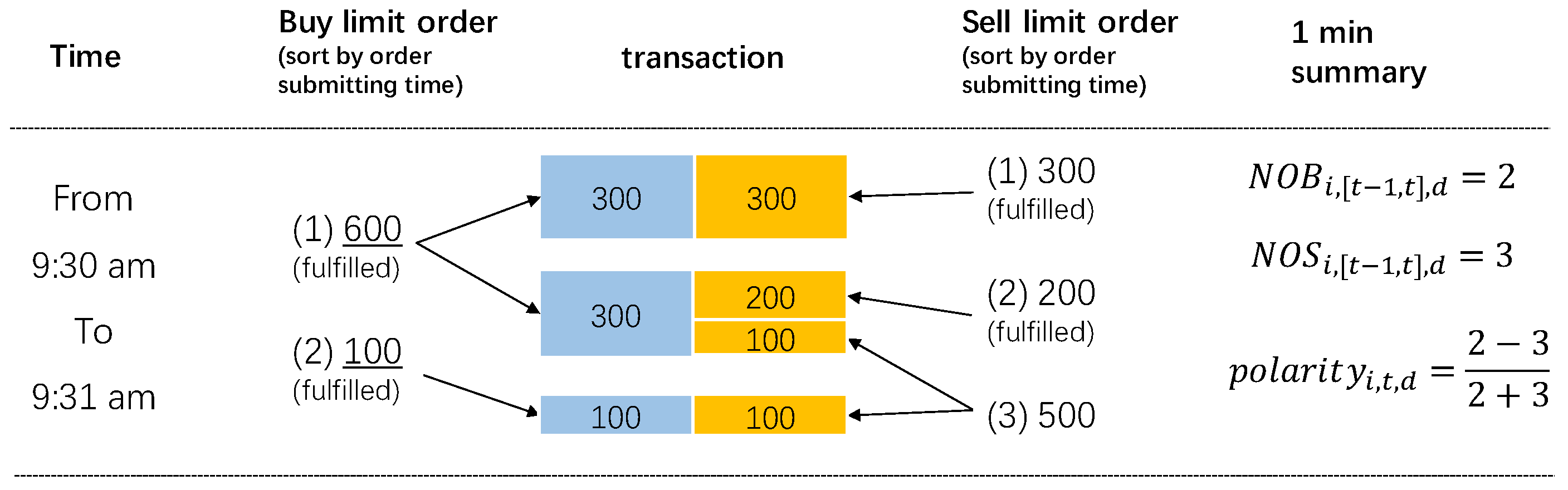
2.1. Trading Polarity
2.2. Data
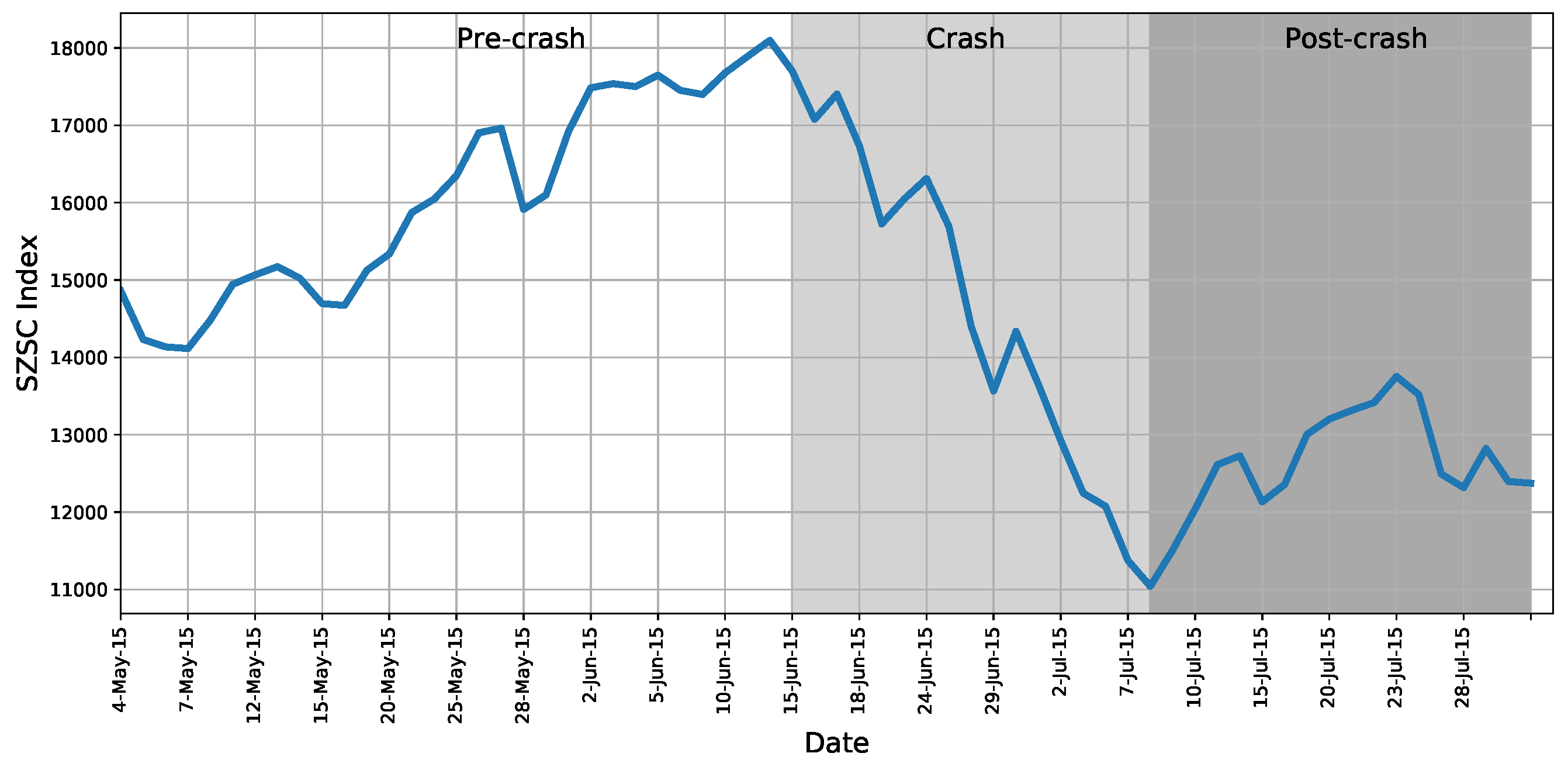
2.2.1. Sample Period: 2015 Stock Market Crash of China
2.2.2. Transaction Records
2.2.3. Stock Prices
3. Results
3.1. Summary Statistics of the Trading Polarity
3.1.1. Market-Level Polarity
3.1.2. Stock-Level Polarity
3.2. Polarity and Return
3.2.1. Market Polarity and Return
3.2.2. Stock Polarity and Return
3.3. The Flipping of Polarity and Stock Returns
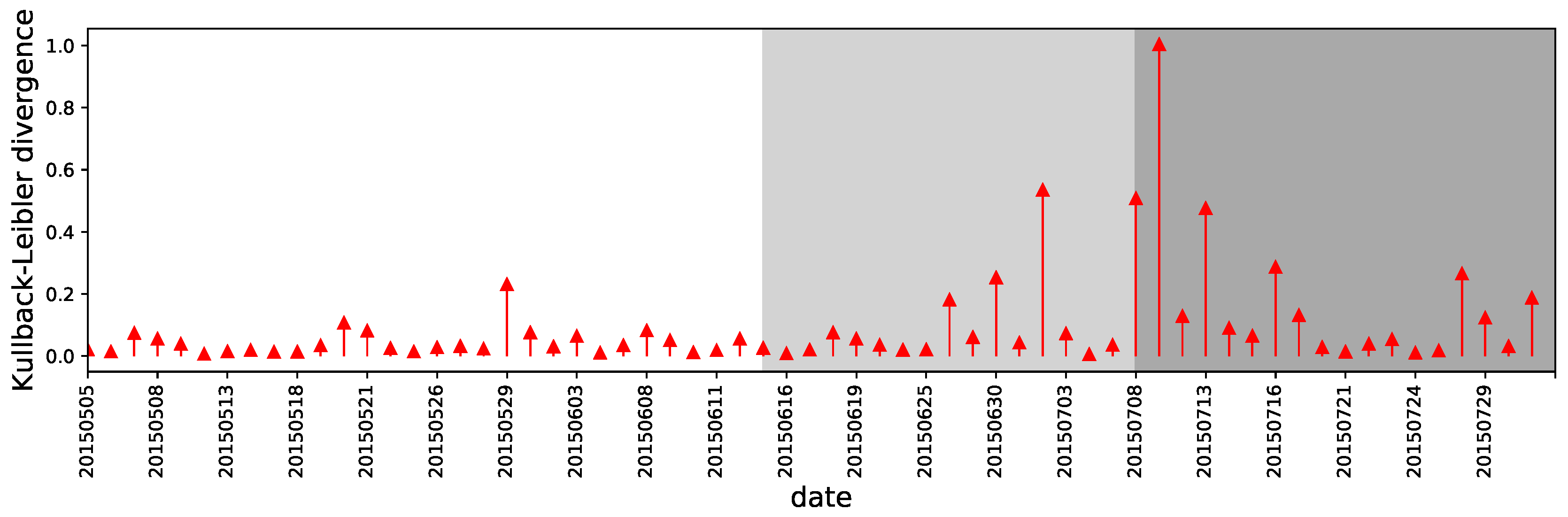
3.4. Using Polarity to Signal the Market Changes
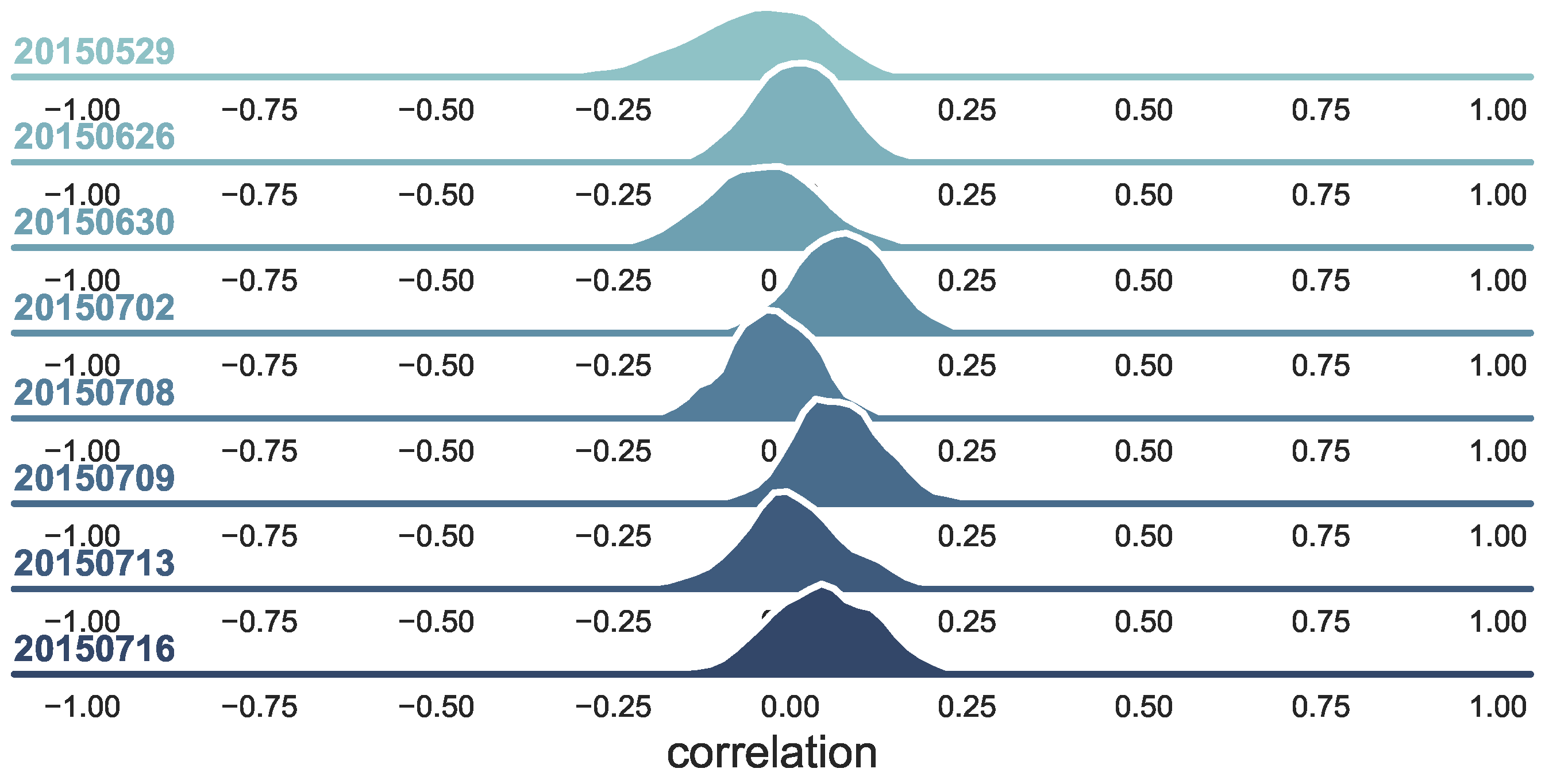
3.4.1. The Changing of the Polarity-Return Correlation
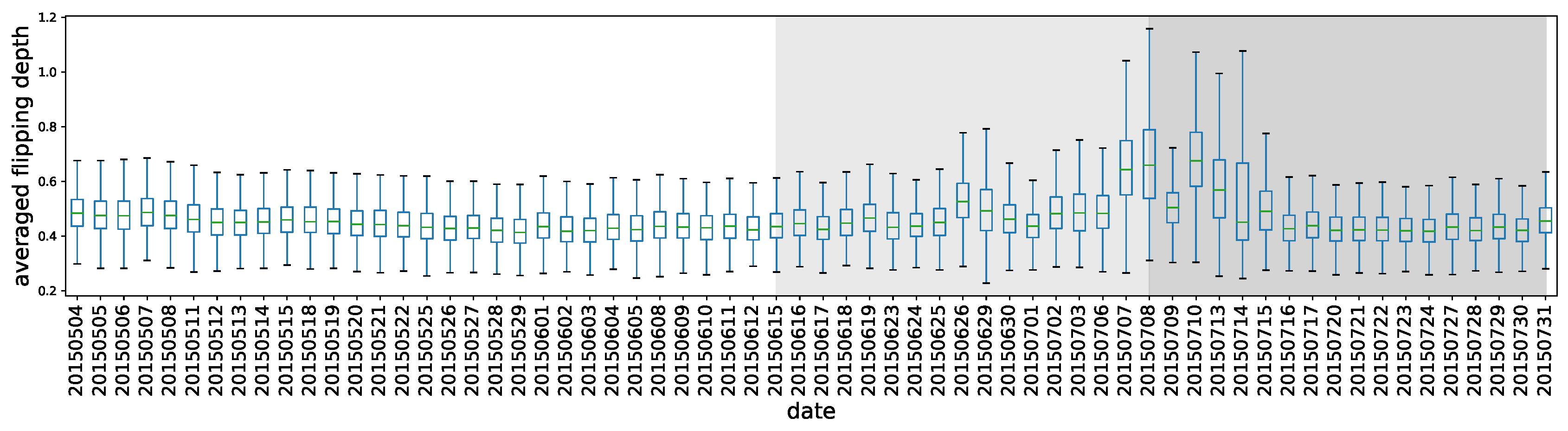
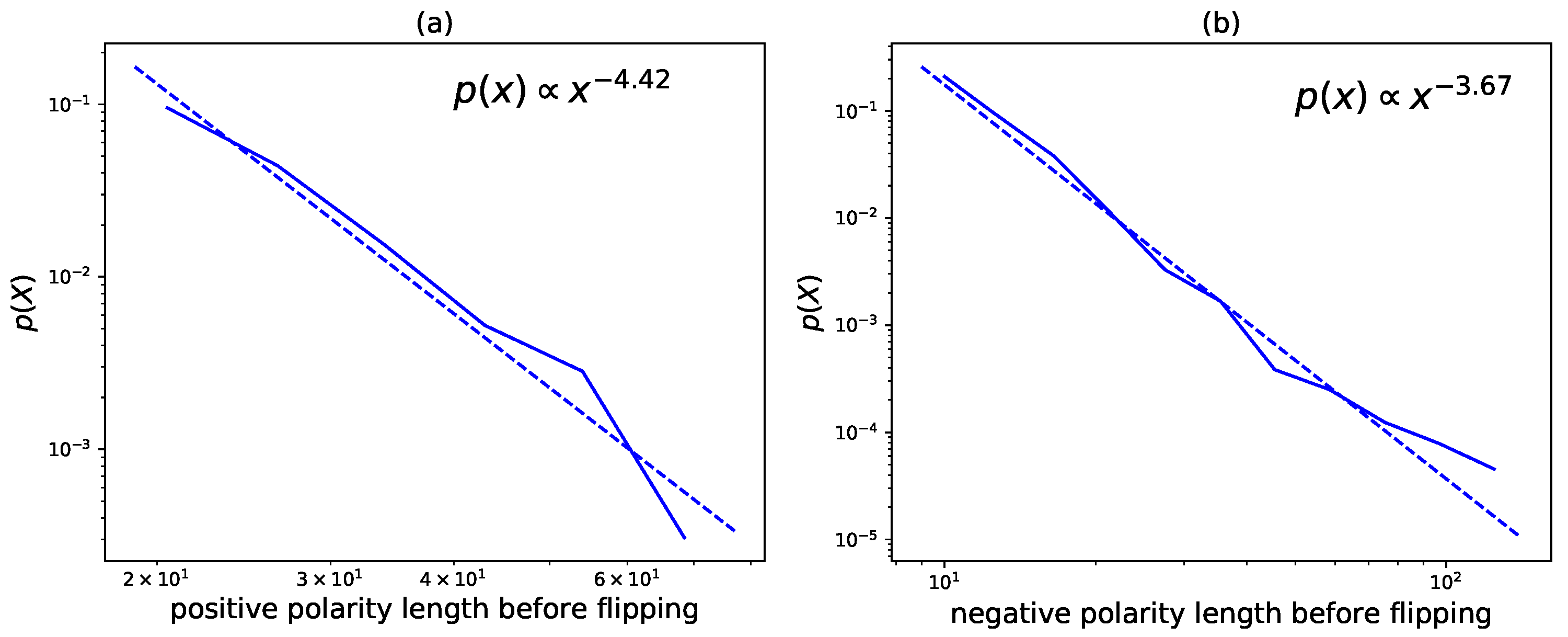
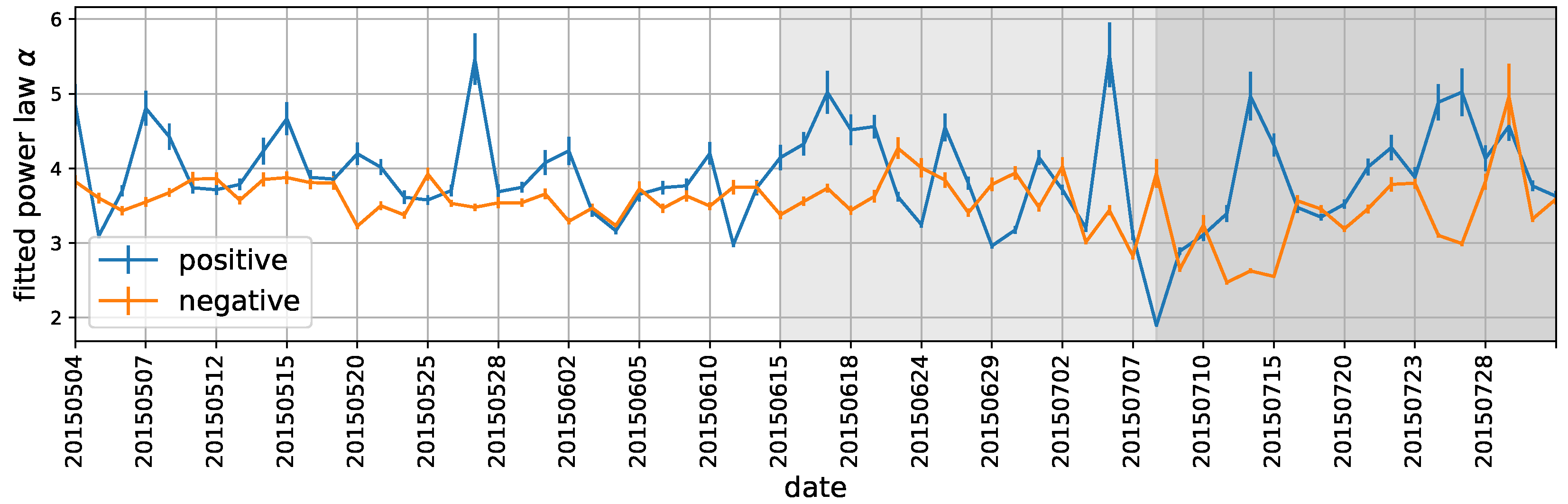
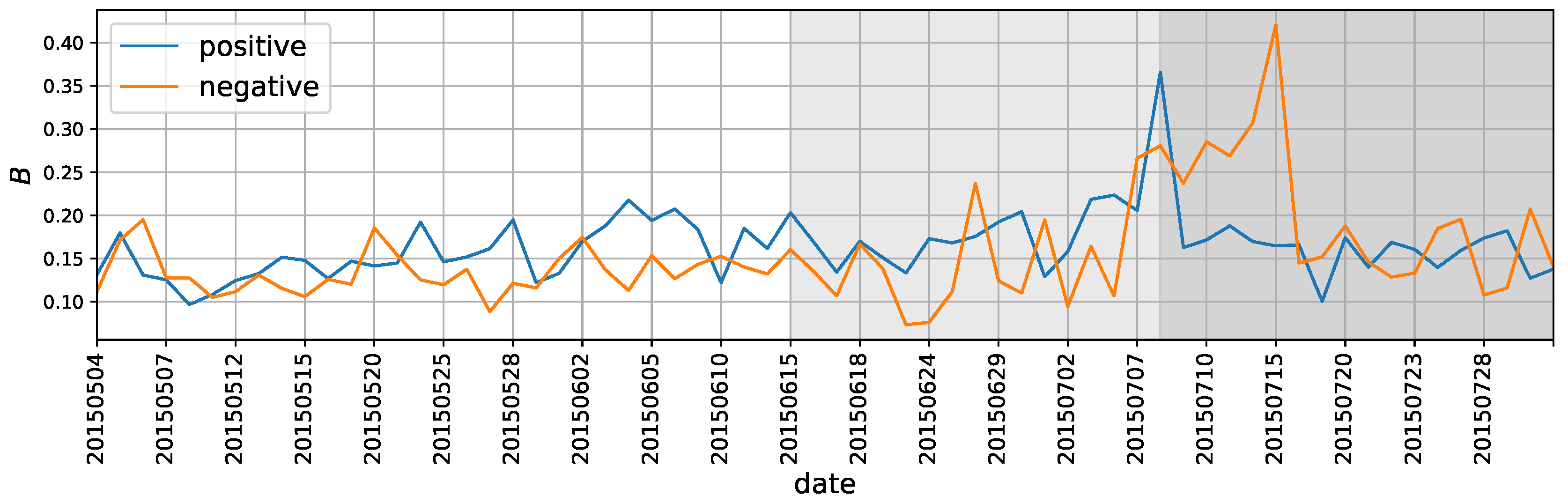
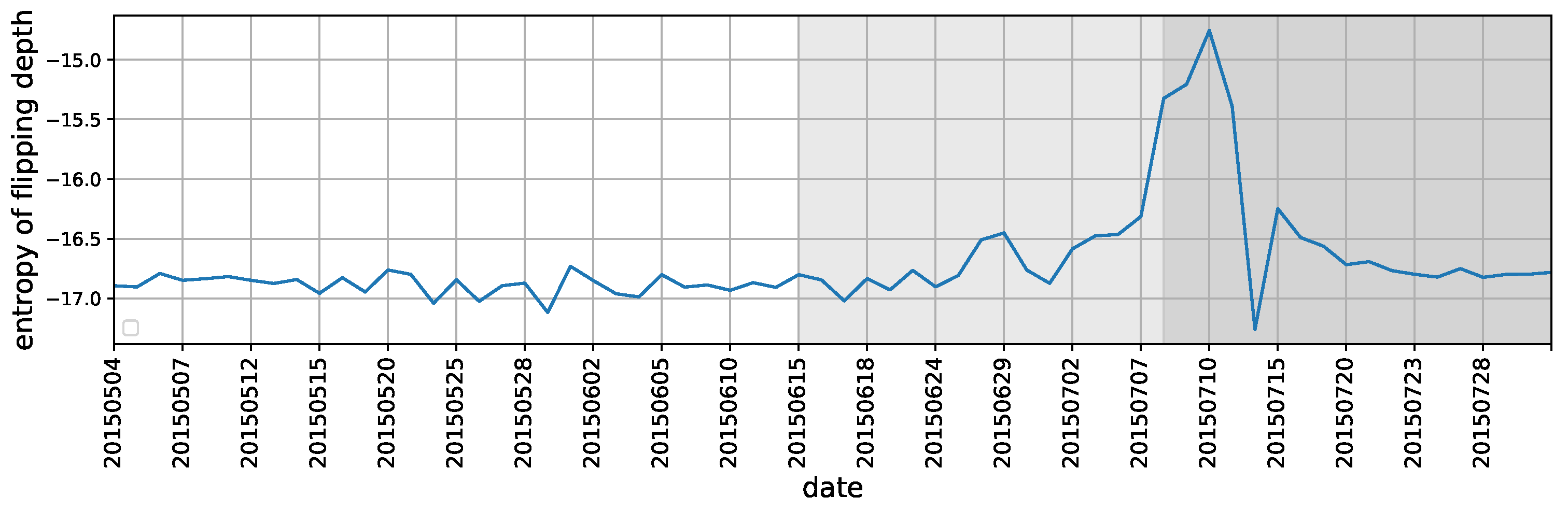
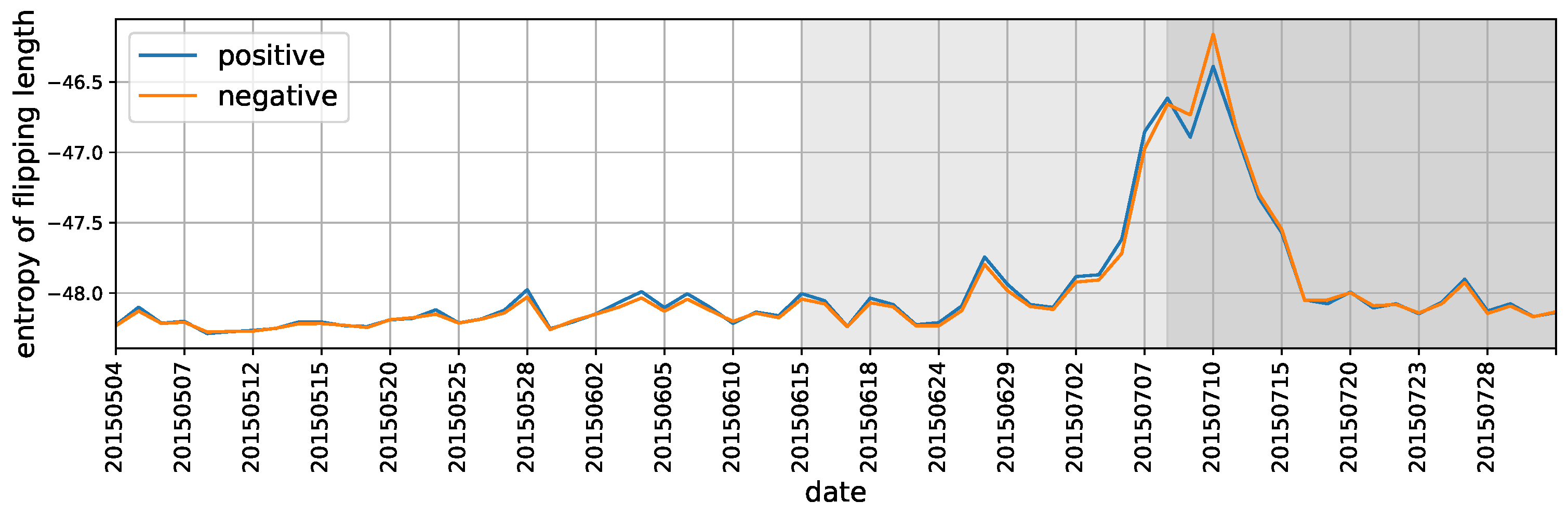
3.4.2. How Does the Flipping Polarity Relates to Market Changes?
- Flipping Depth
- Length before Flipping
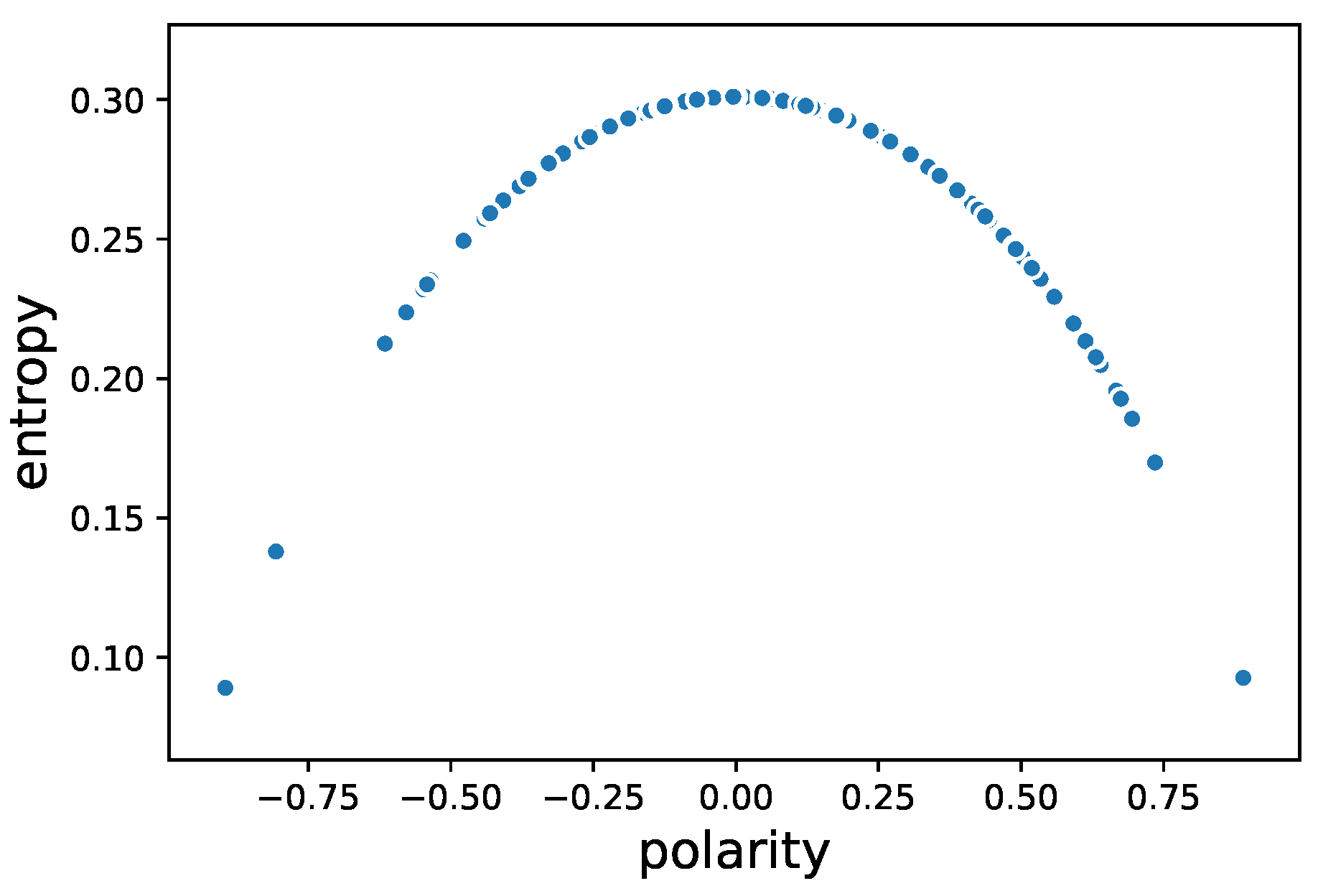
- Using entropy to characterizing the state of market
3.4.3. Market Polarity and Emotions
4. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, Z.; Xu, K.; Zhao, J. Tales of emotion and stock in China: Volatility, causality and prediction. World Wide Web 2017. [Google Scholar] [CrossRef]
- Shiller, R.J. Investor Behavior in the October 1987 Stock Market Crash: Survey Evidence. Working Paper 2446, National Bureau of Economic Research. 1987. Available online: https://www.nber.org/papers/w2446 (accessed on 21 January 2017).
- Lu, S.; Zhao, J.; Wang, H.; Ren, R. Herding boosts too-connected-to-fail risk in stock market of China. Phys. Stat. Mech. Its Appl. 2018, 505, 945–964. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, G.; Wang, W.; Chen, Y.; Huang, J.; Ohashi, H.; Stanley, H.E. Herd behavior in a complex adaptive system. Proc. Natl. Acad. Sci. USA 2011, 108, 15058–15063. [Google Scholar] [CrossRef] [PubMed]
- Delpini, D.; Battiston, S.; Caldarelli, G.; Riccaboni, M. Systemic risk from investment similarities. PLoS ONE 2019, 14, e0217141. [Google Scholar] [CrossRef]
- Lu, S.; Zhao, J.; Wang, H. The Emergence of Critical Stocks in Market Crash. Front. Phys. 2020, 8, 49. [Google Scholar] [CrossRef]
- Lakonishok, J.; Shleifer, A.; Vishny, R.W. The Impact of Institutional Trading on Stock Prices. J. Financ. Econ. 1992, 32, 23–43. [Google Scholar] [CrossRef]
- Wermers, R. Mutual Fund Herding and the Impact on Stock Prices. J. Financ. 1999, 54, 581–622. [Google Scholar] [CrossRef]
- Sias, R.W. Institutional Herding. Rev. Financ. Stud. 2004, 17, 165–206. [Google Scholar] [CrossRef]
- Grinblatt, M.; Keloharju, M.; Linnainmaa, J.T. IQ, trading behavior, and performance. J. Financ. Econ. 2012, 104, 339–362. [Google Scholar] [CrossRef]
- Kaniel, R.; Saar, G.; Titman, S. Individual Investor Trading and Stock Returns. J. Financ. 2008, 63, 273–310. [Google Scholar] [CrossRef]
- Kaniel, R.; Liu, S.; Saar, G.; Titman, S. Individual Investor Trading and Return Patterns around Earnings Announcements. J. Financ. 2012, 67, 639–680. [Google Scholar] [CrossRef]
- Chordia, T.; Subrahmanyam, A. Order imbalance and individual stock returns: Theory and evidence. J. Financ. Econ. 2004, 72, 485–518. [Google Scholar] [CrossRef]
- Preis, T.; Schneider, J.J.; Stanley, H.E. Switching processes in financial markets. Proc. Natl. Acad. Sci. USA 2011, 108, 7674–7678. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.J.; Li, M.X.; Xu, H.C.; Chen, W.; Zhou, W.X.; Stanley, H.E. Quantifying immediate price impact of trades based on the k-shell decomposition of stock trading networks. EPL Europhys. Lett. 2016, 116, 28006. [Google Scholar] [CrossRef]
- Bhattacharya, U.; Kuo, W.Y.; Lin, T.C.; Zhao, J. Do superstitious traders lose money? Manag. Sci. 2017, 64, 3772–3791. [Google Scholar] [CrossRef]
- Mantegna, R.N.; Stanley, H.E. Introduction to Econophysics: Correlations and Complexity in Finance; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Fan, Y.; Li, M.; Chen, J.; Gao, L.; Di, Z.; Wu, J. Network of econophysicists: A weighted network to investigate the development of econophysics. Int. J. Mod. Phys. 2004, 18, 2505–2511. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Yuen, A.; Perakakis, P. Impact of stock market structure on intertrade time and price dynamics. PLoS ONE 2014, 9, e92885. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, J.; Chen, Q.; Wang, Y. Socioeconomic implications of donation distributions. Phys. Stat. Mech. Its Appl. 2011, 390, 4325–4331. [Google Scholar] [CrossRef]
- Huang, J. Experimental econophysics: Complexity, self-organization, and emergent properties. Phys. Rep. 2015, 564, 1–55. [Google Scholar] [CrossRef]
- Zhang, T.; Jiang, G.J.; Zhou, W.X. Order imbalance and stock returns: New evidence from the Chinese stock market. Account. Financ. 2020. [Google Scholar] [CrossRef]
- Ren, F.; Zhou, W.X. Dynamic evolution of cross-correlations in the Chinese stock market. PloS ONE 2014, 9, e97711. [Google Scholar] [CrossRef] [PubMed]
- France24. Almost Half of China’s Firms Halt Trading as Market Dives. Available online: http://www.france24.com/en/20150708-almost-half-chinese-firms-suspend-trading-market-dives (accessed on 14 August 2020).
- Wood, R.A.; McInish, T.H.; Ord, J.K. An investigation of transactions data for NYSE stocks. J. Financ. 1985, 40, 723–739. [Google Scholar] [CrossRef]
- Dufour, A.; Engle, R.F. Time and the price impact of a trade. J. Financ. 2000, 55, 2467–2498. [Google Scholar] [CrossRef]
- Huang, R.D.; Masulis, R.W. Trading activity and stock price volatility: Evidence from the London Stock Exchange. J. Empir. Financ. 2003, 10, 249–269. [Google Scholar] [CrossRef]
- Lillo, F.; Farmer, J.D.; Mantegna, R.N. Econophysics: Master curve for price-impact function. Nature 2003, 421, 129–130. [Google Scholar] [CrossRef]
- Grinblatt, M.; Keloharju, M. How distance, language, and culture influence stockholdings and trades. J. Financ. 2001, 56, 1053–1073. [Google Scholar] [CrossRef]
- Grinblatt, M.; Keloharju, M. Sensation seeking, overconfidence, and trading activity. J. Financ. 2009, 64, 549–578. [Google Scholar] [CrossRef]
- Mizuno, T.; Nakano, T.; Takayasu, M.; Takayasu, H. Traders’ strategy with price feedbacks in financial market. Phys. Stat. Mech. Its Appl. 2004, 344, 330–334. [Google Scholar] [CrossRef][Green Version]
- Schmidt, A.F.; Finan, C. Linear regression and the normality assumption. J. Clin. Epidemiol. 2018, 98, 146–151. [Google Scholar] [CrossRef]
- Hayashi, F. Econometrics; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Ordonez, G. The asymmetric effects of financial frictions. J. Political Econ. 2013, 121, 844–895. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; Huang, J. Heterogeneous preferences, decision-making capacity, and phase transitions in a complex adaptive system. Proc. Natl. Acad. Sci. USA 2009, 106, 8423–8428. [Google Scholar] [CrossRef] [PubMed]
- Alstott, J.; Bullmore, E.; Plenz, D. Powerlaw: A Python package for analysis of heavy-tailed distributions. PLoS ONE 2014, 9, e85777. [Google Scholar] [CrossRef] [PubMed]
- Barabasi, A.L. The origin of bursts and heavy tails in human dynamics. Nature 2005, 435, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.I.; Barabási, A.L. Burstiness and memory in complex systems. EPL Europhys. Lett. 2008, 81, 48002. [Google Scholar] [CrossRef]
- Kraskov, A.; Stogbauer, H.; Grassberger, P. Estimating Mutual Information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Z.; Zhao, J.; Su, C. Weibo sentiments and stock return: A time-frequency view. PLoS ONE 2017, 12, e0180723. [Google Scholar] [CrossRef]
- Bordino, I.; Battiston, S.; Caldarelli, G.; Cristelli, M.; Ukkonen, A.; Weber, I. Web search queries can predict stock market volumes. PLoS ONE 2012, 7, e40014. [Google Scholar] [CrossRef]

| Panel A: Descriptive Statistics | ||||||||
| Mean | Std.dev. | Skewness | ||||||
| 4 May 2015–31 Jul 2015 | 0.07 | 0.11 | − 0.17 | |||||
| pre-crash | 0.07 | 0.06 | 0.61 | |||||
| crash | 0.14 | 0.10 | − 0.11 | |||||
| post-crash | 0.02 | 0.13 | − 0.14 | |||||
| Panel B: 1 min Autocorrelations | ||||||||
| lag 1 | lag 2 | lag 3 | lag 4 | lag 5 | lag 10 | lag 15 | lag 30 | |
| 4 May 2015–31 Jul 2015 | 0.92 | 0.87 | 0.82 | 0.77 | 0.72 | 0.55 | 0.45 | 0.21 |
| pre-crash | 0.92 | 0.86 | 0.80 | 0.74 | 0.69 | 0.49 | 0.39 | 0.12 |
| crash | 0.93 | 0.89 | 0.84 | 0.80 | 0.77 | 0.64 | 0.56 | 0.34 |
| post-crash | 0.93 | 0.88 | 0.82 | 0.78 | 0.75 | 0.60 | 0.48 | 0.26 |
| Panel A: Descriptive Statistics | ||||||||
| Mean | Std.dev | Skewness | Cap | Mean | Std.dev | Skewness | ||
| 4 May–31 Jul | 0.08 | 0.34 | −0.17 | small | 0.07 | 0.33 | −0.13 | |
| mid | 0.08 | 0.34 | −0.18 | |||||
| large | 0.08 | 0.34 | −0.25 | |||||
| pre-crash | 0.07 | 0.33 | −0.22 | small | 0.06 | 0.33 | −0.16 | |
| mid | 0.07 | 0.33 | −0.23 | |||||
| large | 0.08 | 0.32 | −0.31 | |||||
| crash | 0.14 | 0.34 | −0.11 | small | 0.12 | 0.34 | −0.11 | |
| mid | 0.14 | 0.34 | −0.11 | |||||
| large | 0.14 | 0.34 | −0.11 | |||||
| post-crash | 0.04 | 0.35 | −0.18 | small | 0.05 | 0.34 | −0.14 | |
| mid | 0.04 | 0.35 | −0.18 | |||||
| large | 0.02 | 0.36 | −0.25 | |||||
| Panel B: 1 min autocorrelations | ||||||||
| lag 1 | lag 2 | lag 3 | lag 4 | lag 5 | lag 10 | lag 15 | lag 30 | |
| May–Jul | 0.46 | 0.31 | 0.25 | 0.21 | 0.20 | 0.15 | 0.10 | 0.03 |
| pre-crash | 0.46 | 0.31 | 0.25 | 0.21 | 0.19 | 0.15 | 0.09 | 0.03 |
| crash | 0.47 | 0.29 | 0.22 | 0.20 | 0.20 | 0.12 | 0.10 | 0.01 |
| post-crash | 0.45 | 0.32 | 0.27 | 0.22 | 0.21 | 0.15 | 0.11 | 0.04 |
| Panel A: 4 May to 31 Jul. | ||||
| lag k | average coefficient | percent positive | percent positive and significant | percent negative and significant |
| 0 | −0.0061 | 14.06% | 0.00% | 43.75% |
| 1 | 0.0025 | 73.44% | 23.44% | 1.56% |
| 2 | 0.0017 | 67.19% | 21.88% | 6.25% |
| 3 | 0.0018 | 67.19% | 12.50% | 1.56% |
| 4 | 0.0009 | 65.63% | 7.81% | 4.69% |
| 5 | −0.0007 | 45.31% | 3.13% | 12.50% |
| Panel B: 4 May to 14 Jun (pre-crash). | ||||
| lag k | average coefficient | percent positive | percent positive and significant | percent negative and significant |
| 0 | −0.0068 | 13.33% | 0.00% | 53.33% |
| 1 | 0.0034 | 86.67% | 40.00% | 0.00% |
| 2 | 0.0031 | 73.33% | 30.00% | 0.00% |
| 3 | 0.0019 | 73.33% | 10.00% | 0.00% |
| 4 | 0.0005 | 53.33% | 3.33% | 3.33% |
| 5 | −0.0012 | 46.67% | 3.33% | 16.67% |
| Panel C: 15 Jun to 7 Jul (crash). | ||||
| lag k | average coefficient | percent positive | percent positive and significant | percent negative and significant |
| 0 | −0.0084 | 13.33% | 0.00% | 33.33% |
| 1 | 0.0039 | 80.00% | 13.33% | 6.67% |
| 2 | 0.0013 | 73.33% | 13.33% | 6.67% |
| 3 | 0.0018 | 53.33% | 13.33% | 0.00% |
| 4 | 0.0019 | 73.33% | 6.67% | 6.67% |
| 5 | −0.0014 | 33.33% | 0.00% | 20.00% |
| Panel D: 8 Jul to 31 Jul (post-crash). | ||||
| lag k | average coefficient | percent positive | percent positive and significant | percent negative and significant |
| 0 | −0.0029 | 16.67% | 0.00% | 38.89% |
| 1 | −0.0002 | 44.44% | 5.56% | 0.00% |
| 2 | −0.0006 | 50.00% | 11.11% | 16.67% |
| 3 | 0.0017 | 72.22% | 16.67% | 5.56% |
| 4 | 0.0011 | 83.33% | 16.67% | 5.56% |
| 5 | 0.0008 | 55.56% | 5.56% | 0.00% |
| Panel A: 4 May to 31 Jul | ||||
| lag k | average coefficient | percent positive | percent positive and significant | percent negative and significant |
| 0 | −0.0009 | 23.13% | 1.55% | 31.45% |
| 1 | 0.0008 | 77.22% | 16.27% | 0.54% |
| 2 | 0.0006 | 75.40% | 13.70% | 0.54% |
| 3 | 0.0003 | 64.62% | 7.70% | 1.33% |
| 4 | 0.0000 | 54.08% | 3.69% | 2.31% |
| 5 | 0.0000 | 50.36% | 2.69% | 2.76% |
| Panel B: 4 May to 14 Jun (pre-crash). | ||||
| lag k | average coefficient | percent positive | percent positive and significant | percent negative and significant |
| 0 | −0.0013 | 10.92% | 0.32% | 46.13% |
| 1 | 0.0004 | 70.16% | 11.19% | 0.87% |
| 2 | 0.0006 | 80.01% | 16.83% | 0.34% |
| 3 | 0.0004 | 74.34% | 11.43% | 0.49% |
| 4 | 0.0002 | 62.16% | 5.34% | 1.17% |
| 5 | 0.0001 | 54.57% | 3.33% | 2.01% |
| Panel C: 15 Jun to 7 Jul (crash). | ||||
| lag k | average coefficient | percent positive | percent positive and significant | percent negative and significant |
| 0 | −0.0007 | 34.23% | 2.43% | 18.71% |
| 1 | 0.0012 | 82.60% | 18.34% | 0.23% |
| 2 | 0.0007 | 72.24% | 11.44% | 0.58% |
| 3 | 0.0002 | 57.89% | 4.59% | 1.66% |
| 4 | −0.0001 | 48.54% | 2.19% | 2.88% |
| 5 | −0.0001 | 45.72% | 1.98% | 3.57% |
| Panel D: 8 Jul to 31 Jul (post-crash). | ||||
| lag k | average coefficient | percent positive | percent positive and significant | percent negative and significant |
| 0 | −0.0005 | 38.02% | 3.31% | 13.46% |
| 1 | 0.0013 | 87.20% | 25.33% | 0.13% |
| 2 | 0.0005 | 68.92% | 9.50% | 0.94% |
| 3 | 0.0000 | 50.53% | 2.91% | 2.80% |
| 4 | −0.0002 | 42.34% | 1.65% | 4.19% |
| 5 | −0.0001 | 45.71% | 2.02% | 3.63% |
| Variable | Average Coefficient | Percent Positive | Percent Positive and Significant | Percent Negative and Significant | |
|---|---|---|---|---|---|
| May–Jul | positive length | 0.0010 | 81.0% | 49.2% | 12.7% |
| negative length | −0.0021 | 17.5% | 11.1% | 49.2% | |
| depth | −0.0003 | 19.0% | 3.2% | 65.1% | |
| polarity | −0.202 | 0% | 0% | 100% | |
| pre-crash | positive length | 0.0008 | 73.3% | 43.3% | 13.3% |
| negative length | −0.0029 | 6.7% | 0.0% | 53.3% | |
| depth | −0.0004 | 10% | 3.3% | 70% | |
| polarity | −0.2221 | 0% | 0% | 100% | |
| crash | positive length | 0.0010 | 93.3% | 66.7% | 6.7% |
| negative length | −0.0031 | 26.7% | 20% | 60% | |
| depth | −0.0006 | 13.3% | 0% | 80% | |
| polarity | −0.2118 | 0% | 0% | 100% | |
| post-crash | positive length | 0.0015 | 83.3% | 44.4% | 16.7% |
| negative length | 0.0001 | 27.8% | 22.2% | 33.3% | |
| depth | 0.0000 | 38.9% | 5.6% | 44.4% | |
| polarity | −0.1602 | 0% | 0% | 100% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.; Zhao, J.; Wang, H. Trading Imbalance in Chinese Stock Market—A High-Frequency View. Entropy 2020, 22, 897. https://doi.org/10.3390/e22080897
Lu S, Zhao J, Wang H. Trading Imbalance in Chinese Stock Market—A High-Frequency View. Entropy. 2020; 22(8):897. https://doi.org/10.3390/e22080897
Chicago/Turabian StyleLu, Shan, Jichang Zhao, and Huiwen Wang. 2020. "Trading Imbalance in Chinese Stock Market—A High-Frequency View" Entropy 22, no. 8: 897. https://doi.org/10.3390/e22080897
APA StyleLu, S., Zhao, J., & Wang, H. (2020). Trading Imbalance in Chinese Stock Market—A High-Frequency View. Entropy, 22(8), 897. https://doi.org/10.3390/e22080897





