Gintropy: Gini Index Based Generalization of Entropy
Abstract
:1. Introduction
1.1. Motivation
1.2. Basics
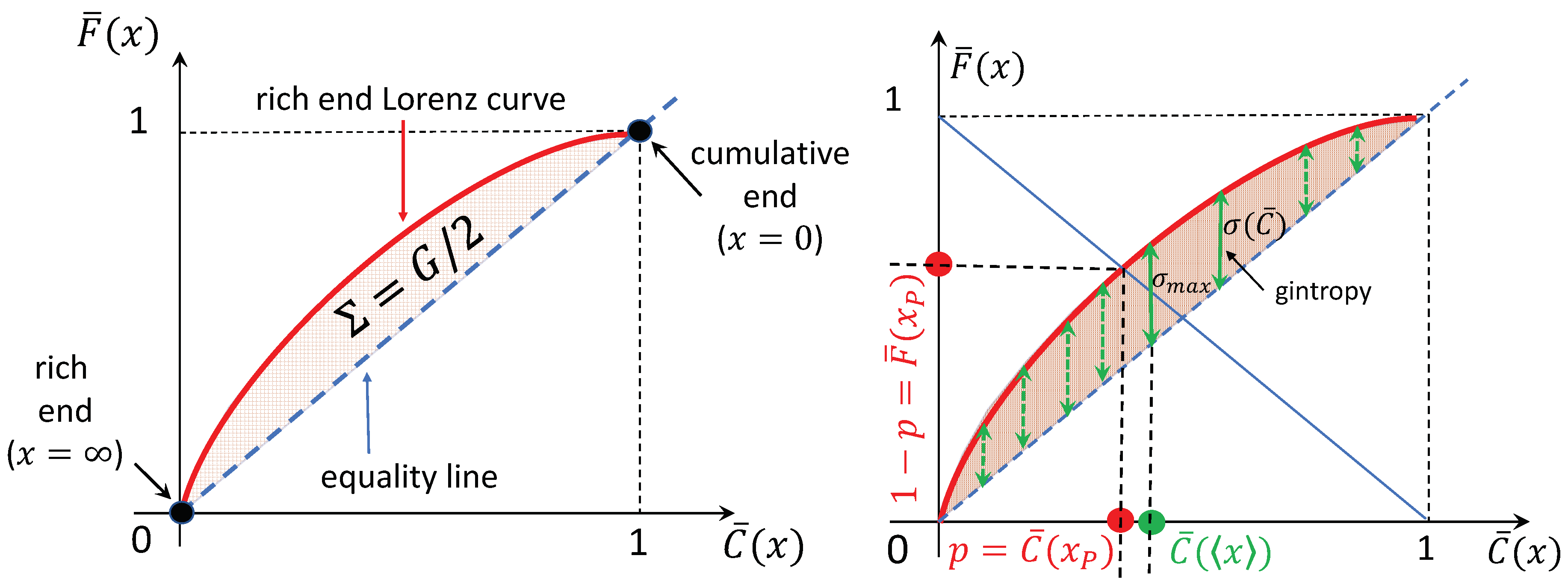
2. Gross Inequality in General
- The gintropy is never negative: is proven by inspecting the integraland taking the first form for , the second form for the opposite case. This implies that the rich-end wealth fraction is always bigger or equal to the population fraction possessing it.
- The gintropy is maximal at , , since changes its sign exactly there and only there.
- According to Equation (8) at the Pareto-point, the gintropy equals , and therefore, for the Pareto point, holds for the rich fraction. Since , in order to get a Pareto point: , i.e., the maximum of the gintropy has to be bigger than this difference value. As a consequence for the Pareto Point, we have a restriction imposed by the maximal gintropy .
- The expectation value of gintropy is the half of the gini index: .
- The integral of gintropy over the base value x is the non-Poissonity index, , with being the variance of x. The proof of this statement uses the same mathematical trick as the one in Equation (12).
- For some particular PDFs, looks like an entropy density formula, . We present important examples in the next section.
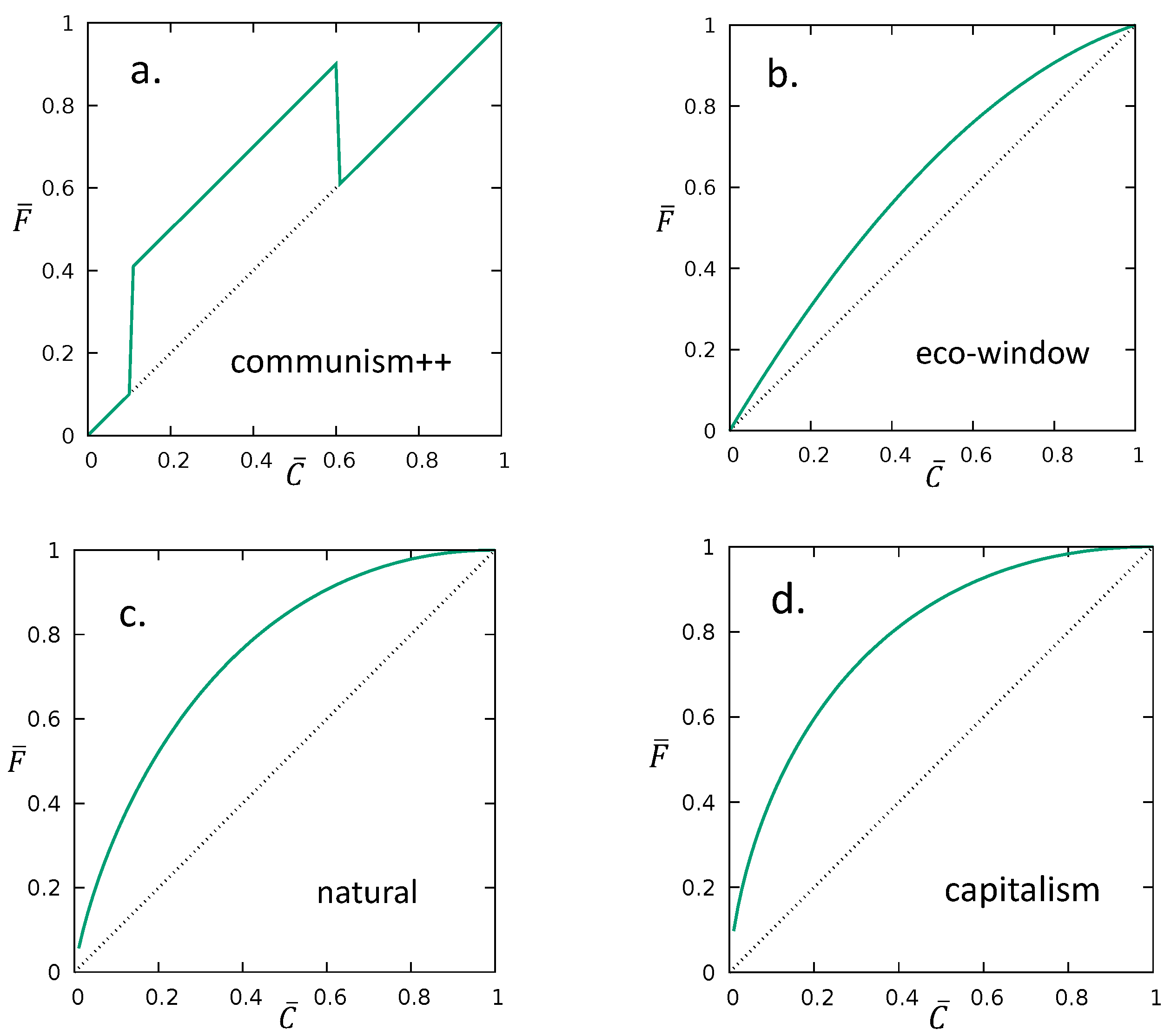
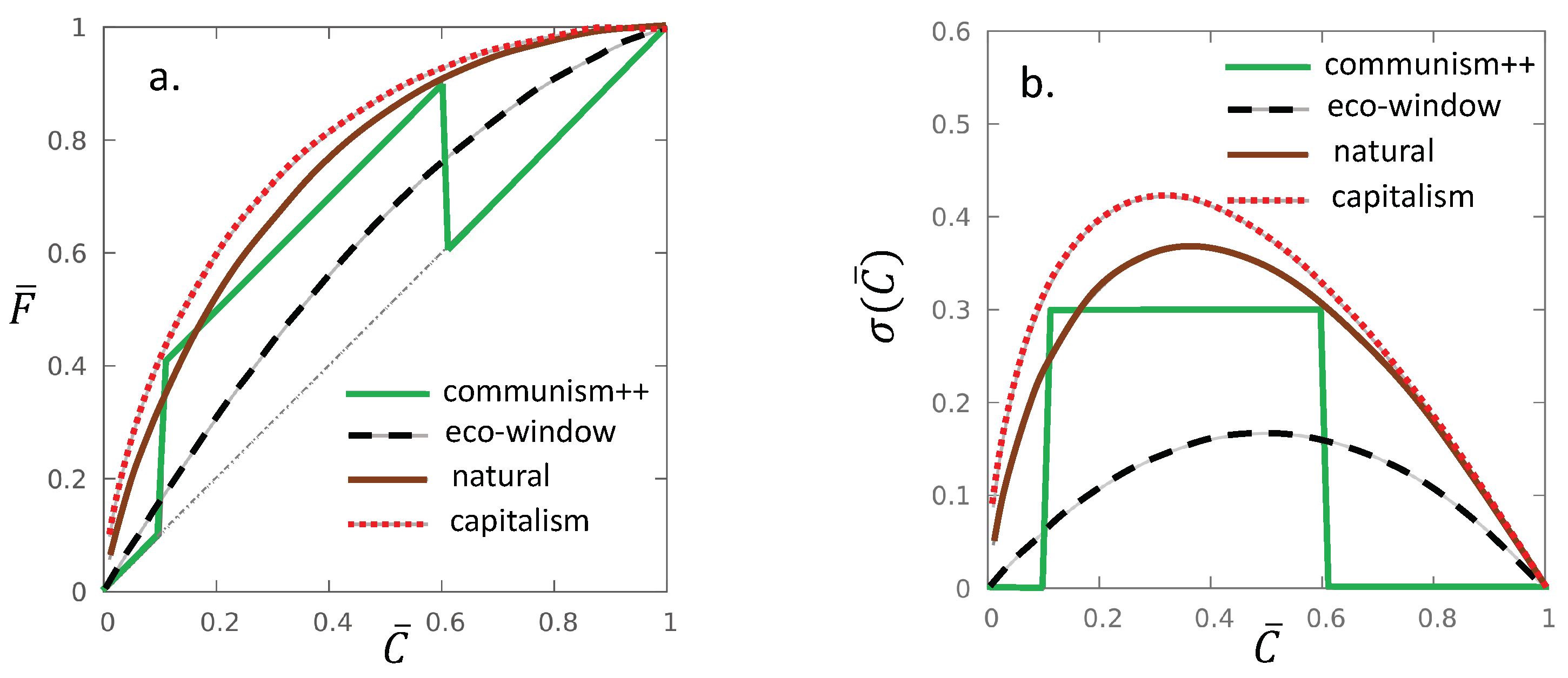
3. Important Examples
3.1. Communism
3.2. Communism++
3.3. Eco-Window
3.4. Natural Distribution
3.5. Capitalism
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thurner, S.; Hanel, R.; Corominas-Murtra, B. The three faces of entropy for complex systems- information, thermodynamics and the maxent principle. Phys. Rev. E 2017, 96, 032124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amigo, J.; Balogh, S.; Hernandez, S. A Brief review of Generalized Entropies. Entropy 2020, 22, 813. [Google Scholar] [CrossRef] [Green Version]
- Gini, C. Sulla misura della concentrazione e della variabilitá dei caratteri. Lettere Arti 1914, 73, 1203–1248. [Google Scholar]
- Lorenz, M.O. Methods of measuring the concentration of wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar] [CrossRef]
- Marmani, S.; Ficcadenti, V.; Kaur, P.; Dhesi, G. Entropic Analysis of Votes Expressed in Italian Elections between 1948 and 2018. Entropy 2020, 22, 523. [Google Scholar] [CrossRef]
- Atkinson, A.B. On the measurement of inequality. J. Econ. Theory 1970, 2, 244–263. [Google Scholar] [CrossRef]
- Shorrocks, A.F. The Class of Additivity Decomposable Inequality Measures. Econometrica 1980, 48, 613–625. [Google Scholar] [CrossRef] [Green Version]
- Pareto, V. Cours d’ economie politique. Political Sci. Q. 1896, 11, 750–751. [Google Scholar]
- Pareto, V. The New Theories of economics. J. Political Econ. 1897, 5, 485–502. [Google Scholar] [CrossRef]
- Schumpeter, J.A. Vilfredo Pareto (1848–1923). Q. J. Econ. 1949, 63, 147–173. [Google Scholar] [CrossRef]
- Dunford, R.; Su, Q.; Tamang, E. The Pareto Principle. Plymouth Stud. Sci. 2014, 7, 140–148. [Google Scholar]
- Levy, M.; Solomon, S. New evidence for the power-law distribution of wealth. Physica A 1997, 242, 90–94. [Google Scholar] [CrossRef]
- Piketty, I. Capital in the Twenty-First, Century; Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Sinha, S. Evidence for the Power-law tail of the wealth-distribution in India. Physica A 2006, 359, 555–562. [Google Scholar] [CrossRef] [Green Version]
- Dragulescu, A.; Yakovenko, V.M. Statistical mechanics of money. Eur. Phys. J. B 2000, 17, 723–729. [Google Scholar] [CrossRef] [Green Version]
- Dragulescu, A.; Yakovenko, V.M. Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Physica A 2001, 299, 213–221. [Google Scholar] [CrossRef] [Green Version]
- Neda, Z.; Gere, I.; Biro, T.S.; Toth, G.; Derzsy, N. Scaling in income inequalities and its dynamical origin. Physica A 2020, 549, 124491. [Google Scholar] [CrossRef] [Green Version]
- Molala, R. Entropy, Information Gain, Gini Index—The Crux of a Decision Tree. Available online: https://blog.clairvoyantsoft.com (accessed on 12 May 2020).
- Iritani, J.; Kuga, K. Duality between the Lorenz curves and the income distribution functions. Econ. Stud. Q. 1983, 34, 9–21. [Google Scholar]
- Thistle, P.D. Duality between generalized Lorenz curves and distribution functions. Econ. Stud. Q. 1989, 40, 183–187. [Google Scholar]
- Aaberge, R. Characterizations of Lorenz curves and income distributions. Soc. Choice Welf. 2000, 17, 639–653. [Google Scholar] [CrossRef]
- Kleiber, C. The Lorenz curve in economics and econometrics. In Advances on Income Inequality and Concentration Measures, Proceedings of the Gini-Lorenz Centennial Conference, Siena, Italy, 23–26 May 2005; Collected Papers in Memory of Corrado Gini and Max O. Lorenz; Betti, G., Lemmi, A., Eds.; Routledge: London, UK, 2008. [Google Scholar]
- Bíró, T.S.; Néda, Z. Unidirectional random growth with resetting. Physica A 2018, 499, 335–361. [Google Scholar] [CrossRef] [Green Version]
- Dogum, C. A new model of personal income distributiuons: Specification and estimation. Econ. Appliquée 1977, 30, 413–437. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- McDonald, J.B. Some generalized functions for the size distribution of income. Econometrica 1984, 52, 647–663. [Google Scholar] [CrossRef]
- Taillie, C. Lorenz ordering within the generalized gamma family of income distributions. Stat. Distrib. Sci. Work 1981, 6, 181–192. [Google Scholar]
- Wilfling, B.; Krämer, W. Lorenz ordering of Singh-Maddala income distributions. Econ. Lett. 1993, 43, 53–57. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Mezard, M. Wealth condensation in a simple model of economy. Physica A 2000, 282, 536–545. [Google Scholar] [CrossRef] [Green Version]
- Kleiber, C.; Kotz, S. A characterization of income distributions in terms of generalized Gini coefficients. Soc. Choice Welf. 2002, 19, 789–794. [Google Scholar] [CrossRef]
- Yitzhaki, S. On an extension of the Gini inequality index. Int. Econ. Rev. 1983, 24, 617–628. [Google Scholar] [CrossRef]
| G | |||
|---|---|---|---|
| natural | |||
| capitalism | |||
| eco-window | |||
| communism++ | |||
| communism | 0 | 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biró, T.S.; Néda, Z. Gintropy: Gini Index Based Generalization of Entropy. Entropy 2020, 22, 879. https://doi.org/10.3390/e22080879
Biró TS, Néda Z. Gintropy: Gini Index Based Generalization of Entropy. Entropy. 2020; 22(8):879. https://doi.org/10.3390/e22080879
Chicago/Turabian StyleBiró, Tamás S., and Zoltán Néda. 2020. "Gintropy: Gini Index Based Generalization of Entropy" Entropy 22, no. 8: 879. https://doi.org/10.3390/e22080879
APA StyleBiró, T. S., & Néda, Z. (2020). Gintropy: Gini Index Based Generalization of Entropy. Entropy, 22(8), 879. https://doi.org/10.3390/e22080879





