Non-Hermitian Floquet Phases with Even-Integer Topological Invariants in a Periodically Quenched Two-Leg Ladder
Abstract
1. Introduction
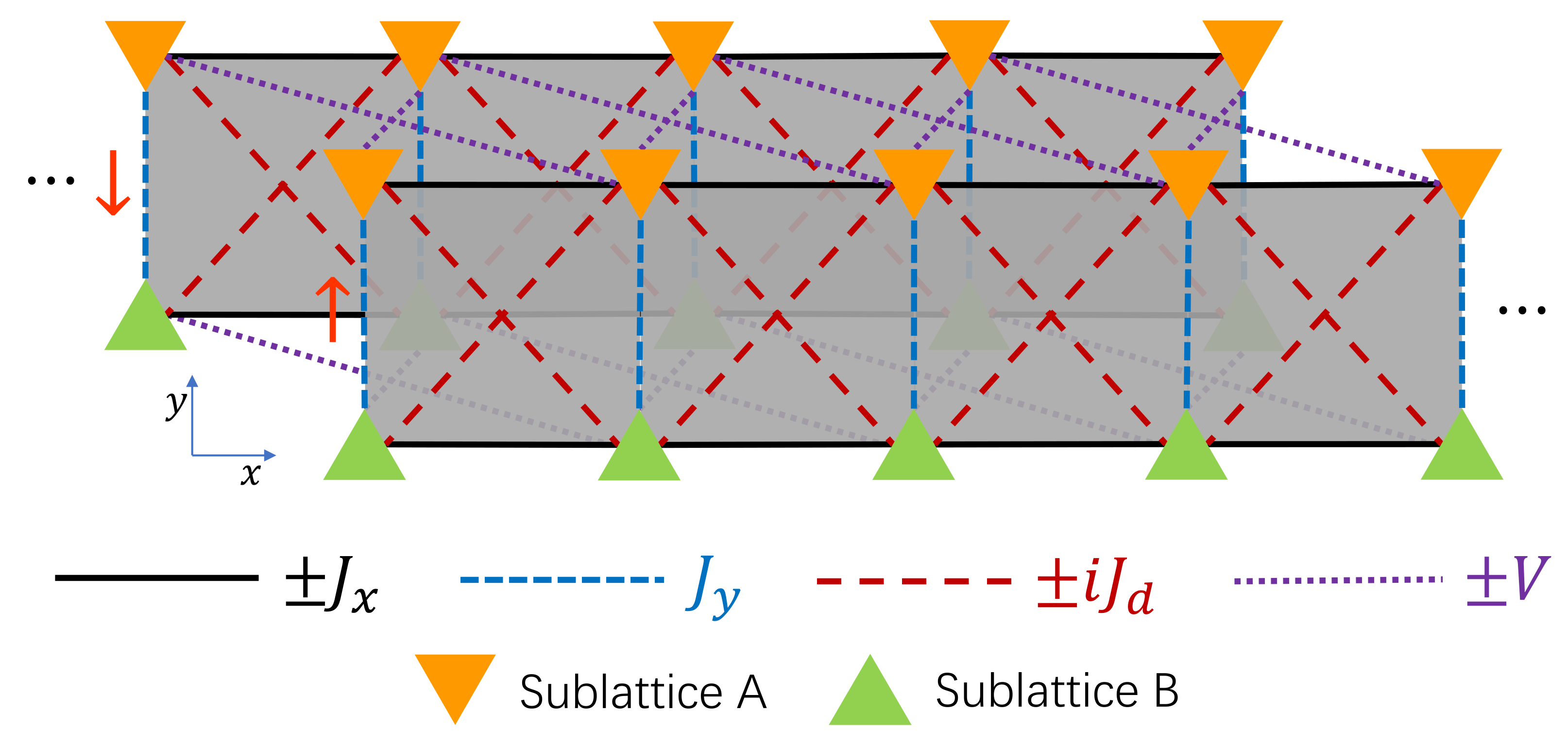
2. Model and Symmetry
3. Topological Invariants and Phase Diagrams
4. Edge States and Bulk-Edge Correspondence
5. Dynamical Probe to the Topological Phases
6. Conclusions
Funding
Conflicts of Interest
References
- Ashida, Y.; Gong, Z.; Ueda, M. Non-Hermitian Physics. arXiv 2020, arXiv:2006.01837. [Google Scholar]
- Yoshida, T.; Peters, R.; Kawakami, N.; Hatsugai, Y. Exceptional band touching for strongly correlated systems in equilibrium. arXiv 2020, arXiv:2002.11265. [Google Scholar]
- Bergholtz, E.J.; Budich, J.C.; Kunst, F.K. Exceptional Topology of Non-Hermitian Systems. arXiv 2020, arXiv:1912.10048. [Google Scholar]
- Ghatak, A.; Das, T. New topological invariants in non-Hermitian systems. J. Phys. Condens. Matter 2019, 31, 263001. [Google Scholar] [CrossRef]
- Alvarez, V.M.M.; Vargas, J.E.B.; Berdakin, M.; Foa Torres, L.E.F. Topological states of non-Hermitian systems. Eur. Phys. J. Spec. Top. 2018, 227, 1295. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
- Mostafazadeh, A.; Batal, A. Physical aspects of pseudo-Hermitian and PT-symmetric quantum mechanics. J. Phys. A Math. Gen. 2004, 37, 11645–11679. [Google Scholar] [CrossRef]
- Foa Torres, L.E.F. Perspective on Topological States of Non-Hermitian Systems. J. Phys. Mater. 2020, 3, 014002. [Google Scholar] [CrossRef]
- Kawabata, K.; Shiozaki, K.; Ueda, M.; Sato, M. Symmetry and Topology in Non-Hermitian Physics. Phys. Rev. X 2019, 9, 041015. [Google Scholar] [CrossRef]
- Gong, Z.; Ashida, Y.; Kawabata, K.; Takasan, K.; Higashikawa, S.; Ueda, M. Topological Phases of Non-Hermitian Systems. Phys. Rev. X 2018, 8, 031079. [Google Scholar] [CrossRef]
- Zhou, H.; Lee, J.Y. Periodic table for topological bands with non-Hermitian symmetries. Phys. Rev. B 2019, 99, 235112. [Google Scholar] [CrossRef]
- Shen, H.; Zhen, B.; Fu, L. Topological Band Theory for Non-Hermitian Hamiltonians. Phys. Rev. Lett. 2018, 120, 146402. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.-H.; Chen, S. Topological classification of defects in non-Hermitian systems. Phys. Rev. B 2019, 100, 144106. [Google Scholar] [CrossRef]
- Lieu, S.; McGinley, M.; Cooper, N.R. Tenfold Way for Quadratic Lindbladians. Phys. Rev. Lett. 2020, 124, 040401. [Google Scholar] [CrossRef] [PubMed]
- Wojcik, C.C.; Sun, X.-Q.; Bzdusˇek, T.; Fan, S. Homotopy characterization of non-Hermitian Hamiltonians. Phys. Rev. B 2020, 101, 205417. [Google Scholar] [CrossRef]
- Li, Z.; Mong, M.S. Homotopical classification of non-Hermitian band structures. arXiv 2019, arXiv:1911.02697. [Google Scholar]
- Borgnia, D.S.; Kruchkov, A.J.; Slager, R.-J. Non-Hermitian Boundary Modes and Topology. Phys. Rev. Lett. 2020, 124, 056802. [Google Scholar] [CrossRef]
- Lee, J.Y.; Ahn, J.; Zhou, H.; Vishwanath, A. Topological Correspondence between Hermitian and Non-Hermitian Systems: Anomalous Dynamics. Phys. Rev. Lett. 2019, 123, 206404. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, Q.-H.; Wang, H.; Gong, J. Dynamical quantum phase transitions in non-Hermitian lattices. Phys. Rev. A 2018, 98, 022129. [Google Scholar] [CrossRef]
- Zhu, B.; Ke, Y.; Zhong, H.; Lee, C. Dynamic winding number for exploring band topology. Phys. Rev. Res. 2020, 2, 023043. [Google Scholar] [CrossRef]
- Doppler, J.; Mailybaev, A.A.; Böhm, J.; Kuhl, U.; Girschik, A.; Libisch, F.; Milburn, T.J.; Rabl, P.; Moiseyev, N.; Rotter, S. Dynamically encircling an exceptional point for asymmetric mode switching. Nature 2016, 537, 76–80. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.U.; Zhen, B.; Soljačić, M.; Khajavikhan, M.; Christodoulides, D.N. Dynamically Encircling Exceptional Points: Exact Evolution and Polarization State Conversion. Phys. Rev. Lett. 2017, 118, 093002. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-L.; Wang, S.; Hou, B.; Chan, C.T. Dynamically Encircling Exceptional Points: In situ Control of Encircling Loops and the Role of the Starting Point. Phys. Rev. X 2018, 8, 021066. [Google Scholar] [CrossRef]
- Li, J.; Harter, A.K.; Liu, J.; Melo, L.D.; Joglekar, Y.N.; Luo, L. Observation of parity-time symmetry breaking transitions in a dissipative Floquet system of ultracold atoms. Nat. Commun. 2019, 10, 855. [Google Scholar] [CrossRef]
- Gou, W.; Chen, T.; Xie, D.; Xiao, T.; Deng, T.-S.; Gadway, B.; Yi, W.; Yan, B. Tunable Nonreciprocal Quantum Transport through a Dissipative Aharonov-Bohm Ring in Ultracold Atoms. Phys. Rev. Lett. 2020, 124, 070402. [Google Scholar] [CrossRef]
- Zeuner, J.M.; Rechtsman, M.C.; Plotnik, Y.; Lumer, Y.; Nolte, S.; Rudner, M.S.; Segev, M.; Szameit, A. Observation of a Topological Transition in the Bulk of a Non-Hermitian System. Phys. Rev. Lett. 2015, 115, 040402. [Google Scholar] [CrossRef]
- Weimann, S.; Kremer, M.; Plotnik, Y.; Lumer, Y.; Nolte, S.; Makris, K.G.; Segev, M.; Rechtsman, M.C.; Szameit, A. Topologically protected bound states in photonic parity-time-symmetric crystals. Nat. Mater. 2016, 16, 433. [Google Scholar] [CrossRef]
- Wang, K.; Qiu, X.; Xiao, L.; Zhan, X.; Bian, Z.; Sanders, B.C.; Yi, W.; Xue, P. Observation of emergent momentum-time skyrmions in parity-time-symmetric non-unitary quench dynamics. Nat. Commun. 2019, 10, 2293. [Google Scholar] [CrossRef]
- Xiao, L.; Deng, T.; Wang, K.; Zhu, G.; Wang, Z.; Yi, W.; Xue, P. Non-Hermitian bulk–boundary correspondence in quantum dynamics. Nat. Phys. 2020. [Google Scholar] [CrossRef]
- Zhu, W.; Fang, X.; Li, D.; Sun, Y.; Li, Y.; Jing, Y.; Chen, H. Simultaneous Observation of a Topological Edge State and Exceptional Point in an Open and Non-Hermitian Acoustic System. Phys. Rev. Lett. 2018, 121, 124501. [Google Scholar] [CrossRef]
- Shen, C.; Li, J.; Peng, X.; Cummer, S.A. Synthetic exceptional points and unidirectional zero reflection in non-Hermitian acoustic systems. Phys. Rev. Mater. 2018, 2, 125203. [Google Scholar] [CrossRef]
- Gao, H.; Xue, H.; Wang, Q.; Gu, Z.; Liu, T.; Zhu, J.; Zhang, B. Observation of topological edge states induced solely by non-Hermiticity in an acoustic crystal. Phys. Rev. B 2020, 101, 180303. [Google Scholar] [CrossRef]
- Hofmann, T.; Helbig, T.; Schindler, F.; Salgo, N.; Brzezińska, M.; Greiter, M.; Kiessling, T.; Wolf, D.; Vollhardt, A.; Kabaši, A.; et al. Reciprocal skin effect and its realization in a topolectrical circuit. Phys. Rev. Res. 2020, 2, 023265. [Google Scholar] [CrossRef]
- Helbig, T.; Hofmann, T.; Imhof, S.; Abdelghany, M.; Kiessling, T.; Molenkamp, L.W.; Lee, C.H.; Szameit, A.; Greiter, M.; Thomale, R. Generalized bulk-boundary correspondence in non-Hermitian topolectrical circuits. Nat. Phys. 2020. [Google Scholar] [CrossRef]
- Liu, S.; Ma, S.; Yang, C.; Zhang, L.; Gao, W.; Xiang, Y.J.; Cui, T.J.; Zhang, S. Gain- and Loss-Induced Topological Insulating Phase in a Non-Hermitian Electrical Circuit. Phys. Rev. Appl. 2020, 13, 014047. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, W.; Geng, J.; Song, X.; Ye, X.; Duan, C.-K.; Rong, X.; Du, J. Observation of parity-time symmetry breaking in a single-spin system. Science 2019, 364, 878–880. [Google Scholar] [CrossRef]
- Harari, G.; Bandres, M.A.; Lumer, Y.; Rechtsman, M.C.; Chong, Y.D.; Khajavikhan, M.; Christodoulides, D.N.; Segev, M. Topological insulator laser: Theory. Science 2018, 359, 4003. [Google Scholar] [CrossRef]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359, 4005. [Google Scholar] [CrossRef]
- Kartashov, Y.V.; Skryabin, D.V. Two-Dimensional Topological Polariton Laser. Phys. Rev. Lett. 2019, 122, 083902. [Google Scholar] [CrossRef]
- Wiersig, J. Enhancing the Sensitivity of Frequency and Energy Splitting Detection by Using Exceptional Points: Application to Microcavity Sensors for Single-Particle Detection. Phys. Rev. Lett. 2014, 112, 203901. [Google Scholar] [CrossRef]
- Lau, H.-K.; Clerk, A.A. Fundamental limits and non-reciprocal approaches in non-Hermitian quantum sensing. Nat. Commun. 2018, 9, 4320. [Google Scholar] [CrossRef] [PubMed]
- Hodaei, H.; Hassan, A.U.; Wittek, S.; Garcia-Gracia, H.; ElGanainy, R.; Christodoulides, D.N.; Khajavikhan, M. Enhanced sensitivity at higher-order exceptional points. Nature 2017, 548, 187–191. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Özdemir, S.K.; Zhao, G.; Wiersig, J.; Yang, L. Exceptional Points Enhance Sensing in an Optical Microcavity. Nature 2017, 548, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Bagchi, B.; Mallik, S.; Quesne, C. Generating Complex Potentials with Real Eigenvalues in Supersymmetric Quantum Mechanics. Int. J. Mod. Phys. A 2001, 16, 2859. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Pseudo-supersymmetric quantum mechanics and isospectral pseudo-Hermitian Hamiltonians. Nucl. Phys. 2002, 640, 419. [Google Scholar] [CrossRef]
- Andrianov, A.A.; Cannata, F.; Sokolov, A.V. Non-linear supersymmetry for non-Hermitian, non-diagonalizable Hamiltonians: I. General properties. Nucl. Phys. B 2007, 773, 107. [Google Scholar] [CrossRef][Green Version]
- Rosas-Ortiz, O.; Castanos, O.; Schuch, D. New supersymmetry-generated complex potentials with real spectra. J. Phys. A Math. Theor. 2015, 48, 445302. [Google Scholar] [CrossRef]
- Principe, M.; Castaldi, G.; Consales, M.; Cusano, A.; Galdi, V. Supersymmetry-Inspired Non-Hermitian Optical Couplers. Sci. Rep. 2015, 5, 8568. [Google Scholar] [CrossRef]
- Zhou, L.; Gong, J. Non-Hermitian Floquet topological phases with arbitrarily many real-quasienergy edge states. Phys. Rev. B 2018, 98, 205417. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, J. Non-Hermitian Floquet topological phases in the double-kicked rotor. Phys. Rev. A 2019, 100, 053608. [Google Scholar] [CrossRef]
- Zhou, L. Dynamical characterization of non-Hermitian Floquet topological phases in one dimension. Phys. Rev. B 2019, 100, 184314. [Google Scholar] [CrossRef]
- Zhou, L. Non-Hermitian Floquet topological superconductors with multiple Majorana edge modes. Phys. Rev. B 2020, 101, 014306. [Google Scholar] [CrossRef]
- Pan, J.; Zhou, L. Non-Hermitian Floquet second order topological insulators in periodically quenched lattices. arXiv 2020, arXiv:2004.06283. [Google Scholar]
- Yuce, C. PT symmetric Floquet topological phase. Eur. Phys. J. D 2015, 69, 184. [Google Scholar] [CrossRef][Green Version]
- Turker, Z.; Tombuloglu, S.; Yuce, C. PT symmetric Floquet topological phase in SSH model. Phys. Lett. A 2018, 382, 2013–2016. [Google Scholar] [CrossRef]
- Li, M.; Ni, X.; Weiner, M.; Alù, A.; Khanikaev, A.B. Topological phases and nonreciprocal edge states in non-Hermitian Floquet insulators. Phys. Rev. B 2019, 100, 045423. [Google Scholar] [CrossRef]
- Zhang, X.; Gong, J. Non-Hermitian Floquet topological phases: Exceptional points, coalescent edge modes, and the skin effect. Phys. Rev. B 2020, 101, 045415. [Google Scholar] [CrossRef]
- Longhi, S. Floquet exceptional points and chirality in non-Hermitian Hamiltonians. J. Phys. A Math. Theor. 2017, 50, 505201. [Google Scholar] [CrossRef]
- Chitsazi, M.; Li, H.; Ellis, F.M.; Kottos, T. Experimental Realization of Floquet -Symmetric Systems. Phys. Rev. Lett. 2017, 119, 093901. [Google Scholar] [CrossRef]
- León-Montiel, R.d.J.; Quiroz-Juárez, M.A.; Domínguez-Juárez, J.L.; Quintero-Torres, R.; Aragón, J.L.; Harter, A.K.; Joglekar, Y.N. Observation of slowly decaying eigenmodes without exceptional points in Floquet dissipative synthetic circuits. Commun. Phys. 2018, 1, 88. [Google Scholar]
- Lee, C.H.; Longhi, S. Ultrafast and Anharmonic Rabi Oscillations between Non-Bloch-Bands. arXiv 2020, arXiv:2003.10763. [Google Scholar]
- Wu, H.; An, J.-H. Floquet Topological Phases of Non-Hermitian Disordered Systems. arXiv 2020, arXiv:2003.08055. [Google Scholar]
- He, P.; Huang, Z.-H. Floquet-engineering and simulating exceptional rings with a quantum spin system. arXiv 2020, arXiv:2005.02703. [Google Scholar]
- Ryu, S.; Schnyder, A.P.; Furusaki, A.; Ludwig, A.W.W. Topological insulators and superconductors: Tenfold way and dimensional hierarchy. New J. Phys. 2010, 12, 065010. [Google Scholar] [CrossRef]
- Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conf. Proc. 2009, 1134, 22. [Google Scholar]
- Creutz, L. End States, Ladder Compounds, and Domain-Wall Fermions. Phys. Rev. Lett. 1999, 83, 2636. [Google Scholar] [CrossRef]
- Kremer, M.; Petrides, I.; Meyer, E.; Heinrich, M.; Zilberberg, O.; Szameit, A. A square-root topological insulator with non-quantized indices realized with photonic Aharonov-Bohm cages. Nat. Commun. 2020, 11, 907. [Google Scholar] [CrossRef]
- Mukherjee, S.; Liberto, M.D.; Öhberg, P.; Thomson, R.R.; Goldman, N. Experimental Observation of Aharonov-Bohm Cages in Photonic Lattices. Phys. Rev. Lett. 2018, 121, 075502. [Google Scholar] [CrossRef]
- Kang, J.H.; Han, J.H.; Shin, Y. Creutz ladder in a resonantly shaken 1D optical lattice. New J. Phys. 2020, 22, 013023. [Google Scholar] [CrossRef]
- Li, X.; Zhao, E.; Liu, W.V. Topological states in a ladder-like optical lattice containing ultracold atoms in higher orbital bands. Nat. Commun. 2013, 4, 1523. [Google Scholar] [CrossRef]
- Gligorić, G.; Leykam, D.; Maluckov, A. Influence of different disorder types on Aharonov-Bohm caging in the diamond chain. Phys. Rev. A 2020, 101, 023839. [Google Scholar] [CrossRef]
- Liberto, M.D.; Mukherjee, S.; Goldman, N. Nonlinear dynamics of Aharonov-Bohm cages. Phys. Rev. A 2019, 100, 043829. [Google Scholar] [CrossRef]
- Sun, N.; Lim, L.-K. Quantum charge pumps with topological phases in a Creutz ladder. Phys. Rev. B 2017, 96, 035139. [Google Scholar] [CrossRef]
- Kuno, Y.; Orito, T.; Ichinose, I. Flat-band many-body localization and ergodicity breaking in the Creutz ladder. New J. Phys. 2020, 22, 013032. [Google Scholar] [CrossRef]
- Kuno, Y. Extended flat-bands, entanglement and topological properties in a Creutz ladder. Phys. Rev. B 2020, 101, 184112. [Google Scholar] [CrossRef]
- Zurita, J.; Creffield, C.E.; Platero, G. Topology and Interactions in the Photonic Creutz and Creutz-Hubbard Ladders. Adv. Quantum Technol. 2019, 3, 1900105. [Google Scholar] [CrossRef]
- Sticlet, D.; Seabra, L.; Pollmann, F.; Cayssol, J. From fractionally charged solitons to Majorana bound states in a one-dimensional interacting model. Phys. Rev. B 2014, 89, 115430. [Google Scholar] [CrossRef]
- Jünemann, J.; Piga, A.; Ran, S.-J.; Lewenstein, M.; Rizzi, M.; Bermudez, A. Exploring Interacting Topological Insulators with Ultracold Atoms: The Synthetic Creutz-Hubbard Model. Phys. Rev. X 2017, 7, 031057. [Google Scholar] [CrossRef]
- Yang, F.; Perrin, V.; Petrescu, A.; Garate, I.; Hur, K.L. From topological superconductivity to quantum Hall states in coupled wires. Phys. Rev. B 2020, 101, 085116. [Google Scholar] [CrossRef]
- Haller, A.; Rizzi, M.; Filippone, M. Drude weight increase by orbital and repulsive interactions in fermionic ladders. Phys. Rev. Res. 2020, 2, 023058. [Google Scholar] [CrossRef]
- Santos, R.A.; Béri, B. Fractional topological insulator precursors in spin-orbit fermion ladders. Phys. Rev. B 2019, 100, 235122. [Google Scholar] [CrossRef]
- Hetényi, B.; Yahyavi, M. Topological insulation in a ladder model with particle-hole and reflection symmetries. J. Phys. Condens. Matter 2018, 30, 10LT01. [Google Scholar] [CrossRef] [PubMed]
- Gholizadeh, S.; Yahyavi, M.; Hetényi, B. Extended Creutz ladder with spin-orbit coupling: A one-dimensional analog of the Kane-Mele model. Europhys. Lett. 2018, 122, 27001. [Google Scholar] [CrossRef]
- Zhou, L.; Du, Q. Floquet topological phases with fourfold-degenerate edge modes in a driven spin-1/2 Creutz ladder. Phys. Rev. A 2020, 101, 033607. [Google Scholar] [CrossRef]
- Asbóth, J.K. Symmetries, topological phases, and bound states in the one-dimensional quantum walk. Phys. Rev. B 2012, 86, 195414. [Google Scholar] [CrossRef]
- Asbóth, J.K.; Obuse, H. Bulk-boundary correspondence for chiral symmetric quantum walks. Phys. Rev. B 2013, 88, 121406. [Google Scholar] [CrossRef]
- Roy, R.; Harper, F. Periodic table for Floquet topological insulators. Phys. Rev. B 2017, 96, 155118. [Google Scholar] [CrossRef]
- Yao, S.; Wang, Z. Edge States and Topological Invariants of Non-Hermitian Systems. Phys. Rev. Lett. 2018, 121, 086803. [Google Scholar] [CrossRef]
- Martinez Alvarez, V.M.; Barrios Vargas, J.E.; Foa Torres, L.E.F. Non-Hermitian robust edge states in one-dimension: Anomalous localization and eigenspace condensation at exceptional points. Phys. Rev. B 2018, 97, 121401. [Google Scholar] [CrossRef]
- Xiong, Y. Why does bulk boundary correspondence fail in some non-hermitian topological models. J. Phys. Commun. 2018, 2, 035043. [Google Scholar] [CrossRef]
- Longhi, S. Half-spectral unidirectional invisibility in non-Hermitian periodic optical structures. Opt. Lett. 2015, 40, 5694. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; El-Ganainy, R. Non-Hermitian photonics based on parity-time symmetry. Nat. Photonics 2017, 11, 752. [Google Scholar] [CrossRef]
- Zhou, L.; Gong, J. Floquet topological phases in a spin-1/2 double kicked rotor. Phys. Rev. A 2018, 97, 063603. [Google Scholar] [CrossRef]
- Song, F.; Yao, S.; Wang, Z. Non-Hermitian Topological Invariants in Real Space. Phys. Rev. Lett. 2019, 123, 246801. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, J. The bulk-edge correspondence in three simple cases. Rev. Math. Phys. 2020, 32, 2030003. [Google Scholar] [CrossRef]
- Mondragon-Shem, I.; Hughes, T.L.; Song, J.; Prodan, E. Topological Criticality in the Chiral-Symmetric AIII Class at Strong Disorder. Phys. Rev. Lett. 2014, 113, 046802. [Google Scholar] [CrossRef]
- Song, J.; Prodan, E. AIII and BDI topological systems at strong disorder. Phys. Rev. B 2014, 89, 224203. [Google Scholar] [CrossRef]
- Cardano, F.; D’Errico, A.; Dauphin, A.; Maffei, M.; Piccirillo, B.; Lisio, C.d.; Filippis, G.D.; Cataudella, V.; Santamato, E.; Marrucci, L.; et al. Detection of Zak phases and topological invariants in a chiral quantum walk of twisted photons. Nat. Commun. 2017, 8, 15516. [Google Scholar] [CrossRef]
- Maffei, M.; Dauphin, A.; Cardano, F.; Lewenstein, M.; Massignan, P. Topological characterization of chiral models through their long time dynamics. New J. Phys. 2018, 20, 013023. [Google Scholar] [CrossRef]
- Nakagawa, M.; Slager, R.-J.; Higashikawa, S.; Oka, T. Wannier representation of Floquet topological states. Phys. Rev. B 2020, 101, 075108. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Zhou, L.; Pan, J.; Gong, J. Coupled-wire construction of static and Floquet second-order topological insulators. Phys. Rev. B 2019, 99, 045441. [Google Scholar] [CrossRef]
- Haller, A.; Massignan, P.; Rizzi, M. Detecting topology through dynamics in interacting fermionic wires. arXiv 2020, arXiv:2001.09074. [Google Scholar]
- D’Errico, A.; Colandrea, F.D.; Barboza, R.; Dauphin, A.; Lewenstein, M.; Massignan, P.; Marrucci, L.; Cardano, F. Bulk detection of time-dependent topological transitions in quenched chiral models. Phys. Rev. Res. 2020, 2, 023119. [Google Scholar] [CrossRef]
- Meier, E.J.; An, F.A.; Dauphin, A.; Maffei, M.; Massignan, P.; Hughes, T.L.; Gadway, B. Observation of the topological Anderson insulator in disordered atomic wires. Science 2018, 362, 929. [Google Scholar] [CrossRef]
- Xie, D.; Deng, T.-S.; Xiao, T.; Gou, W.; Chen, T.; Yi, W.; Yan, B. Topological Quantum Walks in Momentum Space with a Bose-Einstein Condensate. Phys. Rev. Lett. 2020, 124, 050502. [Google Scholar] [CrossRef] [PubMed]




© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L. Non-Hermitian Floquet Phases with Even-Integer Topological Invariants in a Periodically Quenched Two-Leg Ladder. Entropy 2020, 22, 746. https://doi.org/10.3390/e22070746
Zhou L. Non-Hermitian Floquet Phases with Even-Integer Topological Invariants in a Periodically Quenched Two-Leg Ladder. Entropy. 2020; 22(7):746. https://doi.org/10.3390/e22070746
Chicago/Turabian StyleZhou, Longwen. 2020. "Non-Hermitian Floquet Phases with Even-Integer Topological Invariants in a Periodically Quenched Two-Leg Ladder" Entropy 22, no. 7: 746. https://doi.org/10.3390/e22070746
APA StyleZhou, L. (2020). Non-Hermitian Floquet Phases with Even-Integer Topological Invariants in a Periodically Quenched Two-Leg Ladder. Entropy, 22(7), 746. https://doi.org/10.3390/e22070746




