1. Introduction
Randomness is often an important resource in information processing. This is true even in the quantum regime, where quantum randomness is often represented by a
random state, a quantum pure state that is drawn uniformly at random from a Hilbert space. A random state is known to be extremely useful and is used in numerous quantum information protocols, from communication [
1,
2,
3] and computation tasks [
4,
5,
6] to benchmarking quantum devices [
7,
8,
9,
10]. The origin of its usefulness can be traced back to the counter-intuitive property of a random state that it is typically extremely highly entangled.
Quantum randomness is also the key to understanding the physics in complex quantum many-body systems. In the last decade, based on various measures of quantum randomness, such as scrambling [
11,
12], operator entanglement [
13,
14], and out-of-time-ordered correlators [
15], quantum randomness in various complex quantum many-body systems has been intensely studied. It eventually turns out that randomness is indeed the key to connect the physics in quantum chaotic systems and that of quantum black hole, revealing an exotic relation between them [
16,
17,
18]. The measures used in the analyses are all to elucidate entanglement of a random state. Hence, entanglement of a random state plays a crucial role in the approach.
The entanglement of a random state is often called
generic entanglement of quantum states due to the fact that a random state is uniformly distributed in a Hilbert space and can be considered to represent generic properties of quantum pure states. Generic entanglement has been especially studied in terms of a bi-partition of the system. It was first pointed out that in terms of the entanglement entropy, generic entanglement in a large system is typically extremely concentrated around a nearly, but not exactly, maximum value [
19,
20,
21,
22,
23]. The analysis was then extended to a probabilistic statement [
24], revealing the relation with quantum statistical mechanics [
25], and to the higher moments of the distribution of entanglement entropy [
26,
27,
28,
29,
30,
31,
32,
33]. In particular, higher moments were studied in great detail using the technique of random matrix theory. It was shown that the probability density function of the distribution has two singularities, splitting the distribution into three different
entanglement phases with different entanglement spectra. Since the entanglement spectrum characterizes topological orders of the state, this implies that there exists yet another intriguing relation between a random state and an exotic quantum many-body physics.
There is also a close relation between generic entanglement and quantum error correction, one of the key concepts in quantum information science. It is well-known that a randomly chosen unitary is typically a good encoder of quantum information [
34,
35,
36]. It is recently pointed out that a certain property of generic entanglement is responsible for this [
37]. Hence, revealing the properties of generic entanglement will help our understanding of why quantum error correction works well, even providing real applications of generic entanglement in quantum information science.
Most of these studies of generic entanglement focus on the random state that is uniformly distributed over the whole Hilbert space. However, quantum many-body systems often have symmetry, restricting the distribution of states into that over the invariant subspace of the symmetry. Hence, the aforementioned results about generic entanglement cannot be directly applied to complex quantum many-body systems with symmetry. It is also worth pointing out that symmetry is the guiding principle in many-body physics, allowing us to understand intriguing many-body phenomena, such as thermal and quantum phase transitions, in a unified manner. Thus, it will be interesting to take symmetry into account in the study of generic entanglement.
In this paper, we address the question of how symmetry of quantum systems changes the properties of generic entanglement. We specifically investigate bipartite entanglement of random states in invariant subspaces. To this end, we first provide a general formula that is useful to analyze the distribution of entanglement over a random state in any subspace. We then apply the formula to investigate the generic entanglement in invariant subspaces associated with a given symmetry. We especially consider three symmetries, 1. axial symmetry that leads to the conservation law of a component of angular momentum, 2. permutation symmetry that characterizes indistinguishable bosons and fermions, and 3. translation symmetry that defines the structure of a lattice. We particularly focus on these symmetries since the axial symmetry is the one used in Ref. [
37] that pointed out the relation between generic entanglement and quantum error correction, the permutation symmetry is commonly believed to result in weak entanglement, and the translation symmetry is important in relation to the area law of entanglement. We however note that the formula we derive can be applied to any symmetries. We then find that compared to generic entanglement of a random state without symmetry, the axial and permutation symmetries reduce the amount of entanglement by a constant and a significant degree, respectively, while the translation symmetry does not lead to a significant reduction. We also numerically study whether the distribution of entanglement over random states in invariant subspaces has phase-transition-like behaviors. Although it is less conclusive due to a large finite-size effect, we show that certain entanglement phases seem to exist even when a random state has permutation or translation symmetry.
This paper is organized as follows. We start with preliminaries in
Section 2 and overview properties of generic entanglement in
Section 3. In
Section 4, our main technical tool in the analysis is provided. We then investigate generic entanglement with axial, permutation, and translation symmetries in
Section 5,
Section 6 and
Section 7, respectively. We finally numerically analyze possible entanglement phases of random states with symmetry in
Section 8. After we make a remark on the feasibility of generic entanglement in
Section 9, we conclude with a summary and discussions in
Section 10.
2. Preliminaries
Throughout the paper, we consider a quantum system composed of n qudits, whose Hilbert space is , and its bi-partition into subsystems A and , which consist of with and qudits, respectively. We assume that . For Hilbert spaces, and operators, we often write the systems on which they are defined in the superscript. For instance, is the Hilbert space associated with the system , and is an operator X acting on the system A. A reduced operator on A of is denoted simply by , i.e., . We denote by I the identity operator, and by projection onto some subspace.
2.1. Haar Measure, Haar Random Unitaries, and Haar Random States
On a unitary group with finite degree, there exists the unique unitarily invariant probability measure, known as the
Haar measure. We denote it by
, which satisfies the following properties: for any subset
of unitaries and for any unitary
U,
The integral is taken over the whole unitary group. When a unitary
U is chosen from the unitary group uniformly at random with respect to the Haar measure
, we denote it by
and call it a
Haar random unitary.
Let be a Haar random unitary acting on a Hilbert space . The state obtained by applying U to a fixed canonical pure state is called a Haar random state. With a slight abuse of notation, we denote a Haar random state as . Due to the uniform distribution of a Haar random unitary, the distribution of a Haar random state does not depend on the choice of the canonical state and is uniform in the Hilbert space . Thus, it is often used to study generic properties of quantum pure states. In this paper, we often use the Haar measure on the unitary group acting on a subspace of a Hilbert space . The Haar measure on the unitary group acting only on the subspace is denoted by .
Since the Haar measure is a probability measure, we can think of an average of a function of a state over the Haar measure . We denote the average by . Similarly, the probability with respect to the Haar measure is denoted by .
2.2. Entanglement Entropy, and Entanglement Spectrum
For a pure state
in
, we quantify the amount of entanglement with respect to the bi-partition
A and
by the von Neumann entropy of the reduced density matrix
in
A. That is, we use
as a measure of bi-partite entanglement of
, where
is the von Neumann entropy. The measure
is often referred to as the
entanglement entropy of
and takes the value between 0 for separable states and
for maximally entangled states.
For a given pure state , the distribution of the eigenvalues of the reduced density matrix in decreasing order is called an entanglement spectrum of in A.
3. Generic Entanglement without Symmetry
It is well-known that a random state in an
n-qudit system
is typically extremely highly entangled between
A and
, which has been extensively studied in the literature [
19,
20,
21,
22,
23,
24,
26,
27,
28,
29,
30,
31,
32,
33]. For instance, the average entanglement entropy of a Haar random state satisfies [
19,
20,
21,
22,
23,
24]
Since the maximum value of the entanglement entropy is
, this implies that the average is exponentially close to the maximum when
. This statement was later strengthened to the probabilistic statement that the entanglement entropy of a random state strongly concentrates around its average [
24].
Theorem 1 (Theorem III.3 in Ref. [
24]).
Let
be a composite system, , and n and be the number of qudits in
and A, respectively, that satisfy . For a random state in , it holds that , Since the probability is close to 1 doubly exponentially in the number n of qudits in , this clearly shows that it is extremely unlikely that the entanglement entropy of a random state takes the value far from its average.
Theorem 1 is not only of theoretical interest, but also has implications onto many topics in quantum physics. In particular, in the context of the condensed-matter physics, where qudits are often aligned on a lattice, a pure state is said to obey the volume law of entanglement when the entanglement entropy of the state is proportional to the number of qudits in the subsystem. Although the volume law does not hold in most many-body systems, it is expected to hold when the dynamics of the system is sufficiently scrambling, which is likely to be the key feature bridging quantum chaos and quantum gravity. Hence, the volume law of entanglement is considered to be one of the diagnostic features of complex many-body quantum systems. In this context, Theorem 1, stating that a state generated by a random unitary dynamics typically obeys the volume law of entanglement, implies that typical unitary dynamics without any restriction should be highly chaotic.
The entanglement entropy of a Haar random state also has an intriguing property, namely ‘phase transitions’ of the distribution [
26,
27,
28,
29,
30,
31,
32,
33]. This was first studied based on the purity of reduced density matrices, and was then extended to the Rényi entropies and eventually to the von Neumann entropy, i.e., the entanglement entropy. The probability density function of the entanglement entropy
over a Haar random state
has two singularities when
. Thus, the distribution of the entanglement entropy is split into three regimes, which are sometimes called
separable,
typical, and
maximally entangled phases. Each entanglement phase has a different characteristic entanglement spectrum. Thus, although the average of entanglement entropy of a Haar random state is nearly maximum, its distribution has a rather rich structure.
The main question in this paper is how symmetry of quantum states affects these properties of generic entanglement. This is of crucial importance when we are interested in the implications of generic entanglement on the physics in complex quantum many-body systems with symmetry.
4. Concentration of Entanglement Entropy of a Random State in a Subspace
To investigate the entanglement entropy of a random state with symmetry, we use the same technical tool as used to show Theorem 1, which is the so-called
concentration phenomena of the Haar measure [
38]. It states that any real-valued function of a Haar random state strongly concentrates around its average if the function is sufficiently smooth. As the entanglement entropy is a real-valued function, it can be directly applied to the question we are interested in, leading to the following Theorem.
Theorem 2. Let be the Hilbert space of an n-qudit system , and be any -dimensional subspace. Let and be a state on the subsystem A and , defined byrespectively, where is the projection onto . Then, for a random state in , and , it holds thatwhereand . Theorem 2 is a slight generalization of Theorem 1, so that it is applicable to any subspace
. In the case of
, Theorem 2 nearly recovers Theorem 1 except that the probability in Equation (
6) is worse than that in Equation (
4). This is because the latter probability is obtained by using the median rather than the average. Using the same technique, it will be possible to slightly improve Equation (
6).
Proof of Theorem 2. The proof is based on Levy’s lemma [
38]. We particularly use the lemma in the form given in Ref. [
24], which is tailored to the entanglement entropy: for any
, it holds that
where
is the average of
over the probability measure
on
. In the following, we show that
.
We first use the monotonicity of the Rényi entropy, i.e.,
. Further using the Jensen’s inequality, we obtain
We then introduce a system
of
X for
, whose Hilbert space
is isomorphic to
, and denote by
and
the identity and the swap operator on
, respectively. They are explicitly given by
where
is an orthonormal basis in
. Note that the definition of
does not depend on the choice of the basis. Using these operators and the so-called swap trick, i.e.,
for any operator
P and
Q on
X, it follows that
Hence, it suffices to compute
, which can be explicitly done using the unitary invariance of the Haar measure.
For any unitary
acting on the subspace
, it holds that
Due to the Schur-Weyl duality, this implies that
is given by a linear combination of the unitary representations of permutations between
and
, or equivalently, a linear combination of
and
. In terms of the operators defined on
, they are respectively given by
We now have
for some coefficients
and
. The coefficients are determined from the conditions that
Noting that
and
, we obtain
and so,
We thus arrive at
It is straightforward that
To compute
, we expand the swap operator
as
where
is an orthonormal basis in
. This allows us to explicitly write down
as
where we used the swap trick. We further expand
as
by using an orthogonal basis
in
. Note that
are un-normalized. Using this notation, we have
leading to
We then use the relation that
and obtain
Altogether, we have
Substituting this into Equation (
8), we obtain the desired statement. □
Theorem 2 implies that when , the entanglement entropy of a random state in the subspace is typically more than . Hence, when we are interested in the entanglement entropy of a random state in the subspace , what we need to do is to compute , , and .
5. Generic Entanglement of States with an Axial Symmetry
Based on Theorem 2, we now study generic entanglement when a random state has symmetry. We start with a simple case of an axial symmetry of qubit-systems. This is because the relation between generic entanglement and quantum error correcting codes [
37] is particularly pointed out when the system has an axial symmetry.
Suppose that the system consists of
n-qubits and has an axial symmetry. Without loss of generality, we assume that the symmetry is around the
Z-axis. Each invariant subspace is then characterized by the
Z-component of angular momentum, or equivalently, the number
m of up-spins as follows:
where
with
being the spin-
Z operator on
n qubits, i.e.,
with
being the spin-
Z operators acting on the
ith qubit. The dimension
of each subspace
is given by
. We consider the entanglement entropy
of a random state
, where
is the Haar measured on the subspace
.
Since each subspace
can be spanned by the basis consisting of product states,
for
, which we simply denote by
, can be simply obtained as
where
is the projection onto the subspace of
spanned by the states with
ℓ up-spins. We similarly have
Thus, the
is given by
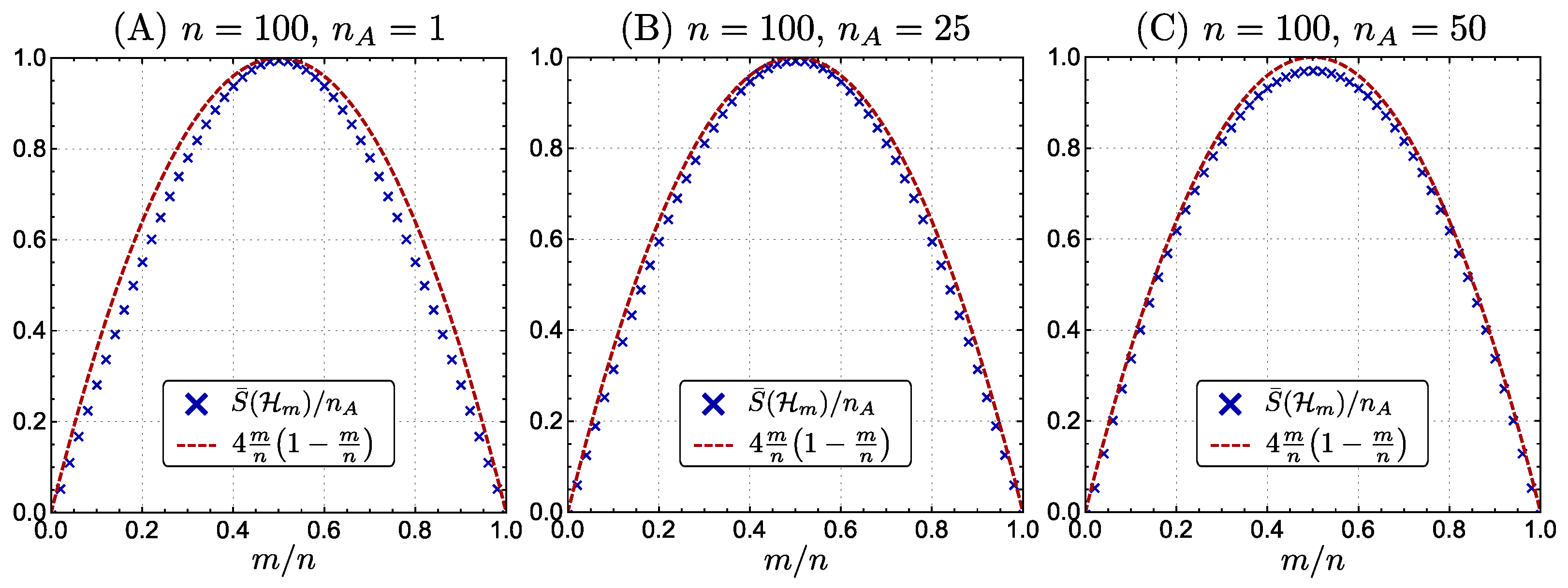
In
Figure 1, we plot
as a function of
for a fixed
n, and also the function
. Since they coincide well, we approximate
by a quadratic function.
Using this expression and denoting
m by
with
, we obtain from Theorem 2 that a random state
in the subspace
with a fixed
Z-axis angular momentum
satisfies
for any
. Note that we used a trivial bound
on
. This implies that as far as
is constant, the state still obeys the volume law, i.e., the entanglement entropy is proportional to the number of qubits
in the subsystem
A. In this sense, the axial symmetry does not change the volume law of entanglement. However, recalling that the entanglement entropy of a Haar random state of qubits without any symmetry is ≈
, the axial symmetry can reduce the entanglement entropy by a constant degree since Equation (
38) shows that the coefficient of
is
that can be smaller than 1.
6. Generic Entanglement of States with Permutation Symmetry
We next investigate the entanglement entropy of a random state with the permutation symmetry. It is often argued that a state with permutation symmetry is generally weakly entangled [
39,
40]. Based on Theorem 2, we here quantitatively justify that this common belief indeed holds for most permutation symmetric states.
We especially consider the symmetric and antisymmetric subspaces in
of
n qudits, which are respectively defined by
where
is the permutation group of degree
n, and
is a unitary representation of
. The dimensions
of
are given by
and
, respectively. Note that
becomes non-trivial if and only if
. From the physics point of view, the symmetric (antisymmetric) subspace is a Hilbert space of indistinguishable bosons (fermions).
Let us first consider the entropy of a state
, where
is the projection onto the symmetric/anti-symmetric subspace in
. Due to the special properties of the permutation symmetry, it turns out that
. To see this, we use another expression of
, that is
where
in the integral is a unitary acting on a single qudit,
is the unitary group of degree
d, and
is any state in
. This is a consequence of Schur’s lemma [
41] and the fact that the symmetric and anti-symmetric subspaces are irreducible representations of
that acts as
onto
.
For the symmetric subspace, we can take
as a product state
. Then, we have
In the last line, we again used Shur’s lemma and the fact that
. For the anti-symmetric subspace, we similarly obtain
To check the support of
, we decompose
into the form of
, where
(
) is an orthonormal product basis in
. For any
i, the state
should be also anti-symmetric because, for any permutation
,
. Recalling that
, we obtain
, implying that
for any
i. Thus, the support of
is
. Again using the Schur’s lemma and the fact that the anti-symmetric subspace is irreducible, we obtain
It is now straightforward to compute
for
as
, where
, leading to
We also have
since, by taking the partial trace, symmetric and anti-symmetric states remain in the symmetric and anti-symmetric subspaces, respectively. Note that this also guarantees that trivial upper bounds of the entanglement entropy for symmetric/anti-symmetric states are given by
.
From Theorem 2, we finally obtain the following: for any
, a random state
in the symmetric/anti-symmetric subspace in
satisfies
Since
and
when
, the right-hand side is extremely close to 1. Hence, we conclude that the entanglement entropy for symmetric/anti-symmetric random states in a small subsystem
A extremely concentrates between
and
.
To be more concrete, let us consider special cases of
d. For simplicity, we ignore
. We first look at the entanglement entropy of a random state in the symmetric space, which typically takes the following value:
where
for
is the binary entropy. We especially note that when
, the entanglement entropy
for a random symmetric state is typically ≈
, and fails to satisfy the volume law of entanglement. Thus, our result implies that the volume law fails to hold when the many-body system is permutation symmetric and consists of the particles with a constant degree of freedom, so that
. A simple example may be many-body systems composed of indistinguishable bosons. We however note that this result is a consequence of the facts that symmetric states remain symmetric by taking the partial trace and that the symmetric subspace is small.
On the other hand, for the anti-symmetric random states, we have
where
. Note that
since the anti-symmetric space is non-trivial only when
. Since the entanglement entropy of the random state without any symmetry is typically
in terms of
, we conclude that the anti-symmetric condition of the state typically reduces the entanglement entropy by the factor
.
7. Generic Entanglement of States with Translation Symmetry
As the last, but not least, instance of symmetry, we consider translation symmetry, which is one of the most common symmetries in many-body systems. We especially consider the case where qudits are aligned on a one-dimensional line with the periodic boundary condition and
A is an interval of the line. The corresponding group
is generated by the shifting operator
T, which shifts every qudit to the next site. Since
is the identity due to the periodic boundary condition, the Hilbert space
is decomposed into discrete momentum subspaces such as
, where
. Here, each subspace is defined by
and
is a unitary representation of
T. This decomposition corresponds to a discrete version of Bloch’s theorem. For simplicity, we consider only the case where
n is a prime number. This simplifies the analysis, but we expect that nearly the same result holds even when
n is not prime with a slight modification.
To investigate the entanglement entropy, we first provide a basis in
and explicitly write down the projector
onto the subspace. Let
be the set of
n-dit sequences,
, and
be the set
, where
for
is the
n-dit sequence whose components are all
a. Let
be an equivalent class of
by the translation group
,
. We construct a basis in
using the state
for
. Note that none of
is a zero vector due to the assumption that
n is a prime number. The basis is given by
and, for
,
Clearly, the dimension
of each subspace is given by
Using these bases, we derive a upper bound of
for
, from which we obtain a lower bound of
. Since
A and
can be treated in the same way, we consider only
, which can be expanded as
where
and
(
for all
). The off-diagonal terms
(
) are non-zero if and only if there exists
(
for
) such that
for some
. Here, we used the notation that
. Hence, if the number of
i’s (
) in
a differs from that in
b,
. This means that
is decomposed into positive operators
on the Hilbert spaces spanned by states with configurations
c containing
of
i’s (
);
where
runs from 0 to
under the condition that
. Thus
is given by
The dimension of the support of
is
.
From a counting argument, the diagonal terms in
are obtained as
where
with
being the delta function. For the off-diagonal terms, we show that the absolute value of each of them is not greater than
. For a fixed
a,
b, and
k, there exists at most one
v that satisfies Equation (
60) due to the assumption that
n is a prime number. Recalling that
since
, an off-diagonal term of
is a summation of at most
terms, where each term has coefficient
for some
. Thus, all off-diagonal terms of
are bounded from above by
where
is an indicator function that
if there exists
v satisfying Equation (
60) for
and
otherwise.
By substituting the diagonal terms, Equation (
63), and the upper bounds of off-diagonal terms, Equation (
64), into Equation (
62), we obtain an upper bound of
as
where
As
, we have
Similarly, we can derive an upper bound for
as
Based on these lower bounds, we obtain
Using a trivial upper bound
on
for any
, we arrive at our conclusion: for any
and for
, it holds that
for any
, where
. Since the entanglement entropy for any state is bounded from above by
, this implies that the entanglement entropy of a random state with translation symmetry concentrates between
and
. Hence, translation symmetry changes the generic entanglement only slightly.
8. Entanglement Phases and Symmetries
We finally investigate how symmetries affect the entanglement phases. The original analyses of entanglement phases are based on the technique of the random matrix theory [
26,
27,
28,
29,
30,
31,
32,
33]. We here present numerical calculations of the entanglement entropy of random states in various invariant subspaces associated with symmetry. We especially consider a random symmetric state, and a random translation invariant state for
,
, and
. All numerics are done by sampling pure states from an invariant subspace of the symmetry. We have used the so-called Hurwitz parametrization of a state, based on which a parametrization of a Haar random state is known [
42].
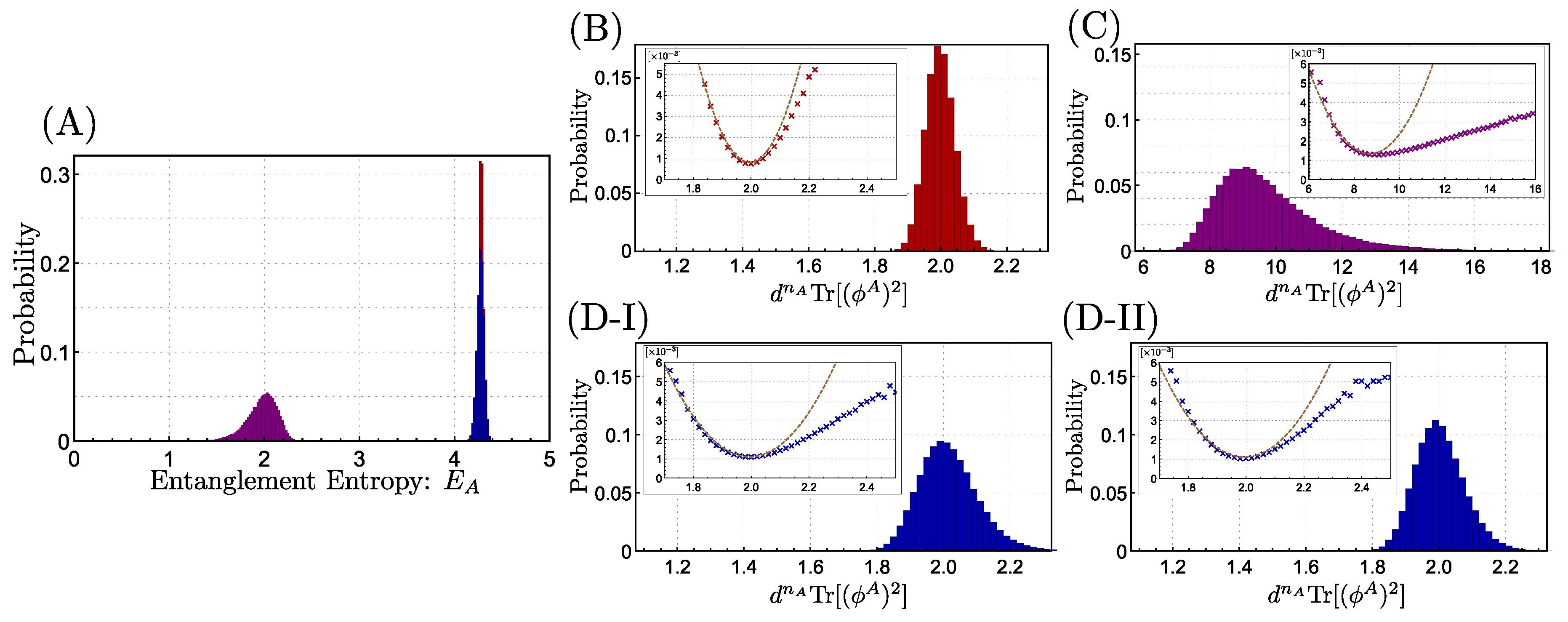
In
Figure 2, we provide the distributions of entanglement of random states in the subspaces. Panel (A) is in terms of the entanglement entropy, where we depict the distribution over a Haar random state in the whole Hilbert space
(red), that in the symmetric subspace
(purple), and that in the translation invariant subspace
with
(blue). As we showed analytically, the distribution of random symmetric state significantly differs from the fully random one, whereas that of the random translation invariant state does not. It is however hard to observe any features of entanglement phases since the distribution is highly concentrated.
Panels (B), (C), (D-I), and (D-II) are the distribution of entanglement in terms of the rescaled purity
R of a reduced density matrix defined by
Note that
and is less when the state
is more entangled. Panels (B), (C), (D-I), and (D-II) are, respectively, for a random state in the whole Hilbert space, a random symmetric state, a random translation invariant state with
, and a translation invariant state with
.
Let us first check the distribution in the whole Hilbert space (Panel (B)). In this case, the probability density function was studied in great detail [
31], with which we compare our numerical result. In terms of the rescaled purity, it is known that the probability density function
over a random state in the whole space has two singularities in the asymptotic limit
: one is at
, and the other is at
. These two singularities split the distribution into three entangled phases, namely the maximally entangled phase for
, the typical phase for
, and the separable phase
. In our numerics, it is hard to clearly observe the singularities. In particular, there is no feature of the phase transition at
at all. This is simply because the probability density function
for
scales as
. Thus, for
,
, which is intractable by a numerical sampling method. On the other hand, a trace of the phase transition at
can be observed from our numerical plot. In particular, by looking at the inset of Panel (B), where we plotted
as a function of
s, we observe that the function is quadratic when
, but gradually becomes less for
. This is consistent with the analysis in Ref. [
31] and can be considered as a feature of the phase transition at
. Note that the phase transition at
is pointed out to be sensitive to the finite-size effect, resulting in the feature less drastic in our numerics with
being 5.
We now move onto the distributions of the rescaled purity for a random symmetric state and random translation invariant states, which are shown in Panels (C) and (D), respectively. For random translation invariant states, the
is chosen to be 0 and
in Panels (D-I) and (D-II), respectively, but similar behaviors are observed for other
’s. Although we do not observe clear singularities, which is similar to the case of a random state in the whole space, the insets show that
where
. This change of the scaling in terms of
s shall indicate the presence of the phase transition between the typical and the separable phases. Hence, it seems that even when the state has permutation or translation symmetry, the typical and the separable phases exist. On the other hand, it remains open whether the maximally entangled phase exists for random symmetric/translation invariant states.
9. Is Generic Entanglement with Symmetry Physical?
Before we conclude the paper, we make a remark on the question of whether generic entanglement is physically feasible. In the case of generic entanglement without symmetry, this question arises from the fact that a Haar random state cannot be efficiently generated by quantum circuits even approximately. Hence, it takes exponentially long time for the distribution of a Haar random state to be achieved by any physical dynamics as far as it consists of a-few-body interactions.
Although it is true that a Haar random state is not physically feasible, recent developments of the theory of
unitary designs [
43] show that the distribution mimicking lower statistical moments of a Haar random state can be quickly generated by quantum circuits [
44,
45,
46,
47,
48] or even by Hamiltonian dynamics [
49,
50]. Also, much evidence was obtained that showed that chaotic dynamics result in properties similar to those of a Haar random state [
16,
17,
18,
51,
52,
53]. In particular, entanglement properties of a Haar random state can be approximately reproduced in many different ways [
54,
55,
56,
57]. Thus, generic entanglement, although it is an idealization in a strict sense, shall be considered to capture characteristic properties of complex quantum many-body systems and hence, physically feasible.
Regarding the generic entanglement of quantum states with symmetry, an interesting question from this perspective is that: is it possible to efficiently implement a random state
with symmetry by quantum circuits or by the dynamics of quantum many-body systems? A natural way to achieve this is to first generate a random state by the aforementioned means and then change the basis into symmetric one. It will be however more interesting from the physics perspective if one can find a way that has natural interpretations in terms of Hamiltonian dynamics with reasonably physical Hamiltonian, such as those with few-body interactions and with less time-dependence. To do so in a rigorous manner, it is highly desired to investigate physically feasible constructions of unitary designs with symmetry, which we may call
symmetric unitary designs. Since unitary designs transform any pure state to the one that has similar properties of Haar random states, applying a symmetric unitary design to a pure state will reproduce generic entanglement of random states with symmetry that we clarified in this paper. Hence, by exploiting physically natural constructions of symmetric unitary designs, the connection of our analysis to complex quantum many-body systems with symmetry will be much more elaborated. Note, however, that a couple of results have been obtained along a similar line [
58,
59], which already indicates that generic entanglement of random states with symmetry reveals characteristic features in those systems.
10. Summary and Discussions
In this paper, we studied how symmetry affects the properties of generic entanglement. Specifically, we investigated the entanglement entropy of a Haar random state in the invariant subspace with respect to a given symmetry. The main technical tool is the concentration formula for the entanglement entropy of a random state. We have first extended it to the one applicable for any subspace, and then applied it to invariant subspaces of axial, permutation, and translation symmetries. It turns out that compared to the entanglement entropy of a random state in the whole Hilbert space, the axial symmetry often reduces entanglement by a constant degree, and that there is a significant reduction by the permutation symmetry. In contrast, the translation symmetry does not reduce entanglement entropy so much, implying that the same properties of generic entanglement without symmetry shall be observed even in the systems with translation symmetry.
Towards the problem of how symmetry affects generic entanglement, these results imply that even when a random state has symmetry, the concentration formula still holds as shown in Theorem 2. In contrast, it is likely that imposing symmetry reduces entanglement, at least for the symmetries we considered in this paper. The degree of reduction is, however, highly dependent on what symmetry is imposed. By closely looking at our results, it is observed that the degree of reduction is related to the size of the invariant subspaces of the symmetry. Whether this is always the case for any symmetry will be left open as a future problem.
We have also numerically studied the presence of the entanglement phases that are observed for a Haar random state without symmetry. Our numerical analysis is far from conclusive due to the fact that the entanglement phases are sensitive to the finite-size effect, we showed that the typical and separable phases seem to exist even when the state has permutation or the translation symmetry.
We think that our analysis opens a number of open questions. First, as we mentioned above, it is important to clarify whether or not imposing symmetry always reduces entanglement entropy and, if so, whether the degree of reduction is always determined by the size of the invariant subspaces. Although we may naturally expect these to be true, we dealt only with abelian symmetries in this paper. Hence, there still remains a possibility that a random state with non-abelian symmetry may result in more exotic features of entanglement.
It will be also interesting to investigate multipartite entanglement of a random state with symmetry. In the case of a Haar random state without symmetry, this is addressed in Refence [
60], where it was shown that most Haar random states are too entangled to be useful as computational resources. Recalling that entanglement is likely to be reduced by imposing symmetry, it may be possible to use random states with symmetry, for instance the one with permutation symmetry, as a computational resource. Thus, investigating multipartite entanglement of random states is not only of theoretical interest but may also be of practical use.
It is also important to address generic entanglement of mixed states. There are however a number of difficulties around the question. First, unlike the pure state, where a random state can be uniquely defined using the uniqueness of the Haar measure, there is no unique or a priori way to define random mixed states. Although there are several attempts to define random mixed states, e.g., in Ref. [
24], it seems that no consensus has been made yet. It is also difficult to evaluate entanglement of mixed states since the entropy of a reduced density matrix is no longer a measure of entanglement. Hence, addressing generic entanglement of mixed states, though it is an interesting problem, may need more elaborate technique.