Patient No-Show Prediction: A Systematic Literature Review
Abstract
1. Introduction
2. Methods
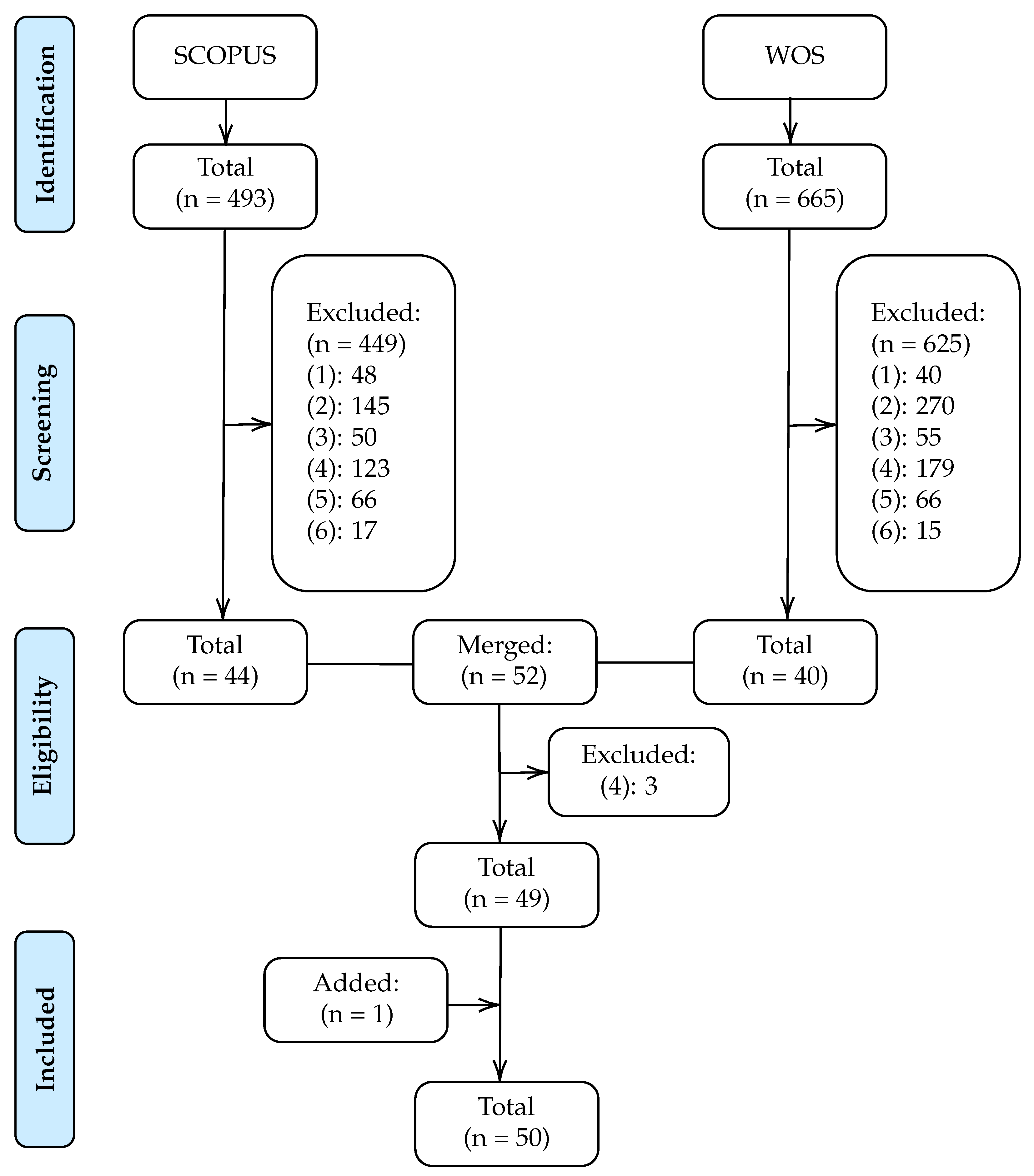
2.1. Bibliographic Databases and Search Criteria
2.2. Study Selection
- The article does not focus on the field of health. For example, articles that focus on predicting no-shows on airplanes or in restaurants.
- The article does not focus on predicting no-shows. For instance, articles in the health field that focus on predicting a dependent variable other than no-shows such as treatment non-adherence.
- The article focuses exclusively on developing a scheduling system.
- The article focuses only on identifying which factors are related to the non-attendance of the patient without focusing on classification rates or other performance measures.
- The article analyses the incidence of a factor in the no-show rate. For example, the impact of sending phone reminders on reducing the no-show rate.
- The article provides only descriptive statistics on the relationship between the factors and the no-show dependent variable.
2.3. Summary Measures
- (i)
- Year of publication.
- (ii)
- Characteristics of the database. Number of patients, number of appointments and duration of the data collection.
- (iii)
- No-show rate. Percentage of no-show on the whole database.
- (iv)
- Set-up. Performance evaluation framework used. It is given by a triplet [x, y, z] that contains the data proportion employed for train, validation, and test, respectively, or by “CV” if a cross-validation framework was employed.
- (v)
- New patients. Indicate if patient’s first visit is included in the analysis.
- (vi)
- Prediction model. Classification model used in the classification problem.
- (vii)
- Performance Measures. Metrics used to evaluate the model performance and its value.
- (viii)
- Feature selection. Whether or not variable selection was applied, and if so, which technique was used. This is complemented with information on the most important variables found in each study.
- (ix)
- Service: If the study was conducted in a primary care center, in a specialty, or both.
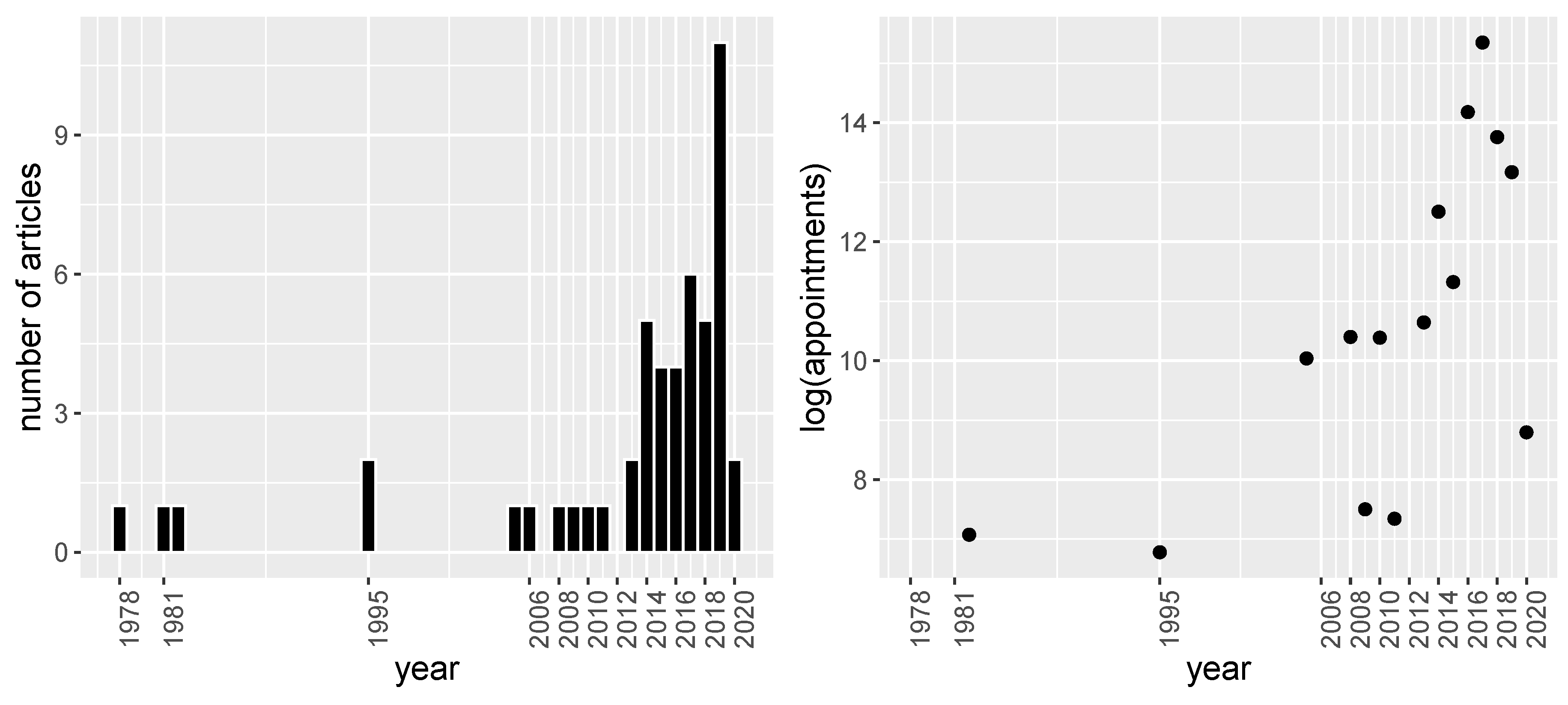
3. Results
3.1. Regression Models
3.2. Tree Based Models
3.3. Neural Networks
3.4. Markov Based Models
3.5. Bayesian Models
3.6. Ensemble/Stacking Methods
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ACC | Accuracy |
| ARM | Association Rule Mining |
| AUC | Area under the receiver operating characteristic curve |
| BN | Bayesian Network |
| BU | Bayesian Update |
| CHAID | Chi-squared automatic interaction detector |
| CV | Cross Validation |
| DT | Decision Tree |
| EHR | Electronic Health Records |
| GA | Genetic Algorithm |
| GB | Gradient Boosting |
| LD | Linear Discriminant |
| LR | Logistic Regression |
| MAS | Mean Absolute Error |
| MELR | Mixed effects Logistic Regression |
| MM | Markov model |
| MSE | Mean Squared Error |
| NN | Neural Network |
| NPV | Negative Predictive Value |
| PRISMA | Preferred Reporting Items for Systematic Reviews and Meta-analyses |
| PPV | Positive Predictive Value |
| RF | Random Forest |
| RMSE | Root Mean Squared Error |
| SACI | Opposition-based Self-Adaptive Cohort Intelligence |
| Sens | Sensitivity |
| SUMER | Sums of exponential for regression |
| WOS | Web of Science |
References
- Martin, C.; Perfect, T.; Mantle, G. Non-attendance in primary care: The views of patients and practices on its causes, impact and solutions. Fam. Pract. 2005, 22, 638–643. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.G.; Wilson-Witherspoon, P.; Probst, J.C. Time and money: Effects of no-shows at a family practice residency clinic. Fam. Med. 2001, 33, 522–527. [Google Scholar] [PubMed]
- Kennard, J. UK: Missed Hospital Appointments Cost NHS £ 600 million. Digit. J. 2009. [Google Scholar]
- Schectman, J.M.; Schorling, J.B.; Voss, J.D. Appointment adherence and disparities in outcomes among patients with diabetes. J. Gen. Intern. Med. 2008, 23, 1685. [Google Scholar] [CrossRef] [PubMed]
- Chariatte, V.; Berchtold, A.; Akré, C.; Michaud, P.A.; Suris, J.C. Missed appointments in an outpatient clinic for adolescents, an approach to predict the risk of missing. J. Adolesc. Health 2008, 43, 38–45. [Google Scholar] [CrossRef]
- Satiani, B.; Miller, S.; Patel, D. No-show rates in the vascular laboratory: Analysis and possible solutions. J. Vasc. Interv. Radiol. 2009, 20, 87–91. [Google Scholar] [CrossRef]
- Daggy, J.; Lawley, M.; Willis, D.; Thayer, D.; Suelzer, C.; DeLaurentis, P.C.; Turkcan, A.; Chakraborty, S.; Sands, L. Using no-show modeling to improve clinic performance. Health Inform. J. 2010, 16, 246–259. [Google Scholar] [CrossRef]
- Hasvold, P.E.; Wootton, R. Use of telephone and SMS reminders to improve attendance at hospital appointments: A systematic review. J. Telemed. Telecare 2011, 17, 358–364. [Google Scholar] [CrossRef]
- Cayirli, T.; Veral, E. Outpatient scheduling in health care: A review of literature. Prod. Oper. Manag. 2003, 12, 519–549. [Google Scholar] [CrossRef]
- Gupta, D.; Denton, B. Appointment scheduling in health care: Challenges and opportunities. IIE Trans. 2008, 40, 800–819. [Google Scholar] [CrossRef]
- Ahmadi-Javid, A.; Jalali, Z.; Klassen, K.J. Outpatient appointment systems in healthcare: A review of optimization studies. Eur. J. Oper. Res. 2017, 258, 3–34. [Google Scholar] [CrossRef]
- Dantas, L.F.; Fleck, J.L.; Oliveira, F.L.C.; Hamacher, S. No-shows in appointment scheduling—A systematic literature review. Health Policy 2018, 122, 412–421. [Google Scholar] [CrossRef] [PubMed]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Ann. Intern. Med. 2009, 151, 264–269. [Google Scholar] [CrossRef] [PubMed]
- Dervin, J.V.; Stone, D.L.; Beck, C.H. The no-show patient in the model family practice unit. J. Fam. Pract. 1978, 7, 1177–1180. [Google Scholar] [PubMed]
- Goldman, L.; Freidin, R.; Cook, E.F.; Eigner, J.; Grich, P. A multivariate approach to the prediction of no-show behavior in a primary care center. Arch. Intern. Med. 1982, 142, 563–567. [Google Scholar] [CrossRef]
- Lee, V.J.; Earnest, A.; Chen, M.I.; Krishnan, B. Predictors of failed attendances in a multi-specialty outpatient centre using electronic databases. BMC Health Hervices Res. 2005, 5, 51. [Google Scholar] [CrossRef]
- Qu, X.; Rardin, R.L.; Tieman, L.; Wan, H.; Williams, J.A.S.; Willis, D.R.; Rosenman, M.B. A statistical model for the prediction of patient non-attendance in a primary care clinic. In Proceedings of the IIE Annual Conference, Orlando, FL, USA, 20–24 May 2006; p. 1. [Google Scholar]
- Alaeddini, A.; Yang, K.; Reddy, C.K.; Yu, S. A probabilistic model for predicting the probability of no-show in hospital appointments. Health Care Manag. Sci. 2011, 14, 146–157. [Google Scholar] [CrossRef]
- Alaeddini, A.; Yang, K.; Reeves, P.; Reddy, C.K. A hybrid prediction model for no-shows and cancellations of outpatient appointments. IIE Trans. Healthc. Syst. Eng. 2015, 5, 14–32. [Google Scholar] [CrossRef]
- Cronin, P.R.; DeCoste, L.; Kimball, A.B. A multivariate analysis of dermatology missed appointment predictors. JAMA Dermatol. 2013, 149, 1435–1437. [Google Scholar] [CrossRef]
- Norris, J.B.; Kumar, C.; Chand, S.; Moskowitz, H.; Shade, S.A.; Willis, D.R. An empirical investigation into factors affecting patient cancellations and no-shows at outpatient clinics. Decis. Support Syst. 2014, 57, 428–443. [Google Scholar] [CrossRef]
- Ma, N.L.; Khataniar, S.; Wu, D.; Ng, S.S.Y. Predictive analytics for outpatient appointments. In Proceedings of the 2014 International Conference on Information Science & Applications (ICISA), Amman, Jordan, 29–30 December 2014; pp. 1–4. [Google Scholar]
- Huang, Y.L.; Hanauer, D.A. Patient no-show predictive model development using multiple data sources for an effective overbooking approach. Appl. Clin. Inform. 2014, 5, 836–860. [Google Scholar] [PubMed]
- Woodward, B.; Person, A.; Rebeiro, P.; Kheshti, A.; Raffanti, S.; Pettit, A. Risk prediction tool for medical appointment attendance among HIV-infected persons with unsuppressed viremia. AIDS Patient Care STDs 2015, 29, 240–247. [Google Scholar] [CrossRef] [PubMed]
- Torres, O.; Rothberg, M.B.; Garb, J.; Ogunneye, O.; Onyema, J.; Higgins, T. Risk factor model to predict a missed clinic appointment in an urban, academic, and underserved setting. Popul. Health Manag. 2015, 18, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Blumenthal, D.M.; Singal, G.; Mangla, S.S.; Macklin, E.A.; Chung, D.C. Predicting non-adherence with outpatient colonoscopy using a novel electronic tool that measures prior non-adherence. J. Gen. Intern. Med. 2015, 30, 724–731. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Erdem, E.; Shi, J.; Masek, C.; Woodbridge, P. Large-scale assessment of missed opportunity risks in a complex hospital setting. Inform. Health Soc. Care 2016, 41, 112–127. [Google Scholar] [CrossRef]
- Harris, S.L.; May, J.H.; Vargas, L.G. Predictive analytics model for healthcare planning and scheduling. Eur. J. Oper. Res. 2016, 253, 121–131. [Google Scholar] [CrossRef]
- Huang, Y.L.; Hanauer, D.A. Time dependent patient no-show predictive modelling development. Int. J. Health Care Qual. Assur. 2016, 29, 475–488. [Google Scholar] [CrossRef] [PubMed]
- Kurasawa, H.; Hayashi, K.; Fujino, A.; Takasugi, K.; Haga, T.; Waki, K.; Noguchi, T.; Ohe, K. Machine- learning-based prediction of a missed scheduled clinical appointment by patients with diabetes. J. Diabetes Sci. Technol. 2016, 10, 730–736. [Google Scholar] [CrossRef]
- Alaeddini, A.; Hong, S.H. A Multi-way Multi-task Learning Approach for Multinomial Logistic Regression. Methods Inf. Med. 2017, 56, 294–307. [Google Scholar]
- Goffman, R.M.; Harris, S.L.; May, J.H.; Milicevic, A.S.; Monte, R.J.; Myaskovsky, L.; Rodriguez, K.L.; Tjader, Y.C.; Vargas, D.L. Modeling patient no-show history and predicting future outpatient appointment behavior in the veterans health administration. Mil. Med. 2017, 182, e1708–e1714. [Google Scholar] [CrossRef]
- Harvey, H.B.; Liu, C.; Ai, J.; Jaworsky, C.; Guerrier, C.E.; Flores, E.; Pianykh, O. Predicting no-shows in radiology using regression modeling of data available in the electronic medical record. J. Am. Coll. Radiol. 2017, 14, 1303–1309. [Google Scholar] [CrossRef] [PubMed]
- Gromisch, E.S.; Turner, A.P.; Leipertz, S.L.; Beauvais, J.; Haselkorn, J.K. Who is not coming to clinic? A predictive model of excessive missed appointments in persons with multiple sclerosis. Mult. Scler. Relat. Disord. 2020, 38, 101513. [Google Scholar] [CrossRef] [PubMed]
- Mieloszyk, R.J.; Rosenbaum, J.I.; Bhargava, P.; Hall, C.S. Predictive modeling to identify scheduled radiology appointments resulting in non-attendance in a hospital setting. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Korea, 11–15 July 2017; pp. 2618–2621. [Google Scholar]
- Ding, X.; Gellad, Z.F.; Mather, C.; Barth, P.; Poon, E.G.; Newman, M.; Goldstein, B.A. Designing risk prediction models for ambulatory no-shows across different specialties and clinics. J. Am. Med Inform. Assoc. 2018, 25, 924–930. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Betancourt, B.; Goldstein, B.A.; Steorts, R.C. Prediction of appointment no-shows using electronic health records. J. Appl. Stat. 2020, 47, 1220–1234. [Google Scholar] [CrossRef]
- Lenzi, H.; Ben, Â.J.; Stein, A.T. Development and validation of a patient no-show predictive model at a primary care setting in Southern Brazil. PLoS ONE 2019, 14, e0214869. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Tang, S.Y.; Johnson, J.; Lubarsky, D.A. Individualized No-show Predictions: Effect on Clinic Overbooking and Appointment Reminders. Prod. Oper. Manag. 2019, 28, 2068–2086. [Google Scholar] [CrossRef]
- Ahmad, M.U.; Zhang, A.; Mhaskar, R. A predictive model for decreasing clinical no-show rates in a primary care setting. Int. J. Healthc. Manag. 2019. [Google Scholar] [CrossRef]
- Chua, S.L.; Chow, W.L. Development of predictive scoring model for risk stratification of no-show at a public hospital specialist outpatient clinic. Proc. Singap. Healthc. 2019, 28, 96–104. [Google Scholar] [CrossRef]
- Dantas, L.F.; Hamacher, S.; Oliveira, F.L.C.; Barbosa, S.D.; Viegas, F. Predicting Patient No-show Behavior: A Study in a Bariatric Clinic. Obes. Surg. 2019, 29, 40–47. [Google Scholar] [CrossRef]
- Dove, H.G.; Schneider, K.C. The usefulness of patients’ individual characteristics in predicting no-shows in outpatient clinics. Med. Care 1981, 19, 734–740. [Google Scholar] [CrossRef]
- Bean, A.B.; Talaga, J. Predicting appointment breaking. Mark. Health Serv. 1995, 15, 29. [Google Scholar]
- Glowacka, K.J.; Henry, R.M.; May, J.H. A hybrid data mining/simulation approach for modelling outpatient no-shows in clinic scheduling. J. Oper. Res. Soc. 2009, 60, 1056–1068. [Google Scholar] [CrossRef]
- Lotfi, V.; Torres, E. Improving an outpatient clinic utilization using decision analysis-based patient scheduling. Socio-Econ. Plan. Sci. 2014, 48, 115–126. [Google Scholar] [CrossRef]
- Devasahay, S.R.; Karpagam, S.; Ma, N.L. Predicting appointment misses in hospitals using data analytics. MHealth 2017, 3. [Google Scholar] [CrossRef] [PubMed]
- Alloghani, M.; Aljaaf, A.J.; Al-Jumeily, D.; Hussain, A.; Mallucci, C.; Mustafina, J. Data Science to Improve Patient Management System. In Proceedings of the 2018 11th International Conference on Developments in eSystems Engineering (DeSE), Cambridge, UK, 2–5 September 2018; pp. 27–30. [Google Scholar]
- Praveena, M.A.; Krupa, J.S.; SaiPreethi, S. Statistical Analysis of Medical Appointments Using Decision Tree. In Proceedings of the 2019 Fifth International Conference on Science Technology Engineering and Mathematics (ICONSTEM), Chennai, India, 14–15 March 2019; Volume 1, pp. 59–64. [Google Scholar]
- AlMuhaideb, S.; Alswailem, O.; Alsubaie, N.; Ferwana, I.; Alnajem, A. Prediction of hospital no-show appointments through artificial intelligence algorithms. Ann. Saudi Med. 2019, 39, 373–381. [Google Scholar] [CrossRef] [PubMed]
- Aladeemy, M.; Adwan, L.; Booth, A.; Khasawneh, M.T.; Poranki, S. New feature selection methods based on opposition-based learning and self-adaptive cohort intelligence for predicting patient no-shows. Appl. Soft Comput. 2020, 86, 105866. [Google Scholar] [CrossRef]
- Snowden, S.; Weech, P.; McClure, R.; Smye, S.; Dear, P. A neural network to predict attendance of paediatric patients at outpatient clinics. Neural Comput. Appl. 1995, 3, 234–241. [Google Scholar] [CrossRef]
- Dravenstott, R.; Kirchner, H.L.; Strömblad, C.; Boris, D.; Leader, J.; Devapriya, P. Applying Predictive Modeling to Identify Patients at Risk to No-Show. In Proceedings of the IIE Annual Conference, Montreal, QC, Canada, 31 May–3 June 2014; p. 2370. [Google Scholar]
- Dashtban, M.; Li, W. Deep learning for predicting non-attendance in hospital outpatient appointments. In Proceedings of the 52nd Annual Hawaii International Conference on System Sciences (HICSS), Maui, HI, USA, 8–11 January 2019; pp. 3731–3740. [Google Scholar]
- Levy, V. A predictive tool for nonattendance at a specialty clinic: An application of multivariate probabilistic big data analytics. In Proceedings of the 2013 10th International Conference and Expo on Emerging Technologies for a Smarter World (CEWIT), Melville, NY, USA, 21–22 October 2013; pp. 1–4. [Google Scholar]
- Mohammadi, I.; Wu, H.; Turkcan, A.; Toscos, T.; Doebbeling, B.N. Data Analytics and Modeling for Appointment No-show in Community Health Centers. J. Prim. Care Community Health 2018, 9. [Google Scholar] [CrossRef]
- Topuz, K.; Uner, H.; Oztekin, A.; Yildirim, M.B. Predicting pediatric clinic no-shows: A decision analytic framework using elastic net and Bayesian belief network. Ann. Oper. Res. 2018, 263, 479–499. [Google Scholar] [CrossRef]
- Lee, G.; Wang, S.; Dipuro, F.; Hou, J.; Grover, P.; Low, L.L.; Liu, N.; Loke, C.Y. Leveraging on Predictive Analytics to Manage Clinic No Show and Improve Accessibility of Care. In Proceedings of the 2017 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Tokyo, Japan, 19–21 October 2017; pp. 429–438. [Google Scholar]
- Elvira, C.; Ochoa, A.; Gonzalvez, J.C.; Mochón, F. Machine-Learning-Based No Show Prediction in Outpatient Visits. Int. J. Interact. Multimed. Artif. Intell. 2018, 4, 29–34. [Google Scholar] [CrossRef]
- Srinivas, S.; Ravindran, A.R. Optimizing outpatient appointment system using machine learning algorithms and scheduling rules: A prescriptive analytics framework. Expert Syst. Appl. 2018, 102, 245–261. [Google Scholar] [CrossRef]
- Ahmadi, E.; Garcia-Arce, A.; Masel, D.T.; Reich, E.; Puckey, J.; Maff, R. A metaheuristic-based stacking model for predicting the risk of patient no-show and late cancellation for neurology appointments. IISE Trans. Healthc. Syst. Eng. 2019, 9, 272–291. [Google Scholar] [CrossRef]
- Deyo, R.A.; Inui, T.S. Dropouts and broken appointments: A literature review and agenda for future research. Med. Care 1980, 10, 1146–1157. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Wang, G.; Guan, G. Weighted Mean Squared Deviation Feature Screening for Binary Features. Entropy 2020, 22, 335. [Google Scholar] [CrossRef]
- Furmańczyk, K.; Rejchel, W. Prediction and Variable Selection in High-Dimensional Misspecified Binary Classification. Entropy 2020, 22, 543. [Google Scholar] [CrossRef]
| Keywords | |
|---|---|
| non-attendance OR missed-appointment* OR no-show* | |
| (i) | OR broken-appointment* OR missed-clinic-appointment* |
| OR appointment-no-show* | |
| (ii) | predict* |
| (iii) | (i) AND (ii) |
| Articles | Patients | Appointments | Months | Service | No-Show Rate | Set-Up | New Patient | Feature Selection | Model | Performance Measures |
|---|---|---|---|---|---|---|---|---|---|---|
| Dervin et al., 1978 | 291 | - | × | Primary Care | 27 | [1,0,0] | × | - | LR, LD | 67.4 (ACC) |
| Dove and Schneider, 1981 | 1333 | - | 12 | Specialty | 24.5 | [1,0,0] | × | embedded | DT | 14.8 (MAE) |
| Goldman et al., 1982 | 376 | 1181 | 6 | Primary Care | 18 | [2/3,0,1/3] | - | filter | LR | - |
| Snowden et al., 1995 | 190 | - | 6 | Specialty | 20 | [3/4,0,1/4] | × | - | NN | 91.11 (ACC) |
| Bean and Talaga, 1995 | - | 879 | 4 | Both | 38.1 | [1,0,0] | - | - | DT | - |
| Lee et al., 2005 | 22,864 | 22,864 | 48 | Specialty | 21 | [1,0,0] | - | - | LR | 0.84 (AUC) |
| Qu et al., 2006 | - | - | 24 | Primary Care | - | [1,0,0] | × | - | LR | 3.6 (RMSE) |
| Chariatte et al., 2008 | 2193 | 32,816 | 96 | Specialty | - | [1,0,0] | - | - | MM | - |
| Glowacka et al., 2009 | - | 1809 | 9 | Both | - | [1,0,0] | × | - | ARM | - |
| Daggy et al., 2010 | 5446 | 32,394 | 36 | Specialty | 15.2 | [2/3,0,1/3] | - | wrapper | LR | 0.82 (AUC) |
| Alaeddini et al., 2011 | 99 | 1543 | 2 | - | - | [1/3,1/3,1/3] | × | - | LR-BU | 79.9 (ACC) |
| Cronin et al., 2013 | - | 41,893 | 22 | Specialty | 18.6 | [1,0,0] | × | filter | LR | - |
| Levy, 2013 | 4774 | - | 12 | Specialty | 16 | [1/2,1/4,1/4] | × | - | BN | 60–65 (Sens) |
| Norris et al., 2014 | 88,345 | 858,579 | 60 | Primary Care | 9.9 | [3/5,0,2/5] | - | filter | LR, DT | 81.5 (ACC) |
| Dravenstott et al., 2014 | - | 103,152 | 24 | Both | 9.1 | [0.60,0.15,0.25] | - | filter | NN | 87 (ACC) |
| Lotfi and Torres, 2014 | 367 | 367 | 5 | Specialty | 16 | [0.55, 0, 0.45] | × | embedded | DT | 78 (ACC) |
| Huang and Hanauer, 2014 | 7988 | 104,799 | 120 | Specialty | 11.2 | [4/5,0,1/5] | × | filter | LR | 86.1 (ACC) |
| Ma et al., 2014 | - | 279,628 | 6 | Primary Care | 19.2 | [1/3,1/3,1/3] | × | - | LR, DT | 65 (ACC) |
| Alaeddini et al., 2015 | 99 | 1543 | 2 | - | 22.6 | [1/3,1/3,1/3] | × | - | LR-BU | 0.072 (MSE) |
| Blumenthal et al., 2015 | 1432 | - | 22 | Specialty | 13.69 | [0.78,0,0.22] | × | filter | LR | 0.702 (AUC) |
| Torres et al., 2015 | 11,546 | 163,554 | 29 | Specialty | 45 | [7/10,0,3/10] | × | filter | LR | 0.71 (AUC) |
| Woodward et al., 2015 | 510 | - | 8 | Specialty | 27.25 | [1,0,0] | × | filter | LR | - |
| Peng et al., 2016 | - | 881,933 | 24 | - | - | [1,0,0] | × | - | LR | 0.706 (AUC) |
| Kurasawa et al., 2016 | 879 | 16,026 | 39 | Specialty | 5.8 | 10 Fold CV | - | embedded | L2-LR | 0.958 (AUC) |
| Harris et al., 2016 | +79,346 | 4,760,733 | 60 | - | 8.9 | [1/10,0, 9/10] | - | - | SUMER | 0.706 (AUC) |
| Huang and Hanauer, 2016 | 7291 | 93,206 | 120 | Specialty | 17 | [2/3,0,1/3] | × | filter | LR | 0.706 (AUC) |
| Lee et al., 2017 | - | 1 million | 24 | Specialty | 25.4 | [2/3,0,1/3] | × | - | GB | 0.832 (AUC) |
| Alaeddini and Hong, 2017 | - | 410 | - | Specialty | - | 5 Fold CV | × | embedded | L1/L2-LR | 80 (ACC) |
| Goffman et al., 2017 | - | 21,551,572 | 48 | Specialty | 13.87 | [5/8,0,3/8] | × | wrapper | LR | 0.713 (AUC) |
| Devasahay et al., 2017 | 410,069 | - | 11 | Specialty | 18.59 | [1,0,0] | × | embedded | LR, DT | 4–23 (Sens) |
| Harvey et al., 2017 | - | 54,652 | 3 | Specialty | 6.5 | [1,0,0] | × | wrapper | LR | 0.753 (AUC) |
| Mieloszyk et al., 2017 | - | 554,611 | 192 | Specialty | - | 5 Fold CV | × | - | LR | 0.77 (AUC) |
| Mohammadi et al., 2018 | 73,811 | 73,811 | 27 | Specialty | 16.7 | 10 * [7/10,0,3/10] | × | - | LR, NN, BN | 0.86 (AUC) |
| Srinivas and Ravindran, 2018 | - | 76,285 | - | Primary Care | - | [2/3,0,1/3] | × | - | Stacking | 0.846 (AUC) |
| Ding et al., 2018 | - | 2,232,737 | 36 | Specialty | 13-32 | [2/3,0,1/3] | × | embedded | L1-LR | 0.83 (AUC) |
| Elvira et al., 2018 | 323,664 | 2,234,119 | 20 | Specialty | 10.6 | [3/5,1/5,1/5] | × | embedded | GB | 0.74 (AUC) |
| Topuz et al., 2018 | 16,345 | 105,343 | 78 | Specialty | - | 10 Fold CV | × | embedded | L1-L2-BN | 0.691 (AUC) |
| Chua and Chow, 2019 | - | 75,677 | 24 | Specialty | 28.6 | [0.35,0.15,0.50] | × | filter | LR | 0.72 (AUC) |
| Alloghani et al., 2018 | - | - | 12 | - | 18.1 | [3/4,0,1/4] | × | - | DT, LR | 3–25 (Sens) |
| AlMuhaideb et al., 2019 | - | 1,087,979 | 12 | Specialty | 11.3 | 10 Fold CV | × | embedded | DT | 76.5 (ACC) |
| Dantas et al., 2019 | 2660 | 13,230 | 17 | Specialty | 21.9 | [3/4,0,1/4] | × | filter | LR | 71 (ACC) |
| Dashtban and Li, 2019 | 150,000 | 1,600,000 | 72 | Primary Care | - | [0.63, 0.12, 25] | × | - | NN | 0.71 (AUC) |
| Ahmadi et al., 2019 | - | 194,458 | 36 | Specialty | 23 | [70(CV),30] | × | wrapper | GA-RF | 0.697 (AUC) |
| Lin et al., 2019 | - | 2,000,000 | 36 | Specialty | 18 | [0.8,0,0.2] | × | embedded | Bay. Lasso | 0.70–0.92 (AUC) |
| Lenzi et al., 2019 | 5637 | 40,740 | 36 | Primary Care | 13 | [1/2,0,1/2] | × | wrapper | MELR | 0.81 (AUC) |
| Praveena et al., 2019 | - | 100,000 | - | Specialty | 20 | [1,0,0] | × | - | LR, DT | 89.6 (ACC) |
| Li et al., 2019 | 42,903 | 115,751 | 12 | Specialty | 18 | [0.80,0,0.20] | × | - | MELR | 0.886 (AUC) |
| Ahmad et al., 2019 | - | 10,329 | 48 | Primary Care | - | [2/3,0,1/3] | × | - | Probit R. | 0.70 (AUC) |
| Gromisch et al., 2020 | 3742 | - | 24 | Specialty | - | [1,0,0] | × | x | LR | 75 (Sens) |
| Aladeemy et al., 2020 | - | 6599 | 10 | Primary Care | 18.58 | [0.70,0,0.30] | × | wrapper | SACI-DT | 0.72 (AUC) |
| Articles | Patient Demographic | Medical History | Appointment Detail | Patient Behaviour | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age | Gender | Language | Race/Etnicity | Employment | Marital Status | Economic Status | Education Level | Insurance/Paym. | ZIP Code | Distance/Transp. | Religion | Access to Phone | Clinic | Specialty | Previous Visits | Provider | Referral Source | Diagnosis | Case Duration | First/Follow-Up | Month | Weekday | Visit Time | Holiday Indicator | Same Day Visit | Weather | Season | Visit Interval | Lead Time | Waiting Time | Scheduling Mode | Prev. No-Show | Prev. Cancel | Last Visit Status | Visit Late | Satisfaction | |
| Dervin et al., 1978 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||
| Dove and Schneider, 1981 | ∘ | × | ∘ | × | ∘ | × | ∘ | ||||||||||||||||||||||||||||||
| Goldman et al., 1982 | ∘ | × | ∘ | × | × | × | ∘ | ∘ | × | × | ∘ | × | × | ||||||||||||||||||||||||
| Snowden et al., 1995 | × | × | ∘ | ∘ | ∘ | ∘ | ∘ | × | × | × | × | ∘ | × | × | × | ∘ | × | × | |||||||||||||||||||
| Bean and Talaga, 1995 | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||||||
| Lee et al., 2005 | ∘ | × | ∘ | × | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||
| Qu et al., 2006 | ∘ | ∘ | ∘ | ∘ | × | ∘ | |||||||||||||||||||||||||||||||
| Chariatte et al., 2008 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||||
| Glowacka et al., 2009 | ∘ | ∘ | × | × | × | ∘ | ∘ | ∘ | ∘ | ∘ | × | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||
| Daggy et al., 2010 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | × | × | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||
| Alaeddini et al., 2011 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||
| Cronin et al., 2013 | ∘ | × | ∘ | ∘ | × | ∘ | × | ∘ | ∘ | ||||||||||||||||||||||||||||
| Levy, 2013 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||||
| Norris et al., 2014 | ∘ | ∘ | ∘ | ∘ | × | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||
| Dravenstott et al., 2014 | ∘ | × | ∘ | ∘ | ∘ | × | ∘ | × | ∘ | × | ∘ | × | ∘ | ∘ | ∘ | ||||||||||||||||||||||
| Lotfi and Torres | × | × | × | × | × | × | × | ∘ | ∘ | × | |||||||||||||||||||||||||||
| Huang and Hanauer, 2014 | ∘ | × | ∘ | ∘ | ∘ | ∘ | × | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||
| Ma et al., 2014 | ∘ | × | ∘ | ∘ | × | ∘ | × | ∘ | × | ∘ | ∘ | ∘ | × | ∘ | × | ||||||||||||||||||||||
| Alaeddini et al., 2015 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||
| Blumenthal et al., 2015 | × | ∘ | ∘ | × | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||||
| Torres et al., 2015 | ∘ | ∘ | ∘ | × | × | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||
| Woodward et al., 2015 | × | × | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||||||
| Peng et al., 2016 | ∘ | ∘ | ∘ | ∘ | × | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||
| Kurasawa et al., 2016 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||||
| Harris et al., 2016 | ∘ | ||||||||||||||||||||||||||||||||||||
| Huang and Hanauer, 2016 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | × | ∘ | ∘ | ∘ | × | × | ∘ | ||||||||||||||||||||||||
| Lee et al., 2017 | ∘ | × | × | ∘ | × | ∘ | × | × | × | × | × | ∘ | ∘ | × | ∘ | ∘ | × | ∘ | × | × | × | × | × | × | ∘ | ∘ | × | × | × | ∘ | ∘ | ||||||
| Alaeddini and Hong, 2017 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||
| Goffman et al., 2017 | ∘ | ∘ | ∘ | × | ∘ | ∘ | ∘ | × | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||
| Devasahay et al., 2017 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||
| Harvey et al., 2017 | ∘ | ∘ | × | ∘ | × | ∘ | × | ∘ | ∘ | × | ∘ | ∘ | × | ∘ | ∘ | ||||||||||||||||||||||
| Mieloszyk et al., 2017 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||
| Mohammadi et al., 2018 | ∘ | × | × | ∘ | × | × | ∘ | × | ∘ | × | × | ∘ | × | × | ∘ | ∘ | × | ∘ | |||||||||||||||||||
| Srinivas and Ravindran, 2018 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||
| Chua and Chow, 2019 | ∘ | × | ∘ | × | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||
| Ding et al., 2018 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||
| Elvira et al., 2018 | ∘ | × | × | ∘ | ∘ | ∘ | × | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||
| Topuz et al., 2018 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||
| Alloghani et al., 2018 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | × | ∘ | |||||||||||||||||||||||||||
| AlMuhaideb et al., 2019 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||
| Dantas et al., 2019 | × | × | × | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||
| Dashtban and Li, 2019 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||||
| Ahmadi et al., 2019 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||
| Lin et al., 2019 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||
| Lenzi et al., 2019 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||
| Praveena et al., 2019 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | |||||||||||||||||||||||||||||||
| Li et al., 2019 | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||
| Ahmad et al., 2019 | ∘ | × | × | ∘ | ∘ | × | × | ∘ | |||||||||||||||||||||||||||||
| Gromisch et al., 2020 | ∘ | × | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ∘ | ||||||||||||||||||||||||||||
| Aladeemy et al., 2020 | × | × | × | × | × | ∘ | × | ∘ | × | × | ∘ | ∘ | × | ||||||||||||||||||||||||
| Articles | No-Show Rate | AUC | Accuracy | Sensitivity | Specificity | PPV | NPV | Precision | Recall | RMSE | MSE | MAE | F-Measure | G-Measure | TOTAL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dervin et al., 1978 | × | × | 1 | ||||||||||||
| Dove and Schneider, 1981 | × | × | × | 2 | |||||||||||
| Goldman et al., 1982 | × | 0 | |||||||||||||
| Snowden et al., 1995 | × | × | × | × | 3 | ||||||||||
| Bean and Talaga, 1995 | × | 0 | |||||||||||||
| Lee et al., 2005 | × | × | × | × | × | 4 | |||||||||
| Qu et al., 2006 | × | 1 | |||||||||||||
| Chariatte et al., 2008 | 0 | ||||||||||||||
| Glowacka et al., 2009 | 0 | ||||||||||||||
| Daggy et al., 2010 | × | × | 1 | ||||||||||||
| Alaeddini et al., 2011 | × | × | 2 | ||||||||||||
| Cronin et al., 2013 | × | 0 | |||||||||||||
| Levy, 2013 | × | × | × | 2 | |||||||||||
| Norris et al., 2014 | × | × | × | × | 3 | ||||||||||
| Dravenstott et al., 2014 | × | × | × | × | × | × | × | 6 | |||||||
| Lotfi and Torres, 2014 | × | × | × | × | × | × | 5 | ||||||||
| Huang and Hanauer, 2014 | × | × | 1 | ||||||||||||
| Ma et al., 2014 | × | × | 1 | ||||||||||||
| Alaeddini et al., 2015 | × | × | × | 2 | |||||||||||
| Blumenthal et al., 2015 | × | × | × | × | × | × | × | 6 | |||||||
| Torres et al., 2015 | × | × | 1 | ||||||||||||
| Woodward et al., 2015 | × | 0 | |||||||||||||
| Peng et al., 2016 | × | 1 | |||||||||||||
| Kurasawa et al., 2016 | × | × | × | × | × | 4 | |||||||||
| Harris et al., 2016 | × | × | 1 | ||||||||||||
| Huang and Hanauer, 2016 | × | × | 1 | ||||||||||||
| Lee et al., 2017 | × | × | × | × | 3 | ||||||||||
| Alaeddini and Hong, 2017 | × | × | 2 | ||||||||||||
| Goffman et al., 2017 | × | × | 1 | ||||||||||||
| Devasahay et al., 2017 | × | × | × | × | × | 4 | |||||||||
| Harvey et al., 2017 | × | × | 1 | ||||||||||||
| Mieloszyk et al., 2017 | × | 1 | |||||||||||||
| Mohammadi et al., 2018 | × | × | × | × | × | 4 | |||||||||
| Srinivas and Ravindran, 2018 | × | × | × | × | 4 | ||||||||||
| Ding et al., 2018 | × | × | 1 | ||||||||||||
| Elvira et al., 2018 | × | × | × | × | × | × | × | 6 | |||||||
| Topuz et al. | × | × | × | 3 | |||||||||||
| Chua and Chow, 2019 | × | × | 1 | ||||||||||||
| Alloghani et al., 2018 | × | × | × | × | × | 4 | |||||||||
| AlMuhaideb et al., 2019 | × | × | × | × | × | 4 | |||||||||
| Dantas et al., 2019 | × | × | × | × | 3 | ||||||||||
| Dashtban and Li, 2019 | × | × | × | × | 4 | ||||||||||
| Ahmadi et al., 2019 | × | × | × | × | 3 | ||||||||||
| Lin et al., 2019 | × | × | 1 | ||||||||||||
| Lenzi et al., 2019 | × | × | 1 | ||||||||||||
| Praveena et al., 2019 | × | × | × | × | × | × | 5 | ||||||||
| Li et al., 2019 | × | × | 1 | ||||||||||||
| Ahmad et al., 2019 | × | 1 | |||||||||||||
| Gromisch et al., 2020 | × | × | × | 3 | |||||||||||
| Aladeemy et al., 2020 | × | × | × | × | 3 | ||||||||||
| TOTAL | 38 | 29 | 21 | 17 | 17 | 6 | 6 | 4 | 4 | 1 | 2 | 1 | 1 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carreras-García, D.; Delgado-Gómez, D.; Llorente-Fernández, F.; Arribas-Gil, A. Patient No-Show Prediction: A Systematic Literature Review. Entropy 2020, 22, 675. https://doi.org/10.3390/e22060675
Carreras-García D, Delgado-Gómez D, Llorente-Fernández F, Arribas-Gil A. Patient No-Show Prediction: A Systematic Literature Review. Entropy. 2020; 22(6):675. https://doi.org/10.3390/e22060675
Chicago/Turabian StyleCarreras-García, Danae, David Delgado-Gómez, Fernando Llorente-Fernández, and Ana Arribas-Gil. 2020. "Patient No-Show Prediction: A Systematic Literature Review" Entropy 22, no. 6: 675. https://doi.org/10.3390/e22060675
APA StyleCarreras-García, D., Delgado-Gómez, D., Llorente-Fernández, F., & Arribas-Gil, A. (2020). Patient No-Show Prediction: A Systematic Literature Review. Entropy, 22(6), 675. https://doi.org/10.3390/e22060675





