Chaos Control and Synchronization of a Complex Rikitake Dynamo Model
Abstract
1. Introduction
2. A Complex Chaotic Rikitake Dynamo System
2.1. Symmetry
2.2. Dissipation
2.3. Equilibria and Stability
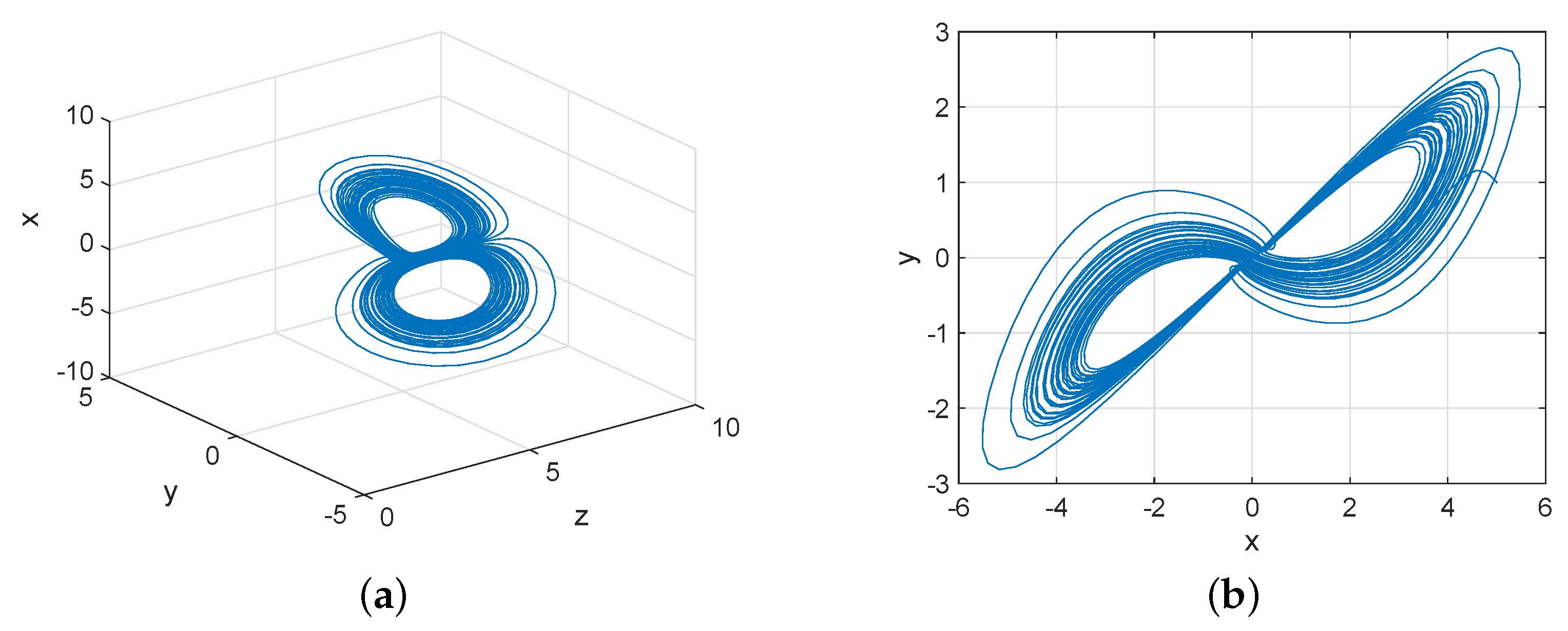
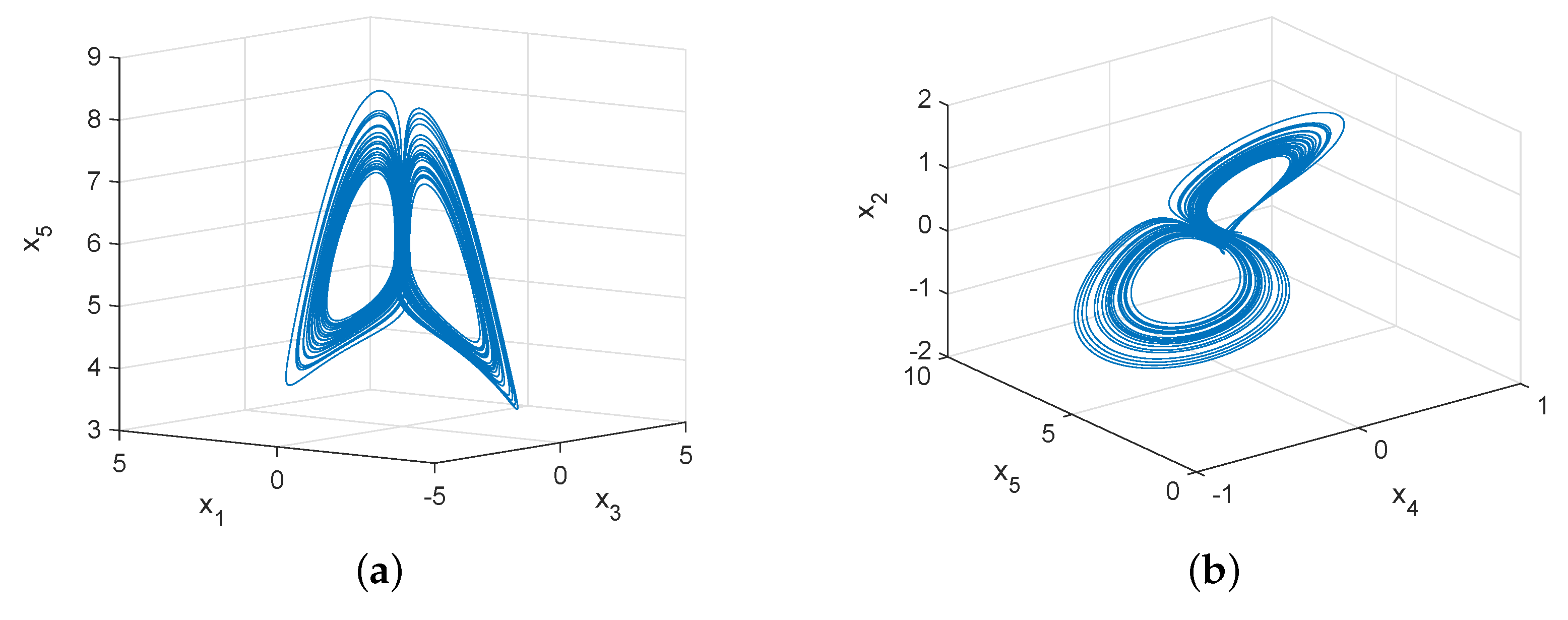
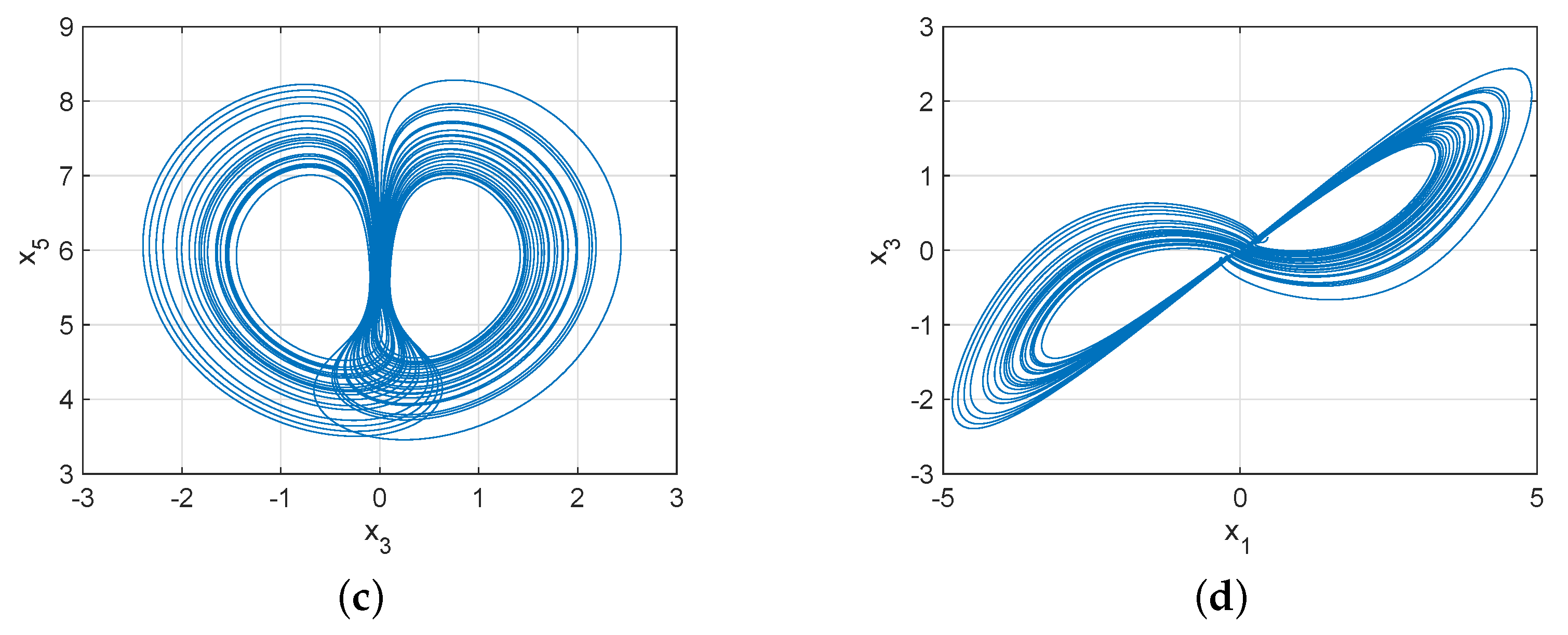
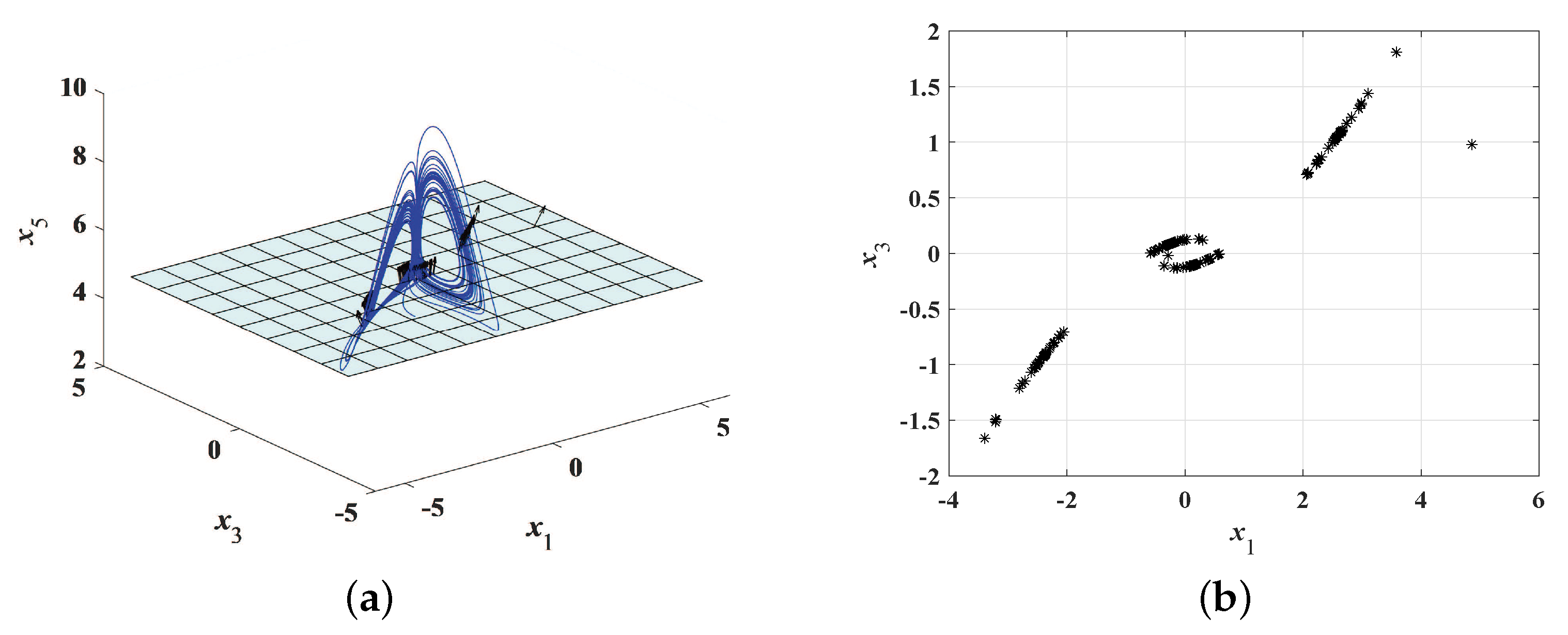
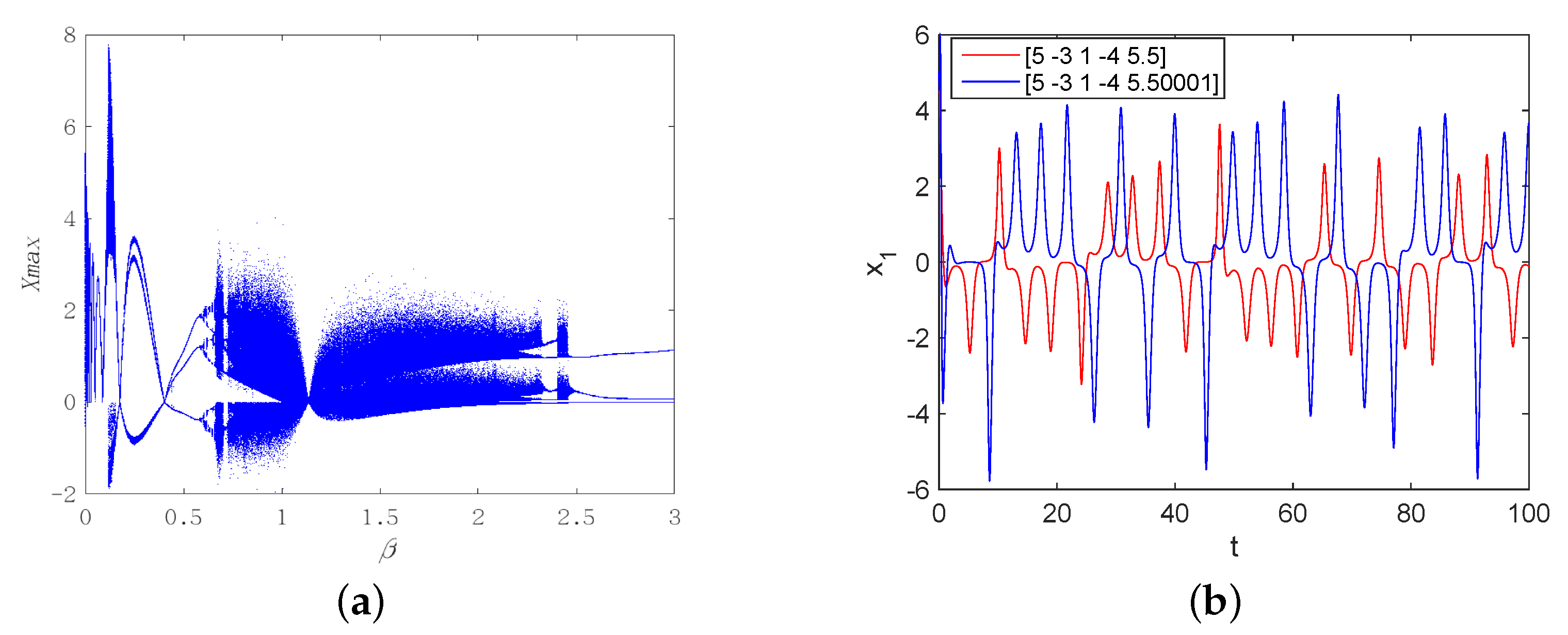
2.4. Chaotic Behavior and Attractors
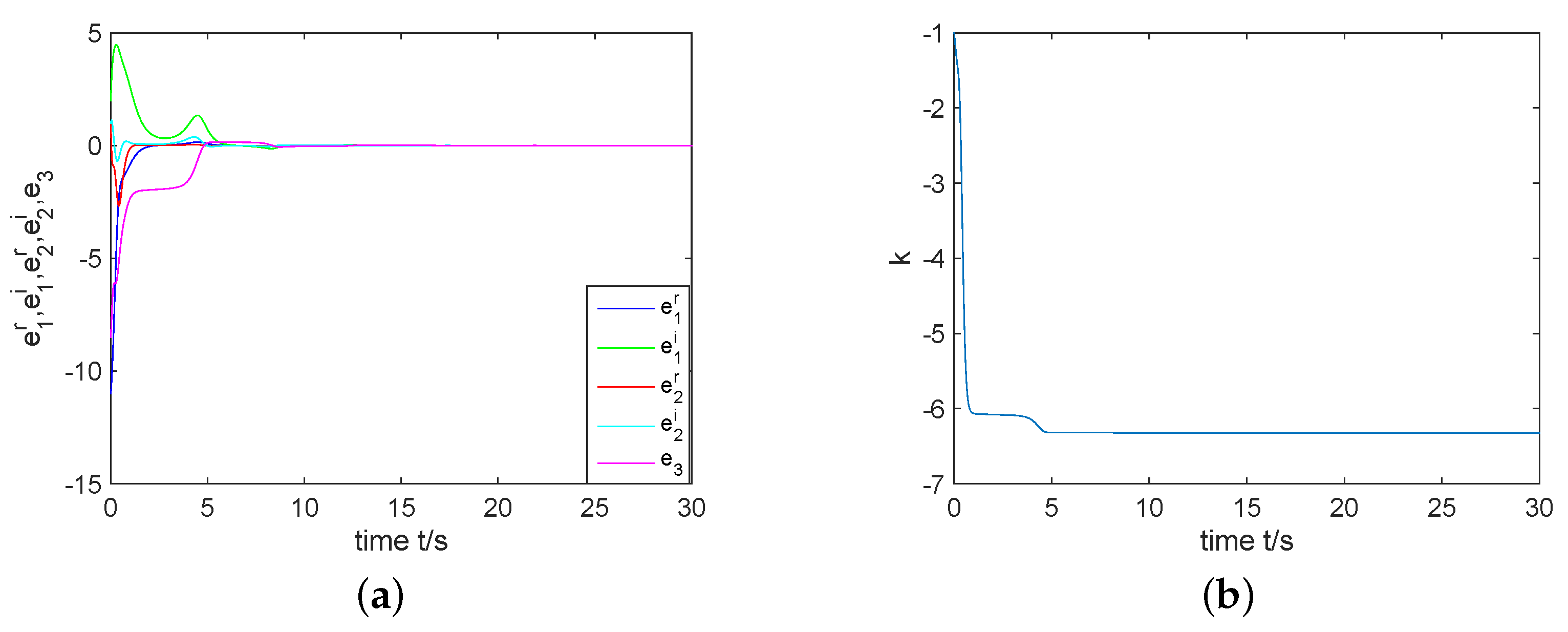
3. Chaos Control
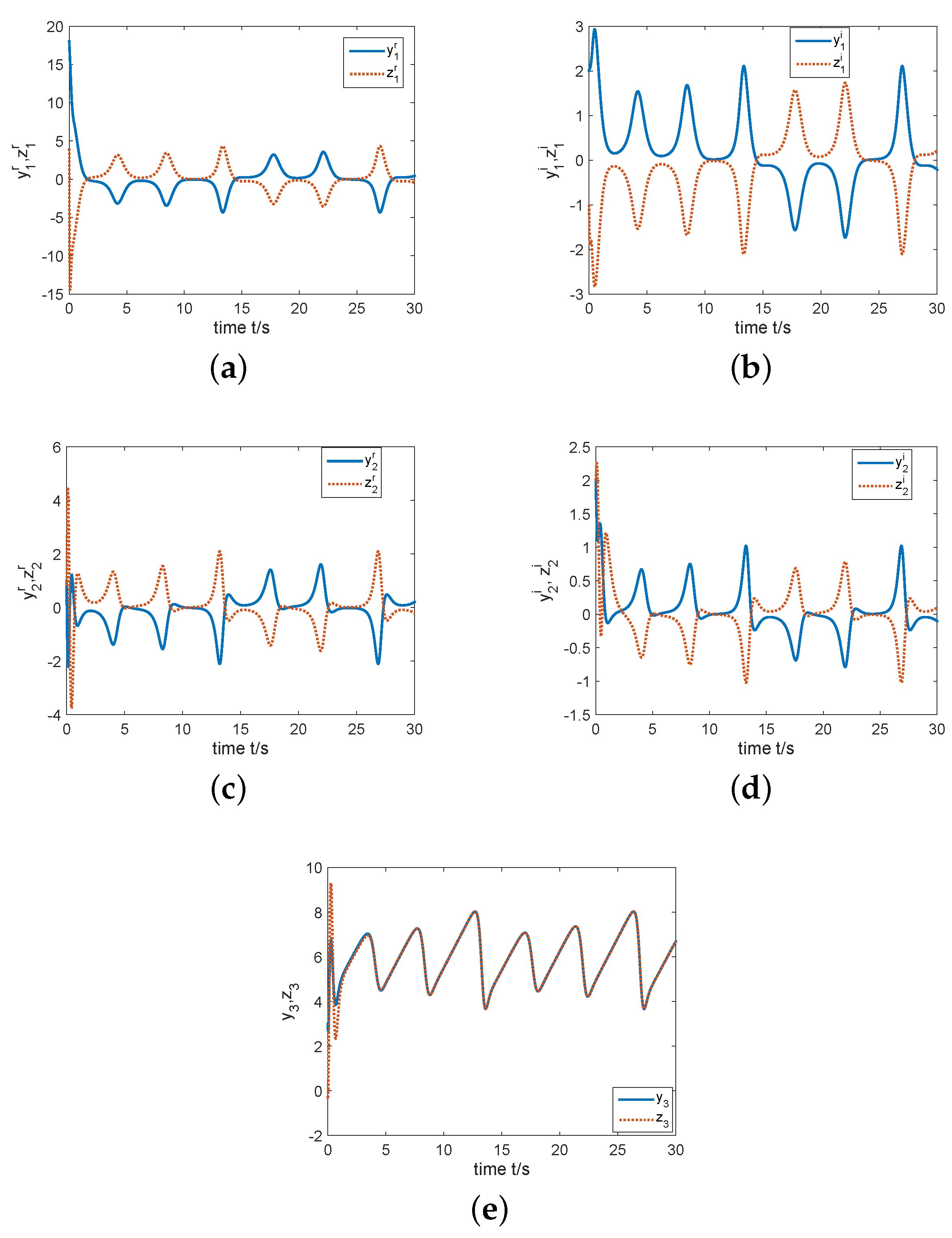
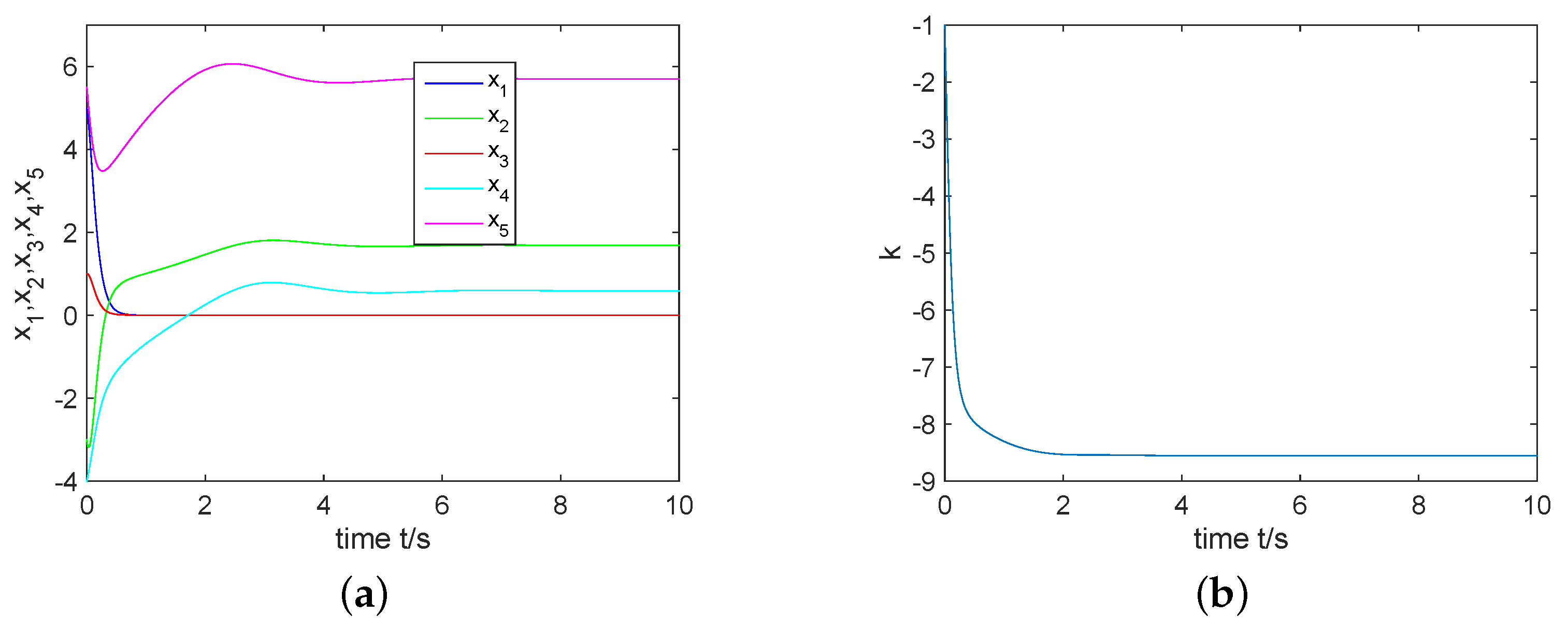
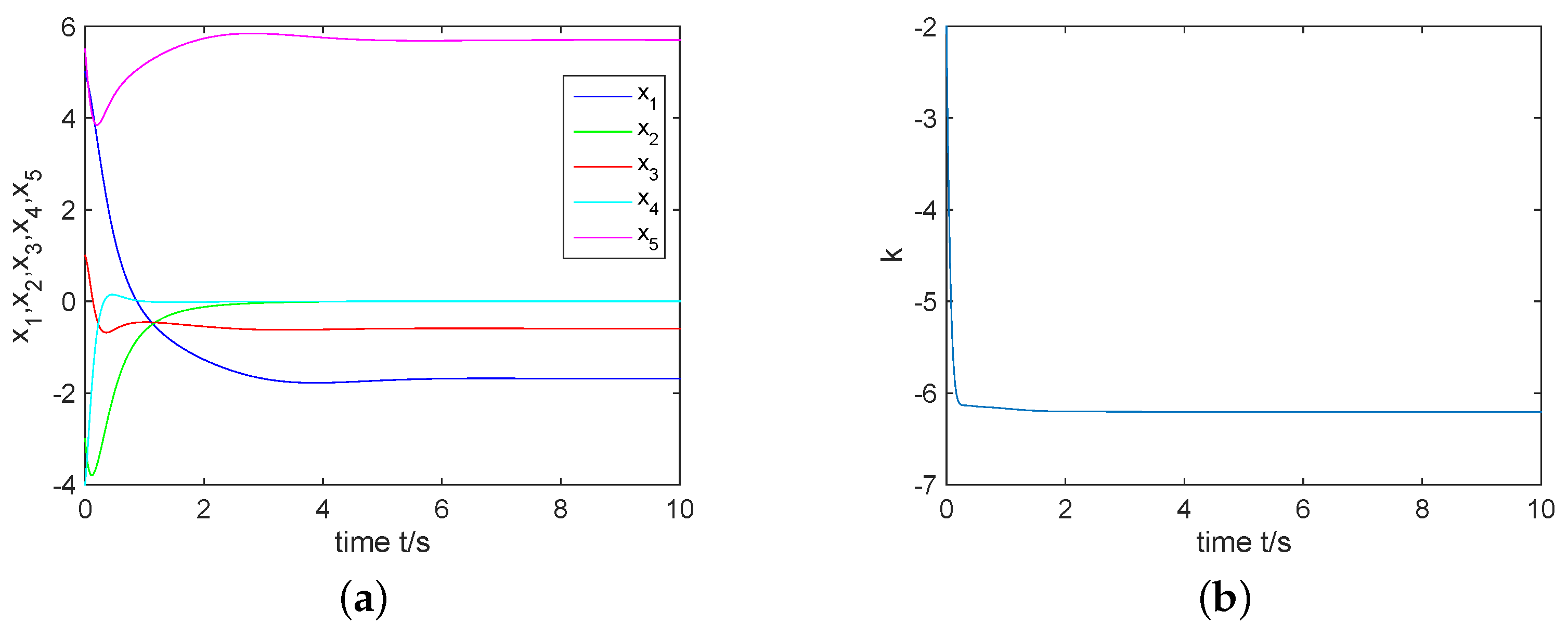
4. Synchronization Scheme
- 1.
- 2.
- 3.
4.1. The Existence of Synchronization in the Complex Rikitake System
4.2. CS of the Complex Rikitake System
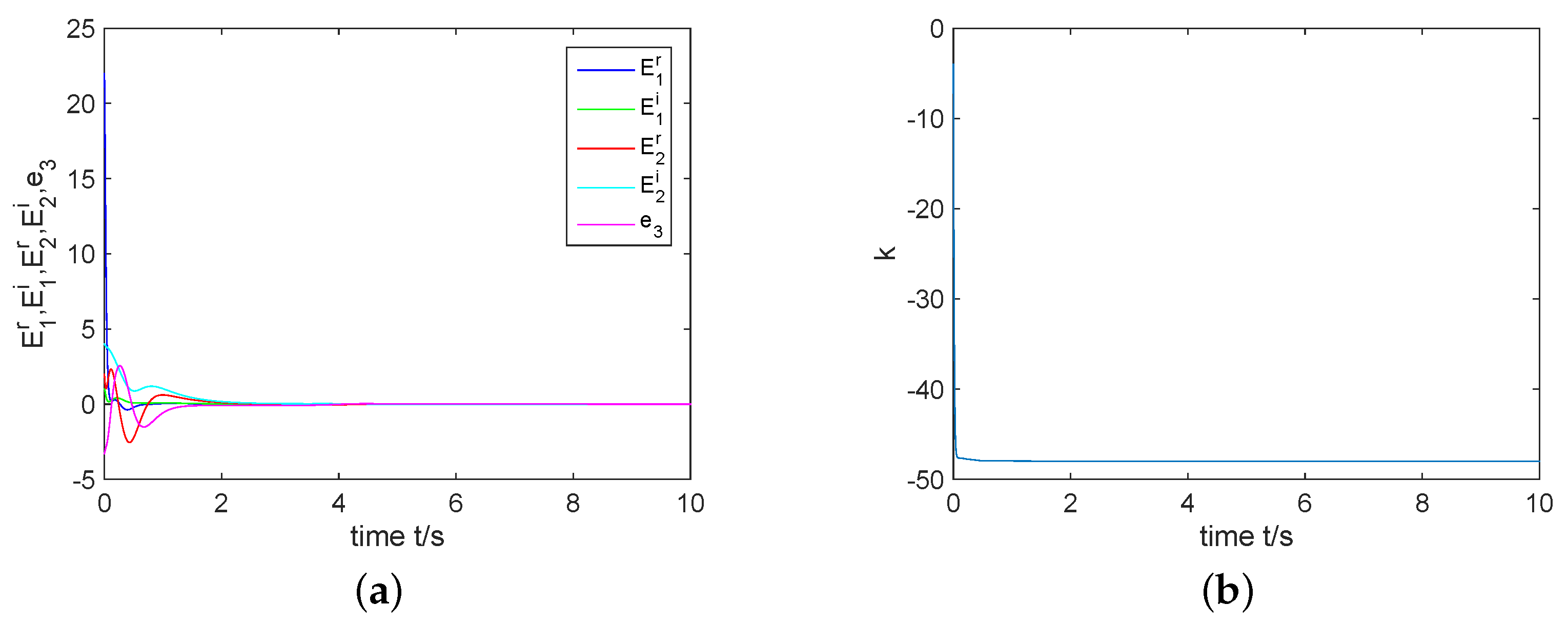
4.3. The Coexistence of CS and AS in the Complex Rikitake System
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ott, E.; Gerbogi, C.; Yorke, J.A. Controlling chaos. Phys. Rev. Lett. 1990, 64, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–824. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Dong, X. On feedback control of chaotic continuous time systems. IEEE Trans. Circuits Syst. I 1993, 40, 591–601. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, W.; Wei, Z.C.; Zhang, S.W. Dynamics and delayed feedback control for a 3D jerk system with hidden attractor. Nonlinear Dyn. 2015, 82, 577–588. [Google Scholar] [CrossRef]
- Rajagopal, K.; Guessas, L.; Vaidyanathan, S.; Karthikeyan, A.; Srinivasan, A. Dynamical analysis and FPGA implementation of a novel hyperchaotic system and its synchronization using adaptive sliding mode control and genetically optimized PID control. Math. Probl. Eng. 2017, 2017, 1–14. [Google Scholar] [CrossRef]
- Rajagopal, K.; Laarem, G.; Karthikeyan, A.; Srinivasan, A. FPGA implementation of adaptive sliding mode control and genetically optimized PID control for fractional-order induction motor system with uncertain load. Adv. Differ. Equ. 2017, 2017, 1–20. [Google Scholar] [CrossRef]
- Chu, J.; Hu, W.W. Control chaos for permanent magnet synchronous motor base on adaptive backstepping of error compensation. Int. J. Autom. Comput. 2016, 9, 163–174. [Google Scholar] [CrossRef]
- Adloo, H.; Roopaei, M. Review article on adaptive synchronization of chaotic systems with unknown parameters. Nonlinear Dyn. 2011, 65, 141–159. [Google Scholar] [CrossRef]
- Guo, R.W. A simple adaptive controller for chaos and hyperchaos synchronization. Phys. Lett. A 2008, 372, 5593–5597. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H. Multivariate permutation entropy and its application for complexity analysis of chaotic systems. Physica A 2016, 461, 812–823. [Google Scholar] [CrossRef]
- Guo, R.W. A Projective synchronization of a class of chaotic systems by dynamic feedback control method. Nonlinear Dyn. 2017, 90, 53–64. [Google Scholar] [CrossRef]
- Wang, Z.X.; Guo, R.W. Hybrid synchronization problem of a class of chaotic systems by an universal control method. Symmetry 2018, 10, 552. [Google Scholar] [CrossRef]
- Jiang, C.M.; Zada, A.; Şenel, M.T.; Li, T.X. Synchronization of bidirectional N-coupled fractional-order chaotic systems with ringconnection based on antisymmetric structure. Adv. Differ. Equ. 2019, 2019, 1–16. [Google Scholar] [CrossRef]
- Li, H.M.; Yang, Y.F.; Zhou, Y.; Li, C.L.; Qian, K.; Li, Z.Y.; Du, J.R. Dynamics and synchronization of a memristor-based chaotic system with no equilibrium. Complexity 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Fowler, A.C.; Gibbon, J.D.; McGuinness, M.J. The complex Lorenz equations. Physica D 1982, 4, 139–163. [Google Scholar] [CrossRef]
- Liu, S.T.; Zhang, F.F. Complex function projective synchronization of complex chaotic system and its applications in secure communications. Nonlinear Dyn. 2014, 76, 1087–1097. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Abo-Dahab, S.M. Dynamical properties and complex anti synchronization with applications to secure communications for a novel chaotic complex nonlinear model. Chaos Solitons Fractals 2018, 106, 273–284. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Kadir, A.; Xu, Y. Image encryption using complex hyper chaotic system by injecting impulse into parameters. Appl. Math. Comput. 2019, 360, 83–93. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Bountis, T.; Mahmoud, E.E. Active control and global synchronization of the complex Chen and Lü systems. Int. J. Bifurc. Chaos 2007, 17, 4295–4308. [Google Scholar] [CrossRef]
- Sun, B.J.; Li, M.; Zhang, F.F.; Wang, H.; Liu, J.W. The characteristics and self-time-delay synchronization of two-time-delay complex Lorenz system. J. Franklin Inst. 2019, 356, 334–350. [Google Scholar] [CrossRef]
- Singh, J.P.; Roy, B.K. Hidden attractors in a new complex generalised Lorenz hyperchaotic system, its synchronisation using adaptive contraction theory, circuit validation and application. Nonlinear Dyn. 2018, 92, 373–394. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Complete synchronization of chaotic complex nonlinear systems with uncertain parameters. Nonlinear Dyn. 2010, 62, 875–882. [Google Scholar] [CrossRef]
- Liu, P.; Liu, S.T. Adaptive anti-synchronization of chaotic complex nonlinear systems with unknown parameters. Nonlinear Anal.-Real World Appl. 2010, 12, 3046–3055. [Google Scholar] [CrossRef]
- Mahmoud, G.M.; Mahmoud, E.E. Lag synchronization of hyperchaotic complex nonlinear systems. Nonlinear Dyn. 2012, 67, 1613–1622. [Google Scholar] [CrossRef]
- Zhou, X.B.; Jiang, M.R.; Huang, Y.Q. Combination synchronization of three identical or different nonlinear complex hyperchaotic systems. Entropy 2013, 15, 3746–3761. [Google Scholar] [CrossRef]
- Mahmoud, E.E. Complex complete synchronization of two non-identical hyperchaotic complex nonlinear systems. Math. Methods Appl. 2014, 37, 321–328. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Abualnaja, K.M. Complex lag synchronization of two identical chaotic complex nonlinear systems. Cent. Eur. J. Phys. 2014, 12, 63–69. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Abood, F.S. A new nonlinear chaotic complex model and it’s complex anti lag synchronization. Complexity 2017, 2017, 3848953. [Google Scholar] [CrossRef]
- Sun, J.W.; Cui, G.Z.; Wang, Y.F.; Shen, Y. Combination complex synchronization of three chaotic complex systems. Nonlinear Dyn. 2015, 79, 953–963. [Google Scholar] [CrossRef]
- Jiang, C.M.; Liu, S.T. Generalized combination complex synchronization of new hyperchaotic complex Lü-like systems. Adv. Differ. Equ. 2015, 2015, 214. [Google Scholar] [CrossRef]
- Rikitake, T. Oscillations of a system of disk dynamos. Proc. Camb. Philos. Soc. 1958, 54, 89–95. [Google Scholar] [CrossRef]
- Keisuke, I. Chaos in the Rikitake two-disk dynamo system. Earth Planet Sci. Lett. 1980, 51, 451–457. [Google Scholar]
- Frederickson, P.; Kaplan, J.L.; Yorke, J.A. The Lyapunov dimension of strange attractors. J. Differ. Equ. 1983, 44, 185–207. [Google Scholar] [CrossRef]
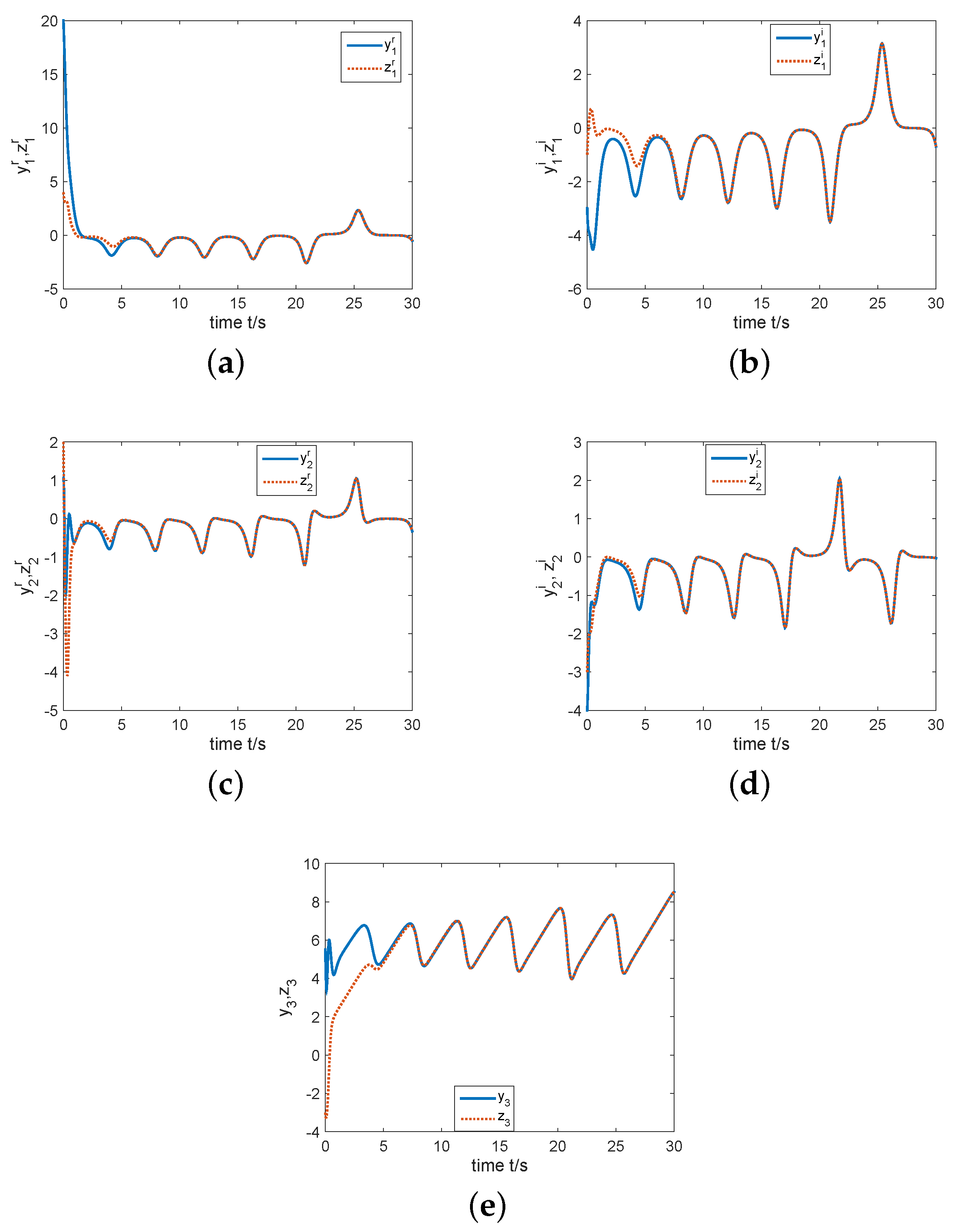
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, W.; Wu, Z.; Xiao, Y.; Jiang, C. Chaos Control and Synchronization of a Complex Rikitake Dynamo Model. Entropy 2020, 22, 671. https://doi.org/10.3390/e22060671
Pang W, Wu Z, Xiao Y, Jiang C. Chaos Control and Synchronization of a Complex Rikitake Dynamo Model. Entropy. 2020; 22(6):671. https://doi.org/10.3390/e22060671
Chicago/Turabian StylePang, Wenkai, Zekang Wu, Yu Xiao, and Cuimei Jiang. 2020. "Chaos Control and Synchronization of a Complex Rikitake Dynamo Model" Entropy 22, no. 6: 671. https://doi.org/10.3390/e22060671
APA StylePang, W., Wu, Z., Xiao, Y., & Jiang, C. (2020). Chaos Control and Synchronization of a Complex Rikitake Dynamo Model. Entropy, 22(6), 671. https://doi.org/10.3390/e22060671