Particle Swarm Contour Search Algorithm
Abstract
1. Introduction
2. Problem Definition
3. Related Works
- Set the start pixel and the current pixel c to be the encountered black pixel. Set the current direction d to “”
- Examine the neighbours of c in a clockwise order from the current direction. The first encountered black pixel is the next pixel on the contour. If , the found pixel is saved as the second pixel . If no point is found, the contour consists of a single pixel and the algorithm terminates.
- Set the step direction from the current pixel to the new pixel as the new direction. If the direction is diagonal, it is set to a counterclockwise of this direction.
- If the current point and the new point are identical to the starting point and the second point s, respectively, a complete contour is found. If not, repeat from step 2 with the current point and direction set to the new point and direction.
4. Particle Swarm Optimisation
5. Particle Swarm Contour Search (PSCS)
| Algorithm1: Baseline PSCS algorithm |
| Input: S, , , , A, ; Output: A; ∅; ∅;  |
5.1. Initialisation
5.2. Object Search Phase
| Algorithm 2: PSCS global search phase |
 |
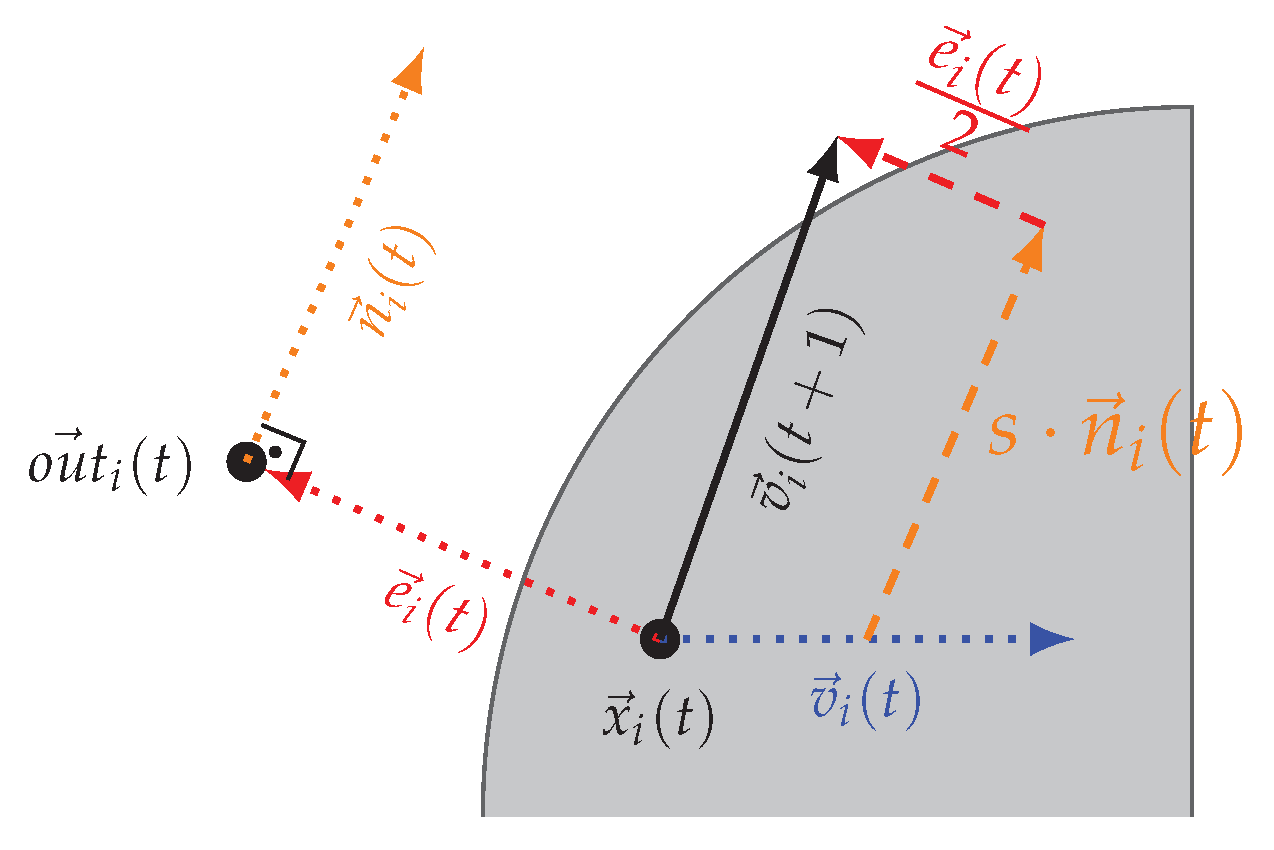
5.3. Contour Search Phase
| Algorithm 3: PSCS contour seach and trace phase |
| Input: ; Output: A;  |
5.4. Contour Trace Phase
6. Evaluation
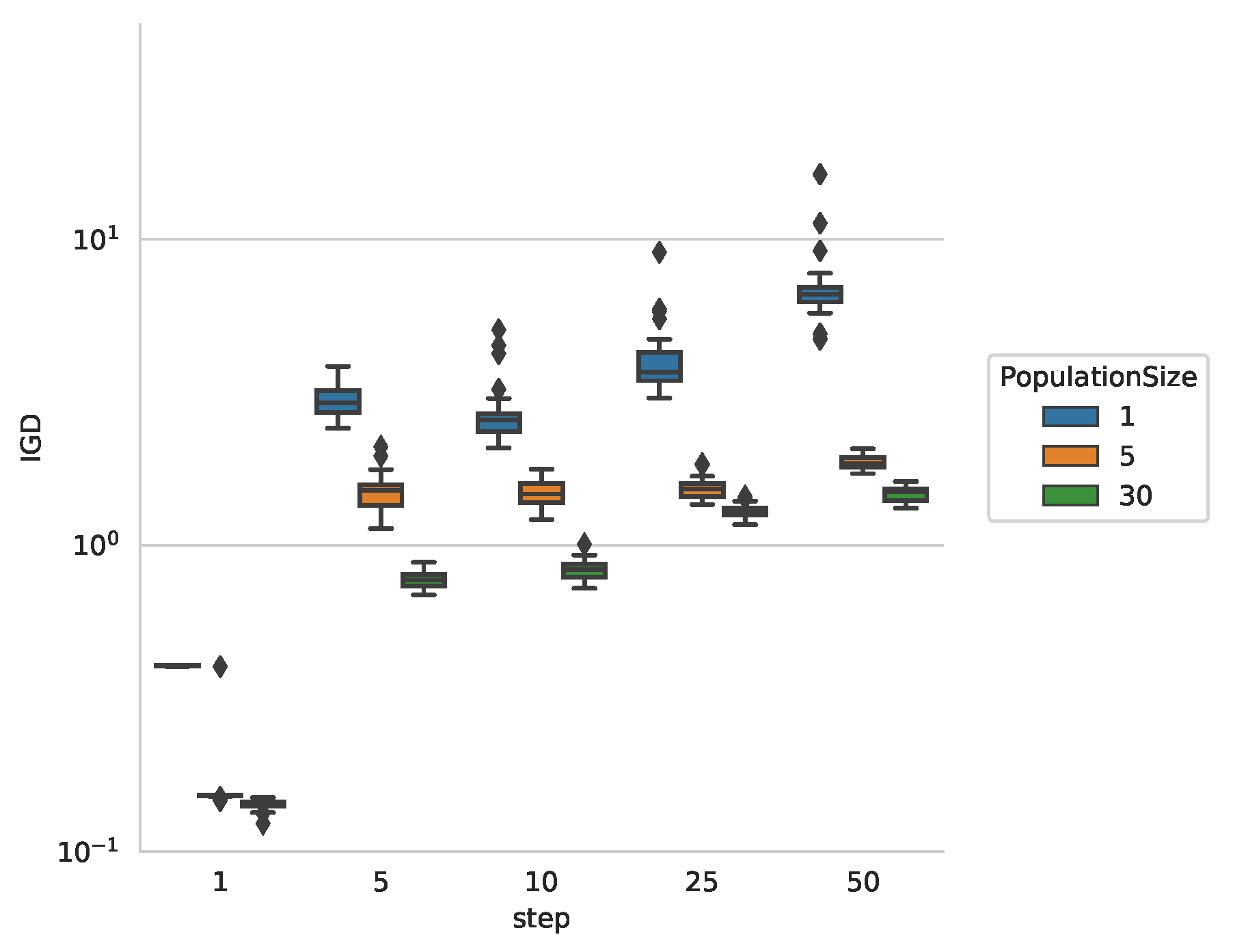
6.1. Parameter Setting
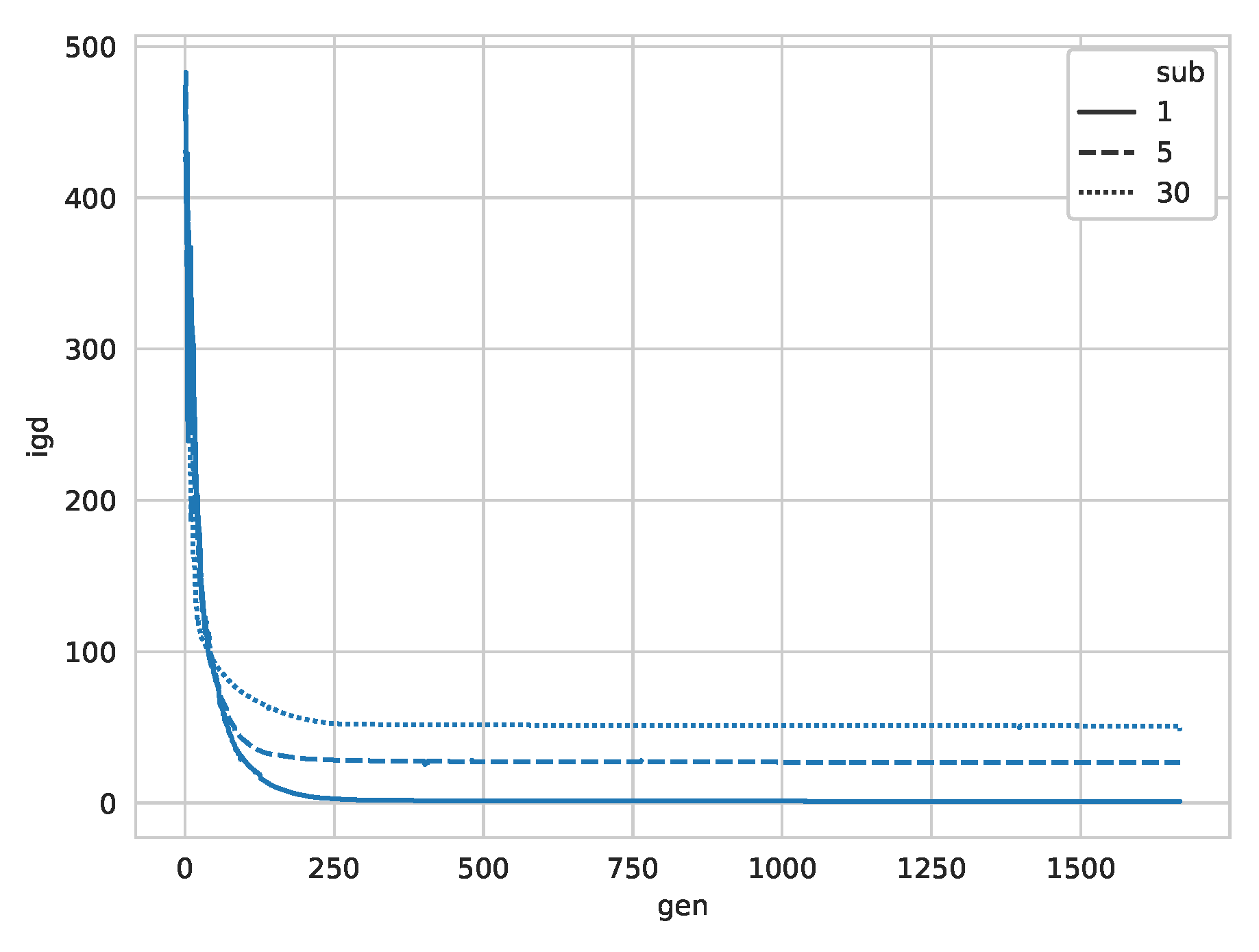
6.2. Experiments
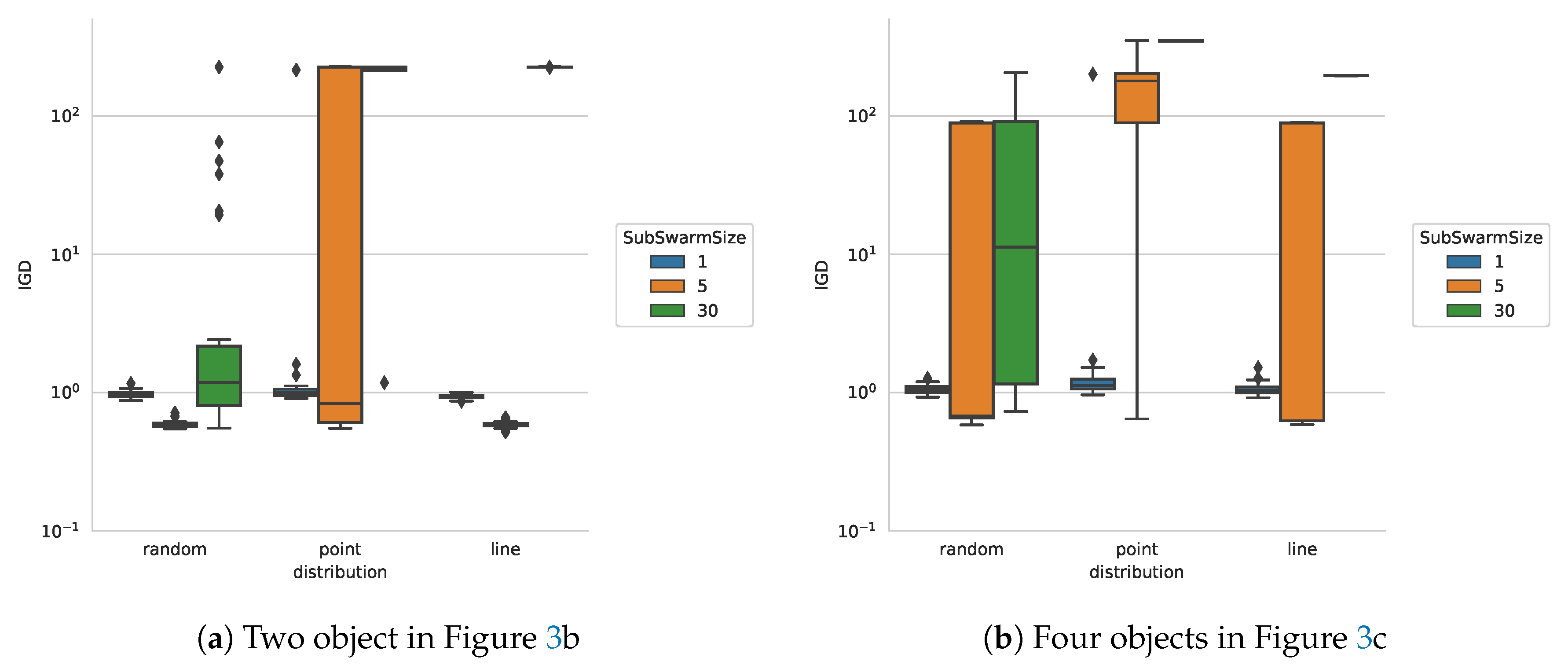
6.3. Experiments on Different Shapes
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PSCS | Particle Swarm Contour Search |
| PSO | Particle Swarm Optimisation |
| IGD | Inverted Generational Distance |
References
- Canny, J.F. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Seo, J.; Chae, S.; Shim, J.; Kim, D.; Cheong, C.; Han, T.D. Fast Contour-Tracing Algorithm Based on a Pixel-Following Method for Image Sensors. Sensors 2016, 16, 353. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization (PSO). In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Li, X. Adaptively choosing neighbourhood bests using species in a particle swarm optimizer for multimodal function optimization. In Genetic and Evolutionary Computation Conference; Springer: Berlin/Heidelberg, Germany, 2004; pp. 105–116. [Google Scholar]
- Zambrano-Bigiarini, M.; Clerc, M.; Rojas, R. Standard particle swarm optimisation 2011 at cec-2013: A baseline for future pso improvements. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2337–2344. [Google Scholar]
- Kulkarni, R.V.; Venayagamoorthy, G.K. Particle swarm optimization in wireless-sensor networks: A brief survey. IEEE Trans. Syst. Man, Cybern. Part (Appl. Rev.) 2010, 41, 262–267. [Google Scholar] [CrossRef]
- Mostaghim, S.; Steup, C.; Witt, F. Energy aware particle swarm optimization as search mechanism for aerial micro-robots. In Proceedings of the 2016 IEEE Symposium Series on Computational Intelligence (SSCI), Athens, Greece, 6–9 December 2016; pp. 1–7. [Google Scholar]
- Poli, R. Analysis of the Publications on the Applications of Particle Swarm Optimisation. J. Artif. Evol. Appl. 2008, 2008, 1–10. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. In Readings in Computer Vision; Elsevier: Amsterdam, The Netherlands, 1987; pp. 184–203. [Google Scholar]
- Yitzhaky, Y.; Peli, E. A method for objective edge detection evaluation and detector parameter selection. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1027–1033. [Google Scholar] [CrossRef]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Duda, R.O.; Munson, J.H. Graphical-Data-Processing Research Study and Experimental Investigation; Technical Report; Stanford Research Institute: Menlo Park, CA, USA, 1967. [Google Scholar]
- Suzuki, S.; Abe, K. Topological structural analysis of digitized binary images by border following. Comput. Vision Graph. Image Process. 1985, 30, 32–46. [Google Scholar] [CrossRef]
- Oldewage, E.T.; Engelbrecht, A.P.; Cleghorn, C.W. The Importance of Component-Wise Stochasticity in Particle Swarm Optimization. In Swarm Intelligence; Dorigo, M., Birattari, M., Blum, C., Christensen, A.L., Reina, A., Trianni, V., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 264–276. [Google Scholar]
- Yang, S.; Wang, M.; Jiao, L. A quantum particle swarm optimization. In Proceedings of the 2004 Congress on Evolutionary Computation, CEC2004, Portland, OR, USA, 19–23 June 2004; Volume 1, pp. 320–324. [Google Scholar] [CrossRef]
- Blackwell, T.M.; Bentley, P.J. Dynamic search with charged swarms. In Proceedings of the 4th Annual Conference on Genetic and Evolutionary Computation; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2002; pp. 19–26. [Google Scholar]
- Blackwell, T.; Branke, J. Multi-swarm optimization in dynamic environments. In Workshops on Applications of Evolutionary Computation; Springer: Berlin/Heidelberg, Germany, 2004; pp. 489–500. [Google Scholar]
- Bradski, G. The OpenCV Library. Available online: https://www.drdobbs.com/open-source/the-opencv-library/184404319 (accessed on 16 March 2020).
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]



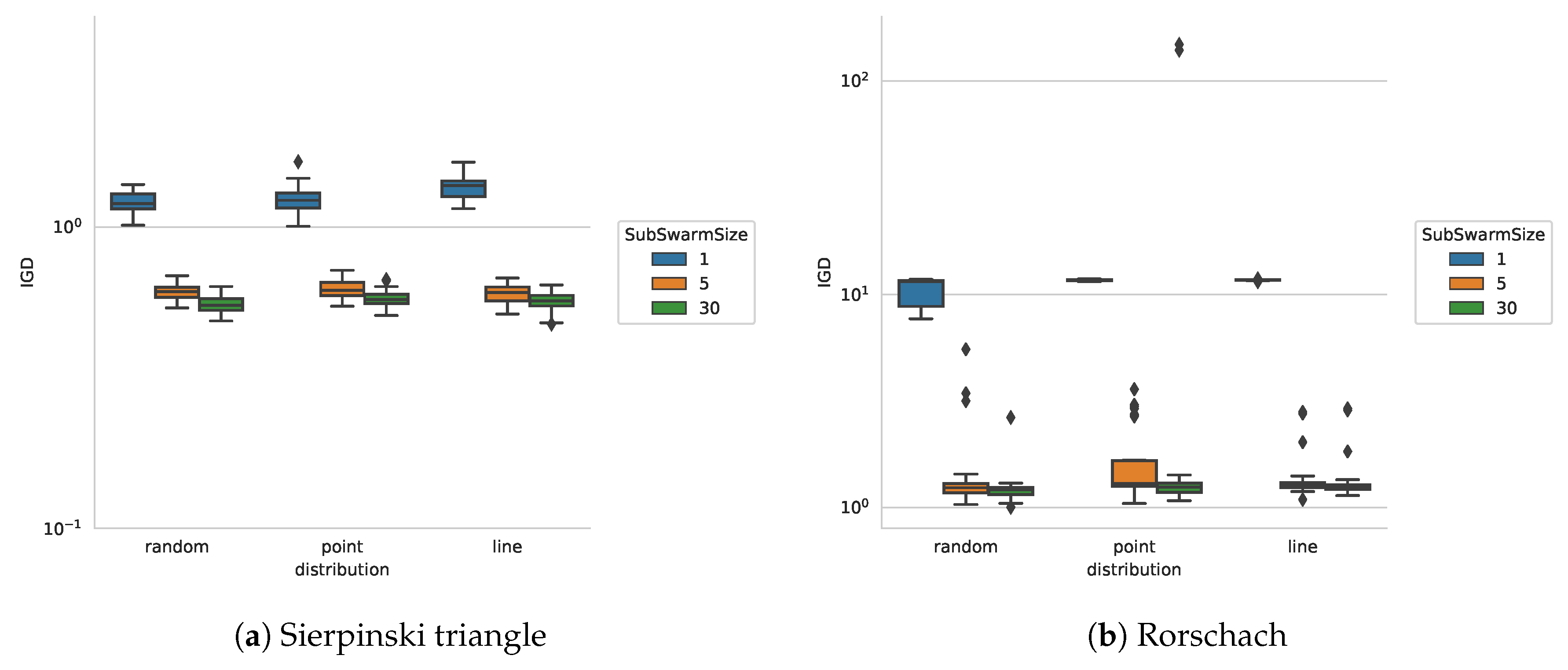
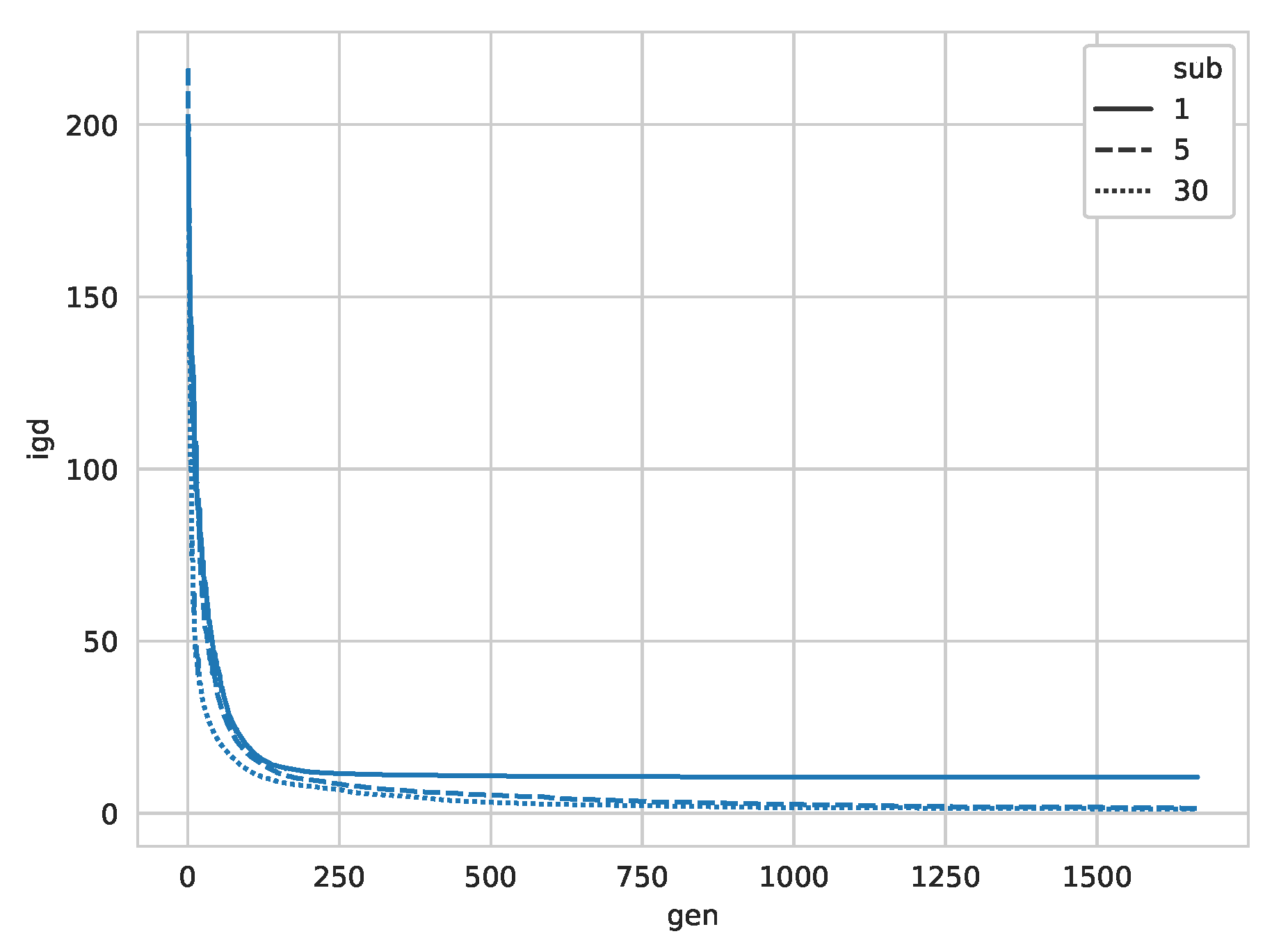
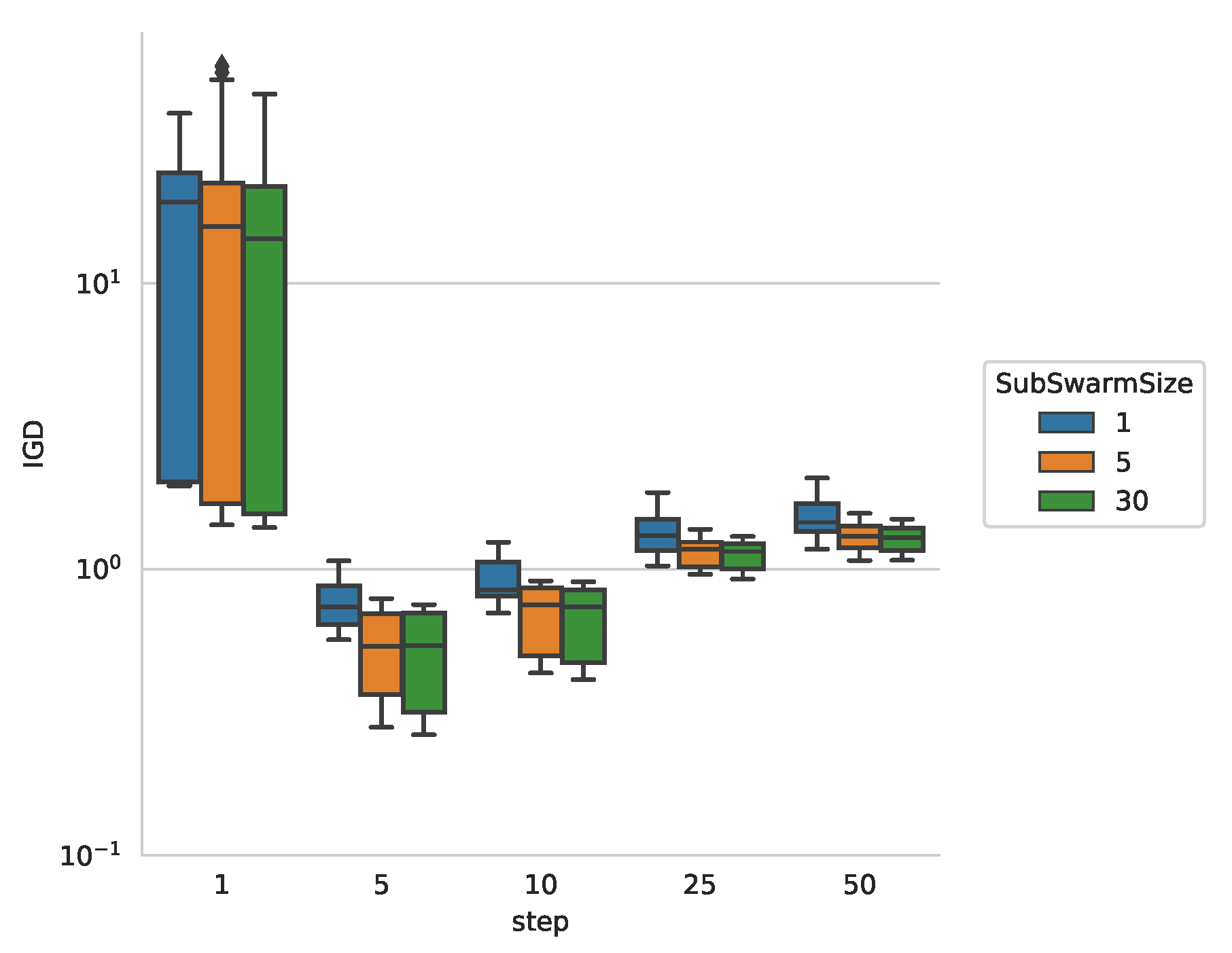
| Category | Parameter | Values |
|---|---|---|
| General | Population Size | 1,5,30 |
| Sub-swarm Size | 1,5,30 | |
| initial distribution | Line, Point, Random | |
| Contour search/trace phase | Step-size s | 1,5,10,25,50 |
| Threshold | 25 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weikert, D.; Mai, S.; Mostaghim, S. Particle Swarm Contour Search Algorithm. Entropy 2020, 22, 407. https://doi.org/10.3390/e22040407
Weikert D, Mai S, Mostaghim S. Particle Swarm Contour Search Algorithm. Entropy. 2020; 22(4):407. https://doi.org/10.3390/e22040407
Chicago/Turabian StyleWeikert, Dominik, Sebastian Mai, and Sanaz Mostaghim. 2020. "Particle Swarm Contour Search Algorithm" Entropy 22, no. 4: 407. https://doi.org/10.3390/e22040407
APA StyleWeikert, D., Mai, S., & Mostaghim, S. (2020). Particle Swarm Contour Search Algorithm. Entropy, 22(4), 407. https://doi.org/10.3390/e22040407







