Some Remarks about Entropy of Digital Filtered Signals
Abstract
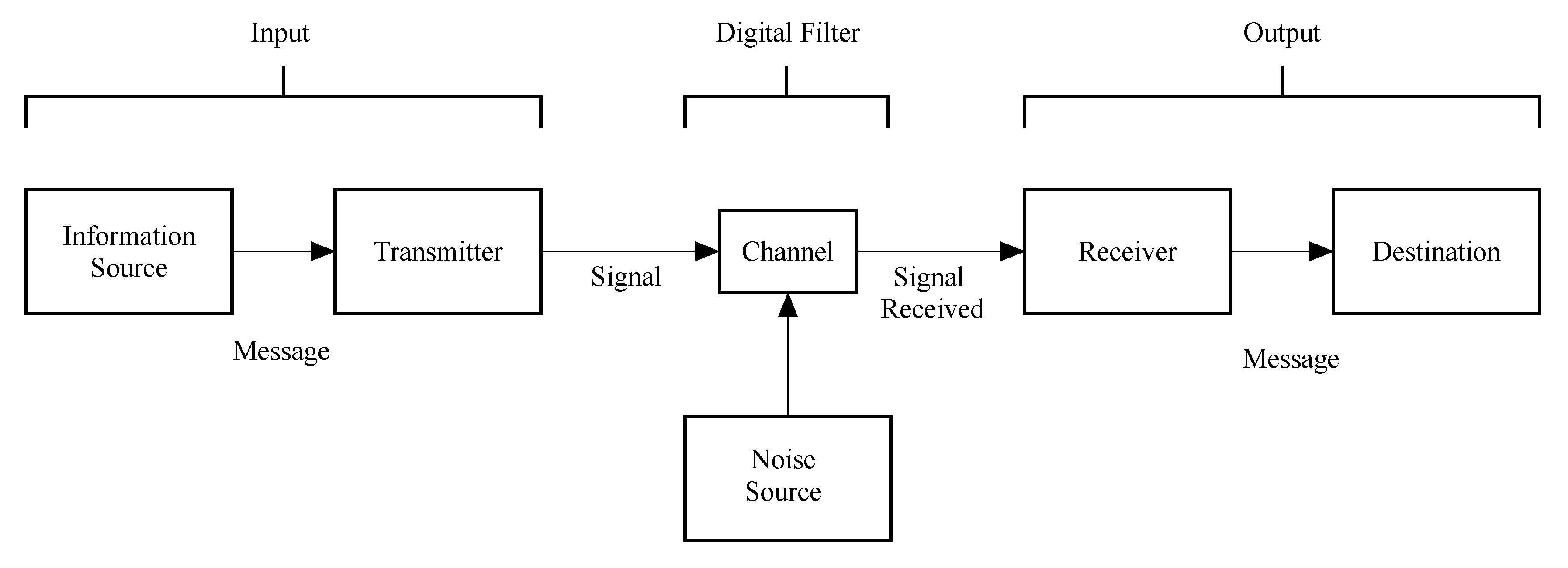
1. Introduction
2. Materials and Methods
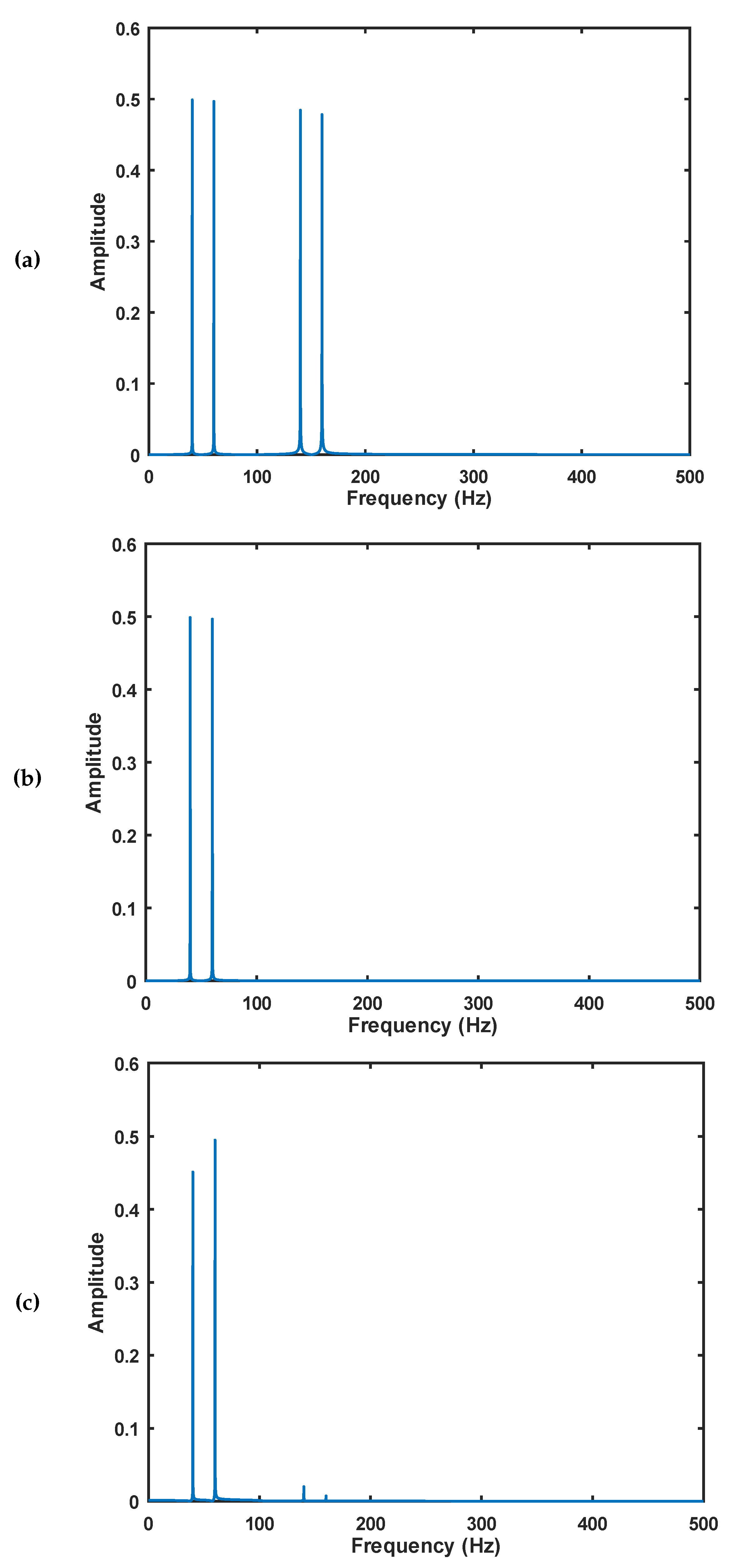
2.1. IIR Filter
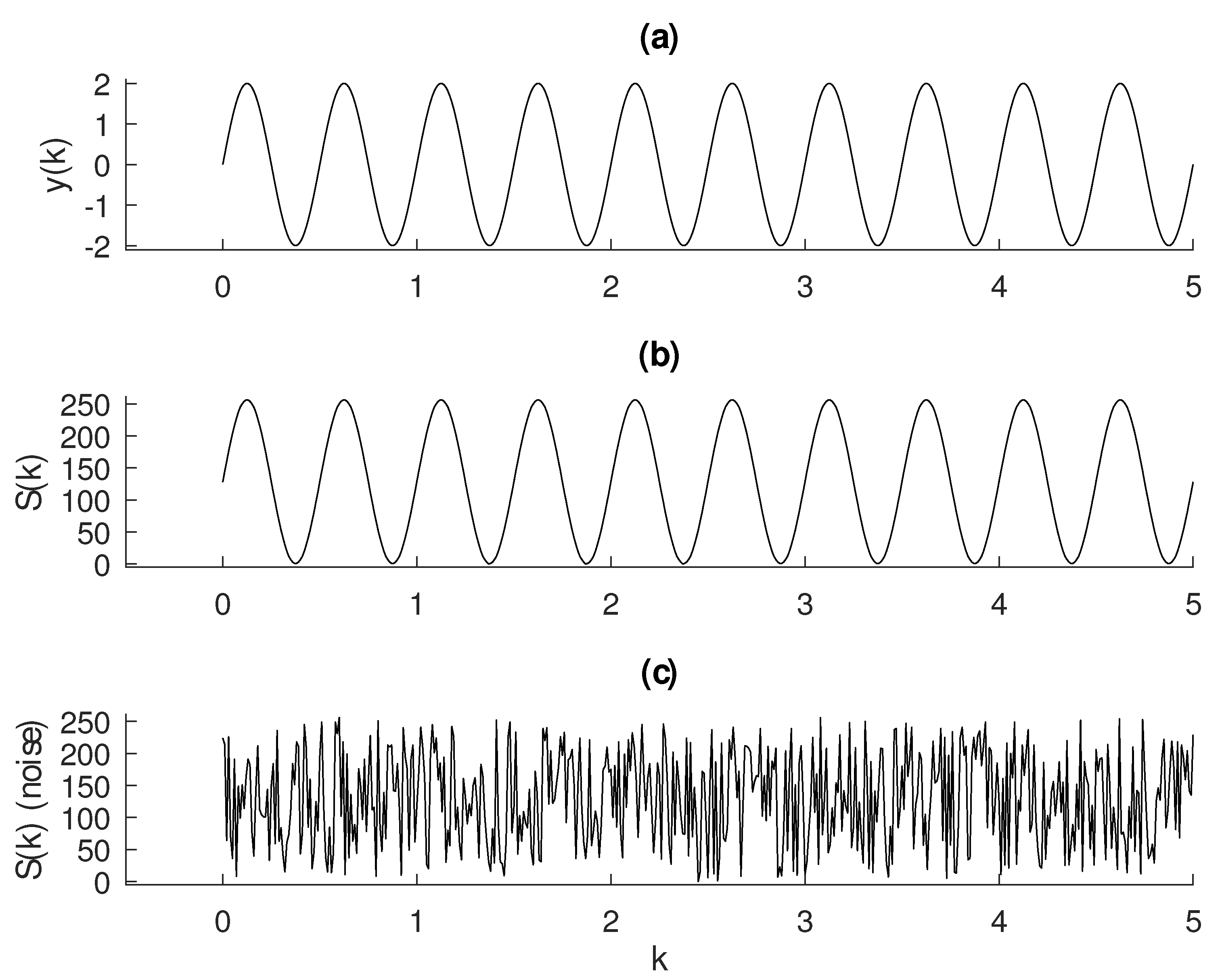
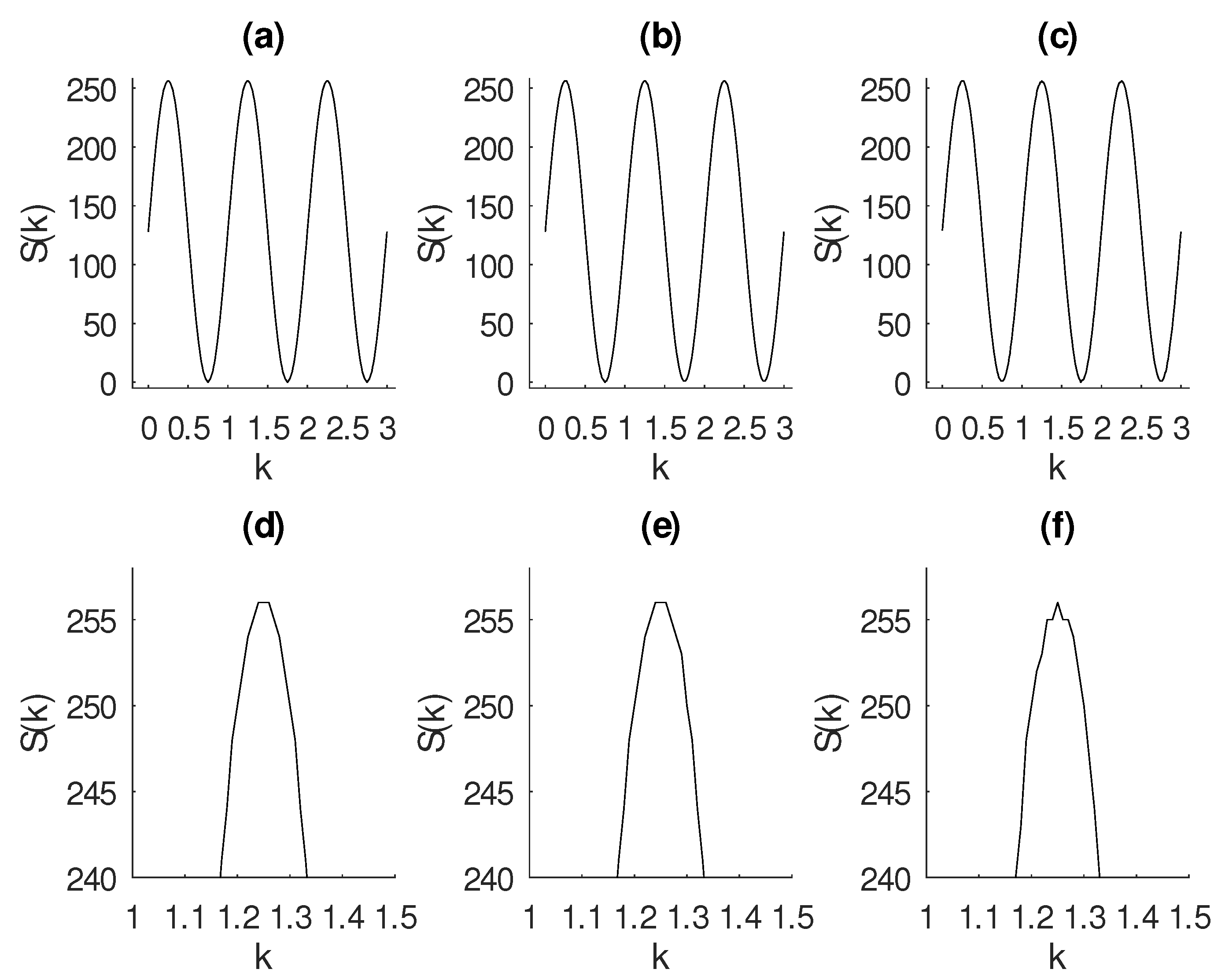
2.2. Quantization Error
2.3. Entropy
2.4. Entropy to Detect Noise
2.5. Numerical Experiments
2.5.1. Numerical Experiment 1
- Step 1:
- Use the commands butter, cheby, or ellip of Octave to generate the poles and zeros of the transfer function according to Equation (1).
- Step 2:
- Choose number of bits and calculate quantization error according to Equation (6).
- Step 3:
- Step 4:
- The signal is filtered using 50 different combinations described by Equations (7) and (8).
- Step 5:
- Apply the standardization procedure to the filtered signal according Equation (15).
- Step 6:
- Calculate the mean and standard deviation of the entropy from the 50 filtered signals.
2.5.2. Numerical Experiment 2
- Step 1:
- Use the command ellip of Octave to generate the poles and zeros of the transfer function (Equation (1)).
- Step 2:
- Choice of input signal (Table 3).
- Step 3:
- The signal is filtered using 50 values of within 1024 to 6024.
- Step 4:
- Apply the standardisation procedure to the filtered signal according Equation (15)
- Step 5:
- Filter signal using Equation (5).
- Step 6:
- Compute the mean and standard deviation of entropy of the filtered signal.
2.5.3. Numerical Experiment 3
- Step 1:
- Use the command butter, cheby, or ellip of Octave to generate the poles and zeros of the transfer function, Equation (1).
- Step 2:
- Filter signal using Equations (5).
- Step 3:
- The signal is filtered using 50 different values of within 1024 to 6024.
- Step 4:
- Apply the standardisation procedure to the filtered signal according Equation (15).
- Step 5:
- Compute the mean and standard deviation of entropy of the filtered signal.
- Step 6:
- Change the order of the filter from 1 to 8 for each of the steps 1 to 5.
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lai, E. Practical Digital Signal Processing; Elsevier: Oxford, UK, 2003. [Google Scholar]
- Giurgiutiu, V. Structural Health Monitoring: With Piezoelectric Wafer Active Sensors; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Antoniou, A. Digital Signal Processing; McGraw-Hill: New York, NY, USA, 2016. [Google Scholar]
- Grout, I. Digital Systems Design with FPGAs and CPLDs; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Wolf, M. Embedded System Interfacing: Design for the Internet-of-Things (IoT) and Cyber-Physical Systems (CPS); Morgan Kaufmann: Cambridge, MA, USA, 2019. [Google Scholar]
- Smith, S. Digital Signal Processing: A Practical Guide for Engineers and Scientists; Elsevier: Burlington, MA, USA, 2013. [Google Scholar]
- Mitra, S.K.; Kuo, Y. Digital Signal Processing: A Computer-Based Approach; McGraw-Hill: New York, NY, USA, 2006; Volume 2. [Google Scholar]
- Frey, D.R. Chaotic digital encoding: An approach to secure communication. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1993, 40, 660–666. [Google Scholar] [CrossRef]
- Kuo, S.M.; Morgan, D.R. Active Noise Control Systems; Wiley: New York, NY, USA, 1996; Volume 4. [Google Scholar]
- Johns, A.T.; Salman, S.K. Digital Protection for Power Systems; IET: London, UK, 1995. [Google Scholar]
- Bruce, E.N. Biomedical Signal Processing and Signal Modeling; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Cameron, R.J.; Kudsia, C.M.; Mansour, R.R. Microwave Filters for Communication Systems: Fundamentals, Design, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Shukl, P.; Singh, B. Recursive Digital Filter Based Control for Power Quality Improvement of Grid Tied Solar PV System. In Proceedings of the 2018 8th IEEE India International Conference on Power Electronics (IICPE), Jaipur, India, 13–15 December 2018; pp. 1–6. [Google Scholar]
- Wu, K.C. Power Converters with Digital Filter Feedback Control; Academic Press: London, UK, 2016. [Google Scholar]
- Ozpolat, E.; Karakaya, B.; Kaya, T.; Gulten, A. FPGA-based digital Filter Design for Biomedical Signal. In Proceedings of the 2016 XII International Conference on Perspective Technologies and Methods in MEMS Design (MEMSTECH), Lviv, Ukraine, 20–24 April 2016; pp. 70–73. [Google Scholar]
- Daniels, R.C.; Gregers-Hansen, V. Code inverse filtering for complete sidelobe removal in binary phase coded pulse compression systems. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 256–261. [Google Scholar]
- Gaydecki, P. A real time programmable digital filter for biomedical signal enhancement incorporating a high-level design interface. Physiol. Meas. 2000, 21, 187–196. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.S.; Yazdanpanah, B.; Kumar, P.R. Removal of noise from electrocardiogram using digital FIR and IIR filters with various methods. In Proceedings of the 2015 International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, India, 2–4 April 2015; pp. 0157–0162. [Google Scholar]
- Patel, J.J.; Parmar, K.R.; Mewada, H.N. Design of FIR filter for burst mode demodulator of satellite Receiver. In Proceedings of the 2016 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2016; pp. 0686–0690. [Google Scholar]
- Cernak, M.; Asaei, A.; Hyafil, A. Cognitive speech coding: Examining the impact of cognitive speech processing on speech compression. IEEE Signal Process. Mag. 2018, 35, 97–109. [Google Scholar] [CrossRef]
- Saxena, M.C.; Upadhyaya, M.V.; Gupta, H.K.; Sharma, A. Denoising of ECG Signals Using FIR & IIR Filter: A Performance Analysis. In Proceedings of the International Conference on Emerging Trends in Expert Applications & Security, Jaipur, India, 17–18 February 2018; Volume 2, pp. 51–58. [Google Scholar]
- Liu, M.; Hao, H.; Xiong, P.; Lin, F.; Hou, Z.; Liu, X. Constructing a guided filter by exploiting the butterworth filter for ECG signal enhancement. J. Med. Biol. Eng. 2018, 38, 980–992. [Google Scholar] [CrossRef]
- Tian, X.; Daigle, H.; Jiang, H. Feature detection for digital images using machine learning algorithms and image processing. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018; pp. 1562–1575. [Google Scholar]
- Sun, S.; Xu, L.; Cao, Z.; Huang, A.; Yang, W. Digital recursive demodulator based on Kalman filter. IEEE Trans. Instrum. Meas. 2017, 66, 3138–3147. [Google Scholar] [CrossRef]
- Wang, S.; Wu, G.; Su, F.; Chen, J. Simultaneous microwave photonic analog-to-digital conversion and digital filtering. IEEE Photonics Technol. Lett. 2018, 30, 343–346. [Google Scholar] [CrossRef]
- Ling, W.K. Nonlinear Digital Filters: Analysis and Applications; Academic Press: London, UK, 2010. [Google Scholar]
- Zhao, B.; Lian, Y.; Niknejad, A.M.; Heng, C.H. A Low-Power Compact IEEE 802.15.6 Compatible Human Body Communication Transceiver With Digital Sigma–Delta IIR Mask Shaping. IEEE J. Solid-State Circuits 2019, 54, 346–357. [Google Scholar] [CrossRef]
- V. Davidek, M.; Antosova, B.P. Finite Word-Length Effects in Digital State-Space Filters. Radioengineering 1999, 8, 7–10. [Google Scholar]
- Liu, B. Effect of finite word length on the accuracy of digital filters—A review. IEEE Trans. Circuit Theory 1971, 18, 670–677. [Google Scholar] [CrossRef]
- Butterweck, H.J.; Ritzerfeld, J.; Werter, M. Finite wordlength effects in digital filters. AEÜ 1989, 43, 76–89. [Google Scholar]
- Cheng, H.M.; Chiu, G.C. Finite precision controller implementation-limitation on sample rate. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Kobe, Japan, 20–24 July 2003; Volume 1, pp. 634–639. [Google Scholar]
- Mullis, C.; Roberts, R. Synthesis of minimum roundoff noise fixed point digital filters. IEEE Trans. Circuits Syst. 1976, 23, 551–562. [Google Scholar] [CrossRef]
- Hwang, S. Minimum uncorrelated unit noise in state-space digital filtering. IEEE Trans. Acoust. Speech Signal Process. 1977, 25, 273–281. [Google Scholar] [CrossRef]
- Rader, C.M.; Gold, B. Digital filter design techniques in the frequency domain. Proc. IEEE 1967, 55, 149–171. [Google Scholar] [CrossRef]
- Goodall, R.M.; Donoghue, B. Very high sample rate digital filters using the δ operator. IEE Proc. G (Circuits Devices Syst.) 1993, 140, 199–206. [Google Scholar] [CrossRef]
- Jones, S.; Goodall, R.; Gooch, M. Targeted processor architectures for high-performance controller implementation. Control Eng. Pract. 1998, 6, 867–878. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for Floating-Point Arithmetic; IEEE Std 754-2019 (Revision of IEEE 754-2008); IEEE: New York, NY, USA, 2019; pp. 1–84. [Google Scholar]
- Nepomuceno, E.G. Convergence of recursive functions on computers. J. Eng. 2014, 2014, 560–562. [Google Scholar] [CrossRef]
- Nepomuceno, E.G.; Martins, S.A.M. A lower bound error for free-run simulation of the polynomial NARMAX. Syst. Sci. Control Eng. 2016, 4, 50–58. [Google Scholar] [CrossRef]
- Nepomuceno, E.; Martins, S.; Amaral, G.; Riveret, R. On the lower bound error for discrete maps using associative property. Syst. Sci. Control Eng. 2017, 5, 462–473. [Google Scholar] [CrossRef]
- Milani, F.L.; Lacerda Júnior, W.R.; Martins, S.A.M.; Nepomuceno, E.G. Influência de softwares e sistemas operacionais na Simulação de modelos dinâmicos Não Lineares. In Proceedings of the XXI Congresso Brasileiro de Automâtica, Vitória, Brazil, 9–12 September 2016. (In Portuguese). [Google Scholar]
- DeBrunner, L.S. Reducing Complexity of FIR Filter Implementations for Low Power Applications. In Proceedings of the 2007 Conference Record of the Forty-First Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–7 November 2007; pp. 1407–1411. [Google Scholar]
- Mehrnia, A.; Willson, A.N. A Lower Bound for the Hardware Complexity of FIR Filters. IEEE Circuits Syst. Mag. 2018, 18, 10–28. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Badii, R.; Broggi, G.; Derighetti, B.; Ravani, M.; Ciliberto, S.; Politi, A.; Rubio, M.A. Dimension increase in filtered chaotic signals. Phys. Rev. Lett. 1988, 60, 979–982. [Google Scholar] [CrossRef] [PubMed]
- Madan, R.N. Maximum Entropy Method and Digital Filter Design. In Maximum Entropy and Bayesian Methods; Springer: Dordrecht, The Netherlands, 1993; pp. 49–54. [Google Scholar]
- DeBrunner, V.E.; DeBrunner, L.S.; Coone, S.; Xiaojuan, H. Using entropy to build efficient FIR digital filters. In Proceedings of the 3rd IEEE Signal Processing Education Workshop. 2004 IEEE 11th Digital Signal Processing Workshop, Taos Ski Valley, NM, USA, 1–4 August 2004; pp. 97–101. [Google Scholar]
- Oppenheim, A.V.; Weinstein, C.J. Effects of finite register length in digital filtering and the fast Fourier transform. Proc. IEEE 1972, 60, 957–976. [Google Scholar] [CrossRef]
- Bose, N.K.; Kim, K. Boundary implications for frequency response of interval FIR and IIR filters. IEEE Trans. Signal Process. 1991, 39, 2167–2173. [Google Scholar] [CrossRef]
- Wan, S.; Zhang, X.; Dou, L. Shannon Entropy of Binary Wavelet Packet Subbands and Its Application in Bearing Fault Extraction. Entropy 2018, 20, 260. [Google Scholar] [CrossRef]
- Noonan, J.P.; Basu, P. Information Theory Preliminaries. In Signal and Image Restoration: Information-Theoretic Approaches; SPIE: Bellingham, WA, USA, 2011; pp. 3–10. [Google Scholar]
- Jayawardena, A.W.; Xu, P.; Li, W.K. Modified correlation entropy estimation for a noisy chaotic time series. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 023104. [Google Scholar] [CrossRef]
- Luo, Y.; Du, M.; Liu, J. A symmetrical image encryption scheme in wavelet and time domain. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 447–460. [Google Scholar] [CrossRef]
- Beghdadi, A.; Khellaf, A. A noise-filtering method using a local information measure. IEEE Trans. Image Process. 1997, 6, 879–882. [Google Scholar] [CrossRef]
- Figlus, T.; Gnap, J.; Skrúcaný, T.; Šarkan, B.; Stoklosa, J. The Use of Denoising and Analysis of the Acoustic Signal Entropy in Diagnosing Engine Valve Clearance. Entropy 2016, 18, 253. [Google Scholar] [CrossRef]
- Nardo, L.G.; Nepomuceno, E.G.; Arias-Garcia, J.; Butusov, D.N. Image encryption using finite-precision error. Chaos Solitons Fractals 2019, 123, 69–78. [Google Scholar] [CrossRef]
- Eaton, J.W.; Bateman, D.; Hauberg, S. Gnu Octave; Network Thoery: London, UK, 1997. [Google Scholar]
| Difference of SNR (dB) | Difference of ESN (dB) | |
|---|---|---|
| 0.0200 | ||
| 0.0192 | ||
| 0.0183 | ||
| 0.0175 | ||
| 0.0167 | ||
| 0.0158 | ||
| 0.0150 | ||
| 0.0142 | ||
| 0.0133 | ||
| 0.0125 |
| Type Filters | Butterworth | Chebyshev | Elliptic |
|---|---|---|---|
| High-pass | 14 | 8 | 6 |
| Low-pass | 14 | 8 | 6 |
| Passband | 5 | 4 | 3 |
| Stopband | 5 | 4 | 3 |
| Signal | Complete Signal | Ideally Filtered Signal |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
| Type Filters | WL | Butterworth | Chebyshev | Elliptic |
|---|---|---|---|---|
| Low-pass | 16 | |||
| 32 | ||||
| High-pass | 16 | |||
| 32 | ||||
| Passband | 16 | |||
| 32 | ||||
| Stopband | 16 | |||
| 32 |
| Signal | Original | Ideally Filtered | Elliptic |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 |
| Order | Butterworth | Chebyshev | Elliptic |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| r | – | 0.700 | 0.760 |
| p-value | – | 0.052 | 0.030 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borges, V.S.; Nepomuceno, E.G.; Duque, C.A.; Butusov, D.N. Some Remarks about Entropy of Digital Filtered Signals. Entropy 2020, 22, 365. https://doi.org/10.3390/e22030365
Borges VS, Nepomuceno EG, Duque CA, Butusov DN. Some Remarks about Entropy of Digital Filtered Signals. Entropy. 2020; 22(3):365. https://doi.org/10.3390/e22030365
Chicago/Turabian StyleBorges, Vinícius S., Erivelton G. Nepomuceno, Carlos A. Duque, and Denis N. Butusov. 2020. "Some Remarks about Entropy of Digital Filtered Signals" Entropy 22, no. 3: 365. https://doi.org/10.3390/e22030365
APA StyleBorges, V. S., Nepomuceno, E. G., Duque, C. A., & Butusov, D. N. (2020). Some Remarks about Entropy of Digital Filtered Signals. Entropy, 22(3), 365. https://doi.org/10.3390/e22030365







