A Note on Wavelet-Based Estimator of the Hurst Parameter
Abstract
1. Introduction
- The changes of bias and variance with all different Hs, different data lengths, different s and different wavelets;
- The relations of selected with data length and H;
- The initialization for initial approximation wavelet coefficients which introduces errors in used detailed wavelet coefficients.
- The inaccurate bias correction caused by correlations of wavelet coefficients.
- The method of simulation for FBM is not enough exact that the empirical bias is caused.
2. Wavelet-Based Estimator
2.1. Definitions and Properties
- For fixed j, the are independent and identically distributed;
- The processes and , , are independent.
2.2. Two Wavelet-Based Estimators
The First Estimator
The Second Estimator
Explicit Formula of theTwo Estimators
Variance Comparison
2.3. Calculation of Wavelet Coefficients
2.4. The Initialization Method
3. Simulation of FBM
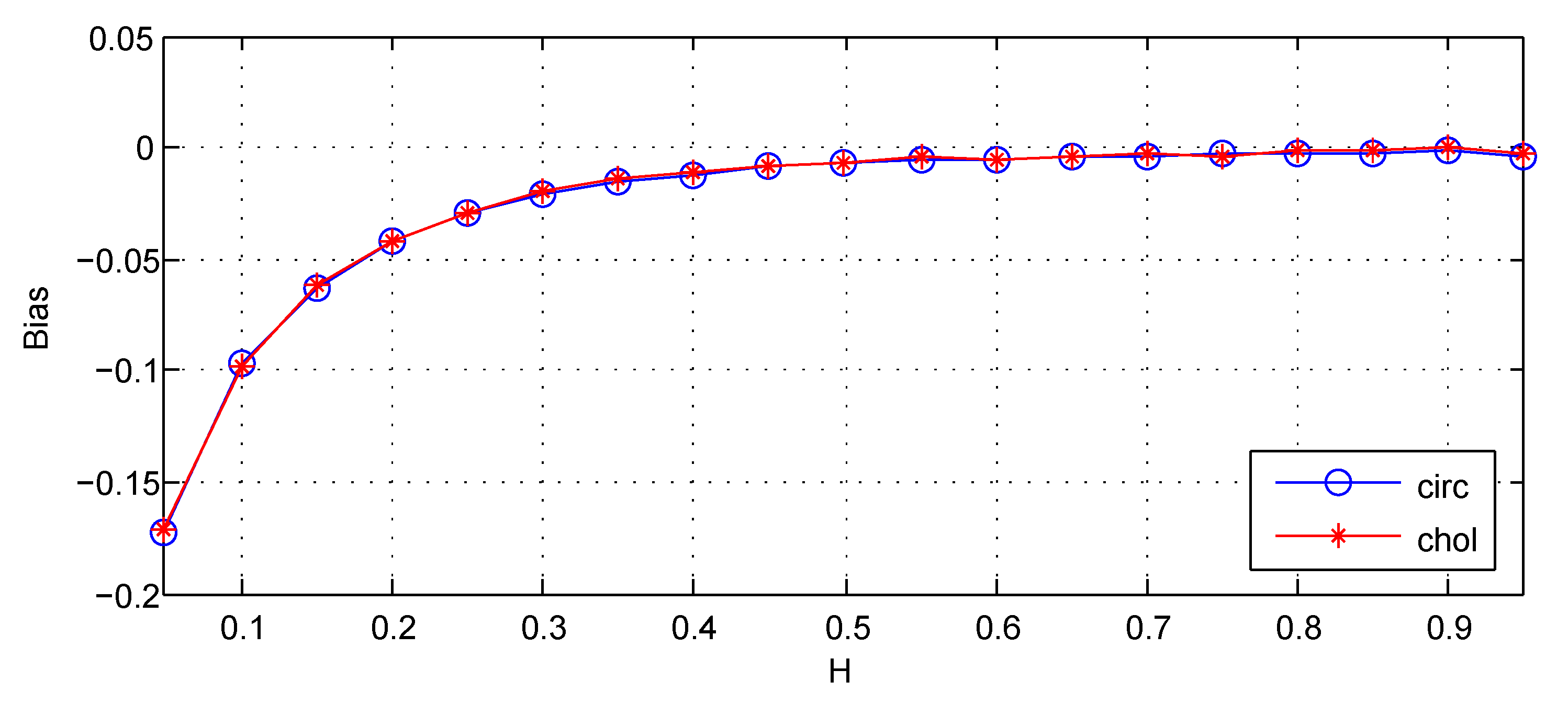
The Cholesky Method
The Circulant Embedding Method
4. Simulation Results and Discussions
4.1. Selection of Parameters
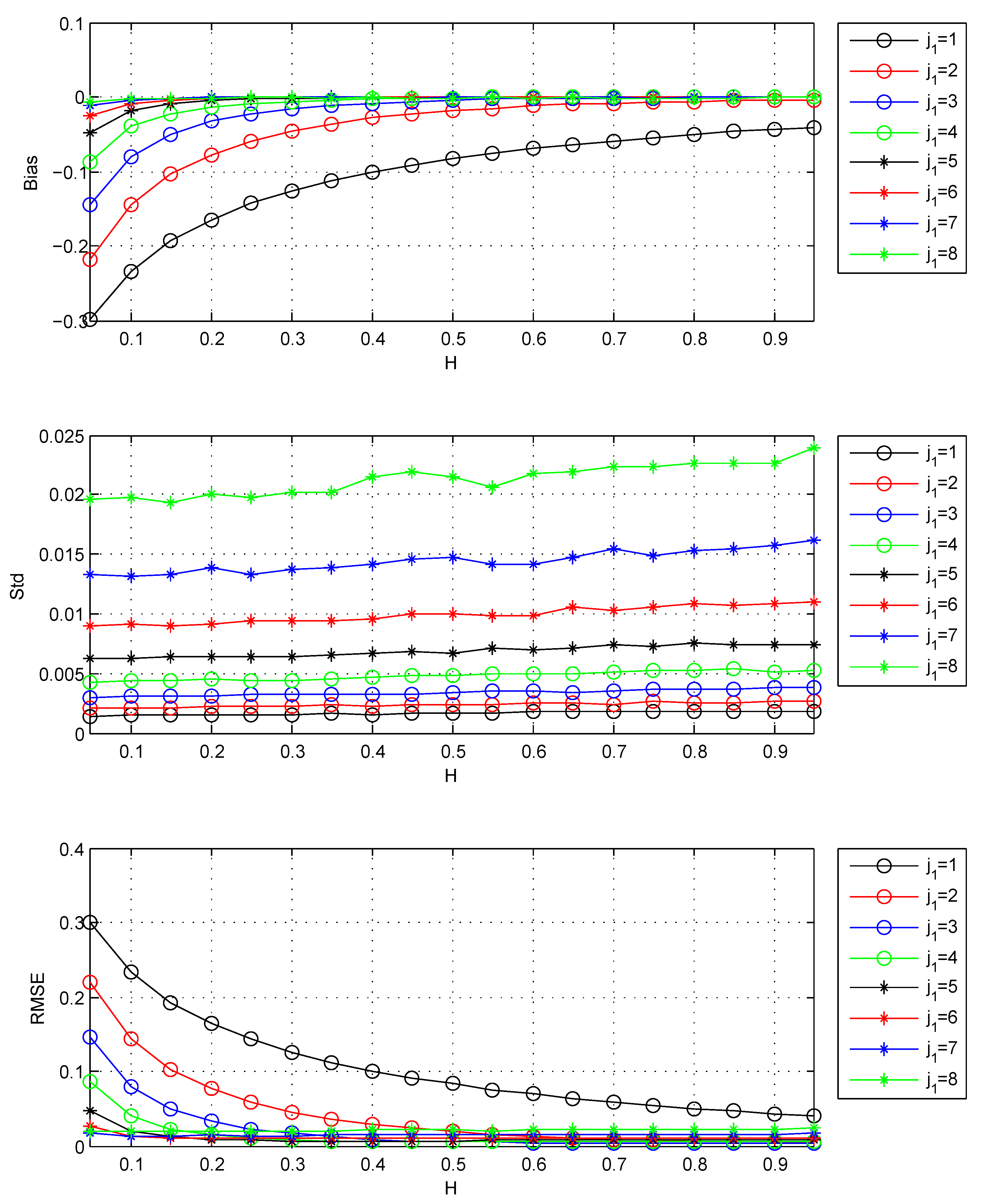
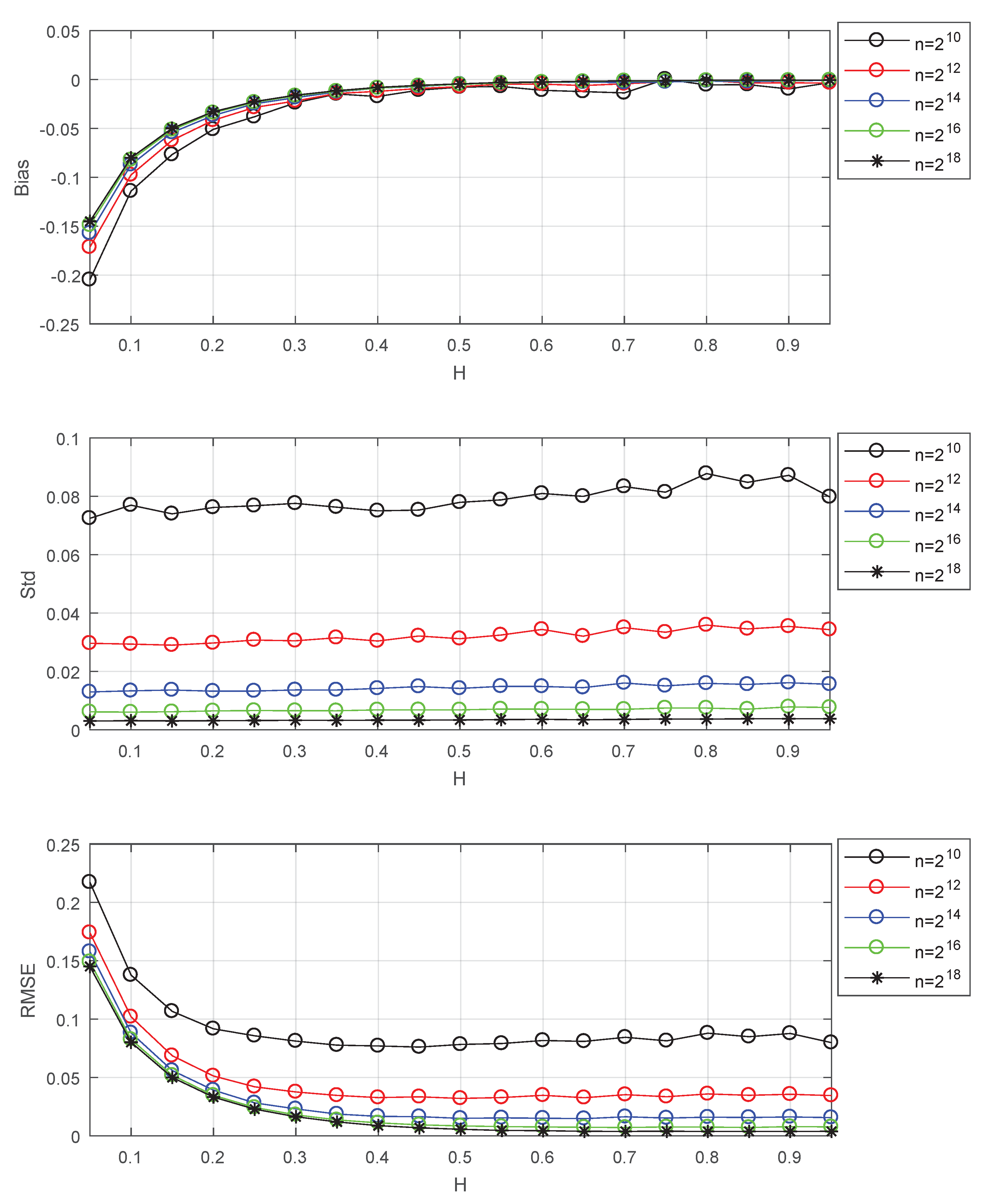
4.2. Results and Discussions on Empirical Bias
- The initialization for given in (27) introduces errors in , and the initialization errors are significant on small octaves but decrease with increasing j.
- The inaccurate bias correction for (under independent assumptions) caused by correlations of wavelet coefficients.
- The method of simulation for FBM is not enough exact that the empirical bias is caused.
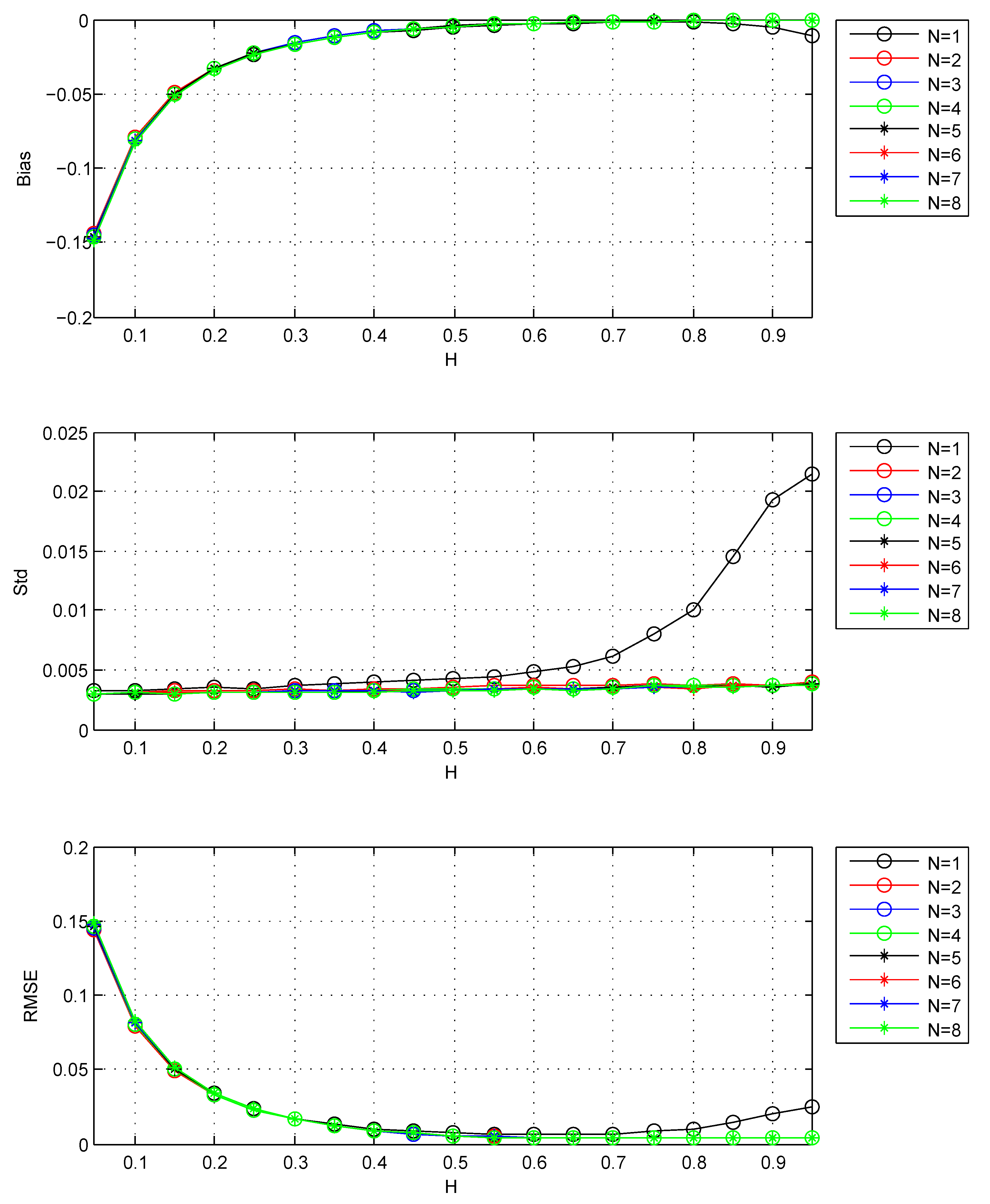
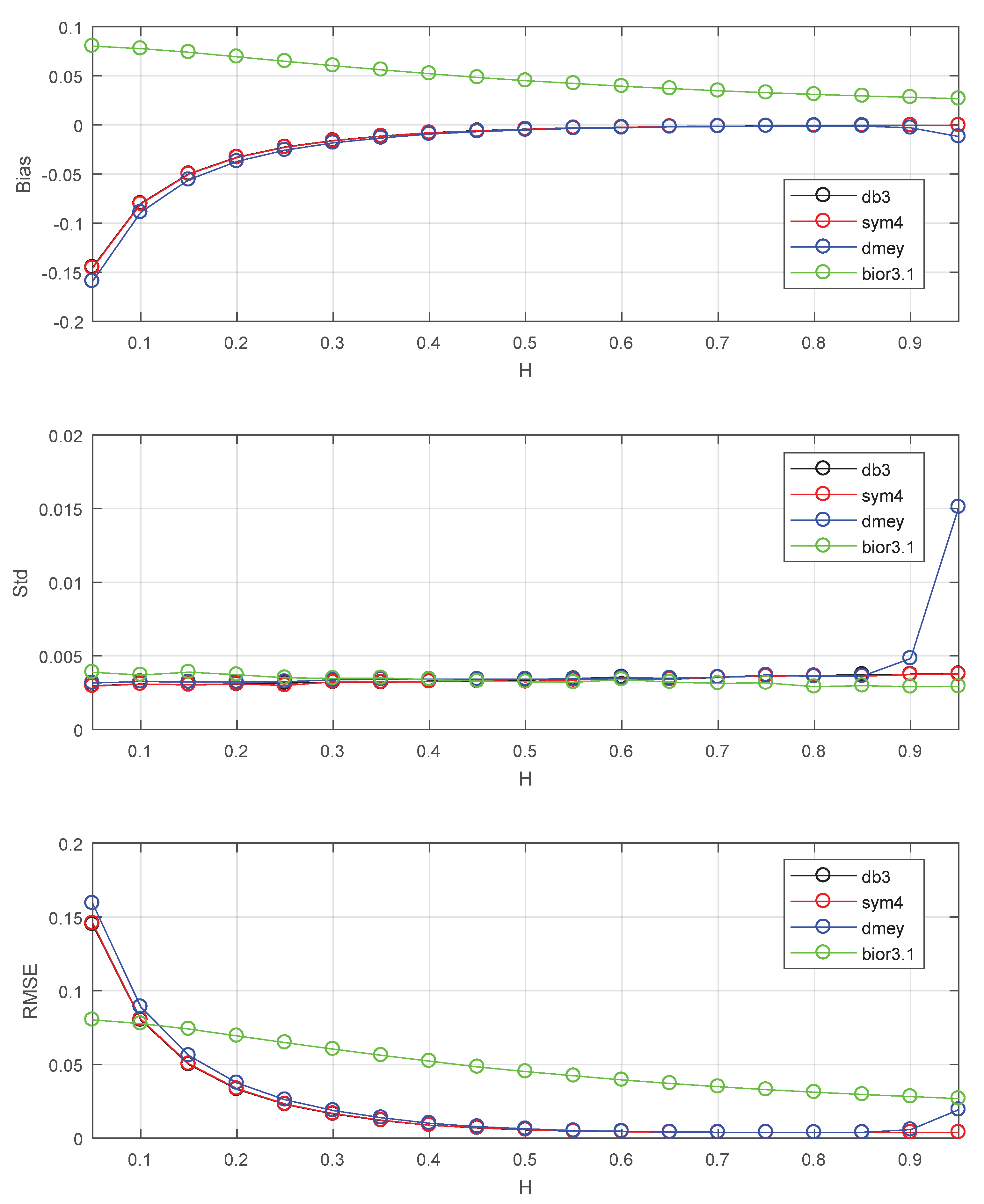
- The increase of N and change of wavelet made no improvements to the empirical bias. The chosen of biorthogonal wavelet makes the empirical bias worse.
- The increase of leads to the decrease of empirical bias.
- The empirical bias increases with the decrease of H. when choosing and , the empirical bias of estimator can be ignored for . So the estimator is suitable to detect the long-range dependence (can be described by ).
Comparison of Estimators
Comparison of Simulation Methods
4.3. Analysis of the Initialization Method
4.4. Analysis of Noise Effects
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Liang, S.Y.; Yang, J.; Li, B. Long range dependence prognostics for bearing vibration intensity chaotic time series. Entropy 2016, 18, 23. [Google Scholar] [CrossRef]
- Liu, C.; Yang, Z.; Shi, Z.; Ma, J.; Cao, J. A gyroscope signal denoising method based on empirical mode decomposition and signal reconstruction. Sensors 2019, 19, 5064. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Chan, C.; Li, B.; Song, X. Multi-sensor fusion methodology for enhanced land vehicle positioning. Inform. Fusion 2019, 46, 51–62. [Google Scholar] [CrossRef]
- Dou, C.; Wei, X.; Lin, J. Fault diagnosis of gearboxes using nonlinearity and determinism by generalized Hurst exponents of shuffle and surrogate data. Entropy 2018, 20, 364. [Google Scholar] [CrossRef]
- Wu, L.; Chen, L.; Ding, Y.; Zhao, T. Testing for the source of multifractality in water level records. Physica A 2018, 508, 824–839. [Google Scholar] [CrossRef]
- Graves, T.; Gramacy, R.; Watkins, N.; Franzke, C. A brief history of long memory: Hurst, Mandelbrot and the road to ARFIMA, 1951–1980. Entropy 2017, 19, 437. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar]
- Mandelbrot, B.; Van Ness, J. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, J.; Liang, X.; Liu, N. Function extension based real-time wavelet de-noising method for projectile attitude measurement. Sensors 2020, 20, 200. [Google Scholar] [CrossRef]
- He, K.; Xia, Z.; Si, Y.; Lu, Q.; Peng, Y. Noise reduction of welding crack AE signal based on EMD and wavelet packet. Sensors 2020, 20, 761. [Google Scholar] [CrossRef]
- Nicolis, O.; Mateu, J.; Contreras-Reyes, J.E. Wavelet-based entropy measures to characterize two-dimensional fractional Brownian fields. Entropy 2020, 22, 196. [Google Scholar] [CrossRef]
- Li, J.; Ke, L.; Du, Q. Classification of heart sounds based on the wavelet fractal and twin support vector machine. Entropy 2019, 21, 472. [Google Scholar] [CrossRef]
- Ramírez-Pacheco, J.C.; Trejo-Sánchez, J.A.; Cortez-González, J.; Palacio, R.R. Classification of fractal signals using two-parameter non-extensive wavelet entropy. Entropy 2017, 19, 224. [Google Scholar] [CrossRef]
- Flandrin, P. Wavelet analysis and synthesis of fractional Brownian motion. IEEE Trans. Inf. Theory 1992, 38, 910–917. [Google Scholar] [CrossRef]
- Abry, P.; Gonçalvès, P.; Flandrin, P. Wavelets, spectrum analysis and 1/f processes. In Wavelets and Statistics; Antoniadis, A., Oppenheim, G., Eds.; Springer: New York, NY, USA, 1995; Section 2; Volume 103, pp. 15–29. [Google Scholar] [CrossRef]
- Delbeke, L.; Van Assche, W. A wavelet based estimator for the parameter of self-similarity of fractional Brownian motion. In Proceedings of the 3rd International Conference on Approximation and Optimization in the Caribbean (Puebla, 1995), Puebla, Mexico, 8–13 October 1995; Volume 24, pp. 65–76. [Google Scholar]
- Abry, P.; Veitch, D. Wavelet analysis of long-range-dependent traffic. IEEE Trans. Inf. Theory 1998, 44, 2–15. [Google Scholar] [CrossRef]
- Veitch, D.; Abry, P. A wavelet-based joint estimator of the parameters of long-range dependence. IEEE Trans. Inf. Theory 1999, 45, 878–897. [Google Scholar] [CrossRef]
- Abry, P.; Flandrin, P.; Taqqu, M.; Veitch, D. Wavelets for the analysis, estimation and synthesis of scaling data. In Self-Similar Network Traffic and Performance Evaluation; Park, K., Willinger, W., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; pp. 39–88. [Google Scholar]
- Abry, P.; Flandrin, P.; Taqqu, M.S.; Veitch, D. Self-similarity and long-range dependence through the wavelet lens. In Theory and Applications of Long-Range Dependence; Doukhan, P., Oppenheim, G., Taqqu, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 527–556. [Google Scholar]
- Abry, P.; Helgason, H.; Pipiras, V. Wavelet-based analysis of non-Gaussian long-range dependent processes and estimation of the Hurst parameter. Lith. Math. J. 2011, 51, 287–302. [Google Scholar] [CrossRef]
- Rea, W.; Oxley, L.; Reale, M.; Brown, J. Estimators for long range dependence: An empirical study. arXiv 2009, arXiv:0901.0762. [Google Scholar]
- Soltani, S.; Simard, P.; Boichu, D. Estimation of the self-similarity parameter using the wavelet transform. Signal Process. 2004, 84, 117–123. [Google Scholar] [CrossRef]
- Shen, H.; Zhu, Z.; Lee, T.C. Robust estimation of the self-similarity parameter in network traffic using wavelet transform. Signal Process. 2007, 87, 2111–2124. [Google Scholar] [CrossRef]
- Park, J.; Park, C. Robust estimation of the Hurst parameter and selection of an onset scaling. Stat. Sin. 2009, 19, 1531–1555. [Google Scholar]
- Feng, C.; Vidakovic, B. Estimation of the Hurst exponent using trimean estimators on nondecimated wavelet coefficients. arXiv 2017, arXiv:1709.08775. [Google Scholar]
- Kang, M.; Vidakovic, B. MEDL and MEDLA: Methods for assessment of scaling by medians of log-squared nondecimated wavelet coefficients. arXiv 2017, arXiv:1703.04180. [Google Scholar]
- Wu, L.; Ding, Y. Estimation of self-similar Gaussian fields using wavelet transform. Int. J. Wavelets Multiresolut. Inf. Process. 2015, 13, 1550044. [Google Scholar] [CrossRef]
- Wu, L.; Ding, Y. Wavelet-based estimator for the Hurst parameters of fractional Brownian sheet. Acta Math. Sci. 2017, 37B, 205–222. [Google Scholar] [CrossRef]
- Wu, L.; Ding, Y. Wavelet-based estimations of fractional Brownian sheet: Least squares versus maximum likelihood. J. Comput. Appl. Math. 2020, 371, 112609. [Google Scholar] [CrossRef]
- Bardet, J.M.; Lang, G.; Oppenheim, G.; Philippe, A.; Stoev, S.; Taqqu, M.S. Semi-parametric estimation of the long-range dependence parameter: A survey. In Theory and Applications of Long-Range Dependence; Doukhan, P., Oppenheim, G., Taqqu, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 557–577. [Google Scholar]
- Tewfik, A.H.; Kim, M. Correlation structure of the discrete wavelet coefficients of fractional Brownian motion. IEEE Trans. Inf. Theory 1992, 38, 904–909. [Google Scholar] [CrossRef]
- Dijkerman, R.W.; Mazumdar, R.R. On the correlation structure of the wavelet coefficients of fractional Brownian motion. IEEE Trans. Inf. Theory 1994, 40, 1609–1612. [Google Scholar] [CrossRef]
- Abry, P.; Delbeke, L.; Flandrin, P. Wavelet based estimator for the self-similarity parameter of α-stable processes. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Phoenix, AZ, USA, 15–19 March 1999; Volume 3, pp. 1729–1732. [Google Scholar] [CrossRef]
- Veitch, D.; Taqqu, M.S.; Abry, P. Meaningful MRA initialization for discrete time series. Signal Process. 2000, 80, 1971–1983. [Google Scholar] [CrossRef]
- Abry, P.; Flandrin, P. On the initialization of the discrete wavelet transform algorithm. IEEE Signal Process. Lett. 1994, 1, 32–34. [Google Scholar] [CrossRef]
- Veitch, D.; Abry, P.; Taqqu, M.S. On the automatic selection of the onset of scaling. Fractals 2003, 11, 377–390. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables and Stochastic Processes; Tata McGraw-Hill Education: New York, NY, USA, 2002. [Google Scholar]
- Davies, R.B.; Harte, D.S. Tests for Hurst effect. Biometrika 1987, 74, 95–101. [Google Scholar] [CrossRef]
- Dieker, T. Simulation of Fractional Brownian Motion. Master’s Thesis, University of Twente, Amsterdam, The Netherlands, 2004. [Google Scholar]
- Kroese, D.P.; Botev, Z.I. Spatial process simulation. In Stochastic Geometry, Spatial Statistics and Random Fields; Spodarev, E., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 369–404. [Google Scholar] [CrossRef]
- Dietrich, C.; Newsam, G.N. Fast and exact simulation of stationary Gaussian processes through circulant embedding of the covariance matrix. SIAM J. Sci. Comput. 1997, 18, 1088–1107. [Google Scholar] [CrossRef]
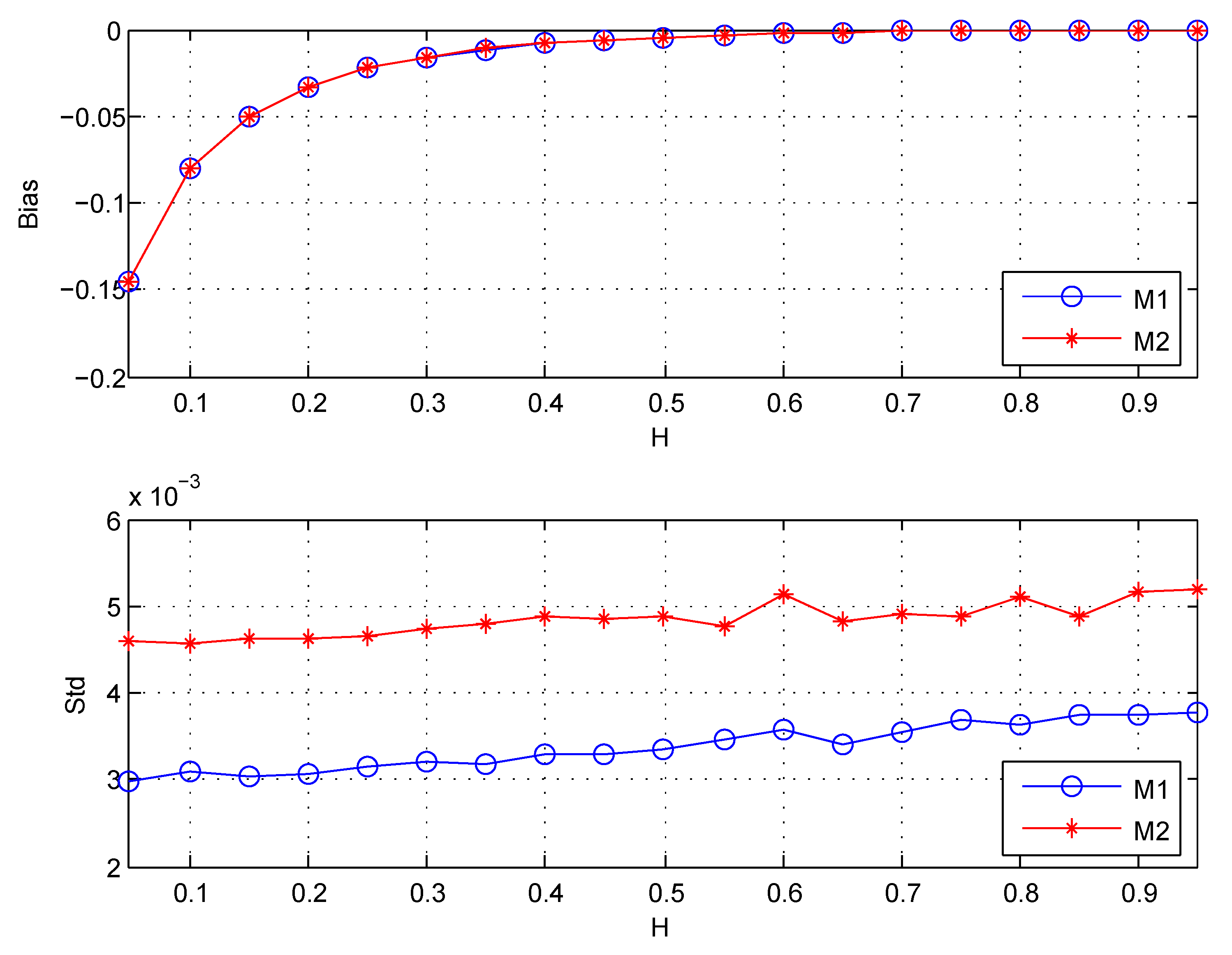


| H | Bias | Std | RMSE | Bias | Std | RMSE | ||
|---|---|---|---|---|---|---|---|---|
| 0.05 | 7 | −0.0122 | 0.0133 | 0.0180 | 3 | −0.1450 | 0.0030 | 0.1451 |
| 0.10 | 6 | −0.0087 | 0.0091 | 0.0126 | 3 | −0.0801 | 0.0031 | 0.0801 |
| 0.15 | 6 | −0.0046 | 0.0090 | 0.0101 | 3 | −0.0499 | 0.0030 | 0.0500 |
| 0.20 | 5 | −0.0056 | 0.0064 | 0.0085 | 3 | −0.0330 | 0.0031 | 0.0331 |
| 0.25 | 5 | −0.0032 | 0.0063 | 0.0071 | 3 | −0.0226 | 0.0032 | 0.0228 |
| 0.30 | 5 | −0.0019 | 0.0063 | 0.0066 | 3 | −0.0160 | 0.0032 | 0.0163 |
| 0.35 | 4 | −0.0038 | 0.0045 | 0.0059 | 3 | −0.0115 | 0.0032 | 0.0119 |
| 0.40 | 4 | −0.0023 | 0.0047 | 0.0052 | 3 | −0.0081 | 0.0033 | 0.0087 |
| 0.45 | 4 | −0.0019 | 0.0048 | 0.0052 | 3 | −0.0060 | 0.0033 | 0.0068 |
| 0.50 | 4 | −0.0012 | 0.0048 | 0.0049 | 3 | −0.0044 | 0.0033 | 0.0056 |
| 0.55 | 3 | −0.0030 | 0.0034 | 0.0046 | 3 | −0.0030 | 0.0034 | 0.0046 |
| 0.60 | 3 | −0.0025 | 0.0036 | 0.0044 | 3 | −0.0025 | 0.0036 | 0.0044 |
| 0.65 | 3 | −0.0018 | 0.0034 | 0.0038 | 3 | −0.0018 | 0.0034 | 0.0038 |
| 0.70 | 3 | −0.0014 | 0.0035 | 0.0038 | 3 | −0.0014 | 0.0035 | 0.0038 |
| 0.75 | 3 | −0.0013 | 0.0037 | 0.0039 | 3 | −0.0013 | 0.0037 | 0.0039 |
| 0.80 | 3 | −0.0008 | 0.0036 | 0.0037 | 3 | −0.0008 | 0.0036 | 0.0037 |
| 0.85 | 3 | −0.0006 | 0.0037 | 0.0038 | 3 | −0.0006 | 0.0037 | 0.0038 |
| 0.90 | 3 | −0.0006 | 0.0037 | 0.0038 | 3 | −0.0006 | 0.0037 | 0.0038 |
| 0.95 | 3 | −0.0006 | 0.0038 | 0.0038 | 3 | −0.0006 | 0.0038 | 0.0038 |
| H | n | Bias | Std | RMSE | Bias | Std | RMSE | ||
|---|---|---|---|---|---|---|---|---|---|
| 2 | −0.0632 | 0.0473 | 0.0789 | 3 | −0.0239 | 0.0776 | 0.0811 | ||
| 3 | −0.0220 | 0.0305 | 0.0376 | 3 | −0.0220 | 0.0305 | 0.0376 | ||
| 0.3 | 4 | −0.0080 | 0.0202 | 0.0217 | 3 | −0.0186 | 0.0136 | 0.0231 | |
| 4 | −0.0063 | 0.0096 | 0.0115 | 3 | −0.0167 | 0.0065 | 0.0179 | ||
| 5 | −0.0019 | 0.0063 | 0.0066 | 3 | −0.0160 | 0.0032 | 0.0163 | ||
| 2 | −0.0276 | 0.0479 | 0.0553 | 3 | −0.0078 | 0.0779 | 0.0783 | ||
| 2 | −0.0231 | 0.0202 | 0.0307 | 3 | −0.0073 | 0.0312 | 0.0320 | ||
| 0.5 | 3 | −0.0048 | 0.0142 | 0.0149 | 3 | −0.0048 | 0.0142 | 0.0149 | |
| 3 | −0.0050 | 0.0068 | 0.0085 | 3 | −0.0050 | 0.0068 | 0.0085 | ||
| 4 | −0.0012 | 0.0048 | 0.0049 | 3 | −0.0044 | 0.0033 | 0.0056 | ||
| 2 | −0.0109 | 0.0526 | 0.0537 | 3 | −0.0056 | 0.0878 | 0.0879 | ||
| 2 | −0.0061 | 0.0233 | 0.0241 | 3 | −0.0010 | 0.0359 | 0.0359 | ||
| 0.8 | 2 | −0.0062 | 0.0106 | 0.0123 | 3 | −0.0015 | 0.0159 | 0.0160 | |
| 3 | −0.0010 | 0.0074 | 0.0075 | 3 | −0.0010 | 0.0074 | 0.0075 | ||
| 3 | −0.0008 | 0.0036 | 0.0037 | 3 | −0.0008 | 0.0036 | 0.0037 |
| H | 0.05 | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 | 0.35 | 0.40 | 0.45 | 0.50 |
|---|---|---|---|---|---|---|---|---|---|---|
| 2.41 | 2.18 | 2.32 | 2.27 | 2.16 | 2.19 | 2.27 | 2.22 | 2.18 | 2.13 | |
| H | 0.55 | 0.60 | 0.65 | 0.70 | 0.75 | 0.80 | 0.85 | 0.90 | 0.95 | |
| 1.92 | 2.08 | 2.00 | 1.94 | 1.76 | 1.95 | 1.71 | 1.89 | 1.88 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L. A Note on Wavelet-Based Estimator of the Hurst Parameter. Entropy 2020, 22, 349. https://doi.org/10.3390/e22030349
Wu L. A Note on Wavelet-Based Estimator of the Hurst Parameter. Entropy. 2020; 22(3):349. https://doi.org/10.3390/e22030349
Chicago/Turabian StyleWu, Liang. 2020. "A Note on Wavelet-Based Estimator of the Hurst Parameter" Entropy 22, no. 3: 349. https://doi.org/10.3390/e22030349
APA StyleWu, L. (2020). A Note on Wavelet-Based Estimator of the Hurst Parameter. Entropy, 22(3), 349. https://doi.org/10.3390/e22030349




