A Two-Stage Mutual Information Based Bayesian Lasso Algorithm for Multi-Locus Genome-Wide Association Studies
Abstract
1. Introduction
2. Materials and Methods
2.1. Statistical Framework
2.2. Simulation Experiments
2.3. Real Data and Preprocessing
2.4. Mutual Information
2.5. SCAD
2.6. Likelihood Ratio Test
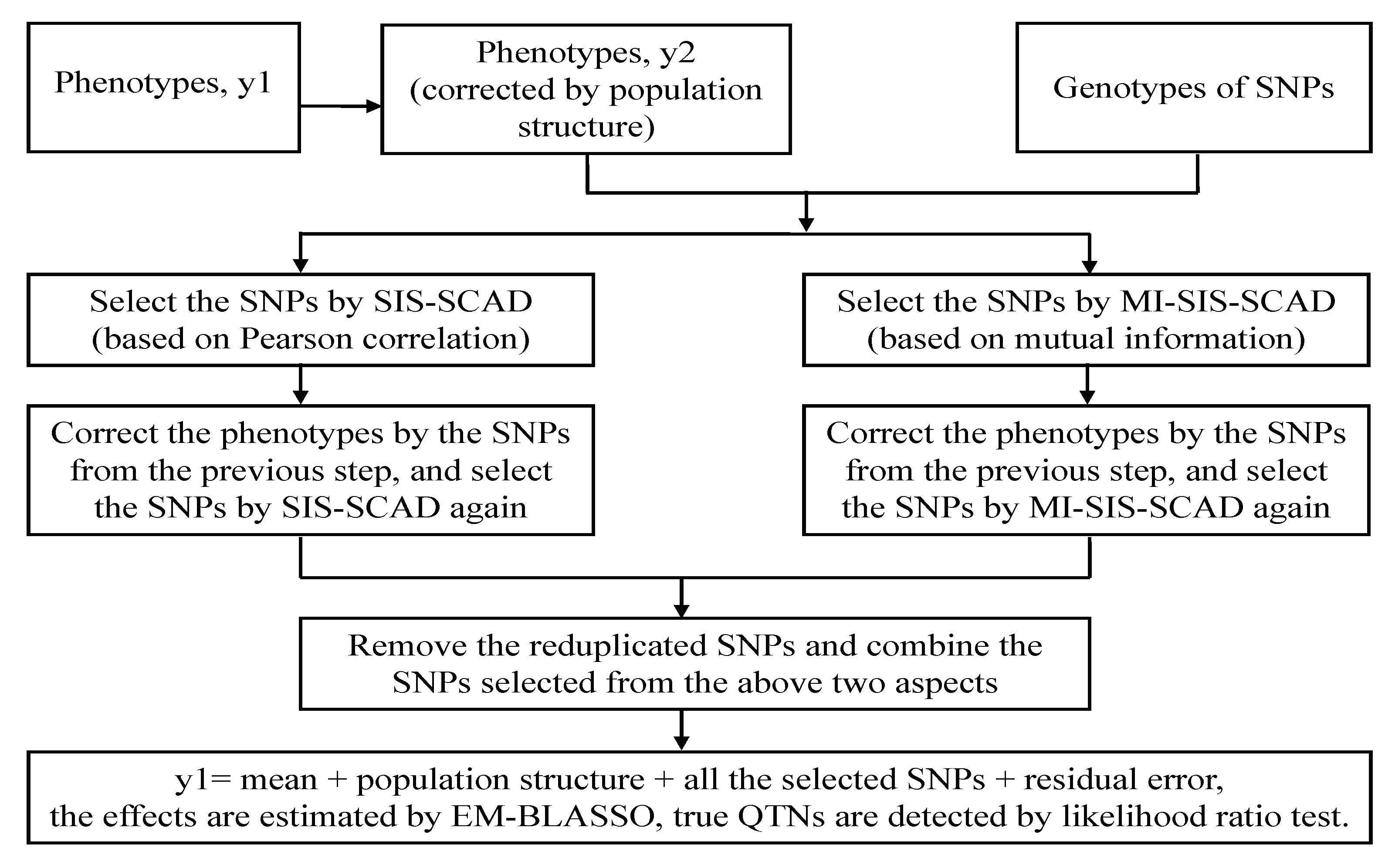
2.7. A Two-Stage Mutual Information Based Bayesian Lasso (MBLASSO) Method
- Step 1: Correct the initial phenotype vector () by the fixed effects, which indicate the population structure in our model.
- Step 2: Calculate the Pearson correlation of the ith SNP with the corrected phenotype (), that is,where is the ith SNP genotype value of the jth individual, is the corrected phenotype value of the jth individual, is the average of the genotype value of the ith SNP, is the mean of the corrected phenotype value of all individuals, and is a vector of Pearson correlation coefficients.
- Step 3: Sort the components of vector in descending order and define a subset:where is one of the two sizes recommended by Fan and Lv [11], and it is more appropriate in our work. Suppose that there are SNPs corresponding to , , for the reason that more than one SNP may share a common Pearson correlation coefficient; the subset consisting of these SNPs is denoted as , are the orders of the selected SNPs in all the p SNPs. Then implement SCAD to estimate the effects. Select the SNPs with nonzero effect to form another subset , , and . The SNPs in correspond to Type I in Pearson correlation screening. This Pearson correlation based SIS followed by SCAD is called SIS-SCAD [11].
- Step 4: Undertake ISIS-SCAD [11] to revive those non-negligible SNPs that are single uncorrelated but jointly correlated with phenotype, only one iteration is implemented here. Firstly correct the phenotype in Step 1 () by the SNPs selected by SIS-SCAD in Step 3, that is,where is estimated by SCAD, and then repeat SIS-SCAD to the rest of the SNPs, which results in another subset of SNPs, . The SNPs in correspond to Type II in Pearson correlation screening. The union of the two disjoint subsets and is denoted as , , whose size is k, .
- Step 5: Under the same conditions as in Step 2, calculate the mutual information of the ith SNP and the corrected phenotype () byand is a vector of mutual information for all of the p SNPs with the corrected phenotype. is the joint probability, and are the marginal probabilities of and , separately.
- Step 6: Similar to Step 3, sort the components of vector in descending order and define another subset:Assume that SNPs corresponding to , , because more than one SNP may share a public mutual information with phenotype. The subset is . Then use SCAD to estimate the effects of SNPs in and select the SNPs with nonzero effect to constitute a new subset , , and . The SNPs in correspond to Type I in mutual information screening. We call this mutual information based SIS followed by SCAD as MI-SIS-SCAD.
- Step 7: Refering to Step 4, correct the phenotype in Step 1 () by SNPs selected by MI-SIS-SCAD, and repeat MI-SIS-SCAD once for to the remaining of the SNPs, which generates a subset of SNPs, . The SNPs in correspond to Type II in mutual information screening. The union of the disjoint subsets and is denoted as , , the size of which is , . We call this process as MI-ISIS-SCAD.
- Step 8: Gather the SNPs selected from Steps 4 and 7 and remove the reduplicated ones. Then obtain a new subset of SNPs, that is, , the size of which is .
- Step 9: Use EM-BLASSO to estimate the effect of the SNPs from and further eliminate the SNPs with zero effect, the source code for EM-BLASSO can be found at https://CRAN.R-project.org/package=mrMLM, where we can also download the program of ISIS EM-BLASSO. Note that the phenotype vector in this step refers to the original one ().
- Step 10: Apply the likelihood ratio test to identify the true QTNs, and set the significant criterion as .
3. Results
3.1. The Overlap Ratio between Pearson Correlation and Mutual Information Based Screening in MBLASSO
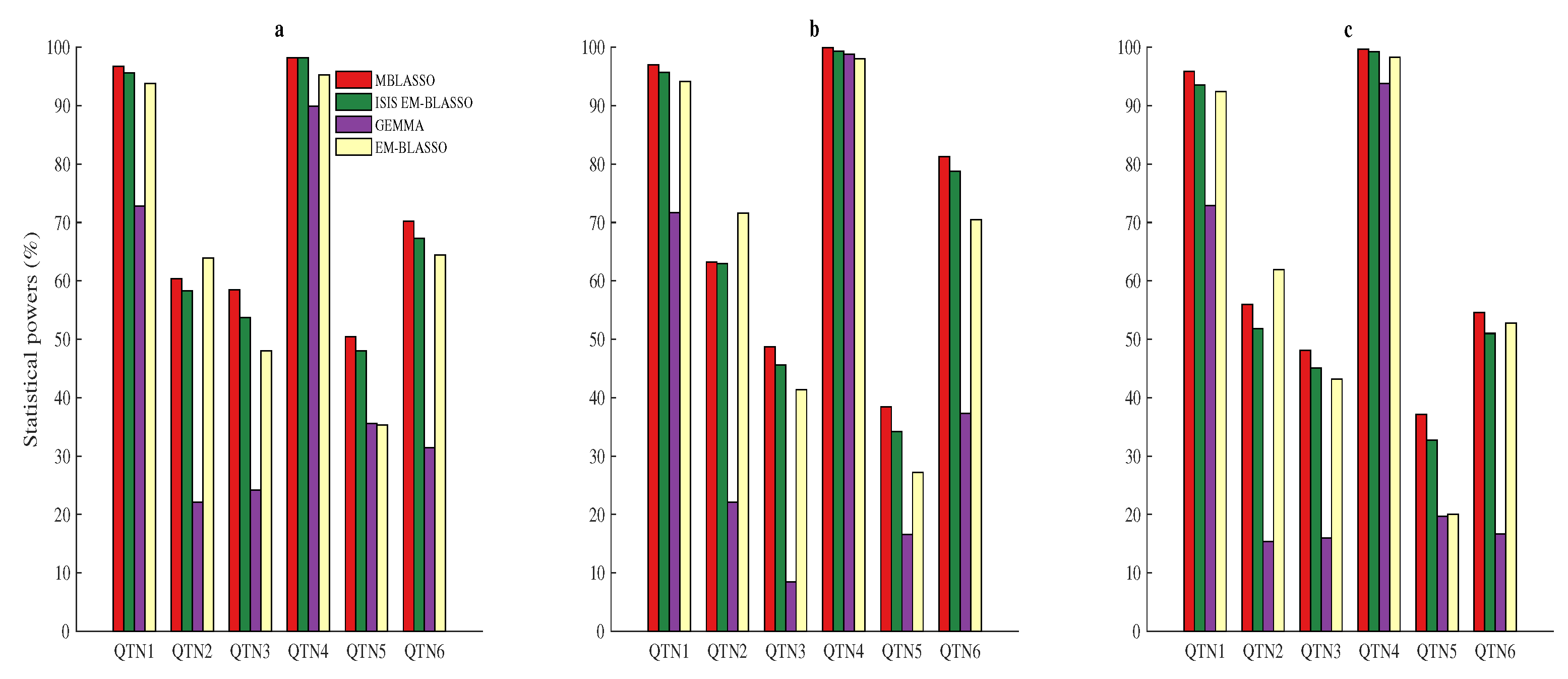
3.2. Statistical Power for QTN Detection
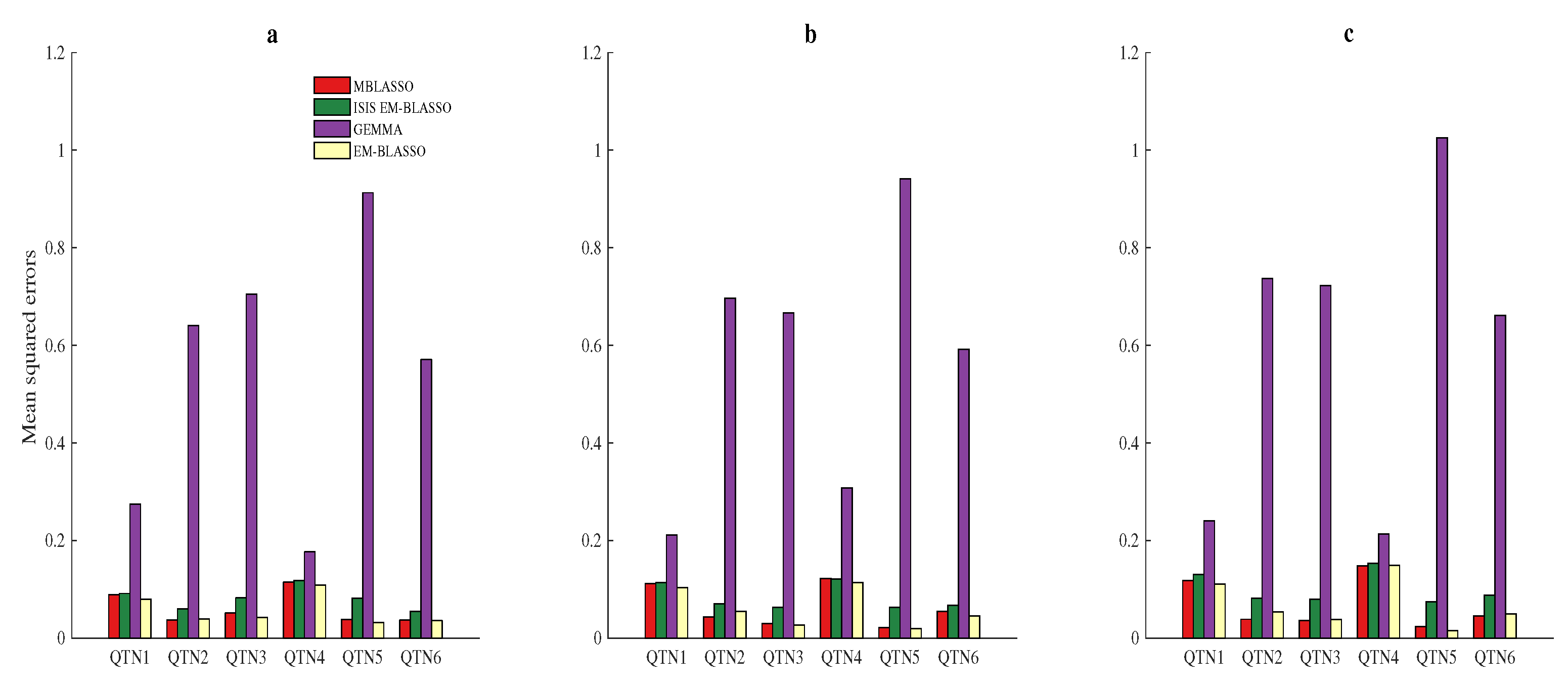
3.3. Average Accuracy for QTN Effects
3.4. Type 1 Error Ratio
3.5. Computational Efficiency
3.6. Arabidopsis Thaliana Dataset Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yu, J.; Pressoir, G.; Briggs, W.H.; Bi, I.V.; Yamasaki, M.; Doebley, J.F.; McMullen, M.D.; Gaut, B.S.; Nielsen, D.M.; Holland, J.B. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 2006, 38, 203–208. [Google Scholar] [CrossRef]
- Kang, H.M.; Zaitlen, N.A.; Wade, C.M.; Kirby, A.; Heckerman, D.; Daly, M.J.; Eskin, E. Efficient control of population structure in model organism association mapping. Genetics 2008, 178, 1709–1723. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ersoz, E.; Lai, C.Q.; Todhunter, R.J.; Tiwari, H.K.; Gore, M.A.; Bradbury, P.J.; Yu, J.; Arnett, D.K.; Ordovas, J.M.; et al. Mixed linear model approach adapted for genome-wide association studies. Nat. Genet. 2010, 42, 355–360. [Google Scholar] [CrossRef] [PubMed]
- Lippert, C.; Listgarten, J.; Liu, Y.; Kadie, C.M.; Davidson, R.I.; Heckerman, D. FaST linear mixed models for genome-wide association studies. Nat. Methods 2011, 8, 833–835. [Google Scholar] [CrossRef]
- Zhou, X.; Stephens, M. Genome-wide efficient mixed model analysis for association studies. Nat. Genet. 2012, 44, 821–824. [Google Scholar] [CrossRef]
- Tamba, C.L.; Ni, Y.L.; Zhang, Y.M. Iterative sure independence screening EM-Bayesian LASSO algorithm for multi-locus genome-wide association studies. PLoS Comput. Biol. 2017, 13, e1005357. [Google Scholar] [CrossRef]
- Wu, T.T.; Chen, Y.F.; Hastie, T.; Sobel, E.; Lange, K. Genome-wide association analysis by lasso penalized logistic regression. Bioinformatics 2009, 25, 714–721. [Google Scholar] [CrossRef]
- Cho, S.; Kim, H.; Oh, S.; Kim, K.; Taesung, P. Elastic-net regularization approaches for genome-wide association studies of rheumatoid arthritis. BMC Proc. 2009, 3, S25. [Google Scholar] [CrossRef]
- Li, J.; Das, K.; Fu, G.; Li, R.; Wu, R. The Bayesian lasso for genome-wide association studies. Bioinformatics 2011, 27, 516–523. [Google Scholar] [CrossRef]
- Xu, S. An expectation-maximization algorithm for the Lasso estimation of quantitative trait locus effects. Heredity 2010, 105, 483–494. [Google Scholar] [CrossRef]
- Fan, J.; Lv, J. Sure independence screening for ultrahigh dimensional feature space. J. R. Stat. Soc. Ser. B 2008, 70, 849–911. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zou, H. The adaptive Lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Li, G.; Peng, H.; Zhang, J.; Zhu, L. Robust rank correlation based screening. Ann. Stat. 2012, 40, 1846–1877. [Google Scholar] [CrossRef]
- Li, R.; Zhong, W.; Zhu, L. Feature screening via distance correlation learning. J. Am. Stat. Assoc. 2012, 107, 1129–1139. [Google Scholar] [CrossRef]
- Li, R.; Liu, J.; Lou, L. Variable selection via partial correlation. Statistica Sinica 2017, 27, 983–996. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, J.; Zhu, X.; Ye, M.; Sun, L.; Lacaze, X.; Wu, R. 2HiGWAS: A unifying high-dimensional platform to infer the global genetic architecture of trait development. Brief. Bioinform. 2015, 16, 905–911. [Google Scholar] [CrossRef]
- Cui, Y.; Zhang, F.; Zhou, Y. The application of multi-locus GWAS for the detection of salt-tolerance loci in rice. Front. Plant Sci. 2018, 9, 1464. [Google Scholar] [CrossRef]
- Liu, J.; Ye, M.; Zhu, S.; Jiang, L.; Sang, M.; Gan, J.; Wang, Q.; Huang, M.; Wu, R. Two-stage identification of SNP effects on dynamic poplar growth. Plant J. 2018, 93, 286–296. [Google Scholar] [CrossRef]
- Fan, J.; Han, F.; Liu, H. Challenges of big data analysis. Nat. Sci. Rev. 2014, 1, 293–314. [Google Scholar] [CrossRef]
- Jing, P.J.; Shen, H.B. MACOED: A multi-objective ant colony optimization algorithm for SNP epistasis detection in genome-wide association studies. Bioinformatics 2015, 31, 634–641. [Google Scholar] [CrossRef] [PubMed]
- Reshef, D.N.; Reshef, Y.A.; Finucane, H.K.; Grossman, S.R.; Mcvean, G.; Turnbaugh, P.J.; Lander, E.S.; Mitzenmacher, M.; Sabeti, P.C. Detecting novel associations in large data sets. Science 2011, 334, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Atwell, S.; Huang, Y.S.; Vilhjalmsson, B.J.; Willems, G.; Horton, M.; Li, Y.; Meng, D. Genome-wide association study of 107 phenotypes in Arabidopsis thaliana inbred lines. Nature 2010, 465, 627–631. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.B.; Feng, J.Y.; Ren, W.L.; Huang, B.; Zhou, L.; Wen, Y.J.; Zhang, J.; Dunwell, J.M.; Xu, S.; Zhang, Y.M. Improving power and accuracy of genome-wide association studies via a multi-locus mixed linear model methodology. Sci. Rep. 2016, 6, 19444. [Google Scholar] [CrossRef] [PubMed]
- Togninalli, M.; Seren, Ü.; Freudenthal, J.A.; Monroe, J.G.; Meng, D.; Nordborg, M.; Weigel, D.; Borgwardt, K.; Korte, A.; Grimm, D.G. AraPheno and the AraGWAS Catalog 2020: A major database update including RNA-Seq and knockout mutation data for Arabidopsis thaliana. Nucleic Acids Res. 2019, 48, D1063–D1068. [Google Scholar] [CrossRef]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.R.; Bender, D.; Maller, J.; Sklar, P.; Bakker, P.I.W.D.; Daly, M.J. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef]
- Alexander, D.H.; Novembre, J.; Lange, K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 2009, 19, 1655–1664. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ren, W.L.; Wen, Y.J.; Dunwell, J.M.; Zhang, Y.M. pKWmEB: Integration of Kruskal-Wallis test with empirical Bayes under polygenic background control for multi-locus genome-wide association study. Heredity 2018, 120, 208–218. [Google Scholar] [CrossRef]
- Berardini, T.Z.; Mundodi, S.; Reiser, L.; Huala, E.; Garcia-Hernandez, M.; Zhang, P.; Mueller, L.A.; Yoon, J.; Doyle, A.; Lander, G.; et al. Functional annotation of the Arabidopsis genome using controlled vocabularies. Plant Physiol. 2004, 135, 745–755. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Feng, J.Y.; Ni, Y.L.; Wen, Y.J.; Niu, Y.; Tamba, C.L.; Yue, C.; Song, Q.; Zhang, Y.M. pLARmEB: Integration of least angle regression with empirical Bayes for multilocus genome-wide association studies. Heredity 2017, 118, 517–524. [Google Scholar] [CrossRef] [PubMed]
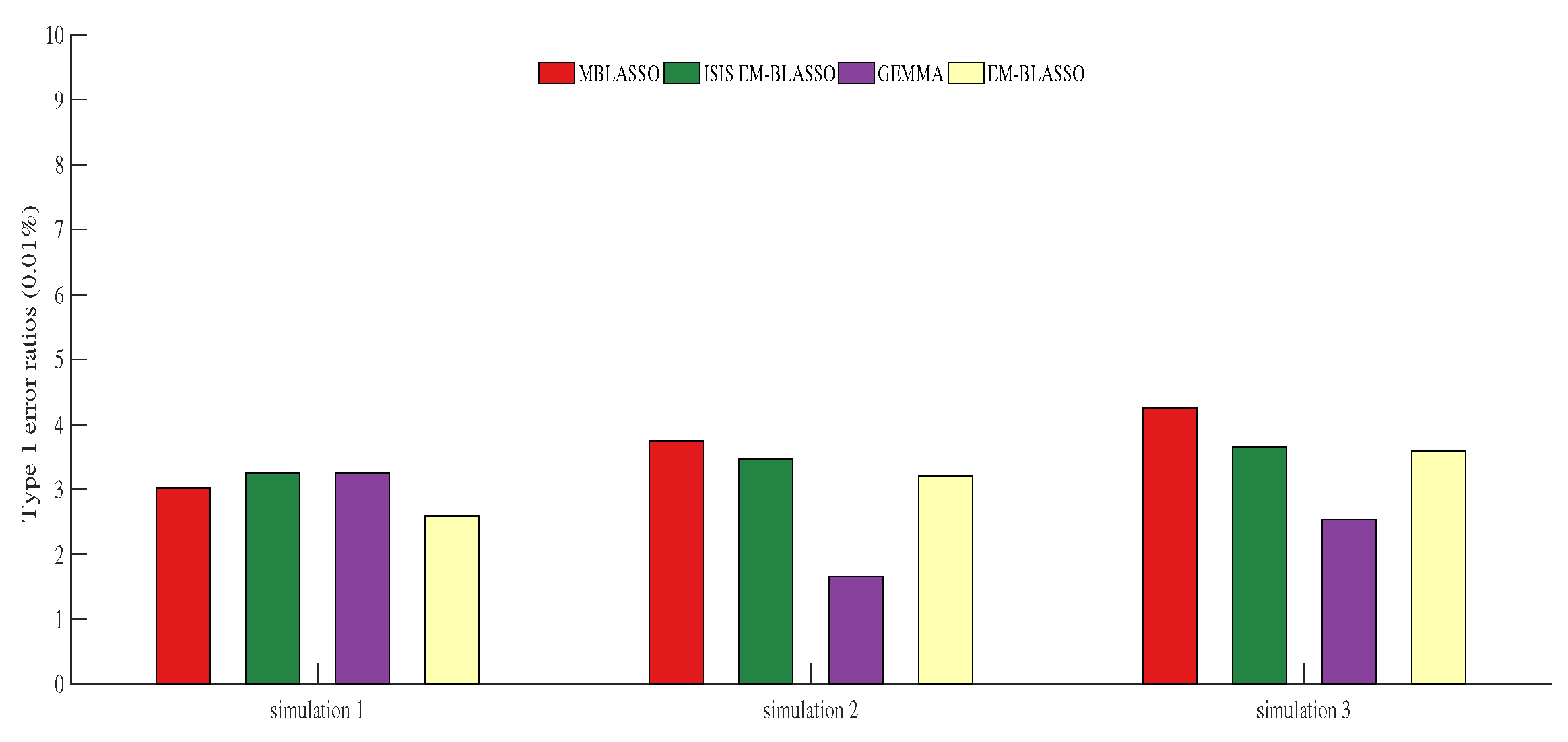
| Simulations | Pearson Correlation Screening | Mutual Information Screening | ||||
|---|---|---|---|---|---|---|
| Type I | Type II | Total | Type I | Type II | Total | |
| 1 | 0.470 (15.8) | 0.086 (50.4) | 0.184 (66.2) | 0.417 (18.2) | 0.298 (15.5) | 0.356 (33.7) |
| 2 | 0.452 (16.6) | 0.091 (50.3) | 0.181 (66.9) | 0.398 (19.0) | 0.285 (17.5) | 0.334 (36.5) |
| 3 | 0.457 (14.6) | 0.090 (50.8) | 0.173 (65.4) | 0.383 (18.4) | 0.278 (17.4) | 0.323 (35.8) |
| Traits | MBLASSO | ISIS EM-BLASSO | GEMMA | EM-BLASSO | ||||
|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | AIC | BIC | |
| LDV | −360.543 | −307.436 | −318.966 | −275.230 | 1312.693 | 1322.065 | −113.638 | −104.266 |
| SDV | −169.269 | −114.028 | −140.485 | −85.245 | 1356.907 | 1372.251 | 149.095 | 149.095 |
| 2W | −103.363 | −51.957 | −65.172 | −7.718 | 584.000 | 587.024 | 148.247 | 160.342 |
| 4W | −124.109 | −74.084 | −98.993 | −54.527 | 1253.281 | 1258.839 | 22.893 | 39.568 |
| Traits | MBLASSO | ISIS EM-BLASSO | GEMMA | EM-BLASSO |
|---|---|---|---|---|
| LDV | 5/17 | 3/14 | 0/3 | 0/3 |
| SDV | 4/18 | 2/18 | 1/5 | 0/0 |
| 2W | 2/17 | 1/19 | 0/1 | 0/4 |
| 4W | 3/18 | 2/16 | 1/2 | 0/6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Yu, Z.; An, J.; Han, G.; Ma, Y.; Tang, R. A Two-Stage Mutual Information Based Bayesian Lasso Algorithm for Multi-Locus Genome-Wide Association Studies. Entropy 2020, 22, 329. https://doi.org/10.3390/e22030329
Guo H, Yu Z, An J, Han G, Ma Y, Tang R. A Two-Stage Mutual Information Based Bayesian Lasso Algorithm for Multi-Locus Genome-Wide Association Studies. Entropy. 2020; 22(3):329. https://doi.org/10.3390/e22030329
Chicago/Turabian StyleGuo, Hongping, Zuguo Yu, Jiyuan An, Guosheng Han, Yuanlin Ma, and Runbin Tang. 2020. "A Two-Stage Mutual Information Based Bayesian Lasso Algorithm for Multi-Locus Genome-Wide Association Studies" Entropy 22, no. 3: 329. https://doi.org/10.3390/e22030329
APA StyleGuo, H., Yu, Z., An, J., Han, G., Ma, Y., & Tang, R. (2020). A Two-Stage Mutual Information Based Bayesian Lasso Algorithm for Multi-Locus Genome-Wide Association Studies. Entropy, 22(3), 329. https://doi.org/10.3390/e22030329





