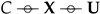Variational Information Bottleneck for Unsupervised Clustering: Deep Gaussian Mixture Embedding
Abstract
1. Introduction
2. Proposed Model
2.1. Inference Network Model
- One of the components of the GMM is chosen according to a categorical variable C.
- The data are generated from the cth component of the GMM, i.e., .
- Encoder maps to a latent representation according to .
- 3.1.
- The encoder is modeled with a DNN , which maps to the parameters of a Gaussian distribution, i.e., .
- 3.2.
- The representation is sampled from .

2.2. Generative Network Model
- One of the components of the GMM is chosen according to a categorical variable C, with a prior distribution .
- The representation is generated from the cth component, i.e., .
- The decoder maps the latent representation to , which is the reconstruction of the source by using the mapping .
- 3.1
- The decoder is modeled with a DNN that maps to the estimate , i.e., .
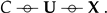
3. Proposed Method
3.1. Brief Review of Variational Information Bottleneck for Unsupervised Learning
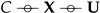 , it is easy to see that for all values of ). Noting that is constant with respect to , maximizing over is equivalent to maximizing:
, it is easy to see that for all values of ). Noting that is constant with respect to , maximizing over is equivalent to maximizing: 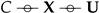 (for a detailed treatment, please look at Appendix B); and follows from the definition of in (8).
(for a detailed treatment, please look at Appendix B); and follows from the definition of in (8).3.2. Proposed Algorithm: VIB-GMM
| Algorithm 1 VIB-GMM algorithm for unsupervised learning. |
|
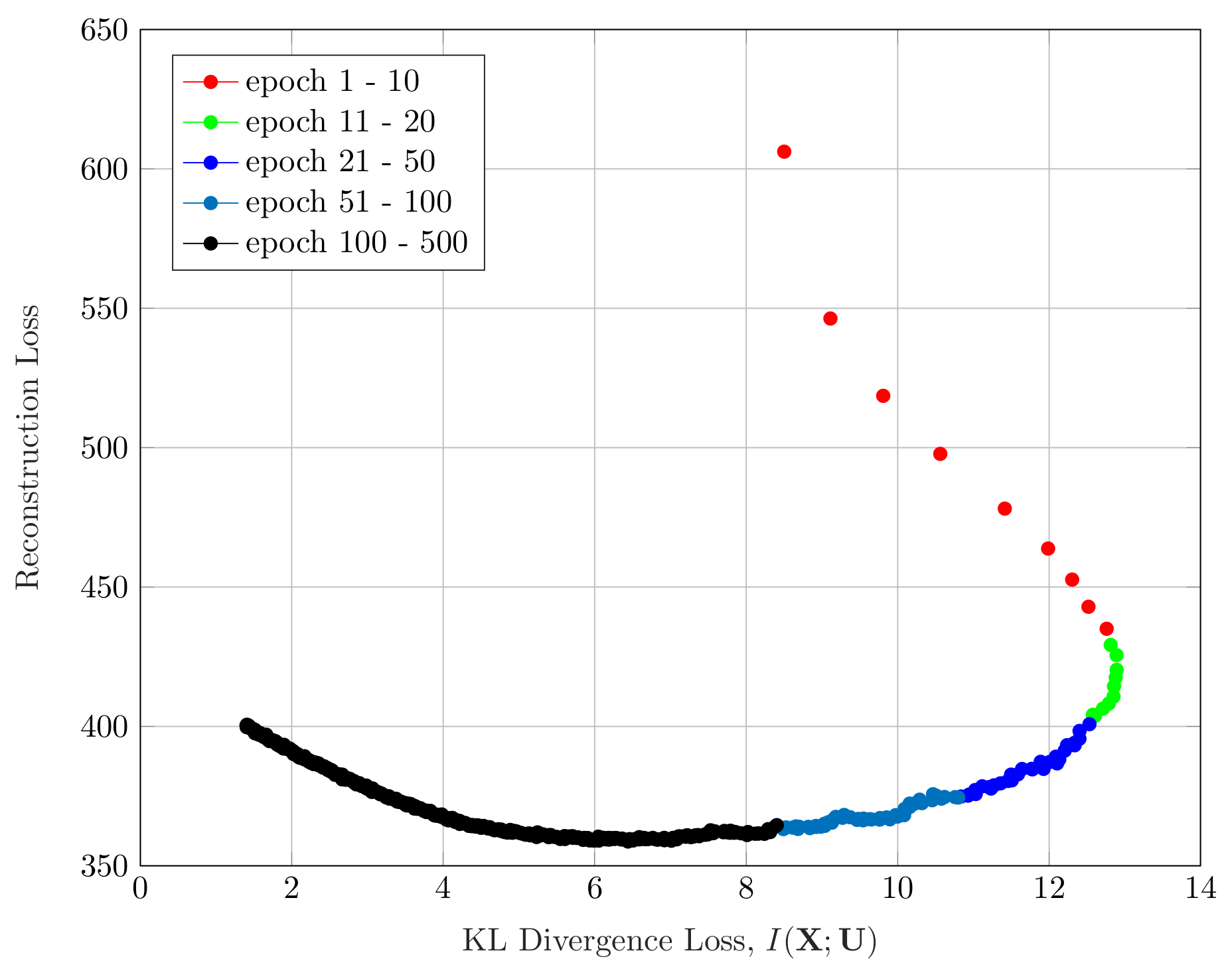
3.3. Effect of the Hyperparameter
| Algorithm 2 Annealing algorithm pseudocode. |
|
4. Experiments
4.1. Description of the Datasets Used
4.2. Network Settings and Other Parameters
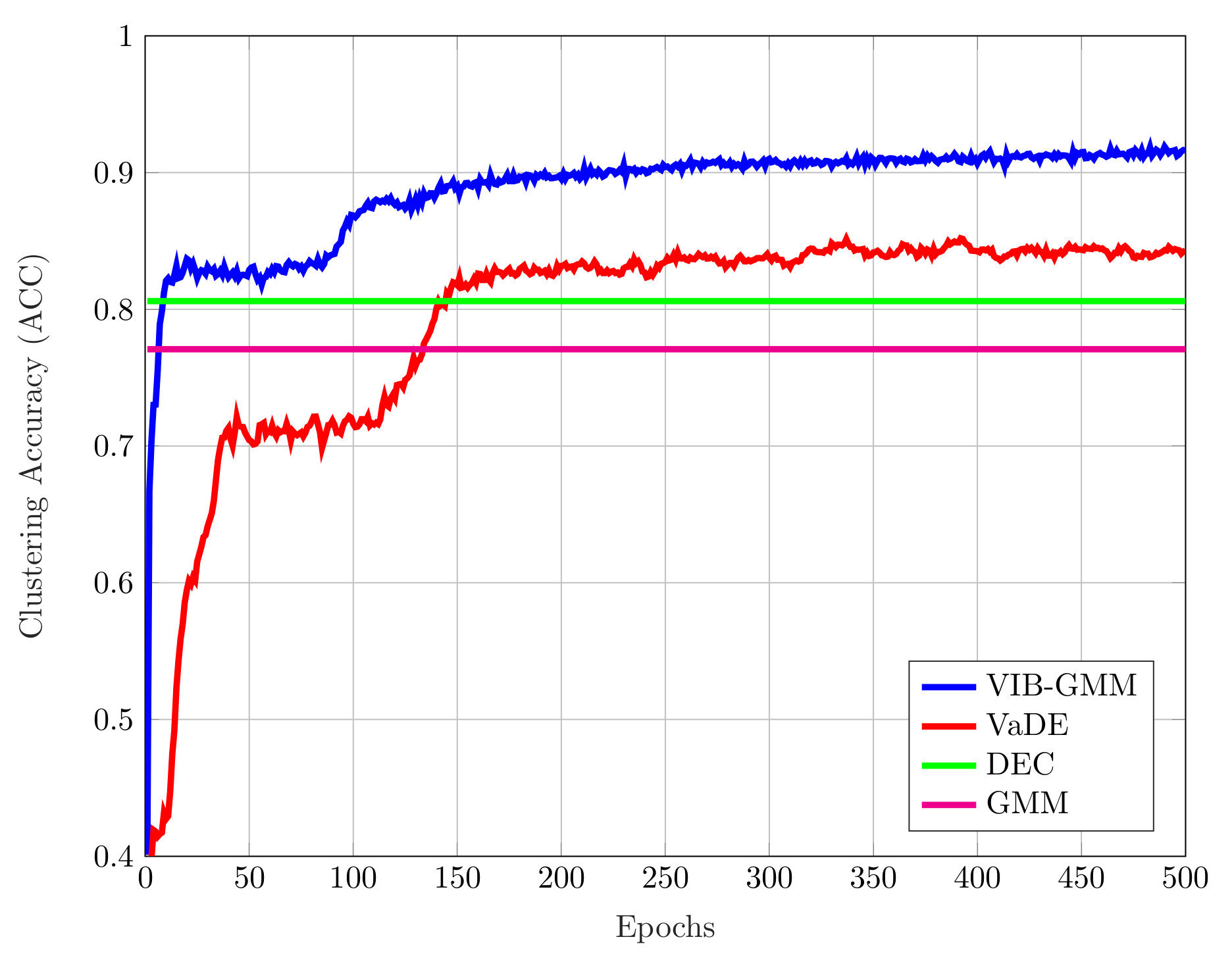
4.3. Clustering Accuracy
4.4. Visualization on the Latent Space
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Proof of Lemma 1
Appendix B. Alternative Expression
References
- Sculley, D. Web-scale K-means clustering. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; pp. 1177–1178. [Google Scholar]
- Huang, Z. Extensions to the k-means algorithm for clustering large datasets with categorical values. Data Min. Knowl. Disc. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-means clustering algorithm. J. R. Stat. Soc. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1977, 39, 1–38. [Google Scholar]
- Ding, C.; He, X. K-means clustering via principal component analysis. In Proceedings of the 21st International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004. [Google Scholar]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Roweis, S. EM algorithms for PCA and SPCA. In Proceedings of the Advances in Neural Information Processing Systems 10, Denver, CO, USA, 1–6 December 1997; pp. 626–632. [Google Scholar]
- Hofmann, T.; Scholkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. In Proceedings of the 37th Annual Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 22–24 September 1999; pp. 368–377. [Google Scholar]
- Slonim, N.; Tishby, N. Document clustering using word clusters via the information bottleneck method. In Proceedings of the 23rd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Athens, Greece, 24–28 July 2000; pp. 208–215. [Google Scholar]
- Slonim, N. The Information Bottleneck: Theory and Applications. Ph.D. Thesis, Hebrew University, Jerusalem, Israel, 2002. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. In Proceedings of the 2nd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1278–1286. [Google Scholar]
- Alemi, A.A.; Fischer, I.; Dillon, J.V.; Murphy, K. Deep variational information bottleneck. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Lewis, D.D.; Yang, Y.; Rose, T.G.; Li, F. A new benchmark collection for text categorization research. J. Mach. Learn. Res. 2004, 5, 361–397. [Google Scholar]
- Coates, A.; Ng, A.; Lee, H. An analysis of single-layer networks in unsupervised feature learning. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 215–223. [Google Scholar]
- Jiang, Z.; Zheng, Y.; Tan, H.; Tang, B.; Zhou, H. Variational deep embedding: An unsupervised and generative approach to clustering. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 1965–1972. [Google Scholar]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised deep embedding for clustering analysis. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 478–487. [Google Scholar]
- Guo, X.; Gao, L.; Liu, X.; Yin, J. Improved deep embedded clustering with local structure preservation. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 1753–1759. [Google Scholar]
- Dilokthanakul, N.; Mediano, P.A.M.; Garnelo, M.; Lee, M.C.H.; Salimbeni, H.; Arulkumaran, K.; Shanahani, M. Deep unsupervised clustering with Gaussian mixture variational autoencoders. arXiv 2017, arXiv:1611.02648. [Google Scholar]
- Min, E.; Guo, X.; Liu, Q.; Zhang, G.; Cui, J.; Long, J. A survey of clustering with deep learning: From the perspective of network architecture. IEEE Access 2018, 6, 39501–39514. [Google Scholar] [CrossRef]
- Hershey, J.R.; Olsen, P.A. Approximating the Kullback Leibler divergence between Gaussian mixture models. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, HI, USA, 15–20 April 2007; pp. 317–320. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Achille, A.; Soatto, S. Information dropout: Learning optimal representations through noisy computation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2897–2905. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Schwartz-Ziv, R.; Tishby, N. Opening the black box of deep neural networks via information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res 2008, 9, 2579–2605. [Google Scholar]
- Estella-Aguerri, I.; Zaidi, A. Distributed variational representation learning. IEEE Trans. Pattern Anal. Mach. Intell. 2020, in press. [Google Scholar] [CrossRef] [PubMed]
- Estella-Aguerri, I.; Zaidi, A. Distributed information bottleneck method for discrete and Gaussian sources. In Proceedings of the International Zurich Seminar on Information and Communication, Zürich, Switzerland, 21–23 February 2018. [Google Scholar]
- Zaidi, A.; Estella-Aguerri, I.; Shamai (Shitz), S. On the information bottleneck problems: Models, connections, applications and information theoretic views. Entropy 2020, 22, 151. [Google Scholar] [CrossRef]
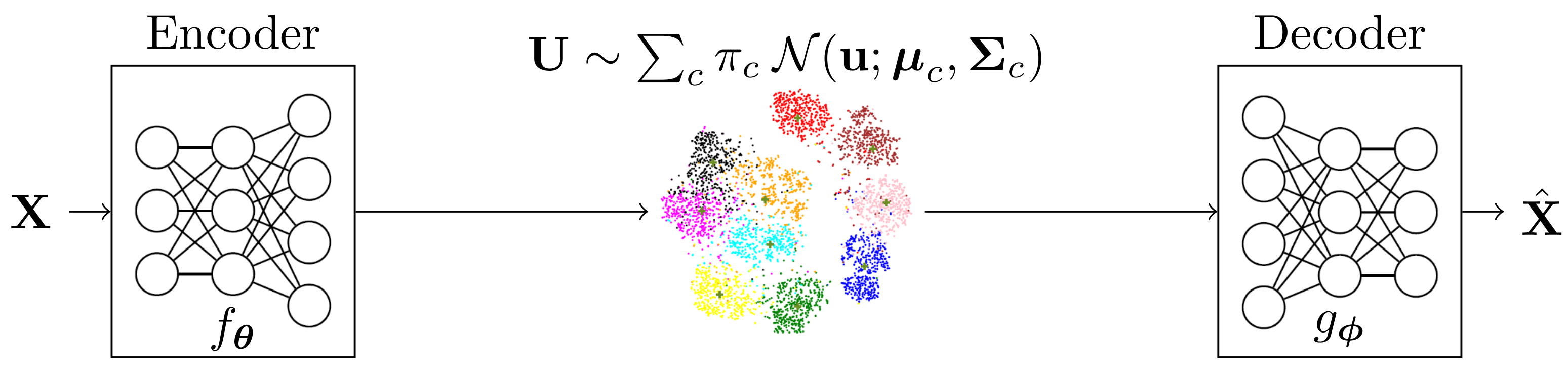



| MNIST | STL-10 | ||||
|---|---|---|---|---|---|
| Best Run | Average Run | Best Run | Average Run | ||
| GMM | 44.1 | 40.5 (1.5) | 78.9 | 73.3 (5.1) | |
| DEC | 80.6 | ||||
| VaDE | 91.8 | 78.8 (9.1) | 85.3 | 74.1 (6.4) | |
| VIB-GMM | (5.9) | (5.6) | |||
| MNIST | REURTERS10K | ||||
|---|---|---|---|---|---|
| Best Run | Average Run | Best Run | Average Run | ||
| DEC | 84.3 | 72.2 | |||
| VaDE | 94.2 | 93.2 (1.5) | 79.8 | 79.1 (0.6) | |
| VIB-GMM | (0.1) | (0.4) | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uğur, Y.; Arvanitakis, G.; Zaidi, A. Variational Information Bottleneck for Unsupervised Clustering: Deep Gaussian Mixture Embedding. Entropy 2020, 22, 213. https://doi.org/10.3390/e22020213
Uğur Y, Arvanitakis G, Zaidi A. Variational Information Bottleneck for Unsupervised Clustering: Deep Gaussian Mixture Embedding. Entropy. 2020; 22(2):213. https://doi.org/10.3390/e22020213
Chicago/Turabian StyleUğur, Yiğit, George Arvanitakis, and Abdellatif Zaidi. 2020. "Variational Information Bottleneck for Unsupervised Clustering: Deep Gaussian Mixture Embedding" Entropy 22, no. 2: 213. https://doi.org/10.3390/e22020213
APA StyleUğur, Y., Arvanitakis, G., & Zaidi, A. (2020). Variational Information Bottleneck for Unsupervised Clustering: Deep Gaussian Mixture Embedding. Entropy, 22(2), 213. https://doi.org/10.3390/e22020213