Emergence of Network Motifs in Deep Neural Networks
Abstract
1. Introduction
2. Methods
2.1. Neural Network Architectures
2.2. Learning Environments
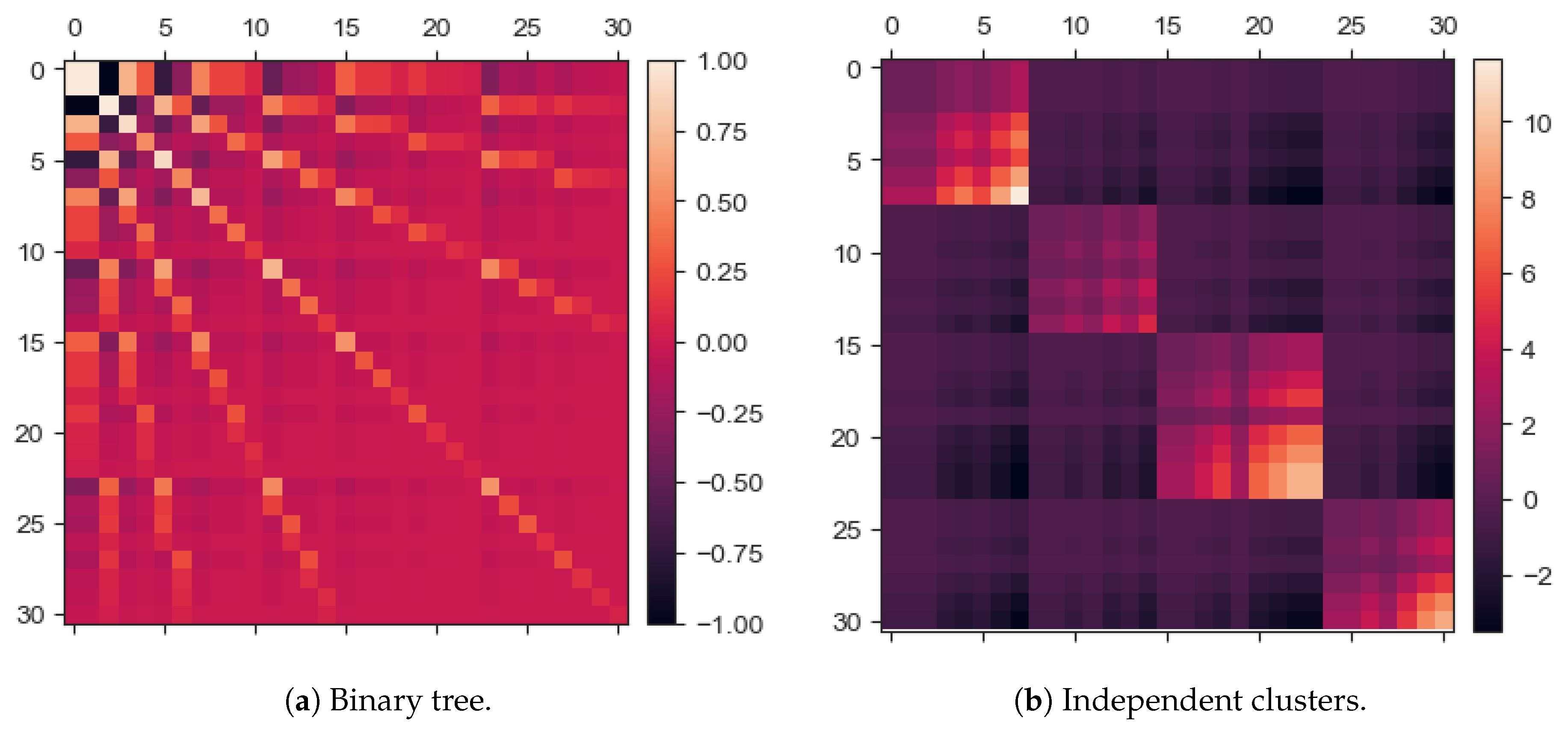
2.2.1. Binary Tree Data Set
2.2.2. Independent Clusters Data Set
2.3. Initial Conditions
2.4. Task and Learning Dynamics
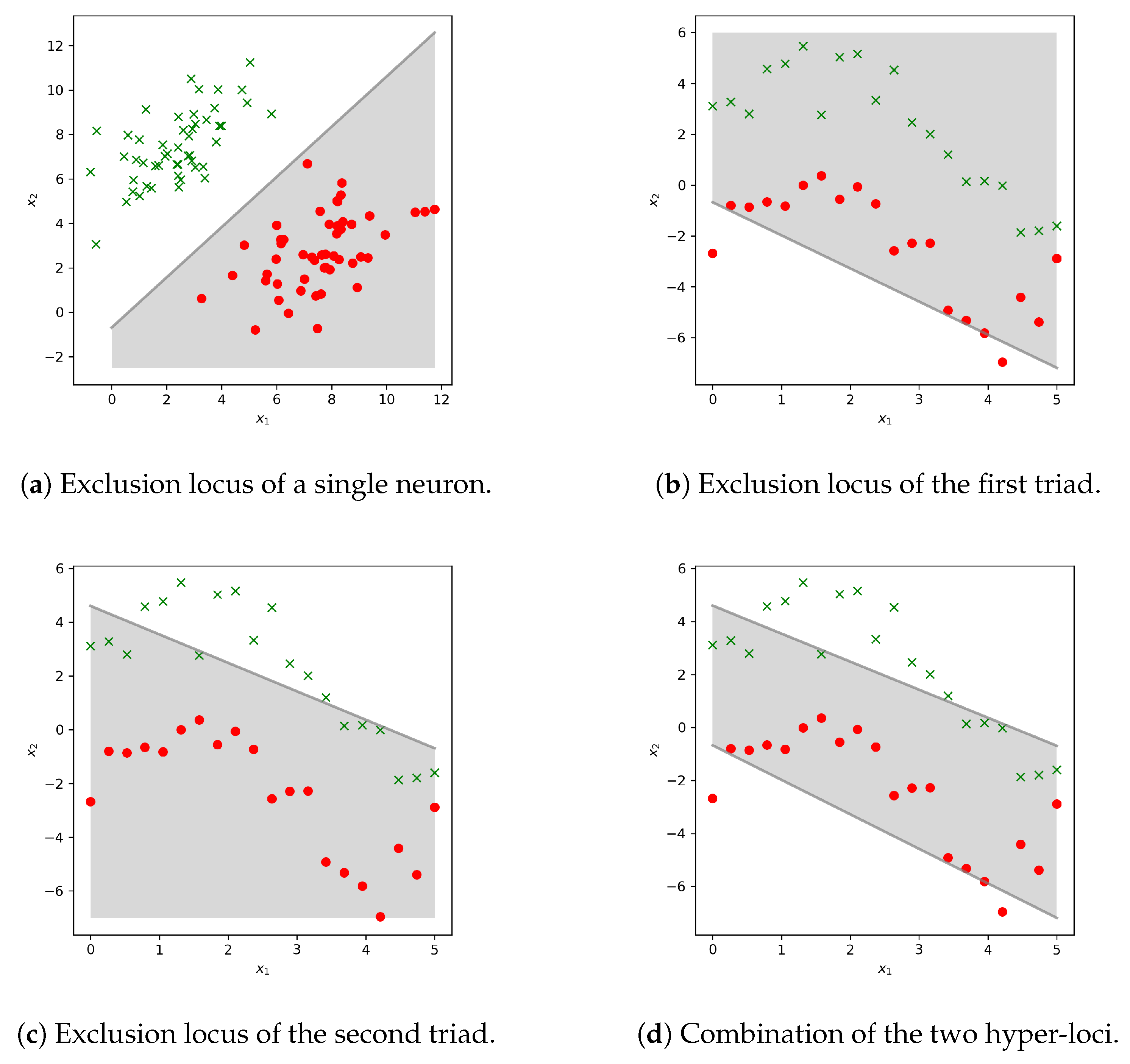
2.5. Mining Network Motifs
2.6. Biological Analogy: Neurons and Protein Kinases
- the kinases of a first layer, the concentration of which is denoted as , with ;
- the target kinase of a second layer, the concentration of which is denoted Y;
- the rate of phosphorylation , being the rate of kinase .
- If then target unit Y activates and propagated the signal forward in the system to a third layer. But
- If then Y is not sufficiently triggered to propagate the signal, that is, to phosphorylate the next unit.
3. Results
3.1. Learning Efficacy
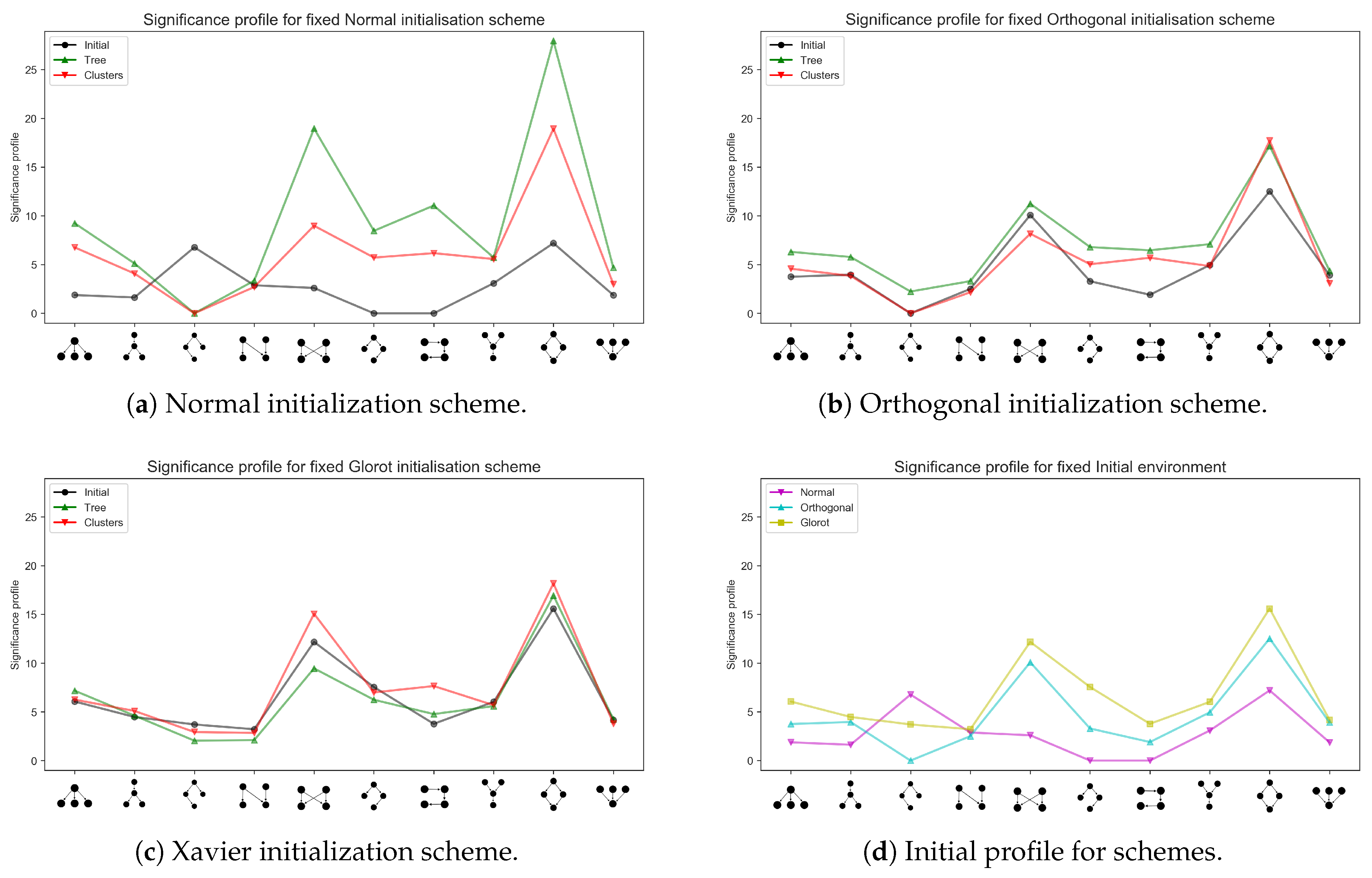
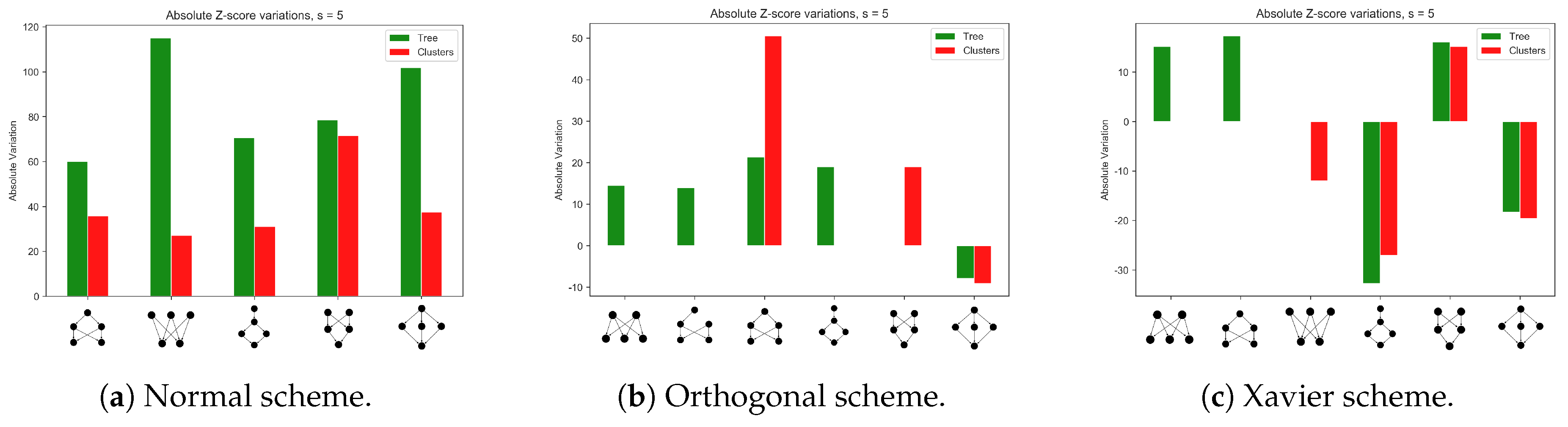
3.2. Emerging Network Motifs
4. Discussion
- larger motifs may be seen as arrangements of smaller motifs, for example “Diamonds combine to form multi-layer perceptron motifs” [25];
- these smaller motifs arrangement gives rise to more complex computation: “Adding additional layers can produce even more detailed functions in which the output activation region is formed by the intersection of many different regions defined by the different weights of the perceptron” [9];
- domain representation is carried out by the composition of subsequent non-linear modules, which “transform the representation of one level (starting with the raw input) into a representation at a higher, slightly more abstract level” [10];
5. Final Remarks and Further Improvements
5.1. Evaluation with Other Classes of Deep Learning Models
5.2. Presence of Combinatorial Biases
5.3. Sensitivity to Free Parameters
5.4. Scalability
5.5. Alternatives to Motifs Mining Algorithms
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
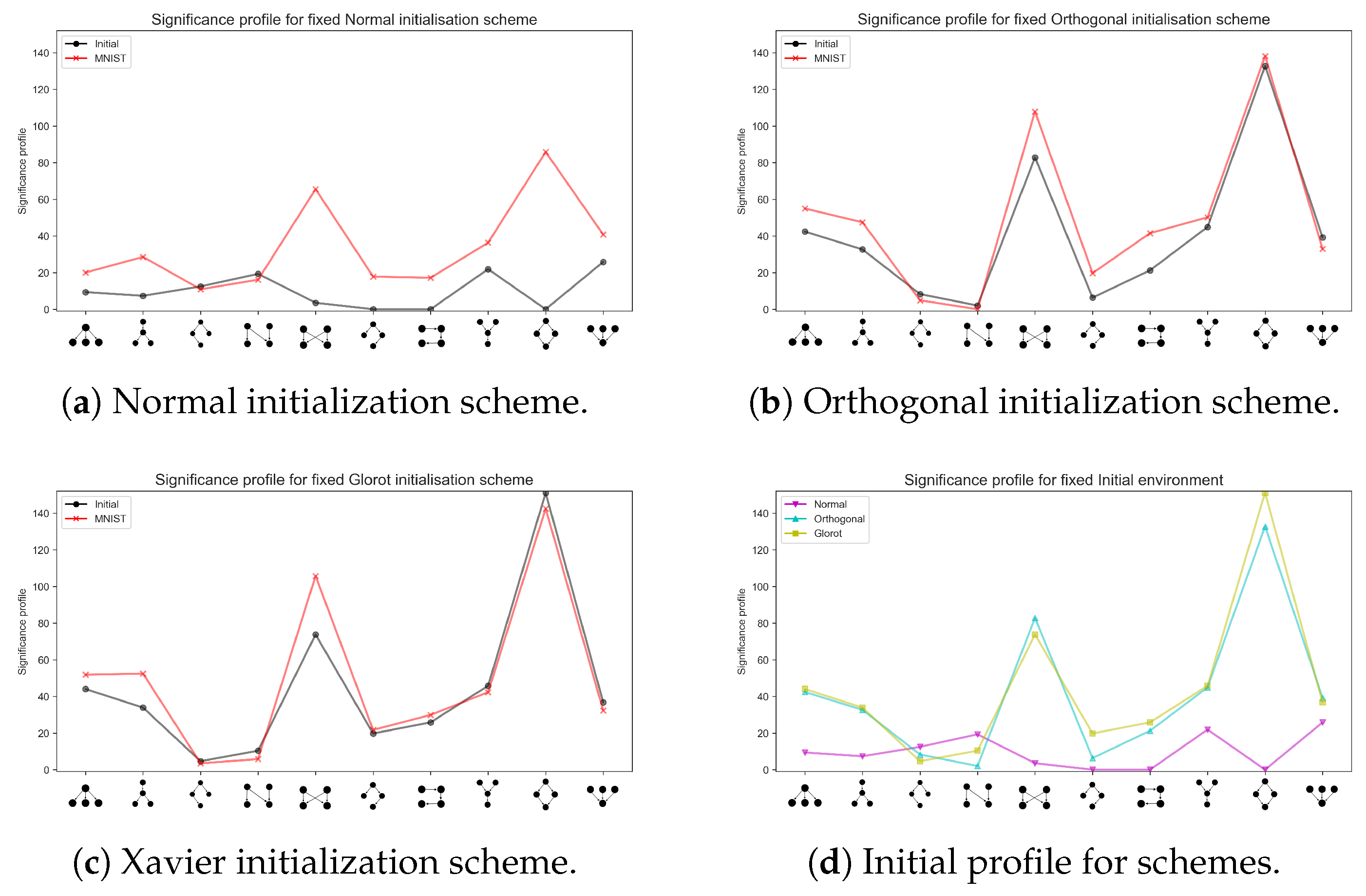
Appendix A. Robustness of Simulations
Appendix A.1. Different Network Architectures for the Synthetic Data Sets
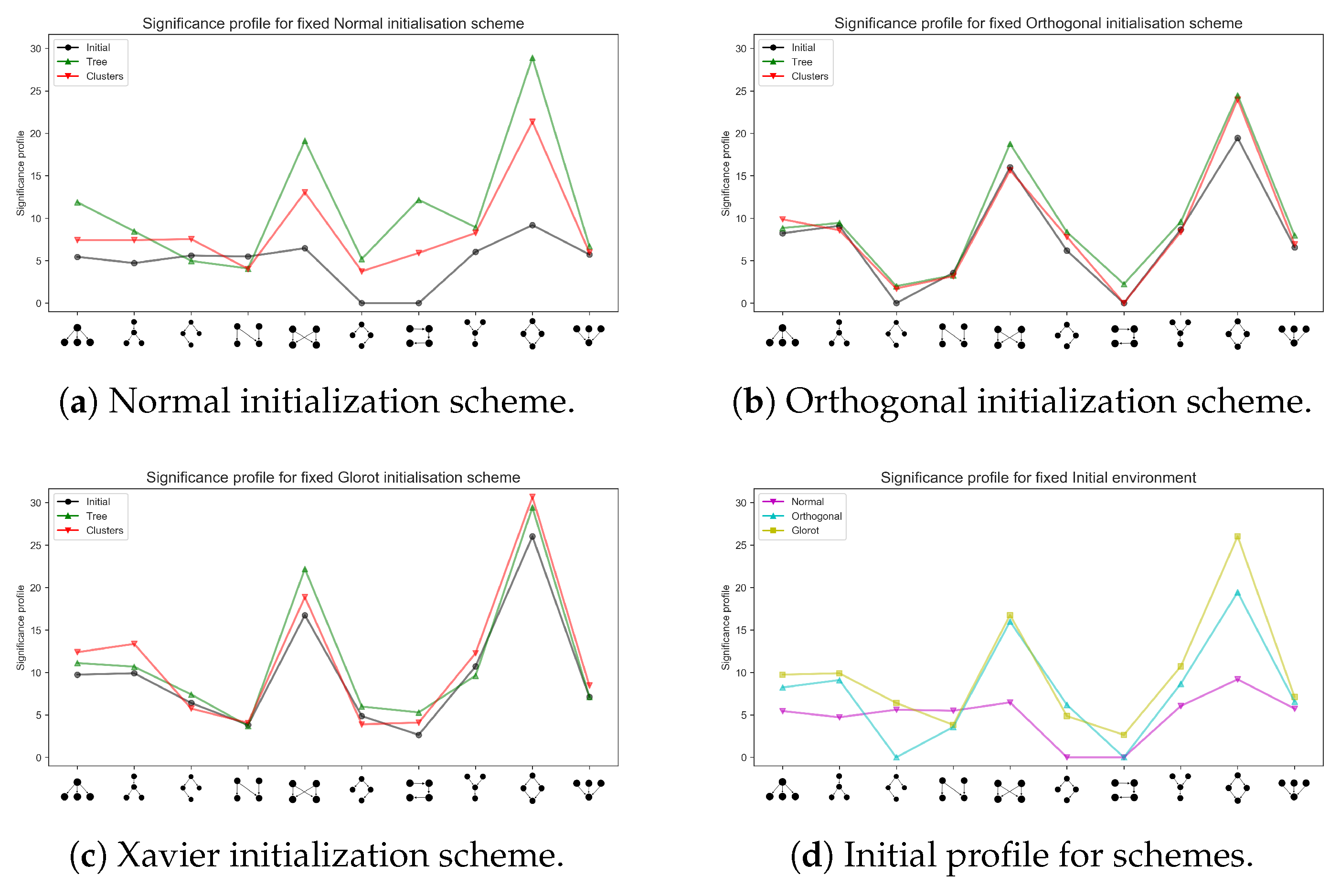
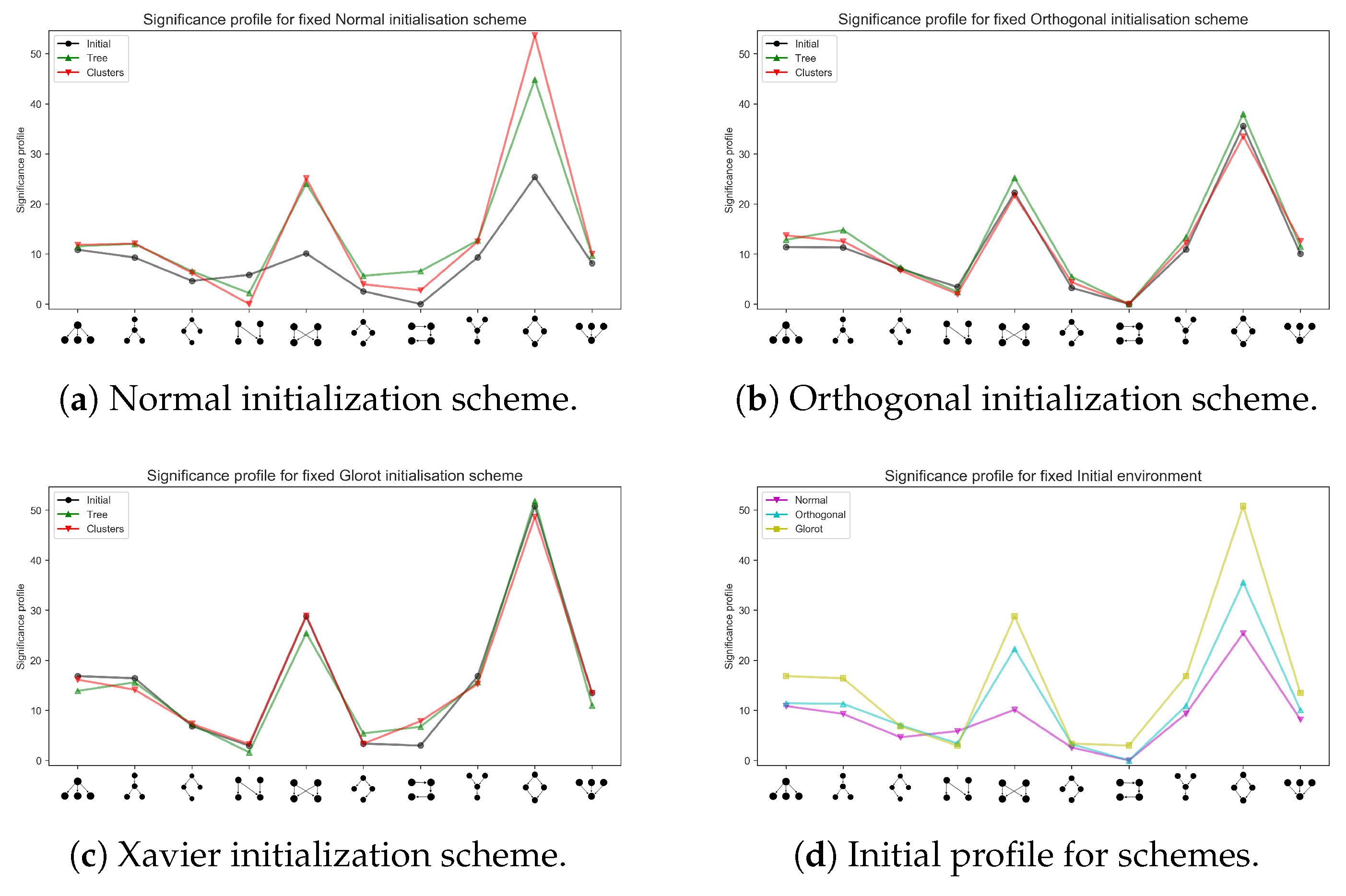
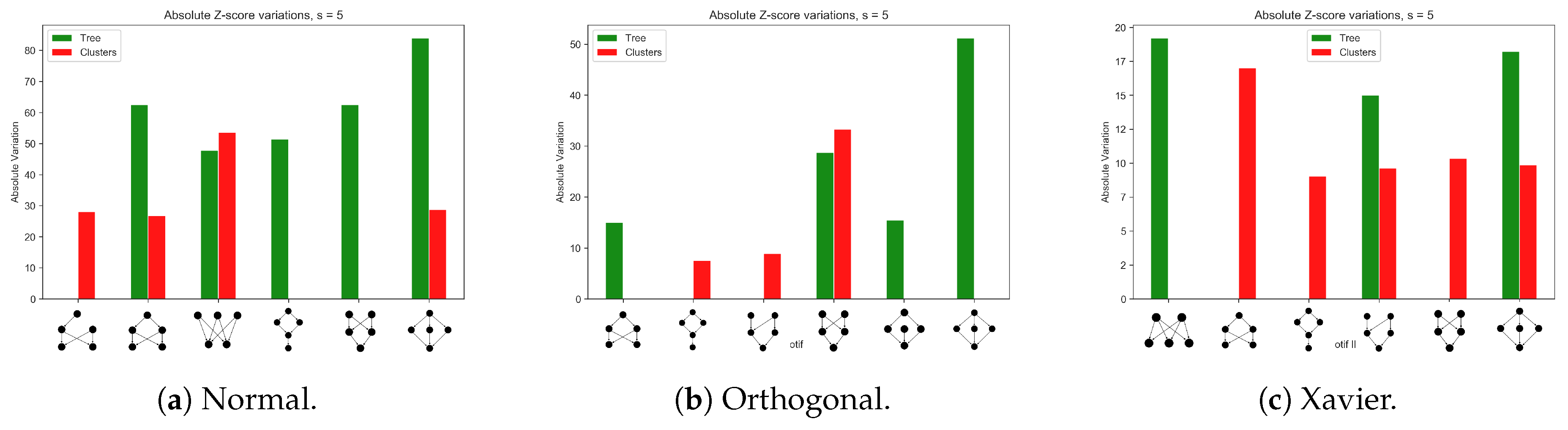
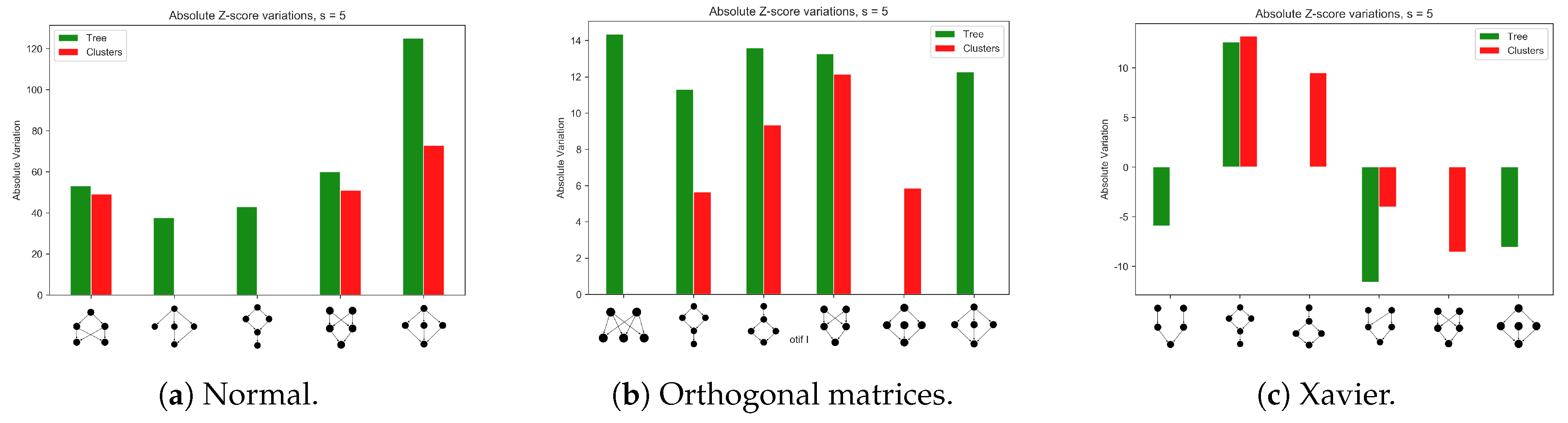
Appendix A.2. Training a Larger Network with the MNIST Data Set

Appendix B. Data Sets Generation
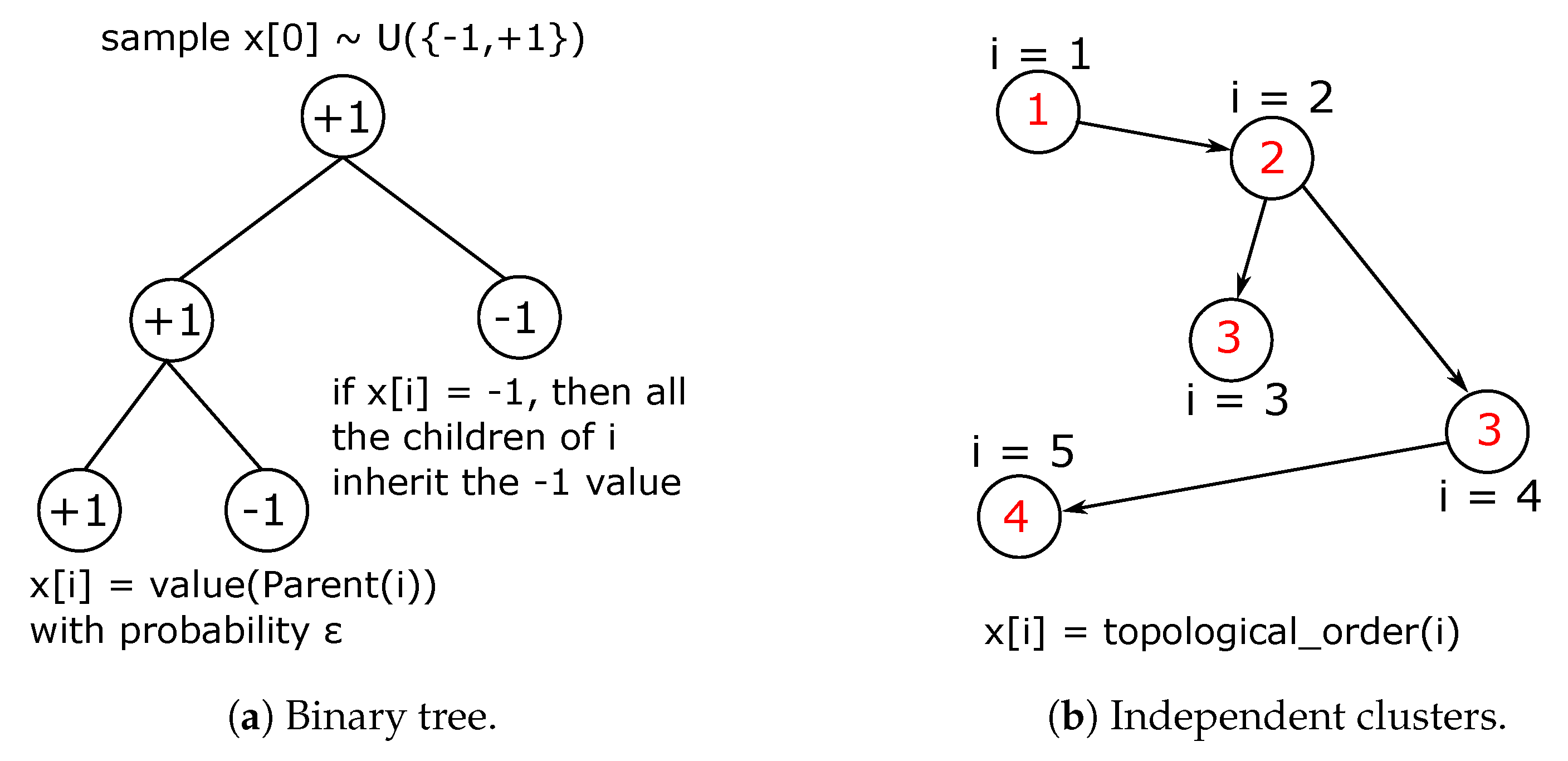
Appendix B.1. Binary Tree Data Set

Appendix B.1.1. Single Pattern Generation
- (1)
- The probabilistic threshold is fixed a priori. The smaller its value, the less variability in the data set.
- (2)
- Root attains the values with probability .
- (3)
- Root’s children attain values or in a mutually exclusive fashion. The following convention is adopted: if the root node attains the value , then the left child inherits the same value. Else, the left child attains the value and the right child has assigned the value .
- (4)
- From the third level (children of root’s children), the progeny of any node that has value also has to have value. On the other hand, if one node has value , its value is inherited (again mutually exclusively) by its children according to a probabilistic decision rule.
- If , the left child inherits the value, and the right child, alongside with its progeny, assume the opposite value;
- Else, is it the right child to assume the value .
Appendix B.1.2. Complete Data Set
| Algorithm A1 Binary tree. Single feature generation |
| 1. Compute , . M is a free parameter |
| 2. |
| 3. tree = |
| 4. |
| 5. Define a small as probabilistic threshold |
| 6. |
| 7. Value of root |
| 8. |
| 9. if Root node has value then |
| 10. |
| 11. The left child inherits the value |
| 12. |
| 13. And the right child inherits the value |
| 14. |
| 15. else |
| 16. |
| 17. The left child inherits the value |
| 18. |
| 19. And the right child inherits the value |
| 20. |
| 21. end if |
| 22. |
| 23. for All the other nodes indexed do |
| 24. |
| 25. if Node i has value then |
| 26. |
| 27. Sample |
| 28. |
| 29. if then |
| 30. |
| 31. Left child of i = ; Right child of i = |
| 32. |
| 33. else |
| 34. |
| 35. Left child of i = ; Right child of i = |
| 36. |
| 37. end if |
| 38. |
| 39. else |
| 40. |
| 41. Both the children of i inherit its value |
| 42. |
| 43. end if |
| 44. |
| 45. end for |
| 46. |
| 47. values generated, |
| 48. |
| Algorithm A2 Binary tree. One-hot activation vectors, that is, labels |
| 1. Choose level of distinction L |
| 2. |
| 3. |
| 4. |
| 5. for do |
| 6. |
| 7. for do |
| 8. |
| 9. if the first entries of equal then |
| 10. |
| 11. |
| 12. |
| 13. end if |
| 14. |
| 15. end for |
| 16. |
| 17. end for |
| 18. |
| 19. for do |
| 20. |
| 21. if then |
| 22. |
| 23. Eliminate column i of |
| 24. |
| 25. end if |
| 26. |
| 27. end for |
| 28. |
Appendix B.2. Independent Clusters Data Set
| Algorithm A3 Independent clusters. Simulated melting to partition the graph |
| 1. Choose the number of classes |
| 2. |
| 3. Set , , |
| 4. |
| 5. Generate s.t. , |
| 6. |
| 7. Include the indexes of the points generate in a list, which is the set of the vertices of the graph |
| 8. |
| 9. Fully connect the vertices to form a fully connected graph and group the vertices and the set of the edges in the graph data structure, . |
| 10. |
| 11. Note that since 2-dimensional coordinates will be useful, is a dictionary of keys (nodes indexes ) and values (list with the point coordinates, ). |
| 12. |
| 13. for T increasing do |
| 14. |
| 15. for All the edges do |
| 16. |
| 17. if Length of edge (for example) then |
| 18. |
| 19. Remove edge e |
| 20. |
| 21. end if |
| 22. |
| 23. end for |
| 24. |
| 25. end for |
| 26. |
| 27. Plot the remaining edges and check if only independent fully connected components have survived. |
| 28. |
| Algorithm A4 Independent clusters. Single pattern generation |
| 1. Here i indexes a single random variable. This kernel is used as many times as the number of samples the user wants to generate. is the whole data item, initialised with each slot set to . Note: in the data set actually generated, the value of the nodes are set to their topological orders, with no ancestral sampling implemented. |
| 2. |
| 3. Set = |
| 4. |
| 5. Sample |
| 6. |
| 7. for all the vertices in cluster L do |
| 8. |
| 9. if Topological Order of i is 1 then |
| 10. |
| 11. |
| 12. |
| 13. else |
| 14. |
| 15. |
| 16. |
| 17. end if |
| 18. |
| 19. end for |
| 20. |
| 21. |
| 22. |
Appendix B.2.1. Single Pattern Generation
Appendix B.2.2. Complete Data Set
Appendix C. Pre-Processing

References
- Newman, M. Networks: An Introduction; Oxford University Press, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef]
- Caldarelli, G. Complex Networks; EOLSS Publications: Abu Dhabi, UAE, 2010. [Google Scholar]
- Newman, M.E.; Barabasi, A.L.; Watts, D.J. The Structure and Dynamics of Networks: (Princeton Studies in Complexity); Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks: Principles, Methods and Applications; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network Motifs: Simple Building Blocks of Complex Networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef] [PubMed]
- Lenski, R.E.; Ofria, C.; Pennock, R.T.; Adami, C. The evolutionary origin of complex features. Nature 2003, 423, 139. [Google Scholar] [CrossRef] [PubMed]
- Vespignani, A. Evolution thinks modular. Nat. Genet. 2003, 35, 118–119. [Google Scholar] [CrossRef] [PubMed]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits; Chapman & Hall/CRC Mathematical and Computational Biology, Taylor & Francis: London, UK, 2006; pp. 27–30, 106–115. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G.E. Deep learning. Nature 2015, 521. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 16 December 2019).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. Adv. Neural Inf. Process. Syst. 2014, 27, 3104–3112. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484. [Google Scholar] [CrossRef]
- Montavon, G.; Samek, W.; Müller, K.R. Methods for interpreting and understanding deep neural networks. Digit. Signal Process. 2018, 73, 1–15. [Google Scholar] [CrossRef]
- Saxe, A.M.; McClelland, J.L.; Ganguli, S. A mathematical theory of semantic development in deep neural networks. Proc. Natl. Acad. Sci. USA 2019, 116, 11537–11546. [Google Scholar] [CrossRef]
- Testolin, A.; Piccolini, M.; Suweis, S. Deep learning systems as complex networks. J. Complex Netw. 2018, 521. [Google Scholar] [CrossRef]
- Testolin, A.; Zorzi, M. Probabilistic models and generative neural networks: Towards an unified framework for modeling normal and impaired neurocognitive functions. Front. Comput. Neurosci. 2016, 10, 73. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Saxe, A.; McClelland, J.; Ganguli, S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Wernicke, S.; Rasche, F. FANMOD: A tool for fast network motif detection. Bioinformatics 2006, 22, 1152–1153. [Google Scholar] [CrossRef]
- Wernicke, S. Efficient Detection of Network Motifs. IEEE/ACM Trans. Comput. Biol. Bioinform. 2006, 3, 347–359. [Google Scholar] [CrossRef] [PubMed]
- Masoudi-Nejad, A.; Schreiber, F.; Kashani, Z.R. Building blocks of biological networks: A review on major network motif discovery algorithms. IET Syst. Biol. 2012, 6, 164–174. [Google Scholar] [CrossRef]
- Alon, U. Network motifs: Theory and experimental approaches. Nat. Rev. Genet. 2007, 8. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Milo, R.; Itzkovitz, S.; Kashtan, N.; Levitt, R.; Shen-Orr, S.; Ayzenshtat, I.; Sheffer, M.; Alon, U. Superfamilies of Evolved and Designed Networks. Science 2004, 303, 1538–1542. [Google Scholar] [CrossRef]
- Wuchty, S.; Oltvai, Z.N.; Barabási, A.L. Evolutionary conservation of motif constituents in the yeast protein interaction network. Nat. Genet. 2003, 35, 176–179. [Google Scholar] [CrossRef]
- Salakhutdinov, R.; Hinton, G. Deep boltzmann machines. In Artificial Intelligence and Statistics; van Dyk, D., Welling, M., Eds.; PMLR: Clearwater, FL, USA, 2009; pp. 448–455. [Google Scholar]
- Zorzi, M.; Testolin, A.; Stoianov, I.P. Modeling language and cognition with deep unsupervised learning: A tutorial overview. Front. Psychol. 2013, 4, 515. [Google Scholar] [CrossRef]
- Testolin, A.; Stoianov, I.; Sperduti, A.; Zorzi, M. Learning orthographic structure with sequential generative neural networks. Cogn. Sci. 2016, 40, 579–606. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep Learning for Computer Vision: A Brief Review. Comput. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Piperno, A. Isomorphism Test for Digraphs with Weighted Edges. In Proceedings of the 17th International Symposium on Experimental Algorithms (SEA 2018); Leibniz International Proceedings in Informatics (LIPIcs); Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2018; Volume 103, pp. 30:1–30:13. [Google Scholar] [CrossRef]
- McKay, B.D.; Piperno, A. Practical graph isomorphism, II. J. Symb. Comput. 2014, 60, 94–112. [Google Scholar] [CrossRef]
- Raina, R.; Madhavan, A.; Ng, A.Y. Large-scale deep unsupervised learning using graphics processors. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 873–880. [Google Scholar]
- Testolin, A.; Stoianov, I.; De Filippo De Grazia, M.; Zorzi, M. Deep unsupervised learning on a desktop PC: A primer for cognitive scientists. Front. Psychol. 2013, 4, 251. [Google Scholar] [CrossRef]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Choobdar, S.; Ribeiro, P.; Silva, F. Motif Mining in Weighted Networks. In Proceedings of the 12nd IEEE ICDM Workshop on Data Mining in Networks, Brussels, Belgium, 10 December 2012; pp. 210–217. [Google Scholar] [CrossRef]
- Onnela, J.P.; Saramäki, J.; Kertész, J.; Kaski, K. Intensity and coherence of motifs in weighted complex networks. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef]
- Kemp, C.; Tenenbaum, J.B. The discovery of structural form. Proc. Natl. Acad. Sci. USA 2008, 105, 10687–10692. [Google Scholar] [CrossRef]




| Network | Layer | Units | Activation |
|---|---|---|---|
| 240120 | Input | 31 | – |
| Hidden 1 | 20 | ReLU | |
| Hidden 2 | 10 | ReLU | |
| Output | 4 | Sotfmax | |
| 250120 | Input | 31 | – |
| Hidden 1 | 20 | ReLU | |
| Hidden 2 | 20 | ReLU | |
| Output | 4 | Sotfmax | |
| 180112 | Input | 31 | – |
| Hidden 1 | 30 | ReLU | |
| Hidden 2 | 30 | ReLU | |
| Output | 4 | Sotfmax |
| Initialization | Initial | Tree | Clusters |
|---|---|---|---|
| Normal | |||
| Orthogonal | |||
| Glorot |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zambra, M.; Maritan, A.; Testolin, A. Emergence of Network Motifs in Deep Neural Networks. Entropy 2020, 22, 204. https://doi.org/10.3390/e22020204
Zambra M, Maritan A, Testolin A. Emergence of Network Motifs in Deep Neural Networks. Entropy. 2020; 22(2):204. https://doi.org/10.3390/e22020204
Chicago/Turabian StyleZambra, Matteo, Amos Maritan, and Alberto Testolin. 2020. "Emergence of Network Motifs in Deep Neural Networks" Entropy 22, no. 2: 204. https://doi.org/10.3390/e22020204
APA StyleZambra, M., Maritan, A., & Testolin, A. (2020). Emergence of Network Motifs in Deep Neural Networks. Entropy, 22(2), 204. https://doi.org/10.3390/e22020204






