Bright-Dark and Multi Solitons Solutions of (3 + 1)-Dimensional Cubic-Quintic Complex Ginzburg–Landau Dynamical Equation with Applications and Stability
Abstract
1. Introduction
2. Mathematical Model
3. Elucidation of Proposed Methods
3.1. Modified Extended Simple Equation Technique
3.2. Exp()-Expansion Method
3.3. Proposed F-Expansion Method
4. Solitons Solutions of (31)-Dimensional Cubic-Quintic Complex Ginzburg–Landau Equation
4.1. Solitons Solutions by Extended SEM
4.2. Solitons Solutions by the Exp()-Expansion Method
4.3. Solitons Solutions by the Proposed F-Expansion Method
5. Modulation Instability
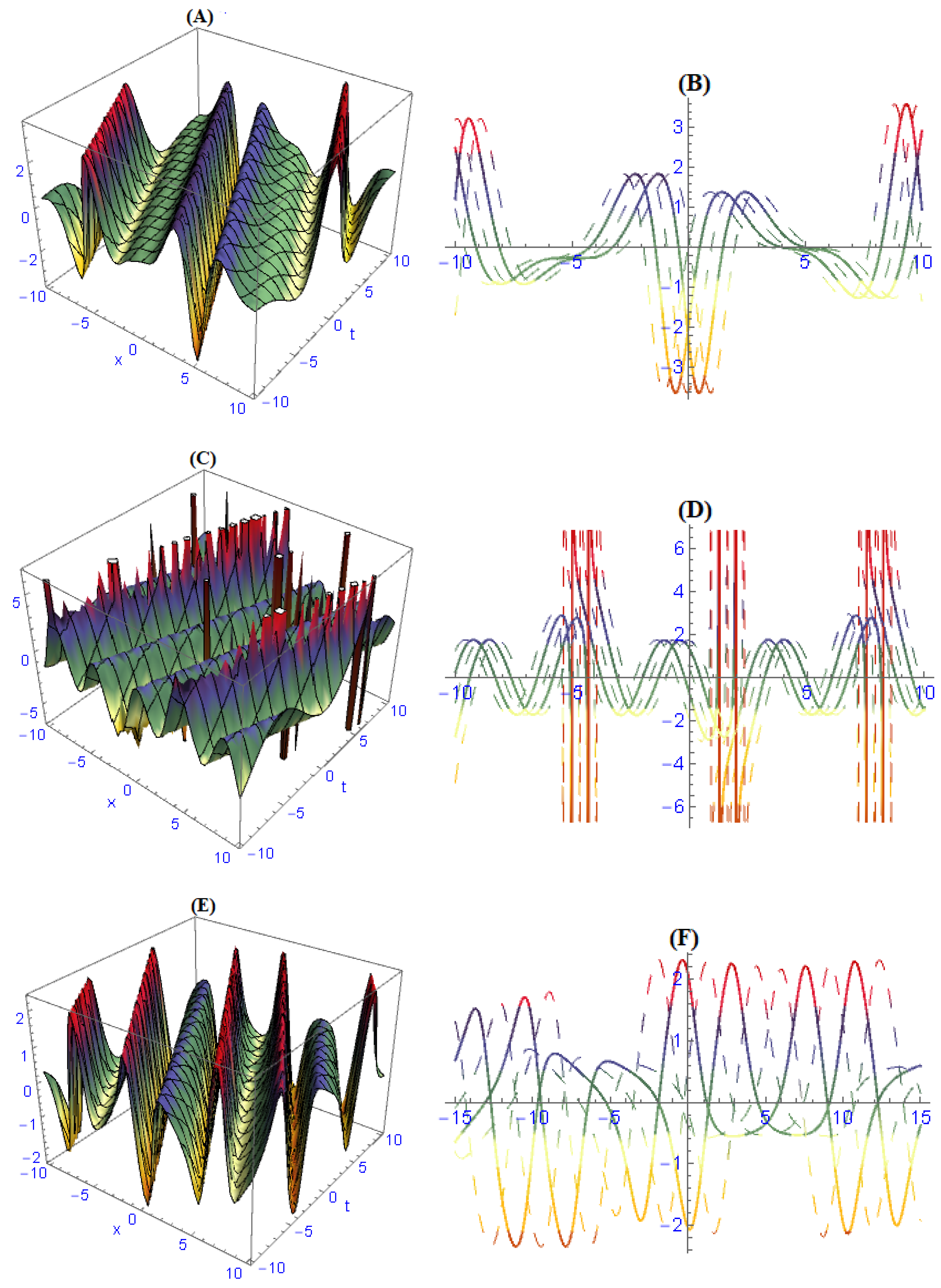
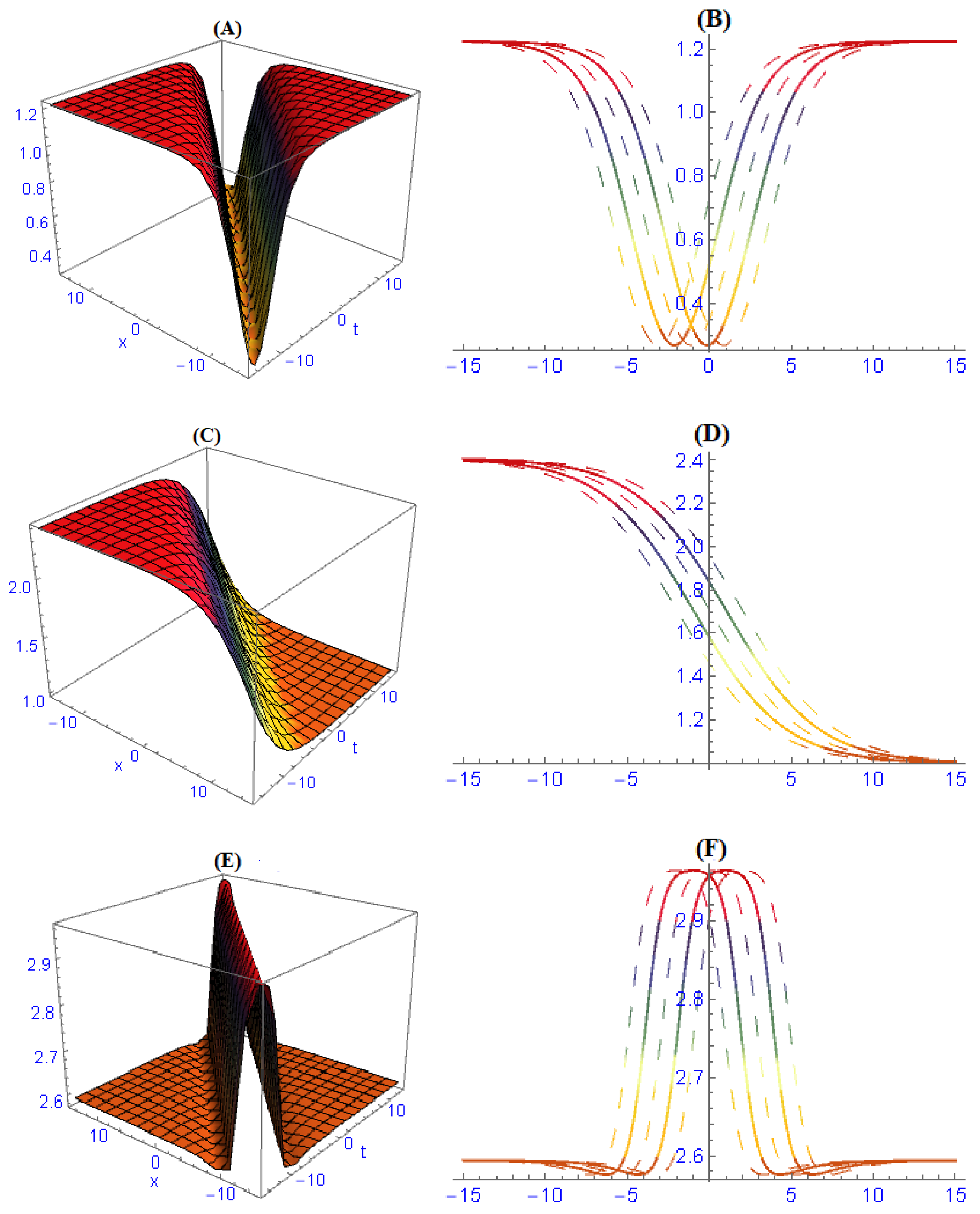
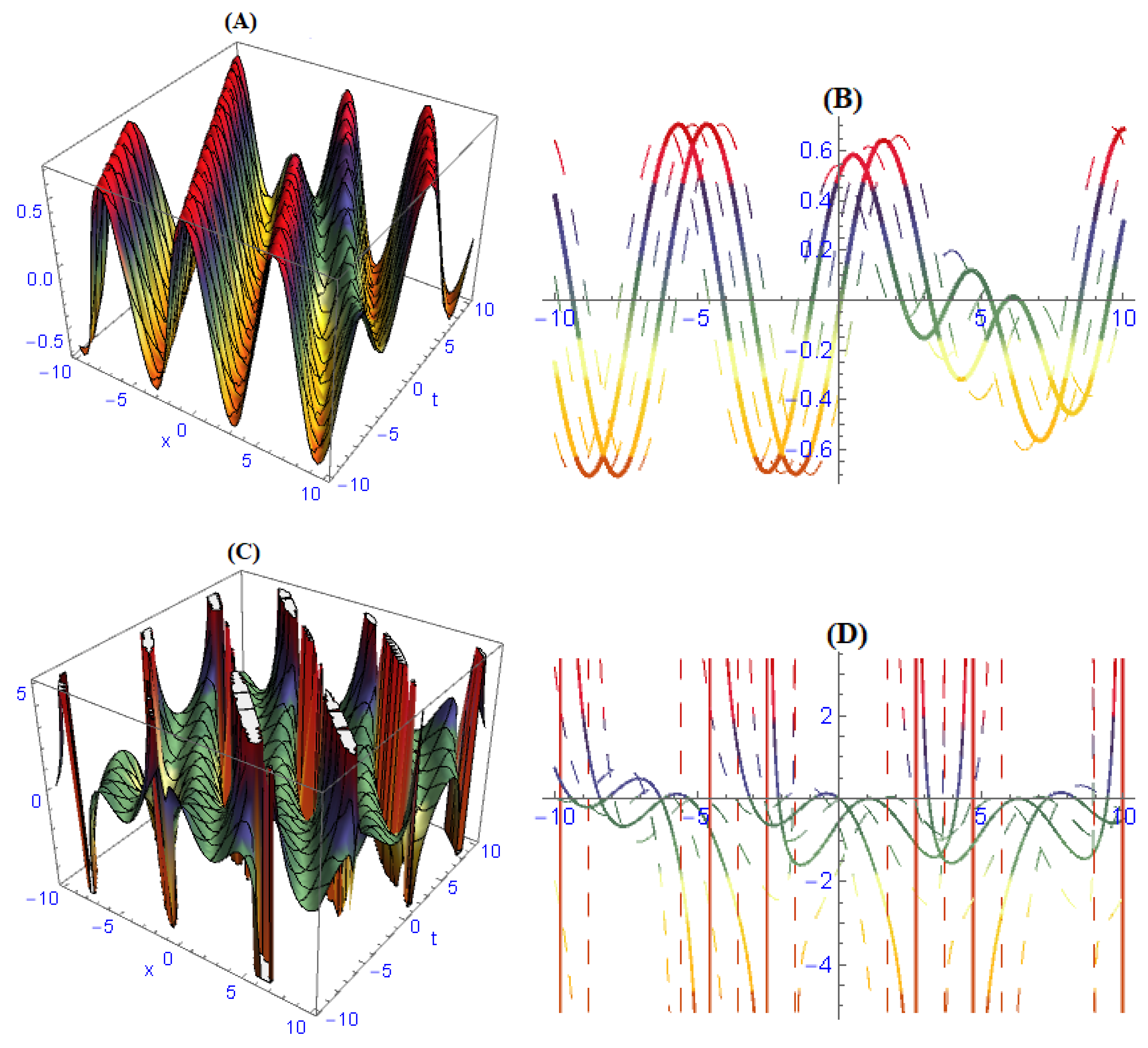
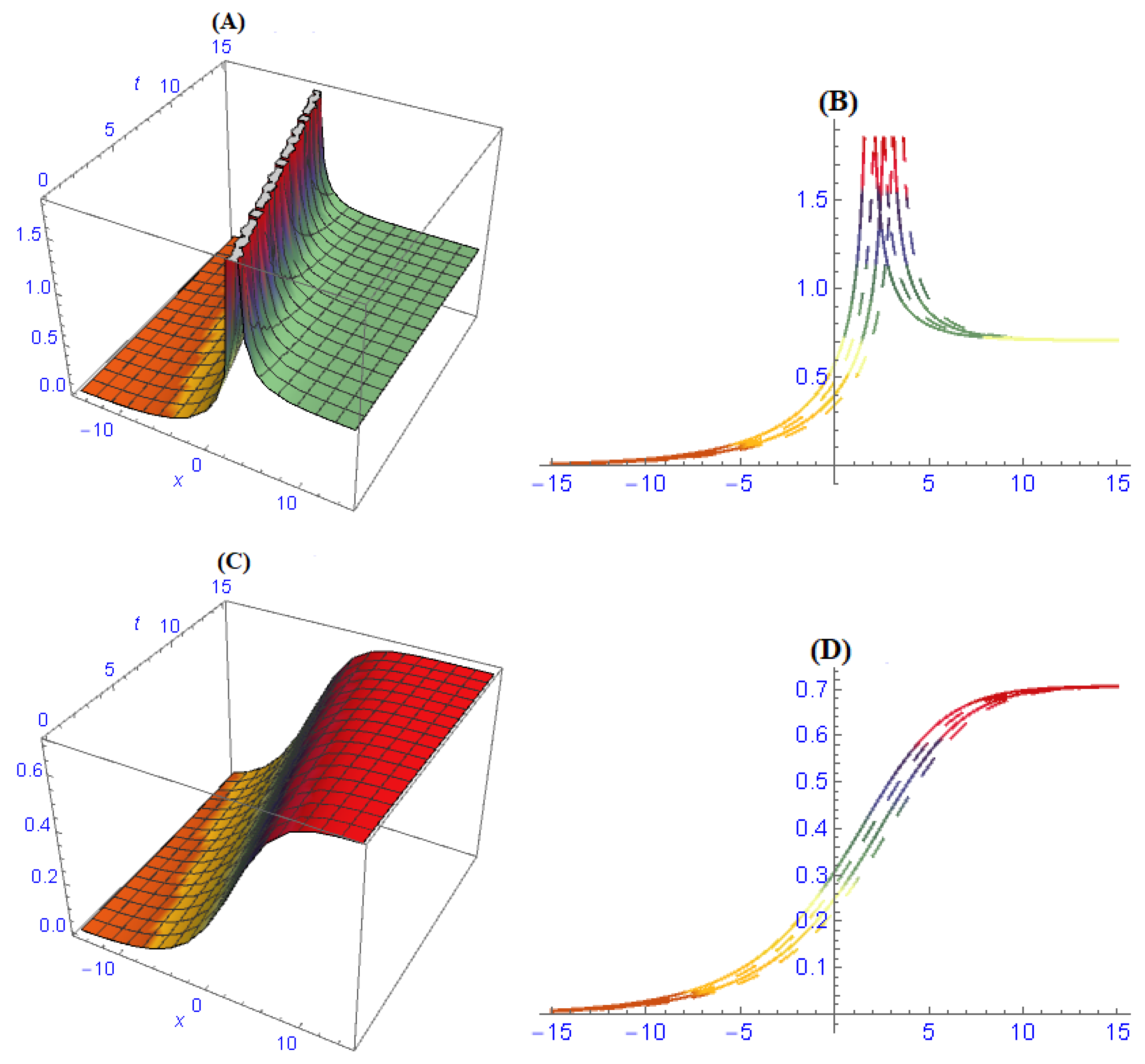
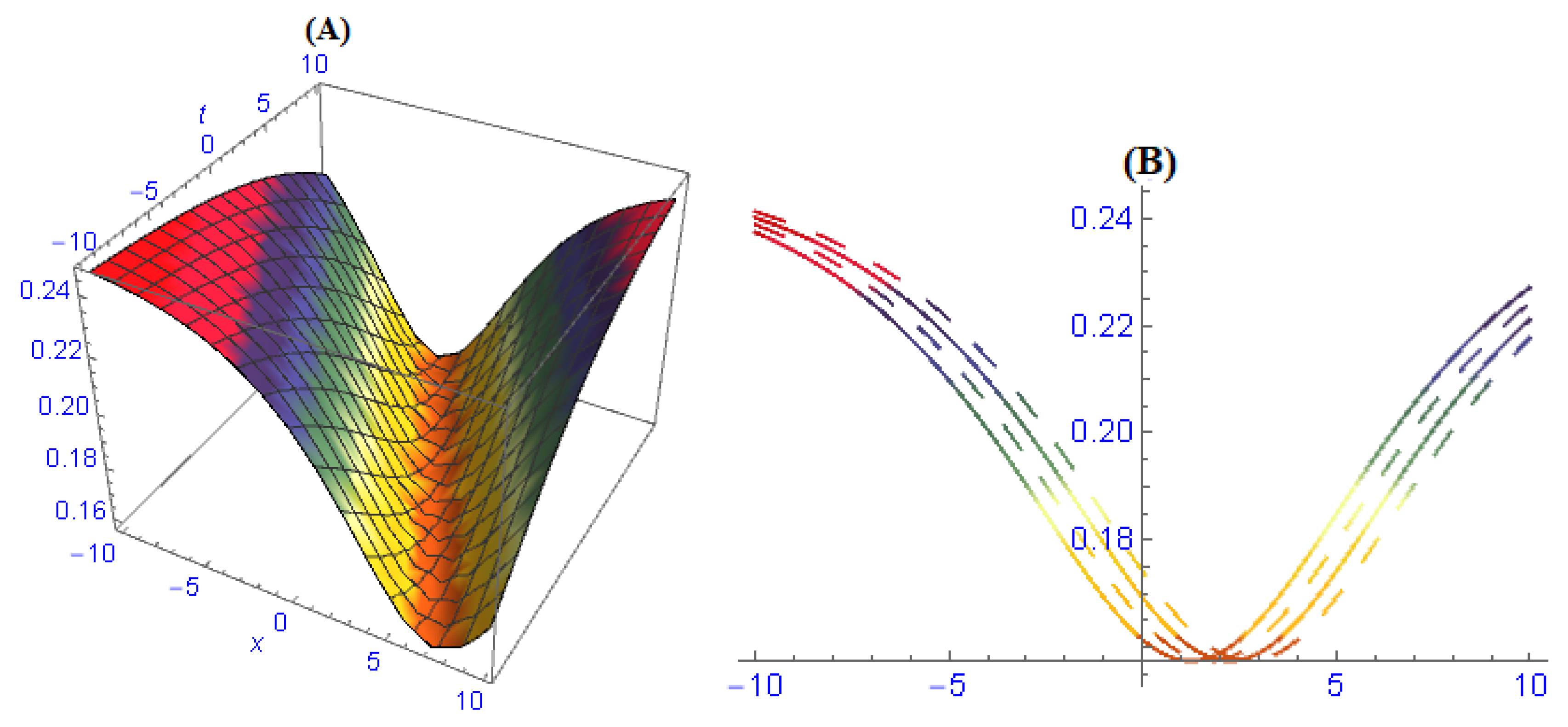
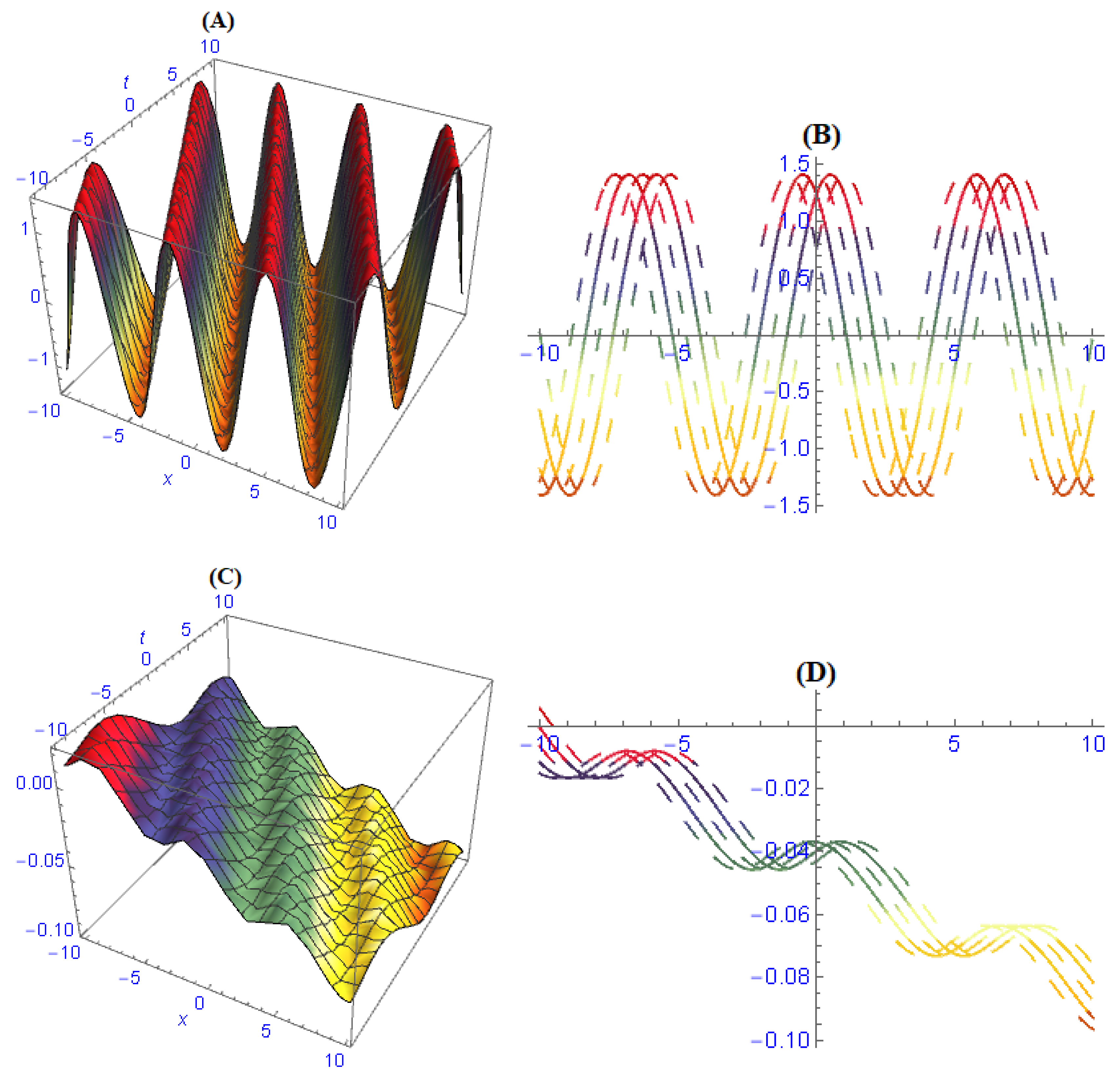
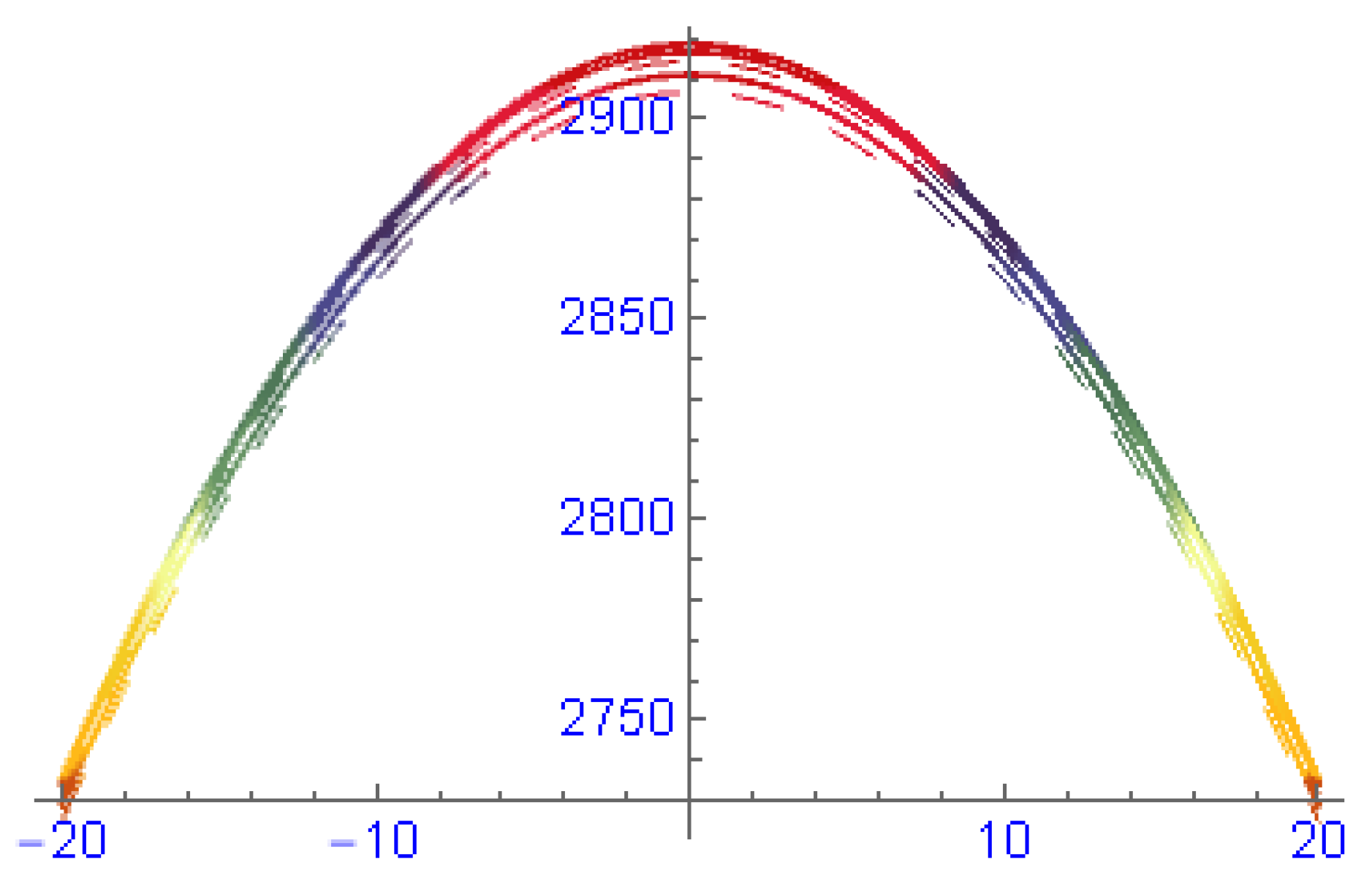
6. Discussion of Results and Their Physical Interpretation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lopez-Mariscal, C.; Gutierrez-Vega, J.C. In your phase: All about optical vortices. Opt. Photonics News 2009, 20, 10–13. [Google Scholar]
- Desyatnikov, A.S.; Kivshar, Y.S.; Torner, L. Optical Vortices and Vortex Solitons. Prog. Opt. 2005, 47, 291–391. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Nasreen, N.; Lu, D.; Arshad, M. Optical solitons of nonlinear Schrödinger equation with second order spatiotemporal dispersion and its modulation instability. Optik 2018, 161, 221–229. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D. Modulation stability and dispersive optical solitons solutions of higher order nonlinear Schrödinger equation and its applications in mono-mode optical fibers. Superlattices Microstruct. 2018, 113, 419–429. [Google Scholar] [CrossRef]
- Khater, M.; Attia, R.A.; Lu, D. Explicit Lump Solitary Wave of Certain Interesting (3 + 1)-Dimensional Waves in Physics via Some Recent Traveling Wave Methods. Entropy 2019, 21, 397. [Google Scholar] [CrossRef]
- Aissat, A.; Mohammedi, T.; Alshehri, B. A geo-numerical approach for the classification of fixed points in the reduced model of the cubic–quintic complex Ginzburg–Landau equation. Optik 2015, 126, 5325–5330. [Google Scholar] [CrossRef]
- Lu, D.; Yue, C.; Arshad, M. Traveling Wave Solutions of Space-Time Fractional Generalized Fifth-Order KdV Equation. Adv. Math. Phys. 2017, 2017, 6743276. [Google Scholar] [CrossRef]
- Inc, M.; Bildic, N. Non-perturbative solution of the Ginzburg–Landau equation. Math. Comput. Appl. 2000, 5, 113–117. [Google Scholar]
- Li, B.; Yang, C. Global well-posedness of the time-dependent Ginzburg–Landau superconductivity model in curved polyhedra. J. Math. Anal. Appl. 2017, 451, 102–116. [Google Scholar] [CrossRef][Green Version]
- Biswas, A. Temporal 1-soliton solution of the complex Ginzburg–Landau equation with power law nonlinearity. Prog. Electromagn. Res. 2009, 96, 1–7. [Google Scholar] [CrossRef]
- Rougemont, J. Space-time invariant measures, entropy, and dimension for stochastic Ginzburg–Landau Equations. Commun. Math. Phys. 2002, 225, 423–448. [Google Scholar] [CrossRef][Green Version]
- LU, D.; Seadawy, A.R.; Arshad, M. Application of simple equation method on unstable nonlinear Schrödinger equations. Optik 2017, 140, 136–144. [Google Scholar] [CrossRef]
- Succi, S. Lattice quantum mechanics: An application to Bose–Einstein condensation. Int. J. Mod. Phys. C 1998, 9, 1577–1585. [Google Scholar] [CrossRef]
- Palpacelli, S.; Succi, S.; Spigler, R. Ground-state computation of Bose–Einstein condensates by an imaginary-time quantum lattice Boltzmann scheme. Phys. Rev. E 2007, 76, 036712. [Google Scholar] [CrossRef]
- Palpacelli, S.; Succi, S. Quantum lattice Boltzmann simulation of expanding Bose–Einstein condensates in random potentials. Phys. Rev. E 2008, 77, 066708. [Google Scholar] [CrossRef]
- Zhong, L.H.; Feng, S.D.; Dong, P.; Gao, S.T. Lattice Boltzmann schemes for the nonlinear Schrödinger equation. Phys. Rev. E 2006, 74, 036704. [Google Scholar] [CrossRef]
- Akhmediev, N.N.; Afanasjev, V.V. Stability of the pulse like solutions of the quintic complex Ginzburg–Landau equation. J. Opt. Soc. Am. B 1996, 3, 1439–1449. [Google Scholar]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851–1089. [Google Scholar] [CrossRef]
- Aranson, I.S.; Kramer, L. The world of the complex Ginzburg–Landau equation. Rev. Mod. Phys. 2002, 74, 99–143. [Google Scholar] [CrossRef]
- Gao, H.; Wang, X. On the global existence and small dispersion limit for a class of complex Ginzburg–Landau equations. Math. Meth. Appl. Sci. 2009, 32, 1396–1414. [Google Scholar] [CrossRef]
- Marcq, P.; Chate, H.; Conte, R. Exact solutions of the one-dimensional, quintic complex Ginzburg–Landau equation. Physica D 1994, 73, 305–317. [Google Scholar] [CrossRef]
- Charbonneau, J. Introduction to the Ginzburg–Landau Equations; V6T 1Z1; Department of Physics and Astronomy, University of British Columbia: Vancouver, BC, Canada, 2005. [Google Scholar]
- Ortega, J.B.; Sardella, E.; Aguiar, J.A. Superconducting properties of a parallelepiped mesoscopic superconductor: A comparative study between the 2D and 3D Ginzburg–Landau models. Phys. Lett. A 2015, 379, 732–737. [Google Scholar] [CrossRef]
- Siddheshwar, P.G. A series solution for the Ginzburg–Landau equation with a time-periodic coefficient. Appl. Math. 2010, 1, 542–554. [Google Scholar] [CrossRef]
- Mihalache, D.; Mazilu, D.; Lederer, F.; Kartashov, Y.V.; Crasovan, L.C.; Torner, L.; Malomed, B.A. Stable vortex tori in the three-dimensional cubic-quintic Ginzburg–Landau equation. Phys. Rev. Lett. 2006, 97, 073904. [Google Scholar] [CrossRef] [PubMed]
- Mihalache, D.; Mazilu, D.; Skarka, V.; Malomed, B.A.; Leblond, H.; Aleksic, N.B.; Lederde, F. Stable topological modes in two-dimensional Ginzburg–Landau models with trapping potentials. Phys. Rev. A 2010, 82, 023813. [Google Scholar] [CrossRef]
- Skarka, V.; Aleksic, N.B.; Leblond, H.; Malomed, B.A.; Mihalache, D. Varieties of stable vertical solitons in Ginzburg–Landau media with radially inhomo-geneous losses. Phys. Rev. Lett. 2010, 105, 213901. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Yan, G.W. Lattice Boltzmann model for the complex Ginzburg–Landau equation. Phys. Rev. E 2010, 81, 066705. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Yan, G.W. Numerical studies based on higher-order accuracy lattice Boltzmann model for the complex Ginzburg–Landau equation. J. Sci. Comput. 2012, 52, 656–674. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Yan, G.W. Three-dimensional lattice Boltzmann model for the complex Ginzburg–Landau equation. J. Sci. Comput. 2014, 60, 660–683. [Google Scholar] [CrossRef]
- Fleischer, J.W.; Segev, M.; Efremidis, N.K.; Christodoulides, D.N. Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices. Nature 2003, 422, 147–150. [Google Scholar] [CrossRef]
- Benzi, R.; Succi, S.; Vergassola, M. The lattice Boltzmann equation: Theory and applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Jeffery, K.; Pollack, R.; Rovelli, C. On the Statistical Mechanics of Life: Schrödinger Revisited. Entropy 2019, 21, 1211. [Google Scholar] [CrossRef]
- Arshad, M.; Lu, D.; Rehman, M.-U.; Ahmed, I.; Sultan, A.M. Optical Solitary Wave and Elliptic function Solutions of Fokas-Lenells Equation in Presence of Perturbation Terms and its Modulation Instability. Phys. Scr. 2019, 94, 105202. [Google Scholar] [CrossRef]
- Correa, F.; Martínez, C.; Troncoso, R. Hairy black hole entropy and the role of solitons in three dimensions. J. High Energy Phys. 2012, 2012, 136. [Google Scholar] [CrossRef]
- Lu, D.; Seadawy, A.R.; Wang, J.; Arshad, M.; Farooq, U. Solitons Solutions of Generalized Third-Order Nonlinear Schrodinger Equation by two Mathematical Methods and its Stability. Pramana-J. Phys. 2019, 93, 44. [Google Scholar] [CrossRef]
- Navickas, Z.; Bikulciene, L.; Rahula, M.; Ragulskis, M. Algebraic operator method for the construction of solitary solutions to nonlinear differential equations. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1374–1389. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D.; Wang, J. Travelling wave solutions of Drinfel’d–Sokolov–Wilson, Whitham–Broer–Kaup and (2+1)-dimensional Broer–Kaup–Kupershmit equations and their applications. Chin. J. Phys. 2017, 140, 136–144. [Google Scholar] [CrossRef]
- Arnous, A.H.; Seadawy, A.R.; Alqahtani, R.T.; Biswas, A. Optical solitons with complex Ginzburg–Landau equation by modified simple equation method. Optik 2017, 55, 780–797. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Arshad, M.; Lu, D. Stability analysis of new exact traveling-wave solutions of new coupled KdV and new coupled Zakharov–Kuznetsov systems. Eur. Phys. J. Plus 2017, 132, 162. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, G.; Wang, M. Lattice Boltzmann simulations for the vortex tori pattern in the three-dimensional cubic-quintic complex Ginzburg–Landau equation. J. Comput. Phys. 2016, 306, 311–319. [Google Scholar] [CrossRef]
- Inc, M.; Aliyu, A.I.; Yusu, A.; Baleanu, D. Optical Solitons and Modulation Instability Analysis with (3 + 1)-Dimensional Nonlinear Shrödinger Equation. Superlattices Microstruct. 2017, 112, 296–302. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, C.; Lu, D.; Arshad, M.; Nasreen, N.; Qian, X. Bright-Dark and Multi Solitons Solutions of (3 + 1)-Dimensional Cubic-Quintic Complex Ginzburg–Landau Dynamical Equation with Applications and Stability. Entropy 2020, 22, 202. https://doi.org/10.3390/e22020202
Yue C, Lu D, Arshad M, Nasreen N, Qian X. Bright-Dark and Multi Solitons Solutions of (3 + 1)-Dimensional Cubic-Quintic Complex Ginzburg–Landau Dynamical Equation with Applications and Stability. Entropy. 2020; 22(2):202. https://doi.org/10.3390/e22020202
Chicago/Turabian StyleYue, Chen, Dianchen Lu, Muhammad Arshad, Naila Nasreen, and Xiaoyong Qian. 2020. "Bright-Dark and Multi Solitons Solutions of (3 + 1)-Dimensional Cubic-Quintic Complex Ginzburg–Landau Dynamical Equation with Applications and Stability" Entropy 22, no. 2: 202. https://doi.org/10.3390/e22020202
APA StyleYue, C., Lu, D., Arshad, M., Nasreen, N., & Qian, X. (2020). Bright-Dark and Multi Solitons Solutions of (3 + 1)-Dimensional Cubic-Quintic Complex Ginzburg–Landau Dynamical Equation with Applications and Stability. Entropy, 22(2), 202. https://doi.org/10.3390/e22020202






