New Interfaces and Approaches to Machine Learning When Classifying Gestures within Music
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Gestural Interfaces and Biometric Data
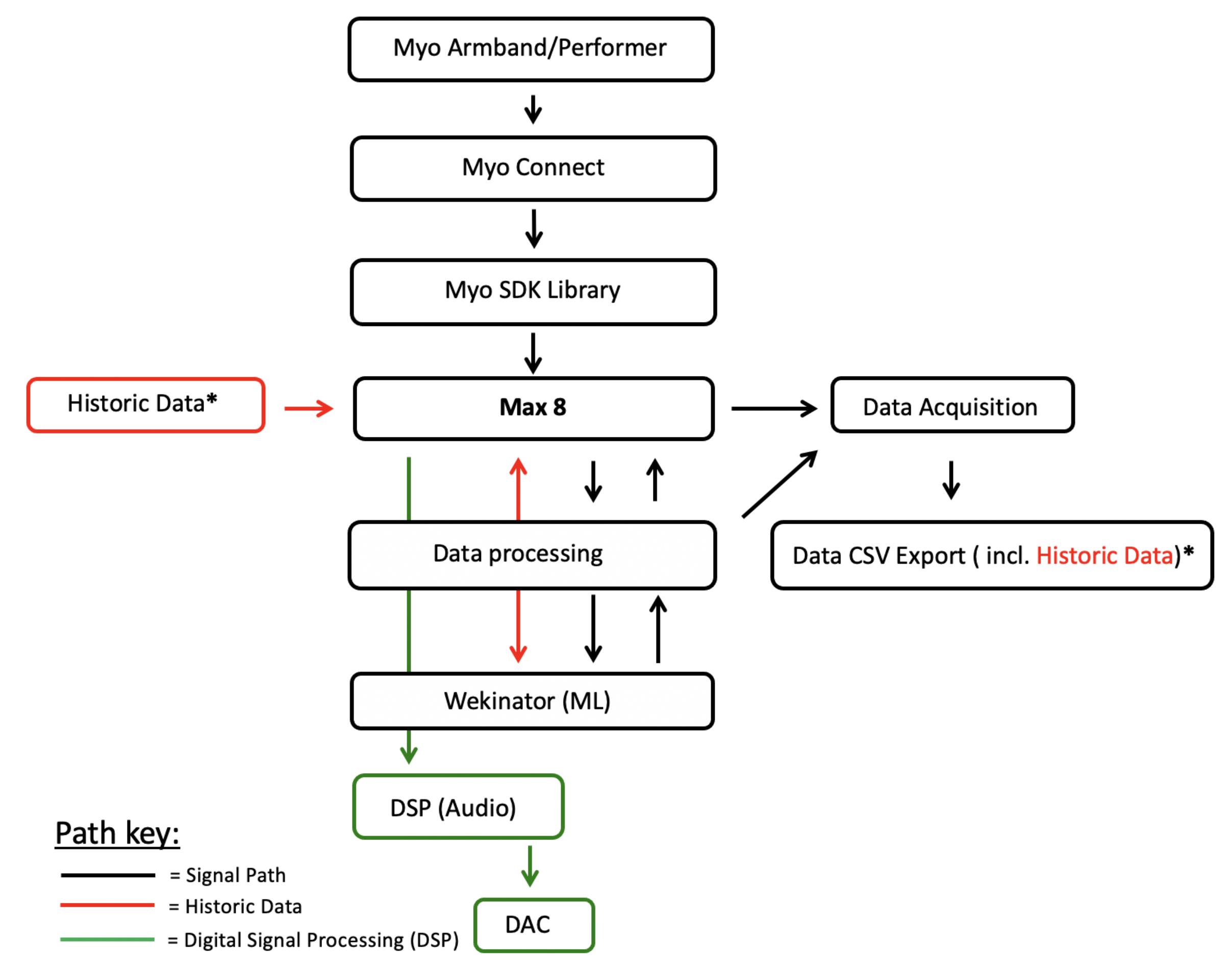
3.1.1. Gestural Interface: The Myo Armband
3.1.2. Transmitted Data
3.1.3. Usage Issues of the Myo
- Calibration: Muscle activity within a Myo user’s arm is unique to the individual [39]. Therefore, users must calibrate the Myo to ensure data reliability. Failing to calibrate the Myo before use will invalidate acquired data as measurement is altered; for example, not providing a point of origin in space for IMU data.
- Placement: Careful placement of the Myo must be observed and standardised. See Figure 2b. This is because incorrect placement will skew all EMG results. A change in rotation of the Myo, between future participants or users, will change the orientation of electrodes (measuring EMG data) and therefore affect data or system validity. We placed the Myo in the same position for data acquisition, model training and testing. This also allowed us to observe how gestural amplitude relates to the returned ML model accuracies.
3.2. Planning Performance Gestures for Model Testing
- Right arm positioned above head (gesture 1): This gesture requires the performer to extend their right arm above the head, linearly. We used the Euler angle ’pitch’ (IMU) to measure this gesture, yielding low data variation because of the linearity of the dataset. Due to this linearity, the model input will position itself very closely to model output. This gesture is therefore most suited to a continuous model. This gesture does not use EMG data; it is used in this study to see if the same behaviour occurs between ML models trained with EMG and IMU data. Musically, it is aimed to measure the dynamic movement of pianist’s arms, typically performed theatrically during performance; if a simple raising of the arm demonstrates any significance amongst model accuracy/behaviour, we can then elaborate on better complex IMU-measured gestures. This gesture was inspired by piano practice, as seen in a piece of music by [40] called Suspensions, where the performer lifts the arm above the head to shape sounds over time via DSP; demonstrating how theatrical piano gestures (which do not traditionally produce sound) can become musical when applied to interactive music practice. The performed strength (amplitude) of this gesture is relative to returned model accuracies. We measure it via observing minimum and maximum values for Euler angle pitch and the data distribution of each trained model (see Section 3.3.1 for more information on this process). A video example of the performance of this gesture can be found at the following link: performance of gesture 1 (https://www.dropbox.com/s/a250u5ga3sgvyxu/Gesture1.mov?dl=0).
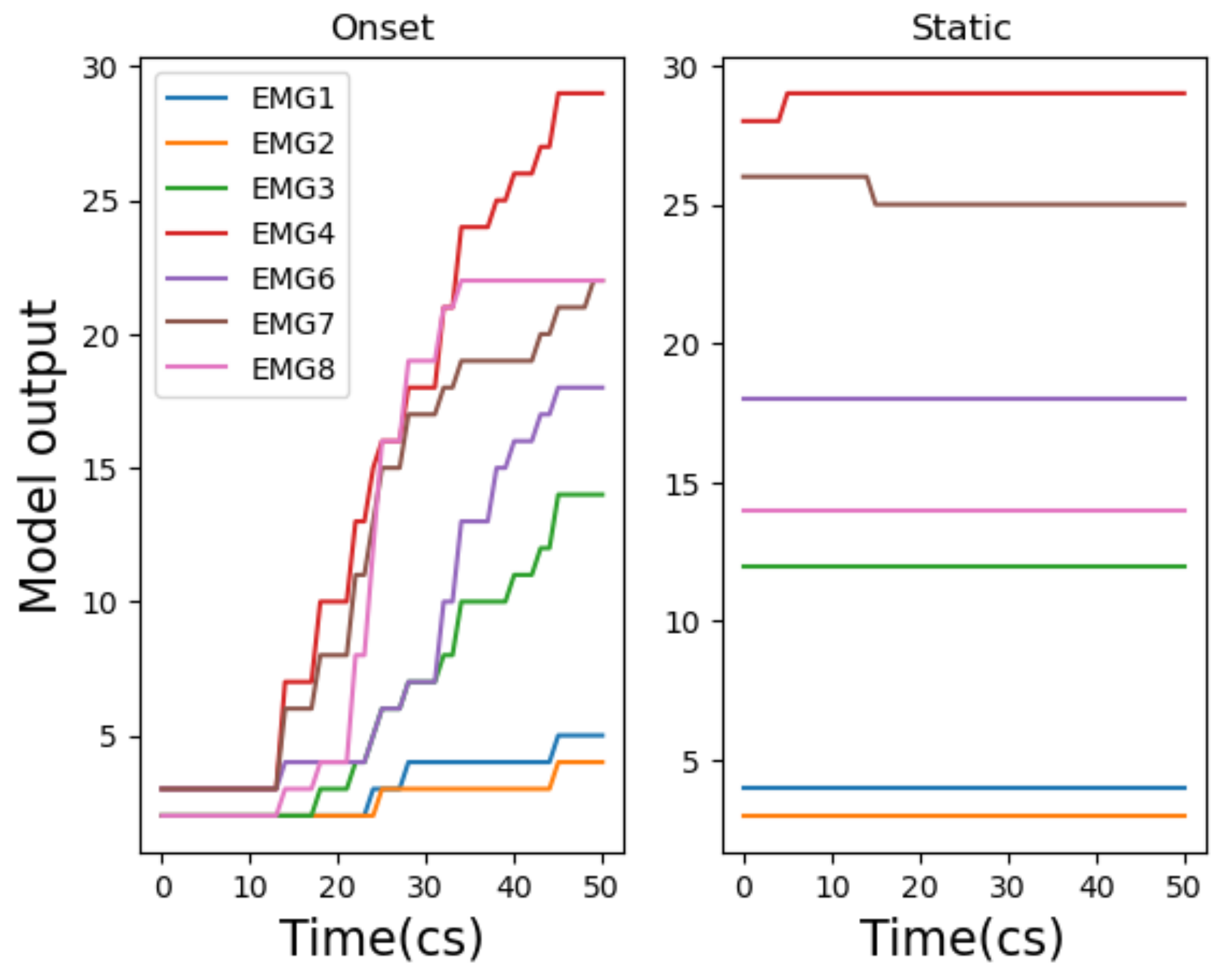
- Spread fingers and resting arm (gesture 2): This gesture is executed by: (a) extending all digits on the right hand (b) putting the arm back to a relaxed position. Gesture position (b) was developed to examine model prediction efficacy of position (a) when shifting between the two states. This gesture navigates between two fixed states. Therefore, it was logical that a classifier model was most suitable for this gesture. This gesture targets all 8 EMG electrodes on the Myo interface (see Figure 2b). This gesture is inspired by the need of a pianist to access a number of musical intervals (an interval is the distance in pitch between two different musical notes, measured by numerical value and determined musical quality [41]) with one hand; when playing melodies, chords, scales and arpeggios. In piano practice, the ability of the pianist to play large intervals is dependent on an individual pianist’s hand span; defined by age, gender and ethnic differences amongst pianists [42]. The average interval range available to pianists is from a second to a maximum of a ninth or tenth [42]; the latter being harder to achieve. This gesture negates such differences because the Myo GI measures EMG activity relative to the pianist and translates it in to a musical outcome; a large desired interval (i.e., a 10th) can therefore be digitally mapped during interactive music practice, if unable to be played. Through musical repertoire, this gesture was influenced by the tenth musical interval (i.e., found in the right hand part, in bar 3, of Harry Ruby’s tenth interval rag [43]), where the piece is composed around the difficult to perform (on average) tenth interval. We measured the performed strength of this gesture via the minimum and maximum MAV values returned across all 8 EMG electrodes of the Myo armband, as well as observing data distribution; we used the MAV to measure performance strength because it is typically used with EMG signals to estimate muscle amplitude [30] (refer to Section 3.3.1 for more information on this method). A video example of the performance of this gesture can be found via the following link: performance of gesture 2 (https://www.dropbox.com/s/mor7ccjyyhr13ry/Gesture2.mov?dl=0).
- Scalic fingering (gesture 3): This gesture is performed by extending and isolating pressure on each individual digit of the right hand, including: thumb (i); index finger (ii); middle finger (iii); ring finger (iv); little finger (v). This gesture was created to understand and execute a nuanced detailing of EMG data, as muscle behaviour for moving individual digits is much more finely detailed than gestures activated by large and pronounced muscle groups (i.e., gesture 2) [25]. It was also chosen because literature on this topic does not use all five digits when examining such a gesture, whereas the maximum number of digits used to train a ML system is four [24,44]. Musically, the use of all five digits is fundamentally important when playing piano music; through scales, chords, arpeggios and melodies. We base this gesture on the first 5 notes (with fingering pattern) found in the upper bass clef voicing, within the first bar of Hanon’s scale exercise (no.1 in C), taken from his iconic piano exercise book The Virtuoso Pianist [45]; this is because fingers i–v are used to achieve focused pitches/fingering. Albeit, even though this gesture focuses on a single scale, it should be noted that scalic playing compromises wider piano playing.This gesture aims to allow performers to create a piano DMI, through emulation of the Hanon scale. Finger ML classification can be used, via this gesture, to replicate piano performance away from the instrument; in other words, playing ’tabletop’ piano. The advantage of this approach is an increased mobility of piano performance; however, it also means that this approach could be further used to simulate piano performance and build novel DMIs (e.g., via interacting with 3D digital instruments). The mobile instrument approach has particular interest in the field for this reason [24,25,27]. The identification of fine EMG detailing is done, for this gesture, via post-processing and the application of a MAV function (discussed in Section 3.3.1). The DTW model has been targeted for this gesture because each individual digit needs to be accounted for as a single-fire, discrete, state. This gesture targets all 8 EMG electrodes on the Myo interface (see Figure 2a) and uses the MAV function, across all electrodes, to estimate the performance amplitude of this gesture (discussed in Section 3.3.1). A video example of the performance of this gesture can be found via the following link: performance of gesture 3 (https://www.dropbox.com/s/tg6wa7uap38y3c9/Gesture3.mov?dl=0).
3.2.1. Onset Vs. Static Gestures for Model Training in Wekinator
3.3. Data Structuring and Acquisition
- Acquisition: Data were acquired from the Myo SDK at 10 ms per entry. This acquisition frequency was deemed ample in order to see significant data trends. Gestures 1 and 2 were recorded with 4 iterations over 16 s. Gesture 3 was recorded with 5 iterations in 20 s. Gesture 3 was recorded with a longer length of time because the gesture is much more complex than gestures 1–2. We used a digital metronome to synchronise the data acquisition software with gesture performance.
- Pre-processing and structuring: Data were pre-processed following acquisition via unpacking and structuring/labelling all Myo data (i.e., IMU and EMG) to an array (see Section 3.1.2 for a summary of data types).
3.3.1. Data Post-Processing
3.4. Machine Learning within Wekinator
3.4.1. Ml Models in Wekinator
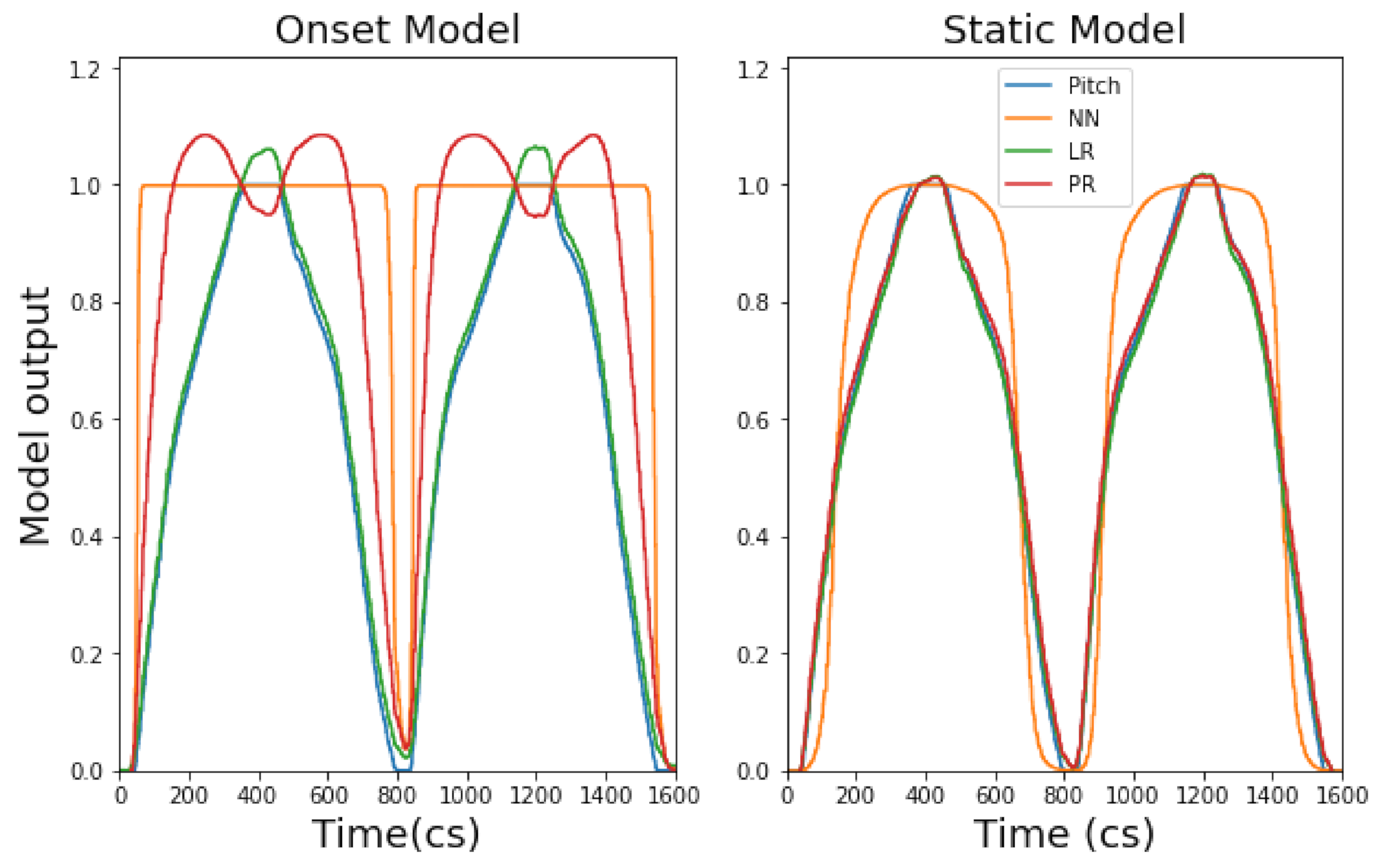
- Continuous models: Continuous models in Wekinator include (i) linear regression (LR), (ii) polynomial regression (PR) and (iii) neural network (NN). These can be considered regression models. They are useful for modelling real-time model inputs versus model outputs over time. They do not make categorical classifications, unlike classifier or DTW models offered in Wekinator. They are useful in music practice because their model output type (regressive) can be used to continuously alter an audio signal (via DSP) over time. However, each continuous model in Wekinator provides different methods and behaviours to do this (see Appendix A for an explanation of how each continuous model functions and their application to music).
- Classifier models: Classification models in Wekinator include (i) k-nearest neighbour (k-NN), (ii) AdaBoost.M1 (ABM1), (iii) DT, (iv) support vector machine (SVM), (v) naive Bayes (NB) and (vi) decision stump (DS). These models are important to understand because their gestural predictions affect interactive music practice. A weak classification model is not reliable or desirable to use within a temporal art form, relying on immediacy. Therefore, how they arrive at those decisions is of interest. Their output is categorical (e.g., classes 1–5) and they are useful in music practice for defining fixed sequence points within a gesture. However, they do not apply a real-time mapping to audio signals, unlike continuous models do. See Appendix B for details regarding how the classifier models offered in Wekinator operate at an algorithmic level and how they apply to music practice.
- Dynamic time warping: DTW is a model that looks to predict a pattern over a time series. It is best used when attempting to predict a pattern, within an attribute, in spite of fluctuations in timing [47]. The algorithm aligns the trained model with fluctuations over the time series, hence the namesake. This model is very useful in music practice because it attempts to predict a music gesture (using the trained template) regardless of timing issues. Therefore, it compensates for subtle timing variances in how a music performer actions a specific gesture; a common issue in music practice. The DTW model output is a single-fire message every time the model predicts a gesture; useful in music when a performer wants to trigger a fixed music event only when a gesture is performed.
3.4.2. Training Ml Models in Wekinator Using Real-Time Data
3.4.3. Running Ml Models in Wekinator Using Historic Data
3.4.4. Optimising Trained Ml Models in Wekinator
3.4.5. Ml Model Example Length within Wekinator
4. Results
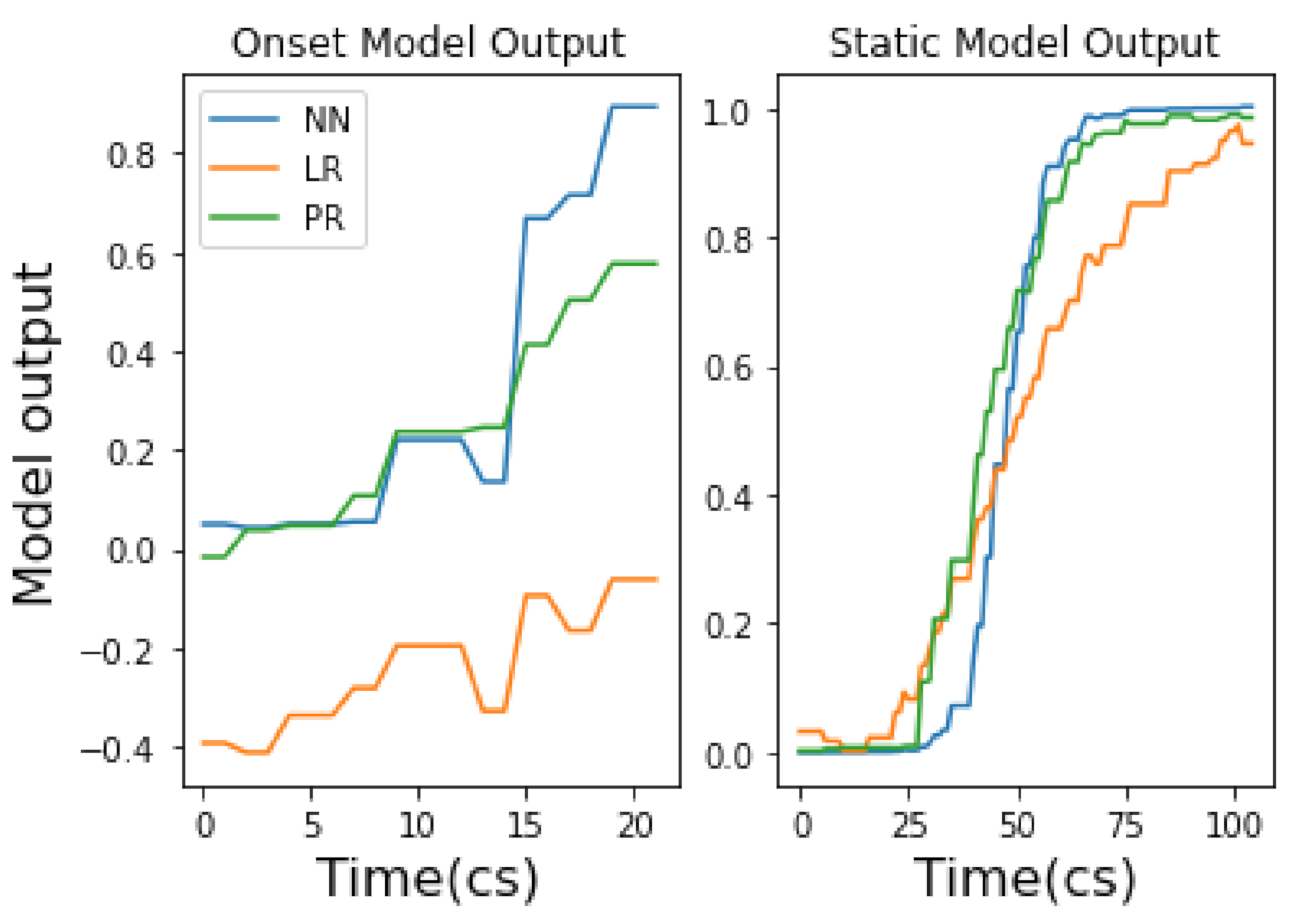
4.1. Model Evaluations (Static Models)
4.1.1. Continuous Models
4.1.2. Classifier Models
4.1.3. Dynamic Time Warping
4.2. Model Evaluations (Onset Models)
4.2.1. Continuous Models
4.2.2. Classifier Models
4.2.3. Dynamic Time Warping Models
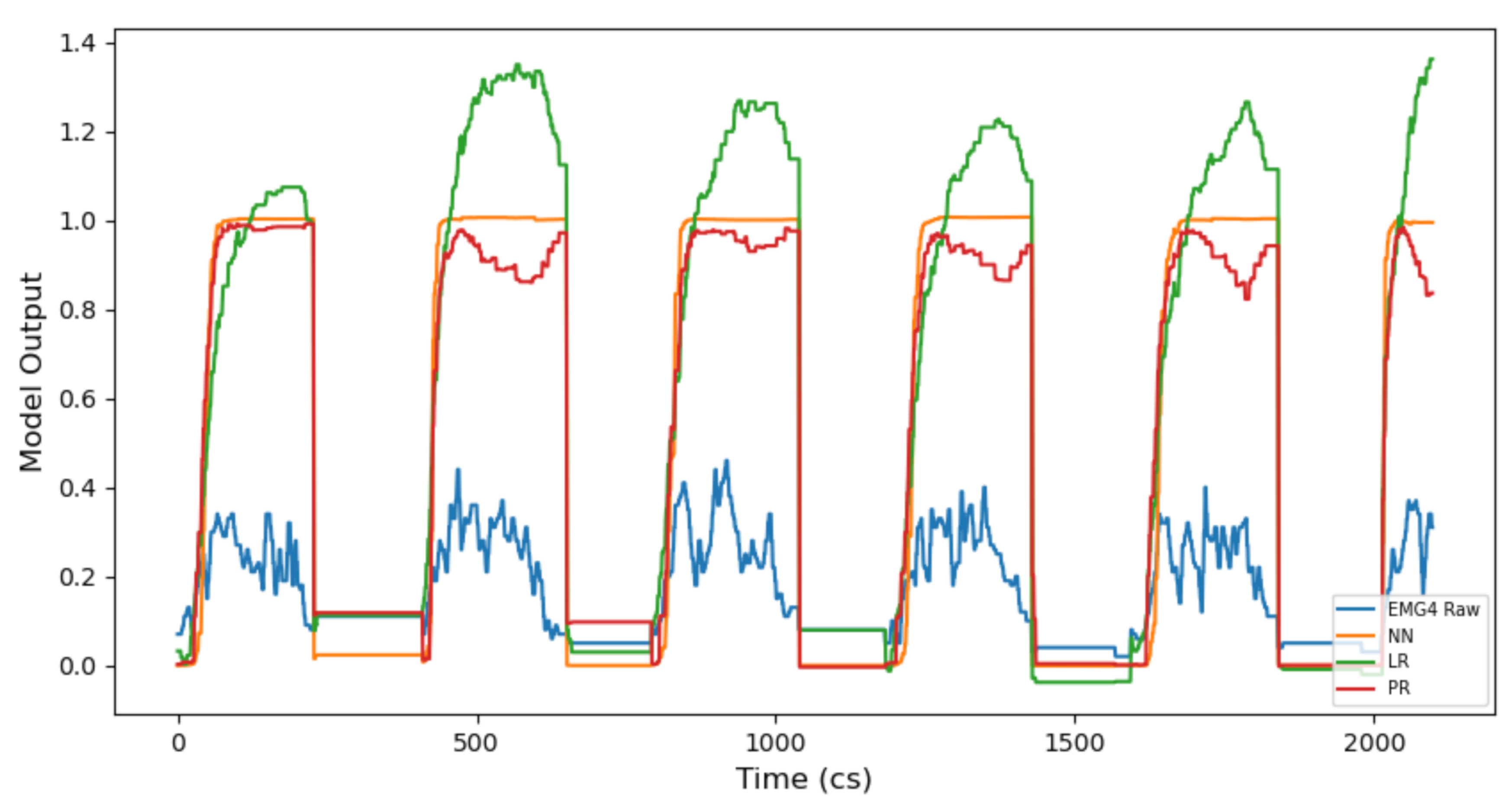
4.3. Running Supervised Models with Historical Gesture Data
4.3.1. Continuous Models
4.3.2. Classifier Models
4.3.3. Dynamic Time Warping Models
4.4. Number of Model Examples vs. Model Accuracy
4.4.1. Continuous Models
4.4.2. Classifier Models
4.4.3. Dynamic Time Warping Models
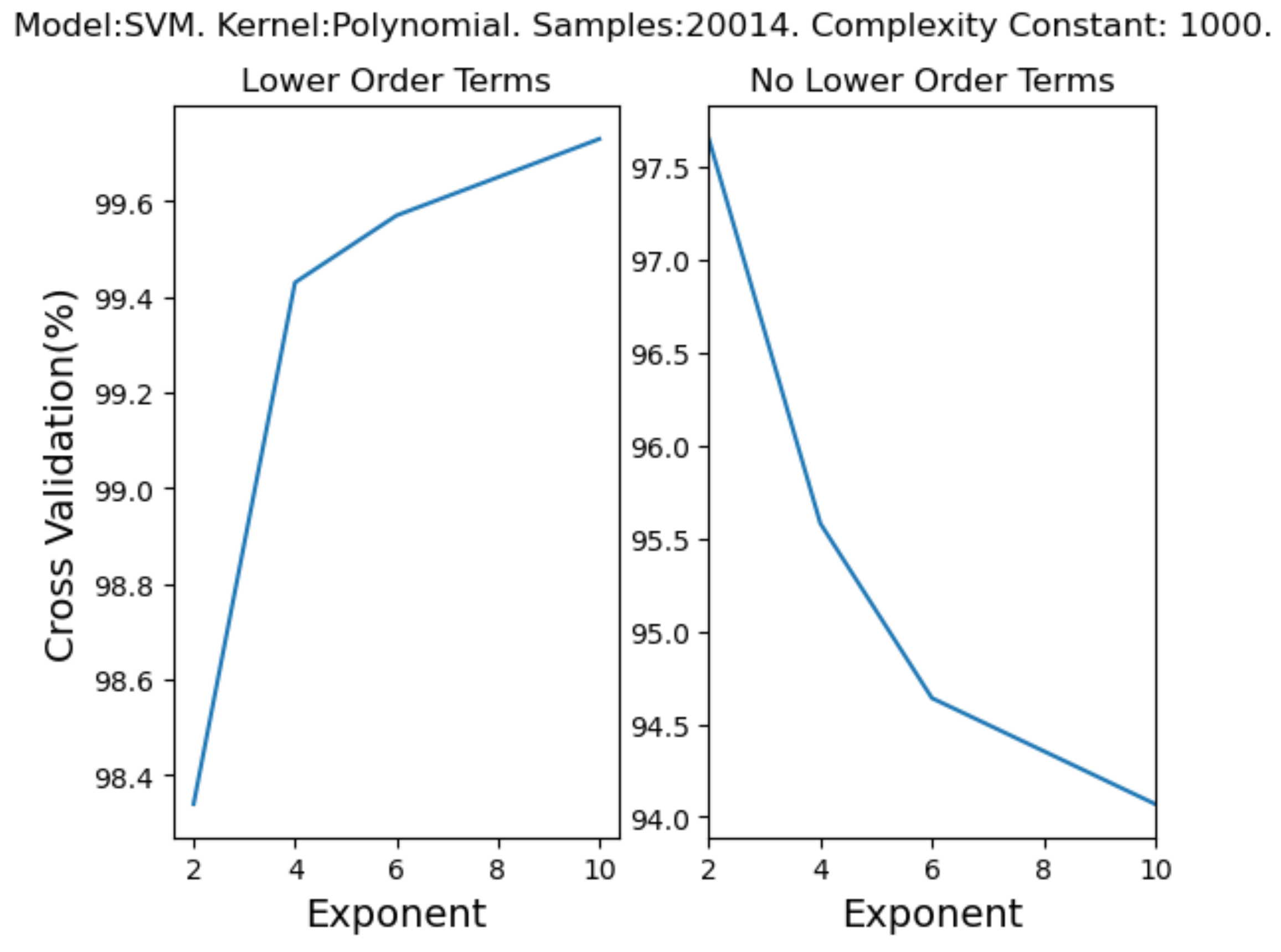
4.5. Impact of Data Type and Post-Processing on Model Accuracy
4.6. Optimising Supervised Learning Models for Gestures 1–3 in Wekinator
4.7. Reflections on Model Choice When Classifying Performance Gestures 1–3 in Wekinator
- Pre-process, post-process and select the best data type for the chosen performance gesture from this study; using a MAV function for a gesture reliant on EMG information and Euler pitch data for a gesture measuring a linear upwards vector (i.e., elevation); refer to Section 3.3 and Section 3.3.1 regarding this process.
- Inform chosen gesture type by addressing this question: is the perceived onset (attack time) of the gesture vital to the particular music process and aims? Answering ’yes’ will direct the practitioner to record your chosen gesture in Wekinator, including the onset of your gesture. Answering ’no’ will direct the practitioner to record the gesture statically, without the onset; refer to Section 3.2.1 for a description of both gesture types.
- Establishing chosen gesture type then informs model choice. We suggest that there are two model types to choose from: prediction via generating a fixed music event or live music event. A fixed music event will require a classifier model, whereas a live music event will require a continuous or DTW model. However, the choice between a continuous and DTW model, for a live event, will have an important consequence; choosing only a continuous model for a live music event will provide the user an additional layer of musical information regarding the disparate mapping behaviour of each algorithm (i.e., NN, LR and PR—see Section 4.1.1 for mapping behaviour. The direct implication of this concept on music is discussed in Section 5).
- Next, the practitioner should choose their particular algorithm within the model type chosen (refer to Section 4 to inform this decision through observing model accuracy).
- Record the chosen gesture (from this study) using the Wekinator GUI. Refer to Section 4.4 when deciding on number of examples for best practice regarding the chosen model(s) type.
- Next, optimise the model(s) (refer to Section 4.6 for information regarding the optimisation of classifier and DTW models).
- Train model(s) and then run Wekinator for the composition process.
5. Interactive Music Composition
5.1. Model Output: Interactive Music Composition
5.1.1. Continuous Models
5.1.2. Classifier Models
5.1.3. Dynamic Time Warping Models
5.2. Ml Findings to Facilitate Novel Dmis: Gesture 3 as a Tabletop Piano
5.3. Ml Model Mapping Behaviour as a Creative Application within Music
5.4. Using Historic Gesture Data within Music Practice
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Linear Regression: LR is a model that makes a prediction when observing the relationship between an independent (x) and dependent variable (y). It expresses the model prediction class as a linear combination of model attributes. It is especially useful when model attributes and class/outcome are numerical. It uses the least square method, derived from all model input data points, to find a line of best fit when modelling the relationship between the independent variable and dependent variable [55]. It is useful in interactive music practice because linear relationships between model input and output can create strict action–sound relationships; in this sense, they provide a reliable signal mapping when applying DSP to an audio signal. An LR approach can be expressed as follows, where represents the model input, represents the y-intercept, indicates the constant and y indicates the predicted value:
- Polynomial Regression: A PR model is built upon the foundations of a linear regression model (finding a line of best fit linearly). However, a polynomial builds upon this by creating a line of best fit polynomially (using several terms to do so). This is done by increasing the exponent of the model input . This model is useful in interactive music practice because it provides a less strict action-sound mapping (in comparison to the LR model). Due to the fact there are more terms, it gives the performer the option to use a ’smoother’ and non-linear way of mapping model inputs when applying PR model output to audio signals. A PR approach can be expressed as follows, where represents the model input, represents the y-intercept, and indicate the constant and y indicates the predicted value:
- Neural Network: The NN in Wekinator is an MPNN [56]. This model is based on a backpropogation framework to classify instances and is composed of a network of low-level processing elements, which work together to produce an accurate and complex output [57]. The NN model is composed of three core elements: an input layer (e.g., inputs from GIs in Wekinator), a hidden layer and an output layer. The backpropogation algorithm performs learning on a multilayer feed-forward NN [57]. At model training, it iteratively uses backpropogation to adjust the weights of the hidden layer(s), in order for the model to become more accurate. Model parameters, such as number of nodes per hidden layers, or number of hidden layers used, can be adjusted in Wekinator (see Table A8 for more information on NN parameters). An NN is useful in interactive music practice because the model gives a stabilised/smoothened model output value (in comparison to LR and PR models), due to the fact that the model uses a sigmoid activation function (mapping input values between 0 and 1) at the model output layer.
Appendix B
- k-Nearest neighbour: The k-NN model is a classification algorithm which makes predictions based on the proximity of new model input data to the assigned value of k [58]. If , then the algorithm will look for the closest data point to the input feature (i.e., its nearest neighbour) and make a respective classification. However, if , then the model will regard the 100 closest points to the input feature and make a respective classification; both approaches will disparately affect the classification outcome. Therefore, the model uses the value of k to assign a class to new data, based on the proximity of new data to the labelled data in the trained dataset.
- AdaBoost.M1: The ABM1 algorithm is a popular boosting algorithm that takes weak classifiers/learners and improves their performance. This is done in Wekinator via choosing a base classifier: a DT or a DS (see Table A7 for more information). Initially, the ABM1 model assigns a weight to all features/attributes introduced to the model (all weights are defined by attributes). The weight is then iteratively redefined based on errors made on the training data by the base classifier chosen [59].
- Decision Tree (J48): The DT is a model based on the C4.5 algorithm used to generate DTs [60]. The DT graphically represents the classification process. Due to this, it is very useful for discovering the significance of certain attributes within datasets. In Wekinator, the DT is a univariate tree [61] that uses model attributes as tree internal nodes. It makes classifications by following a procedure: constructing the tree, calculating information gain and pruning. On construction, each model attribute is assessed in terms of its information gain and then pruned. Pruning a tree allows the user to discard any irrelevant information, within the dataset (attributes), when making classifications [61].
- Support Vector Machine: The SVM model assesses observations, from model attributes, and their distance to a defined linear class margin; this is referred to as a maximum margin hyperplane [55]. This hyperplane aims to create a margin which achieves the best separation between classes and does not move closer to each class than it has to [55]. The observations that are closest to the margin are called support vectors. This classification method seeks to accommodate for low bias and high variance in the model. It also ensures that the model is not sensitive to outliers when new data are introduced to the (trained) model. However, the SVM model can also perform a non-linear classification (via the kernel chosen for the model, see Table A7 for all kernels available).
- Naive Bayes: The NB algorithm is a classification model that ignores syntax and treats attribute observations as independent of the class [62]. It calculates the probability of observations belonging to a class by an attribute observation vector. This can be described as follows, where P denotes probability, is an attribute observation vector (at ith iteration) and C is a class label [62]:
- Decision Stump: A DS model is a single-layer DT that uses a single level to split an attribute from the root of the tree [63].
Appendix C
| Gesture No. | Trained Model Input Parameter | Min. Value | Max. Value | Input Data Distribution |
|---|---|---|---|---|
| 1 | Euler pitch | 49 | 72.92 |  |
| 2 | EMG1 | 2 | 6 |  |
| EMG2 | 2 | 13 |  | |
| EMG3 | 2 | 26 |  | |
| EMG4 | 2 | 34 |  | |
| EMG5 | 2 | 14 |  | |
| EMG6 | 2 | 26 |  | |
| EMG7 | 6 | 25 |  | |
| EMG8 | 2 | 4 |  | |
| 3 (i) | EMG1 | 2 | 5 |  |
| EMG2 | 2 | 13 |  | |
| EMG3 | 2 | 32 |  | |
| EMG4 | 2 | 42 |  | |
| EMG5 | 2 | 23 |  | |
| EMG6 | 2 | 25 |  | |
| EMG7 | 2 | 37 |  | |
| EMG8 | 2 | 16 |  | |
| 3 (ii) | EMG1 | 2 | 5 |  |
| EMG2 | 2 | 10 |  | |
| EMG3 | 4 | 32 |  | |
| EMG4 | 2 | 23 |  | |
| EMG5 | 2 | 12 |  | |
| EMG6 | 2 | 24 |  | |
| EMG7 | 2 | 41 |  | |
| EMG8 | 2 | 28 |  | |
| 3 (iii) | EMG1 | 2 | 6 |  |
| EMG2 | 2 | 10 |  | |
| EMG3 | 2 | 13 |  | |
| EMG4 | 2 | 14 |  | |
| EMG5 | 2 | 13 |  | |
| EMG6 | 2 | 21 |  | |
| EMG7 | 2 | 36 |  | |
| EMG8 | 2 | 36 |  | |
| 3 (iv) | EMG1 | 2 | 7 |  |
| EMG2 | 2 | 19 |  | |
| EMG3 | 2 | 37 |  | |
| EMG4 | 2 | 33 |  | |
| EMG5 | 2 | 29 |  | |
| EMG6 | 2 | 24 |  | |
| EMG7 | 2 | 30 |  | |
| EMG8 | 2 | 27 |  | |
| 3 (v) | EMG1 | 2 | 6 |  |
| EMG2 | 2 | 18 |  | |
| EMG3 | 2 | 35 |  | |
| EMG4 | 2 | 28 |  | |
| EMG5 | 2 | 23 |  | |
| EMG6 | 2 | 18 |  | |
| EMG7 | 2 | 27 |  | |
| EMG8 | 2 | 14 |  |
| Gesture No. | Trained Model Input Parameter | Min. Value | Max. Value | Input Data Distribution |
|---|---|---|---|---|
| 1 | Euler pitch | 48.88 | 72.05 |  |
| 2 | EMG1 | 2 | 6 |  |
| EMG2 | 2 | 11 |  | |
| EMG3 | 2 | 27 |  | |
| EMG4 | 2 | 34 |  | |
| EMG5 | 2 | 13 |  | |
| EMG6 | 2 | 16 |  | |
| EMG7 | 6 | 17 |  | |
| EMG8 | 4 | 12 | 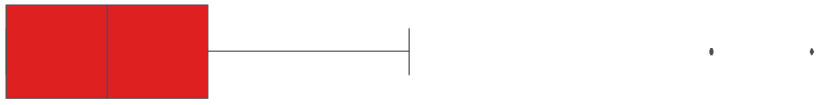 | |
| 3 (i) | EMG1 | 1 | 8 |  |
| EMG2 | 2 | 11 |  | |
| EMG3 | 2 | 32 |  | |
| EMG4 | 2 | 46 |  | |
| EMG5 | 2 | 26 |  | |
| EMG6 | 2 | 27 |  | |
| EMG7 | 2 | 38 |  | |
| EMG8 | 2 | 33 |  | |
| 3 (ii) | EMG1 | 1 | 10 |  |
| EMG2 | 2 | 6 |  | |
| EMG3 | 2 | 22 |  | |
| EMG4 | 2 | 30 |  | |
| EMG5 | 2 | 25 |  | |
| EMG6 | 2 | 19 |  | |
| EMG7 | 2 | 35 |  | |
| EMG8 | 2 | 39 |  | |
| 3 (iii) | EMG1 | 1 | 11 |  |
| EMG2 | 2 | 5 |  | |
| EMG3 | 2 | 7 |  | |
| EMG4 | 2 | 18 |  | |
| EMG5 | 2 | 22 |  | |
| EMG6 | 2 | 17 |  | |
| EMG7 | 2 | 31 |  | |
| EMG8 | 2 | 42 |  | |
| 3 (iv) | EMG1 | 1 | 9 |  |
| EMG2 | 2 | 13 | 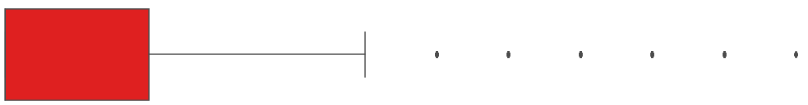 | |
| EMG3 | 2 | 35 |  | |
| EMG4 | 2 | 38 |  | |
| EMG5 | 2 | 27 |  | |
| EMG6 | 2 | 24 |  | |
| EMG7 | 2 | 28 |  | |
| EMG8 | 2 | 30 |  | |
| 3 (v) | EMG1 | 1 | 7 |  |
| EMG2 | 2 | 14 |  | |
| EMG3 | 2 | 34 |  | |
| EMG4 | 2 | 38 |  | |
| EMG5 | 2 | 24 |  | |
| EMG6 | 2 | 20 |  | |
| EMG7 | 2 | 23 |  | |
| EMG8 | 2 | 20 |  |
| Gesture No. | Trained Model Input Parameter | Min. Value | Max. Value | Input Data Distribution |
|---|---|---|---|---|
| 1 | Euler pitch | 48.78 | 69.96 |  |
| 2 | EMG1 | 2 | 6 |  |
| EMG2 | 2 | 12 |  | |
| EMG3 | 2 | 31 |  | |
| EMG4 | 2 | 37 |  | |
| EMG5 | 2 | 14 |  | |
| EMG6 | 2 | 19 |  | |
| EMG7 | 3 | 24 |  | |
| EMG8 | 2 | 9 |  | |
| 3 | EMG1 | 2 | 10 |  |
| EMG2 | 2 | 13 |  | |
| EMG3 | 5 | 36 |  | |
| EMG4 | 13 | 40 |  | |
| EMG5 | 12 | 30 |  | |
| EMG6 | 10 | 26 |  | |
| EMG7 | 15 | 33 |  | |
| EMG8 | 11 | 38 |  |
| Gesture No. | Trained Model Input Parameter | Min. Value | Max. Value | Input Data Distribution |
|---|---|---|---|---|
| 1 | Euler pitch | 47.92 | 70.81 |  |
| 2 | EMG1 | 2 | 6 |  |
| EMG2 | 2 | 13 |  | |
| EMG3 | 2 | 29 |  | |
| EMG4 | 2 | 34 |  | |
| EMG5 | 2 | 11 |  | |
| EMG6 | 2 | 22 |  | |
| EMG7 | 2 | 26 |  | |
| EMG8 | 2 | 11 |  | |
| 3 | EMG1 | 2 | 14 |  |
| EMG2 | 2 | 17 |  | |
| EMG3 | 2 | 37 |  | |
| EMG4 | 2 | 41 |  | |
| EMG5 | 2 | 36 |  | |
| EMG6 | 2 | 28 |  | |
| EMG7 | 2 | 32 | 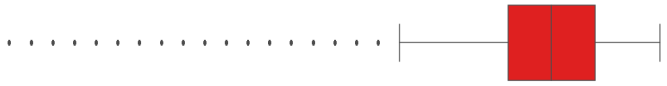 | |
| EMG8 | 2 | 42 |  |
| Gesture No. | Trained Model Input Parameter | Min. Value | Max. Value | Input Data Distribution |
|---|---|---|---|---|
| 1 | Euler pitch | 69.83 | 70.20 |  |
| 2 | EMG1 | 5 | 6 |  |
| EMG2 | 11 | 13 |  | |
| EMG3 | 25 | 28 |  | |
| EMG4 | 30 | 35 |  | |
| EMG5 | 12 | 14 |  | |
| EMG6 | 14 | 16 |  | |
| EMG7 | 18 | 23 |  | |
| EMG8 | 8 | 11 |  | |
| 3 | EMG1 | 2 | 7 |  |
| EMG2 | 2 | 21 |  | |
| EMG3 | 4 | 42 |  | |
| EMG4 | 2 | 40 |  | |
| EMG5 | 2 | 31 |  | |
| EMG6 | 2 | 27 |  | |
| EMG7 | 2 | 50 |  | |
| EMG8 | 2 | 38 |  |
| Gesture No. | Trained Model Input Parameter | Min. Value | Max. Value | Input Data Distribution |
|---|---|---|---|---|
| 1 | Euler pitch | 49.59 | 69.71 |  |
| 2 | EMG1 | 2 | 8 |  |
| EMG2 | 2 | 19 |  | |
| EMG3 | 2 | 37 |  | |
| EMG4 | 2 | 37 |  | |
| EMG5 | 2 | 14 |  | |
| EMG6 | 2 | 20 |  | |
| EMG7 | 2 | 30 |  | |
| EMG8 | 2 | 16 |  | |
| 3 | EMG1 | 2 | 12 |  |
| EMG2 | 2 | 23 |  | |
| EMG3 | 2 | 36 |  | |
| EMG4 | 2 | 41 |  | |
| EMG5 | 2 | 33 |  | |
| EMG6 | 2 | 33 |  | |
| EMG7 | 2 | 41 |  | |
| EMG8 | 2 | 35 |  |
Appendix D

Appendix E
| Model Type | Model | Available Customisable Parameters for Each Classifier Model |
|---|---|---|
| Classifier | KNN | Number of neighbours (k). |
| ABM1 | 2 base classifiers: decision tree and decision stump. Number of training rounds customisable for each base classifier. | |
| SVM | 3 kernels to choose: linear, polynomial and radial basis function (RBF). Choice to use lower-order terms for polynomial kernel. Complexity constant modifiable for all kernels. Exponent of chosen complexity constant modifiable for polynomial kernel. Gamma of chosen complexity constant modifiable for RBF kernel. |
| Model Type | Model | Available Customisable Parameters for Each Continuous Model |
|---|---|---|
| Continuous | NN | Number of hidden layers customisable (maximum 3). Number of nodes per hidden layer, for number of hidden layers chosen, also customisable. |
| LR | Three feature selection choices: no feature selection; M5 feature selection and greedy feature selection. The user can choose whether colinear inputs are removed—or not removed—for each feature selection. | |
| PR | Three feature selection choices: no feature selection, M5 feature selection and greedy feature selection. The user can choose whether colinear inputs are removed—or not removed—for each feature selection. The user can also choose the polynomial exponent (positive integer) number for each feature selection chosen. |
| Model | Matches Computed: | Downsample: | Continuous Matches Use: | Other Parameters: |
|---|---|---|---|---|
| DTW | Continuously while running | So examples have max length of By constant rate Don’t downsample | A minimum length of | Match width |
| Only once running stops | A min length equal to the shortest example | Match hop size |
References
- Tanaka, A. Sensor-based musical instruments and interactive music. In The Oxford Handbook of Computer Music; Dean, R.T., Ed.; Oxford University Press: Oxford, UK, 2011. [Google Scholar] [CrossRef]
- Miranda, E.R.; Wanderley, M.M. New Digital Musical Instruments: Control and Interaction beyond the Keyboard (Computer Music and Digital Audio Series); AR Editions, Inc.: Middleton, WI, USA, 2006. [Google Scholar]
- Hayward, P. Danger! Retro-Affectivity! The cultural career of the theremin. Convergence 1997, 3, 28–53. [Google Scholar] [CrossRef]
- Finamore, E. A Tribute to the Synth: How Synthesisers Revolutionised Modern Music. Available online: https://www.bbc.co.uk/programmes/articles/3ryZCdlXtpkNG3yRl3Y7pnh/a-tribute-to-the-synth-how-synthesisers-revolutionised-modern-music (accessed on 8 September 2020).
- Torre, G.; Andersen, K.; Baldé, F. The Hands: The making of a digital musical instrument. Comput. Music J. 2016, 40, 22–34. [Google Scholar] [CrossRef]
- Rose, J. k-bow: The Palimpolin Project. Available online: http://www.jonroseweb.com/e_vworld_k-bow.php (accessed on 8 September 2020).
- Bongers, B. An interview with Sensorband. Comput. Music J. 1998, 22, 13–24. [Google Scholar] [CrossRef]
- Wu, D.; Li, C.; Yin, Y.; Zhou, C.; Yao, D. Music composition from the brain signal: Representing the mental state by music. Comput. Intell. Neurosci. 2010, 2010. [Google Scholar] [CrossRef] [PubMed]
- Jackson, B. Thalmic Labs Myo armband hits consumer release, for sale on Amazon. Available online: https://www.itbusiness.ca/news/thalmic-labs-myo-armband-hits-consumer-release-for-sale-on-amazon/54056 (accessed on 8 September 2020).
- Nymoen, K.; Haugen, M.R.; Jensenius, A.R. Mumyo–evaluating and exploring the myo armband for musical interaction. In International Conference on New Interfaces For Musical Expression; NIME: Gonzales, LA, USA, 2015; pp. 215–218. [Google Scholar]
- Fiebrink, R.; Trueman, D.; Cook, P.R. A Meta-Instrument for Interactive, On-the-Fly Machine Learning. In International Conference on New Interfaces For Musical Expression; NIME: Pittsburgh, PA, USA, 2009; pp. 280–285. [Google Scholar]
- Schedel, M.; Fiebrink, R. A demonstration of bow articulation recognition with Wekinator and K-Bow. In International Computer Music Conference; ICMC: Huddersfield, UK, 2011. [Google Scholar]
- Santini, G. Synesthesizer: Physical modelling and machine learning for a color-based synthesizer in virtual reality. In International Conference on Mathematics and Computation in Music; Springer: Madrid, Spain, 2019; pp. 229–235. [Google Scholar] [CrossRef]
- Hantrakul, L.; Kondak, Z. GestureRNN: A neural gesture system for the Roli Lightpad Block. In New Interfaces for Musical Expression; NIME: Blacksburg, VA, USA, 2018; pp. 132–137. [Google Scholar]
- Fiebrink, R.; Cook, P.R.; Trueman, D. Human model evaluation in interactive supervised learning. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems; Association for Computing Machinery: New York, NY, USA, 2011; CHI ’11; pp. 147–156. [Google Scholar] [CrossRef]
- Caramiaux, B.; Tanaka, A. Machine Learning of Musical Gestures: Principles and Review. In International Conference on New Interfaces for Musical Expression; NIME: Daejeon, Korea, 2013; pp. 513–518. [Google Scholar]
- Tanaka, A.; Di Donato, B.; Zbyszynski, M.; Roks, G. Designing gestures for continuous sonic interaction. In International Conference on New Interfaces for Musical Expression; NIME: Porto Alegre, Brazil, 2019; pp. 180–185. [Google Scholar]
- North. Myo Connect, SDK and Firmware Downloads. Available online: https://support.getmyo.com/hc/en-us/articles/360018409792-Myo-Connect-SDK-and-firmware-downloads (accessed on 8 September 2020).
- Marin, G.; Dominio, F.; Zanuttigh, P. Hand gesture recognition with leap motion and kinect devices. In IEEE International Conference on Image Processing; IEEE: Paris, France, 2014; pp. 1565–1569. [Google Scholar] [CrossRef]
- Kosmopoulos, D.I.; Doulamis, A.; Doulamis, N. Gesture-based video summarization. In IEEE International Conference on Image Processing; IEEE: Genova, Italy, 2005; Volume 3. [Google Scholar] [CrossRef]
- Trigueiros, P.; Ribeiro, F.; Reis, L.P. A comparison of machine learning algorithms applied to hand gesture recognition. In 7th Iberian Conference on Information Systems and Technologies; IEEE: Madrid, Spain, 2012; pp. 1–6. [Google Scholar]
- Han, S.; Ho Yu, T.; Zhang, P.; Isaac, E.; Liu, B.; Cabezas, R.; Vajda, P.; Wang, R. Using deep neural networks for accurate hand-tracking on Oculus Quest. Available online: https://ai.facebook.com/blog/hand-tracking-deep-neural-networks/ (accessed on 8 September 2020).
- Benalcázar, M.E.; Motoche, C.; Zea, J.A.; Jaramillo, A.G.; Anchundia, C.E.; Zambrano, P.; Segura, M.; Palacios, F.B.; Pérez, M. Real-time hand gesture recognition using the Myo armband and muscle activity detection. In Proceedings of the 2017 IEEE Second Ecuador Technical Chapters Meeting (ETCM), Salinas, Ecuador, 16–20 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Dalmazzo, D.; Ramirez, R. Air violin: A machine learning approach to fingering gesture recognition. In Proceedings of the 1st ACM SIGCHI International Workshop on Multimodal Interaction for Education; ACM Press: Glasgow, UK, 2017; pp. 63–66. [Google Scholar] [CrossRef]
- Ruan, X.; Wang, Q.; Liu, R.; Fan, J.; Liu, J. Air-Ukulele: Finger Movement Detection Based on sEMG for Ukulele playing. In Proceedings of the Sixth International Symposium of Chinese CHI; ACM: Montreal, QC, Canada, 2018; pp. 132–135. [Google Scholar] [CrossRef]
- Di Donato, B.; Dooley, J.; Hockman, J.; Hall, S.; Bullock, J. MyoSpat: A hand-gesture controlled system for sound and light projections manipulation. In International Computer Music Conference; ICMC: Shanghai, China, 2017. [Google Scholar]
- Erdem, C.; Martin, C.; Lan, Q.; Tørresen, J.; Fuhrer, J.; Jensenius Refsum, A. Towards Playing in the ‘Air’: Modeling Motion–Sound Energy Relationships in Electric Guitar Performance Using Deep Neural Networks. In 17th Sound and Music Computing Conference; SMC: Torino, Italy, 2020; pp. 177–184. [Google Scholar]
- Dalmazzo, D.; Ramírez, R. Bowing Gestures Classification in Violin Performance: A Machine Learning Approach. Front. Psychol. 2019, 10, 344. [Google Scholar] [CrossRef] [PubMed]
- Arief, Z.; Sulistijono, I.A.; Ardiansyah, R.A. Comparison of five time series EMG features extractions using Myo Armband. In International Electronics Symposium; IEEE: Surabaya, Indonesia, 2015; pp. 11–14. [Google Scholar] [CrossRef]
- Phinyomark, A.; Quaine, F.; Laurillau, Y.; Thongpanja, S.; Limsakul, C.; Phukpattaranont, P. EMG Amplitude Estimators Based on Probability Distribution for Muscle-Computer Interface. Fluct. Noise Lett. 2013, 12, 1350016. [Google Scholar] [CrossRef]
- Phinyomark, A.; Khushaba, R.N.; Scheme, E. Feature Extraction and Selection for Myoelectric Control Based on Wearable EMG Sensors. Sensors 2018, 18, 1615. [Google Scholar] [CrossRef] [PubMed]
- Françoise, J.; Schnell, N.; Borghesi, R.; Bevilacqua, F. Probabilistic models for designing motion and sound relationships. In International Conference on New Interfaces For Musical Expression; NIME: London, UK, 2014; pp. 287–292. [Google Scholar]
- Calegario, F.; Wanderley, M.M.; Huot, S.; Cabral, G.; Ramalho, G. A Method and Toolkit for Digital Musical Instruments: Generating Ideas and Prototypes. IEEE MultiMed. 2017, 24, 63–71. [Google Scholar] [CrossRef]
- Jensenius, A.R.; Wanderley, M.M.; Godøy, R.I.; Leman, M. Musical gestures: Concepts and methods in research. In Musical Gestures: Sound, Movement, and Meaning; Godøy, R.I., Leman, M., Eds.; Routledge: Abingdon, UK, 2010; pp. 12–35. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine learning and data mining. Commun. ACM 1999, 42, 30–36. [Google Scholar] [CrossRef]
- Bini, S.A. Artificial intelligence, machine learning, deep learning, and cognitive computing: What do these terms mean and how will they impact health care? J. Arthroplast. 2018, 33, 2358–2361. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Dagnino, A. An initial study of predictive machine learning analytics on large volumes of historical data for power system applications. In IEEE International Conference on Big Data; IEEE: Washington, DC, USA, 2014; pp. 952–959. [Google Scholar] [CrossRef]
- North. What is the Wireless Range of Myo? Available online: https://support.getmyo.com/hc/en-us/articles/202668603-What-is-the-wireless-range-of-Myo- (accessed on 8 September 2020).
- North. Creating a Custom Calibration Profile for Your Myo Armband. Available online: https://support.getmyo.com/hc/en-us/articles/203829315-Creating-a-custom-calibration-profile-for-your-Myo-armband (accessed on 8 September 2020).
- Tanaka, A. Sarah Nicolls performs Suspensions, by Atau Tanaka. Available online: https://www.youtube.com/watch?v=HumBMPJUroQ (accessed on 10 January 2020).
- EarMaster. What are Intervals in Music? Available online: https://www.earmaster.com/wiki/music-memos/what-are-intervals-in-music.html (accessed on 10 April 2020).
- Pianists for Alternatively Sized Keyboards. Gender Differences. Available online: http://paskpiano.org/hand-span-data/ (accessed on 10 June 2020).
- RagtimeDorianHenry. 10th Interval Rag by Harry Ruby (1923, Ragtime piano). Available online: https://www.youtube.com/watch?v=L5hK-OF9Kx8 (accessed on 10 February 2020).
- Zadeh, A.S.; Calitz, A.; Greyling, J. Evaluating a biosensor-based interface to recognize hand-finger gestures using a Myo armband. In Proceedings of the Annual Conference of the South African Institute of Computer Scientists and Information Technologists; SAICSIT: New York, NY, USA, 2018; pp. 229–238. [Google Scholar] [CrossRef]
- Hanon-online.com. Piano Technique Exercise N∘1 in C. Available online: https://www.hanon-online.com/the-virtuoso-pianist-part-i/hanon-exercise-n-1/ (accessed on 10 February 2020).
- Rafiee, J.; Rafiee, M.A.; Yavari, F.; Schoen, M.P. Feature extraction of forearm EMG signals for prosthetics. Expert Syst. Appl. 2011, 38, 4058–4067. [Google Scholar] [CrossRef]
- Berndt, D.J.; Clifford, J. Using Dynamic Time Warping to Find Patterns in Time Series. In Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining; AAAI Press: Seattle, DC, USA, 1994; AAAIWS’94; pp. 359–370. [Google Scholar]
- Sammut, C.; Webb, G.I. (Eds.) Decision Stump. In Encyclopedia of Machine Learning; Springer US: Boston, FL, USA, 2010; pp. 262–263. [Google Scholar] [CrossRef]
- Rhodes, C.; Allmendinger, R.; Climent, R. New Interfaces for Classifying Performance Gestures in Music. In International Conference on Intelligent Data Engineering and Automated Learning; IDEAL: Manchester, UK, 2019; pp. 31–42. [Google Scholar]
- Hunt, A.; Wanderley, M.M. Mapping performer parameters to synthesis engines. Organised Sound 2002, 7, 97–108. [Google Scholar] [CrossRef]
- Winkler, T. Composing Interactive Music: Techniques and Ideas Using Max; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Dobrian, C. ADSR Amplitude Envelope. Available online: https://music.arts.uci.edu/dobrian/maxcookbook/adsr-amplitude-envelope (accessed on 8 September 2020).
- Hermann, T. Taxonomy and definitions for sonification and auditory display. In Proceedings of the 14th International Conference on Auditory Display; ICAD: Paris, France, 2008. [Google Scholar]
- Turchet, L.; Fischione, C.; Essl, G.; Keller, D.; Barthet, M. Internet of musical things: Vision and challenges. IEEE Access 2018, 6, 61994–62017. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 4th ed.; Elsevier: Cambridge, MA, USA, 2017. [Google Scholar]
- Scurto, H.; Fiebrink, R. Grab-and-play mapping: Creative machine learning approaches for musical inclusion and exploration. In International Computer Music Conference; ICMC: Utrecht, The Netherlands, 2016. [Google Scholar]
- Arora, R. Comparative analysis of classification algorithms on different datasets using WEKA. Int. J. Comput. Appl. 2012, 54, 21–25. [Google Scholar] [CrossRef]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy k-nearest neighbor algorithm. IEEE Trans. Syst. Man Cybern. 1985, SMC-15, 580–585. [Google Scholar] [CrossRef]
- Cortes, E.A.; Martinez, M.G.; Rubio, N.G. Multiclass corporate failure prediction by Adaboost. M1. Int. Adv. Econ. Res. 2007, 13, 301–312. [Google Scholar] [CrossRef]
- Quinlan, J. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1992. [Google Scholar]
- Bhargava, N.; Sharma, G.; Bhargava, R.; Mathuria, M. Decision tree analysis on j48 algorithm for data mining. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 1114–1119. [Google Scholar]
- Rish, I. An empirical study of the naive Bayes classifier. IJCAI Workshop Empir. Methods Artif. Intell. 2001, 3, 41–46. [Google Scholar]
- Zhao, Y.; Zhang, Y. Comparison of decision tree methods for finding active objects. Adv. Space Res. 2008, 41, 1955–1959. [Google Scholar] [CrossRef]



| Study | Targeted ML Models | No. Gestures Used | Type of Gestures Used |
|---|---|---|---|
| Tanaka et al. [17] | MPNN and HHMM | 4 | All gestures user-designed in a workshop |
| Dalmazzo and Ramirez [24] | DT and HMM | 4 | 4 fingers (left hand, index to ring fingers) |
| Ruan et al. [25] | MPNN | 3 | 3 fingers (left hand - thumb, index, middle) |
| Di Donato et al. [26] | MPNN and DTW | 6 | 5 activation gestures and 1 modulating gesture (left arm) |
| Erdem et al. [27] | RNN | 6 | 6 gestures (exercises on guitar playing - both arms) |
| Dalmazzo and Ramírez [28] | HHMM and DT | 7 | Violin bowing techniques |
| Model Type | Model | Model Parameters and Their Default Settings | Model Output Range/Type |
|---|---|---|---|
| Continuous (Soft Limits, meaning the maximum model output (0–1) can be exceeded.) | NN | 1 hidden layer. 1 node per hidden layer. | [0.0–1.0] (float) |
| LR | Linear inputs. No feature selection used. Colinear inputs not removed. | ||
| PR | Polynomial exponent = 2. No feature selection used. Colinear inputs not removed. | ||
| Classifier | k-NN | Number of neighbors (k) = 1. | [1–5] (integer) |
| ABM1 | Training rounds = 100. Base classifier = Decision tree. | ||
| DT | Model not customisable. | ||
| SVM | Kernel: linear. Complexity constant: 1. | ||
| NB | Model not customisable. | ||
| DS | Model not customisable. | ||
| DTW | DTW | Matches computed continuously while running. Downsample so examples have max length of: 10. Continuous matches use a minimum length of: 5. Match width: 5. Match hop size: 1. Threshold for prediction set in GUI at scale value of 6 (see Figure A1) | Single fire |
| Gesture No. | Model | TA | CV | Class No. | No. Class Examples |
|---|---|---|---|---|---|
| 1 | NN | 0 | 0 | 0.0 | 4006 |
| LR | 0.01 | 0.01 | 1.0 | 4024 | |
| PR | 0.01 | 0.01 | |||
| 2 | NN | 0 | 0 | 0.0 | 4021 |
| LR | 0.02 | 0.02 | 1.0 | 4016 | |
| PR | 0.02 | 0.02 | |||
| 3 (i) | NN | 0 | 0 | 0.0 | 3911 |
| LR | 0.05 | 0.05 | 1.0 | 4116 | |
| PR | 0.05 | 0.05 | |||
| 3 (ii) | NN | 0 | 0 | 0.0 | 3871 |
| LR | 0.03 | 0.03 | 1.0 | 4136 | |
| PR | 0.03 | 0.03 | |||
| 3 (iii) | NN | 0 | 0 | 0.0 | 3997 |
| LR | 0.05 | 0.05 | 1.0 | 4017 | |
| PR | 0.05 | 0.05 | |||
| 3 (iv) | NN | 0 | 0 | 0.0 | 3882 |
| LR | 0.04 | 0.04 | 1.0 | 4155 | |
| PR | 0.04 | 0.04 | |||
| 3 (v) | NN | 0 | 0 | 0.0 | 3799 |
| LR | 0.03 | 0.03 | 1.0 | 4243 | |
| PR | 0.03 | 0.03 |
| Gesture No. | Model | TA | RRSE TA (%) | CV | RRSE CV (%) | Class No. | No. Class Examples |
|---|---|---|---|---|---|---|---|
| 1 | k-NN | 100 | 0.0117 | 100 | 0.0236 | 1 | 4018 |
| ABM1 | 100 | 0 | 100 | 0 | 2 | 4003 | |
| DT | 100 | 0 | 100 | 0 | |||
| NB | 100 | 0 | 100 | 0 | |||
| SVM | 100 | 0 | 100 | 0 | |||
| DS | 100 | 0 | 100 | 0 | |||
| 2 | k-NN | 100 | 0.0011 | 100 | 0.0015 | 1 | 4042 |
| ABM1 | 100 | 0 | 100 | 0 | 2 | 4009 | |
| DT | 100 | 0 | 100 | 0 | |||
| NB | 100 | 0 | 100 | 0 | |||
| SVM | 100 | 0 | 100 | 0 | |||
| DS | 100 | 0 | 100 | 0 | |||
| 3 | k-NN | 100 | 0.002 | 100 | 0.0036 | 1 | 3939 |
| ABM1 | 100 | 0 | 100 | 0 | 2 | 4033 | |
| DT | 100 | 0 | 100 | 0 | 3 | 3990 | |
| NB | 100 | 0 | 100 | 0 | 4 | 3997 | |
| SVM | 100 | 0 | 100 | 0 | 5 | 4083 | |
| DS | 40.5 | 86.5631 | 40.5 | 86.5631 |
| Model | TA (%) | CV (%) | Examples per Class | % Increase in TA before Post-Processing | % Increase in CV before Post-Processing |
|---|---|---|---|---|---|
| KNN | 100 | 100 | 500 | 0 | 0 |
| ABM1 | 100 | 100 | 0.2 | 0.29 | |
| DT | 100 | 100 | 0.2 | 0.29 | |
| SVM | 100 | 100 | 1.67 | 1.97 | |
| NB | 100 | 100 | 0 | 0 | |
| DS | 100 | 100 | 1.47 | 1.47 | |
| KNN | 100 | 100 | 4000 | 0 | 0.1 |
| ABM1 | 100 | 100 | 0 | 0.01 | |
| DT | 100 | 100 | 0.02 | 0.1 | |
| SVM | 100 | 100 | 1.85 | 1.89 | |
| NB | 100 | 100 | 0.39 | 0.39 | |
| DS | 100 | 100 | 3.27 | 3.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rhodes, C.; Allmendinger, R.; Climent, R. New Interfaces and Approaches to Machine Learning When Classifying Gestures within Music. Entropy 2020, 22, 1384. https://doi.org/10.3390/e22121384
Rhodes C, Allmendinger R, Climent R. New Interfaces and Approaches to Machine Learning When Classifying Gestures within Music. Entropy. 2020; 22(12):1384. https://doi.org/10.3390/e22121384
Chicago/Turabian StyleRhodes, Chris, Richard Allmendinger, and Ricardo Climent. 2020. "New Interfaces and Approaches to Machine Learning When Classifying Gestures within Music" Entropy 22, no. 12: 1384. https://doi.org/10.3390/e22121384
APA StyleRhodes, C., Allmendinger, R., & Climent, R. (2020). New Interfaces and Approaches to Machine Learning When Classifying Gestures within Music. Entropy, 22(12), 1384. https://doi.org/10.3390/e22121384






