A Review of Fractional Order Entropies
Abstract
1. Introduction
2. Fractional-Order Derivatives and Integrals
- The left-side and the right-side Caputo derivatives,
- The left-side and the right-side Grünwald-Letnikov derivatives,
- The Hadamard derivative,
- The left-side and right-side Hilfer derivatives of type ,where and denote the left-side and right-side Riemann-Liouville fractional integrals of order , respectively, defined by:
- The Karcı derivative
- The Liouville, the left-side and the right-side Liouville derivatives,
- The Marchaud, the left-side and the right-side Marchaud derivatives,
- The left-side and the right-side Riemann-Liouville derivatives,
- The Riesz derivative,
- The local Yang derivative,
3. The Concept of Entropy
4. Fractional Generalizations of Entropy
5. Comparison of the Fractional-Order Entropies
5.1. Fractional-Order Entropy of Some Probability Distributions
5.2. Fractional-Order Entropy of Real-World Data
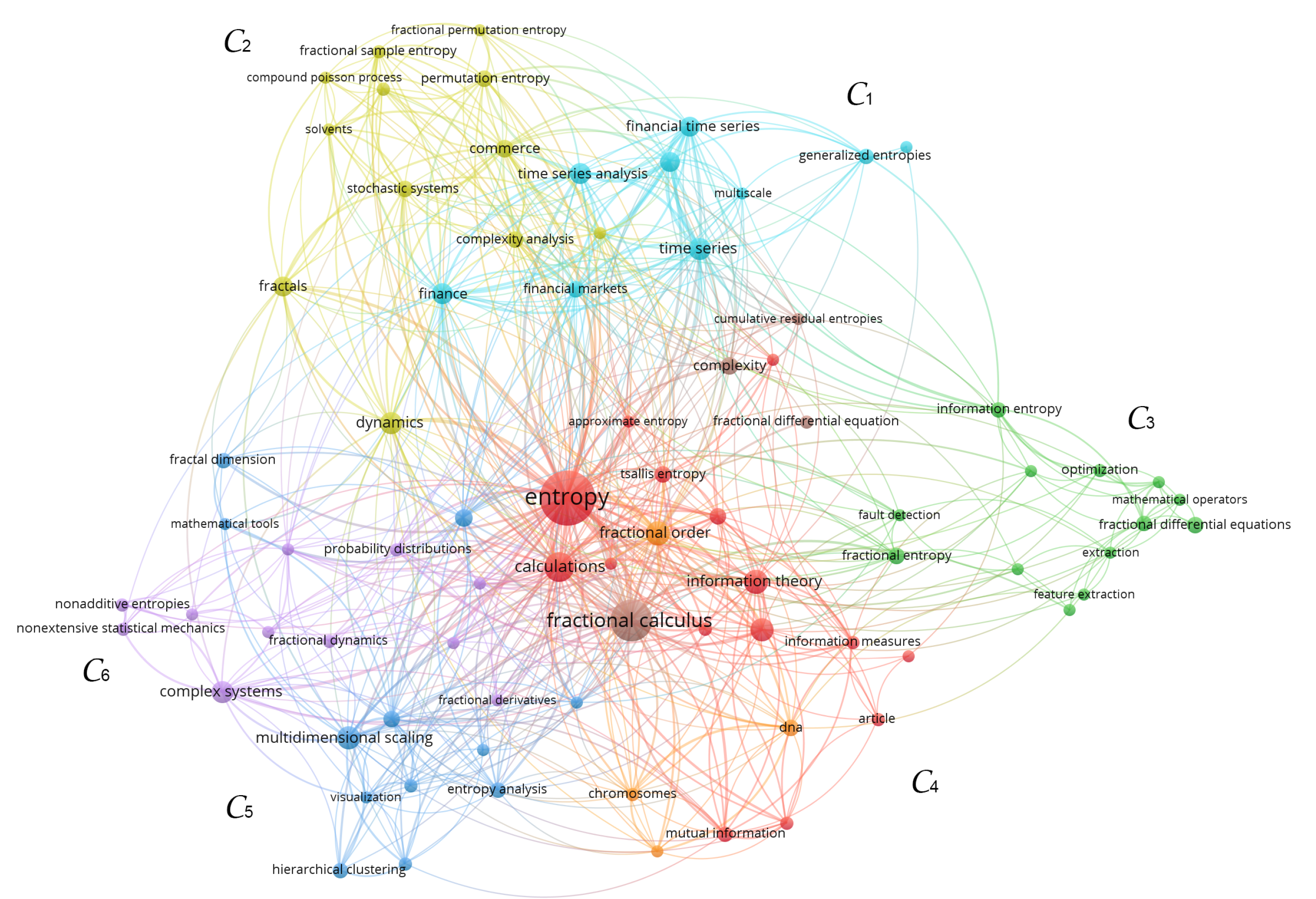
6. Impact and Applications of the Fractional-Order Entropies
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Application of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Samko, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Miller, K.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Plastino, A.; Plastino, A.R. Tsallis entropy and Jaynes’ Information Theory formalism. Braz. J. Phys. 1999, 29, 50–60. [Google Scholar] [CrossRef]
- Li, X.; Essex, C.; Davison, M.; Hoffmann, K.H.; Schulzky, C. Fractional Diffusion, Irreversibility and Entropy. J. Non-Equilib. Thermodyn. 2003, 28, 279–291. [Google Scholar] [CrossRef]
- Mathai, A.; Haubold, H. Pathway model, superstatistics, Tsallis statistics, and a generalized measure of entropy. Phys. A Stat. Mech. Appl. 2007, 375, 110–122. [Google Scholar] [CrossRef]
- Anastasiadis, A. Special Issue: Tsallis Entropy. Entropy 2012, 14, 174–176. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A.; Kiryakova, V. Recent history of the fractional calculus: Data and statistics. In Handbook of Fractional Calculus with Applications: Basic Theory; Kochubei, A., Luchko, Y., Eds.; De Gruyter: Berlin, Germany, 2019; Volume 1, pp. 1–21. [Google Scholar]
- Machado, J.T.; Galhano, A.M.; Trujillo, J.J. On development of fractional calculus during the last fifty years. Scientometrics 2014, 98, 577–582. [Google Scholar] [CrossRef]
- Ionescu, C. The Human Respiratory System: An Analysis of the Interplay between Anatomy, Structure, Breathing and Fractal Dynamics; Series in BioEngineering; Springer: London, UK, 2013. [Google Scholar]
- Lopes, A.M.; Machado, J.T. Fractional order models of leaves. J. Vib. Control. 2014, 20, 998–1008. [Google Scholar] [CrossRef]
- Hilfer, R. Application of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Tarasov, V. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: New York, NY, USA, 2010. [Google Scholar]
- Parsa, B.; Dabiri, A.; Machado, J.A.T. Application of Variable order Fractional Calculus in Solid Mechanics. In Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part A; Baleanu, D., Lopes, A.M., Eds.; De Gruyter: Berlin, Germany, 2019; Volume 7, pp. 207–224. [Google Scholar]
- Lopes, A.M.; Machado, J.A.T. Fractional-order modeling of electro-impedance spectroscopy information. In Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part A; Baleanu, D., Lopes, A.M., Eds.; De Gruyter: Berlin, Germany, 2019; Volume 7, pp. 21–41. [Google Scholar]
- Valério, D.; Ortigueira, M.; Machado, J.T.; Lopes, A.M. Continuous-time fractional linear systems: Steady-state behaviour. In Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part A; Petráš, I., Ed.; De Gruyter: Berlin, Germany, 2019; Volume 6, pp. 149–174. [Google Scholar]
- Tarasov, V.E. On history of mathematical economics: Application of fractional calculus. Mathematics 2019, 7, 509. [Google Scholar] [CrossRef]
- Clausius, R. The Mechanical Theory of Heat: With Its Applications to the Steam-Engine and to the Physical Properties of Bodies; Van Voorst, J., Ed.; Creative Media Partners: Sacramento, CA, USA, 1867. [Google Scholar]
- Boltzmann, L. Vorlesungen über die Principe der Mechanik; Barth, J.A., Ed.; Nabu Press: Charleston, SC, USA, 1897; Volume 1. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Valério, D.; Trujillo, J.J.; Rivero, M.; Machado, J.T.; Baleanu, D. Fractional calculus: A survey of useful formulas. Eur. Phys. J. Spec. Top. 2013, 222, 1827–1846. [Google Scholar] [CrossRef]
- Lopes, A.M.; Tenreiro Machado, J.; Galhano, A.M. Multidimensional Scaling Visualization Using Parametric Entropy. Int. J. Bifurc. Chaos 2015, 25, 1540017. [Google Scholar] [CrossRef]
- Landsberg, P.T.; Vedral, V. Distributions and channel capacities in generalized statistical mechanics. Phys. Lett. A 1998, 247, 211–217. [Google Scholar] [CrossRef]
- Beck, C. Generalised information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Kaniadakis, G. Statistical mechanics in the context of special relativity. Phys. Rev. E 2002, 66, 056125. [Google Scholar] [CrossRef]
- Naudts, J. Generalized thermostatistics based on deformed exponential and logarithmic functions. Phys. A Stat. Mech. Appl. 2004, 340, 32–40. [Google Scholar] [CrossRef]
- Abe, S.; Beck, C.; Cohen, E.G. Superstatistics, thermodynamics, and fluctuations. Phys. Rev. E 2007, 76, 031102. [Google Scholar] [CrossRef]
- Sharma, B.D.; Mittal, D.P. New nonadditive measures of entropy for discrete probability distributions. J. Math. Sci. 1975, 10, 28–40. [Google Scholar]
- Wada, T.; Suyari, H. A two-parameter generalization of Shannon–Khinchin axioms and the uniqueness theorem. Phys. Lett. A 2007, 368, 199–205. [Google Scholar] [CrossRef]
- Bhatia, P. On certainty and generalized information measures. Int. J. Contemp. Math. Sci. 2010, 5, 1035–1043. [Google Scholar]
- Asgarani, S. A set of new three-parameter entropies in terms of a generalized incomplete Gamma function. Phys. A Stat. Mech. Appl. 2013, 392, 1972–1976. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions. EPL (Europhys. Lett.) 2011, 93, 20006. [Google Scholar] [CrossRef]
- Sharma, B.D.; Taneja, I.J. Entropy of type (α, β) and other generalized measures in information theory. Metrika 1975, 22, 205–215. [Google Scholar] [CrossRef]
- Kaniadakis, G. Maximum entropy principle and power-law tailed distributions. Eur. Phys. J. B-Condens. Matter Complex Syst. 2009, 70, 3–13. [Google Scholar] [CrossRef]
- Tarasov, V.E. Lattice model with power-law spatial dispersion for fractional elasticity. Cent. Eur. J. Phys. 2013, 11, 1580–1588. [Google Scholar] [CrossRef]
- Nigmatullin, R.; Baleanu, D. New relationships connecting a class of fractal objects and fractional integrals in space. Fract. Calc. Appl. Anal. 2013, 16, 911–936. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Entropy, relative entropy and mutual information. Elem. Inf. Theory 1991, 2, 1–55. [Google Scholar]
- Ebrahimi, N.; Pflughoeft, K.; Soofi, E.S. Two measures of sample entropy. Stat. Probab. Lett. 1994, 20, 225–234. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Chen, J.; Li, X. Spectral entropy: A complementary index for rolling element bearing performance degradation assessment. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1223–1231. [Google Scholar] [CrossRef]
- Fan, J.L.; Ma, Y.L. Some new fuzzy entropy formulas. Fuzzy Sets Syst. 2002, 128, 277–284. [Google Scholar] [CrossRef]
- Rosso, O.A.; Blanco, S.; Yordanova, J.; Kolev, V.; Figliola, A.; Schürmann, M.; Başar, E. Wavelet entropy: A new tool for analysis of short duration brain electrical signals. J. Neurosci. Methods 2001, 105, 65–75. [Google Scholar] [CrossRef]
- De Oliveira, E.C.; Tenreiro Machado, J.A. A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C. On the ψ-Hilfer fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 72–91. [Google Scholar] [CrossRef]
- Katugampola, U.N. Correction to “What is a fractional derivative?” by Ortigueira and Machado [Journal of Computational Physics, Volume 293, 15 July 2015, Pages 4–13. Special issue on Fractional PDEs]. J. Comput. Phys. 2016, 321, 1255–1257. [Google Scholar] [CrossRef]
- Tarasov, V.E. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- Abdelhakim, A.A.; Machado, J.A.T. A critical analysis of the conformable derivative. Nonlinear Dyn. 2019, 95, 3063–3073. [Google Scholar] [CrossRef]
- Lenzi, E.; Mendes, R.; Da Silva, L. Statistical mechanics based on Rényi entropy. Phys. A Stat. Mech. Appl. 2000, 280, 337–345. [Google Scholar] [CrossRef]
- Parvan, A.; Biró, T. Extensive Rényi statistics from non-extensive entropy. Phys. Lett. A 2005, 340, 375–387. [Google Scholar] [CrossRef]
- Plastino, A.; Casas, M.; Plastino, A. A nonextensive maximum entropy approach to a family of nonlinear reaction–diffusion equations. Phys. A Stat. Mech. Appl. 2000, 280, 289–303. [Google Scholar] [CrossRef]
- Frank, T.; Daffertshofer, A. H-theorem for nonlinear Fokker–Planck equations related to generalized thermostatistics. Phys. A Stat. Mech. Appl. 2001, 295, 455–474. [Google Scholar] [CrossRef]
- Abe, S. A note on the q-deformation-theoretic aspect of the generalized entropies in nonextensive physics. Phys. Lett. A 1997, 224, 326–330. [Google Scholar] [CrossRef]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Dover: New York, NY, USA, 1957. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1963. [Google Scholar]
- Lesche, B. Instabilities of Rényi entropies. J. Stat. Phys. 1982, 27, 419–422. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Tsallis, C. Nonextensive Entropy: Interdisciplinary Applications; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Amigó, J.M.; Balogh, S.G.; Hernández, S. A brief review of generalized entropies. Entropy 2018, 20, 813. [Google Scholar] [CrossRef]
- Namdari, A.; Li, Z. A review of entropy measures for uncertainty quantification of stochastic processes. Adv. Mech. Eng. 2019, 11, 1687814019857350. [Google Scholar] [CrossRef]
- Abe, S. Nonextensive statistical mechanics of q-bosons based on the q-deformed entropy. Phys. Lett. A 1998, 244, 229–236. [Google Scholar] [CrossRef]
- Jackson, F.H. On q-functions and a certain difference operator. Earth Environ. Sci. Trans. R. Soc. Edinb. 1909, 46, 253–281. [Google Scholar] [CrossRef]
- Akimoto, M.; Suzuki, A. Proposition of a New Class of Entropy. J. Korean Phys. Soc. 2001, 38, 460–463. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1965. [Google Scholar]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Yu, S.; Huang, T.Z.; Liu, X.; Chen, W. Information measures based on fractional calculus. Inf. Process. Lett. 2012, 112, 916–921. [Google Scholar] [CrossRef]
- Radhakrishnan, C.; Chinnarasu, R.; Jambulingam, S. A Fractional Entropy in Fractal Phase Space: Properties and Characterization. Int. J. Stat. Mech. 2014, 2014, 460364. [Google Scholar] [CrossRef]
- Wang, Q.A. Extensive generalization of statistical mechanics based on incomplete information theory. Entropy 2003, 5, 220–232. [Google Scholar] [CrossRef]
- Machado, J.T. Fractional Order Generalized Information. Entropy 2014, 16, 2350–2361. [Google Scholar] [CrossRef]
- Bagci, G.B. The third law of thermodynamics and the fractional entropies. Phys. Lett. A 2016, 380, 2615–2618. [Google Scholar] [CrossRef]
- Jalab, H.A.; Subramaniam, T.; Ibrahim, R.W.; Kahtan, H.; Noor, N.F.M. New Texture Descriptor Based on Modified Fractional Entropy for Digital Image Splicing Forgery Detection. Entropy 2019, 21, 371. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science Publisher: New York, NY, USA, 2012. [Google Scholar]
- Karcı, A. New approach for fractional order derivatives: Fundamentals and analytic properties. Mathematics 2016, 4, 30. [Google Scholar] [CrossRef]
- Karcı, A. Fractional order entropy: New perspectives. Optik 2016, 127, 9172–9177. [Google Scholar] [CrossRef]
- Ferreira, R.A.; Tenreiro Machado, J. An Entropy Formulation Based on the Generalized Liouville Fractional Derivative. Entropy 2019, 21, 638. [Google Scholar] [CrossRef] [PubMed]
- Machado, J.T.; Lopes, A.M. Fractional Rényi entropy. Eur. Phys. J. Plus 2019, 134, 217. [Google Scholar] [CrossRef]
- Beliakov, G.; Sola, H.B.; Sánchez, T.C. A Practical Guide to Averaging Functions; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Xu, D.; Erdogmuns, D. Renyi’s entropy, divergence and their nonparametric estimators. In Information Theoretic Learning; Springer: Berlin/Heidelberg, Germany, 2010; pp. 47–102. [Google Scholar]
- Van Eck, N.J.; Waltman, L. Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics 2010, 84, 523–538. [Google Scholar] [CrossRef] [PubMed]
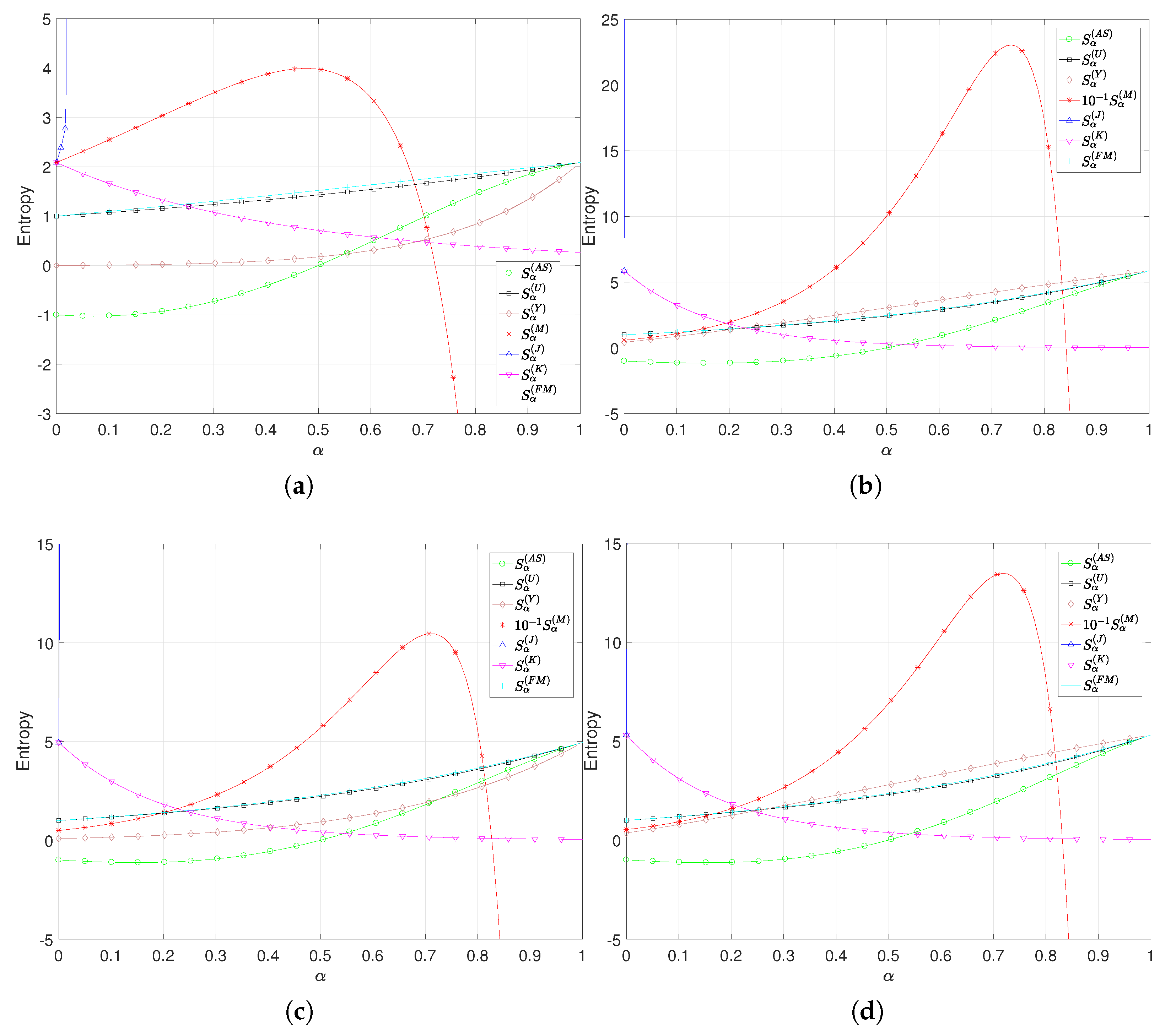
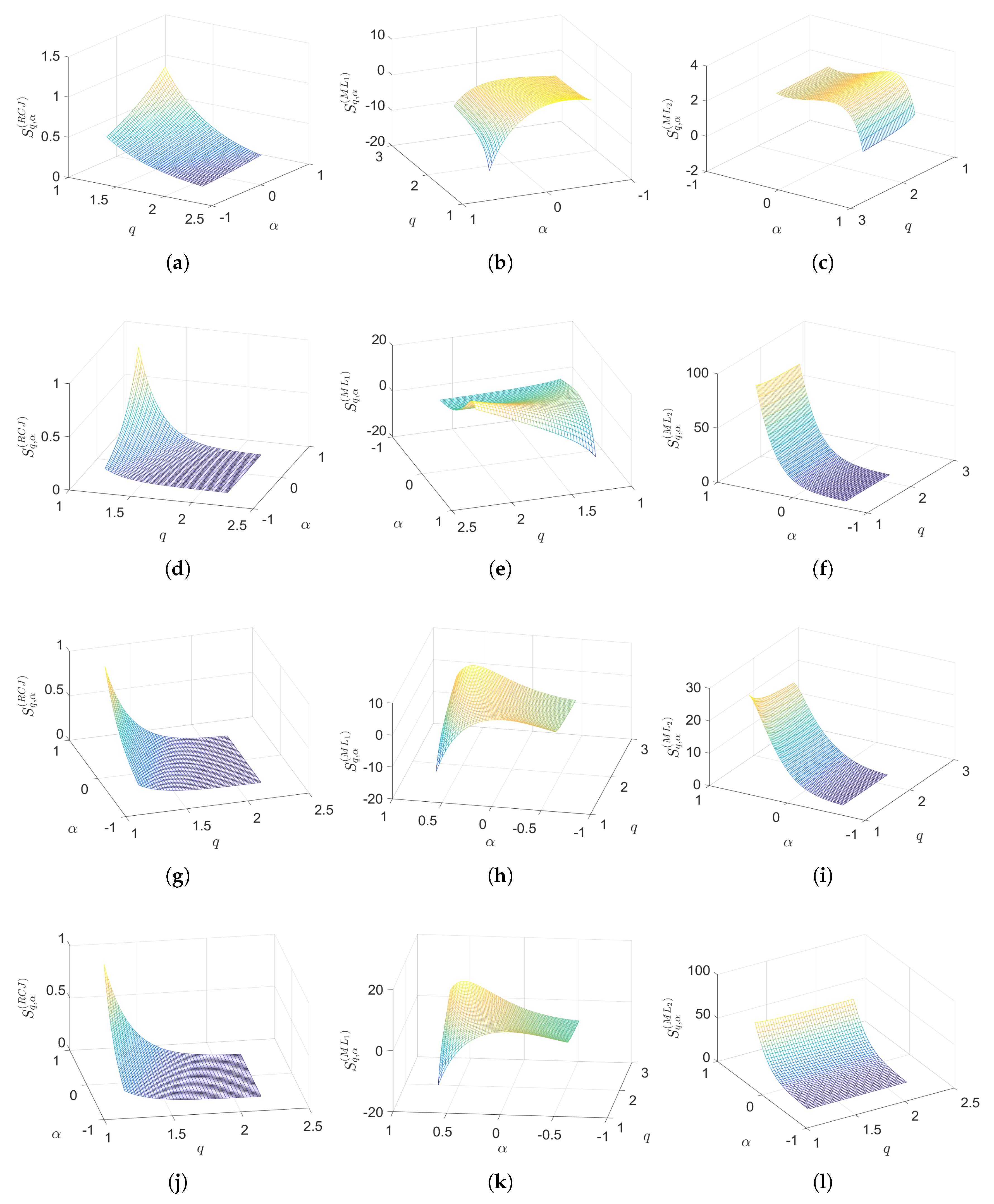
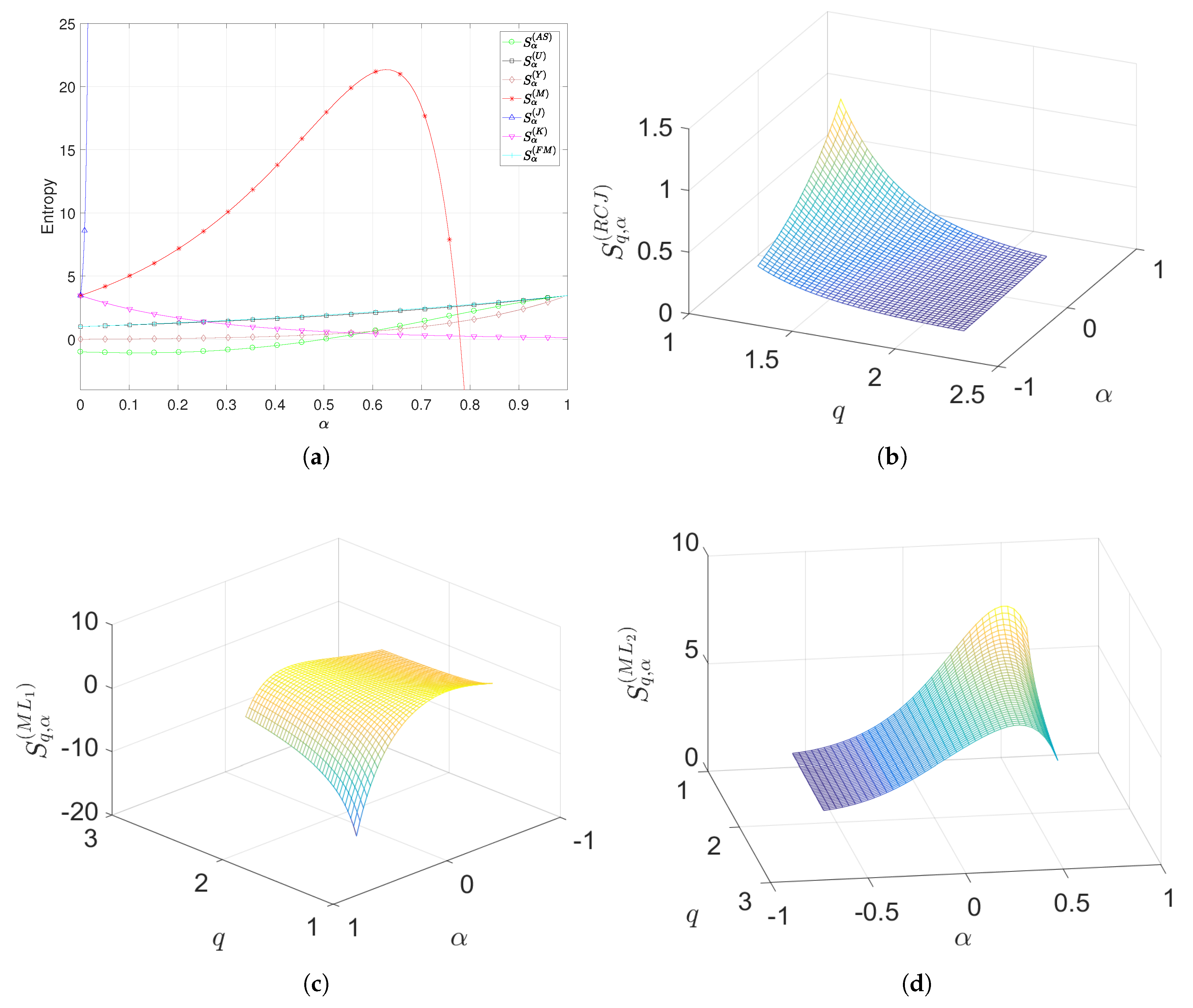
| Distribution | Expression | Parameters | Domain | Order 1-par. Entropy | Order 2-par. Entropy |
|---|---|---|---|---|---|
| Poisson | |||||
| Gaussian | |||||
| Lévy | |||||
| Weibull |
| Entropy | Equation Number | Authors | Reference | N. Citations | Year |
|---|---|---|---|---|---|
| (37) | Akimoto and Suzuki | [67] | 5 | 2001 | |
| (41) | Ubriaco | [69] | 88 | 2009 | |
| (42) | Yu et al. | [70] | 7 | 2012 | |
| (43) | Radhakrishnan et al. | [71] | 3 | 2014 | |
| (46) | Machado | [73] | 79 | 2014 | |
| (47) | Jalab et al. | [75] | 6 | 2019 | |
| (49) | Karcı | [77] | 16 | 2016 | |
| (55) | Ferreira and Machado | [79] | 4 | 2019 | |
| (60) | Machado and Lopes | [80] | 5 | 2019 | |
| (62) | Machado and Lopes | [80] | 5 | 2019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, A.M.; Machado, J.A.T. A Review of Fractional Order Entropies. Entropy 2020, 22, 1374. https://doi.org/10.3390/e22121374
Lopes AM, Machado JAT. A Review of Fractional Order Entropies. Entropy. 2020; 22(12):1374. https://doi.org/10.3390/e22121374
Chicago/Turabian StyleLopes, António M., and José A. Tenreiro Machado. 2020. "A Review of Fractional Order Entropies" Entropy 22, no. 12: 1374. https://doi.org/10.3390/e22121374
APA StyleLopes, A. M., & Machado, J. A. T. (2020). A Review of Fractional Order Entropies. Entropy, 22(12), 1374. https://doi.org/10.3390/e22121374






