A Path-Based Distribution Measure for Network Comparison
Abstract
1. Introduction
2. Methods
2.1. Path Distribution Combined with End Nodes’ Information
2.2. Network Distance between Two Networks
3. Results
3.1. Experiments on Synthetic Networks
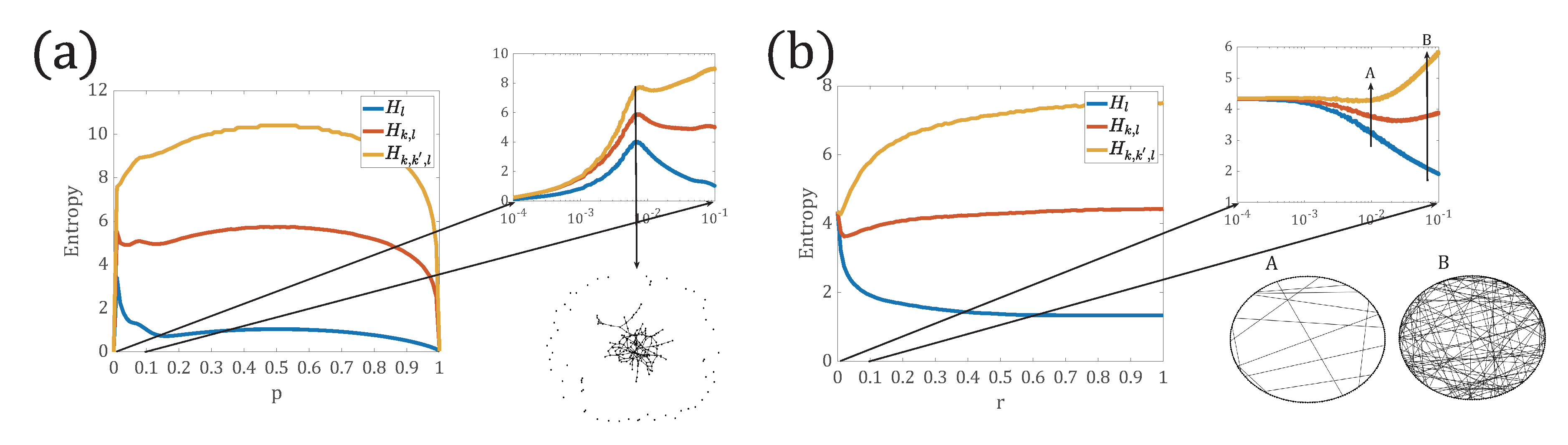
3.1.1. Comparison of Network Entropies Based on Different Path Distributions
3.1.2. Comparison of Network Entropy for Network Models with Different
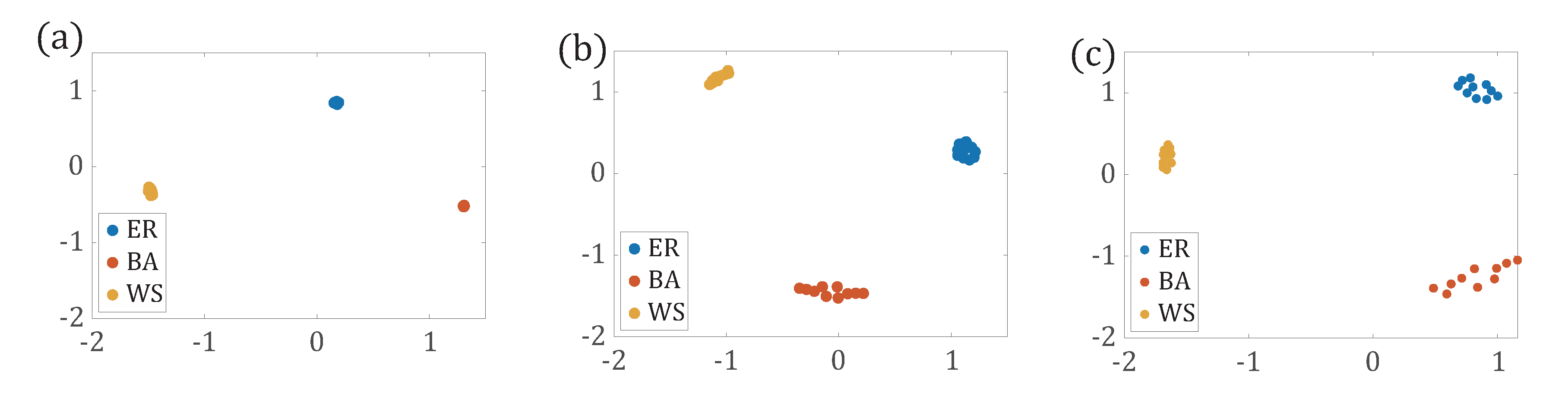
3.1.3. Comparison of Network Distance Based on Different Path Distributions
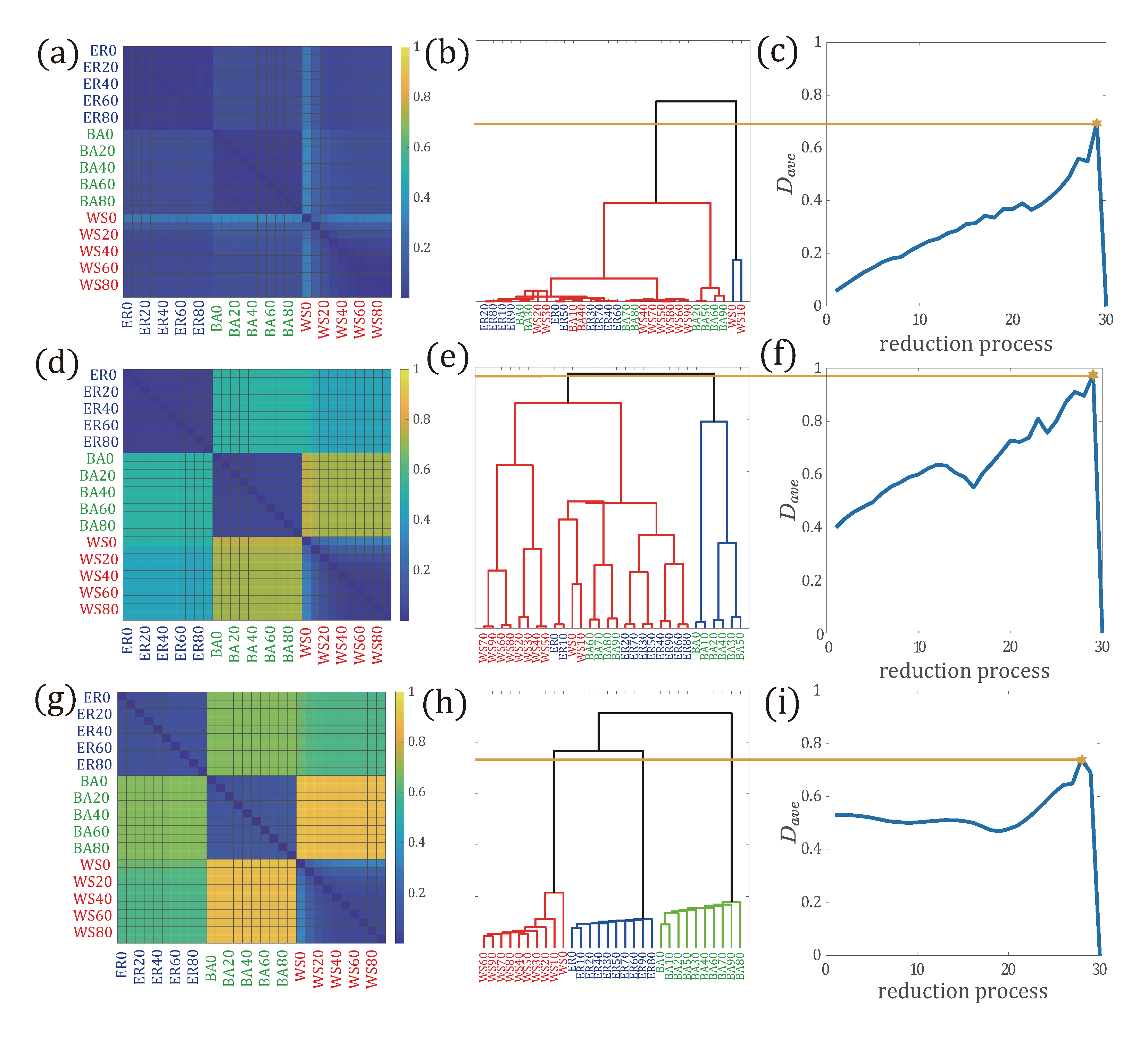
3.2. Application of Network Comparison to Network Reduction in Multilayer Networks
- Step 1:
- Compute the topological distribution, , for each subnetwork . Then compute the distance between each pair of subnetworks and , denoted as and calculated by .
- Step 2:
- Calculate the average distance between all pairs of subnetworks as the objective function, given by,where X is the number of subnetworks. If , let and stop the reduction process.
- Step 3:
- Perform hierarchical clustering of layered networks. Aggregate subnetworks and , whose distance is the minimum, into a new subnetwork . The updated adjacency matrix of the subnetwork , is described as , that is, edges in are the union set of the edges in and .
- Step 4:
- Update the multilayer network G, , that is, removing and from G, and adding to G. Then go to Step 1.
3.2.1. Network Reduction on Synthetic Networks
3.2.2. Network Reduction on Real Data
4. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Mandke, K.; Meier, J.; Brookes, M.J.; O’Dea, R.D.; Van Mieghem, P.; Stam, C.J.; Hillebrand, A.; Tewarie, P. Comparing multilayer brain networks between groups: Introducing graph metrics and recommendations. NeuroImage 2018, 166, 371–384. [Google Scholar] [CrossRef] [PubMed]
- Fraiman, D.; Fraiman, R. An ANOVA approach for statistical comparisons of brain networks. Sci. Rep. 2018, 8, 4746. [Google Scholar] [CrossRef] [PubMed]
- Masuda, N.; Holme, P. Detecting sequences of system states in temporal networks. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef]
- De Domenico, M.; Nicosia, V.; Arenas, A.; Latora, V. Structural reducibility of multilayer networks. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef]
- Van Wijk, B.C.; Stam, C.J.; Daffertshofer, A. Comparing brain networks of different size and connectivity density using graph theory. PLoS ONE 2010, 5, e13701. [Google Scholar] [CrossRef]
- Donnat, C.; Holmes, S. Tracking network dynamics: A survey using graph distances. Ann. Appl. Stat. 2018, 12, 971–1012. [Google Scholar] [CrossRef]
- Levandowsky, M.; Winter, D. Distance between Sets. Nat. Phys. Ence 1972, 235, 60. [Google Scholar] [CrossRef]
- Sanfeliu, A.; Fu, K.S. A distance measure between attributed relational graphs for pattern recognition. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 353–362. [Google Scholar] [CrossRef]
- Wallis, W.D.; Shoubridge, P.; Kraetz, M.; Ray, D. Graph distances using graph union. Pattern Recognit. Lett. 2001, 22, 701–704. [Google Scholar] [CrossRef]
- Gao, X.; Xiao, B.; Tao, D.; Li, X. A survey of graph edit distance. Pattern Anal. Appl. 2010, 13, 113–129. [Google Scholar] [CrossRef]
- Jurman, G.; Visintainer, R.; Riccadonna, S.; Filosi, M.; Furlanello, C. The HIM glocal metric and kernel for network comparison and classification. In Proceedings of the 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Paris, France, 19–21 October 2015; pp. 1–10. [Google Scholar]
- Banerjee, A.; Jost, J. Spectral plot properties: Towards a qualitative classification of networks. Netw. Heterog. Media 2017, 3, 395–411. [Google Scholar] [CrossRef]
- Cai, H.Y.; Zheng, V.W.; Chang, C.C. A Comprehensive Survey of Graph Embedding: Problems, Techniques, and Applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef]
- Shrivastava, A.; Li, P. A new space for comparing graphs. In Proceedings of the 2014 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Beijing, China, 17–20 August 2014; pp. 62–71. [Google Scholar]
- Carpi, L.C.; Schieber, T.A.; Pardalos, P.M.; Marfany, G.; Masoller, C.; Díaz-Guilera, A.; Ravetti, M.G. Assessing diversity in multiplex networks. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Schieber, T.A.; Carpi, L.; Díaz-Guilera, A.; Pardalos, P.M.; Masoller, C.; Ravetti, M.G. Quantification of network structural dissimilarities. Nat. Commun. 2017, 8, 1–10. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J. A layer reduction based community detection algorithm on multiplex networks. Phys. A Stat. Mech. Its Appl. 2017, 471, 244–252. [Google Scholar] [CrossRef]
- Bagrow, J.P.; Bollt, E.M. An information-theoretic, all-scales approach to comparing networks. Appl. Netw. Sci. 2019, 4, 45. [Google Scholar] [CrossRef]
- Stella, M.; De Domenico, M. Distance entropy cartography characterises centrality in complex networks. Entropy 2018, 20, 268. [Google Scholar] [CrossRef]
- Chen, Z.; Dehmer, M.; Shi, Y. A Note on Distance-based Graph Entropies. Entropy 2014, 16, 5416–5427. [Google Scholar] [CrossRef]
- Zenil, H.; Kiani, N.A.; Tegner, J. A Review of Graph and Network Complexity from an Algorithmic Information Perspective. Entropy 2018, 20, 551. [Google Scholar] [CrossRef]
- Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 1972, 2, 113–120. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Meghanathan, N. Correlation Coefficient Analysis of Centrality Metrics for Complex Network Graphs. In Proceedings of the 4th Computer Science On-line Conference: Intelligent Systems in Cybernetics and Automation Theory (CSOC 2015), Zlin, Czech Republic, 27–30 April 2015; pp. 11–20. [Google Scholar] [CrossRef]
- Dehmer, M.; Mowshowitz, A. A history of graph entropy measures. Inf. Sci. 2011, 181, 57–78. [Google Scholar] [CrossRef]
- Demetrius, L.; Manke, T. Robustness and network evolution—An entropic principle. Phys. A Stat. Mech. Its Appl. 2005, 346, 682–696. [Google Scholar] [CrossRef]
- Endres, D.; Schindelin, J. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On random graphs. I. Publ. Math. 1959, 4, 3286–3291. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ’small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabasi, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Kiers, H. Modern multidimensional scaling: Theory and applications. Psychometrika 1999, 64, 683. [Google Scholar]
- Santoro, A.; Nicosia, V. Algorithmic Complexity of Multiplex Networks. Phys. Rev. X 2020, 10, 021069. [Google Scholar] [CrossRef]
- Kivela, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]




| G | |||||
|---|---|---|---|---|---|
| 2.763 | 2.764 | 2.785 | 2.832 | 2.710 | |
| 4.221 | 4.254 | 4.247 | 4.281 | 3.994 | |
| 5.025 | 5.199 | 5.166 | 5.175 | 4.487 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Sun, Z.; Han, Y. A Path-Based Distribution Measure for Network Comparison. Entropy 2020, 22, 1287. https://doi.org/10.3390/e22111287
Wang B, Sun Z, Han Y. A Path-Based Distribution Measure for Network Comparison. Entropy. 2020; 22(11):1287. https://doi.org/10.3390/e22111287
Chicago/Turabian StyleWang, Bing, Zhiwen Sun, and Yuexing Han. 2020. "A Path-Based Distribution Measure for Network Comparison" Entropy 22, no. 11: 1287. https://doi.org/10.3390/e22111287
APA StyleWang, B., Sun, Z., & Han, Y. (2020). A Path-Based Distribution Measure for Network Comparison. Entropy, 22(11), 1287. https://doi.org/10.3390/e22111287






