1. Introduction
Stochastic processes are common in nature or laboratories, and play a major role across traditional disciplinary boundaries (e.g., see [
1,
2]). These stochastic processes often exhibit complex temporal behaviour and even the emergence of order (self-organization). The latter can also be artificially designed to complete an orderly task (guided self-organization) [
3,
4,
5,
6]. In order to study and compare the dynamics of different stochastic processes and self-organization, it is valuable to utilize a measurement which is independent of any specifics of a system [
7,
8,
9,
10,
11] (e.g., physical variables, units, dimensions, etc.). This can be achieved by using information theory based on probability density functions (PDFs) and working in terms of information content or information change, e.g., by quantifying the statistical difference between two states [
12,
13,
14]. Mathematically, we do this by assigning a metric to probability and by using the notion of ‘length’ or ‘distance’ in the statistical space.
One method of measuring the information content in a system is utilizing the Fisher information, which represents the degree of certainty, or order. The opposite is entropy, which is a popular concept for the uncertainty or amount of disorder. Comparing entropy at different times then gives a measure of the difference in information content between the two states, which is known as relative entropy (e.g., see [
15]). Another example is the Wasserstein metric [
16,
17], which provides an exact solution to the Fokker-Planck equation for a gradient flow subject to the minimization of the energy functional defined as the sum of the entropy and potential energy [
18,
19,
20]. This metric has units of a physical length in comparison with other metrics, for instance the dimensionless statistical distance based on the Fisher information metric [
21,
22,
23]. Interestingly, there is a link between the Fisher information and the Wasserstein distance [
24]. Furthermore, the relative entropy can be expressed by the integral of the Fisher information along the same path [
25].
Although quite useful, the relative entropy lacks the locality of a metric as it concerns only about the difference between given two PDFs. For instance, when these two PDFs represent the two states at different times, the relative entropy between them tells us nothing about how one PDF evolves to the other PDF over time or what intermediate states a system passes through between the two PDFs. As a result, it can only inform us of the changes that affect the overall system evolution [
26]. To overcome this limitation, the information length
was proposed in recent works, which quantifies the total number of different states that the system evolves through in time [
27,
28]. This means that the information length is a measure that depends on the evolution path between two states (PDFs). Its formulation allows us to measure local changes in the evolution of the system as well as providing an intriguing link between stochastic processes and geometry [
26].
For instance, the relation between the information length
and the mean value of the initial PDF for the fixed values of all other parameters was invoked as a new way of mapping out an attractor structure in a relaxation problem where any initial PDF relaxes into its equilibrium PDF in the long time limit. Specifically, for the Ornstein-Uhlenbeck (O-U) process driven by a Gaussian white-noise (which is a linearly damped, relaxation problem),
increases linearly with the distance between the mean position of an initial PDF and the stable equilibrium point for further details, see [
28,
29], with its minimum value zero at the stable equilibrium point. This linear dependence manifests that the information length preserves the linear geometry of the underlying Gaussian process, which is lost in other metrics [
26]. For a nonlinear stochastic process with nonlinear damping,
still takes its minimum value at the stable equilibrium point but exhibits a power-law dependence on the distance between the mean value of an initial PDF and the stable equilibrium point. In contrast, for a chaotic attractor,
changes abruptly under an infinitesimal change of the mean value of an initial PDF, reminiscent of the sensitive dependence on initial conditions of the Lyapunov exponent [
30]. These results suggest that
elucidates how different (non)linear forces affect (information) geometry.
With the above background in mind, this paper aims to extend the analysis of the information length of the O-U process to an arbitrary n-th order linear autonomous stochastic processes, providing a basic theoretical framework to be utilized in a large set of problems in both engineering and physics. In particular, we provide a useful analytical result that defines the information diagnostics as a function of the covariance matrix and the mean vector of the system, which enormously reduces the computational cost of numerical simulations of high-order systems.
This is followed by a specific application to a harmonically bound particle system (Kramers equation) for the position x and velocity , with the natural oscillation frequency , subject to a damping constant and a Gaussian white-noise (short-correlated). We find an exact time-dependent joint PDF starting from an initial Gaussian PDF which has a finite-width. Note that as far as we are aware of, our result is original since in literature, the calculation was done only for the case of a delta-function initial PDF. Since this process is governed by the two variables, x and v, we investigate how depends on their initial mean values and . Here, the angular brackets denote the average. Furthermore, the two characteristic time scales associated with and raise the interesting question as to their role in . Thus, we explore how the information length depends on and . Our principle results are as follows: (i) tends to increase linearly with either the deviation of initial mean position or the initial mean velocity from their equilibrium values ; (ii) a linear geometry is thus preserved for our linearly coupled stochastic processes driven by a Gaussian noise; (iii) tends to take its minimum value near the critical damping for the same initial conditions and other parameters.
The remainder of this paper is organized as follows:
Section 2 presents the basic concept of information length and the formulation of our problem. In
Section 3, our main theoretical results are provided (see also
Appendix A). In
Section 4, we apply the results in
Section 3 to analyze a harmonically bound particle system with the natural oscillation frequency
subject to a damping constant
and a Gaussian white-noise. Finally,
Section 5 contains our concluding remarks.
To help readers, we here provide a summary of our notations: and are the sets of real and complex numbers, respectively. represents a column vector of real numbers of dimension n, represents a real matrix of dimension , corresponds to the trace of the matrix , and are the transpose and inverse of matrix , respectively. (Bold-face letters are used to represent vectors and matrices.) In some places, or the prime both are used for the partial derivative with respect to time. Besides, and for , corresponds to the inverse Laplace transform of the complex function . Finally, the average of a random vector is denoted by .
3. General Analytical Results
In the section, we provide the analytical results for Problem 2.1, summarizing the main steps required to calculate information length (
4). To this end, we assume that an initial PDF is Gaussian and then take the advantage of the fact that a linear process driven by a Gaussian noise with an initial Gaussian PDF is always Gaussian. The joint PDF for (
2) and (
3) is thus Gaussian, whose form is provided below.
Proposition 1 (Joint probability).
The system (2) and (3) for a Gaussian random variable at any time t has the following joint PDF whereand is the matrix of elements . Here, is the mean value of while Σ
is the covariance matrix. Proof. For a Gaussian PDF of
, all we need to calculate are the mean and covariance of
and substitute them in the general expression for multi-variable Gaussian distribution (
5). To this end, we first write down the solution of Equation (
2) as follows
By taking the average of Equation (
8), we find the mean value of
of (
8) as follows
which is Equation (
6). On the other hand, to find covariance
, we let
, and use the property
to find
Here
is the initial fluctuation at
. Equation (
10) thus proves Equation (7). Substitution of Equations (
6) and (7) in Equation (
5) thus gives us a joint PDF
☐
Next, in order to calculate the information length from the joint PDF
in Equation (
5), we now use the following Theorem:
Theorem 1 (Information Length).
The information length of the joint PDF of system (2) and (3) is given by the following integral where (recall, a prime denotes ). Proof. To prove this theorem, we use the PDF (
5) in (
4). To simplify the expression, we let
We then compute step by step
as follows:
Now, using Equation (
12) in Equation (
14), we compute the integral
as follows
To calculate the three averages in (
15), we use the properties
[
32],
and
. We then have
We recall that
and
denote the first and second derivative over time of the elements
and
. By substituting (
17) in (
16) and making some arrangements, we obtain
Now with the help of the following relations
[
33],
[
34], and
, we then have
Equation (
19) thus proves Equation (
11). ☐
Given important properties of the covariance matrix eigenvalues (see, e.g., [
35]), it is useful to express Equation (
19) and the information length as a function of these covariance matrix eigenvalues. This is done in the following Corollary.
Corollary 1. Let ’s () be the eigenvalues of the covariance matrix Σ,
and where is an orthonormal matrix whose column vectors are linearly independent eigenvectors of . We can rewrite the information length (11) as Proof. The proof follows straightforwardly from the fact that
is a symmetric matrix which can be diagonalised by finding the orthonormal matrix
such that
. Here
is the diagonal matrix whose entries are the eigenvalues
(recall that
is
i-th the eigenvalue of
). This gives us
This finishes the proof. ☐
It is useful to check that Equation (
20) reproduces the previous result for the O-U process [
36]
where
is the inverse temperature. Here,
denotes the time derivative of
. To show this, we note that for the O-U process, the covariance matrix is a scalar (
) with the value
and thus
while
. Thus,
In sum, for the O-U process, the square of the information velocity (shown in expression (
22)) increases with the ‘roughness’ of the process, as quantified by the squared ratio of the rate of change of the inverse temperature (or precision) and the precision – plus a term that depends upon this precision times the variance of the state velocity.
4. Kramers Equation
In this section we apply our results in
Section 3 to the Kramers equation for a harmonically bound particle [
19,
37]. As noted in Introduction, we investigate the behaviour of the information length when varying various parameters and initial conditions to elucidate how the information geometry is affected by the damping, oscillations, strength of the stochastic noises and initial mean values.
Consider the Kramers equation
Here,
is a natural frequency and
is the damping constant, both positive real numbers.
is a Gaussian white-noise acting on
v with the zero mean value
, with the statistical property
Comparing Equations (
23) and (
24) with Equations (
2) and (
3), we note that
,
,
,
,
,
, and
while the matrix
for (
23) has the element
. Thus, the eigenvalues of
are
.
To find the information length for the system (
23), we use Proposition 1 and Theorem 1. First, Proposition 1 requires the computation of the exponential matrix
involving a rather long algebra with the help of [
38]. The result is:
Here,
is the identity matrix. Similarly, we can show
Using Equations (
25) and (
26) in Equations (
6) and (7), we have the time-dependent (joint) PDF (
5) at any time
t for our system (
23) and (
24). To calculate Equation (
11) with the help of Equations (
25) and (
26), we perform numerical simulations (integrations) for various parameters in Equations (
23) and (
24) as well as initial conditions. Note that while we have simulated many different cases, for illustration, we show some representative cases by varying
D,
,
and
,
in
Section 4.1,
Section 4.2 and
Section 4.3 and
Appendix A, respectively, for the same initial covariance matrix
with elements
and
. Note that the initial marginal distributions of
and
are Gaussian with the same variance
. Results in the limit
are presented in
Section 4.4.
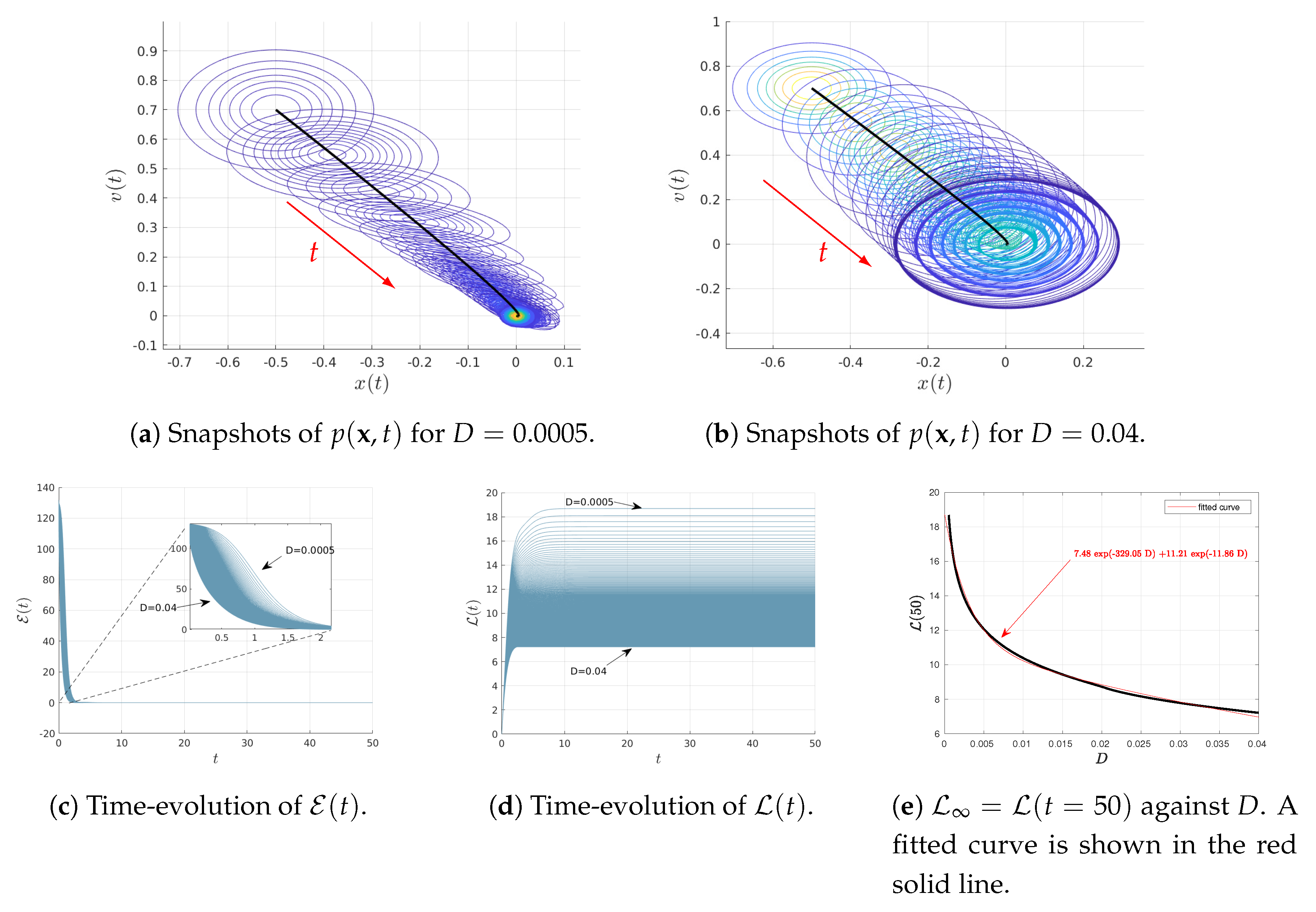
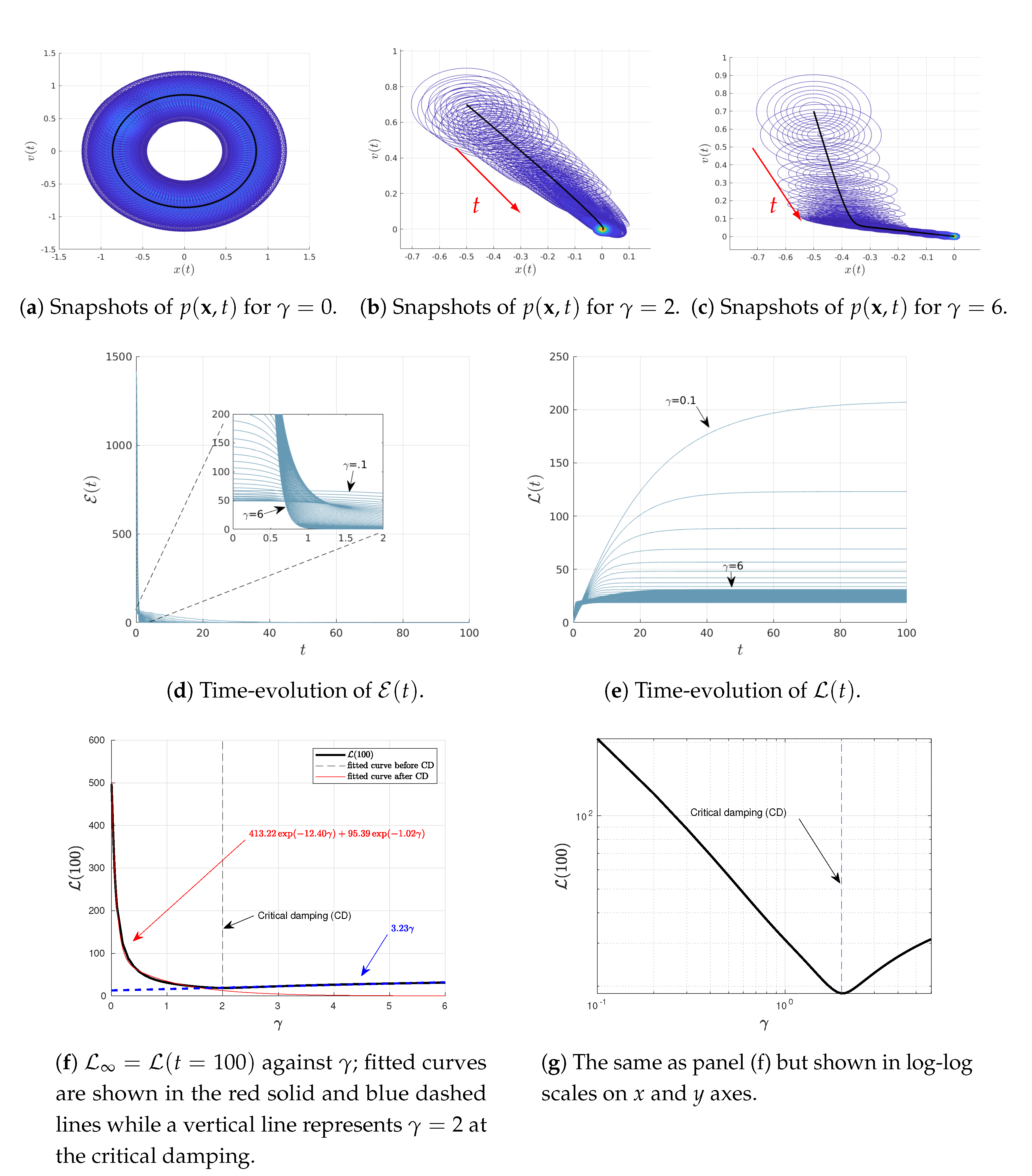
4.1. Varying D
Figure 1 shows the results when varying
D as
for the fixed parameters
and
. The initial joint PDFs are Gaussian with the fixed mean values
,
; as noted above, the covariance matrix
with elements
and
. Consequently, at
, the marginal distributions of
and
are Gaussian PDFs with the same variance
and the mean values
and
, respectively.
Figure 1a,b show the snapshots of time-dependent joint PDF
(in contour plots) for the two different values of
and
, respectively. The black solid represents the phase portrait of the mean value of
and
while the red arrows display the direction of time increase. Note that in
Figure 1b, only some of the initial snapshots of the PDFs are shown for clarity, given the great amount of overlapping between different PDFs.
Figure 1c,d show the time-evolution of the information velocity
and information length
, respectively, for different values of
. It can be seen that the system approaches a stationary (equilibrium) state for
for all values of
D,
approaching constant values (recall
does not change in a stationary state). Therefore, we approximate the total information length as
, for instance. Finally, the total information length
is shown in
Figure 1e. We determine the dependence of
on
D by fitting an exponential function as
(shown in red solid line).
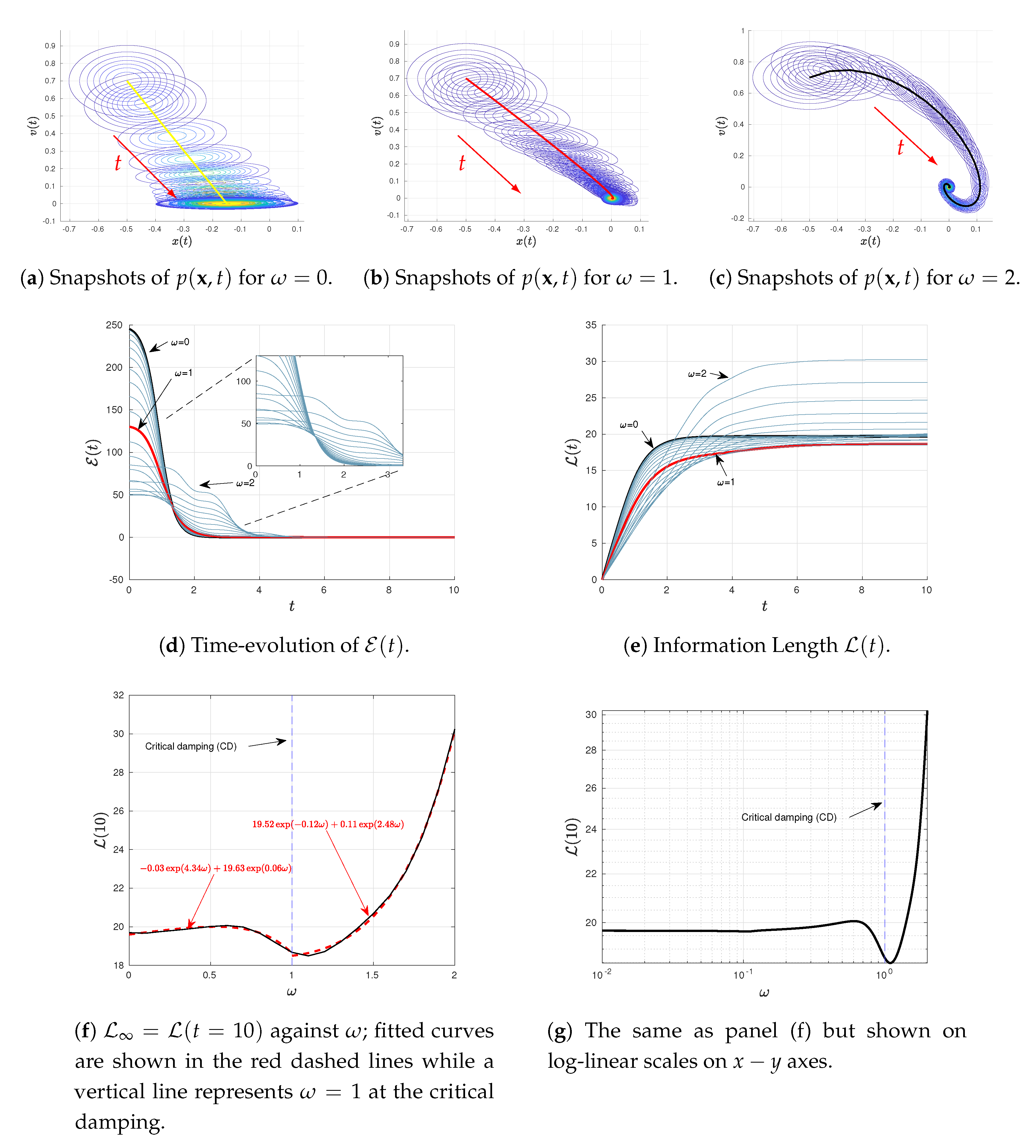
4.2. Varying or
We now explore how results depend on the two parameters
and
, associated with oscillation and damping, respectively. To this end, we use
and the same initial conditions as in
Figure 1 but vary
and
in
Figure 2 and
Figure 3, respectively. Specifically, in different panels of these figures, we show the snapshots of the joint PDF
, the time-evolutions of
and
for different values of
and
, and
against either
or
. From
Figure 2e and
Figure 3e, we can see that the system is in a stationary state for sufficiently large
and
, respectively. Thus, we use
in
Figure 2f,g and
in
Figure 3f,g.
Notably,
Figure 2f,g (shown on linear-linear and log-linear scales on
axes, respectively) exhibit an interesting a non-monotonic dependence of
on
for the fixed
, with the presence of a distinct minimum in
at certain
. Similarly,
Figure 3f,g (shown in linear-linear and log-log scales on
axes, respectively) also shows a non-monotonic dependence of
on
for the fixed
. These non-monotonic dependences are more clearly seen in
Figure 2g and
Figure 3g. A close inspection of these figures then reveals that the minimum value of
occurs close to the critical damping (CD)
; specifically, this happens at
for
in
Figure 2f,g while at
for
in
Figure 3f,g. We thus fit
against
or
depending on whether
or
is smaller/larger than its critical value as follows:
The fitted curves in Equations (
27)–(
30) are superimposed in
Figure 2f and
Figure 3f, respectively. It is important to notice from Equations (
27)–(
30) that
tends to increase as either
for a finite, fixed
(
) or
for a finite, fixed
(
).
Finally, we note that for the critical damping
, the eigenvalue becomes a real double root with the value
. Thus, in this limit, we have that
and
is composed by the following elements
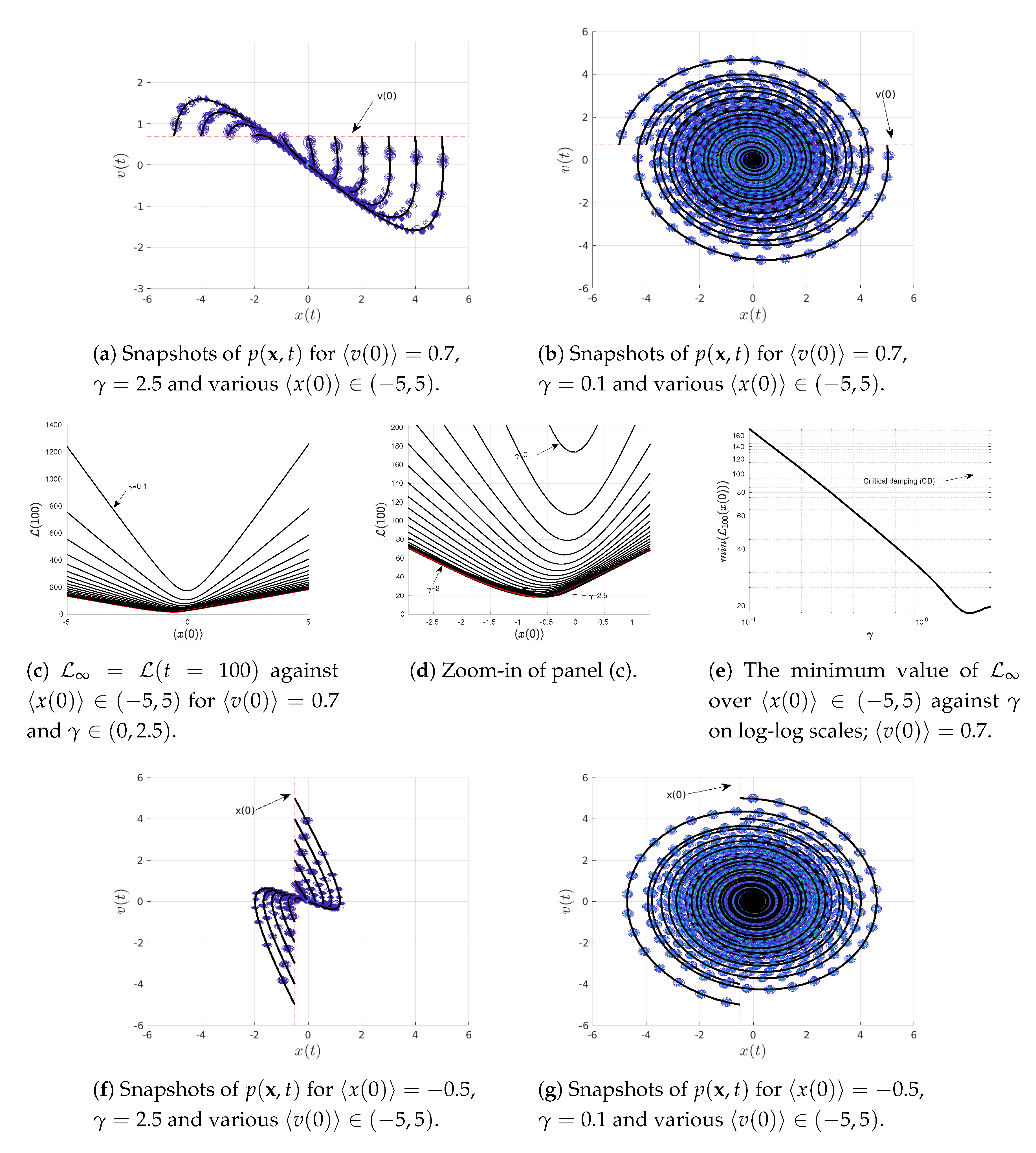
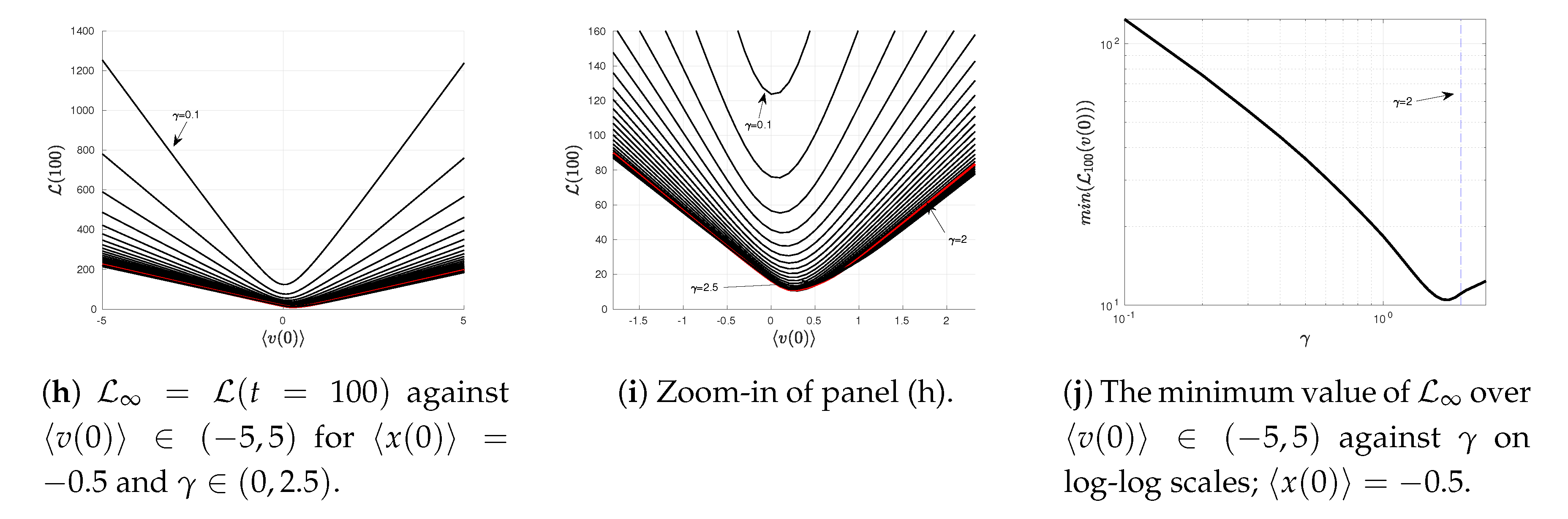
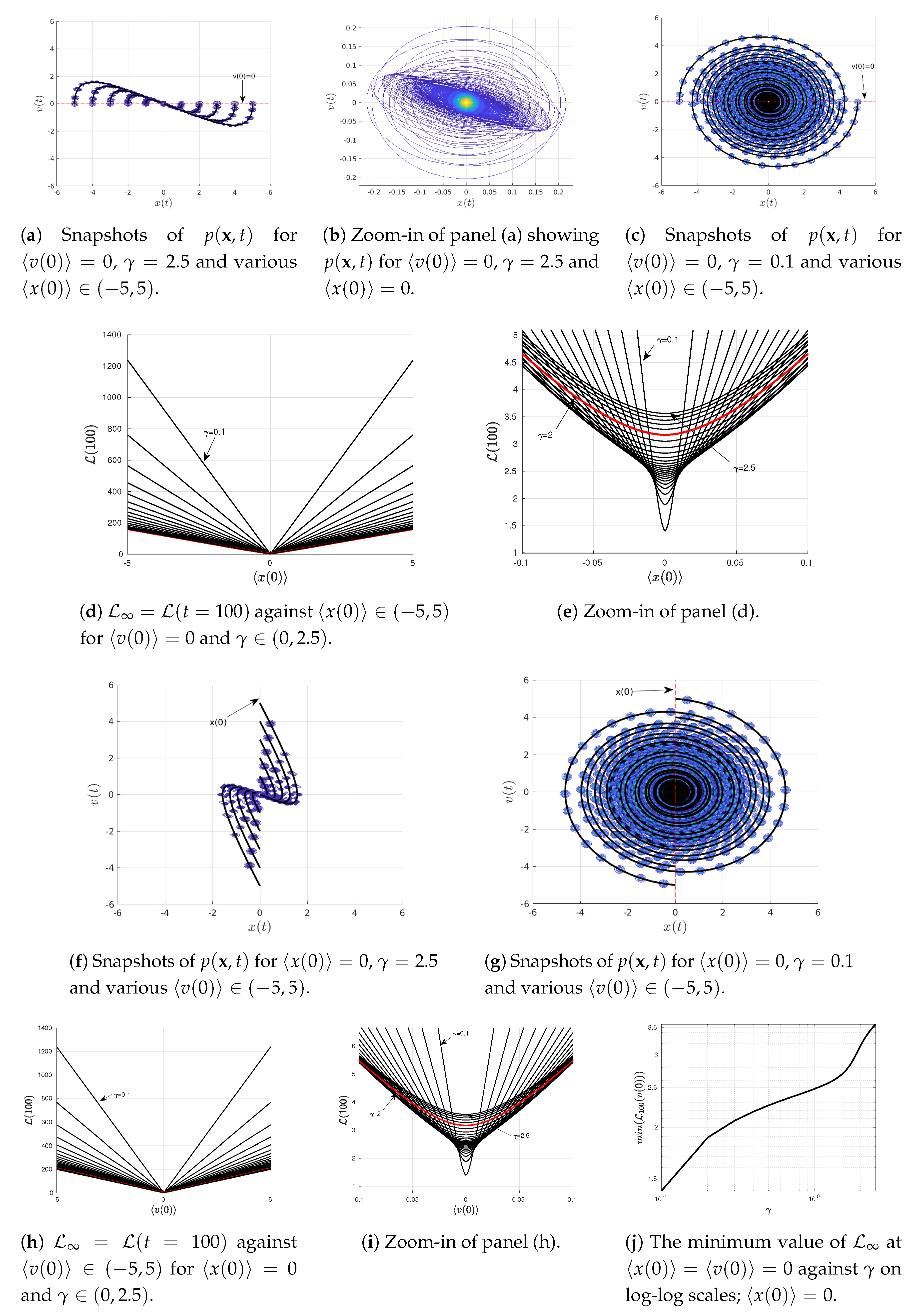
4.3. Varying or
To elucidate the information geometry associated with the Kramer equation (Equations (
23) and (
24)), we now investigate how
behaves near the equilibrium point
. To this end, we scan over
for
in
Figure 4a–e while scanning over
for
in
Figure 4f–i. For our illustrations in
Figure 4, we use the same initial covariance matrix
as in
Figure 1,
Figure 2 and
Figure 3,
and
and a few different values of
(above/below/at the critical value
). We note that the information geometry near a non-equilibrium point is studied in
Appendix A.
Specifically, snapshots of
are shown in
Figure 4a–f for
(above its critical value
) while those in
Figure 4c–g are for
below the critical value 2. By approximating
, we then show how
depends on
and
for different values of
in
Figure 4d,e and
Figure 4h,i, respectively.
Figure 4d,e show the presence of a minimum in
at the equilibrium
(recall
);
is a linear function of
for
, which can be described as
. Here,
and
are constant functions depending on
for a fixed
which represent the slope and the
y-axis intercept, respectively. A non-zero value of
at
is caused by the adjustment (oscillation and damping) of the width of the PDFs in time due to the disparity between the width of the initial and equilibrium PDFs (see
Figure 4b). In other words, even though the mean values remain in equilibrium for all time
, the information length (
11) depends on the covariance matrix
which changes from its initial value to the final equilibrium value as follows
On the other hand,
against
shows parabolic behaviour for small
in
Figure 4e. This is caused by the finite width
of the initial
; we see that
is within the uncertainty of the initial
.
Similarly,
Figure 4h,i exhibit a minimum in
at the equilibrium
(recall
in this case);
is a linear function of
for
described by
(again parabolic for
, see
Figure 4i). Here again,
and
are constant functions depending on
for a fixed
which represent the slope and the
y-axis intercept, respectively.
Finally,
Figure 4j shows in logarithmic scale that the minimum value of
at
monotonically increases with
.
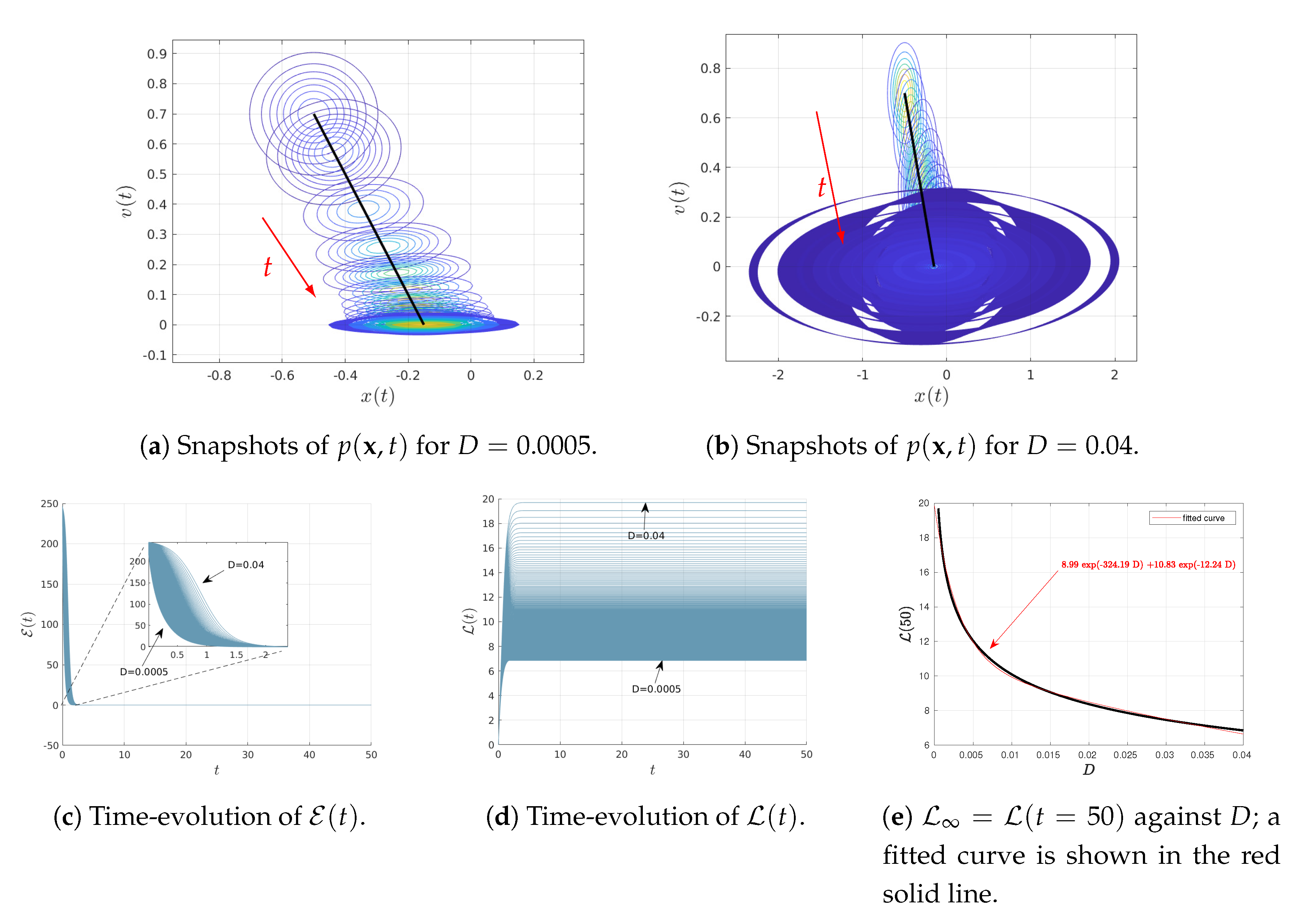
4.4. The Limit Where
When the natural frequency
(i.e., damped-driven system like the O-U process [
36]) in Equation (
23), the two eigenvalues of the matrix
become
and
. It then easily follows that
and
is composed by the elements
To investigate the case of
, we consider the scan over
for the same parameter value
, and the initial conditions as in
Figure 1, apart from using
instead of
.
Figure 5 presents the results – snapshots of
, time evolutions of
,
, and
against
D in
Figure 5a–e. In particular, in
Figure 5e, we identify the dependence of
on
D by fitting the results to the curve
.