Quantum Work Statistics with Initial Coherence
Abstract
1. Introduction
2. Background
2.1. Quantum Work Statistics
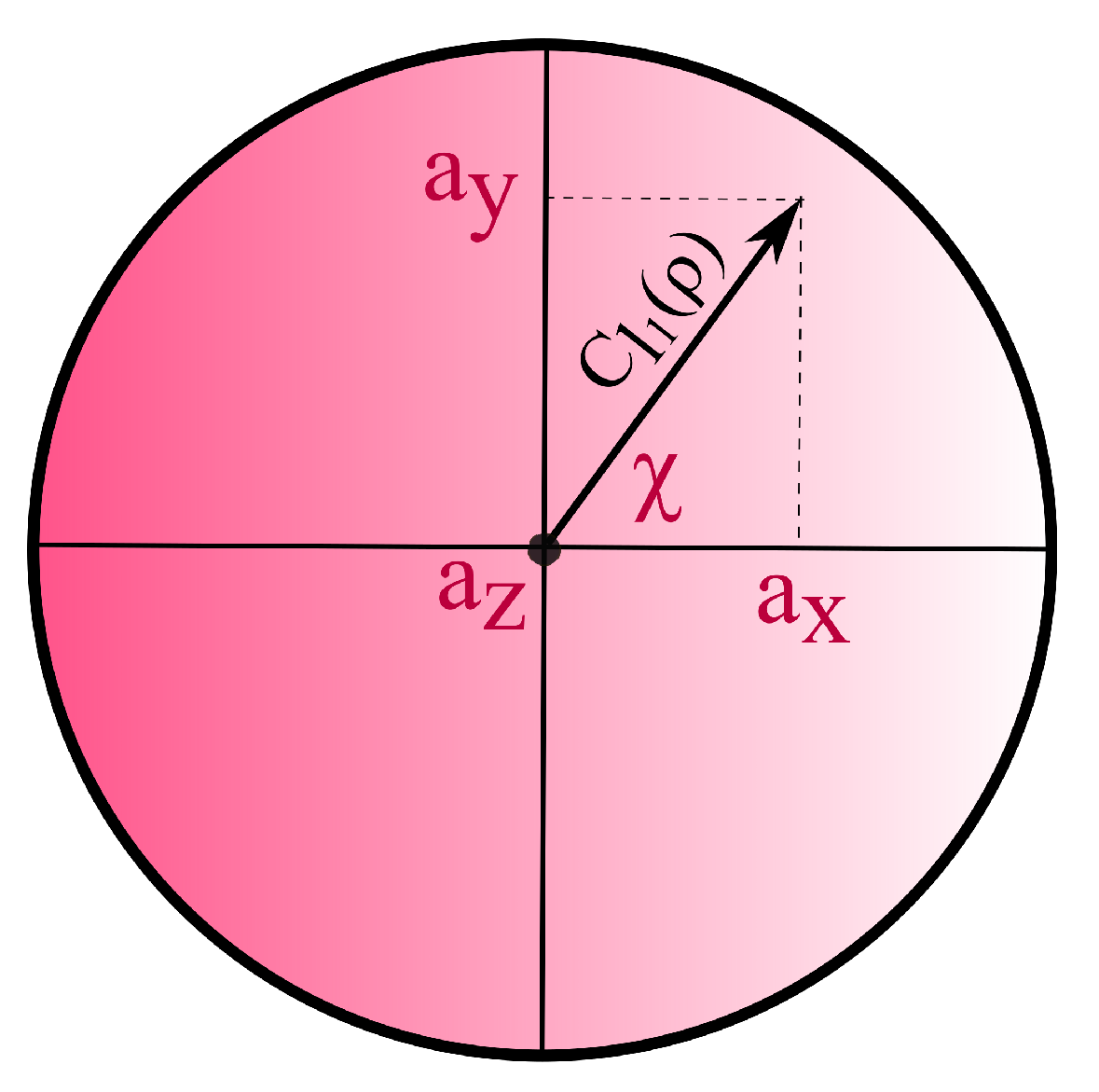
2.2. Coherence Theory
3. Main Results
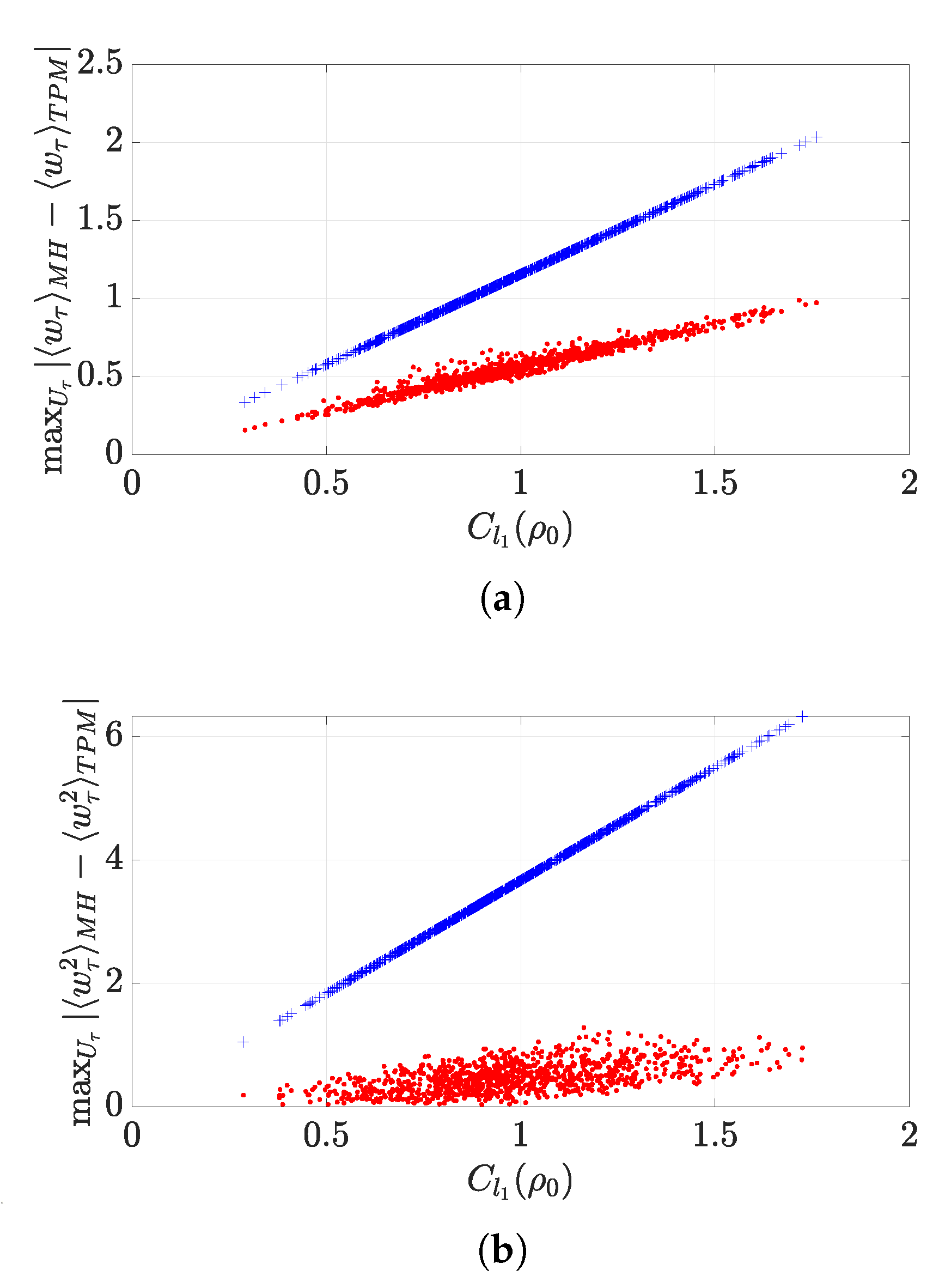
3.1. Distance between the Averages of Work
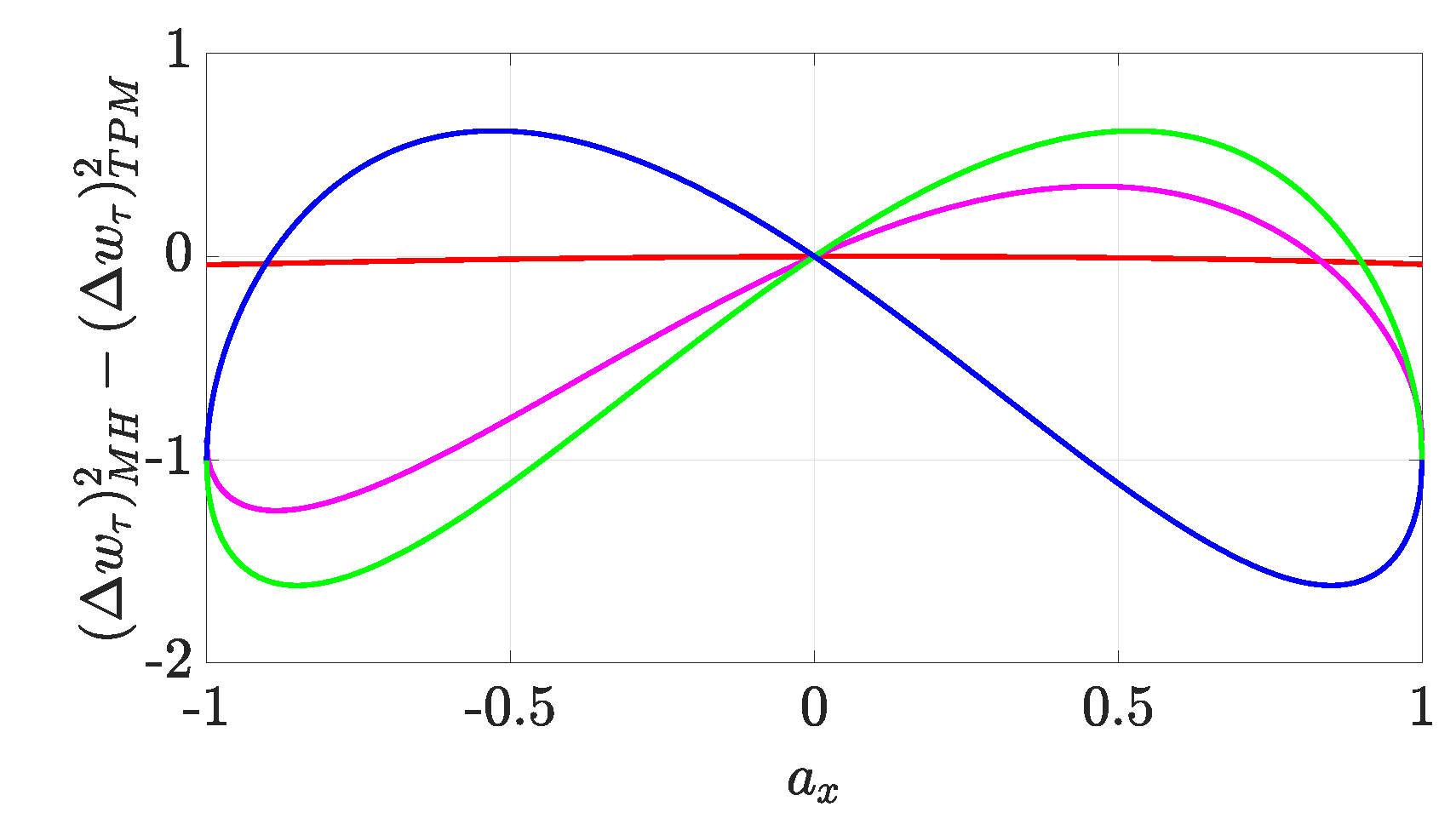
3.2. Distance between the Variances of Work
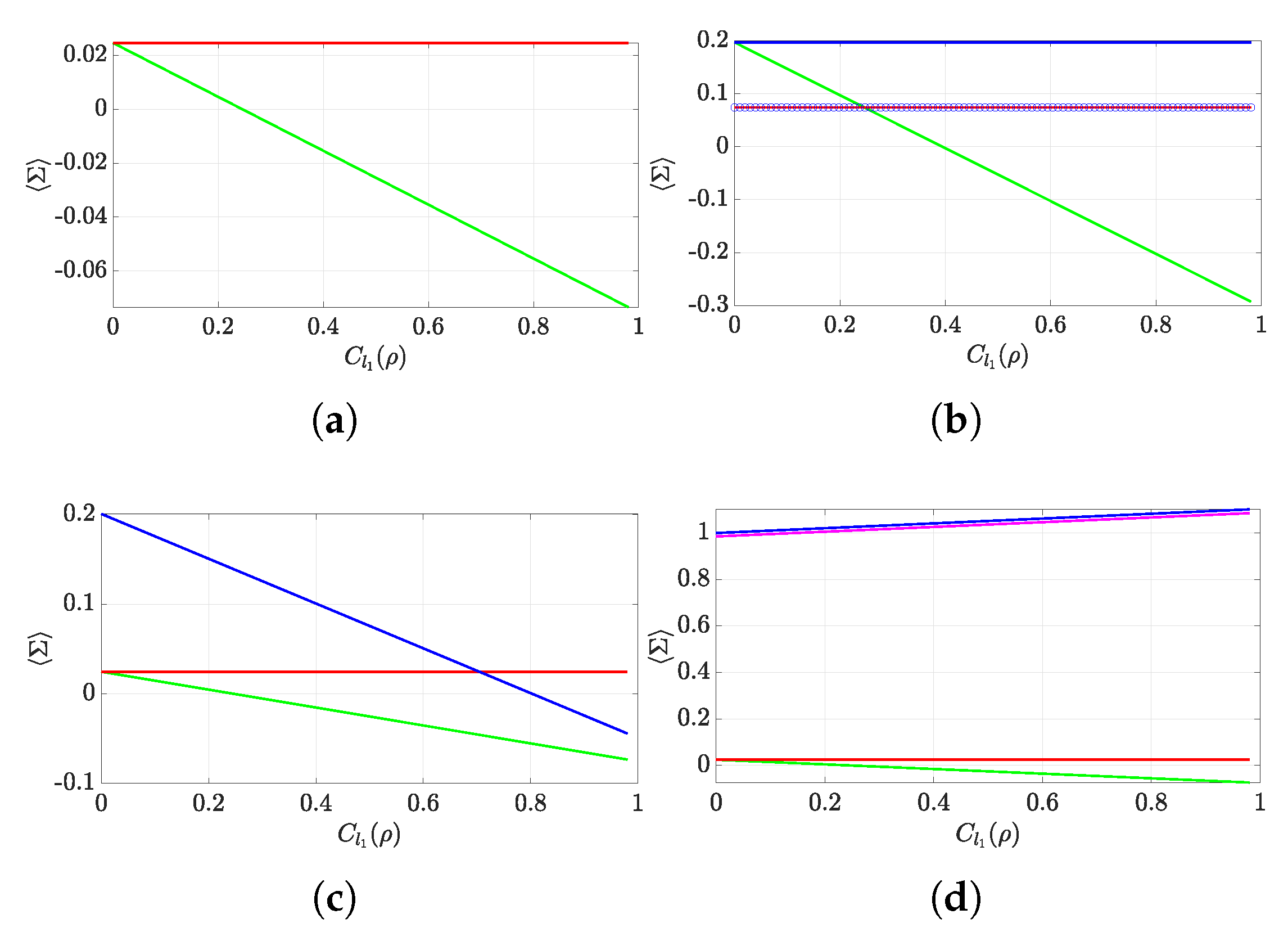
3.3. Study of the Entropy Production
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 1
- Equation (8): The parameterisation of qudit states and unitaries makes finding an exact expression for the absolute difference between average works a difficult task to tackle. However, one can still find an upper bound to such difference as follows:where we have used the triangle inequality and the fact that the coherence of the pure state can never be larger than to achieve the final upper bound.
Appendix B. Proof of Theorem 2
- Equation (10): By using the triangle inequality, the definition of given above and the fact that , we can also provide the following upper bound
- When focusing on qubits, we have
Appendix C. Derivation of Table 1
Appendix D. Proof of Theorem 3
- Equation (17): The Jarzynski equality [42] is only fulfilled when the initial state is at equilibrium. For an arbitrary initial state , the following fluctuation Theorem applies [21]where is a Gibbs state and . From here, we get that the free energy difference in the MH scheme is given byWe use this result in the definition of entropy production and use a cumulant expansion of to find [44]where are the cumulants of the MH work distribution. Note that we do not take the average of , as it does not contain any stochastic variable .In the linear response regime, the first term yields [44], where is the variance of the MH distribution of work. Expanding the second term givesThus, the average entropy production in the linear response regime amounts to
- Equation (18): Let us now have a close look at qubits. For convenience, we consider a qubit prepared in the state , with , and . This ensures that, for small enough , will also be small:Let us suppose the qubit is subjected to a real unitary transformation such that , for . The average entropy production in the linear response regime is then given by Equation (17)where we have used that, for small , . As shown in [44], the TPM average entropy production in the linear response regime, where the initial state is set to be in equilibrium, is given by . Let us compute it for our qubit evolutionwhere we have neglected the terms in . Therefore,
Appendix E. Proof of Corollary 2
Appendix F. Why Can 〈Στ〉MH Be Negative?
References
- Thermodynamics in the Quantum Regime; Binder, F., Correa, L., Gogolin, C., Anders, J., Adesso, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Deffner, S.; Campbell, S. Quantum Thermodynamics: An Introduction to the Thermodynamics of Quantum Information; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019. [Google Scholar]
- Santos, J.P.; Céleri, L.C.; Landi, G.T.; Paternostro, M. The role of quantum coherence in non-equilibrium entropy production. NPJ Quant. Inf. 2019, 5, 23. [Google Scholar] [CrossRef]
- Francica, G.; Goold, J.; Plastina. The role of coherence in the non-equilibrium thermodynamics of quantum systems. Phys. Rev. E 2019, 99, 042105. [Google Scholar] [CrossRef]
- Riechers, P.M.; Gu, M. Initial-State Dependence of Thermodynamic Dissipation for any Quantum Process. arXiv 2020, arXiv:2002.11425. [Google Scholar]
- Sone, A.; Liu, Y.X.; Cappellaro, P. Quantum Jarzynski equality in open quantum systems from the one-time measurement scheme. arXiv 2020, arXiv:2002.06332. [Google Scholar]
- Francica, G.; Binder, F.; Guarnieri, G.; Mitchison, M.T.; Goold, J.; Plastina, F. Quantum coherence and ergotropy. arXiv 2020, arXiv:2006.05424. [Google Scholar]
- Francica, G.; Goold, J.; Plastina, F.; Paternostro, M. Daemonic Ergotropy: Enhanced Work Extraction from Quantum Correlations. NPJ Quant. Inf. 2017, 3, 12. [Google Scholar] [CrossRef]
- Bernards, F.; Kleinmann, M.; Gühne, O.; Paternostro, M. Daemonic Ergotropy: Generalised Measurements and Multipartite Settings. Entropy 2019, 21, 771. [Google Scholar] [CrossRef]
- Miller, H.J.D.; Mohammady, M.H.; Perarnau-Llobet, M.; Guarnieri, G. Thermodynamic uncertainty relation in slowly driven quantum heat engines. arXiv 2020, arXiv:2006.07316. [Google Scholar]
- Miller, H.J.; Scandi, M.; Anders, J.; Perarnau-Llobet, M. Work Fluctuations in Slow Processes: Quantum Signatures and Optimal Control. Phys. Rev. Lett. 2019, 123. [Google Scholar] [CrossRef]
- Scandi, M.; Miller, H.J.D.; Anders, J.; Perarnau-Llobet, M. Quantum work statistics close to equilibrium. arXiv 2019, arXiv:1911.04306. [Google Scholar] [CrossRef]
- Talkner, P.; Lutz, E.; Hänggi, P. Fluctuation theorems: Work is not an observable. Phys. Rev. E 2007, 75, 050102. [Google Scholar] [CrossRef]
- Campisi, M.; Hänggi, P.; Talkner, P. Colloquium: Quantum fluctuation relations: Foundations and applications. Rev. Mod. Phys. 2011, 83, 771. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum system. Rev. Mod. Phys. 2009, 81, 1665. [Google Scholar] [CrossRef]
- Batalhão, T.B.; Souza, A.M.; Mazzola, L.; Auccaise, R.; Sarthour, R.S.; Oliveira, I.S.; Goold, J.; De Chiara, G.; Paternostro, M.; Serra, R.M. Experimental reconstruction of work distribution and study of fluctuation relations in a closed quantum system. Phys. Rev. Lett. 2014, 113, 140601. [Google Scholar] [CrossRef]
- An, S.; Zhang, J.N.; Um, M.; Lv, D.; Lu, Y.; Zhang, J.; Yin, Z.Q.; Quan, H.; Kim, K. Experimental test of the quantum Jarzynski equality with a trapped-ion system. Nat. Phys. 2015, 11, 193–199. [Google Scholar] [CrossRef]
- Peterson, J.P.; Batalhão, T.B.; Herrera, M.; Souza, A.M.; Sarthour, R.S.; Oliveira, I.S.; Serra, R.M. Experimental characterization of a spin quantum heat engine. Phys. Rev. Lett. 2019, 123, 240601. [Google Scholar] [CrossRef]
- Ronzani, A.; Karimi, B.; Senior, J.; Chang, Y.C.; Peltonen, J.T.; Chen, C.; Pekola, J.P. Tunable photonic heat transport in a quantum heat valve. Nat. Phys. 2018, 14, 991–995. [Google Scholar] [CrossRef]
- von Lindenfels, D.; Gräb, O.; Schmiegelow, C.T.; Kaushal, V.; Schulz, J.; Mitchison, M.T.; Goold, J.; Schmidt-Kaler, F.; Poschinger, U.G. Spin Heat Engine Coupled to a Harmonic-Oscillator Flywheel. Phys. Rev. Lett. 2019, 123, 080602. [Google Scholar] [CrossRef]
- Allahverdyan, A.E. Nonequilibrium quantum fluctuations of work. Phys. Rev. E 2014, 90, 032137. [Google Scholar] [CrossRef]
- Micadei, K.; Landi, G.T.; Lutz, E. Quantum Fluctuation Theorems beyond Two-Point Measurements. Phys. Rev. Lett. 2020, 124, 090602. [Google Scholar] [CrossRef]
- Levy, A.; Lostaglio, M. A quasiprobability distribution for heat fluctuations in the quantum regime. arXiv 2019, arXiv:1909.11116. [Google Scholar] [CrossRef]
- Gherardini, S.; Belenchia, A.; Paternostro, M.; Trombettoni, A. The role of quantum coherence in energy fluctuations. arXiv 2020, arXiv:2006.06208. [Google Scholar]
- Solinas, P.; Gasparinetti, S. Full distribution of work done on a quantum system for arbitrary initial states. Phys. Rev. E 2015, 92, 042150. [Google Scholar]
- de Falco, D.; Tamascelli, D. Noise-assisted quantum transport and computation. J. Phys. A Math. Theor. 2013, 22, 5301–5316. [Google Scholar] [CrossRef]
- Solinas, P.; Gasparinetti, S. Probing quantum interference effects in the work distribution. Phys. Rev. A 2016, 94, 052103. [Google Scholar] [CrossRef]
- Terletsky, Y.P. The limiting transition from quantum to classical mechanics. J. Exp. Theor. Phys. 1937, 7, 1290. [Google Scholar]
- Margenau, H.; Hill, R.N. Correlation between measurements in quantum theory. Prog. Theor. Phys. 1961, 26, 722. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Quantum statistics of almost classical assemblies. Phys. Rev. 1933, 44, 37. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef]
- Miller, H.J.D.; Anders, J. Time-reversal symmetric work distributions for closed quantum dynamics in the histories framework. New J. Phys. 2017, 19, 062001. [Google Scholar] [CrossRef]
- Åberg, J. Quantifying Superposition. arXiv 2006, arXiv:0612146. [Google Scholar]
- Braun, D.; Georgeot, B. Quantitative measure of interference. Phys. Rev. A 2006, 73, 022314. [Google Scholar] [CrossRef]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Winter, A.; Yang, D. Operational Resource Theory of Coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef]
- Brandão, F.G.S.L.; Gour, G. Reversible Framework for Quantum Resource Theories. Phys. Rev. Lett. 2015, 115, 070503. [Google Scholar] [CrossRef]
- Bu, K.; Xiong, C. A Note on Cohering Power and De-cohering Power. Quant. Inf. Comput. 2017, 17, 1206–1220. [Google Scholar]
- Ding, X.; Yi, J.; Kim, Y.W.; Talkner, P. Measurement-driven single temperature engine. Phys. Rev. E 2018, 98, 042122. [Google Scholar] [CrossRef]
- Elouard, C.; Herrera-Martí, D.; Huard, B.; Auffèves, A. Extracting Work from Quantum Measurement in Maxwell’s Demon Engines. Phys. Rev. Lett. 2017, 118, 260603. [Google Scholar] [CrossRef]
- Buffoni, L.; Solfanelli, A.; Verrucchi, P.; Cuccoli, A.; Campisi, M. Quantum Measurement Cooling. Phys. Rev. Lett. 2019, 122. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Batalhão, T.B.; Souza, A.M.; Sarthour, R.S.; Oliveira, I.S.; Paternostro, M.; Lutz, E.; Serra, R.M. Irreversibility and the arrow of time in a quenched quantum system. Phys. Rev. Lett. 2015, 115, 190601. [Google Scholar] [CrossRef] [PubMed]
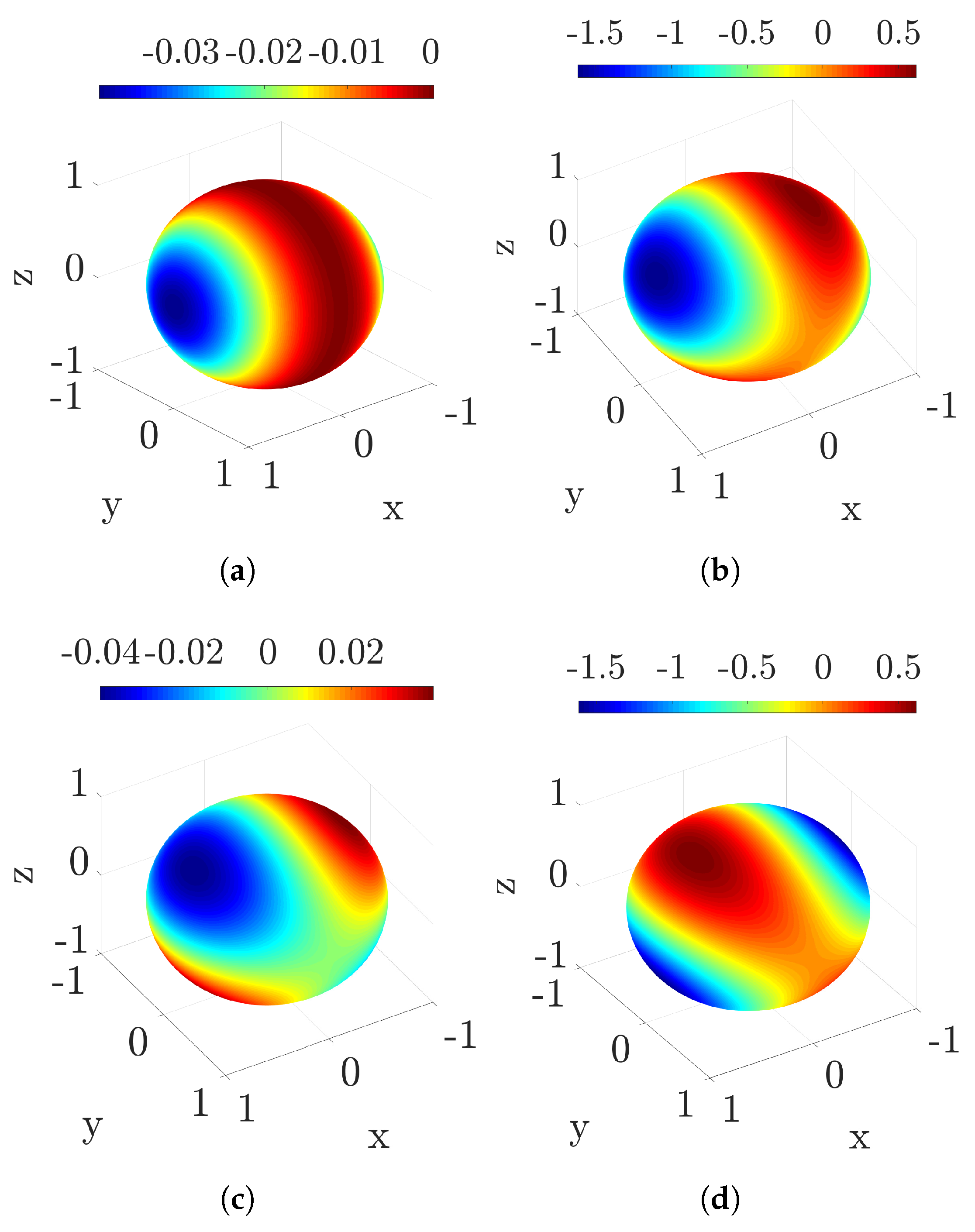
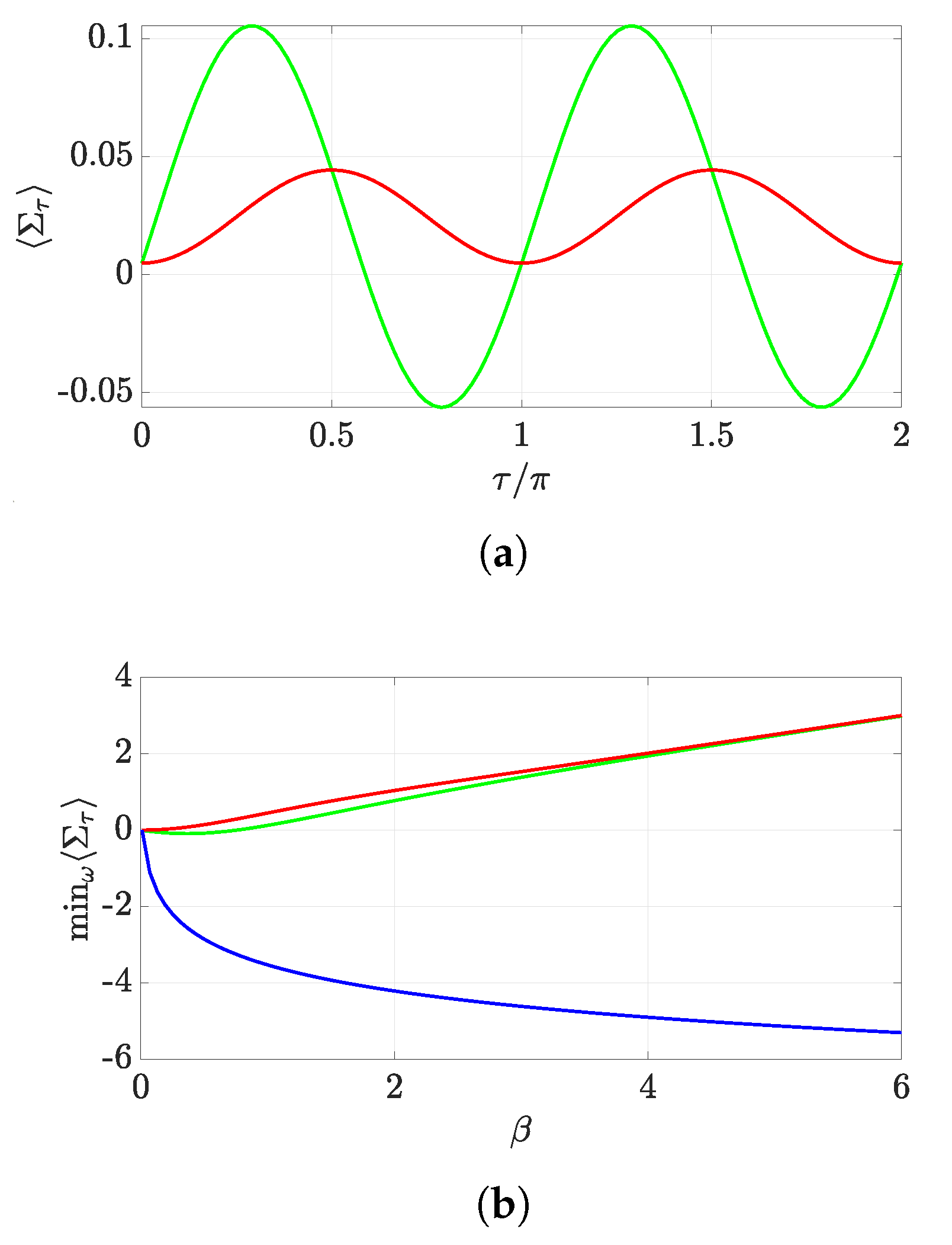
| (a) | ||
| (b) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz, M.G.; Guarnieri, G.; Paternostro, M. Quantum Work Statistics with Initial Coherence. Entropy 2020, 22, 1223. https://doi.org/10.3390/e22111223
Díaz MG, Guarnieri G, Paternostro M. Quantum Work Statistics with Initial Coherence. Entropy. 2020; 22(11):1223. https://doi.org/10.3390/e22111223
Chicago/Turabian StyleDíaz, María García, Giacomo Guarnieri, and Mauro Paternostro. 2020. "Quantum Work Statistics with Initial Coherence" Entropy 22, no. 11: 1223. https://doi.org/10.3390/e22111223
APA StyleDíaz, M. G., Guarnieri, G., & Paternostro, M. (2020). Quantum Work Statistics with Initial Coherence. Entropy, 22(11), 1223. https://doi.org/10.3390/e22111223





