1. Introduction
Aggregation is the process of forming structures through the merging of clusters. This generic process is encountered in a large variety of systems, from polymerization and colloidal aggregation to the clustering of social groups and the merging of galaxies. The mathematical foundations of aggregation were set by Smoluchowski [
1], whose particular interest was in Brownian coagulation. The aggregation equation, more commonly known as Smoluchowski equation, is a rate equation on a distribution of clusters whose size (mass) changes by binary aggregation events. For a discrete population of clusters with integer masses in multiples of a unit mass (“monomer”) it takes the form [
1],
where
is the number concentration of clusters with mass
k and
the aggregation kernel, a rate constant for the merging of masses
i and
j. A large body of literature has focused on the theory of the Smoluchowski equation, the existence of analytic solution and the scaling limit [
2]. Of particular interest is
gelling, a condition that arises under the product kernel
; it refers to the formation of a giant structure, as in polymer gels, and is manifested by the failure of the Smoluchowski equation to conserve mass. This process is commonly described as a phase transition, suggesting the possibility that statistical thermodynamics, a theory developed for equilibrium states of interacting particles, may perhaps be applicable in this clearly irreversible process.
Studies of Smoluchowski aggregation broadly fall in one of two categories, kinetic and stochastic. The kinetic approach is based on Equation (
1) and its solution. Stable solutions conserve mass; gelling is identified as the point where mass conservation breaks down [
3,
4]. Post-gel solutions require additional assumptions as to how the gel and the dispersed phase interact [
5]. The stochastic approach views clusters as entities that merge with probabilities proportional to the aggregation kernel. It was first formulated by Marcus [
6] for a discrete finite population, and its formal mathematical treatment was developed by Lushnikov, who obtained solutions for certain special cases, including gelation [
7,
8,
9,
10,
11]. In Lushnikov’s method all feasible distributions are given a probability, whose evolution in time is tracked via a generating functional. The approach is explicitly probabilistic and views the Smoluchowski equation as the mean-field approximation of the underlying stochastic process [
12]. A different approach within the probabilistic realm makes use of combinatorial methods. This treatment originated with Stockmayer [
13] and was further explored by Spouge [
14,
15,
16,
17]. The combinatorial approach considers the number of ways to build a particular distribution of clusters and assigns probabilities in proportion to that combinatorial weight. The ensemble of distributions is then reduced to the most probable distribution, which is identified by maximizing the combinatorial weight. This approach has two appealing advantages. It deals with a time-free ensemble in which time appears implicitly via the mean cluster mass. More importantly, it brings the problem closer to the viewpoint of statistical mechanics and the notion that an ensemble may be represented in the scaling limit by its most probable element. Stockmayer recognized this connection and his treatment of gelation is replete with references to the theory of phase transitions [
13]. The analogy between aggregation and thermodynamics was not formalized, however. Stockmayer obtained the gel point by mathematical, not thermodynamic methods, and arrived at a post-gel solution that is not consistent with the kinetics of aggregation [
5].
We have previously shown that gelation can be indeed treated as a formal phase transition and have presented solutions for the product kernel in the pre- and post-gel regions [
18] based on our earlier work on the cluster ensemble [
19,
20]. Here we generalize the methodology to formulate a rigorous thermodynamic theory of Smoluchowski aggregation. We begin with a finite population that starts from a well defined state and construct the set of all possible distributions that can be reached in a fixed number of elementary transitions. The probability of distribution in this ensemble is governed by the kinetics of the elementary processes that act on the population. In the thermodynamic limit the most probable distribution is overwhelmingly more probable than all others and is governed by a set of mathematical relationships that we recognize as
thermodynamics. The work is organized as follows. In
Section 2 we define the Smoluchowski ensemble of distributions and their probabilities. In
Section 3 we formulate the probability of distribution in terms of a special functional
W that introduces the partition function and the Shannon entropy of distribution. In
Section 4 we treat the scaling limit and derive the thermodynamic relationships of the Smoluchowski ensemble. In
Section 5 we obtain solutions of the Gibbs form for the classical kernels, constant, sum and product. We analyze the stability and phase behavior of the ensemble in
Section 6 and treat the sol-gel process as a phase transition. In
Section 7 we express the results in the continuous domain and finally offer concluding remarks in
Section 8.
2. The Smoluchowski Ensemble
We consider a population of clusters composed of
units (monomers). In binary aggregation two clusters merge to form a new cluster that conserves mass, via the schematic reaction
The merging of a pair constitutes an elementary stochastic event, whose probability depends on the aggregation kernel
. At the initial state the population consists of
single members (monomers). This distribution constitutes generation
. The next generation is constructed by implementing every possible aggregation event in the distribution of generation
. The set of distributions formed in this manner constitutes the microcanonical ensemble of generation
. We continue recursively to form the ensemble of distributions in generation
g by implementing all possible aggregation events, one at a time, in all distributions of the parent ensemble. We represent a distribution of clusters by the vector
, where
is the number of clusters with
i members. All distributions in generation
g satisfy the conditions
The first condition expresses the fact each elementary event decreases the number of clusters by 1, according to the stoichiometry of binary merging; the second condition expresses the fact that the number of members is conserved. Conversely, any distribution that satisfies the conditions in Equation (
3) is a member of the ensemble of generation
g because it can be formed in
g steps from
M monomers. We view the two equations in Equation (
3) as the constraints that define the ensemble of feasible distributions. We call this ensemble microcanonical to indicate that it is conditioned by two extensive constraints that fix the mean cluster mass
in all distributions of the ensemble.
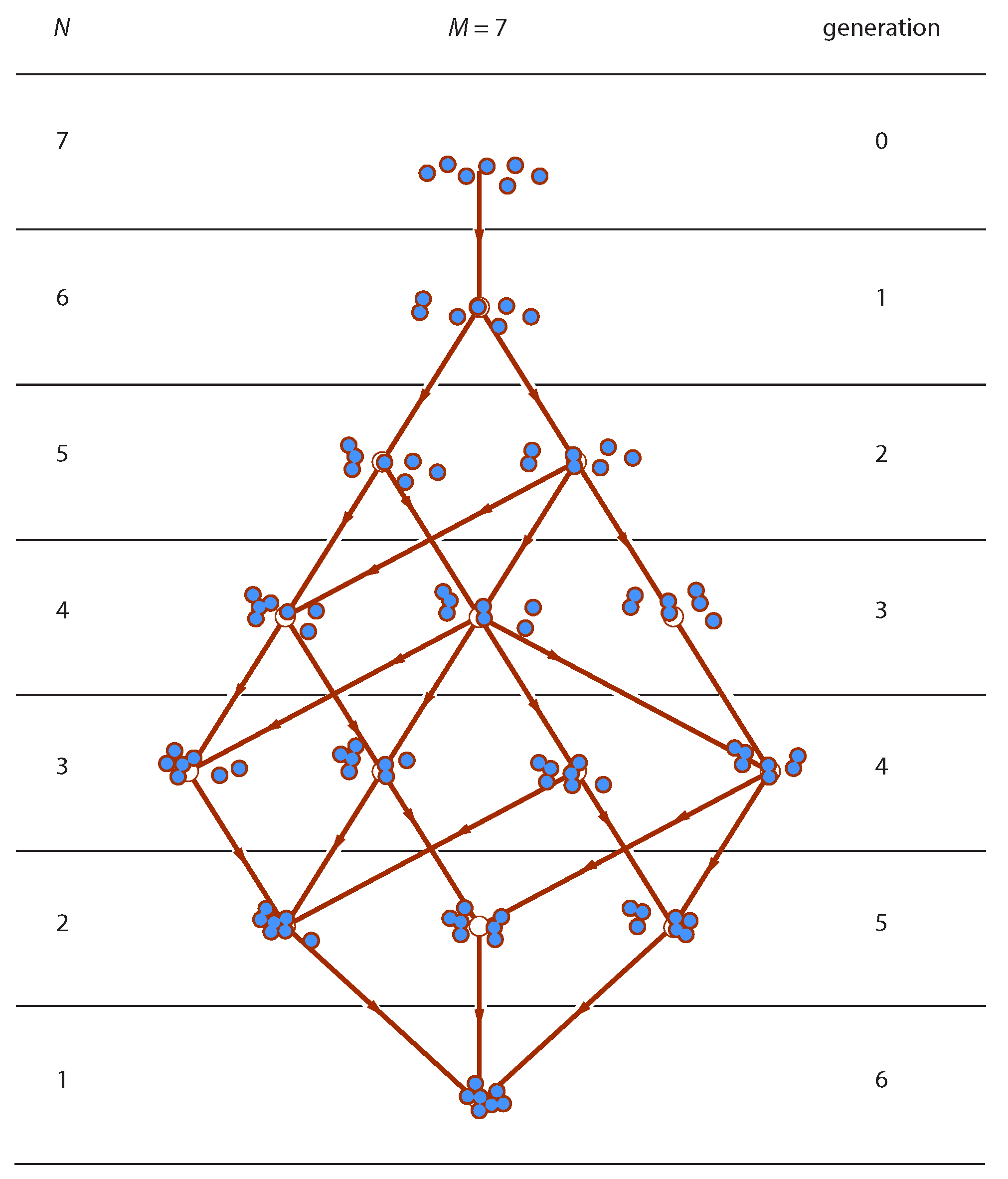
The evolution of the ensemble may be represented in the form of a layered graph (
Figure 1), whose vertices represent distributions and edges represent elementary transitions according to Equation (
2). Edges are directed from parent in generation
to offspring in generation
g. Layers are organized by generation and contain all distributions in a generation. The graph begins in generation
with a distribution of all monomers and ends when all units have joined the same cluster. Stochastic aggregation is a random walk on this graph. A trajectory is a possible sequence of connected edges from top to bottom. Our goal is to establish the probability
of distribution in generation
, in terms the aggregation kernel
for any
M.
2.1. Kinetics
When cluster masses
and
j, in distribution
of generation
, merge to form a cluster of mass
i, the parent distribution
is transformed to offspring distribution
via the transition
This transition is represented by an edge in the graph of
Figure 1. Its rate
is proportional to the number of ways to choose the reactants and the proportionality factor is the aggregation kernel:
The total rate by which parent
produces offspring is
where
is the number of clusters and
is the mean kernel in parent distribution
:
In physical terms the aggregation kernel
is the rate constant for the reaction between masses
i and
j. Its mathematical form may be constructed on the basis of a kinetic model for the particular problem. It is beyond the scope of this work to review the numerous kernels that have been proposed in the literature. We mention a selected few that are important for their physical, mathematical and historical significance, and summarize them in
Table 1.
The Brownian coagulation kernel was derived by Smoluchowski [
1] to describe the kinetics of diffusion limited aggregation in colloidal systems. The constant kernel was adopted by Smoluchowski [
1] as an approximation for the Brownian kernel, a simplification that allows analytic results. This kernel is obtained by setting
in the Brownian kernel. The Flory/Stockmayer kernel [
13,
21] is a model for polymerization of chains composed of monomers with
f functional groups. Assuming no cycles, a polymer with
i monomers contains
unreacted functional groups that are available to react. The Flory/Stockmayer kernel is the product of the unreacted functional groups in the two chains that merge. This kernel leads to gelation [
13]. The product kernel is the limiting form of the Flory/Stockmayer kernel when the number of functional groups approaches infinity. It also leads to gelation, and being a simpler kernel than the Flory/Stockmayer, it serves as the standard model to study gelation. The sum kernel is proportional to the number of units in each cluster. This kernel may be viewed as the limiting form of a Flory/Stockmayer type kernel with two kinds functional groups [
15], but its significance is primarily mathematical as one of a handful of kernels that lead to analytic solutions.
We discuss the constant, sum and product kernel in detail in
Section 5. For now we leave the kernel general and unspecified. We only place the minimum conditions,
, which are required from elementary physical considerations; additionally, we adopt the normalization
.
2.2. Probabilities
We assign a probability
to each distribution
within generation
g and formulate its propagation in proportion to the probability of the parent and the rate of the parent-offspring transition:
Here
is a distribution in generation
g,
is its parent of
in generation
via the reaction
,
is the rate of the reaction, and
is the mean reaction rate in parent generation
:
In both Equations (
8) and (
9) the summations are over all distributions
in generation
. Expressing the transition rate in terms of the aggregation kernel we obtain
with
We may confirm that
as defined in Equation (
8) satisfies normalization over all distributions in the same generation. Beginning with
at the initial state, Equation (
8) uniquely determines the probabilities of all distributions in all future generations.
2.3. Smoluchowski Equation
The mean number of clusters with mass
k in generation
g is
with the summation going over all distributions in the same generation. We will derive the evolution of the mean distribution from parent generation
to generation
g. The probability of distribution
is given by Equation (
8) and is expressed as a summation over its parents
. By the stoichiometry of the transition in Equation (
2), the parent and offspring distributions satisfy
Combining this relationship with (
12) and (
8) the result is (see
Supplementary Material)
The left-hand side is the change in the mean number of
k-mers between generations; the right-hand side is the ensemble average of the production and depletion of
k-mers within all distributions of the parent ensemble. Define the mean time increment
from parent to offspring generation as
then Equation (
14) reads
In the mean-field approximation we reduce the ensemble into a single distribution,
. This resolves the ensemble averages trivially and leads to the governing equation for
:
This is the Smoluchowski equation for binary aggregation, the discrete finite equivalent of Equation (
1). The mean field approximation, which is invoked to obtain (
17), implies that a single distribution is representative of the entire ensemble. In
Section 4 and
Section 6 we examine the conditions under which this is true.
5. Gibbs Distributions
A special type of functional is of the form
whose log is linear in
with functional derivative
. Here
is a function of
i alone and does not depend on
. If the selection functional is given by Equation (
49) the probability of distribution in Equation (
18) takes the form
Probability distributions of this type are called Gibbs distributions [
23] and are frequently encountered in stochastic processes [
24]. Several important results can be obtained in analytic form. In particular, the mean distribution is [
22]:
The result is exact for all
,
.
We apply this selection functional of Equation (
49) to the transition
that converts parent distribution
to offspring
. By the stoichiometry of the transition we have
Inserting into Equation (
31) we obtain
One possible solution that satisfies this equation for all distributions
is
This is not the only possible solution for
W in Equation (
31) and may or may not be acceptable; if it is, we have obtained a Gibbs distribution and the kernel is a Gibbs kernel.
We have identified three kernels for which Equation (
55) is the correct solution. These are the constant kernel,
the sum kernel
and their linear combinations. The product kernel is a
quasi-Gibbs kernel and is discussed in
Section 5.3.
Here we provide detailed solutions for the constant and sum kernels. We will not discuss the linear combination in part because the results are more involved but mainly because this kernel reverts to the sum kernel when cluster masses are large thus it does not contribute to our understanding of aggregation beyond what we learn by studying the constant and sum kernels separately.
5.1. Constant Kernel
With
Equation (
55) gives
for all
i. Accordingly, the ensemble is
unbiased and its partition function is given by Equation (
27):
The mean distribution follows from Equation (
52) and is given by
To obtain the most probable distribution we calculate the parameters
and
q from Equations (
42) and (
43) along with (
58). The differentiations may be done by first replacing the factorials in the partition function with the Stirling expression. Alternatively we may obtain these parameters by the discrete difference form of these derivatives and apply the asymptotic conditions
. The latter method is simpler:
We obtain the MPD from (
39) with
:
For large
this goes over to the exponential distribution
which is the well known result for the constant kernel. Here
x stands for the continuous cluster mass.
5.2. Sum Kernel
The ensemble average of the sum kernel is
We obtain the partition function from Equation (
32). The result is
The factors
that satisfy Equation (
55) are
and the mean distribution follows from (
52),
This is an exact result for all
,
. The parameters
and
q are obtained similarly to those for the constant kernel:
Combining with Equation (
39) we obtain the MPD in the form
with
. We use the Stirling formula for the factorial the MPD in the continuous limit takes the form
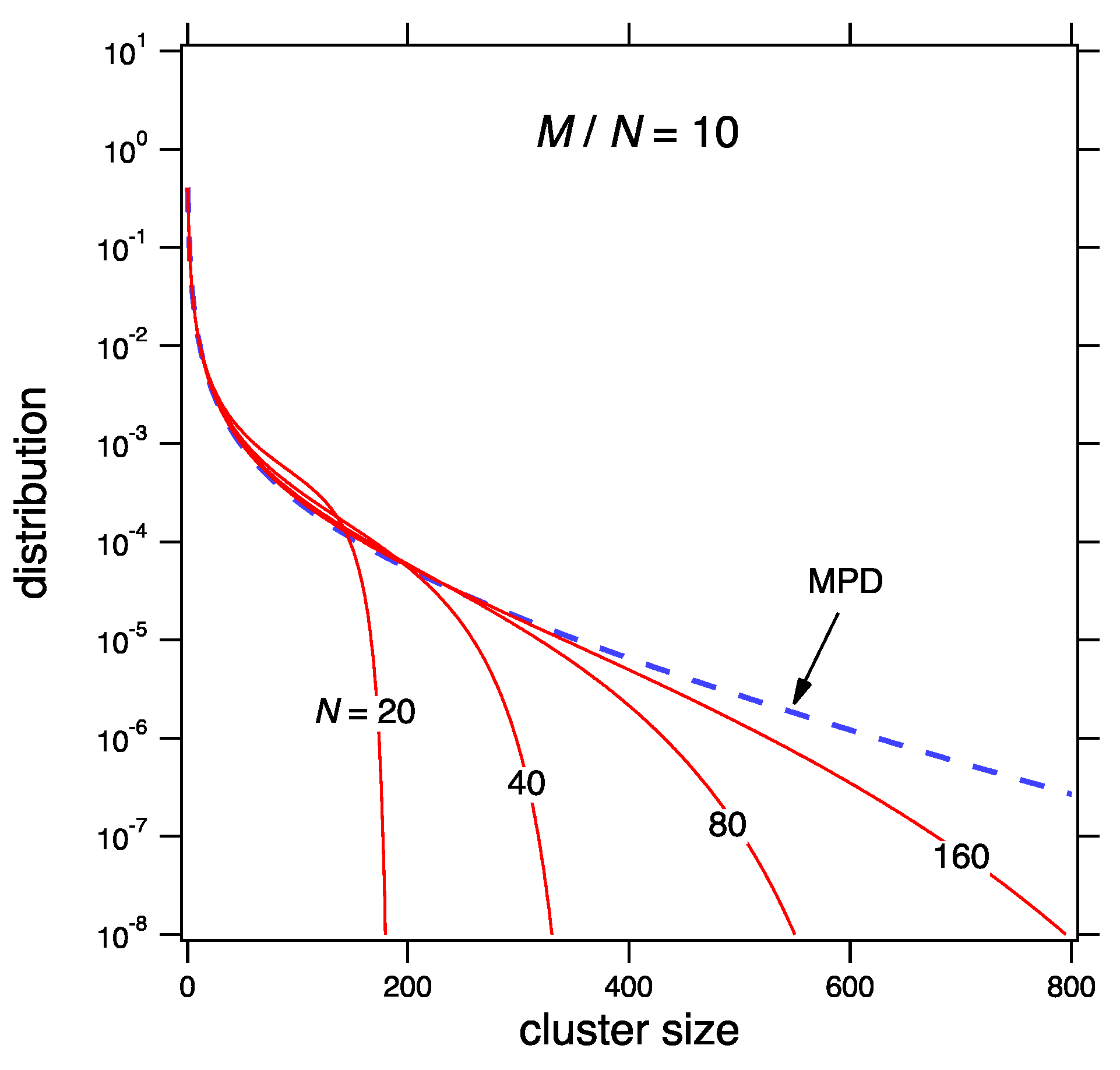
Figure 2 shows the MPD for
and the mean distribution from Equation (
67) at fixed
for various values of
M and
N. In the scaling limit the mean distribution converges to the MPD.
5.3. Quasi-Gibbs Kernels—The Product Kernel
We are able to obtain closed-form expressions for the partition function of the constant and sum kernels and heir linear combinations because they all satisfy the condition
for all
. This states that the mean kernel is the same in all distributions of the ensemble, therefore also equal to the ensemble average kernel. In this case the calculation of the ensemble average kernel is trivial, as it does not require knowledge of the probabilities
. The constant kernel, sum kernel and their linear combinations are the only kernels that satisfy (
72) in the strictest sense, that is, for all
that satisfy the two constraints in (
3). We refer to Equation (
72) as the Gibbs condition because it generates Gibbs distributions. We may relax the requirement that
all distributions obey the Gibbs condition with the milder requirement that it be obeyed by
most distributions. This is the case of the produce kernel. The product kernel is defined
and its mean within distribution
is
Here
and
are the normalized first moment and second moments of
, respectively. In the limit
,
, this scales as
in most distributions except those that contain clusters of the order
M. (The largest cluster size in the ensemble is
and for
it is of the order
M.) According to Equation (
75) the product kernel is a quasi-Gibbs kernel: it satisfies the Gibbs condition in Equation (
72) asymptotically in most but not all feasible distributions. We proceed to obtain the Gibbs distribution of the product kernel and test its validity.
Inserting (
75) into (
32) we obtain the partition function:
We complete the solution by evaluating
from Equation (
55),
The mean distribution is obtained by inserting these results into Equation (
52):
Unlike Equations (
62) and (
67) this result is not exact. This can be demonstrated numerically by the fact this distribution is not normalized to unity and its mean is not
for finite
M,
N; its approaches proper normalization in the asymptotic limit. This failure arises from the fact that Equation (
52) requires a Gibbs probability distribution that strictly applies to all distributions of the
ensemble.
We obtain
and
from Equations (
42) and (
43):
Using
the MPD is
and in the continuous limit
These results are summarized in
Table 3 along with those for the constant and sum kernels.
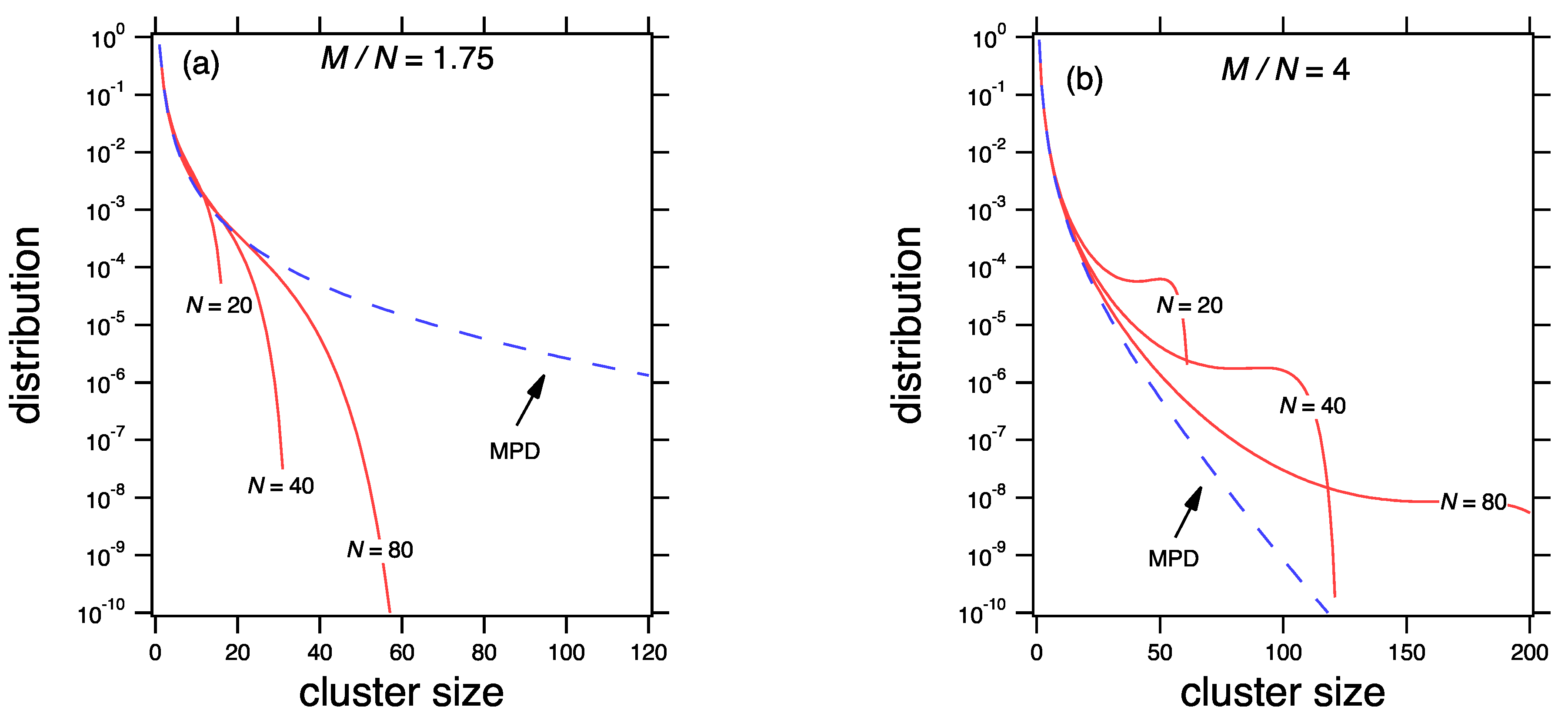
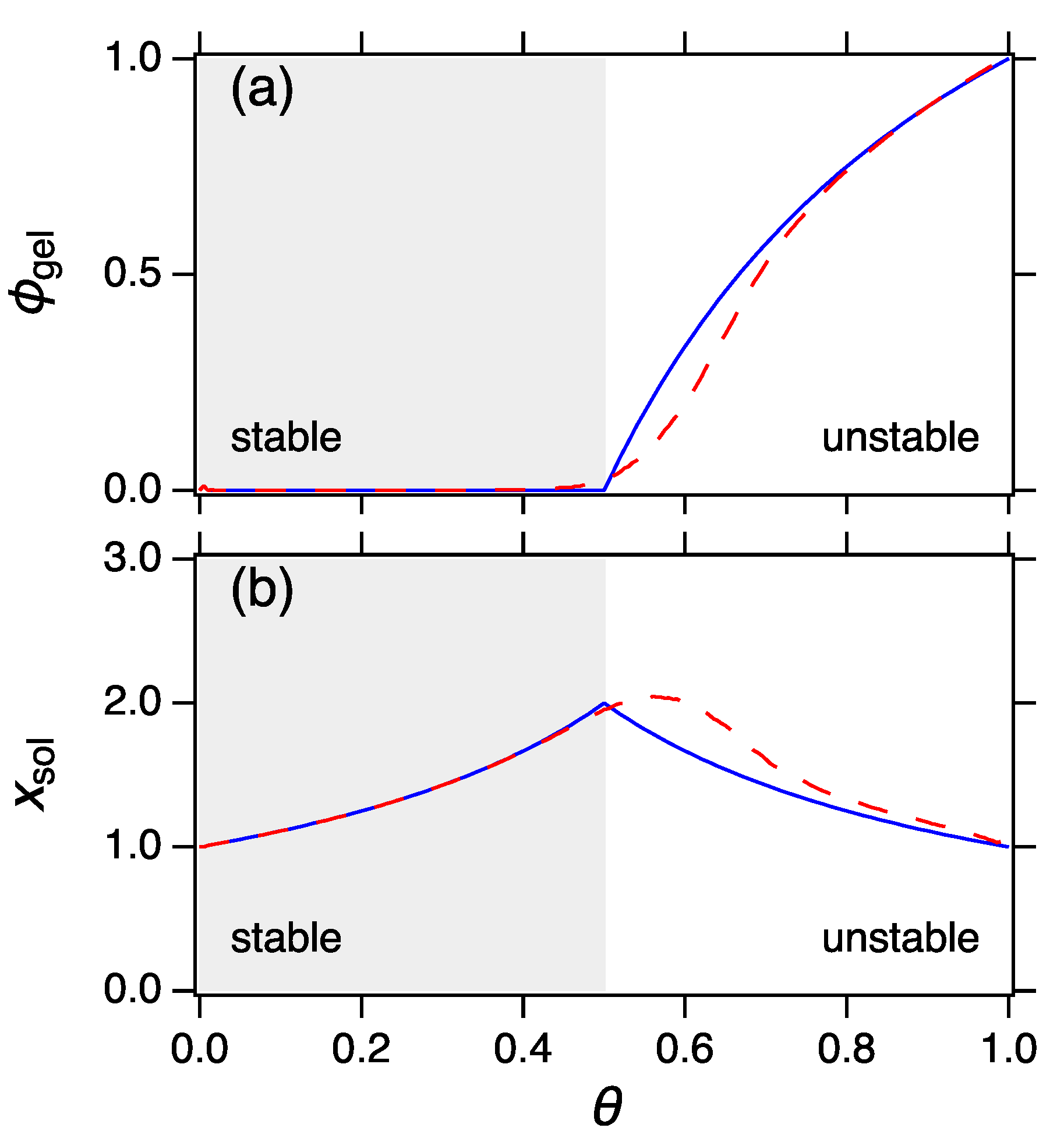
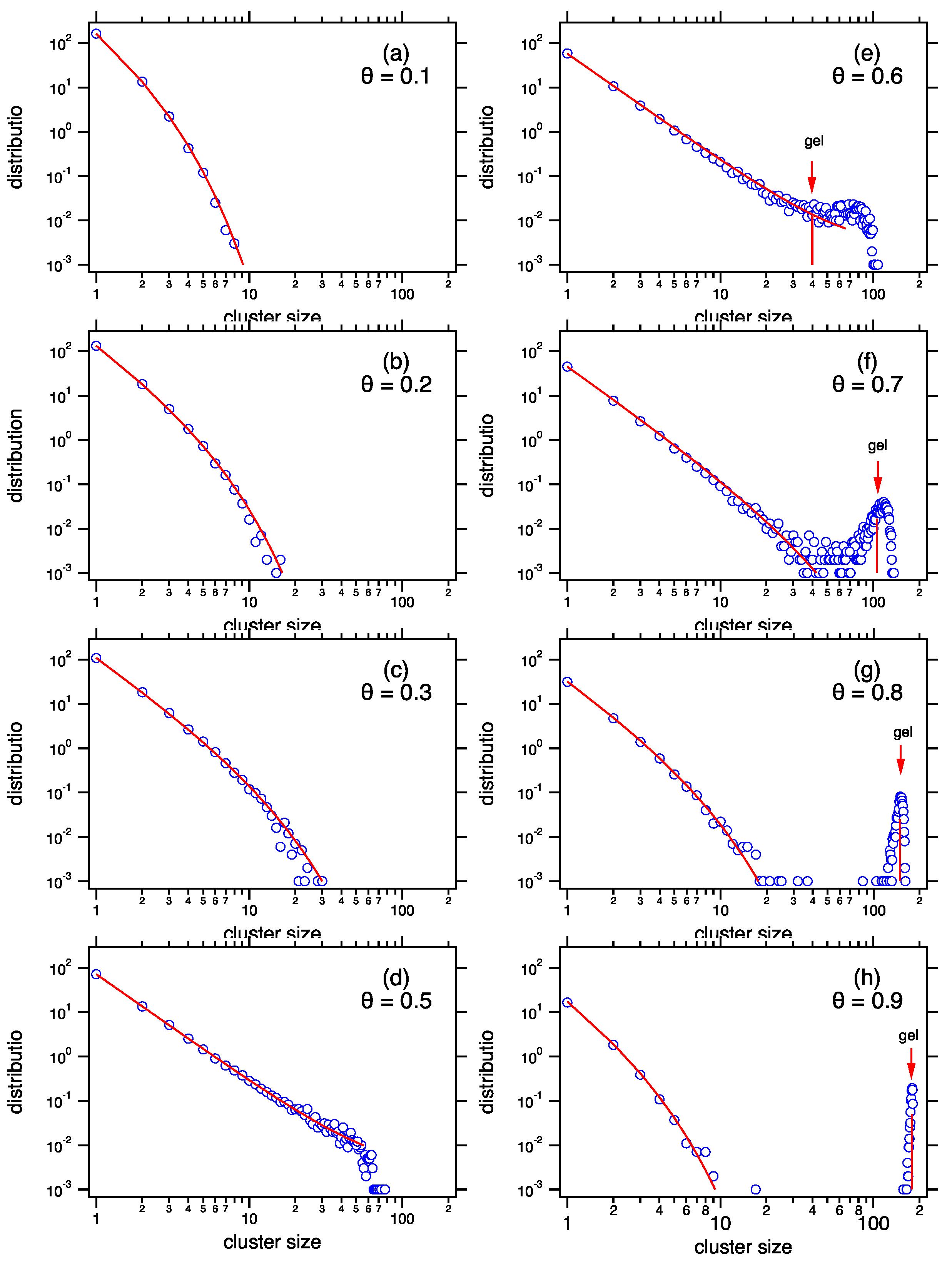
The relationship between the mean and the most probable distribution of the product kernel is shown in
Figure 3 for two values of the mean cluster,
and
. At
the mean distribution calculated from Equation (
78) is not exact but its moments asymptotically approach the correct values as
M and
N are increased at fixed
. At
the behavior is different. A peak develops at the long tail of the distribution. It is pushed to ever larger sizes but never vanishes. In this region the mean distribution from Equation (
78) is not correct: its mean does not converge to
when
M and
N are increased, but to a value smaller than
, which implies that mass conservation is not satisfied. This breakdown is manifestation of
gelation, the emergence of an infinite cluster that is not captured by the mean field theory. The precise nature of the gel phase is discussed in the next section.
7. Continuous Limit
We define the continuous limit by the conditions
Thus in addition to the scaling limit we require the mean cluster size to be much larger than the unit mass, such that the cluster mass may be treated as a continuous variable, which we denote as
x. Equations (
63), (
71) and (
82) refer to this limit. We present the corresponding expressions for the partition function and the selection functional.
In the continuous domain all intensive properties of the ensemble are functions of the mean cluster size
. Thus we write
,
,
, and express the partition function in intensive form
. The MPD is
and satisfies the normalizations
The log of the cluster function
is the functional derivative of the selection functional at the MPD:
and the notation
indicates this function of
x will generally depend on
as well since the functional derivative of non linear functionals depend on the function on which the derivative is evaluated. Since the microcanonical probability peaks sharply about the MPD (we are assuming a stable single-phase state) all ensemble averages revert to averages over the continuous MPD. The ensemble average kernel is then equal to the mean kernel within the MPD
The log of the intensive partition function,
, satisfies
with
These are the intensive forms of Equations (
40) and (
42), respectively. The partition function of aggregation is obtained from Equation (
32) by expressing the summation over
and an integral over
:
The parameter
is obtained from Equation (
102) and
from (
101):
From Equation (
54) we obtain
which expresses a condition on
.
Equations (
97), (
103)–(
106) provide an equivalent mathematical description of Smoluchowski aggregation in the continuous limit. These are accompanied by the variational condition
which is the continuous form of Equation (
48) and is satisfied by all distributions
with mean
. The equality defines the solution to the Smoluchowski process, the MPD,
.
As a demonstration we apply these results to the constant kernel. The right-hand side of Equation (
106) is zero and we obtain
at all times. It follows that
. The parameters
and
q are
and the MPD becomes
This is the well-known solution of the constant kernel in the continuous domain. The partition function of the constant kernel is
and the inequality in Equation (
107) becomes
whose right-hand side is the Shannon entropy of distribution
. For fixed
it is maximized by the exponential distribution, whose entropy is
: the inequality is indeed satisfied.
8. Summary
With the results obtained here we have made contact with several previous works in the literature. The mean distribution for the constant kernel in Equation (
59) was given by Hendriks [
26], who also obtained a recursion for the partition function similar to that in Equation (
30). The combinatorial treatment of Hendriks has in fact several common elements to ours but is limited to the constant and sum kernels and lacks the thermodynamic element of this work. The recursion for the cluster weights in Equation (
55) has appeared in various treatments of aggregation, both deterministic [
2,
27] and stochastic [
15,
17,
26]. The mean distributions in the continuous limit for the mean and sum kernels and for the product kernel in the pre-gel region are well known results in the literature [
2]. The instability of power-law kernels has been discussed by Ziff et al. [
3] in the context of the Smoluchowski equation. These connections to prior literature serve to validate the theory presented here and demonstrate that the thermodynamic treatment provides a unified theory of aggregation that brings previously disconnected results under a single formalism, the
Smoluchowski ensemble.
The Smoluchowski ensemble is a probability space of distributions that are feasible under the rules of binary aggregation. The structure of this space, that is, the connectivity of the graph in
Figure 1, is solely determined by the condition that aggregation is a binary event; the probability measure over this space is determined by the rate expression prescribed by the aggregation model. In Smoluchowski aggregation the rate is directly proportional to the number of clusters that appear on the reactant side of the aggregation reaction and on the aggregation kernel. In the scaling limit the probability of distribution is sharply peaked around a single distribution of the ensemble, its most probable distribution (MPD). In this limit all ensemble averages reduce to averages of the MPD, a distribution that alone suffices to generate all properties of the ensemble. The Smoluchowski coagulation equation is the time evolution of the most probable distribution in the asymptotic limit.
The step that turns the Smoluchowski ensemble into a
thermodynamic ensemble is Equation (
18). It expresses the probability of distribution in terms of two special functionals, the multinomial coefficient
and the selection functional
. This formulation introduces the partition function
as the central property of the ensemble to which al other properties are connected. The thermodynamic calculus, summarized by the equations in
Table 2, is a mathematical consequence of the variational condition that defines the most probable distribution in Equation (
39) as the solution to the constrained maximization of the probability
in Equation (
18). The constraints are given by Equations (
3) that fix the zeroth and first order moments of the distribution. These constraints define a
microcanonical ensemble of distributions with fixed mean
.
The MPD obtained by the method of constrained maximization is stable, provided that the partition function is concave in its independent variables. In extensive terms,
must be concave in
; in intensive terms,
must be concave in
. The two conditions are equivalent and define the stability criterion of the MPD. As in regular thermodynamics, when the stability criterion is violated the system experiences
phase splitting and exists a mixture of two phases—mathematically, as a linear combination of two independent MPD’s. In aggregation these phases are the
sol phase, which is represented by the MPD in Equation (
39) and the
gel phase (giant component), which in the scaling limit is represented by a delta function at
∞. The splitting into a sol and gel phase is treated by the theory in a natural and rigorous manner.
Notably, entropy in this treatment plays no special role. The Shannon entropy of distribution is the log of the multinomial coefficient. In the scaling limit, entropy is a component of the partition function through Equation (
36),
where
is the Shannon functional evaluated at the MPD. In the special case of the constant kernel
. In this case the partition function reduces to the Shannon entropy of the MPD,
and the variational condition reads,
In this form we have recovered the inequality of the second law as stated in statistical thermodynamics: the entropy of the equilibrium distribution (MPD) is at maximum with respect to all feasible distributions, namely, all distributions with the same mean. As is well known this distribution is exponential. The constant kernel is special. With
the probability of distribution is proportional to
; accordingly, all ordered sequences of
N clusters with total mass
M are equally probable. The ordered sequence of cluster masses in this case is analogous to microstate in statistical mechanics and the condition
analogous to the postulate if equal a priori probabilities. In the general case the Shannon entropy and the log of the microcanonical partition function are not the same. The fundamental functional that is maximized is the microcanonical weight
, whose log is
The selection functional incorporates the effect of the aggregation kernel and in this sense it the point of contact between thermodynamics and the mathematical model of the stochastic process that gives rise to the probability space of interest. In Smoluchowski aggregation the model is defined by the transition rate in Equation (
10) and the corresponding governing equation for
W is Equation (
33).
The thermodynamic formalism developed here is not limited to aggregation. Two alternative derivations that make no reference to stochastic process that gives rise to the probability space have been given in References [
20,
28]. As long as
is a homogeneous functional with degree 1, the thermodynamic relationships follow as a direct consequence of the maximization of the microcanonical probability in Equation (
18) under the constraints in Equation (
3). The details of aggregation enter through Equations (
32) and (
33) that give the partition function and selection functional in terms of the aggregation kernel. The approach may be generalized to other processes including growth by monomer addition and breakup. These will be treated elsewhere.