Twin Least Square Support Vector Regression Model Based on Gauss-Laplace Mixed Noise Feature with Its Application in Wind Speed Prediction
Abstract
1. Introduction
2. Related Work
3. TLSSVR Model of G-L Mixed Noise Characteristics
3.1. TLSSVR Model of G-L Mixed Homoscedastic Noise Characteristics
3.2. TLSSVR Model of G-L Mixed Heteroscedastic Noise Characteristics
4. ALM Method Analysis
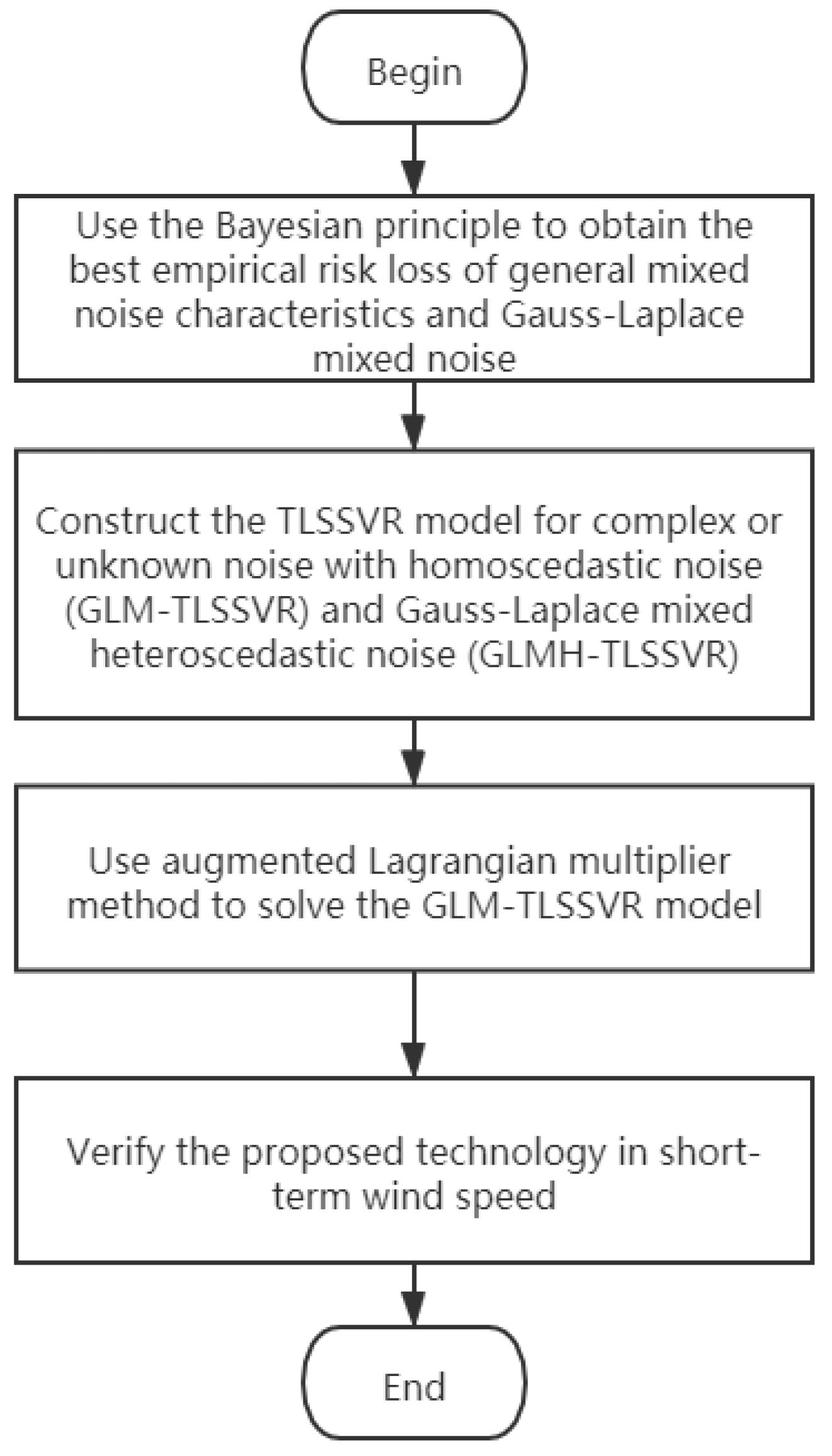
5. Experiments and Discussion
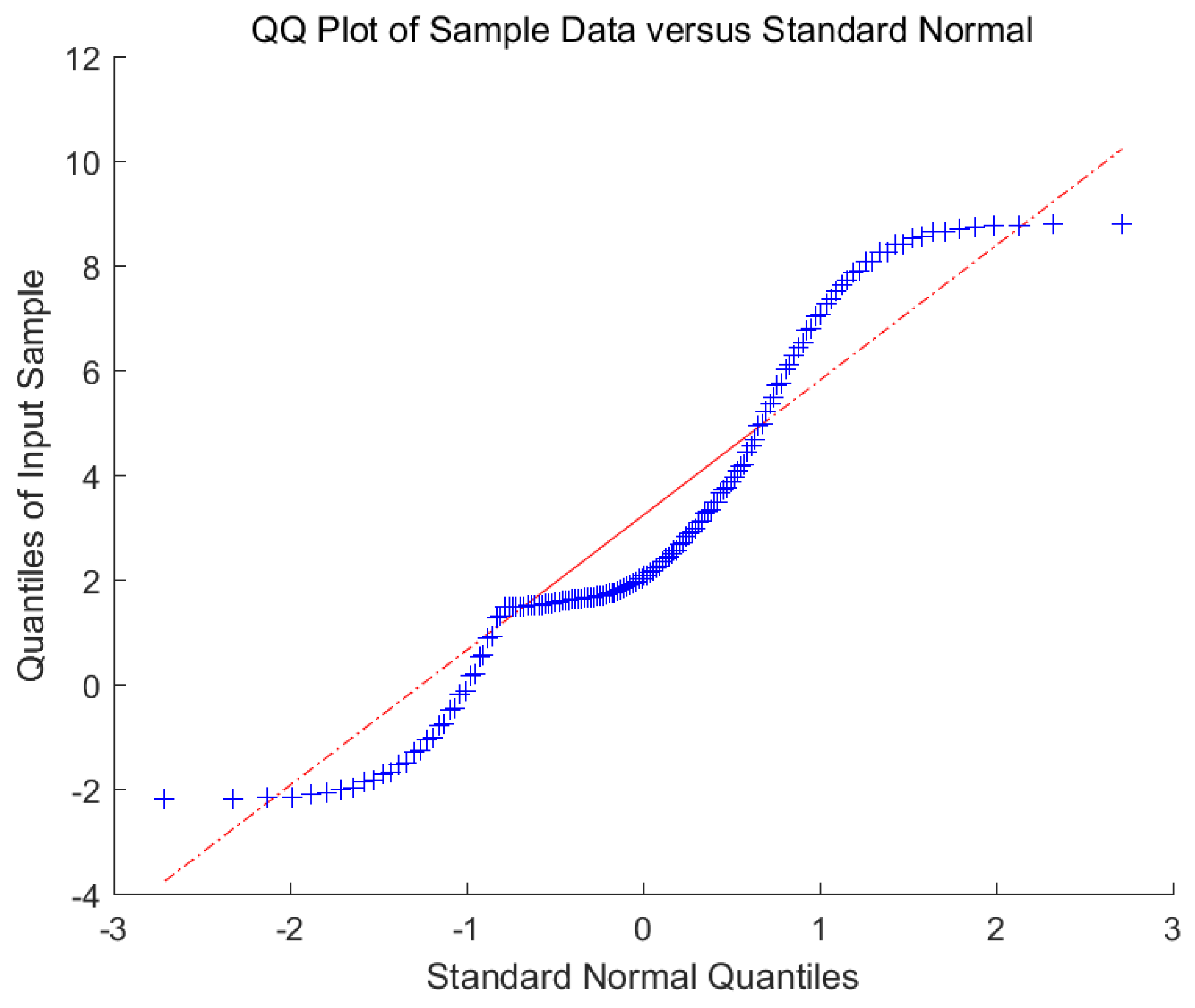
5.1. G-L Mixed Noise Characteristics of Wind Speed
5.2. The Criteria for Algorithm Evaluation
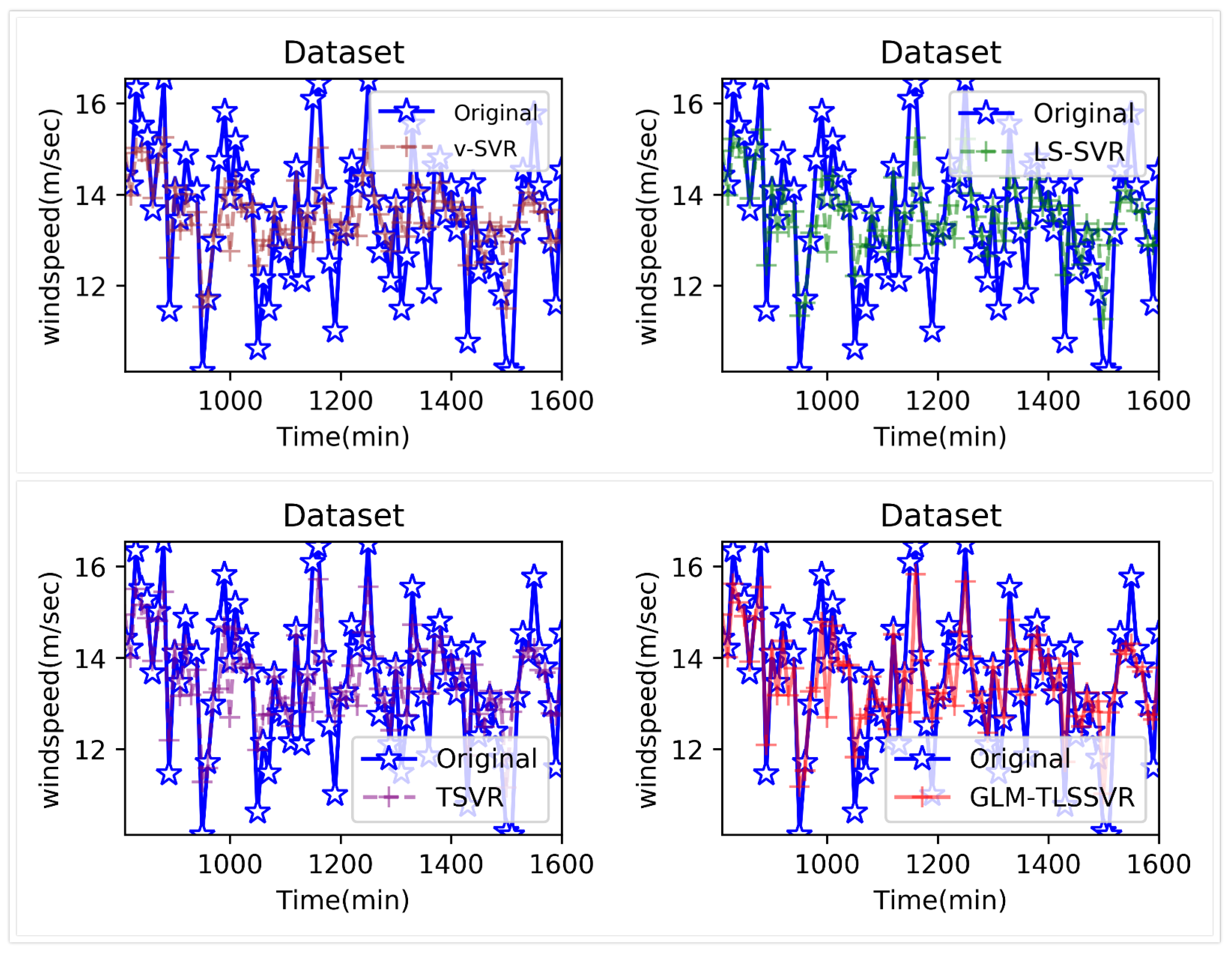
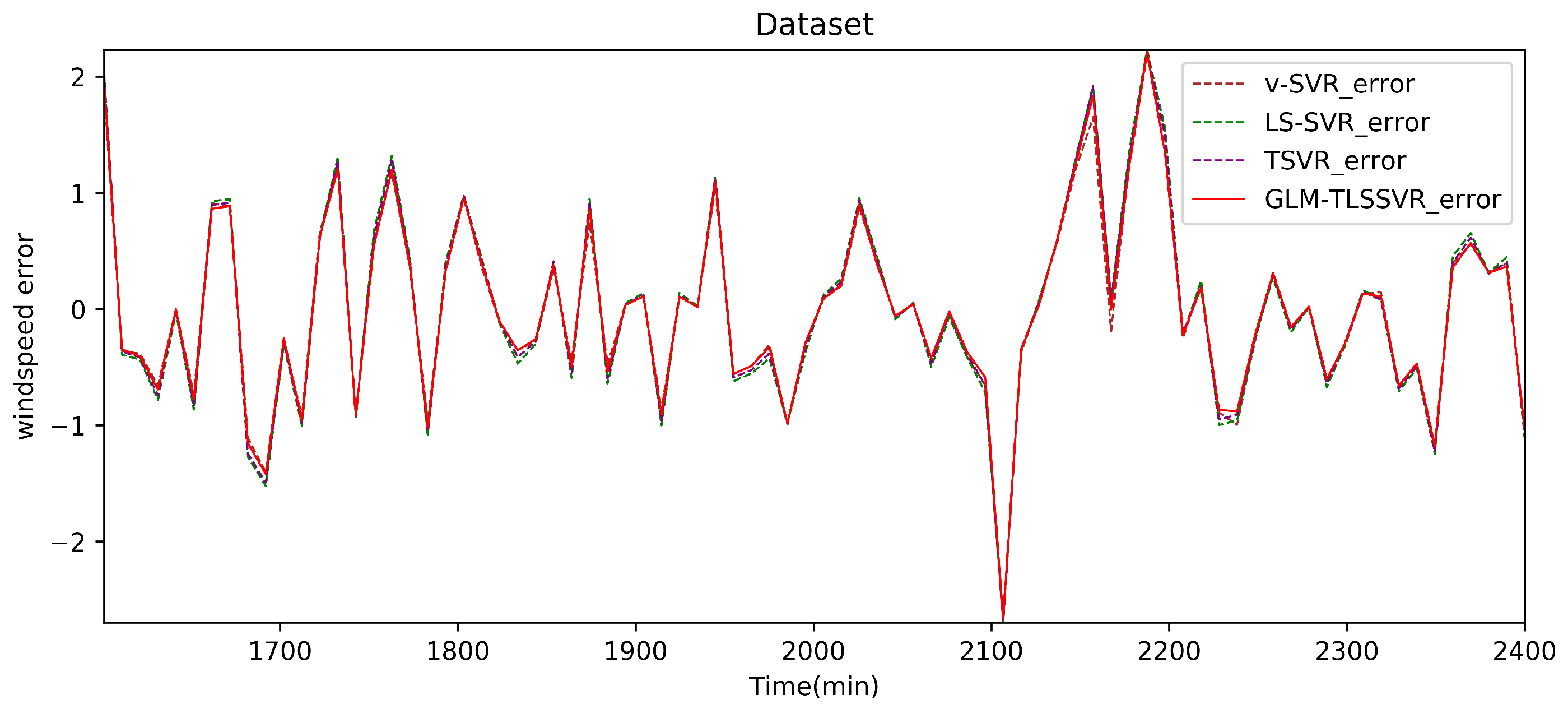
5.3. Application on Predicting the Short-Term Wind Speed
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| -SVR | -Support vector regression |
| LS-SVR | Least squares support vector regression model |
| TSVR | Twin support vector regression model |
| GLM-TLSSVR | Twin LS-SVR model of Gaussian-Laplacian mixed homoscedastic-noise |
| ALM | Augmented Lagrange multiplier method |
References
- Vapnik, V. The Natural of Statistical Learning Theory; Springer: New York, NY, USA, 1995; pp. 521–576. [Google Scholar]
- Debnath, R.; Muramatsu, M.; Takahashi, H. An efficient support vector machine learning method with second-order cone programming for large-scale problems. Appl. Intell. 2005, 23, 219–239. [Google Scholar] [CrossRef]
- Nie, F.; Huang, H.; Cai, X.; Ding, C.H. Efficient and robust feature selection via joint ℓ2, 1-norms minimization. In International Conference on Neural Information Processing Systems; Curran Associates Inc.: New York, NY, USA, 2010; pp. 1813–1821. [Google Scholar]
- Claesen, M.; De Smet, F.; Suykens, J.A.; De Moor, B. A robust ensemble approach to learn from positive and unlabeled data using SVM base models. Neurocomputing 2015, 160, 73–74. [Google Scholar] [CrossRef]
- Osuna, E.; Freund, R.; Girosi, F. Training support vector machines: An application to face detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 130–136. [Google Scholar]
- Lee, S.; Park, C.; Koo, J.-Y. Feature selection in the Laplacian support vector machine. Comput. Stat. Data Anal. 2011, 55, 567–577. [Google Scholar] [CrossRef]
- Chuang, C.-C.; Su, S.-F.; Jeng, J.-T.; Hsiao, C.-C. Robust support vector regression networks for function approximation with outliers. IEEE Trans. Neural Net-Works 2002, 13, 1322–1330. [Google Scholar] [CrossRef]
- Ince, H.; Trafalis, T.B. Support vector machine for regression and applications to financial forecasting. In Proceedings of the International Joint Conference on Neural Networks, IEEE-INNS-ENNS, Como, Italy, 27–27 July 2000. [Google Scholar]
- Pandit, R.; Infield, D. Comparative analysis of binning and support vector regression for wind turbine rotor speed based power curve use in condition monitoring. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Pandit, R.K.; Infield, D.; Kolios, A. Comparison of advanced non-parametric models for wind turbine power curves. IET Renew. Power Gener. 2019, 13, 1503–1510. [Google Scholar] [CrossRef]
- Prasetyowati, A.; Sudiana, D.; Sudibyo, H. Comparison Accuracy W-NN and WD-SVM Method In Predicted Wind Power Model on Wind Farm Pandansimo. In Proceedings of the 2018 4th International Conference on Nano Electronics Research and Education (ICNERE), Hamamatsu, Japan, 27–29 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, X.; Cui, Y.Q.; Zhang, H.S.; Tang, N.N. Research on modeling of wind turbine based on LS-SVM. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009. [Google Scholar] [CrossRef]
- Mohandes, M.A.; Halawani, T.O.; Rehman, S.; Hussain, A.A. Support vector machines for wind speed prediction. Renew. Energy 2003, 29, 939–947. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, Q.H.; Li, L.H.; Foley, A.M.; Srinivasan, D. Approaches to wind power curve modeling: A review and discussion. Renew. Sustain. Energy Rev. 2019, 116, 109422. [Google Scholar] [CrossRef]
- Moustris, K.P.; Zafirakis, D.; Kavvadias, K.A.; Kaldellis, J.K. Wind power forecasting using historical data and artificial neural networks modeling. In Proceedings of the Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (MedPower 2016), Belgrade, Serbia, 6–9 November 2016; pp. 105–106. [Google Scholar]
- Cai, X.; Nan, X.; Gao, B. Oxygen supply Prediction model based on IWO-SVR in bio-oxidation pretreatment. Eng. Lett. 2015, 23, 173–179. [Google Scholar]
- Burges, C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J.; Williamson, R.C.; Bartlett, P.L. New support vector algorithms. Neural Comput. 2000, 12, 1207–1245. [Google Scholar] [CrossRef]
- Deng, N.Y.; Tian, Y.J.; Zhang, C.H. Support Vector Machines: Optimization Based Theory, Algorithms, and Extensions; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Tian, Y.; Shi, Y.; Liu, X. Recent advances on support vector machines research. Technol. Econ. Dev. Econ. 2012, 18, 5–33. [Google Scholar] [CrossRef]
- Sfetsos, A. A comparison of various forecasting techniques applied to mean hourly wind speed time series. Renew. Energy 2008, 21, 23–35. [Google Scholar] [CrossRef]
- Zhao, N.; Ouyang, X.; Gao, C.; Zang, Z. Training an Improved TSVR Based on Wavelet Transform Weight Via Unconstrained Convex Minimization. IAENG Int. J. Comput. Sci. 2019, 46, 264–274. [Google Scholar]
- Doulamis, N.D.; Doulamis, A.D.; Varvarigos, E. Virtual associations of prosumers for smart energy networks under a renewable split market. IEEE Trans. Smart Grid 9.6 2017, 9, 6069–6083. [Google Scholar] [CrossRef]
- Vergados, D.J.; Mamounakis, I.; Makris, P.; Varvarigos, E. Prosumer clustering into virtual microgrids for cost reduction in renewable energy trading markets. Sustain. Energy Grids Netw. 2016, 7, 90–103. [Google Scholar] [CrossRef]
- Hu, Q.H.; Zhang, S.G.; Xie, Z.X.; Mi, J.S.; Wan, J. Noise model based ν-Support vector regression with its application to short-term wind speed forecasting. Neural Netw. 2014, 57, 1–11. [Google Scholar] [CrossRef]
- Zhang, S.G.; Hu, Q.H.; Xie, Z.X.; Mi, J.S. Kernel ridge regression for general noise model with its application. Neurocomputing 2015, 149, 836–846. [Google Scholar] [CrossRef]
- Jiang, P.; Li, P.Z. Research and Application of a New Hybrid Wind Speed Forecasting Model on BSO algorithm. J. Energy Eng. 2017, 143, 04016019. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Du, P.; Wang, J.Z.; Guo, Z.H.; Yang, W.D. Research and application of a novel hybrid forecasting system based on multi-objective optimization for wind speed forecasting. Energy Convers. Manag. 2017, 150, 90–107. [Google Scholar] [CrossRef]
- Jiang, Y.; Huang, G.Q. A hybrid method based on singular spectrum analysis, fifireflfly algorithm, and BP neural network for short-term wind speed forecasting. Energies 2016, 9, 757. [Google Scholar]
- Jiang, Y.; Huang, G.Q. Short-term wind speed prediction: Hybrid of ensemble empirical mode decomposition, feature selection and error correction. Energy Convers. Manag. 2017, 144, 340–350. [Google Scholar] [CrossRef]
- Wang, H.B.; Wang, Y.; Hu, Q.H. Self-adaptive robust nonlinear regression for unknown noise via mixture of Gaussians. Neurocomputing 2017, 235, 274–286. [Google Scholar] [CrossRef]
- Khemchandani, R.; Chandra, S. Twin support vector machines for pattern classification. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 905–910. [Google Scholar]
- Peng, X.J. TSVR: An efficient twin support vector machine for regression. Neural Netw. 2010, 23, 365–372. [Google Scholar] [CrossRef]
- Peng, X.J. Efficient twin parametric insensitive support vector regression model. Neurocomputing 2012, 79, 26–38. [Google Scholar] [CrossRef]
- Peng, X.J.; Xu, D.; Shen, J.D. A twin projection support vector machine for data regression. Neurocomputing 2014, 138, 131–141. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Zhao, J.; Zhao, M. Twin least squares support vector regression. Neurocomputing 2013, 118, 225–236. [Google Scholar] [CrossRef]
- Khemchandani, R.; Goyal, K.; Chandra, S. TWSVR: Regression via twin support vector machine. Neural Netw. 2016, 74, 14–21. [Google Scholar] [CrossRef]
- Shao, Y.H.; Zhang, C.H.; Yang, Z.M.; Jing, L.; Deng, N.Y. An ε-twin support vector machine for regression. Neural Comput. Appl. 2013, 23, 175–185. [Google Scholar] [CrossRef]
- Rastogi, R.; Anand, P.; Chandra, S. A ν-twin support vector machine based regression with automatic accuracy control. Appl. Intell. 2017, 46, 670–683. [Google Scholar] [CrossRef]
- Xu, Y.; Li, X.; Pan, X.; Yang, Z. Asymmetric ν-twin support vector regression. Neural Comput. Appl. 2017, 2, 1–16. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L. A weighted twin support vector regression. Knowl. Based Syst. 2012, 33, 92–101. [Google Scholar] [CrossRef]
- Matei, O.; Pop, P.C.; Vălean, H. Optical character recognition in real environments using neural networks and k-nearest neighbor. Appl. Intell. 2013, 39, 739–748. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L. K-nearest neighbor-based weighted twin support vector regression. Appl. Intell. 2014, 41, 299–309. [Google Scholar] [CrossRef]
- Parastalooi, N.; Amiri, A.; Aliherdari, P. Modified twin support vector regression. Neurocomputing 2016, 211, 84–97. [Google Scholar] [CrossRef]
- Ye, Y.F.; Bai, L.; Hua, X.Y.; Shao, Y.H.; Wang, Z.; Deng, N.Y. Weighted Lagrange ε-twin support vector regression. Neurocomputing 2016, 197, 53–68. [Google Scholar] [CrossRef]
- Chapelle, O. Training a support vector machine in primal. Neural Comput. 2007, 19, 1155–1178. [Google Scholar] [CrossRef]
- Peng, X.J. Primal twin support vector regression and its sparse approximation. Neuro Comput. 2010, 73, 2846–2858. [Google Scholar] [CrossRef]
- Balasundaram, S.; Gupta, D. Training Lagrangian twin support vector regression via uncontrained convex minimization. Knowl. Based Syst. 2014, 59, 85–96. [Google Scholar] [CrossRef]
- Gupta, D. Training primal K-nearest neighbor based weighted twin support vector regression via uncontrained convex minimization. Appl. Intell. 2017, 47, 962–991. [Google Scholar] [CrossRef]
- Balasundaram, S.; Meena, Y. Training primal twin support vector regression via uncontrained convex minimization. Appl. Intell. 2016, 44, 931–955. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, T.; Sun, L.; Wang, W.; Chang, B. LSSVR Model of G-L Mixed Noise-Characteristic with Its Applications. Entropy 2020, 22, 629. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, T.; Sun, L.; Wang, W.; Wang, C.; Mao, W. ν-Support Vector Regression Model Based on Gauss-Laplace Mixture Noise Characteristic for Wind Speed Prediction. Entropy 2019, 21, 1056. [Google Scholar] [CrossRef]
- Rastogi, R.; Anand, P.; Chandra, S. L1-norm Twin Support Vector Machine-based Regression. Optimization 2017, 66, 1895–1911. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, C.; Zhou, T.; Sun, L. Twin Least Squares Support Vector Regression of Heteroscedastic Gaussian Noise Model. IEEE Access 2020, 8, 94076–94088. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Augmented Lagrange Multiplier Functions and Duality in Nonconvex Programming. SIAM J. Control 1974, 12, 268–285. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; pp. 521–620. [Google Scholar]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Shevade, S.; Keerthi, S.S.; Bhattacharyya, C.; Murthy, K. Improvements to the SMO algorithm for SVM regression. IEEE Trans. Neural Netw. 2000, 11, 1188–1193. [Google Scholar] [CrossRef]
- Bordes, A.; Bottou, L.; Gallinari, P. SGD-QN: Careful quasiNewton stochastic gradient descent. J. Mach. Learn. Res. 2009, 10, 1737–1754. [Google Scholar]
- Chalimourda, A.; Schölkopf, B.; Smola, A.J. Experimentally optimal ν in support vector regression for different noise models and parameter settings. Neural Netw. 2004, 17, 127–141. [Google Scholar] [CrossRef]
- Cherkassky, V.; Ma, Y. Practical selection of SVM parameters and noise estimation for SVM regression. Neural Netw. 2004, 17, 113–126. [Google Scholar] [CrossRef]
- Kwok, J.T.; Tsang, I.W. Linear dependency between and the input noise in ε-support vector regression. IEEE Trans. Neural Netw. 2003, 14, 544–553. [Google Scholar] [CrossRef] [PubMed]
- Suykens, J.; Lukas, L.; Vandewalle, J. Sparse approximation using least square vector machines. In Proceedings of the IEEE International Symposium on Circuits and Systems, Geneva, Switzerland, 28–31 May 2000; pp. 757–760. [Google Scholar]





| Parameter | Mathematical Expression |
|---|---|
| MAE | |
| RMSE | |
| SSE | |
| SSR | |
| SST | |
| SSE/SST | |
| SSR/SST |
| Model | MAE (m/s) | RMSE (m/s) | SSE/SST | SSR/SST | teTime (s) |
|---|---|---|---|---|---|
| -SVR | 0.4797 | 0.6799 | 0.2603 | 0.4552 | 0.68 |
| LS-SVR | 0.4434 | 0.6366 | 0.2282 | 0.5064 | 0.66 |
| TSVR | 0.4182 | 0.6161 | 0.2137 | 0.5270 | 0.56 |
| GLM-TLSSVR | 0.4091 | 0.6069 | 0.2074 | 0.5384 | 0.55 |
| Model | MAE (m/s) | RMSE (m/s) | SSE/SST | SSR/SST | teTime (s) |
|---|---|---|---|---|---|
| -SVR | 0.7596 | 1.0041 | 0.4378 | 0.2365 | 0.71 |
| LS-SVR | 0.7131 | 0.9466 | 0.3891 | 0.2932 | 0.68 |
| TSVR | 0.6167 | 0.8546 | 0.3171 | 0.3793 | 0.59 |
| GLM-TLSSVR | 0.5787 | 0.8204 | 0.2923 | 0.4197 | 0.57 |
| Model | MAE (m/s) | RMSE (m/s) | SSE/SST | SSR/SST | teTime (s) |
|---|---|---|---|---|---|
| -SVR | 0.7781 | 0.9877 | 0.4333 | 0.2227 | 0.77 |
| LS-SVR | 0.7252 | 0.9202 | 0.3761 | 0.2714 | 0.69 |
| TSVR | 0.6566 | 0.8485 | 0.3198 | 0.3287 | 0.65 |
| GLM-TLSSVR | 0.6121 | 0.8005 | 0.2847 | 0.3702 | 0.58 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Liu, C.; Wang, W.; Chang, B. Twin Least Square Support Vector Regression Model Based on Gauss-Laplace Mixed Noise Feature with Its Application in Wind Speed Prediction. Entropy 2020, 22, 1102. https://doi.org/10.3390/e22101102
Zhang S, Liu C, Wang W, Chang B. Twin Least Square Support Vector Regression Model Based on Gauss-Laplace Mixed Noise Feature with Its Application in Wind Speed Prediction. Entropy. 2020; 22(10):1102. https://doi.org/10.3390/e22101102
Chicago/Turabian StyleZhang, Shiguang, Chao Liu, Wei Wang, and Baofang Chang. 2020. "Twin Least Square Support Vector Regression Model Based on Gauss-Laplace Mixed Noise Feature with Its Application in Wind Speed Prediction" Entropy 22, no. 10: 1102. https://doi.org/10.3390/e22101102
APA StyleZhang, S., Liu, C., Wang, W., & Chang, B. (2020). Twin Least Square Support Vector Regression Model Based on Gauss-Laplace Mixed Noise Feature with Its Application in Wind Speed Prediction. Entropy, 22(10), 1102. https://doi.org/10.3390/e22101102




