Numerical Study of Nanofluid Irreversibilities in a Heat Exchanger Used with an Aqueous Medium
Abstract
1. Introduction
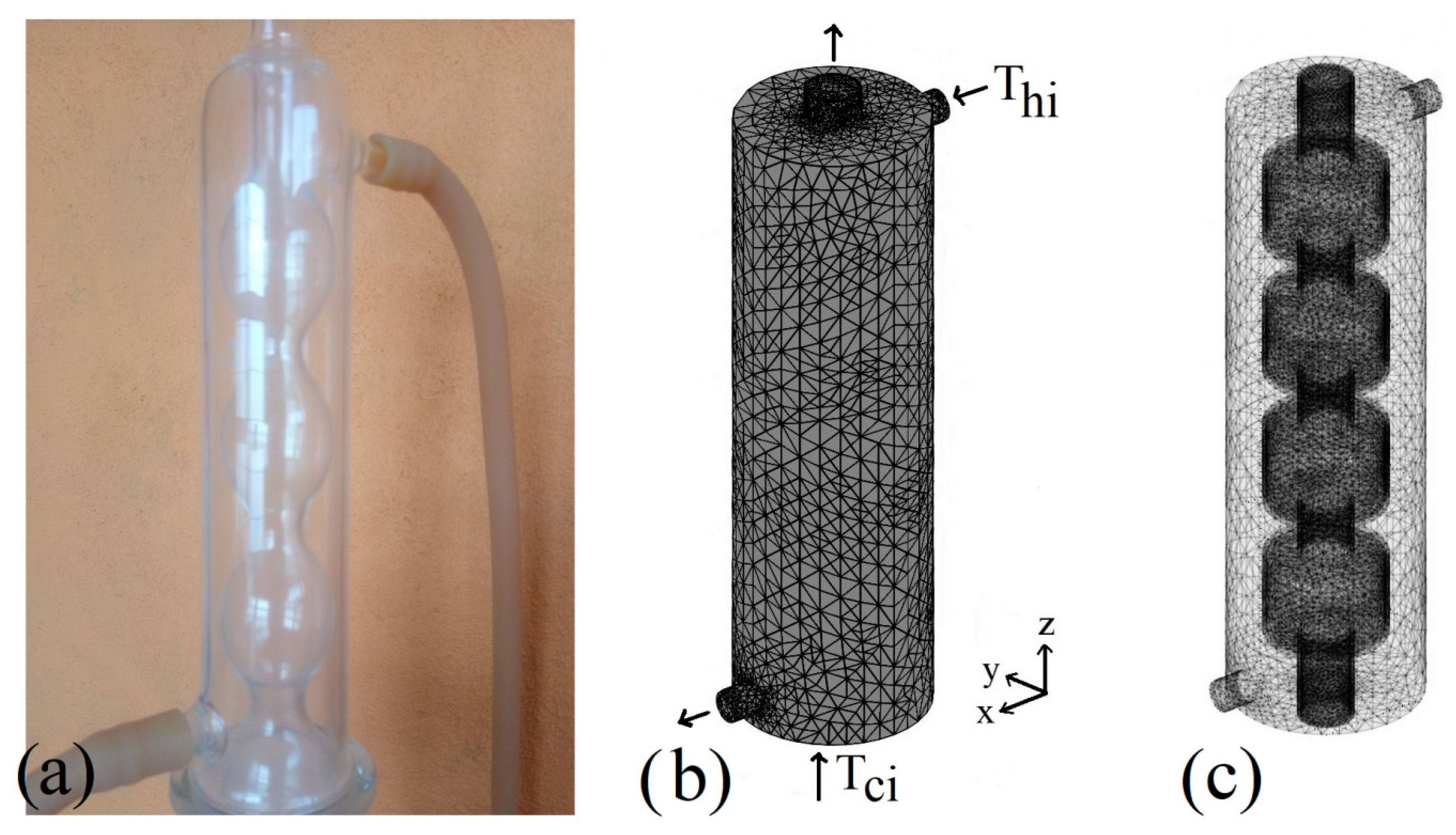
2. Description of the Problem
3. Conservation Equations
4. Entropy Generation Equations
5. Numerical Methods
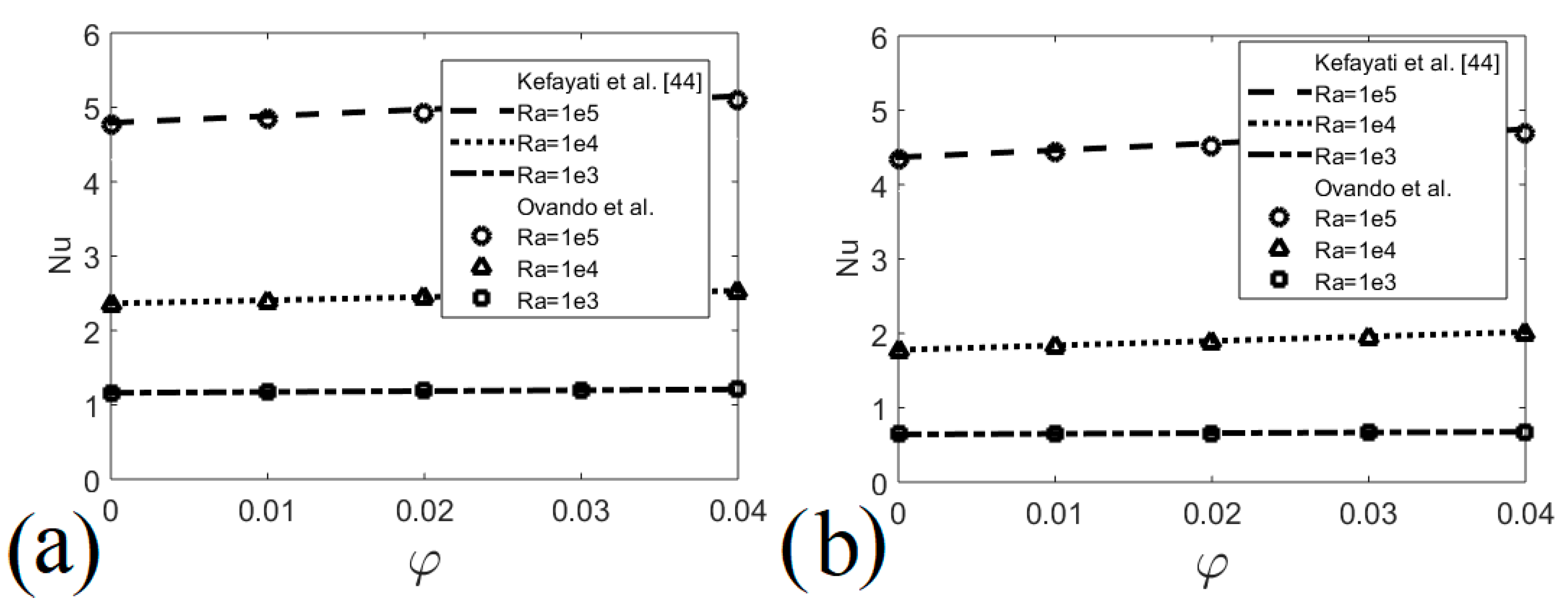
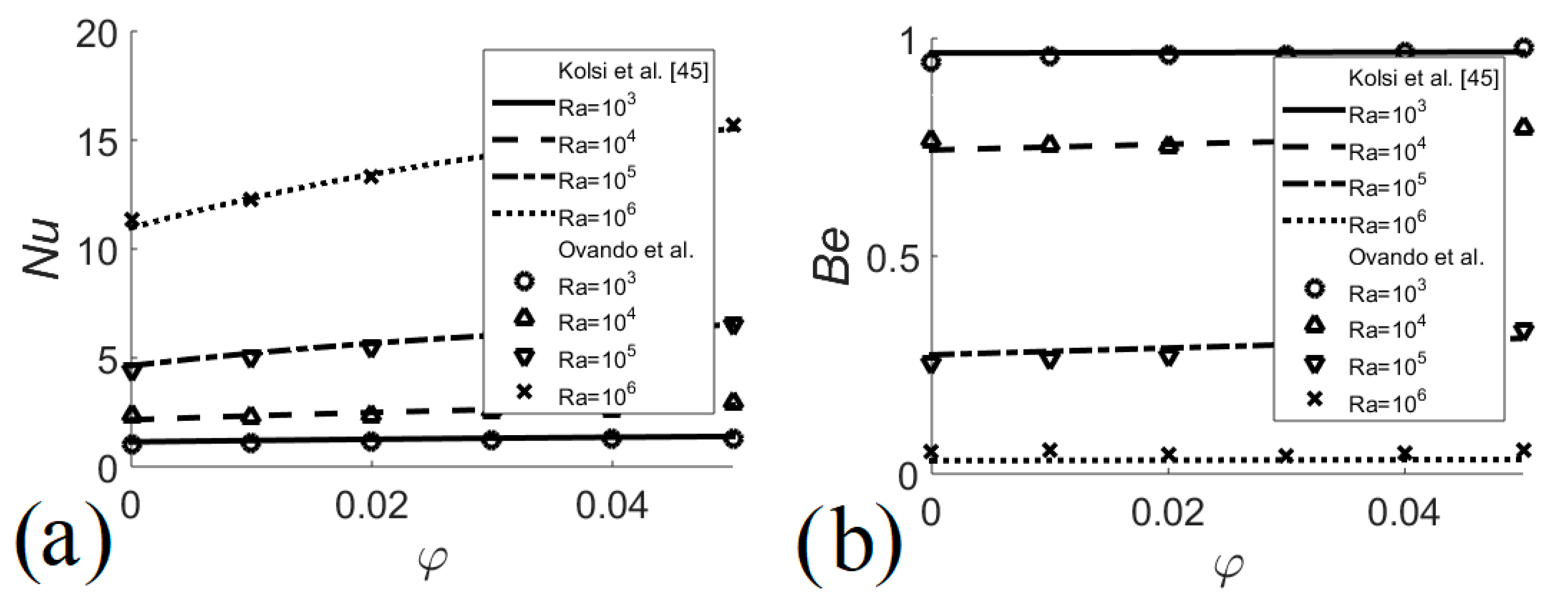
6. Validation
7. Results and Discussion
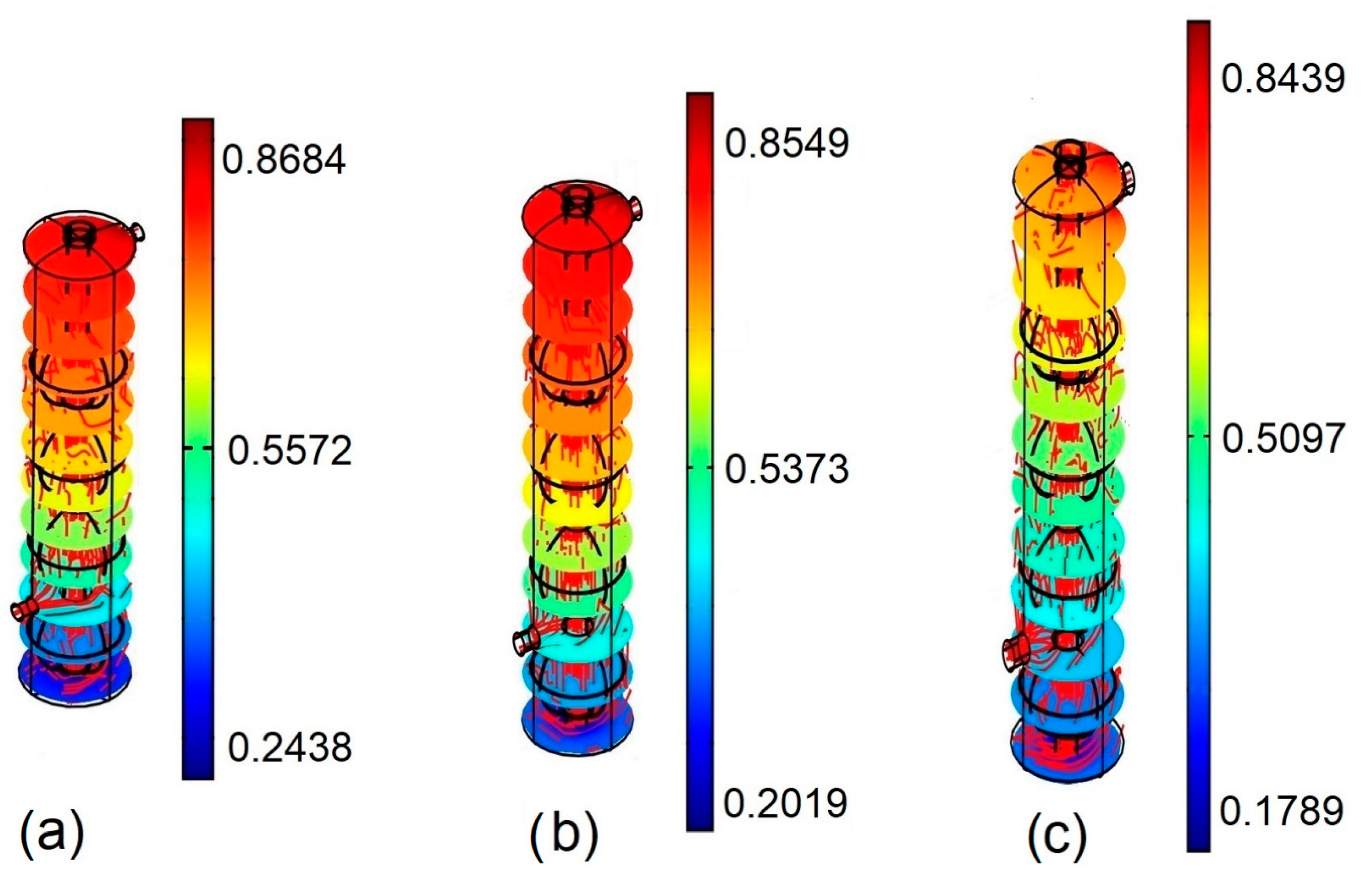
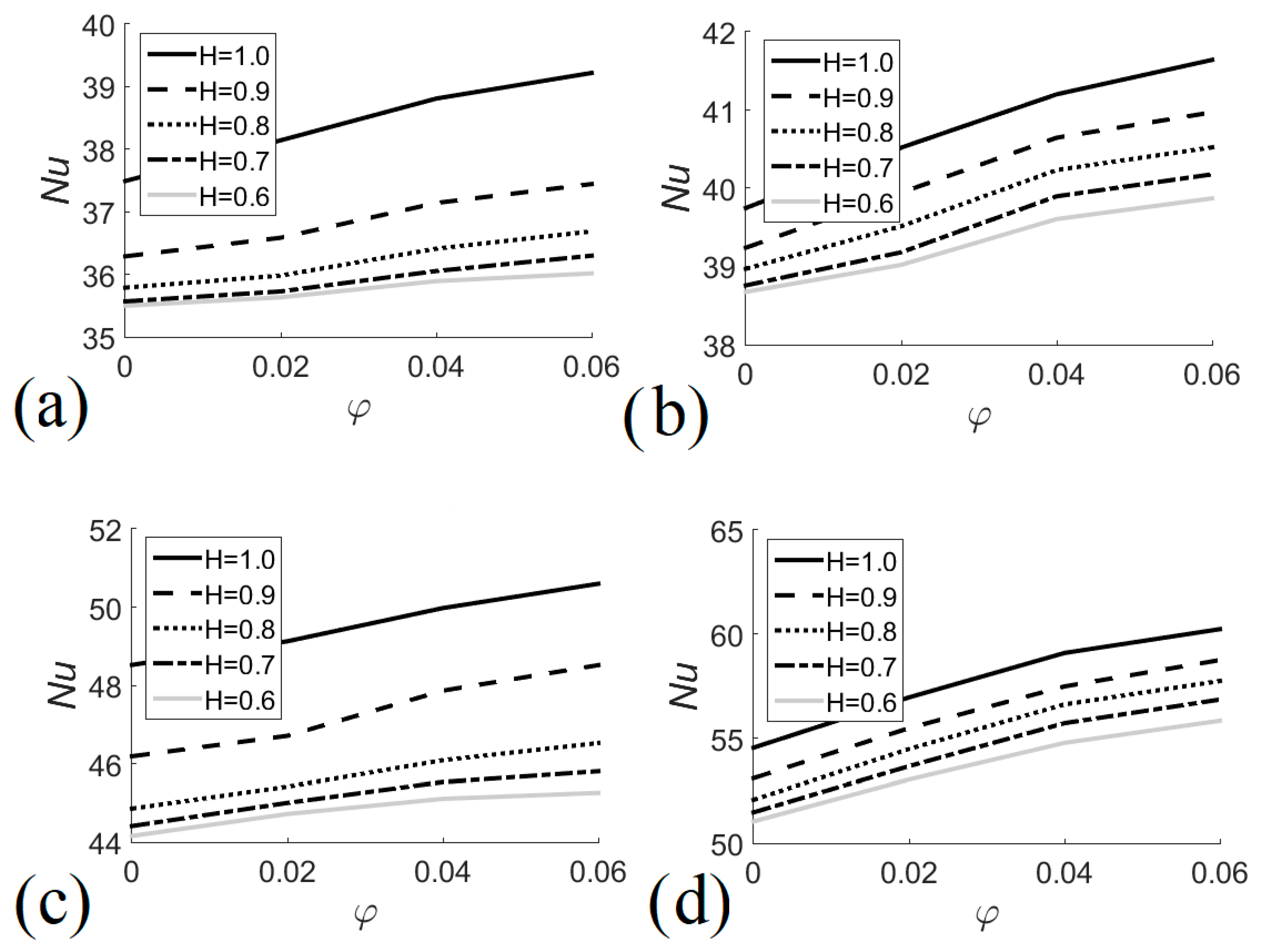
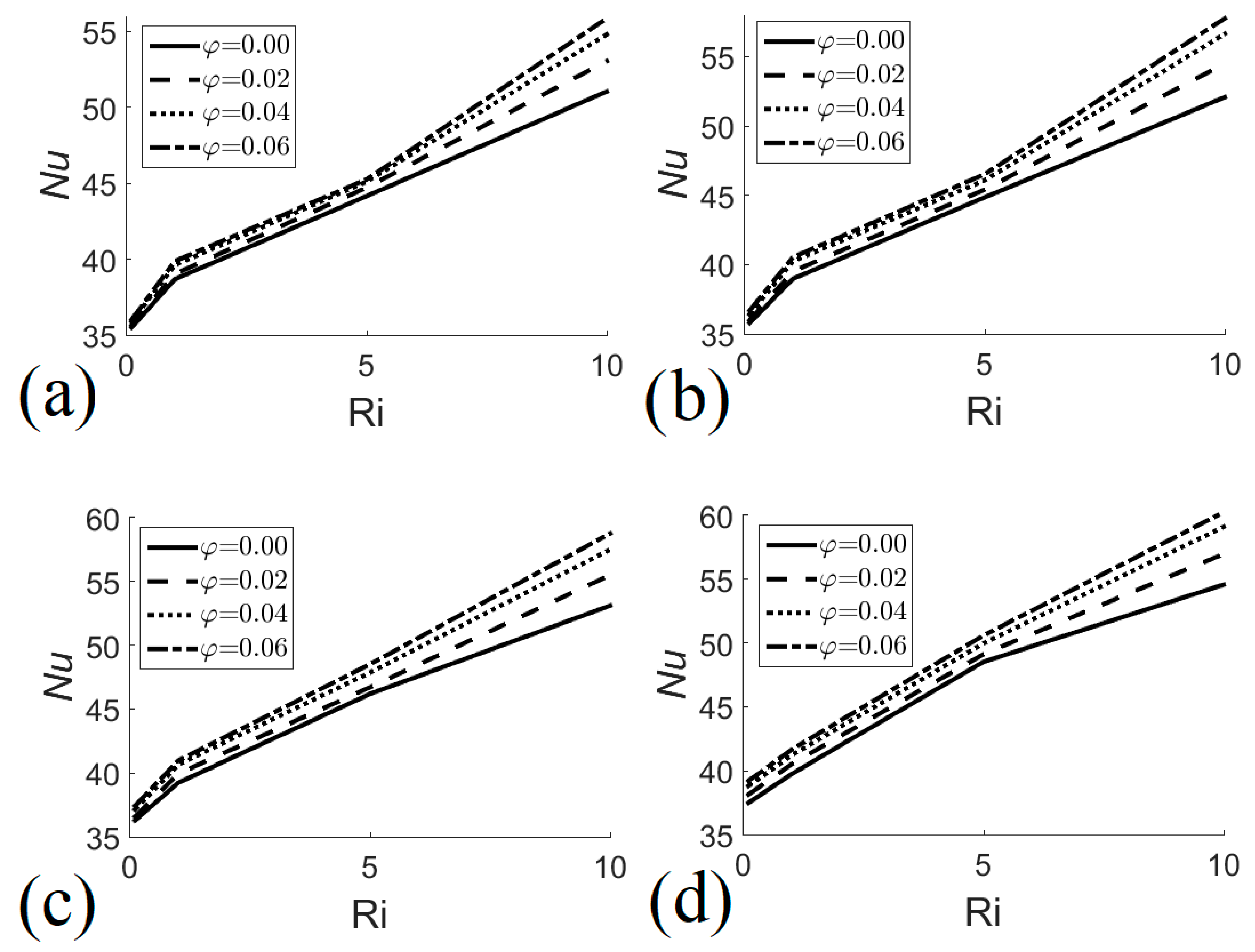
7.1. Heat Transfer
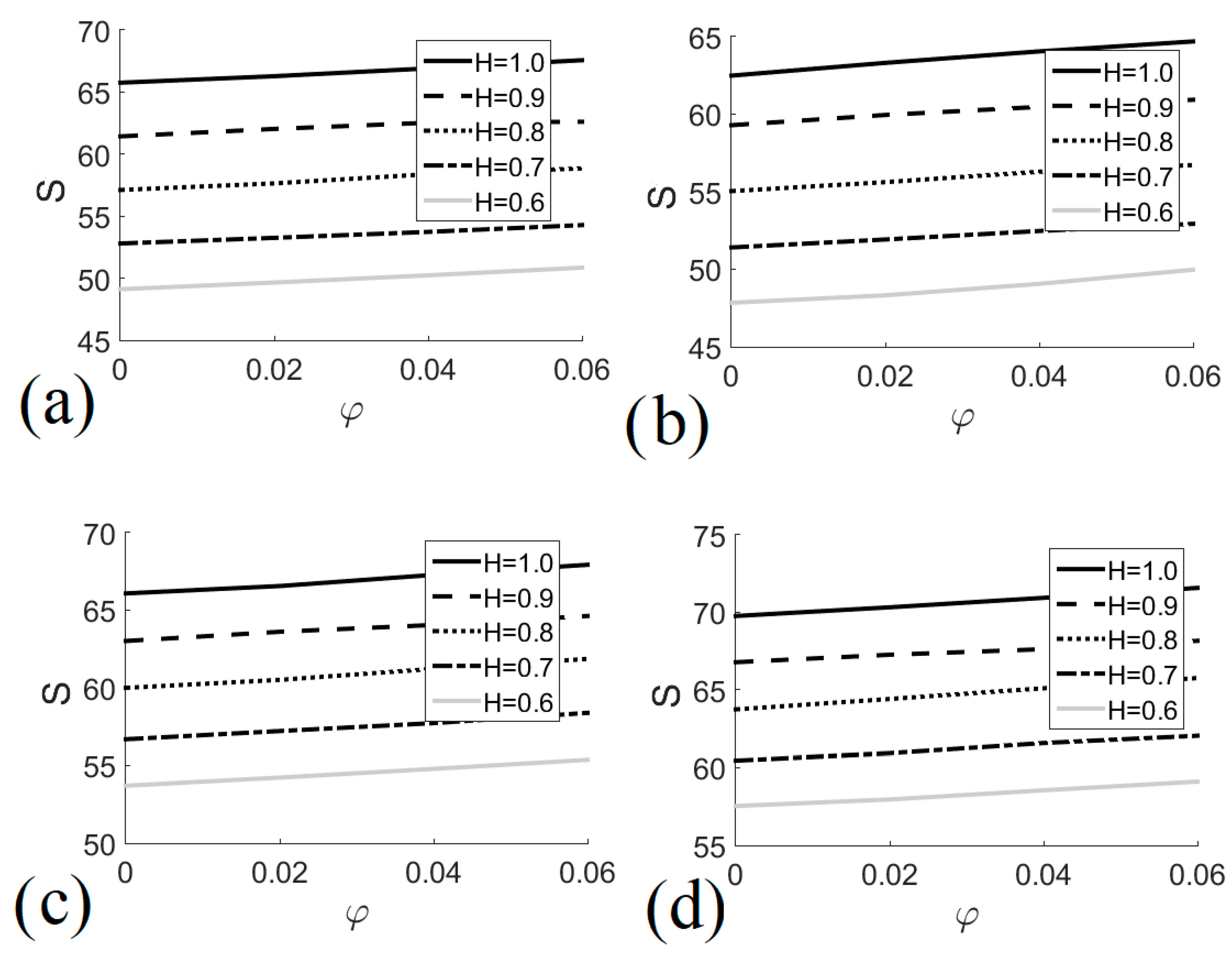
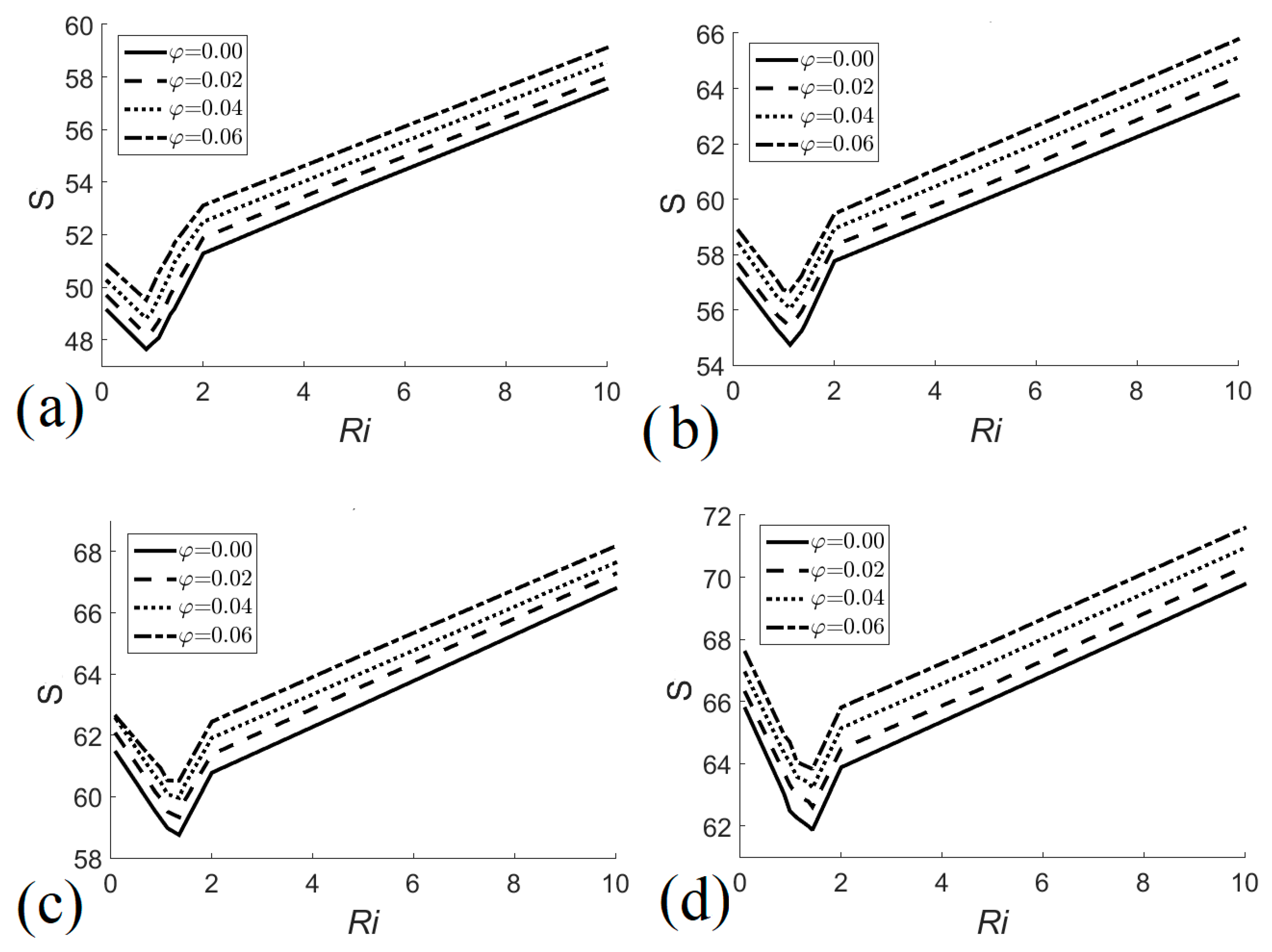
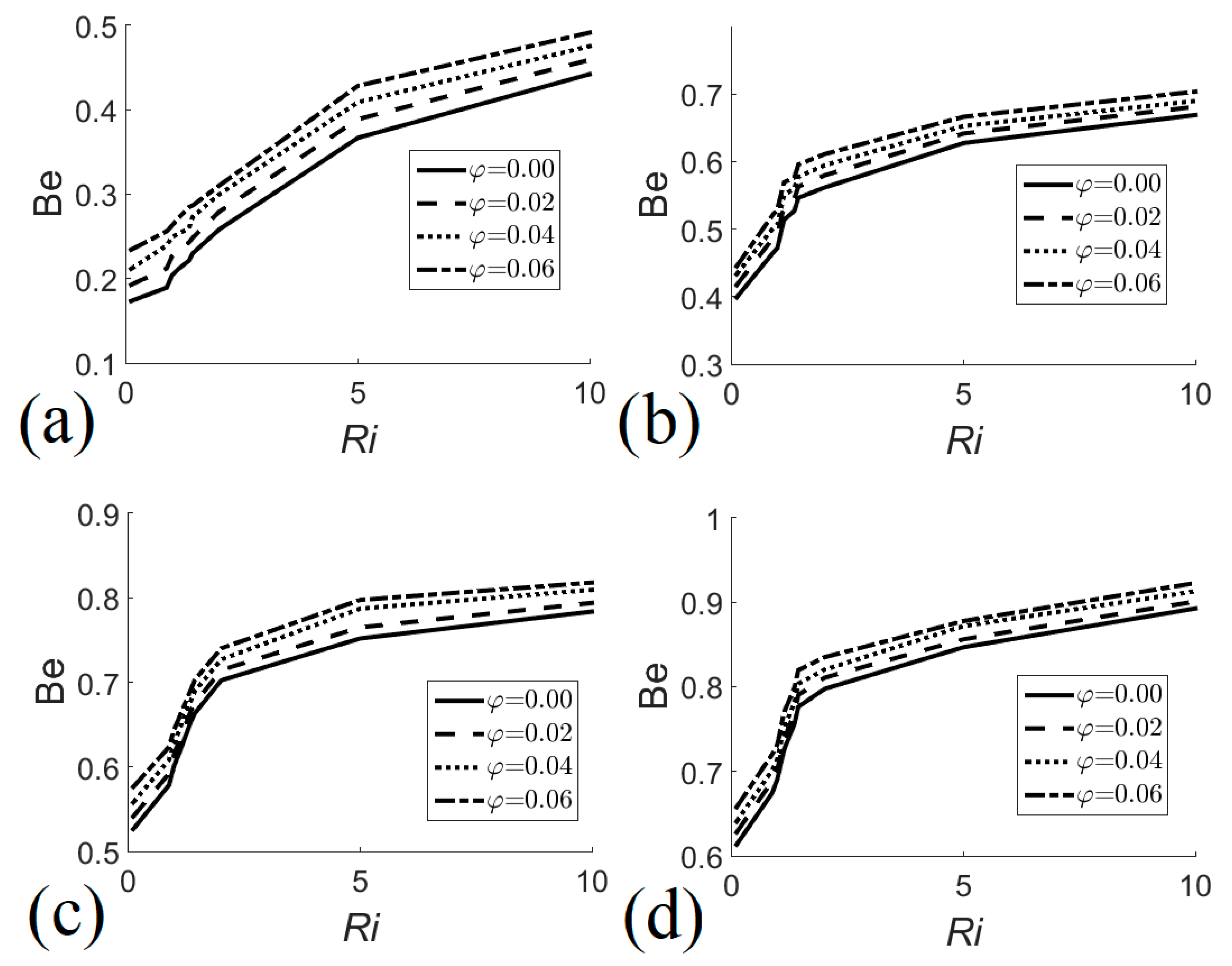
7.2. Entropy Analysis
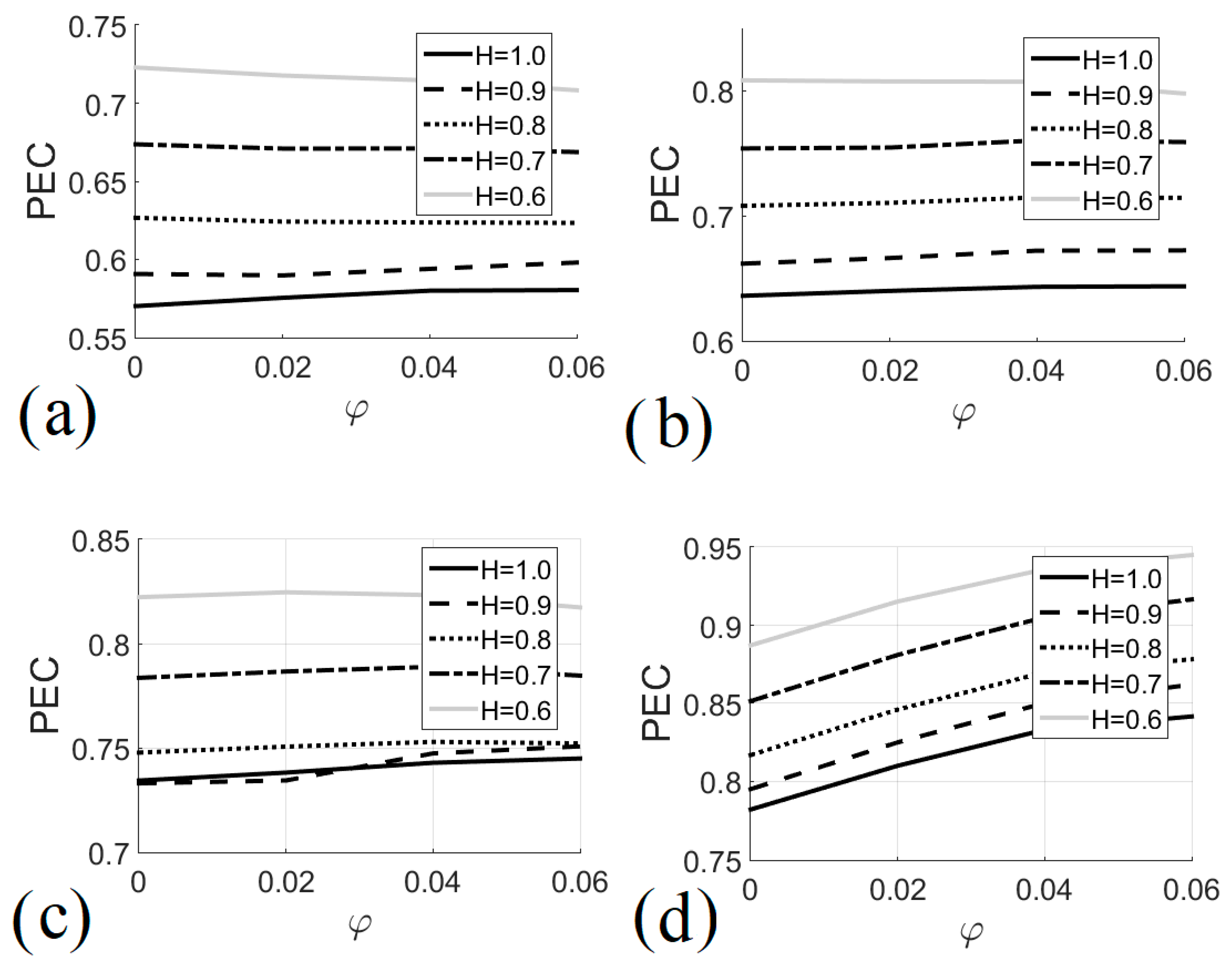
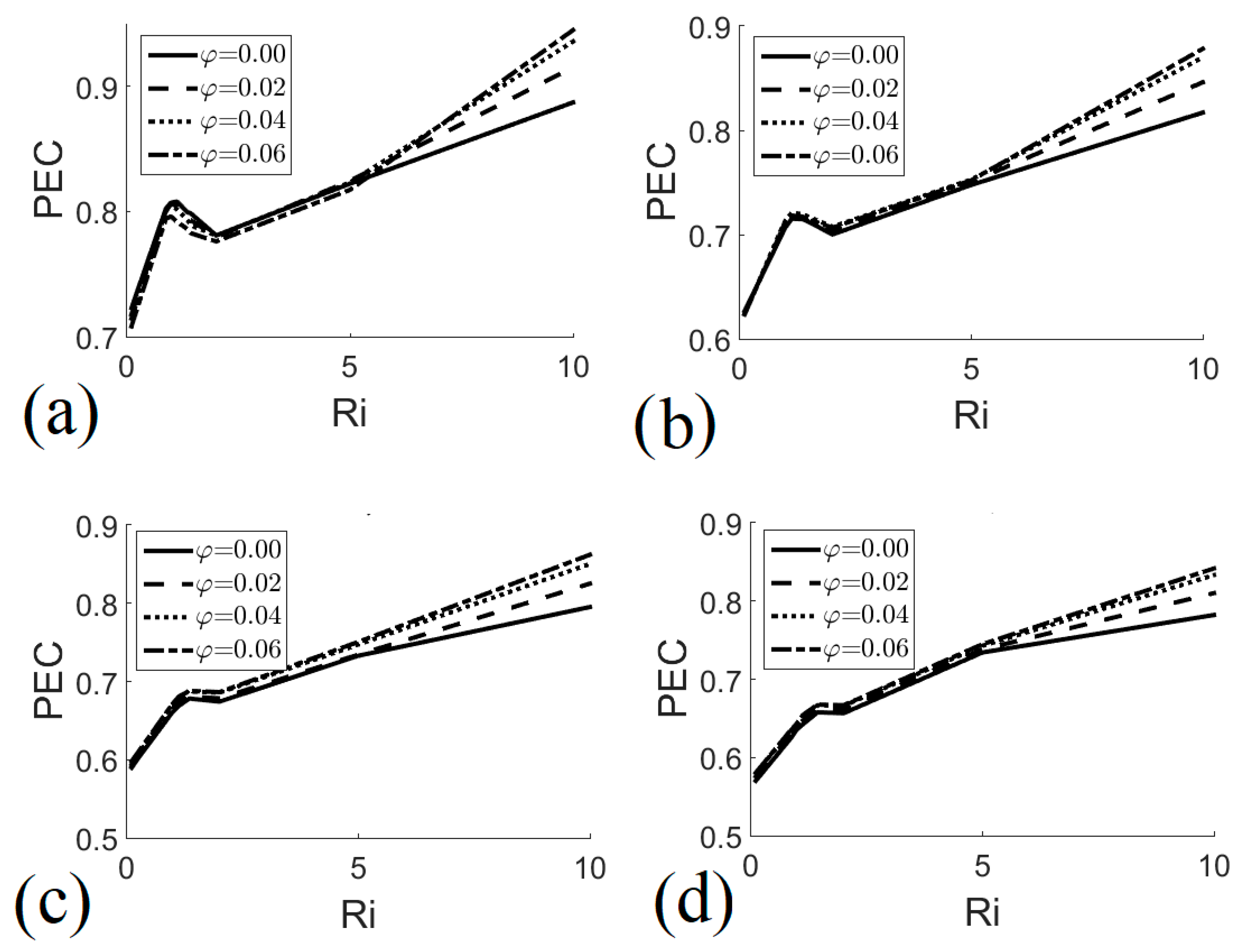
7.3. Performance Evaluation Criterion
8. Conclusions
- The nanofluid used as a heating fluid on the shell side gives off the more energy toward the aqueous medium flowing on the tube side, the larger the size of the heat exchanger.
- Nusselt numbers increase with the increase in nanofluid volume fraction, heat exchanger size, and Richardson number.
- Total entropy generation increases with the increase in nanofluid volume fraction and heat exchanger size; however, irreversibilities decrease when Ri ≈ 1.
- Irreversibilities due to heat transfer become more significant as the size of the heat exchanger increases.
- In general, the criterion used to evaluate the performance of the heat exchanger increases with the Richardson number when Ri < 1 and Ri > 2. On the other hand, PEC is increased by reducing the size of the heat exchanger. The nanofluid volume fraction tends to increase the performance evaluation criterion if Ri > 5.
- The optimal operation of heat exchangers that use aqueous media for oil extraction occurs when H ≥ 0.8, φ = 0.06 and Ri ≈ 1; in this range of parameters the system can operate under conditions of minimum entropy generation which implies the minimization of irreversibilities guaranteeing the efficient use of energy.
- The key achievement of this research is the characterization of the entropy minimization in heat exchangers for the aqueous extraction of oil at low temperatures, which avoids the use of solvents that cause problems in industrial safety, environmental pollution and risks for human health.
- The results obtained in this work would be beneficial in the future to improve the thermal performance of heat exchangers used in food processing, biochemical processes, solar thermal collectors and the chemical industry, guaranteeing the minimization of energy costs in such applications.
- Future research includes multiphase flows, high temperature processes and study of different nanofluids.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | |
| Be | Bejan number |
| Cp | specific heat, J kg−1 K−1 |
| g | acceleration of gravity, ms−2 |
| He | height of heat exchanger, m |
| H | dimensionless height of heat exchanger |
| J | vertical unit vector |
| k | thermal conductivity, W m−1 K−1 |
| n | time step |
| Nu | Average Nusselt number |
| p | pressure, Pa |
| PEC | performance evaluation criterion |
| Pr | Prandtl number |
| Ri | Richardson number |
| Re | Reynolds number |
| S | total dimensionless entropy generation |
| Slf | dimensionless local entropy generation due to fluid friction |
| Slh | dimensionless local entropy generation due to heat transfer |
| T | temperature, °C |
| U, V | dimensionless transverse components of velocity |
| W | dimensionless axial component of velocity |
| Uin | inlet velocity on the shell side, ms−1 |
| X, Y | dimensionless transverse coordinates |
| Z | axial dimensionless coordinate |
| Greek Symbols | |
| α | thermal diffusivity, m2 s−1 |
| β | coefficient of thermal expansion, K−1 |
| ρ | density, kg m−3 |
| Γ | Dirichlet boundary condition in the domain |
| Ω | three-dimensional domain |
| ψ | finite element weight function |
| φ | irreversibility ratio |
| μ | dynamic viscosity, Pa s |
| θ | dimensionless temperature |
| φ | nanofluid volume fraction |
| Sub-indices | |
| nf | nanofluid |
| f | base fluid |
| sol | solid |
| ci | cold fluid inlet |
| hi | hot fluid inlet |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluid with nanoparticles. In Developments and Applications of Non-Newtonian Flows; Siginer, D.A., Wang, H.P., Eds.; ASME FED: New York, NY, USA, 1995; Volume 66, pp. 99–105. [Google Scholar]
- Hamid, M.; Usman, M.; Khan, Z.H.; Haq, R.U.; Wang, W. Heat transfer and flow analysis of Casson fluid enclosed in a partially heated trapezoidal cavity. Int. Commun. Heat Mass Transf. 2019, 108, 104284. [Google Scholar] [CrossRef]
- Hamid, M.; Usman, M.; Haq, R.U.; Khan, Z.H.; Wang, W. Wavelet analysis of stagnation point of non-Newtonian nanofluid. Appl. Math. Mech. 2019, 40, 1211–1226. [Google Scholar] [CrossRef]
- Hamid, M.; Usman, M.; Haq, R.U. Wavelets investigation of Soret and Dufour effects on stagnation point fluid flow in two-dimension with variable thermal conductivity and diffusivity. Phys. Scr. 2019, 94. [Google Scholar] [CrossRef]
- Zaib, A.; Haq, R.U. Magnetohydrodynamics mixed convective flow driven through a static wedge including TiO2 nanomaterial with micropolar liquid: Similarity dual solutions via finite difference method. Proc. Inst. Mech. Eng. J. Mech. Eng. Sci. 2019, 233, 5813–5825. [Google Scholar] [CrossRef]
- Mahmud, S.; Das, P.K.; Hyder, N.; Sadrul Islam, A.K.M. Free convection in an enclosure with vertical wavy walls. Int. J. Therm. Sci. 2002, 41, 440–446. [Google Scholar] [CrossRef]
- Mahmud, S.; Sadrul Islam, A.K.M.; Das, P.K. Numerical prediction of fluid flow and heat transfer in a wavy pipe. J. Therm. Sci. 2001, 10, 133–147. [Google Scholar] [CrossRef]
- Mital, M. Analytical analysis of heat transfer and pumping power of laminar nanofluid developing flow in microchannel. Appl. Therm. Eng. 2013, 50, 429–436. [Google Scholar] [CrossRef]
- Radwan, A.; Ahmed, M. Thermal management of concentrator photovoltaic systems using microchannel heat sink with nanofluid. Sol. Energy 2018, 171, 229–246. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Shuaib, N.H.; Yusoff, M.Z.; Al-Falahi, A.H. Numerical investigations of flow and heat transfer enhancement in a corrugated channel using nanofluid. Int. Commun. Heat Mass Transf. 2011, 38, 1368–1375. [Google Scholar] [CrossRef]
- Ajeel, R.K.; Salim, W.S.I.; Hasnan, K. Thermal and hydraulic characteristic of turbulent nanofluids flow in trapezoidal-corrugated channel: Symmetry and zigzag shaped. Case Stud. Therm. Eng. 2018, 12, 620–635. [Google Scholar] [CrossRef]
- Mohammed, H.A.; Al-Shamani, A.N.; Sheriff, J.M. Thermal and hydraulic characteristics of turbulent nanofluid flow in a rib–groove channel. Int. Commun. Heat Mass Transf. 2012, 39, 1584–1594. [Google Scholar] [CrossRef]
- Ali, M.M.; Alim, M.A.; Ahmed, S.S. Oriented magnetic field effect on mixed convective flow of nanofluid in a grooved channel with internal rotating cylindrical heat source. Int. J. Mech. Sci. 2019, 151, 385–409. [Google Scholar] [CrossRef]
- Namburu, P.K.; Das, D.K.; Tanguturi, K.M.; Vajjha, R.S. Numerical study of turbulent flow and heat transfer characteristics of nanofluids considering variables properties. Int. J. Therm. Sci. 2009, 48, 290–302. [Google Scholar] [CrossRef]
- Ebrahimnia-Bajestan, E.; Niazmand, H.; Duangthongsuk, W.; Wongwises, S. Numerical investigation of effective parameters in convective heat transfer of nanofluids flowing under a laminar flow regime. Int. J. Heat Mass Transf. 2011, 54, 4376–4388. [Google Scholar] [CrossRef]
- Mahmoudi, A.H.; Shahi, M.; Talebi, F. Effect of inlet and outlet location on the mixed convective cooling inside the ventilated cavity subjected to an external nanofluid. Int. Commun. Heat Mass Transf. 2010, 37, 1158–1173. [Google Scholar] [CrossRef]
- Hemmat-Esfe, M.; Abbasian-Arani, A.A.; Yan, W.M.; Afrand, M.; Sina, N. Mixed convection of functionalized DWCNT-water nanofluid in baffled lid-driven cavities. Therm. Sci. 2018, 22, 2503–2514. [Google Scholar] [CrossRef]
- Hamid, M.; Khan, Z.H.; Khan, W.A.; Haq, R.U. Natural convection of water-based carbon nanotubes in a partially heated rectangular fin-shaped cavity with an inner cylindrical obstacle. Phys. Fluids 2019, 31, 103607. [Google Scholar] [CrossRef]
- Haq, R.U.I.; Soomro, F.A.; Oztop, H.F.; Mekkaoui, T. Thermal management of water-based carbon nanotubes enclosed in a partially heated triangular cavity with heated cylindrical obstacle. Int. J. Heat Mass Transf. 2019, 131, 724–736. [Google Scholar] [CrossRef]
- Haq, R.U.I.; Aman, S. Water functionalized CuO nanoparticles filled in a partially heated trapezoidal cavity with inner obstacle: FEM approach. Int. J. Heat Mass Transf. 2019, 128, 401–417. [Google Scholar] [CrossRef]
- Haq, R.U.I.; Soomro, F.A.; Hammouch, Z.; Rehman, S.U.R. Heat exchanger within the partially heated C-shape cavity filled with the water based SWCNTs. Int. J. Heat Mass Transf. 2018, 127, 506–514. [Google Scholar] [CrossRef]
- Cong, R.; Ozaki, Y.; Machado, B.S.; Das, P.K. Constructal design of a rectangular fin in a mixed convective confined environment. Inventions 2018, 3, 27. [Google Scholar] [CrossRef]
- Das, P.K.; Mahmud, S.; Tasnim, S.H.; Sadrul Islam, A.K.M. Effect of surface waviness and aspect ratio on heat tranfer inside a wavy enclosure. Int. J. Numer. Methods Heat Fluid Flow 2003, 13, 1097–1122. [Google Scholar] [CrossRef]
- Ovando-Chacon, G.E.; Ovando-Chacon, S.L.; Prince-Avelino, J.C.; Rodriguez-Leon, A.; Garcia-Arellano, C. Numerical optimization of double-diffusive mixed convection in a rectangular enclosure with a reactant fluid. Heat Transf. Res. 2017, 48, 1651–1668. [Google Scholar] [CrossRef]
- Ovando-Chacon, G.E.; Ovando-Chacon, S.L.; Prince-Avelino, J.C.; Rodriguez-Leon, A.; Garcia-Arellano, C. Simulation of thermal decomposition in an open cavity: Entropy analysis. Braz. J. Chem. Eng. 2019, 36, 335–350. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Heat transfer and entropy generation analyses of nanofluids in helically coiled tube-in-tube heat exchangers. Int. Commun. Heat Mass Transf. 2016, 71, 118–125. [Google Scholar] [CrossRef]
- Kolsi, L.; Lajnef, E.; Aich, W.; Alghamdi, A.; Aichouni, M.A.; Borjini, M.N.; Aissia, H.B. Numerical investigation of combined buoyancy-thermocapillary canvection and entropy generation in 3D cavity filled with Al2O3 nanofluid. Alex. Eng. J. 2017, 56, 71–79. [Google Scholar] [CrossRef]
- Kolsi, L.; Kalidasan, K.; Alghamdi, A.; Borjini, M.N.; Kanna, P.R. Natural convection and entropy geenration in a cubical cavity with twin adiabatic blocks filled by aluminum oxide-water naofluid. Numer. Heat Transf. Appl. 2016, 70, 242–259. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, H.C.; Yang, X.; Shi, L. Entropy generation analysis and performance evaluation of turbulent forced convective heat transfer to nanofluids. Entropy 2017, 19, 108. [Google Scholar] [CrossRef]
- Belhaj, S.; Ben-Beya, B. Magnetoconvection and entropy generation of nanofluid in an enclosure with an isothermal block: Performance evaluation criteria analysis. J. Therm. Sci. Technol. 2018, 13, JTST0019. [Google Scholar] [CrossRef]
- Ismael, M.A.; Armaghani, T.; Chamkha, A.J. Mixed convection and entropy generation in a lid-driven cavity filled with a hybrid nanofluid and heated by a triangular solid. Heat Transf. Res. 2018, 49, 1645–1665. [Google Scholar] [CrossRef]
- Salari, M.; Malekshah, E.H.; Esfe, M.H. Three dimensional simulation of natural convection and entropy generation in an air and MWCNT/water nanofluid filled cuboid as two immiscible fluids with emphasis on the nanofluid height ratios’s effects. J. Mol. Liq. 2017, 227, 223–233. [Google Scholar] [CrossRef]
- Kashani, S.; Ranjbar, A.A.; Mastiani, M.; Mirzaei, H. Entropy generation and natural convection of nanoparticle-water mixture (nanofluid) near water density inversion in an enclosure with various patterns of vertical wavy walls. Appl. Math. Comput. 2014, 226, 180–193. [Google Scholar] [CrossRef]
- Mohammadtabar, M.; Mohammadtabar, F.; Shokri, R.; Sadrzadeh, M. Numerical investigation of entropy generation due to natural convection in a partially heated squared cavity filled with nanofluids. Heat Transf. Eng. 2017, 17, 1506–1521. [Google Scholar] [CrossRef]
- Ting, K.; Mozumder, A.K.; Das, P.K. Effect of surface roughness on heat tranfer and entropy generation of mixed convection in nanofluid. Phys. Fluids 2019, 31, 093602. [Google Scholar] [CrossRef]
- Das, S.; Banu, A.S.; Jana, R.N.; Makinde, O.D. Entropy analysis on MHD pseudo-plastic nanofluid flow through a vertical porous channel with convective heating. Alex. Eng. J. 2015, 54, 325–337. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Mehrez, Z.; El Cafsi, A.; Belghith, A.; Le Quéré, P. MHD effects on heat transfer and entropy generation of nanofluid flow in an open cavity. J. Magn. Magn. Mater. 2015, 374, 214–224. [Google Scholar] [CrossRef]
- Parvin, S.; Chamkha, A.J. An analysis on free convection flow, heat transfer and entropy generation in an odd-shaped cavity filled with nanfluid. Int. Commun. Heat Mass Transf. 2014, 54, 8–17. [Google Scholar] [CrossRef]
- Mehrez, Z.; Bouterra, M.; El Cafsi, A.; Belghith, A. Heat tranfer and entropy generation analysis of nanofluids flow in an open cavity. Comput. Fluids 2013, 88, 363–373. [Google Scholar] [CrossRef]
- Kolsi, L.; Mahian, O.; Oztop, H.F.; Aich, W.; Borjini, M.N.; Abu-Hamdeh, N.; Aissia, H.B. 3D buoyancy-induced flow and entropy generation of nanofluid-filled open cavities having adiabatic diamond shaped obstacles. Entropy 2016, 18, 232. [Google Scholar] [CrossRef]
- Glowinski, R. Numerical Methods for Fluids, Handbook of Numerical Analysis; Part 3; Garlet, P.G., Lions, J.L., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; Volume IX. [Google Scholar]
- Girault, V.; Raviart, P.A. Finite Element Methods for the Navier-Stokes Equations: Theory and Algorithms; Springer: Berlin, Germany, 1986. [Google Scholar]
- Kefayati, G.H.R.; Hosseinnizadeh, S.F.; Gorji, M.; Sajjadi, H. Lattice Boltzmann simulation of natural convection in tall enclosures using water/SiO2 nanofluid. Int. Commun. Heat Mass Transf. 2011, 38, 798–805. [Google Scholar] [CrossRef]
- Kolsi, L.; Hussein, A.K.; Borjini, M.N.; Mohammed, H.A.; Aissia, H.B. Computational analysis of three-dimensional unsteady natural convection and entropy generation in a cubical enclosure filled with water-Al2O3 nanofluid. Arab. J. Sci. Eng. 2014, 39, 7483–7493. [Google Scholar] [CrossRef]
| Nodes of the Mesh | 150,240 | 200,175 | 250,645 | 300,240 | 350,422 |
|---|---|---|---|---|---|
| Ri = 5, H = 0.8, φ = 0.04 | |||||
| Nu | 52.4558 | 48.2885 | 46.7369 | 46.0871 | 45.6941 |
| S | 70.6391 | 64.4988 | 61.9109 | 61.2252 | 60.7875 |
| Be | 0.7429 | 0.6861 | 0.6614 | 0.6527 | 0.6466 |
| Ri = 0.1, H = 0.6, φ = 0.00 | |||||
| Nu | 40.9913 | 37.2716 | 36.1299 | 35.6981 | 35.3727 |
| S | 56.5378 | 51.8838 | 49.7830 | 49.1102 | 48.5662 |
| Be | 0.1995 | 0.1821 | 0.1757 | 0.1735 | 0.1721 |
| Nodes of the Mesh | Texp (°C) | T (°C) | Error |
|---|---|---|---|
| Ri = 5, H = 1.0, φ = 0.04 | |||
| Top | 73.58 | 72.81 | 1.05% |
| Middle | 59.17 | 58.66 | 0.87% |
| Bottom | 38.73 | 38.30 | 1.12% |
| Ri = 5, H = 0.6, φ = 0.04 | |||
| Top | 76.59 | 75.63 | 1.27% |
| Middle | 62.14 | 61.57 | 0.93% |
| Bottom | 42.89 | 42.44 | 1.06% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ovando-Chacon, G.E.; Ovando-Chacon, S.L.; Rodriguez-Leon, A.; Diaz-Gonzalez, M.; Hernandez-Zarate, J.A.; Servin-Martinez, A. Numerical Study of Nanofluid Irreversibilities in a Heat Exchanger Used with an Aqueous Medium. Entropy 2020, 22, 86. https://doi.org/10.3390/e22010086
Ovando-Chacon GE, Ovando-Chacon SL, Rodriguez-Leon A, Diaz-Gonzalez M, Hernandez-Zarate JA, Servin-Martinez A. Numerical Study of Nanofluid Irreversibilities in a Heat Exchanger Used with an Aqueous Medium. Entropy. 2020; 22(1):86. https://doi.org/10.3390/e22010086
Chicago/Turabian StyleOvando-Chacon, Guillermo Efren, Sandy Luz Ovando-Chacon, Abelardo Rodriguez-Leon, Mario Diaz-Gonzalez, Jorge Arturo Hernandez-Zarate, and Alberto Servin-Martinez. 2020. "Numerical Study of Nanofluid Irreversibilities in a Heat Exchanger Used with an Aqueous Medium" Entropy 22, no. 1: 86. https://doi.org/10.3390/e22010086
APA StyleOvando-Chacon, G. E., Ovando-Chacon, S. L., Rodriguez-Leon, A., Diaz-Gonzalez, M., Hernandez-Zarate, J. A., & Servin-Martinez, A. (2020). Numerical Study of Nanofluid Irreversibilities in a Heat Exchanger Used with an Aqueous Medium. Entropy, 22(1), 86. https://doi.org/10.3390/e22010086





